冬日的暖阳在窗外探头,期待和你邂逅。周末快乐,如果不够快乐就去和它拥抱一下吧 ~
今天的周赛整体难度不大,只有最后一题涉及并查集算法,而且数据规模也不大。第一题签到题,数据规模很小,直接模拟,赛后学习了一下别人o(n)的思路,细节我们后面讨论;第二题链表逆转,属于稍微复杂一点的模拟,思路不难但是代码需要时间打磨;第三题根据题目给的加密方式直接反推原码,最后处理掉结尾空格;第四题并查集应用,"能不能交朋友" 这样的情境背景非常适合应用并查集。另外,第二题这样的题是需要一定时间的,遇到这样的情况不妨先做做后面两道,今天的3、4,思路和代码都没有大难点,解决后面两道再来写第二道这样策略也挺好。
5926. 买票需要的时间
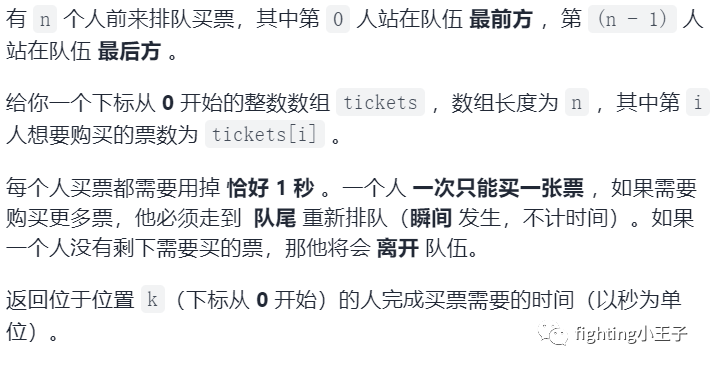


最简单的思路是直接循环模拟。一趟扫描思路是:第k个人买了m张票,则k前面的人最多买了m张票,k后面的人最多买了m-1张票,一次累加就行。下面代码第一个是直接模拟,第二个是一次累加。
class Solution {public:int timeRequiredToBuy(vector<int>& t, int k) {int cnt = 0;while(true){for(int i = 0; i < t.size(); i ++){if(t[i] > 0){t[i] --;cnt ++;if(t[k] == 0) return cnt;}}}return -1;}}
class Solution {public:int timeRequiredToBuy(vector<int>& t, int k) {int sum = 0;for(int i = 0; i < t.size(); i ++){if(i <= k){sum += min(t[i] , t[k]);}else{sum += min(t[i] , t[k] - 1);}}return sum;}};
5927. 反转偶数长度组的节点
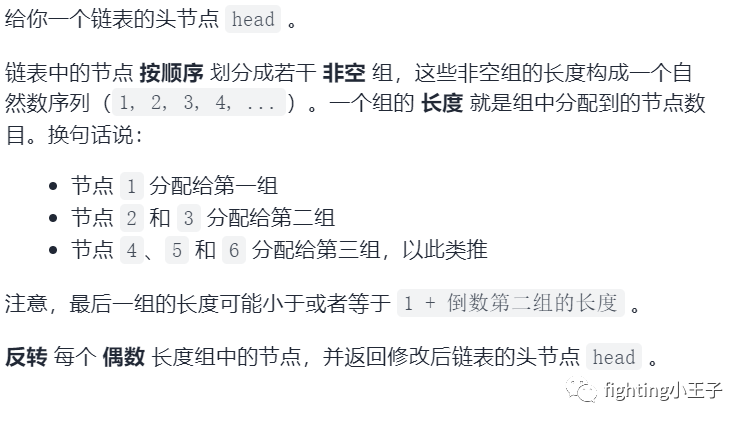
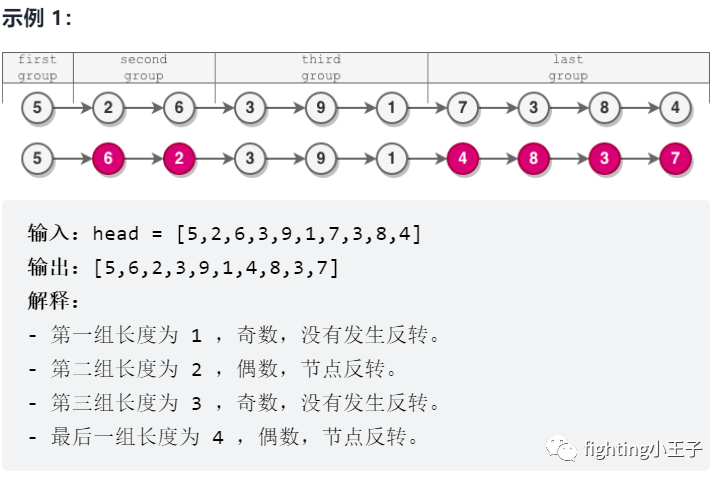

最后一组中元素个数是不确定的,所以必须得模拟。整体思路很简单,第一次取出第一组,第二次取出第二组,偶数个元素的组拎出来逆转后再接到链表里。代码里遍历过程中 i 记录走过的节点数作为是否逆转标志。逆转采用的是头插法,每次取出一个节点插入链表头实现逆转。为了保证链表不断,取出一个组不仅要记录该组的头尾节点在哪(代码中的stay 和 last两个指针),还要记录该组头节点的前一个节点以及尾节点的后一个节点(代码中的pre 和 work两个指针),这样的链表操作的代码看起来很费脑子,自己画一个链表手动跟踪模拟会对你的理解大有帮助。
typedef ListNode* L;class Solution {public:L reverse(L head){if(head == NULL) return head;L t = head;head = head -> next;t -> next = NULL;while(head){L p = head;head = head -> next;p -> next = t;t = p;}return t;}ListNode* reverseEvenLengthGroups(ListNode* head) {if(head == NULL || head -> next == NULL)return head;int cnt = 2;L work = head -> next , last = head , pre = head , stay = head -> next;while(work != NULL){int i = 0;for(i = 0; i < cnt && work != NULL; i ++){last = work;work = work -> next;}if(i % 2 == 0){last -> next = NULL;reverse(stay); // 逆转后last指向的节点变为头 stay指向的节点变为尾pre -> next = last;stay -> next = work;pre = stay;stay = work;last = work;}else{pre = last;stay = work;last = work;}cnt ++;}return head;}};
5928. 解码斜向换位密码
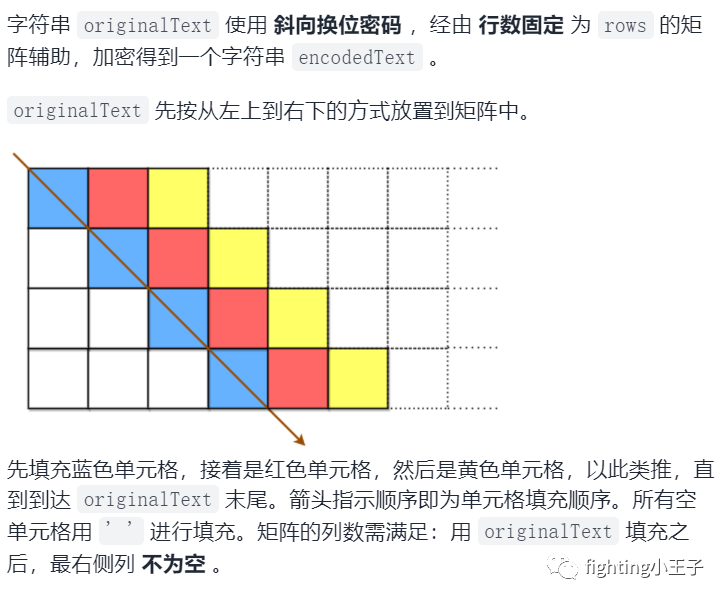
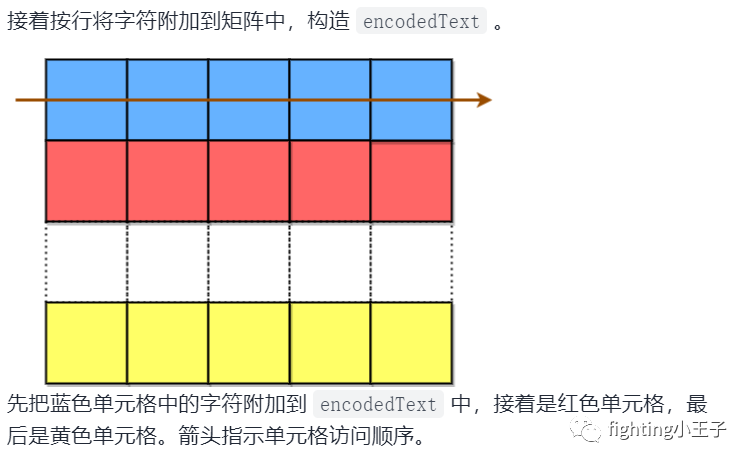
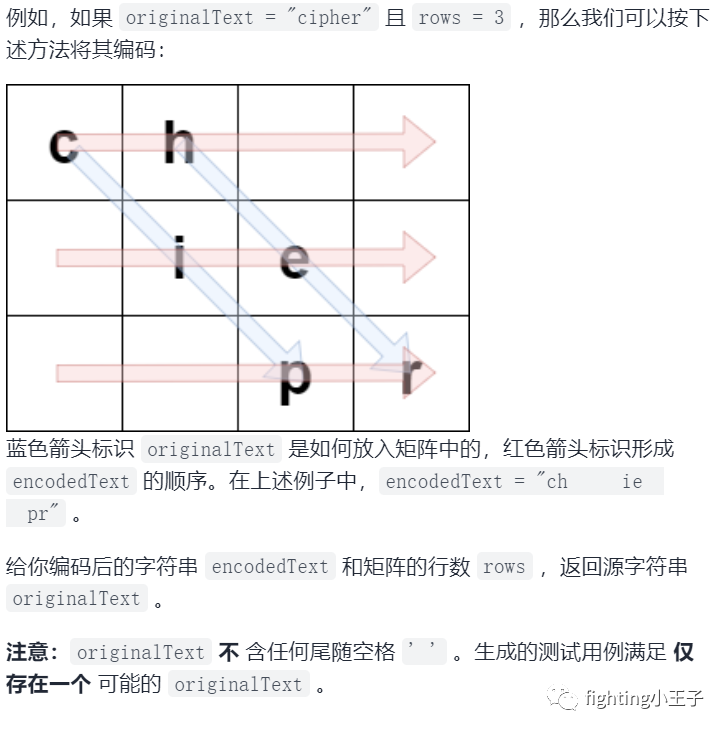


首先根据行数和编码串的长度可以得到矩阵的列数m。第一个元素在加密串的第一个位置,第二个元素在加密串的第1+m+1个位置,中间隔m个元素,对应取元素就可以确定原串了,最后注意去掉结尾的空格就行。时间复杂度o(n加密串长度)。
class Solution {public:string decodeCiphertext(string s, int rows) {int n = rows;int m = s.size() / n;string result;int i = 0;while(i < m){int j = i;bool flag = false;while(j < s.size()){result += s[j];j += m + 1;}i ++;}i = result.size() - 1;while(i >= 0 && result[i] == ' ') i--;return result.substr(0 , i + 1);}};
5929. 处理含限制条件的好友请求



首先,很自然想到用并查集。对于一个请求a,b添加为好友,如果能添加,那么a,b将属于一个好友圈。遍历一遍所有的不可以成为好友的人,比如限制了c,d不能成为好友,如果原本a和c属于同一个好友圈,d和b属于同一个好友圈(a和d,c和b同理),ab不能成为好友,因为二者若成为好友,cd将属于同一个好友圈。总之,将ab能成为好友的前提是,二者成为好友后不会让有限制的两个人处在同一朋友圈。判断两者是否属于同一集合,方便地合并集合,并查集应该是最合适的。
const int N = 1010;class Solution {public:int father[N];int find(int x){if(x == father[x])return x;elsereturn father[x] = find(father[x]);}void join(int x , int y){int fx = find(x) , fy = find(y);if(fx != fy)father[fx] = fy;}vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& re) {vector<bool> ans;for(int i = 0; i < n + 5; i ++)father[i] = i;for(auto &x : re){int a = x[0] , b = x[1];int fa = find(a) , fb = find(b);bool flag = true;for(auto &y : restrictions){int ra = find(y[0]) , rb = find(y[1]);if((ra == fa && rb == fb) || (ra == fb && rb == fa)){flag = false;break;}}if(flag){ans.push_back(true);join(fa , fb);}else{ans.push_back(false);}}return ans;}};






