周末快乐。今天周赛还挺有特点的,1,2题感觉比3,4题要难些。需要现场想的模拟题,相比有思路、可模板的题要"难"些,难在思路形成、代码实现以及特殊情况考虑。第一题模拟;第二题数学推导,或者简单dp,后者可能不那么容易想到;第三题二分查找,首先写了个顺序查,超时后改用了二分优化;第四题dfs暴搜,看题目描述似"关了门",数据规模却"留了窗"。
5918. 统计字符串中的元音子字符串



找出所有连续的元音子串,一个个算。每个串判断前后各可以删除多少个字符,即可得到当前串可构成满足条件的子串数。写了40多行代码,感觉写复杂了,看了一遍题解区大家的思路,都差不多,自认为我的代码逻辑还是比较清晰的。
class Solution {public:bool judge(string s){bool f[5]={false};for(auto &x : s){if(x == 'a') f[0] = true;else if(x == 'e') f[1] = true;else if(x == 'i') f[2] = true;else if(x == 'o') f[3] = true;else if(x == 'u') f[4] = true;}return (f[0] && f[1] && f[2] && f[3] && f[4]);}int count(string s){int front = 1 , last = 0 , n = s.size() , sum = 0;if(!judge(s)) return 0;if(judge(s) && n == 5) return 1;for(int i = 0; i <= n - 5; i ++){last = 0;for(int j = n - 1; j >= i + 4; j --)if(judge(s.substr(i , j - i + 1)))last ++;else break;sum += last;}return sum;}int countVowelSubstrings(string word) {string s = "" ;int sum = 0;for(int i = 0; i < word.size(); i ++){if(word[i] == 'a' || word[i] =='e' || word[i] == 'i' || word[i] == 'o' || word[i] == 'u'){s += word[i];if(i==word.size()-1)sum += count(s);}else{if(s.size() >= 5)sum += count(s);s = "";}}return sum;}};
5919. 所有子字符串中的元音



看似是第二题,但数据规模也不"仁慈",枚举所有子串的做法并不实际。可以计算每个字符属于哪些子串,对于区间[l~r],如果s[i]是元音,0<=l<=i,i<=r<n,那当前这个s[i]就属于此区间,这样的 l 有0~i 即 i+1 个,这样的 r 有i~n 即 n-i 个,所以每个元音s[i]所属区间有(i+1)*(n-i)个,扫描一遍就可以得到所有子串包含的元音总数了。
动态规划的思路也比较简单。dp[i]记录以s[i]结尾的字串中包含的元音个数。如果s[i]不是元音,前面所有的字串最后追加s[i]不改变元音数量,即dp[i] = dp[i - 1]。如果dp[i]是元音,前面每个都多了一个元音s[i],总数就是dp[i-1]+i-1,另外当前s[i]也可以单独成串,所以dp[i] = dp[i-1] + i。这里要注意,此题子串是源串中连续的一个串,所以以 s[i] 为结尾的字串个数就是 i。 最后答案就是所有dp[i]的和。下面的动态规划代码中,dp下标实际有效值是从1开始的,所以相对于s的下标都要偏移1个,dp从0开始没问题的,这里只是个人习惯,这样写可以省去dp[i]=dp[i-1]时的越界判断。
typedef long long ll;class Solution {public:long long countVowels(string word) {ll result = 0 , n = word.size();for(ll i = 0; i < n; i ++){if(word[i] == 'a' || word[i] =='e' || word[i] == 'i' || word[i] == 'o' || word[i] == 'u'){result += (i + 1) * (n - i);}}return result;}};typedef long long ll;class Solution {public:ll dp[100010];long long countVowels(string word) {ll result = 0 , n = word.size();dp[0] = 0;for(ll i = 1; i <= n; i ++){dp[i] = dp[i - 1] ;if(word[i - 1] == 'a' || word[i - 1] =='e' || word[i - 1] == 'i' || word[i - 1] == 'o' || word[i - 1] == 'u'){dp[i] += i;}result += dp[i];}return result;}};
5920. 分配给商店的最多商品的最小值
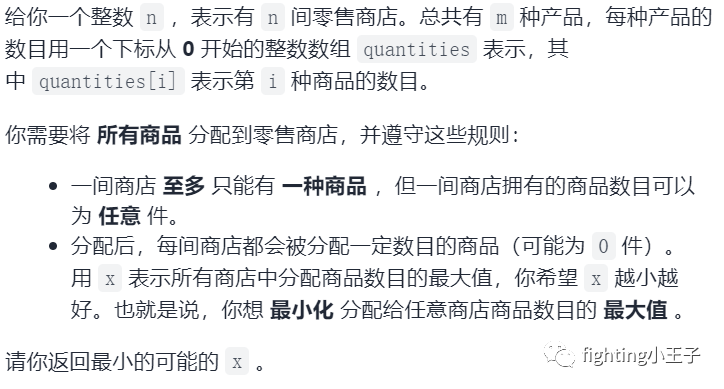

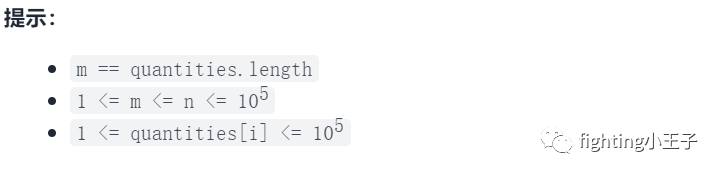
乍一看,把quantities总和除上n,得到一个初始值,然后从这个初始值递增一个个查似乎是很快可以查到,敲完却打脸了,超时。从1-10^5查一个确定的值适合二分。二分的初始值也可以从 把quantities总和除上n 这个值开始,这样二分的区间稍微缩短了一点点,但实际上效果并不明显,很难使二分趟数减1,而求和操作也比较费时,代码更复杂,有点捡了芝麻丢了西瓜吧。二分时间复杂度o(nlongn),此题中n最大10^5,log(10^5)不到15,nlogn不到10^7。
class Solution {public:bool check(int maxn , int n , vector<int>& q){int t = 0;for(int &x : q){t += (x + maxn - 1) / maxn;}return t <= n;}int minimizedMaximum(int n, vector<int>& q) {int l = 1 , r = 1e5 + 4;while(l < r){int mid = (l + r) >> 1;if(check(mid , n , q)){r = mid;}else{l = mid + 1;}}return r;}};
5921. 最大化一张图中的路径价值
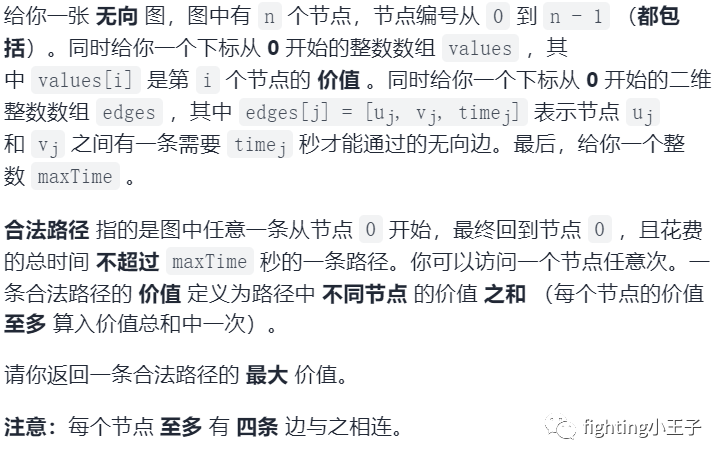


从0号节点出发又回到0号节点,路径长度不超情况下,确定可获得的最大价值。这题给出的是一个图,可能有环可能不连通,想要找到这样的最大价值,好像除了搜索没有其他办法了,但是不加限制暴搜复杂度是很高的。实际上,输入数据有很多限制,这样就确保了暴搜可以在可接受的时间范围内找到答案。maxTime最大是100,time最小是10,说明最多可以走10条路,dfs深度最多是10,每个节点最多4条边,最多搜索4^10次,也就是2^20=1024*1024次。剩下就是写dfs了。
const int N = 1010 , M = 10010; //边数最多 1010 * 4 * 2(每个节点最多四条边,无向)class Solution {public:int h[N] , w[M] , e[M] , ne[M] , idx;vector<int> value;int ans;bool st[N];void add(int a , int b, int c){e[idx] = b;w[idx] = c;ne[idx] = h[a];h[a] = idx ++;}void dfs(int u , int remain_time , int val){if(remain_time < 0)return ;if(u == 0)ans = max(ans , val);for(int i = h[u]; i != -1; i = ne[i]){int j = e[i];int tmpcost = w[i];if(st[j] == false){st[j] = true;dfs(j , remain_time - tmpcost , val + value[j]);st[j] = false;}else{dfs(j , remain_time - tmpcost , val);}}}int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {memset(st , false , sizeof st);memset(h , -1 , sizeof h);idx = 0;ans = 0;value = values;for(auto &x : edges){add(x[0] , x[1] , x[2]);add(x[1] , x[0] , x[2]);}st[0] = true;dfs(0 , maxTime , value[0]);return ans;}};






