5890. 转换字符串的最少操作次数
【题目描述】

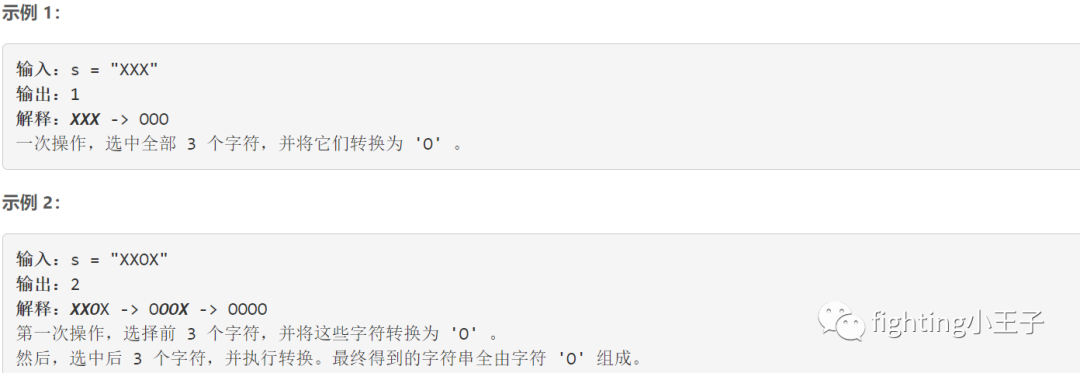

【思路】
【代码】
class Solution {public:int minimumMoves(string s) {int ans=0;for(int i=0;i<s.length();){if(s[i]=='X'){ans++;i+=3;}else if(i+1<s.length() && s[i+1]=='X'){ans++;i+=4;}else if(i+2<s.length() && s[i+2]=='X'){ans++;i+=5;}else i+=3;}return ans;}};
5891. 找出缺失的观测数据
【题目描述】



【思路】
先计算出剩余的n个情况的点数和sum,过滤掉没有答案(点数和小于n或者大于6n)的情况。然后将n个情况都取到使和不超过sum的点数,通过每次给n种情况的点数增1的操作把sum中剩余的点分配到各个情况上,得到一种可行解。
【代码】
class Solution {public:vector<int> missingRolls(vector<int>& rolls, int mean, int n) {int sum=0;sum=accumulate(rolls.begin(),rolls.end(),0);sum=(n+rolls.size())*mean - sum;vector<int> nu;if(sum>n*6 || sum<n) return nu;int x = (sum - (sum%n)) / n;vector<int> ans(n,x);sum = sum - x*n;cout<<sum<<endl;int i=0;while(sum){if(ans[i]<6){sum--;ans[i]++;}i++;i=i%n;}return ans;}};
【题目描述】



【思路】
首先可以把stones初始化成3的余数,每个数变成0,1,2。两者交替进行取数,若Alice取完数后,元素没取完,而且剩下的元素中Bob任取一个都会导致取出元素和为3的倍数,那么必是Alice获胜,否则Bob获胜。Alice为先手,若上述游戏过程进行的轮次为奇数,Alice赢,否则Bob赢,所以关键是确定游戏可进行的轮次。Alice先手第一次只能取1或者2。先不考虑0,倘若第一次Alice取1,由于两者均最佳决策,必定是让自己取出的数不会使取出的总和变成3的倍数,也就接着Bob会取1,同样接下来Alice一定取2,取数的序列为1121212...。若考虑0,0可以插入到1121212...这个序列的第一个元素后的任意位置,所以游戏可进行的轮数就是这个非0串的最大长度加上0的个数。倘若Alice第一次取的是2,同理取数序列变成2212121...,轮数亦同理。
【代码】
class Solution {public:bool stoneGameIX(vector<int>& stones) {int cnt[3]={0};for(auto &x:stones)cnt[x%3]++;int turn=0;int cnt_copy[3]={cnt[0],cnt[1],cnt[2]};if(cnt[1]>0)//Alice 第一次选 1{cnt[1]--;turn = 1 + min(cnt[1],cnt[2]) * 2 + cnt[0];if(cnt[1]>cnt[2])//末尾还可以追加一个 1{cnt[1]--;turn++;}if(turn%2==1 && cnt[1]!=cnt[2]) return true;}if(cnt_copy[2]>0)//Alice 第一次选 2{cnt_copy[2]--;turn = 1 + min(cnt_copy[1] , cnt_copy[2]) * 2 + cnt_copy[0];if(cnt_copy[2] > cnt_copy[1])//末尾还可以追加一个 2{turn++;cnt_copy[2]--;}if(turn%2==1 && cnt_copy[1]!=cnt_copy[2]) return true;}return false;}};
看这题之前我们先看一个经典问题。如何求一个串的字典序最小的指定长度的字串?
思路是这样的。假设输出串为s,长度为n,待求字串长为k。维护一个单调队列,队列中元素单调不减。读入一个待处理字符,若其不小于队尾元素(此处特指ASCII码大小),直接入队,否则不断弹出队尾直到队尾不再大于该元素,再将其入队。求长为k的字典序最小的子串,先将前n-k个元素直接入栈,剩下k个元素。对于剩下的k个元素,每次处理一个,队头出队一个,处理完剩下的k个,一共出队的元素就是k个,即所求答案。恰是单调队列的应用既维护了元素的非递减序,同时又保持元素在源串中的相对顺序,比如abacccbb,这个串处理到单调队列中实际存的就是aabb。至于为什么这样处理出来的子序列就是所求的序列,需要你想想啦,其实也比较明显,我若描述出来您照着我的思路走反而不容易理解,有想法亦可给我留言交流。
【模板】
#include<bits/stdc++.h>using namespace std;int main(){string s="bcaabac";int k=4;string ans;int n=s.size();vector<int> q(n+10);int head=0,rear=-1;for(int i=0;ans.size()<k;i++){while(i<n && head<=rear && s[i]<q[rear])rear--;if(i<n)q[++rear]=s[i];if(i >= n-k)ans+=q[head++];}cout<<ans;return 0;}
回到第四题。
【题目描述】

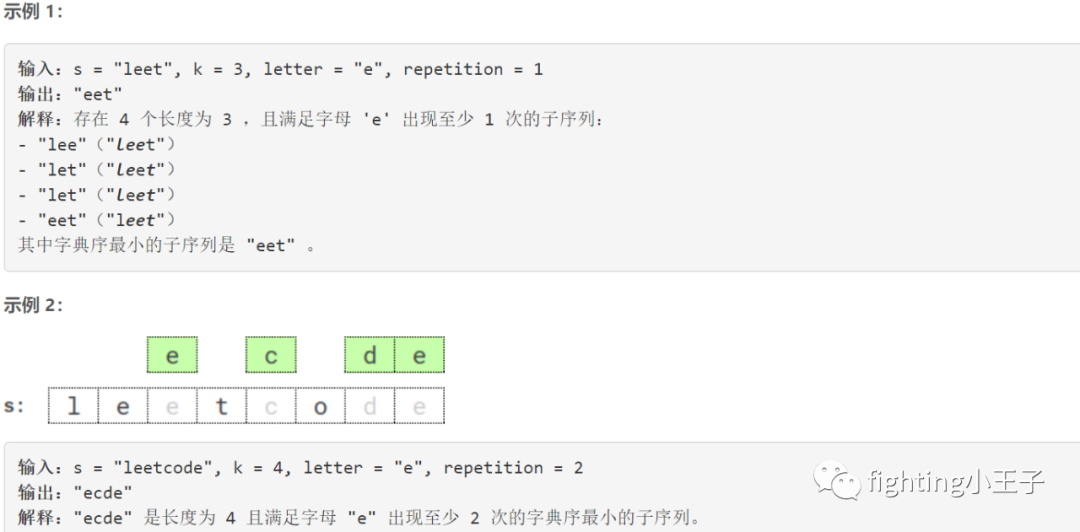

【思路】
这题在上面那个经典问题上提出了一个新要求,要求某个元素要在子序列中出现repetition次。只要稍微改一下就可以了。首先弹出队尾的时候,如果队尾元素是letter,弹出后后面会使得letter不够,则不弹出,直接让该元素进队(此时可能会破坏单调栈非递增的性质,但除letter外的元素是单调不减的)。出队的时候(出队的元素构成结果串ans),如果ans剩余的位置不足以放够letter,那当前出队的这个元素照样出队但不放进ans里,因为ans剩下的位置是letter专属的。
【代码】
class Solution {public:string smallestSubsequence(string s, int k, char letter, int repetition) {int n=s.length();char q[n+10];int head=0,rear=-1;int inQ=0,unread = count(s.begin(),s.end(),letter);cout<<unread<<endl;string ans;for(int i=0;ans.size() < k; i++){while(i<n && head<=rear && s[i] < q[rear]){if(q[rear] == letter){if(inQ + unread <= repetition)break;inQ--;}rear--;}if(i<n){if(s[i] == letter){unread--;inQ++;}q[++rear]=s[i];}if(i>=n-k){if(q[head] == letter){inQ--;repetition--;ans+=q[head];}else if(ans.size()+repetition < k)ans+=q[head];head++;}}return ans;}};






