第253场周赛。本次周赛难度不是特别大,第一名5分钟AK(All-Killed)辽。第一题第二题都是简单模拟,第二题需要多次找最大值,两重循环o(n^2)的方式模拟可能过不了,我用的大顶堆(优先队列)。第三题贪心,如果没做过类似的话贪心的思路比较难想到(但代码确实简洁),我用的是非贪心的思路,借助栈初始化字符串,去掉可匹配的字符;第四题虽然是一个hard级,难点应该就在时间复杂度优化上,二分就行。
keywords:模拟;大顶堆;优先队列;贪心;栈;时间复杂度;整数二分
5838. 检查字符串是否为数组前缀
【题目描述】


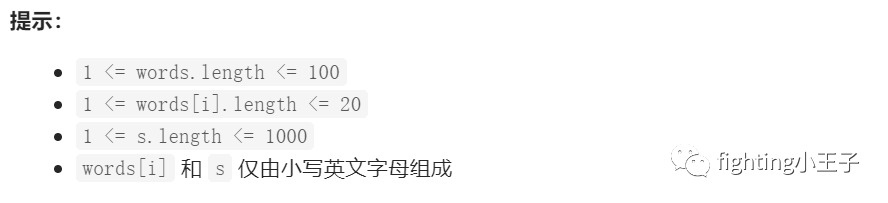
【思路】
简单级难度,数据量很小,直接枚举字符串拼接看能否拼出目标串。
【代码】
class Solution {public:bool isPrefixString(string s, vector<string>& words) {string tmp=words[0];int i=0;while(tmp!=s && i<words.size()-1){tmp+=words[++i];if(tmp.size()>s.size()) break;}return tmp==s;}};
5839. 移除石子使总数最小
【题目描述】



【思路】
题目说得很清楚,每次取最大的那个堆,删掉一半,把剩下的一半留着,重复k次求剩余石子数。石堆的总数是10^5级别,k也是10^5级别,处理一个重新排序后再处理下一个或者处理一个后扫描整个序列找最大值时间复杂度分别为o(n*n*logn)、o(n*n),可能会过不了(没有尝试这两个思路的代码,估计不一定能过,感兴趣的同学可以尝试写一下)。每次都取最大元素类型的时间复杂度优化,在写了这么些次周赛后,很习惯性地想到用堆来解决,C++ STL封装了优先队列(priority_queue),很方便实现大/小顶堆,而时间复杂度也可以优化到o(n*logn)。
【代码】
class Solution {public:int minStoneSum(vector<int>& piles, int k) {priority_queue<int,vector<int>,less<int>> q;int sum=accumulate(piles.begin(),piles.end(),0);for(auto &x:piles)q.push(x);while(k){k--;int top=q.top();q.pop();int minus=top/2;q.push(top-minus);sum-=minus;}return sum;}};
注:accumulate是C++的一个求和函数。
5840. 使字符串平衡的最小交换次数
【题目描述】



【思路】
贪心思路。记左括号为+1,右括号为-1,前缀和小于0时就说明字符串并不平衡。于是只要扫描一遍,找到最大的前缀和maxn,答案就是maxn/2向上取整。
非贪心思路。首先,先了解一下这个 "平衡串" 的定义。其核心是左右左右括号刚好能匹配,如 "[]","[[][]]","[[][][]]","[[[[][][]]]]"都是平衡串,会发现我们把一些能平衡的串给它去掉,剩下的就是"...]]][[[..."这样的串,而且题目保证一定能通过有限次交换是串达到平衡,所以真正要交换的目的就是使"...]]][[[..."这种串达到平衡,于是我们要解决的问题也就是求最少多少次可以让这样的串达到平衡。长度为2的非平衡串只有"][",交换一次就行了。长度为4的非平衡串只有"[]][","]][[","][][","][[]",都最少交换一次即可达到平衡。对于长度不足4的串只要交换一次就可以达到平衡,而对于长度大于4的串,如"]]]]]]][[[[[[["我们的策略是任挑两个"]]"与"[[",交换一次使之变成"[][]",因为长度一定为偶数,这样操作要么就是经过n次已经变成平衡串了,要么就是还剩一个长度为2的非平衡串,再交换一次就行。这种一次交换消掉一个长度为4的不平衡串的策略一定是操作次数最少的,最后的答案也就是"...]]][[[..."这个串长度/4向上取整。
这个非贪心思路其实也多少有点贪心的意思,上述第一个思路像是后者的一个封装了一下的结果,后者则是详述了一下没有做过类似的题而希望解出这道题时一个可能的思考过程。该说说时间复杂度了。n的规模达到10^6,试探性地写的时候每次用字符串查找、删除,去掉s中所有可匹配的"[]",得到"...]]][[[...",这样虽可以帮助我找到思路,但时间复杂度也很高,字符串匹配最快也是o(nlogn),整体复杂度就到了o(n*n*logn),超时无疑。括号匹配的问题当然用栈最为合适,当遇到 ']' 而栈顶是 '[' 时说明就找到了一对匹配串,弹栈就行,否则入栈,时间复杂度o(n)。
【代码】
class Solution {public:int minSwaps(string s) {int idx=s.find("[]");stack<char> stk;for(auto &x:s){if(x==']' && stk.size() && stk.top()=='[')stk.pop();else stk.push(x);}return (stk.size() +3) / 4;}};
注:x/n向上取整就是(x+n-1)/ n。
5841. 找出到每个位置为止最长的有效障碍赛跑路线
【题目描述】



【思路】
对于每一个元素,找前面比它小的所有元素构成一个非递减序列的最大长度。如上示例中,对于元素6,其前面比它小的元素构成的最长非递减序列有[3,5]和[1,5],加上自己,最长的非递减序列长度就是3。处理到元素6时,应该已经知道前面三个元素3,1,5分别能构成的非递减序列最长长度分别为1,1,2。对于元素6,就需要扫描前面每一个小于它元素,尝试将6放入其后,然后找到最长的那个(此例中显然放入5后构成356或者156的非递减序列最长)。思路很明显,但是每个元素都要往前找,时间复杂度达到o(n*n),势必会超时。需要优化。
前面提到这题可以用二分来优化。用二分搜索,那就要求序列必须有序,因此拿什么二分是需要认真思考,且有一定难度的问题。这里有"递增"这个性质的也只有最长非递减序列长度了,每加一个元素,前面的数字可构成的最长非递减序列长度是不会减小的,有递增的性质。这里我的思路是对长度进行二分,对于每个长度 i,用数组a[i]记录下组成长度为 i 的非递减序列的最后一个元素的最小值,如上例中假设当前已处理到元素6,则a[1]=1,a[2]=5,a[3]=6,处理到6时,长度为1的非递减序列有3和1,两个序列最后一个元素最小值为1,长度为2的有15,35,两个序列最后一个元素的最小值为5。这样记录用意是什么?为了二分。有一个新的元素ai需要处理时,直接二分前面元素构成的所有长度,对于长度j,若其最小的结束元素bj>ai,说明ai是不能接在这个序列后的,也就意味着ai也无法接到长度大于j的序列后面,ai只能接在长度小于等于j的序列之后,加上ai元素可构成的最长非递减序列长度就是ai可接入的串的长度+1。而维护最小值记录数组 a 需要分情况考虑,见下图。

这个更新步骤稍微有点难理解的,先理解a[i]记录的是什么,有什么含义,然后结合一个示例手动更新一下a[i]会更容易理解。这题想清楚这步会有难度,我做比赛的时候可能一刻钟左右就AC(Accepted)了(这个速度已经是很慢的了),但写这道题的分析却花了我快两小时。虽然想到这个思路有难度,但这个难度是因为这类题做得不够多,这种 “另辟蹊径” 的二分在我写过的屈指可数的算法题复盘中就有过几次,所以这次周赛我也能勉强写出来,还是要多做,我与5分钟AK的人只有一小段距离——大概是几个宇宙那么长……
【代码】
const int N=100010;int a[N];class Solution {public:vector<int> longestObstacleCourseAtEachPosition(vector<int>& ob) {int cnt=1,n=ob.size();vector<int> ans(n);ans[0]=1;a[1]=ob[0];for(int i=1;i<n;i++){int t=ob[i];int l=1,r=cnt;while(l<r){int mid=(l+r)>>1;if(a[mid]>t) r=mid;else l=mid+1;}if(a[r]>t){ans[i]=r;a[r]=t;}else{ans[i]=r+1;a[r+1]=t;cnt++;}}return ans;}};
坚信 "复利" 的力量。






