第一题模拟，相较于之前的第一题难度稍有提高，不过还是一个简单题；第二题贪心，思路也比较容易想到；第三题动态规划，朴素思路比较容易想到，但是会超时，需要优化；第四题0-1字典树+DFS，需要对字典树比较熟悉，做过最大异或和问题的同学应该能比较快想出思路，0-1字典树是解决最大异或和比较经典的方法。
keywords：模拟；贪心；动态规划；0-1字典树；DFS
5161. 可以输入的最大单词数
题目描述：
思路：
模拟，统计出现过的单词数，若其中包含敲不出的字母则此单词不计入结果中。
代码：
class Solution {public:bool f[27];int canBeTypedWords(string text, string br) {memset(f,false,sizeof f);for(auto &x:br){f[x-'a']=true;}int n=text.length();bool flag=false;int ans=0;for(int i=0;i<n;i++){if(text[i]==' '){if(!flag)ans++;elseflag=false;continue;}if(f[text[i]-'a']) flag=true;}if(flag==false) ans++;return ans;}};
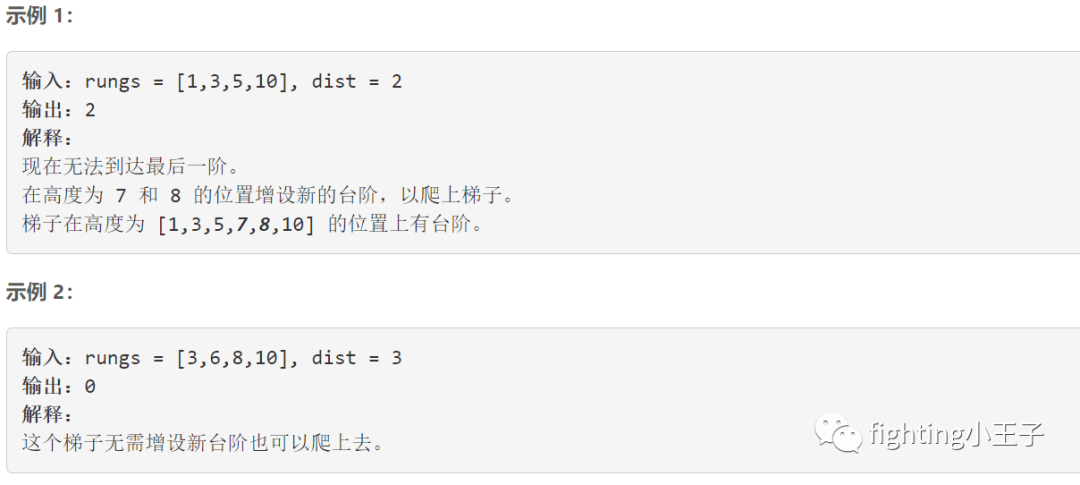
5814. 新增的最少台阶数
题目描述：
思路：
贪心。rungs序列严格递增，只要能够到的就够到，够不到的时候再加梯子就行。够不到的台阶之间加上距离/dist下取整就行。这里需要注意的是下取整操作常规是(x+n-1)/n就行，但是做题的时候遇到了n=1的情况，被卡了一下，所以我的代码里下取整操作分情况写的。
代码：
class Solution {public:int addRungs(vector<int>& rungs, int dist) {int last=0;int ans=0;for(int i=0;i<rungs.size();i++){if((rungs[i]-last)%dist == 0)ans += (rungs[i]-last)/dist - 1;elseans += (rungs[i]-last)/dist;last = rungs[i];}return ans;}};
5815. 扣分后的最大得分
题目描述：
思路：
这题很自然地就想到动态规划。对于每一行每个位置处的最优得分是上一行转移过来的，那对于当前行每个元素可以枚举一遍上面行所有位置转移过来的得分，取最大就行。（说明一下：“从上面某位置转移过来” 是指上一行取了某个列上元素，拿到的了得分，然后到当前行来找最优选择。这里用 “转移” 来描述比较切合动态规划解题的思考套路。）这样的话，每一行需要枚举一遍，而每行中选每个位置可以得到的分又得扫描上一行所有元素来确定，于是时间复杂度为o(n*m*m)，其中n为列数，m为行数，显然，坏的情况下可以达到10^10，会超时。
这个思路主要是在确定某行某个位置的得分时需要将上一行全扫一遍，这样处理一行时间复杂度就o(m*m)了。可以这样考虑。对于当前行某个位置(i,j)，转移过来的最大值要么是由 i-1 行 j 左边的值传过来的，要么是 j 右边值传过来，否则就只可能是(i-1,j)位置传过来的。那么对于左边，我们可以维护一个left_max = max(left_max-1,dp[j])。左边的最大值往右传一个位置就会减少1。同样右边也可以维护一个right_max = max(right_max-1,dp[j])，有了左右转移过来的最大值，那每个位置就可以在o(1)时间确定最终转移到该位置的最大值了。最后时间复杂度降为o(n*m)，可以愉快地看代码了~~
代码：
typedef long long ll;class Solution {public:long long maxPoints(vector<vector<int>>& points) {int n=points.size();int m=points[0].size();vector<ll> dp(m+10,0),work(m+10,0);for(int i=1;i<=n;i++){long long left_max=0;for(int j=1;j<=m;j++){left_max = max(left_max-1 , dp[j]);work[j] = max(work[j],left_max);}long long right_max=0;for(int j=m;j>0;j--){right_max = max(right_max-1 , dp[j]);work[j] = max(work[j] , right_max);}for(int j=1;j<=m;j++)work[j] += points[i-1][j-1];dp = work;}long long ans=0;for(int i=1;i<=m;i++)ans = max(ans , dp[i]);return ans;}};
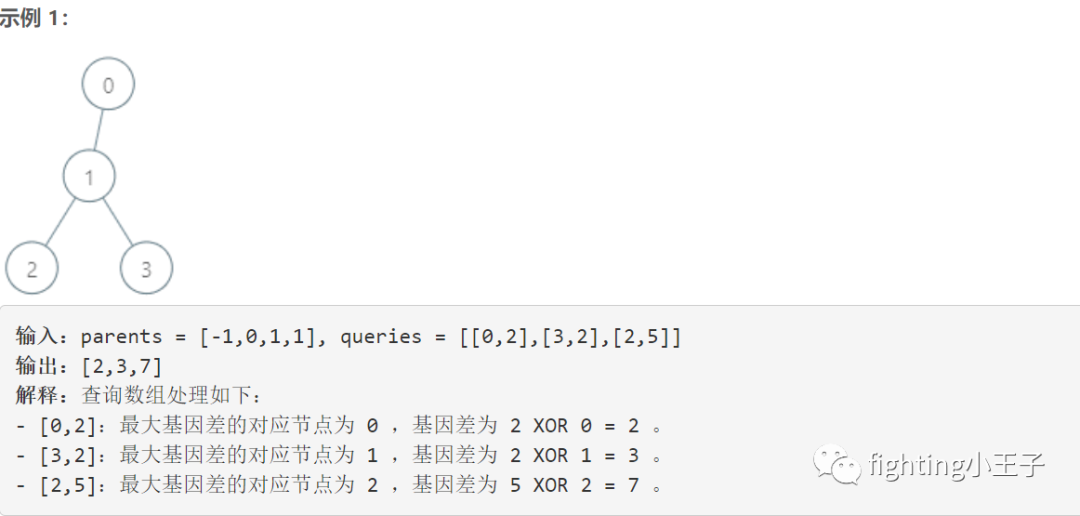
5816. 查询最大基因差
题目描述：
思路：
在第三题写完未优化代码时来写的这个题，粗略一看，二叉树已经建好了，然后直接遍历时间复杂度o(10^4*lg10^5)，好像能过？一顿操作写完代码提交TLM（Time Limit Exceeded）了……想简单了，这是最优情况下的复杂度，而如果二叉树是单支的话时间复杂度就o(10^9)了。
求解异或和的经典方法是0-1字典树（也就是说这里又可以上板子了
）。这里还是简单介绍一下，字典树也是一个用于查找的树，最为经典的应用应该是找多个单词中出现次数最多的前缀，字典树边表示字母，每个节点内存到当前节点为止的所有字母构成的单词串（即根节点到此节点的路径上的所有边组成的单词），这样可以方便地查询、统计公共前缀等信息。而0-1字典树边上存的是0或者1，所以0-1字典树也是一个二叉树。把每个节点的值按二进制位存在0-1字典树中，高层（越靠近根）存高位，叶节点存低位。于是，每次找某个数的最大异或值只要遍历字典树，找对应位上的值与待查数不同的就行，如待查的数当前位为1，那么我们要走0的那条边，二者异或值最大。
每个查询要找的是val与node自己以及所有父辈的异或值最大，也就是说每一个查询我们要能方便地知道该节点的所有父节点。这点恰好dfs能够满足。每次dfs访问到某个节点时，栈中存的都是其父节点，于是我们可以利用这点。每次dfs开始时把u存到字典树中，对u的dfs操作结束后再将u从字典树中删除就行。这里删除操作为减少代码复杂度，只是设一个标志位来对代码进行删除，实际节点占用的存储空间最后全交由操作系统来回收。
代码：
typedef pair<int,int> pii;const int N=20; //10^5 二进制表示不超过20位struct node{int cnt=0;struct node *child[2]{};};void dfs(int u,vector<vector<int>>& children,vector<vector<pii>> &queries,node *trie,vector<int>& ans){node *p=trie;for(int i=N-1;i>=0;i--)//把节点u插入字典树{int next = (u & (1 << i)) ? 1 : 0;if(!p->child[next]){p->child[next]=new node();}p=p->child[next];p->cnt++;}for(auto &q:queries[u]){int val=q.first,id=q.second;p=trie;int tmp=0;for(int i=N-1;i>=0;i--){int next = (val & (1 << i)) ? 0 : 1;if(p->child[next]!=NULL && p->child[next]->cnt!=0){p = p->child[next];tmp = tmp xor (1 << i);}else{if(p->child[next xor 1] == NULL){p->child[next xor 1]=new node();}p = p->child[next xor 1];}}ans[id] = tmp;}for(auto &x:children[u])dfs(x,children,queries,trie,ans);p = trie;for (int i=N-1;i>=0;i--){int next = (u & (1 << i)) ? 1 : 0;p = p->child[next];p->cnt--;}}class Solution {public:vector<int> maxGeneticDifference(vector<int>& parents, vector<vector<int>>& query) {int root;int n=parents.size(),q=query.size();vector<int> ans(q);vector<vector<int>> children(n);for(int i=0;i<n;i++)if(parents[i]==-1)root=i;elsechildren[parents[i]].push_back(i);vector<vector<pii>> queries(n);for(int i=0;i<q;i++){int id=query[i][0],val=query[i][1];queries[id].push_back({val,i});}node *trie = new node();dfs(root,children,queries,trie,ans);return ans;}};
别着急，慢慢来，比较快。
