第一题字符串简单搜索;第二题贪心,思路也容易想到;第三题暴搜,可以用前缀和来降低复杂度;第四题状态压缩dp。
keywords:贪心;暴搜;前缀和;状态压缩;动态规划
正文
————————————————————————————
~~~~~~~~~~~~~~~~~~~~~~~~~~~
5754. 长度为三且各字符不同的子字符串
~~~~~~~~~~~~~~~~~~~~~~~~~~~
题目描述:



代码:
class Solution {public:int countGoodSubstrings(string s) {int cnt=0,n=s.length();for(int i=0;i<n-2;i++)if(s[i]!=s[i+1] && s[i]!=s[i+2] && s[i+1]!=s[i+2]) cnt++;return cnt;}};
~~~~~~~~~~~~~~~~~~~~~~~
5755. 数组中最大数对和的最小值
~~~~~~~~~~~~~~~~~~~~~~~
题目描述:



思路:
凭直觉应该是最小的和最大的配对才能使最大和最小。按这个思路敲出来直接AC了,但还是要不严谨地证一证。

代码:
class Solution {public:int minPairSum(vector<int>& nums) {sort(nums.begin(),nums.end());int minsum=0;int i=0,j=nums.size()-1;while(i<j){minsum=max(minsum,nums[i]+nums[j]);i++;j--;}return minsum;}};
~~~~~~~~~~~~~~~~~~~~
1878. 矩阵中最大的三个菱形和
~~~~~~~~~~~~~~~~~~~~
题目描述:
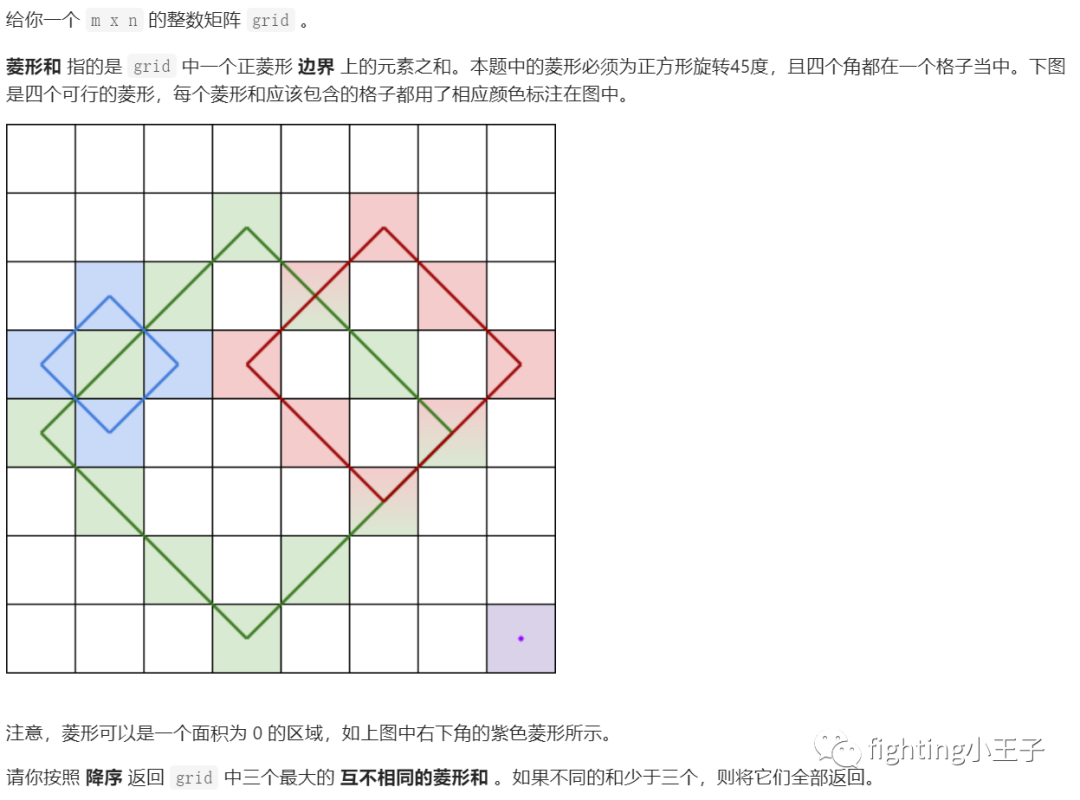
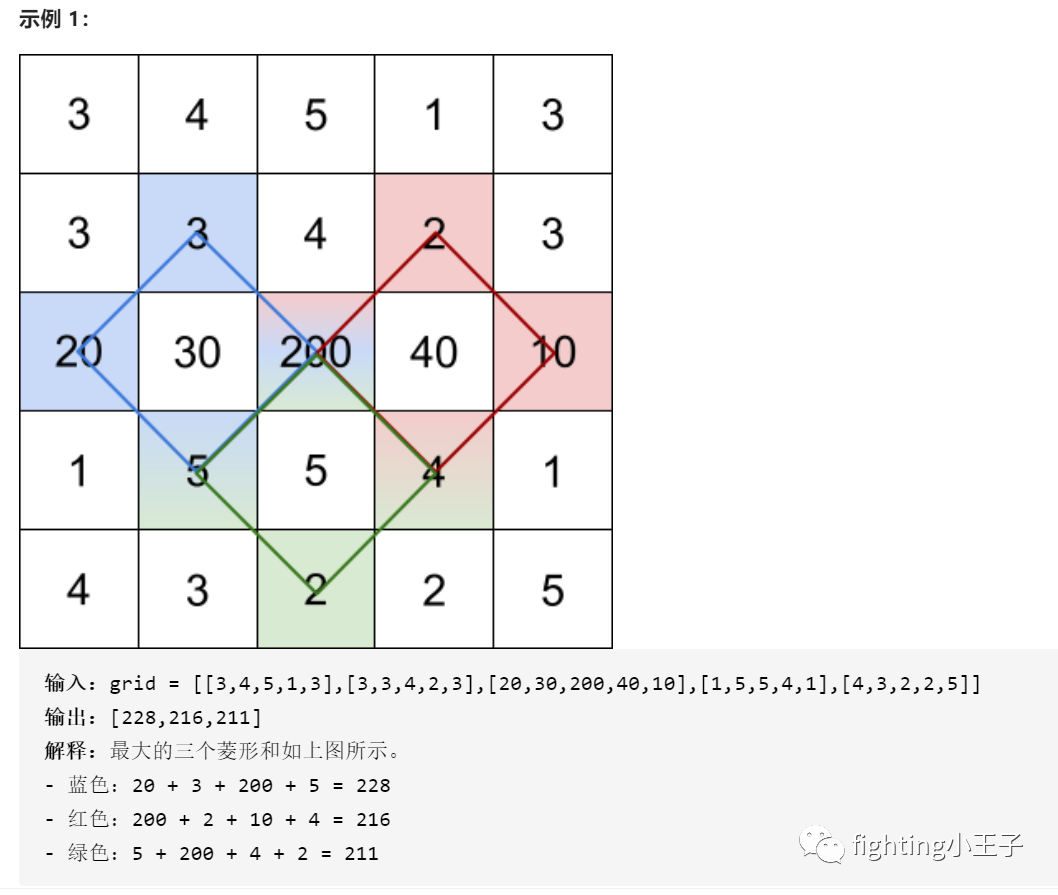

思路:
这题跟上次参加的CCF认证第二题好像,不过那题数据量是1000,这里是100。三重循环可以扫遍所有的菱形,但是求和还需要一重循环,如果直接四重循环的话,复杂度接近o(n^4),可能不能过。内层求和可以用前缀和来处理,这样求和的复杂度可以降到o(1),整体复杂度o(n^3)。
代码:
const int N=110;int s1[N][N],s2[N][N];class Solution {public:vector<int> getBiggestThree(vector<vector<int>>& g) {int n=g.size(),m=g[0].size();for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){s1[i][j]=s1[i-1][j-1]+g[i-1][j-1];s2[i][j]=s2[i-1][j+1]+g[i-1][j-1];}set<int> result;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){result.insert(g[i-1][j-1]);for(int k=1;k+i<=n && i-k>=1 && k+j<=m && j-k>=1;k++){int a=s2[i][j-k]-s2[i-k][j];//[(i,j-k),(i-k,j)) 的和int b=s1[i][j+k]-s1[i-k][j];//[(i,j+k),(i-k,j)) 的和int c=s2[i+k][j]-s2[i][j+k];//[(i+k,j),(i,j+k)) 的和int d=s1[i+k][j]-s1[i][j-k];//[(i+k,j),(i,j-k)) 的和//(i+k,j) 这个点算了两次 (i-k,j)一次也没算result.insert(a+b+c+d - g[i+k-1][j-1] + g[i-k-1][j-1]);}while(result.size()>3) result.erase(result.begin());}}return vector<int>(result.rbegin(),result.rend());}};
代码说明:
k遍历菱形所有可能 “边长”。
求和部分代码可以对着下图看。
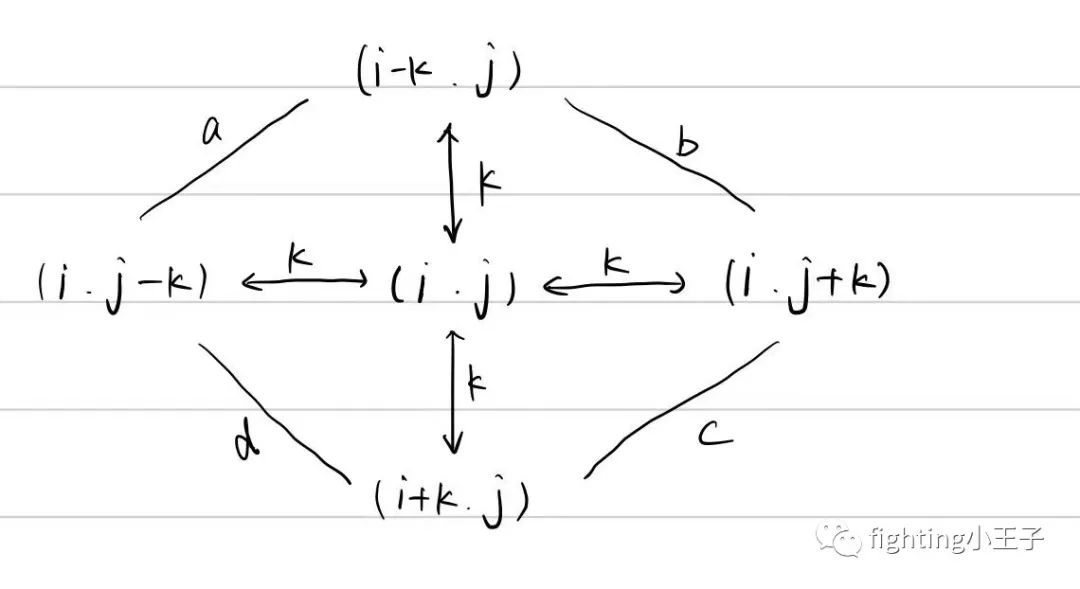
~~~~~~~~~~~~~~~~~~~~~~~
5756. 两个数组最小的异或值之和
~~~~~~~~~~~~~~~~~~~~~~~
题目描述:



思路:
最开始看到n这么小,直接用next_permutation枚举每个序列,但是超时了,玩了个寂寞。n给这样一个数据规模其实是暗示状态压缩了。
设压缩后的状态值为 i ,f[i]表示匹配状态为 i 时的最小异或和。假设 i 用二进制表示为 100101,表示nums2中的第0,3,5这三个数与nums1的前三个数可组成的最小异或和为f[i]。对于nums1的第3个数(下表为2的那个),是与nums2的那个对应,只要都扫描一遍就行。
代码:
class Solution {public:int minimumXORSum(vector<int>& nums1, vector<int>& nums2) {int n=nums1.size(),inf=1e9+10;vector<int> dp(1<<n,inf);dp[0]=0;for(int i=1;i < 1<<n ;i++){int s=0;for(int j=0;j<n;j++)if((i>>j) & 1)s++;for(int j=0;j<n;j++){if((i>>j)&1)dp[i]=min(dp[i],dp[i-(1<<j)]+(nums1[j] xor nums2[s-1]));}}return dp[(1<<n)-1];}};






