之前没做双周赛,感觉leetcode周赛题都还不错,一个半小时4道题的模式也不耽误时间,今天就做了一下刚比完的这场双周赛。
这场还是比较简单,前三道都是模拟,第四题直接搜索,稍微用到了一些前缀和的思想。
1859. 将句子排序
题目描述:
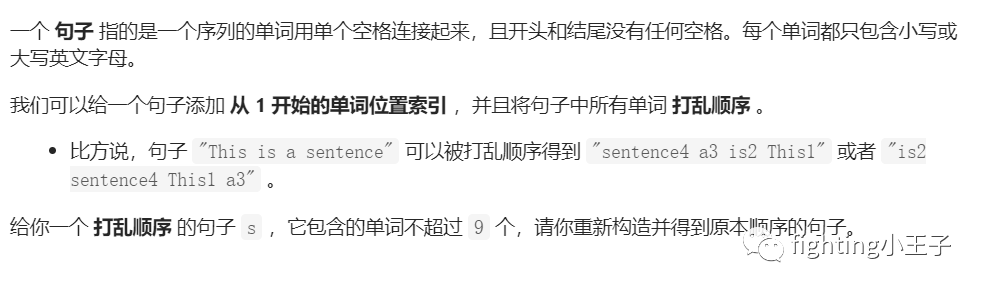
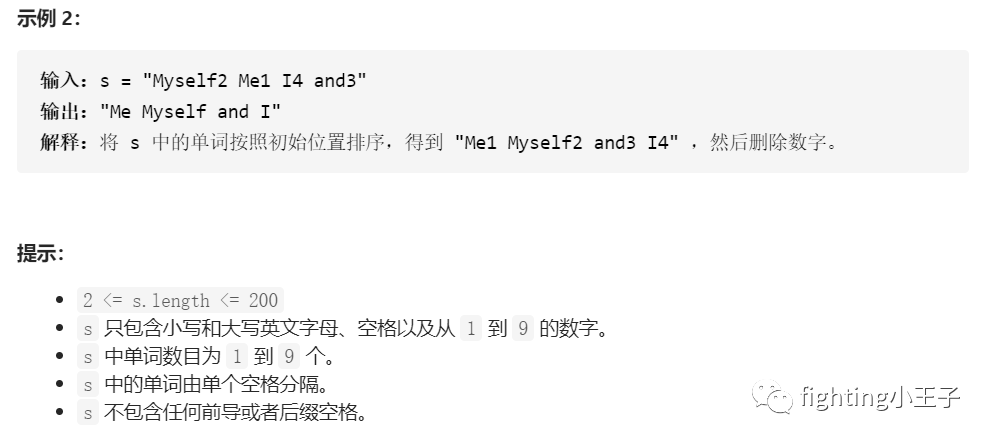
字符串处理,最多10个单词,而且没有多个空格之类的特殊情况处理,还是比较简单的。
代码:
class Solution {public:string word[10]={""};string sortSentence(string s) {int i=0;string tmp="";while(i<=s.length()){if(s[i]==' ' || i==s.length()){if(tmp.length()>0){int id=tmp[tmp.length()-1]-'0';word[id]=tmp.substr(0,tmp.length()-1);}tmp="";}else tmp+=s[i];i++;}string ans;bool block=false;for(int i=1;i<10;i++)if(word[i].length()>0){if(block) ans+=" ";ans+=word[i];block=true;}return ans;}};
1860. 增长的内存泄露
题目描述:


纯模拟了,一个个减。
代码:
class Solution {public:vector<int> memLeak(int memory1, int memory2) {long long i=1;while(i<=memory1 || i<=memory2){if(memory1>=memory2) memory1-=i++;else memory2-=i++;}vector<int> ans;ans.push_back(i);ans.push_back(memory1);ans.push_back(memory2);return ans;}};
1861. 旋转盒子
题目描述:

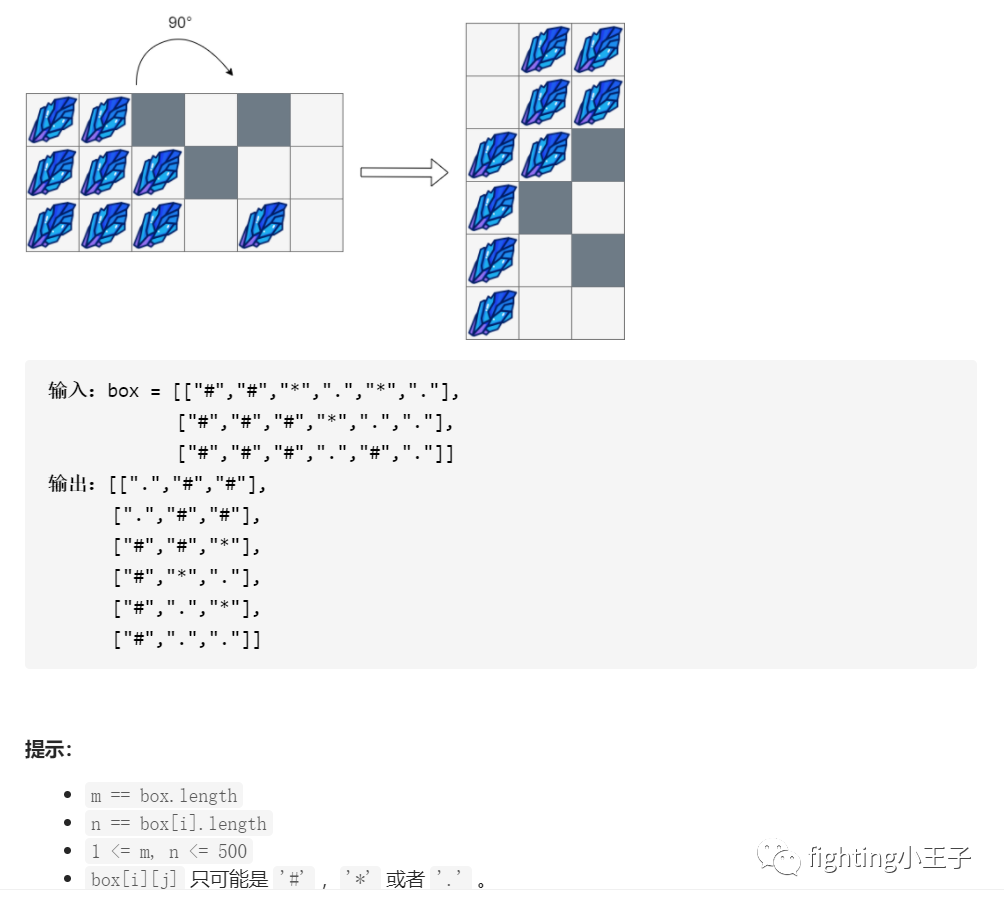
也是模拟,先旋转90度,然后逐列扫。
代码:
class Solution {public:vector<vector<char>> rotateTheBox(vector<vector<char>>& box) {int n=box.size(),m=box[0].size();vector<vector<char>> ans(m,vector<char>(n));for(int i=0;i<n;i++)for(int j=0;j<m;j++)ans[j][n-1-i]=box[i][j];for(int i=0;i<n;i++)//扫描每列{int j=m-1;while(j>0){while(j>0 && ans[j][i]!='.') j--;if(j<=0) break;int t=j-1,cnt=0;while(t>=0 && ans[t][i]!='*'){if(ans[t][i]=='#') cnt++;t--;}int k=j;for(k;j-k<cnt;k--)ans[k][i]='#';for(k;k>t;k--) ans[k][i]='.';if(t<0) break;else j=t;}}return ans;}};
1862. 向下取整数对和
题目描述:

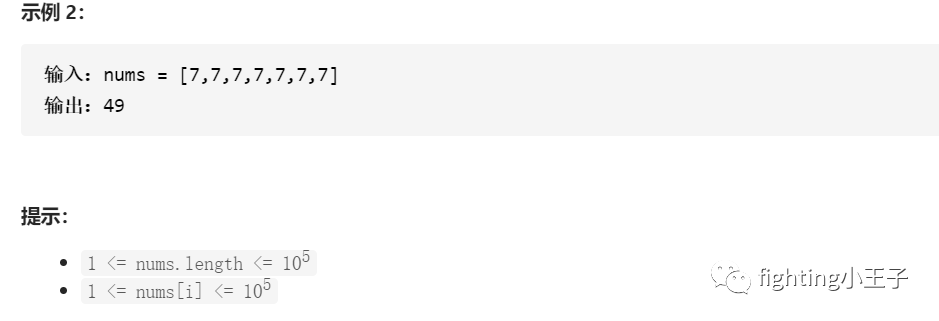
思路:
两重循环扫描求会超时。要想个o(nlogn)的算法才行。nums中每个数小于10^5,可以用一个cnt数组统计nums中每个数出现次数。对于nums中的每个数x,可以这样遍历:
求出[x,x*2),[x*2,x*3)...[x*k,x*(k+1))各个区间中元素个数,对于区间[x*k,x*(k+1)),假设这区间中元素有y个,那么这个区间里所有数除x向下取整结果之和就是k*y。对每个数都扫描一遍所有区间就行,快速统计某个区间内元素总个数,可以对cnt求一次前缀和。前缀和板子咱们已经用过很多次啦。
nums中每个数都在1-10^5之内,咱们可以直接对1-10^5全扫描一遍。也可以只扫描nums的数,这样时间复杂度会比1-10^5全扫更低些,后面两个版本代码都提供了,可以对比一下。
拿1-10^5全扫的方法来看,看似好像对1,好像要扫描10^5次,这样复杂度是不是就是o(N^2)了呢?我曾这样怀疑。但仔细想想实际是这样的:
对于任意一个k,我们要扫描 k,2*k,3*k,4*k,....,x*k直到达到最大值10^5。
于是:
1 要扫 N 次
2 要扫 N/2 次
3 要扫 N/3 次
k 要扫 N/k 次
总共的次数就是N*(1+1/2+1/3+...+1/N)
括号里这是个调和级数,欧拉给出过证明,其和为ln(N+1)+一个无穷小量。所以时间复杂度差不多就是o(NlogN),能过。
代码1:
typedef long long ll;const int N=100010,M=1e9+7;class Solution {public:int cnt[N]={0};int sumOfFlooredPairs(vector<int>& nums) {int ans=0;for(auto &x:nums) cnt[x]++;for(int i=1;i<N;i++) cnt[i]+=cnt[i-1];for(int i=1;i<N;i++)for(int j=1;j*i<N;j++){int l=j*i,r=min(N-1,(j+1)*i-1);int sum=(ll)(cnt[r]-cnt[l-1])*j % M ;ans=(ans+sum*(cnt[i]-cnt[i-1])) % M;}return ans;}};
代码2:
typedef long long ll;const int N=100010,M=1e9+7;class Solution {public:int cnt[N]={0};int sumOfFlooredPairs(vector<int>& nums) {int ans=0;for(auto &x:nums) cnt[x]++;for(int i=1;i<N;i++) cnt[i]+=cnt[i-1];sort(nums.begin(),nums.end());nums.erase(unique(nums.begin(),nums.end()),nums.end());for(auto &x:nums){for(int j=1;j*x<N;j++){int l=j*x,r=min(N-1,(j+1)*x-1);int sum=(ll)(cnt[r]-cnt[l-1])*j % M ;ans=(ans+sum*(cnt[x]-cnt[x-1])) % M;}}return ans;}};
解释一下两个代码中的这两句:
int sum=(ll)(cnt[r]-cnt[l-1])*j % M ;ans=(ans+sum*(cnt[i]-cnt[i-1])) % M;
sum求出的就是对于元素i,[l,r) 上所有元素除x下取整的和。而下面这行又给sum乘了一个(cnt[i]-cnt[i-1]),这是求出 i 出现的次数,也就是可能有多个 i,如样例2,所以要乘一下。
第二个代码比第一个代码扫描更有针对性,只扫nums中出现过的,更快些,下图可以看出运行时间上确实少了一半。而且,代码2中对nums2去重,会耽误时间,如果用一个标记数组来标记省去去重时间执行时间会更少,不过这也是牺牲空间换时间的做法。