这次周赛整体难度不是很大。
1790. 仅执行一次字符串交换能否使两个字符串相等
题目描述:
给你长度相等的两个字符串 s1 和 s2 。一次 字符串交换 操作的步骤如下:选出某个字符串中的两个下标(不必不同),并交换这两个下标所对应的字符。
如果对 其中一个字符串 执行 最多一次字符串交换 就可以使两个字符串相等,返回 true ;否则,返回 false 。
(看一个串是否是另一个串交换两个字符位置而来。)
样例:
输入:s1 = "bank", s2 = "kanb"输出:true解释:例如,交换 s2 中的第一个和最后一个字符可以得到 "bank"
数据约束:
1 <= s1.length, s2.length <= 100s1.length == s2.lengths1 和 s2 仅由小写英文字母组成
AC代码:
bool areAlmostEqual(string s1, string s2) {if(s1==s2) return true;int n=s1.size(),m=s2.size();if(n!=m) return false;for(int i=0;i<n;i++)for(int j=i+1;j<n;j++){swap(s1[i],s1[j]);if(s1==s2) return true;swap(s1[i],s1[j]);}return false;}
1791. 找出星型图的中心节点
题目描述:
有一个无向的 星型 图,由 n 个编号从 1 到 n 的节点组成。星型图有一个 中心 节点,并且恰有 n - 1 条边将中心节点与其他每个节点连接起来。
给你一个二维整数数组 edges ,其中 edges[i] = [ui, vi] 表示在节点 ui 和 vi 之间存在一条边。请你找出并返回 edges 所表示星型图的中心节点。
(对于一个星形图,任意两边,必定有一个重复的端点,而这个点就是我们要找的中心点。)
样例:
输入:edges = [[1,2],[5,1],[1,3],[1,4]]输出:1
数据约束:
3 <= n <= 105edges.length == n - 1edges[i].length == 21 <= ui, vi <= nui != vi题目数据给出的 edges 表示一个有效的星型图
AC代码:
class Solution {public:int cnt[100010];int findCenter(vector<vector<int>>& edges) {int a=edges[0][0],b=edges[0][1];if(a==edges[1][0] || a==edges[1][1]) return a;else return b;}};
1792. 最大平均通过率
题目描述:
一所学校里有一些班级,每个班级里有一些学生,现在每个班都会进行一场期末考试。给你一个二维数组 classes ,其中 classes[i] = [passi, totali] ,表示你提前知道了第 i 个班级总共有 totali 个学生,其中只有 passi 个学生可以通过考试。
给你一个整数 extraStudents ,表示额外有 extraStudents 个聪明的学生,他们 一定 能通过任何班级的期末考。你需要给这 extraStudents 个学生每人都安排一个班级,使得 所有 班级的 平均 通过率 最大 。
一个班级的 通过率 等于这个班级通过考试的学生人数除以这个班级的总人数。平均通过率 是所有班级的通过率之和除以班级数目。
请你返回在安排这 extraStudents 个学生去对应班级后的 最大 平均通过率。与标准答案误差范围在 10-5 以内的结果都会视为正确结果。
样例:
输入:classes = [[1,2],[3,5],[2,2]], extraStudents = 2输出:0.78333解释:你可以将额外的两个学生都安排到第一个班级,平均通过率为 (3/4 + 3/5 + 2/2) / 3 = 0.78333 。
数据约束:
1 <= classes.length <= 105classes[i].length == 21 <= passi <= totali <= 1051 <= extraStudents <= 105
思路:
怎样能使平均值最大?给定一个班级,通过人数为 a,总人数为 b,则通过率为 a/b。若加了一个尖子生到这个班级,则通过人数变为 a+1,总人数为 b+1,通过率为
(a+1) /(b+1)。令 dt = (a+1) /(b+1) - a/b 表示把尖子生加到这个班能增加的通过率。最后的目标是使总通过率最大,那么每个尖子生应该加到能使通过率增加量dt最大的那个班,这样最后的总通过率才最大。
AC代码:
double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {struct node{double dt;int a,b;bool operator < (const node& v) const{return dt<v.dt;}};priority_queue<node> heap;double sum=0;for(auto& c:classes){int a=c[1],b=c[0];sum+=(double)b/a;heap.push({(double)(a-b)/(a*(a+1.0)),a,b});}while(extraStudents -- ){node t=heap.top();heap.pop();int a=t.a+1,b=t.b+1;sum+=t.dt;heap.push({(double)(a-b)/(a*(a+1.0)),a,b});}return sum/classes.size();}
1793. 好子数组的最大分数
题目描述:
给你一个整数数组 nums (下标从 0 开始)和一个整数 k 。
一个子数组 (i, j) 的 分数 定义为 min(nums[i], nums[i+1], ..., nums[j]) * (j - i + 1) 。一个 好 子数组的两个端点下标需要满足 i <= k <= j 。
请你返回 好 子数组的最大可能 分数 。
样例:
输入:nums = [1,4,3,7,4,5], k = 3输出:15解释:最优子数组的左右端点下标是 (1, 5) ,分数为 min(4,3,7,4,5) * (5-1+1) = 3 * 5 = 15 。
数据约束:
1 <= nums.length <= 1051 <= nums[i] <= 2 * 1040 <= k < nums.length
思路:
模板题:
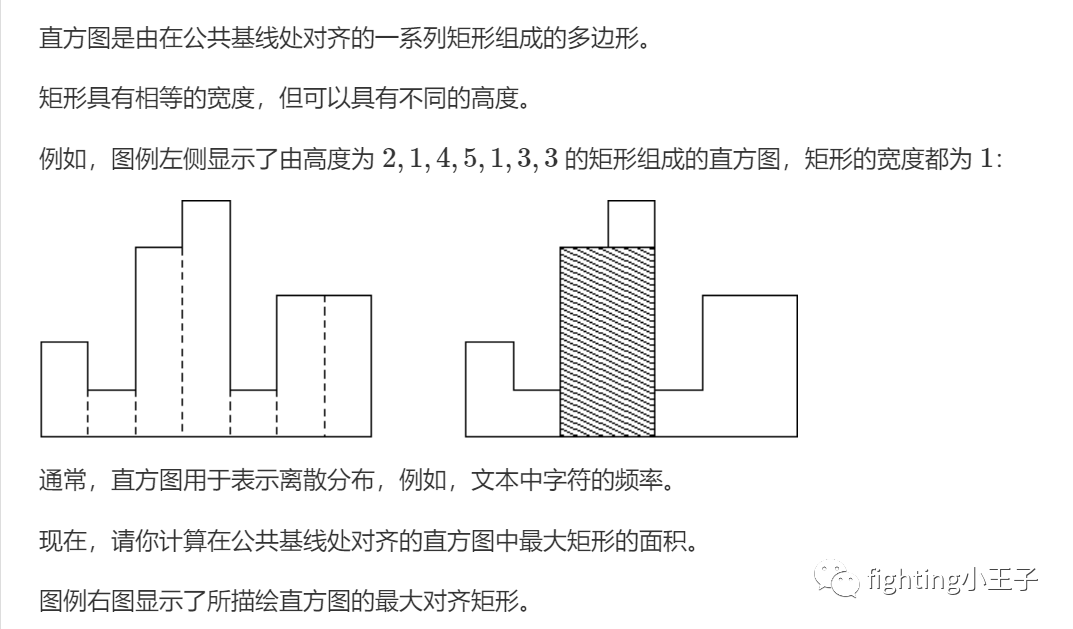
(代码直接粘过来就行……模板还得使劲背呀,大佬们5分钟写完4道题真的太强了。)
对于每个数,找一遍左边第一个比它小的数的位置,右边第一个比它小的数的位置,人后区间长度乘以这个数就行了。
AC代码:
int maximumScore(vector<int>& nums, int k) {int n=nums.size();vector<int> h(n+2,-1),l(n+2),r(n+2),stk(n+2);for(int i=1;i<=n;i++) h[i]=nums[i-1];int tt=0;stk[0]=0;for(int i=1;i<=n;i++){while(h[stk[tt]] >= h[i]) tt--;l[i]=stk[tt];stk[++tt]=i;}tt=0;stk[0]=n+1;for(int i=n;i>=1;i--){while(h[stk[tt]] >= h[i]) tt--;r[i]=stk[tt];stk[++tt]=i;}int sum=0;k++;for(int i=1;i<=n;i++){if(r[i]>k && l[i]<k) sum=max(sum,h[i]*(r[i]-l[i]-1));}return sum;}






