拖了两周了,终于把这场周赛补上了。这次第二、三题有一些难度,第三题卡了很久,在一个社区把我代码上传了后有大佬给我支持初始化爆int的问题,改了就AC了,所以来补坑了。
给你一个二进制字符串 s ,该字符串 不含前导零 。
如果 s 最多包含 一个由连续的 '1' 组成的字段 ,返回 true 。否则,返回 false 。
样例:
输入:s = "1001"输出:false解释:字符串中的 1 没有形成一个连续字段。输入:s = "110"输出:true
数据约束:
1 <= s.length <= 100s[i]
为'0'
或'1's[0]
为'1'
AC代码:
bool checkOnesSegment(string s) {int i=0,j=s.size()-1;while(i<=j && s[i]=='0') i++;while( i<=j && s[j]=='0') j--;for(int k=i;k<=j;k++)if(s[k]=='0') return false;return true;}
1785. 构成特定和需要添加的最少元素
题目描述:
给你一个整数数组 nums ,和两个整数 limit 与 goal 。数组 nums 有一条重要属性:abs(nums[i]) <= limit 。
返回使数组元素总和等于 goal 所需要向数组中添加的 最少元素数量 ,添加元素 不应改变 数组中 abs(nums[i]) <= limit 这一属性。
注意,如果 x >= 0 ,那么 abs(x) 等于 x ;否则,等于 -x 。
样例:
输入:nums = [1,-1,1], limit = 3, goal = -4输出:2解释:可以将 -2 和 -3 添加到数组中,数组的元素总和变为 1 - 1 + 1 - 2 - 3 = -4 。
数据约束:
1 <= nums.length <= 105
1 <= limit <= 10^6
-limit <= nums[i] <= limit
-10^9 <= goal <= 10^9
思路:
不妨记 sum = goal-数组和,先把sum取一下绝对值,因为题目只要求 abs(nums[i]) <= limit即可。而这道题的目的就是将正的sum不断减去0-limit中的一个数使sum=0,而需要减去的最少的数据个数就是最后的答案。很显然,这里用贪心思路,sum>limit时,每次都让sum减去limit就行,只有这样才能让减去的个数最小。所以需要减去的最小的个数就是 sum/limit上取整(上取整操作 上一篇文章提到过:(t+k-1/k) )。
AC代码:
int minElements(vector<int>& nums, int limit, int goal) {long long sum=0;// for(int i=0;i<nums.size();i++) sum+=nums[i];sum=accumulate(nums.begin(),nums.end(),0ll);//和函数return (abs(goal-sum)+limit-1)/limit;}
1786. 从第一个节点出发到最后一个节点的受限路径数
题目描述:
现有一个加权无向连通图。给你一个正整数 n ,表示图中有 n 个节点,并按从 1 到 n 给节点编号;另给你一个数组 edges ,其中每个 edges[i] = [ui, vi, weighti] 表示存在一条位于节点 ui 和 vi 之间的边,这条边的权重为 weighti 。
从节点 start 出发到节点 end 的路径是一个形如 [z0, z1, z2, ..., zk] 的节点序列,满足 z0 = start 、zk = end 且在所有符合 0 <= i <= k-1 的节点 zi 和 zi+1 之间存在一条边。
路径的距离定义为这条路径上所有边的权重总和。用 distanceToLastNode(x) 表示节点 n 和 x 之间路径的最短距离。受限路径 为满足 distanceToLastNode(zi) > distanceToLastNode(zi+1) 的一条路径,其中 0 <= i <= k-1 。
返回从节点 1 出发到节点 n 的 受限路径数 。由于数字可能很大,请返回对 109 + 7 取余 的结果。
样例:
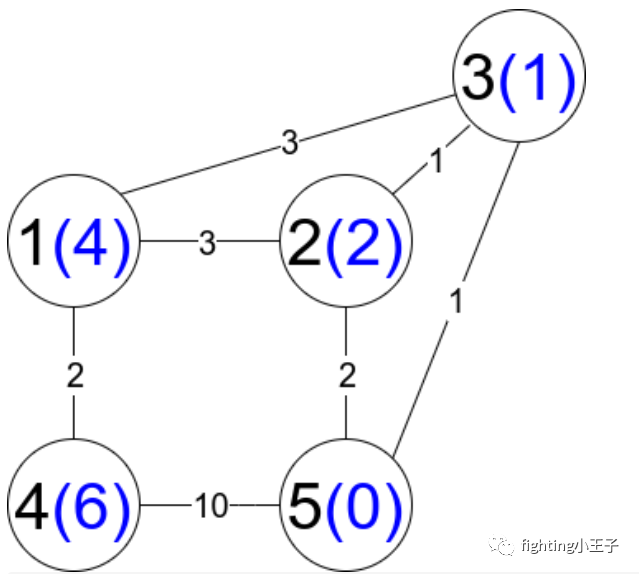
输入:n = 5, edges = [[1,2,3],[1,3,3],[2,3,1],[1,4,2],[5,2,2],[3,5,1],[5,4,10]]输出:3解释:每个圆包含黑色的节点编号和蓝色的 distanceToLastNode 值。三条受限路径分别是:1) 1 --> 2 --> 52) 1 --> 2 --> 3 --> 53) 1 --> 3 --> 5
数据约束:
1 <= n <= 2 * 104n - 1 <= edges.length <= 4 * 104edges[i].length == 31 <= ui, vi <= nui != vi1 <= weighti <= 105任意两个节点之间至多存在一条边任意两个节点之间至少存在一条路径
思路:
最短路+dp。首先求n号节点到每一个节点的最短路,单源最短路,直接dijkstra算法就行。比赛时有的人用spfa写的也过了,但是后面去测试就过不了了,spfa平均时间复杂度是o(n),应该是后面数据加强了,2000的测试点过不了。朴素dijkstra算法估计也不一定能过,最好用优化的。然后是求受限路径数,dp。设f(i)为从i号节点到n号节点的受限路径数,则若i节点可以到j节点,且满足受限条件,则f(i)+=f(j)。
AC代码:
using PII=pair<long long ,long long>;class Solution {public:const long long INF=1e10,MOD=1e9+7;//这里无穷大之前习惯性设置为0x3f3f3f3f,// 会出现爆int错误,导致2000的测试点过不了,注意一下vector<vector<PII>> g;vector<long long> d;vector<int> f;vector<bool> st;int countRestrictedPaths(int n, vector<vector<int>>& edges) {g.resize(n+1);d.resize(n+1,INF);f.resize(n+1,0);st.resize(n+1,false);for(auto& e:edges){int a=e[0],b=e[1],c=e[2];g[a].push_back({b,c});g[b].push_back({a,c});}d[n]=0;priority_queue<PII,vector<PII>,greater<PII>> heap;heap.push({0,n});while(heap.size()){PII t=heap.top();heap.pop();long long distance=t.first;int v=t.second;if(st[v]) continue;st[v]=true;for(auto& e:g[v]){int j=e.first;long long dis=e.second;if(d[j]>distance+dis){d[j]=dis+distance;heap.push({d[j],j});}}}vector<PII> vs;for(int i=1;i<=n;i++) {vs.push_back({d[i],i});}sort(vs.begin(),vs.end());f[n]=1;for(auto& v:vs){long long distance=v.first;int u=v.second;for(auto& p:g[u]){int j=p.first;if(distance>d[j]){f[u]=(f[u]+f[j] )% MOD;}}}return f[1];}};
1787. 使所有区间的异或结果为零
题目描述:
给你一个整数数组 nums 和一个整数 k 。区间 [left, right](left <= right)的 异或结果 是对下标位于 left 和 right(包括 left 和 right )之间所有元素进行 XOR 运算的结果:nums[left] XOR nums[left+1] XOR ... XOR nums[right] 。
返回数组中 要更改的最小元素数 ,以使所有长度为 k 的区间异或结果等于零。
样例:
输入:nums = [1,2,0,3,0], k = 1输出:3解释:将数组 [1,2,0,3,0] 修改为 [0,0,0,0,0]输入:nums = [3,4,5,2,1,7,3,4,7], k = 3输出:3解释:将数组 [3,4,5,2,1,7,3,4,7] 修改为 [3,4,7,3,4,7,3,4,7]
数据约束:
1 <= k <= nums.length <= 20000 <= nums[i] < 210
思路:



(字丑……我尽力了)
AC代码:
class Solution {public:const int M=1024; //nums[i] 异或 nums[j] 最大值为1023const int INF=1e8; //无穷大int s[1024];int minChanges(vector<int>& nums, int k) {int n=nums.size();int m=(n+k-1)/k;vector<vector<int>> f(k+1,vector<int>(M,INF));f[0][0]=0;int sum=0,minv=INF;for(int i=1;i<=k;i++){memset(s,0,sizeof s);int len=m;if(n%k && n%k < i) len--;for(int j=0;j<len;j++)s[nums[j*k+i-1]]++;int maxv=0;for(int j=0;j<1024;j++)if(s[j])maxv=max(maxv,s[j]);sum+=len-maxv,minv=min(minv,maxv);for(int j=0;j<1024;j++)for(int u=0;u<len;u++){int x=nums[u*k+i-1],cost=len-s[x];f[i][j]=min(f[i][j],f[i-1][j^x]+cost);}}return min(sum+minv,f[k][0]);}};






