6.3 RNN高级用法
在本小节中,我们将学习三种高级方法提升RNN的性能和泛化能力。学完本小节你将会掌握使用Keras实现RNN的细节。我们将展示解决天气预报问题的三种思想,建筑顶部安置的传感器会收集相关的时序数据,比如,温度、大气压和湿度。你可以用这些数据预测接下来24小时的天气。这是一个相当有挑战性的问题,也是其它处理时序数据时会遇到的许多常见困难。
本章将会介绍下面的技术:
循环dropout(Recurrent dropout ):它是特殊的、内建的方法,用dropout来解决recurrent layer中的过拟合问题
堆叠循环layer(Stacking recurrent layer):它能提高神经网络的表征能力,但是相应会加重计算的高负载
双向循环layer(Bidirectional recurrent layer ):它能提高神经网络的准确度和减轻遗忘问题,同时以不同的方式为循环神经网络呈现相同的信息
6.3.1 天气预报问题
到目前为止,我们遇到唯一的序列数据是文本数据,比如IMDB数据集和Reuter数据集。但是,人们发现序列数据比自然语言处理的问题更多。在本小节所有的例子,你将会使用天气时序数据集,它由德国马克斯-普朗克研究所气象站监测记录。
在该数据集中,每十分钟记录14个变量(比如,空气温度,大气压,湿度,风度等等),时间跨度将近七年。最早的数据是2003年的,但是本例中选择2009年到2016年的数据。本数据集是学习数值型时序数据的最佳选择。使用该数据集训练一个模型,它输入最近过去的一些数据(几天的数据点),预测将来24小时的空气温度。
下载数据集并解压:
cd ~/Downloadsmkdir jena_climatecd jena_climatewget https://s3.amazonaws.com/keras-datasets/jena_climate_2009_2016.csv.zipunzip jena_climate_2009_2016.csv.zip
下面瞅一下数据:
#Listing 6.28 Inspecting the data of the Jena weather datasetimport osdata_dir = '/users/fchollet/Downloads/jena_climate'fname = os.path.join(data_dir, 'jena_climate_2009_2016.csv')f = open(fname)data = f.read()f.close()lines = data.split('\n')header = lines[0].split(',')lines = lines[1:]print(header)print(len(lines))
上面的代码将输出数据集行数是420,551,每行是一个时间点的数据:一个日期和14个天气相关的值,其文件头如下:
["Date Time","p (mbar)","T (degC)","Tpot (K)","Tdew (degC)","rh (%)","VPmax (mbar)","VPact (mbar)","VPdef (mbar)","sh (g/kg)","H2OC (mmol/mol)","rho (g/m**3)","wv (m/s)","max. wv (m/s)","wd (deg)"]
接着将所有420,551行数据转换成一个Numpy数组
#Listing 6.29 Parsing the dataimport numpy as npfloat_data = np.zeros((len(lines), len(header) - 1))for i, line in enumerate(lines):values = [float(x) for x in line.split(',')[1:]]float_data[i, :] = values
例如,下面的代码是绘制随时间的温度(摄氏度)变化趋势,见图6.18。从图中你可以清晰的看出天气温度的周期性变化。
#Listing 6.30 Plotting the temperature timeseriesfrom matplotlib import pyplot as plttemp = float_data[:, 1] <1> temperature (in degrees Celsius)plt.plot(range(len(temp)), temp)
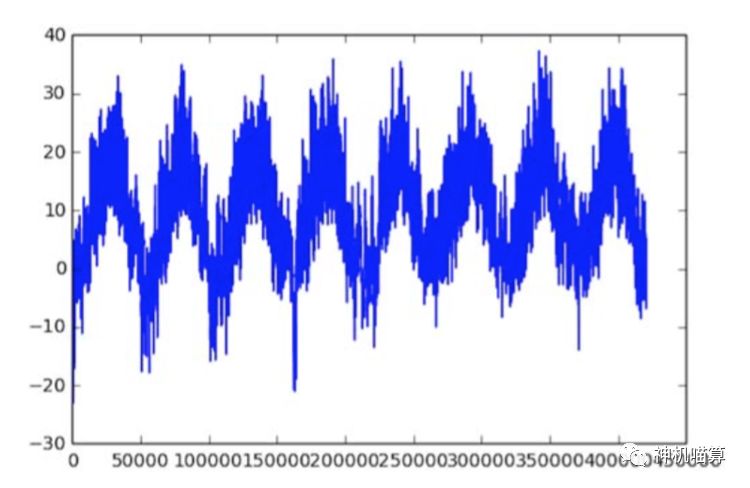
图6.18 数据集中随时间的温度变化趋势图(摄氏度)
下面取十天的温度数据绘制趋势图,见图6.19。由于数据点是每十分钟记录一次,你将得到每天144个数据点。
#Listing 6.31 Plotting the first 10 days of the temperature timeseriesplt.plot(range(1440), temp[:1440])
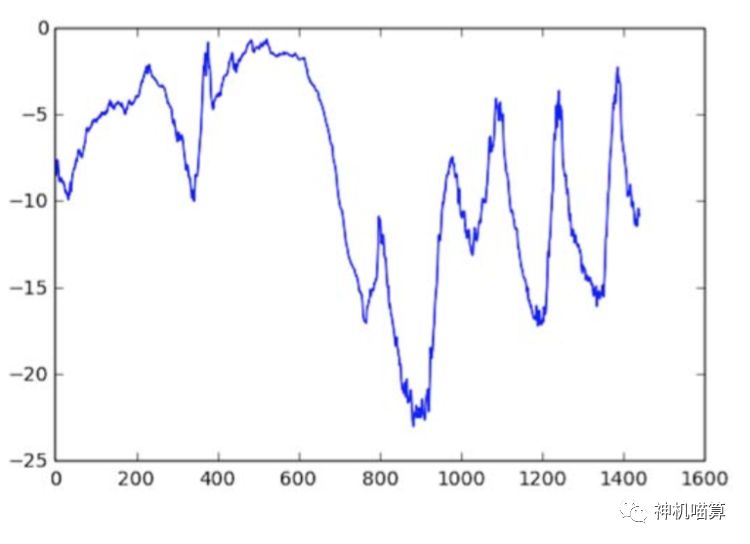
图6.19 前十天的温度变化趋势图(摄氏度)
在上图中,你能看到每天数据的周期性,特别是最近四天更明显。也可以注意到,这十天周期一定是来自相当冷的冬天月份。
如果你想通过过去几个月的数据集来预测下一个月的平均气温,由于数据集按年度是稳定周期性,那这个问题简单。但是按天观察数据集,气温看起相当混乱无序。那我们可以按天进行时序数据预测吗?
6.3.2 准备数据
上述问题的确切描述如下:给定的数据持续lookback个时间步(一个时间步是10分钟),每steps个时间步抽样数据点,那么你可以预测delay个时间步后的气温吗?你将会用到下面的参数值:
lookback = 720 —回放5天的观测值
steps = 6 —每小时抽样一个数据点
delay = 144—预测将来24小时的目标
正式开始前有两件事要做:
将数据集预处理成神经网络要求的输入格式。这步简单:因为数据已是数值型,所以无需任何向量化操作。但是数据集中的时序数据尺度不同,比如,气温典型的在-20到+30,但是大气压用毫巴为单位,大约在1,000左右。你将各自归一化每个时序数据,使其都在相似的尺度范围内。
编写一个Python生成器。其输入当前浮点型数据的数组,生成过去最近的batch数据,除将来目标气温数据外。因为数据集中的样本高度冗余,直接用每个样本将会明显浪费内存。这里用原始数据生成样本数据。
归一化数据,通过减去每个时间点的均值并除以标准差。本例中使用前200,000个时间点的数据作为训练集,所有计算均值和标准差只考虑这部分数据。
#Listing 6.32 Normalizing the datamean = float_data[:200000].mean(axis=0)float_data -= meanstd = float_data[:200000].std(axis=0)float_data /= std
代码6.33显示使用的数据生成器。它生成一个元组(samples, targets),其中samples是一个batch的输入数据,targets是目标气温相应的数组。该生成器的参数如下:
data:浮点型数据的原始数组,其用代码6.32归一化
lookback:输入数据回放多少个时间步
delay :预测将来多少个时间步的目标
min_index 和max_index:数据数组的索引确定时间点的边界。这确保数据集可以分割为验证集和测试集
shuffle:是shuffle样本数据还是按时间顺序排列
batch_size:每个batch的样本数量
step:抽样数据的周期。为了每个小时一个数据点,这里设置为6。
#Listing 6.33 Generator yielding timeseries samples and their targetsdef generator(data, lookback, delay, min_index, max_index,shuffle=False, batch_size=128, step=6):if max_index is None:max_index = len(data) - delay - 1i = min_index + lookbackwhile 1:if shuffle:rows = np.random.randint(min_index + lookback, max_index, size=batch_size)else:if i + batch_size >= max_index:i = min_index + lookbackrows = np.arange(i, min(i + batch_size, max_index))i += len(rows)samples = np.zeros((len(rows),lookback // step,data.shape[-1]))targets = np.zeros((len(rows),))for j, row in enumerate(rows):indices = range(rows[j] - lookback, rows[j], step)samples[j] = data[indices]targets[j] = data[rows[j] + delay][1]yield samples, targets
6.3.3 一个常识性、非机器学习的基线
在使用黑盒神经网络模型解决气温预测问题之前,咱们尝试一个简单的、常识性的方法。作为大体功能的正确性检验,它将建立一个基准线。你必须证明更高级的机器学习模型比该方法更有效。当你试图解决的新问题没有已知的方案,那常识性的基线是有用的。一个典型的例子是不平衡的分类任务,其中某一类别远多于比另外一类。如果你的数据集含有90%的A分类,10%的B分类,那么当出现一个新样本时,分类任务的常识性方法将总是将其预测为“A”分类。这种分类器整体上来讲有90%的准确度,如果有某种机器学习方法的准确度超过90%,那么证明该方法有效。有时一些初级的基线也是非常难超越的。
在本例中,气温序列可以假设为连续变量(明天的气温与今天的相当接近),它是以天为周期的。因此,预测接下来24小时气温的常识性方法将是等于当前的气温。下面我们用平均绝对误差(mean absolute error,MAE)来评估该方法:
np.mean(np.abs(preds - targets))
下面是评估迭代:
#Listing 6.35 Computing the common-sense baseline MAEdef evaluate_naive_method():batch_maes = []for step in range(val_steps):samples, targets = next(val_gen)preds = samples[:, -1, 1]mae = np.mean(np.abs(preds - targets))batch_maes.append(mae)print(np.mean(batch_maes))evaluate_naive_method()
上面的代码返回MAE结果是0.29。因为气温数据归一化后的期望为0,标准差为1,所以这个数字不具有可解释性。我们将MAE 0.29 x temperature_std得到摄氏度为2.57 ̊C。
#Listing 6.36 Converting the MAE back to a Celsius errorcelsius_mae = 0.29 * std[1]
上述结果得到一个相当大的平均绝对误差。现在开始用你的深度学习的知识解决的更好。
6.3.4 基础的机器学习方法
同样地,在进行复杂和高耗时计算成本的模型(比如,RNN)之前,除了要建立一个常识性的基线方法,也要构建一个简单的、低成本的机器学习方法(比如,小型的致密连接(也称为全联接层)的网络模型)来验证。做更进一步的探索时,要确保方法的合理性,以及产生实际的效益。
下面的代码清单展示的是一个全联接模型,其将输入数据打平,然后接着两个Dense layer。注意,最后一个Dense layer并没有激活函数,这是因为本例是一个回归问题。你将使用MAE作为损失函数。因为你的评估数据集和评估指标都与常识性方法相同,所以它们的结果可以直接相比较。
#Listing 6.37 Training and evaluating a densely connected modefrom keras.models import Sequentialfrom keras import layersfrom keras.optimizers import RMSpropmodel = Sequential()model.add(layers.Flatten(input_shape=(lookback // step, float_data.shape[-1]))) model.add(layers.Dense(32, activation='relu'))model.add(layers.Dense(1))model.compile(optimizer=RMSprop(), loss='mae')history = model.fit_generator(train_gen,steps_per_epoch=500, epochs=20, validation_data=val_gen, validation_steps=val_steps)
下面绘制验证集和训练集的损失曲线,见图6.20,代码如下:
#Listing 6.38 Plotting resultsimport matplotlib.pyplot as pltloss = history.history['loss']val_loss = history.history['val_loss']epochs = range(1, len(loss) + 1)plt.figure()plt.plot(epochs, loss, 'bo', label='Training loss')plt.plot(epochs, val_loss, 'b', label='Validation loss')plt.title('Training and validation loss')plt.legend()plt.show()
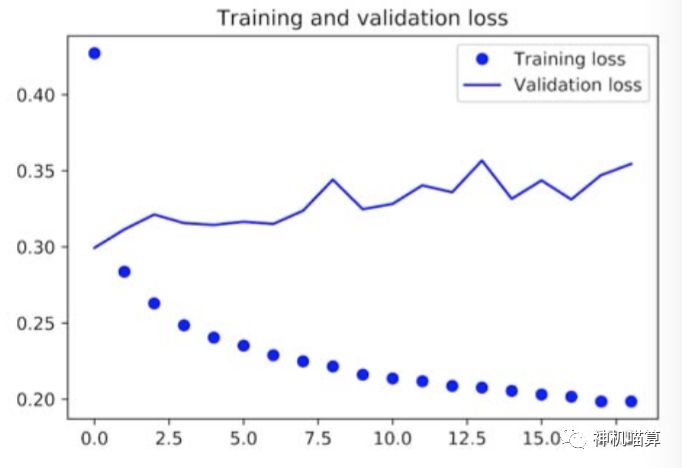
图6.20 简单的致密连接的网络模型在天气预报任务上训练和验证的损失曲线
验证集上的一些损失值接近非机器学习的基线,但是不很稳定。首先,这里显示了基线的价值:基线方法并不是那么容易超越的。常识性的基线方法包含了许多机器学习模型没有学到的、有价值的信息。
你可能会犯嘀咕,如果存在从数据集到目标的一个简单的、性能好的模型,那为什么你训练模型的过程没有学习到呢?这是因为你想得到的简单解决方法与训练设置不符。你正在寻找的模型空间,也即模型假设空间,是两个layer网络参数配置的所有可能的空间。这些网络模型已经相当复杂了。当你用复杂的模型空间寻找一个简单的解决方法,那是学习不到这个简单的、性能好的基线模型。这是机器学习普遍会遇到的问题:除了学习算法是硬编码来找特定的简单模型外,参数型学习算法对于简单问题有时也会找不到简单的解决方案。
6.3.5 RNN基线模型
第一个全联接方法表现的不好,这并不意味着机器学习解决不了该问题。前面的方法首先打平时序数据,这导致输入数据的时间特性丢失。下面来观察下数据本身:序列数据具有顺序和因果关系。你可以尝试一个循环序列处理模型,它可以完美的拟合序列数据。主要是因为它能挖掘数据点之间的时间顺序,而前一个方法忽略了这点。
下面使用Chung在2014年开发的GRU layer(替代,前面小节中介绍的LSTM layer)。GRU(Gated recurrent unit)保留了LSTM的基本思想,但是其运行更简单(虽然GRU可能没有LSTM的表达能力强)。机器学习中你会经常看到计算成本和学习表征能力之间的平衡博弈。
#Listing 6.39 Training and evaluating a GRU-based modelfrom keras.models import Sequentialfrom keras import layersfrom keras.optimizers import RMSpropmodel = Sequential()model.add(layers.GRU(32, input_shape=(None, float_data.shape[-1])))model.add(layers.Dense(1))model.compile(optimizer=RMSprop(), loss='mae')history = model.fit_generator(train_gen,steps_per_epoch=500,epochs=20,validation_data=val_gen,validation_steps=val_steps)
下面的图6.21显示了上述模型的结果,明显看起来好多了。从图中我们发现,其结果明显打败常识性基线方法。也证明了,对于时序问题,这种循环网络的机器学习的价值比致密连接网络要好。
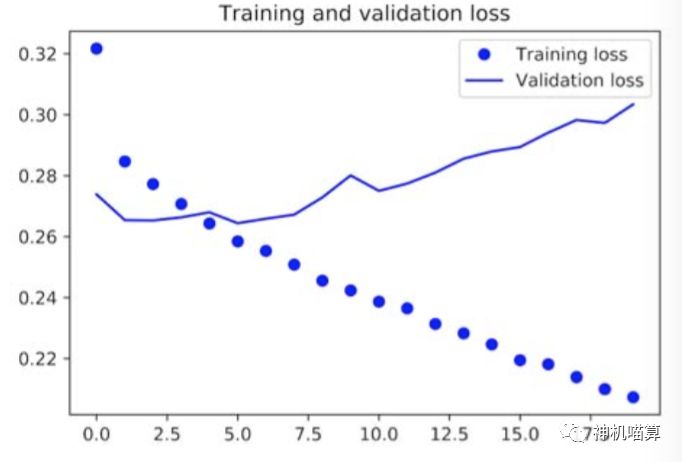
图6.21 GRU在天气预报上的训练集和验证集的损失曲线
新验证集的MAE为~0.265(有点过拟合),还原归一化得到平均绝对值误差为2.35 ̊C。这相比于初始误差2.57 ̊C有相当大的进步,但是仍然有较大的提升空间。
未完待续。。。
Enjoy!
翻译本书系列的初衷是,觉得其中把深度学习讲解的通俗易懂。不光有实例,也包含作者多年实践对深度学习概念、原理的深度理解。最后说不重要的一点,François Chollet是Keras作者。
声明本资料仅供个人学习交流、研究,禁止用于其他目的。如果喜欢,请购买英文原版。
上述内容加入了个人的理解和提炼(若有引起不适,请阅读原文),希望能用通俗易懂、行文流畅的表达方式呈现给新手。
侠天,专注于大数据、机器学习和数学相关的内容,并有个人公众号:bigdata_ny分享相关技术文章。
若发现以上文章有任何不妥,请联系我。







