排列组合算法

Java有货 2020-10-15

904

点击上方「Java有货」关注我们

技术交流群添加方式

添加小编微信:372787553，备注:进群

带您进入Java技术交流群

1. 排列组合公式

我们知道，排列个数的计算公式如下：

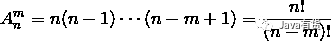
组合个数的计算公式如下：

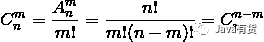
计算排列或组合的数量，通过上面的公式就很容易就算出来了，其Java的实现如下

2. Java 版实现

  /**
   * 计算阶乘数，即n! = n * (n-1) * ... * 2 * 1
   * @param n
   * @return
   */
  private static long factorial(int n) {
    return (n > 1) ? n * factorial(n - 1) : 1;
  }


  /**
   * 计算排列数，即A(n, m) = n!/(n-m)!
   * @param n
   * @param m
   * @return
   */
  public static long arrangement(int n, int m) {
    return (n >= m) ? factorial(n) / factorial(n - m) : 0;
  }


  /**
   * 计算组合数，即C(n, m) = n!/((n-m)! * m!)
   * @param n
   * @param m
   * @return
   */
  public static long combination(int n, int m) {
    return (n >= m) ? factorial(n) / factorial(n - m) / factorial(m) : 0;
  }

有时候，我们不仅需要知道排列或组合的数量，而且需要知道有哪些排列或组合，并列举出所有的排列或组合，人工列举工作量大而且容易出错，那么，如何利用计算机帮忙列举出所有的这些排列或组合呢？
（1）排列
采用递归即可枚举出所有的排列情况，相关Java实现如下：

  /**
   * 排列选择（从列表中选择n个排列）
   * @param dataList 待选列表
   * @param n 选择个数
   */
  public static void arrangementSelect(String[] dataList, int n) {
    System.out.println(String.format("A(%d, %d) = %d", dataList.length, n, arrangement(dataList.length, n)));
    arrangementSelect(dataList, new String[n], 0);
  }


  /**
   * 排列选择
   * @param dataList 待选列表
   * @param resultList 前面（resultIndex-1）个的排列结果
   * @param resultIndex 选择索引，从0开始
   */
  private static void arrangementSelect(String[] dataList, String[] resultList, int resultIndex) {
    int resultLen = resultList.length;
    if (resultIndex >= resultLen) { // 全部选择完时，输出排列结果
      System.out.println(Arrays.asList(resultList));
      return;
    }


    // 递归选择下一个
    for (int i = 0; i < dataList.length; i++) {
      // 判断待选项是否存在于排列结果中
      boolean exists = false;
      for (int j = 0; j < resultIndex; j++) {
        if (dataList[i].equals(resultList[j])) {
          exists = true;
          break;
        }
      }
      if (!exists) { // 排列结果不存在该项，才可选择
        resultList[resultIndex] = dataList[i];
        arrangementSelect(dataList, resultList, resultIndex + 1);
      }
    }
  }

（2）组合
采用递归即可枚举出所有的排列情况，相关Java实现如下：

  /**
   * 组合选择（从列表中选择n个组合）
   * @param dataList 待选列表
   * @param n 选择个数
   */
  public static void combinationSelect(String[] dataList, int n) {
    System.out.println(String.format("C(%d, %d) = %d", dataList.length, n, combination(dataList.length, n)));
    combinationSelect(dataList, 0, new String[n], 0);
  }


  /**
   * 组合选择
   * @param dataList 待选列表
   * @param dataIndex 待选开始索引
   * @param resultList 前面（resultIndex-1）个的组合结果
   * @param resultIndex 选择索引，从0开始
   */
  private static void combinationSelect(String[] dataList, int dataIndex, String[] resultList, int resultIndex) {
    int resultLen = resultList.length;
    int resultCount = resultIndex + 1;
    if (resultCount > resultLen) { // 全部选择完时，输出组合结果
      System.out.println(Arrays.asList(resultList));
      return;
    }


    // 递归选择下一个
    for (int i = dataIndex; i < dataList.length + resultCount - resultLen; i++) {
      resultList[resultIndex] = dataList[i];
      combinationSelect(dataList, i + 1, resultList, resultIndex + 1);
    }
  }

3、测试
（1）完整的测试代码如下

/**
 * 从n个数里取出m个数的排列或组合算法实现
 * @author chengesheng
 * @date 2016年9月28日 下午3:18:34
 */
import java.util.Arrays;
public class MathTest {


  public static void main(String[] args) {
    arrangementSelect(new String[] {
        "1", "2", "3", "4"
    }, 2);
    combinationSelect(new String[] {
        "1", "2", "3", "4", "5"
    }, 3);
  }


  /**
   * 排列选择（从列表中选择n个排列）
   * @param dataList 待选列表
   * @param n 选择个数
   */
  public static void arrangementSelect(String[] dataList, int n) {
    System.out.println(String.format("A(%d, %d) = %d", dataList.length, n, arrangement(dataList.length, n)));
    arrangementSelect(dataList, new String[n], 0);
  }


  /**
   * 排列选择
   * @param dataList 待选列表
   * @param resultList 前面（resultIndex-1）个的排列结果
   * @param resultIndex 选择索引，从0开始
   */
  private static void arrangementSelect(String[] dataList, String[] resultList, int resultIndex) {
    int resultLen = resultList.length;
    if (resultIndex >= resultLen) { // 全部选择完时，输出排列结果
      System.out.println(Arrays.asList(resultList));
      return;
    }


    // 递归选择下一个
    for (int i = 0; i < dataList.length; i++) {
      // 判断待选项是否存在于排列结果中
      boolean exists = false;
      for (int j = 0; j < resultIndex; j++) {
        if (dataList[i].equals(resultList[j])) {
          exists = true;
          break;
        }
      }
      if (!exists) { // 排列结果不存在该项，才可选择
        resultList[resultIndex] = dataList[i];
        arrangementSelect(dataList, resultList, resultIndex + 1);
      }
    }
  }


  /**
   * 组合选择（从列表中选择n个组合）
   * @param dataList 待选列表
   * @param n 选择个数
   */
  public static void combinationSelect(String[] dataList, int n) {
    System.out.println(String.format("C(%d, %d) = %d", dataList.length, n, combination(dataList.length, n)));
    combinationSelect(dataList, 0, new String[n], 0);
  }


  /**
   * 组合选择
   * @param dataList 待选列表
   * @param dataIndex 待选开始索引
   * @param resultList 前面（resultIndex-1）个的组合结果
   * @param resultIndex 选择索引，从0开始
   */
  private static void combinationSelect(String[] dataList, int dataIndex, String[] resultList, int resultIndex) {
    int resultLen = resultList.length;
    int resultCount = resultIndex + 1;
    if (resultCount > resultLen) { // 全部选择完时，输出组合结果
      System.out.println(Arrays.asList(resultList));
      return;
    }


    // 递归选择下一个
    for (int i = dataIndex; i < dataList.length + resultCount - resultLen; i++) {
      resultList[resultIndex] = dataList[i];
      combinationSelect(dataList, i + 1, resultList, resultIndex + 1);
    }
  }


  /**
   * 计算阶乘数，即n! = n * (n-1) * ... * 2 * 1
   * @param n
   * @return
   */
  public static long factorial(int n) {
    return (n > 1) ? n * factorial(n - 1) : 1;
  }


  /**
   * 计算排列数，即A(n, m) = n!/(n-m)!
   * @param n
   * @param m
   * @return
   */
  public static long arrangement(int n, int m) {
    return (n >= m) ? factorial(n) / factorial(n - m) : 0;
  }


  /**
   * 计算组合数，即C(n, m) = n!/((n-m)! * m!)
   * @param n
   * @param m
   * @return
   */
  public static long combination(int n, int m) {
    return (n >= m) ? factorial(n) / factorial(n - m) / factorial(m) : 0;
  }
}

（2）测试结果

A(4, 2) = 12
[1, 2]
[1, 3]
[1, 4]
[2, 1]
[2, 3]
[2, 4]
[3, 1]
[3, 2]
[3, 4]
[4, 1]
[4, 2]
[4, 3]
C(5, 3) = 10
[1, 2, 3]
[1, 2, 4]
[1, 2, 5]
[1, 3, 4]
[1, 3, 5]
[1, 4, 5]
[2, 3, 4]
[2, 3, 5]
[2, 4, 5]
[3, 4, 5]