华为机试：迷宫问题

Hello，小伙伴们，我是知道。

之前在面试华为的时候，在力扣上刷了一些题，根据hr提示，有几题是重点题型，其中有一题就是迷宫问题，今天简单介绍一下：

1. 问题

迷宫问题:

给一个二维列表，表示迷宫(0表示通道，1表示围墙)

给出算法，求一条走出迷宫的路径。

maze = [
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
[1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 1, 1, 0, 1], 
[1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
]

2. 解决思路

2.1 栈——深度优先搜索(回溯法)

思路: 从一个节点开始，任意找下一个能走的点，当找不到能走的点时，退回上一个点寻找是否有其他方向的点  ,并使用栈存储当前路径。

2.2 代码

maze = [
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
[1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 1, 1, 0, 1], 
[1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
]

dirs = [
    lambda x,y: (x - 1, y),   # 上
    lambda x,y: (x, y + 1),   # 右
    lambda x,y: (x + 1, y),   # 下
    lambda x,y: (x, y - 1)    # 左 
]


def maze_path(x1, y1, x2, y2):
    stack = []
    stack.append((x1, y1))
    while(len(stack) > 0):   # 栈空表示没有路
        current_node = stack[-1]  # 当前节点
        # 判断当前是否走到了终点
        if current_node[0] == x2 and current_node[1] == y2:
            # 把路径打印出来
            for p in stack:
                print(p)
            return True

        # x, y四个方向: x, y-1; x+1, y; x, y+1; x-1, y
        for dir in dirs:
            next_node = dir(current_node[0], current_node[1])
            # 如果下一个节点能走
            if maze[next_node[0]][next_node[1]] == 0:
                stack.append(next_node)
                maze[next_node[0]][next_node[1]] = 2  # 表示已经走过
                break
        else:  # 如果4个位置都不能走了，该点就出栈
            maze[current_node[0]][current_node[1]] = 2
            stack.pop()
    else:
        print("无路可走，走投无路")
        return False

maze_path(1, 1, 8, 8)

结果:

(1, 1)
(1, 2)
(2, 2)
(3, 2)
(3, 1)
(4, 1)
(5, 1)
(5, 2)
(5, 3)
(6, 3)
(6, 4)
(6, 5)
(5, 5)
(4, 5)
(4, 6)
(4, 7)
(3, 7)
(3, 8)
(4, 8)
(5, 8)
(6, 8)
(7, 8)
(8, 8)

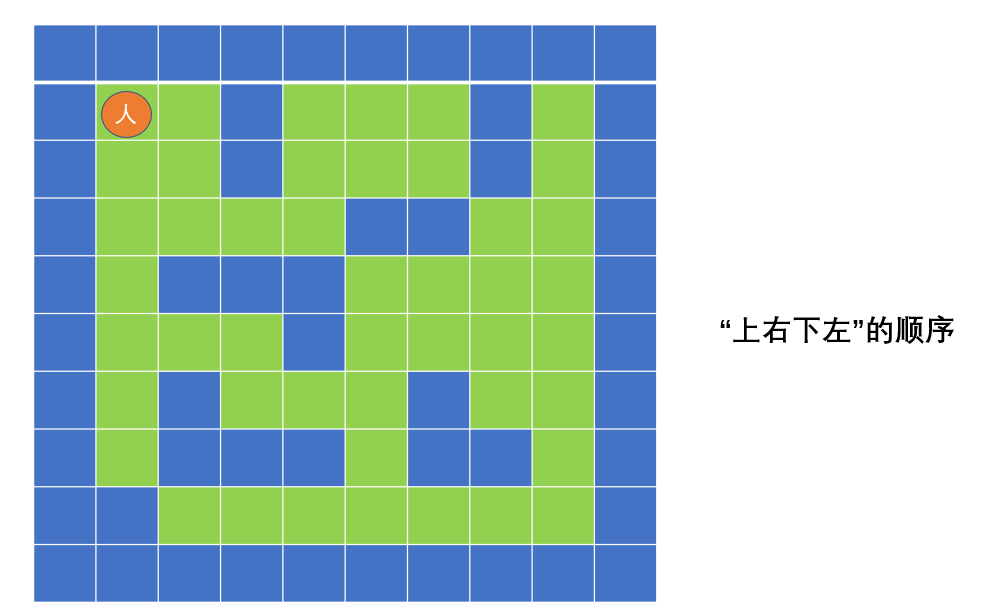
路线为:

有人可能会认为这条路太麻烦了，太长了，这就跟我们的dirs
方向优先权有关了，具体的原理就涉及到了深度优先搜索的知识点了，而深度优先会存在这个问题，但是广度优先不会，因为广度优先的四个方向不存在优先级。如果我们把方向优先级改为：

dirs = [
    lambda x,y: (x + 1, y),   # 下
    lambda x,y: (x, y - 1),    # 左
    lambda x,y: (x - 1, y),   # 上
    lambda x,y: (x, y + 1)   # 右
]

那么结果就是和广度优先搜索一样，是最短路径了：

(1, 1)
(2, 1)
(3, 1)
(4, 1)
(5, 1)
(5, 2)
(5, 3)
(6, 3)
(6, 4)
(6, 5)
(7, 5)
(8, 5)
(8, 6)
(8, 7)
(8, 8)

2.2 队列——广度优先搜索

思路:从一个节点开始，寻找所有接下来能继续走的点，继续不断寻找，直到找到出口。使用队列存储当前正在考虑的节点区别:用队列和栈解决迷宫问题最大的区别在于，栈利用了深度优先搜索的思想，而队列利用了广度优先搜索的思想

代码：

'''
TOPIC: 用队列解决迷宫问题
author: Blue
time: 2020-08-12
QQ: 2458682080
'''

from collections import deque
maze = [
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
[1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 1, 1, 0, 1], 
[1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
]

dirs = [
    lambda x,y: (x, y - 1), 
    lambda x,y: (x + 1, y), 
    lambda x,y: (x, y + 1), 
    lambda x,y: (x - 1, y)
]

def print_r(path):
    cur_node = path[-1]
    real_path = []
    while cur_node[2] != -1:
        real_path.append(cur_node[0:2])
        cur_node = path[cur_node[2]]
    real_path.append(cur_node[0:2])
    real_path.reverse()
    for node in real_path:
        print(node)



def maze_path_queue(x1, y1, x2, y2):
    queue = deque()
    queue.append((x1, y1, -1))
    path = []
    # 队空了，没有路
    while len(queue) > 0:
        cur_node = queue.popleft()
        path.append(cur_node)
        if cur_node[0] == x2 and cur_node[1] == y2:
            print_r(path)
            return True

        for dir in dirs:
            next_node = dir(cur_node[0], cur_node[1])
            if maze[next_node[0]][next_node[1]] == 0:
                # 后续节点进队，记录哪个节点带它来的
                queue.append((next_node[0], next_node[1], len(path)-1))
                maze[next_node[0]][next_node[1]] = 2

    else:
        print("走投无路，无路可走")
        return False

maze_path_queue(1, 1, 8, 8)

结果：

(1, 1)
(2, 1)
(3, 1)
(4, 1)
(5, 1)
(5, 2)
(5, 3)
(6, 3)
(6, 4)
(6, 5)
(7, 5)
(8, 5)
(8, 6)
(8, 7)
(8, 8)

路线为:

其实用队列解决和用栈解决的代码中，最大却别在于这里:

# 用队列解决
 for dir in dirs:
            next_node = dir(cur_node[0], cur_node[1])
            if maze[next_node[0]][next_node[1]] == 0:
                # 后续节点进队，记录哪个节点带它来的
                queue.append((next_node[0], next_node[1], len(path)-1))
                maze[next_node[0]][next_node[1]] = 2

# 用栈解决
for dir in dirs:
            next_node = dir(current_node[0], current_node[1])
            # 如果下一个节点能走
            if maze[next_node[0]][next_node[1]] == 0:
                stack.append(next_node)
                maze[next_node[0]][next_node[1]] = 2  # 表示已经走过
                break

用栈解决的加了break
，用队列解决没有加break
。 栈——深度优先搜索: 只要在当前位置current_node
找到一点next_node
可以继续往下的，就直接将current_node
改为next_node
，就这样先把一条路走到黑，如果最后发现走不通，再返回，走其他路。 队列——广度优先搜索: 在当前位置current_node
找到所有可以走的next_node
，然后再将所有的next_node
的下一步可以走的点也找出来，直到找到终点！