机器学习常见评价指标

在建模的时候，不论是一般机器学习还是深度学习，都要有评价指标进行模型效果的衡量，评价指标是对于一个模型效果的数值型量化。一般来说，评价指标分为分类问题和回归问题，下面知道就分别介绍两类问题的评价指标。

1 分类问题常见评价指标

1.1 基础知识

分类问题中，又可以分为二分类和多分类问题：

• 二分类问题：accuracy
  、precision
  、recall
  、F1-score
  、AUC
  、ROC
  曲线
• 多分类问题：accuracy
  、宏平均、微平均、F1-score
  

在介绍各评价指标的计算方法之前，还要介绍一下TP
(True Positive
)、TN
(True Negative
)、FP
(False Positive
)、FN
(False Negative
)

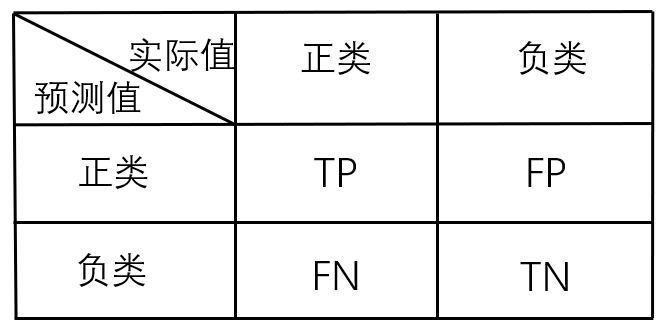
TP
表示将实际标签为正的样本判断为正的样本数量或者比例；FP
表示将实际标签为负的样本判断为正的样本数量或者比例；FN
表示将实际标签为正的样本判断为负的样本数量或者比例；TN
表示将实际标签为负的样本判断为负的样本数量或者比例。

有时候很容易记混，所以我自己有个记忆方法：第一个字母代表是否判断正确，第二个字母代表样本的预测值。

1.2 各指标计算方法

现在网上很多人把precision
和accuracy
、精确率和准确率混为一谈，这其实是错误的，如下图：

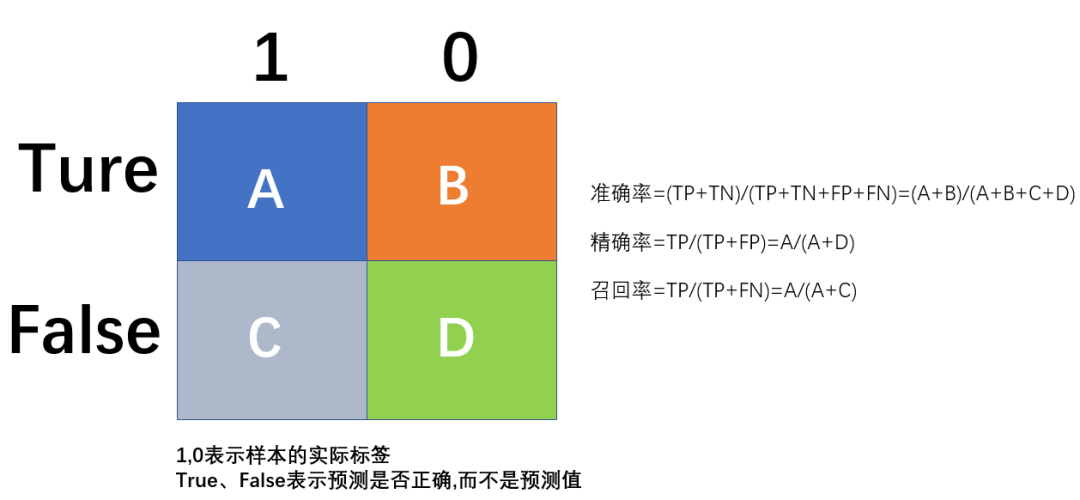
(1) 准确率(Accuracy)

准确率(Accuracy
)表示所有的预测样本中，预测正确的比例，计算方法如下：

(2) 精确率(Precision)

精确率(Precision
)表示预测为正样本的样本中，实际为正样本的比例。精确率考虑的是正样本被预测正确的比例。计算方法如下：

(3) 召回率(Recall)

召回率(Recall
)表示实际为正样本的样本中，预测为正样本的比例。召回率考虑的是正样本的召回的比例。计算方法如下：

(4) F1-socre

其实精确率和召回率之间是存在矛盾的，很多场景下，模型最终结果往往实在精确率和召回率之间找到平衡点。F1-socre
是兼顾精确率和召回率的参数，之所以使用调和平均而不是算术平均，是因为在算术平均中，任何一方对数值增长的贡献相当，任何一方对数值下降的责任也相当；而调和平均在增长的时候会偏袒较小值，也会惩罚精确率和召回率相差巨大的极端情况，很好地兼顾了精确率和召回率。F1-socre
计算方法如下：

(5)AUC值以及ROC曲线

AUC(Area Under ROC Curve)
值为ROC
曲线下面积，表示模型或预测结果的可靠性，越接近1
，可靠性越高。

(6) Macro avg(宏平均)

Macro avg
(宏平均)在为每一指标计算时，会对每一类别赋予相同的权重，即每个类别的指标的算术平均值。可能理解起来比较抽象，看以下例子：

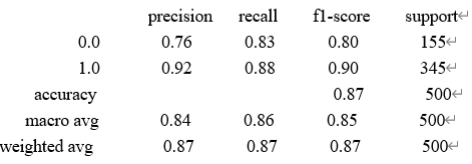
比如macro avg of precision = [precision(C=0)+precision(C=1) ]/ 2 = (0.76+0.92)/2=0.84

(7) Micro avg(微平均)

Micro avg
(微平均)为所有类别的准确率，即所有预测正确的样本数量的比例:

上图中并没有Micro-avg
，但并不妨碍我们计算：

预测对的正样本TP=345*0.88

预测对的负样本TN=155*0.83

(8) weighted-avg(权重平均)

weighted-avg
(权重平均)是因为宏平均在计算的时候，每个类别赋予的权重相同，但如果存在样本不平衡的情况，那这种方法就不适合了，所以权重平均便根据每个类别的样本数量，赋予不同的权重。权重平均其实就是所有类别的F1
加权平均，主要针对F1
值，计算方式如下：

2  回归(预测)问题常见评价指标

回归或预测问题常见评价指标如下：

平均绝对误差(Mean Absolute Error，MAE)
，均方误差(Mean Squared Error，MSE)
，均方根误差(Root Mean Square Error, RMSE)
，均方根误差(Root Mean Squared Error)
, R2(R-Square)

2.1 平均绝对误差(Mean Absolute Error，MAE)

平均绝对误差(Mean Absolute Error，MAE)
是预测值与真实值之差的绝对值，反映了预测值与真实值误差的实际情况，计算公式为

MAE的计算在sklearn中调用代码为:

from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(y_true, y_pred) # y_true为真实值,y_pred为预测值

2.2 均方误差(Mean Squared Error, MSE)

均方误差(Mean Squared Error, MSE)
是预测值与真实值之差平方的期望值。MSE的值越小，说明预测模型描述实验数据具有越好的精确度。计算公式为

MSE的计算在sklearn中调用代码为:

from sklearn.metrics import mean_squared_error
mse = mean_squared_error(y_true, y_pred) # y_true为真实值,y_pred为预测值

2.3 均方根误差(Root Mean Square Error, RMSE)

均方根误差(Root Mean Square Error, RMSE)
是MSE
的平方根，为预测值和真实值差异的样本标准差。均⽅根误差为了说明样本的离散程度，拟合时，RMSE
越小越好。均方根误差与标准差的研究对象不同，均方根误差用来衡量预测值与真实值之间的偏差，而标准差用于衡量一组数据的离散程度。计算公式为

其中，SSE(error sum of squares)
为残差平方和。

RMSE的计算在sklearn中调用代码为:

from sklearn.metrics import mean_squared_error
mse = mean_squared_error(y_true, y_pred) # y_true为真实值,y_pred为预测值
rmse = Sqrt(mse)

2.4 R平方值(R-Squared)

R平方值(R-Squared
)又称拟合优度，反映了回归模型对数据的拟合程度，取值范围为(0,1]
，越接近1
，表明用x
的变化来解释y
值变化的部分就越多,回归的拟合程度就越好。

当然，sklearn中同样可以直接调用:

from sklearn.metrics import r2_score
r2 = r2_score(y_true, y_pred) # y_true为真实值,y_pred为预测值