Bw树索引结构
Bw树的树节点结构与传统B+树相似,内部索引节点包含有序键值对(键值和指针)指向下一层的树节点,叶节点包含键值对(键值和记录)。此外,每个页还包含:1. low-key,表示能存在这个页上的最小键值信息;2. high-key,表示能存在这个页上的最大键值信息;3. side-link,指向同一层次右边的兄弟节点,与B-link树相似。然而,两种不同的特征使得Bw树区别于传统B+树。
首先,Bw树的树节点是逻辑性的,并不占用固定的物理位置。逻辑地址到物理地址的映射关系,通过键值对的方式存储在Bw的核心模块 - 地址映射表(mapping table)中。如下图所示,地址映射表将数据页的逻辑地址映射到真实的物理地址。逻辑地址通过页描述符PID(page identifier)来表示,而物理地址分为两类数据:1. 闪存地址,表示这个页在闪存中的起始地址;2.内存指针,表示这个页在内存中的起始地址。在Bw树中,树节点与树节点之间的链接关系用PID来表示,而不是物理指针。任何一个访问树节点的操作首先需要访问地址映射表,将PID信息转化成树节点的真实物理地址。因此,在每次更新数据页到闪存的过程中,因为树节点间相连接的PID信息并没有发生变化,所以Bw树不需要更新到树的根节点,它只需要将新的树节点的地址信息更新到地址映射表中。
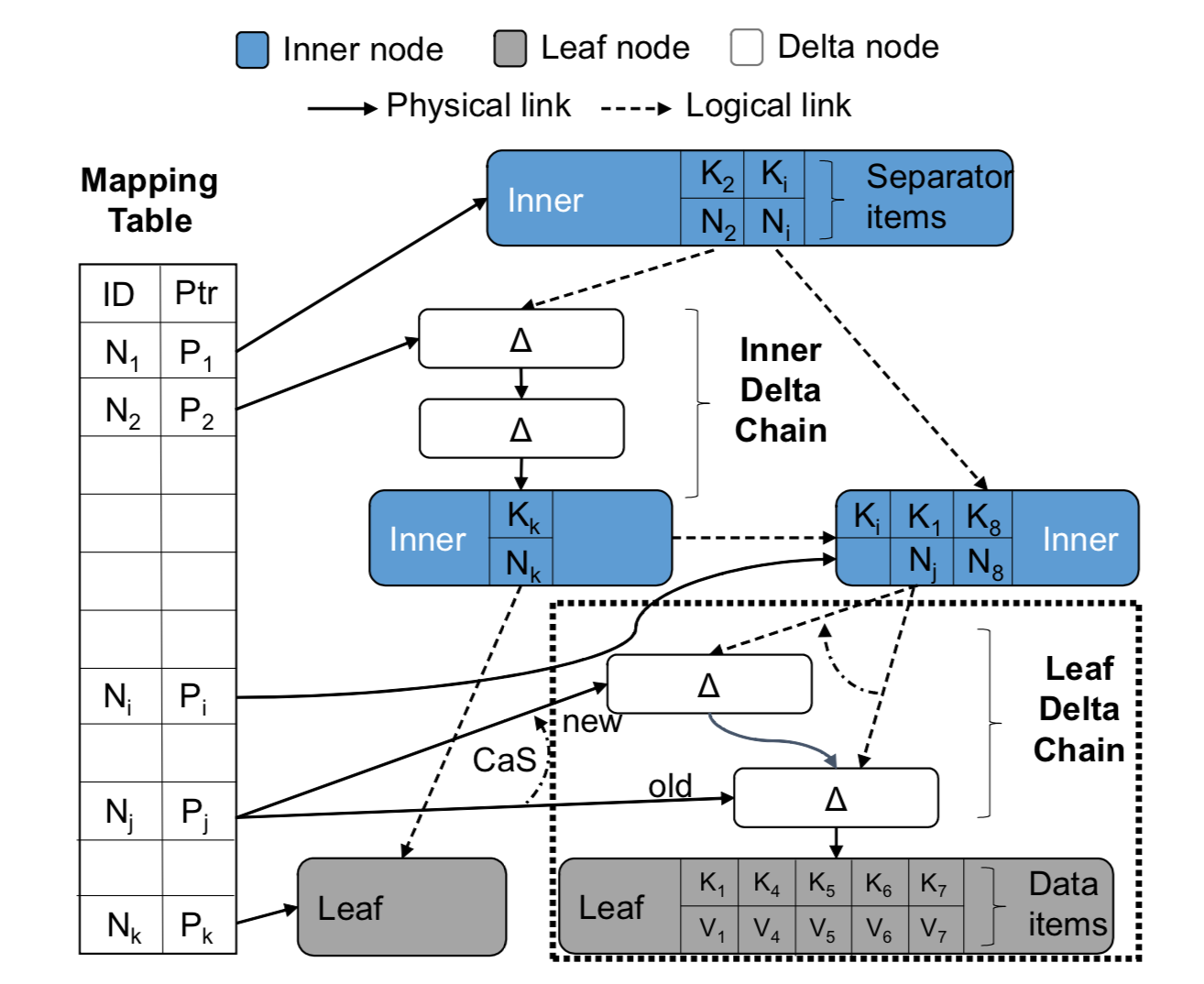
其次,Bw树节点的大小是可伸缩的,这种设计方式使得Bw树在存储真实树节点时具有更高的灵活性。如上图所示,所有的更新操作都不是本地更新的(不会直接修改原数据),而是会创建一个增量记录(delta record,描述修改信息)。每个增量记录包含一个物理指针,指向现存的页数据。然后,Bw树将将增量记录记录到映射表中,增量记录就成为了该数据页的新地址。所以,一个逻辑树节点包含原数据和一系列的增量记录,形成一个单链表结构(delta chain)。这种异地更新机制避免了对处理器缓存中源数据的修改,提高了处理器缓存的效率。此外,这也意味着它没有严格的树节点大小限制,可以在合适的时候再执行分裂操作。下图描述了异地更新所需的关键元信息。


显然,在将增量记录的地址更新到地址映射表前,其它线程不会看到更新操作的中间状态。这一特性使得Bw树可以利用原子操作(Compare-And-Swap,CAS),实现latch-free的树操作。
Bw树的latch-free操作 - 单个树节点的操作
本文首先从最简单的树操作入手,这指的是记录的插入/删除/更新/查询操作,它们只会针对单个数据页产生修改。如下图(a)所示,虚线表示页P的旧地址,实线表示表示更新操作产生的指向原数据的增量记录D。在叶节点层,增量记录包含插入/更新/删除操作三种类型。插入/更新操作的增量记录包含完整的插入信息,而删除操作的增量记录只包含删除的键值信息。此外,每个增量记录包含一个LSN号,这个LSN号将被用于事务恢复机制中,这将在后文中详细叙述。
Bw树利用CAS操作将增量记录的新内存地址记录到映射表中。如果CAS操作成功,这个增量记录就变成了这个数据页的新物理“根”地址,因此就更新了这个页。如果CAS操作失败,这说明有其它线程正在修改这个数据页,所以它会重做该操作。CAS操作保证同时修改该数据页的多个线程中只有一个胜利者,因此保证了操作的正确性。
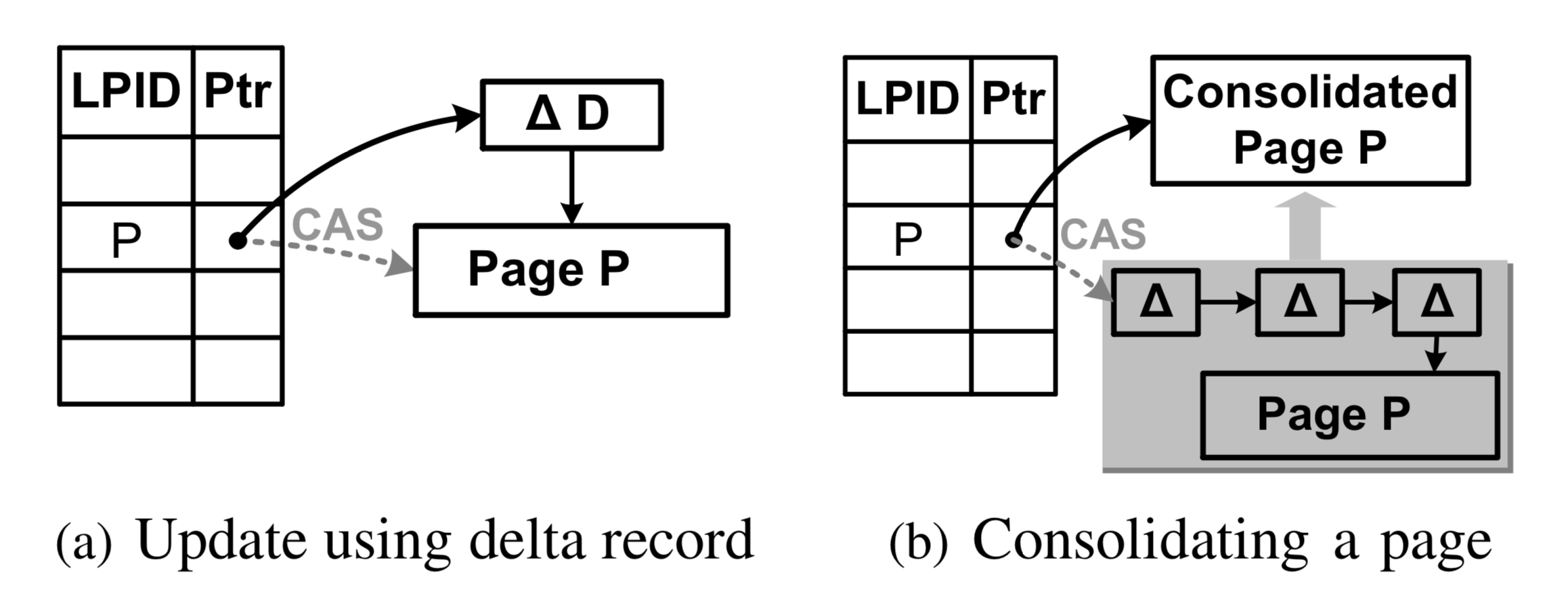
对于页的搜索操作,它需要遍历增量记录链,直到找到第一个目标键值对。如果在增量记录链中没有找到目标键值对,它会在原来的数据页中执行二分查找操作。显然,过长的增量记录链会影响Bw树读操作的性能和存储空间的利用率。所以,当访问增量记录链的操作发现链长超过某个阈值时,它会在执行完操作后执行增量记录链和原数据页的合并操作(consolidate)。
一个页的合并操作同样是通过CAS操作实现的。如上图(b)所示,Bw树执行一个合并操作,虚线表示页P的原地址,而实线表示页P合并后的新地址。Bw树首先创建一个新页,将页P的原数据和所有增量记录合并到这个新页,然后通过CAS操作记录到地址映射表中。如果成功了,它通过垃圾回收,处理原来的页信息和增量记录。如果失败了,说明有其它操作在更新或者合并数据页P,所以该线程会释放新页并放弃这个操作,后续访问该增量记录链的操作会视情况再次执行合并操作。
对于范围查找操作,它往往会指定一个键值范围:(low key,high key)。在Bw树中,范围查找操作会维护一个游标,记录目前搜索的状态信息。当第一次访问包含目标信息的数据页时,Bw树会构建一个记录向量,包含这个页上范围操作所需的所有记录。当该数据页没有被修改时,这可以加速获取下一个键值对信息。当然,在从向量数组中获取记录之前,Bw树会检查是否有其它更新操作影响了这个子查询结果。如果是,Bw树会重建向量数组。
因为Bw树没有用锁保护正在访问的数据对象,所以它也采用epoch-based reclamation机制[7]避免回收正在被访问的数据对象。原理简单来说就是将删除操作分为逻辑删除和物理删除两个步骤,只有在确保一个对象没有被任何操作访问时才可以回收这个对象的物理空间。由于篇幅和时间所限,本文在后续的文章中会单独分析这类垃圾处理机制的原理和实现过程,在此不做赘述,感兴趣的读者可以参考引用[7]这篇文章。
Bw树的latch-free操作 - 多个树节点的操作
Latch-free的并发控制机制不仅使用在单数据页的操作中,而且也用在涉及多个数据页的树节点分裂/合并操作中。当Bw树的逻辑节点大小超出或者低于某个阈值时,这个逻辑节点需要分裂成两个逻辑节点或者与其它兄弟节点合并成一个逻辑节点。这类复杂操作称之为SMO(Index structure modification operation)操作。然而,一个CAS操作无法保证多个数据页的原子性修改。
为了解决这个问题,Bw树借鉴了B-link树的设计,简化了SMO操作(前文《B+树并发控制机制的前世今生》中已经详细分析过B-link树)。以页分裂操作为例,Bw树可以将一个树节点分裂操作分解成两个原子性的“half-split”操作。首先它在子节点层次(叶节点)执行原子性的分裂操作,其次它对父节点执行原子性的插入操作(指向新分裂节点的键值对信息)。如果父节点依然需要分裂,这个过程会可以递归执行。在完成第一次原子性操作后,得益于B-link树结构,即使新分裂的节点还没有插入到父节点中,每个数据页的右指针提供了一种合法的方式去访问新分裂的树节点。具体过程如下:
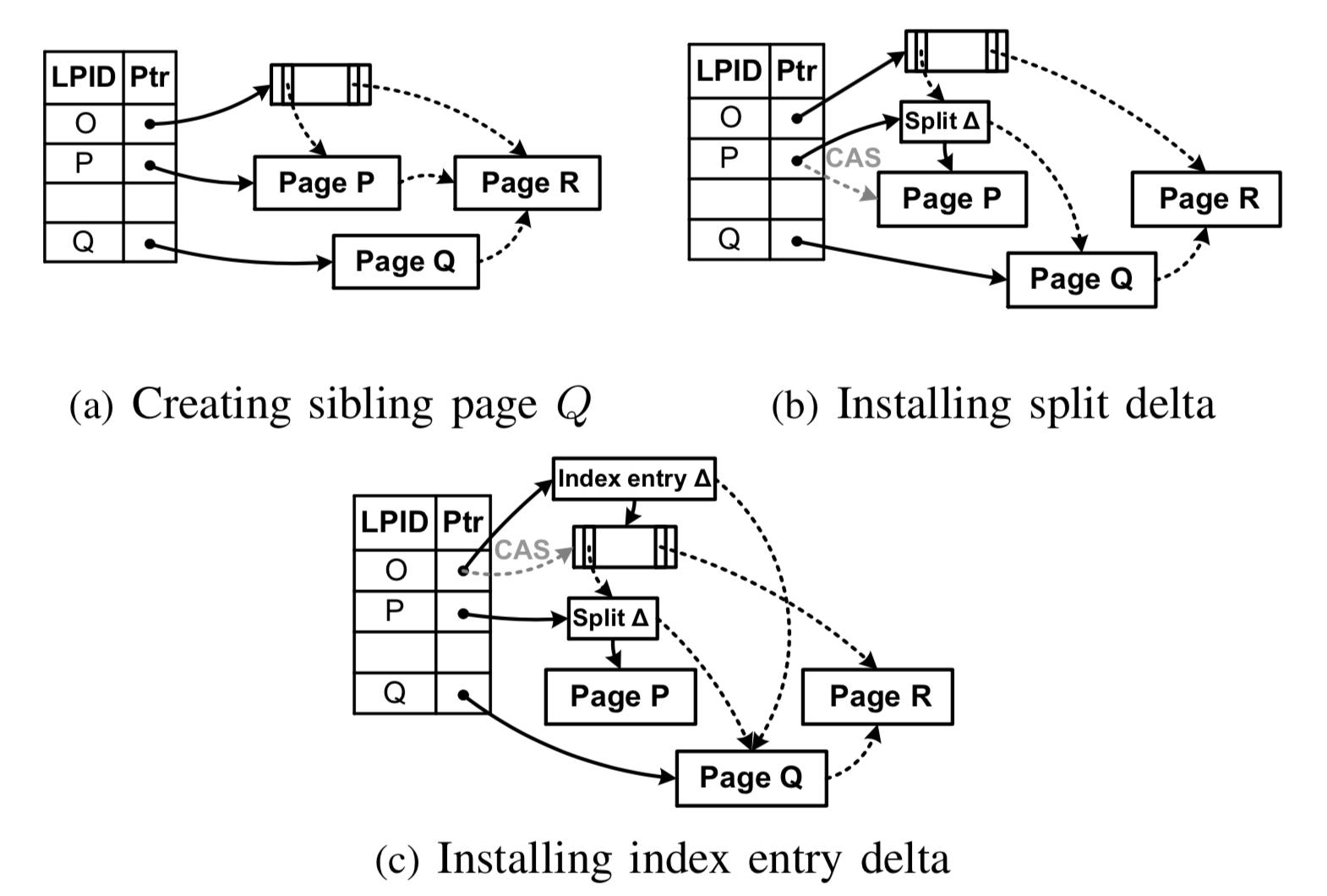
- 子节点的分裂。分为两个步骤:(1) 为了分裂节点P,Bw树会申请一个新节点Q。Q作为P的右兄弟节点, 包含节点P一半的键值对信息,并指向P的原右兄弟节点R。然后,Q的地址信息被记录到地址映射表中。值得注意的是,这个操作不需要使用原子操作(CAS),因为Q目前只会被当前的分裂线程看到。上图(a)中描述了这个场景;(2)修改节点P,删除已经移动到Q的键值对。Bw树会生成一个
分裂增量(split delta),并使用CAS操作加入到节点P的映射表项中。分裂增量包含两部分信息:1. 分裂键值KP,用于表示大于KP的所有键值对已经被移动到其它节点;2. 逻辑指针指向新节点Q。Bw树通过这次CAS操作,判断在split过程中节点P是否被其它线程所修改,如果是则需要重做。自此,Bw树完成了第一个原子操作,上图(b)中描述了这个场景。当上述步骤完成后,即使没有将新的节点Q更新到父节点O中,索引依然是合法的。原因在于所有访问节点Q的数据(键值信息大于KP)的线程首先会访问P,然后根据分裂增量,通过右兄弟指针访问节点Q。 - 父节点的更新。为了让树操作可以直接访问节点Q,Bw树将指向Q的键值对信息插入到P和Q的父亲节点O中,这就是
第二个原子操作。该操作会生成一个索引增量(index delta),它包括:1. 分裂键值KP,用以区分节点P和Q的键值;2. 指向Q的逻辑指针;3.KQ,用以区分节点P和R的键值。Bw树采用和B-link树相似的方式找到父节点(具体看上一篇文章)。即使在父节点被删除的情况,它也能通过epoch-based reclamation判断出父节点的状态,递归到更上层的祖先节点找到合适的父节点。自此,Bw树完成了两个原子操作,上图(c)中描述了这个场景。 因为SMO操作需要2个以上的原子操作,在原子操作之间可能会发生修改相同数据页的更新操作或者其它SMO操作,而SMO操作没有通过锁来避免其它操作看到一个未完成的SMO操作,所以Bw树需要处理SMO操作与有影响的其它SMO/普通更新操作之间的顺序关系,从而使SMO操作整体上像是原子性的。Bw树给出的处理机制是:当某一线程看到未完成的SMO操作时,它会先完成SMO操作,再去执行自己的操作。例如,当其它线程尝试通过兄弟指针访问正确的数据页Q时,它会先完成整个split SMO操作,更新Q的父节点,然后再去执行自己的操作。Bw树通过这种方式,将相互影响的SMO操作与其它操作串行化,避免了很多复杂问题。举两个简单例子:1. 由于Bw树并没有使用锁保护节点P/Q,因此在插入到父节点的过程中,节点P/Q可能被删除,从而导致父节点O指向一个被删除的树节点。通过上述这种方式,这种问题就可以被有效避免。2. 当执行节点P分裂的线程被挂起时,其他线程也可以持续执行,不会因为未完成的P分裂操作而持续等待。这种机制在latch-free的数据结构设计中被广泛使用,称之为the help-along protocol。
此外,当树节点的合法键值对总量少于某个阈值时,它会触发多页之间的合并操作。该操作与分裂操作类似,在此不作赘述,感兴趣的读者可以阅读原文。






