1 研究背景
1.1 死锁检测与消除
分布式环境中的死锁检测比集中式环境中的死锁检测更具挑战性,因为每一个顶点只有整个系统视图的一部分,且 SQL 在并行执行的过程中同时访问数据表的多个部分,每个部分都可能被其他事务锁所阻塞,从而引起一个事务等待多个锁的情况。如表1 所示,当前的死锁检测与消除算法主要有四种:
- 集中式死锁检测,基本思想是选择一个中心节点作为检测器,收集所有节点的锁等待关系,生成全局锁等待图(WFG),应用案例为TiDB[1]。这种方法的缺点是典型应用的锁等待关系通常较为简单,整合所有局部 WFG的开销较大;
- 死锁预防策略,基本思想是在死锁发生之前通过 Wound-Wait,Wait-Die 等策略有选择地杀死事务,应用案例为Google Spanner[2]。这种方法的缺点是大量不会导致死锁的事务被杀掉,用户无法接受;
- 路径推动算法,基本思想是在每个顶点构建局部WFG,每个顶点将其本地WFG发送到多个相邻节点,并重复此过程。直到某个顶点有足够的视图来宣布死锁,应用案例为 CockroachDB[3]。这种方法的缺点是多个顶点会检测到同一个死锁,每个顶点都试图通过杀死一些事务来消除死锁,这可能具有多杀性;
- 边追逐算法,基本思想就是沿着事务 WFG 的边传播具有特殊意义的消息,死锁产生的环路关系最终将导致消息返回到它的发起者处,从而提示死锁的存在,应用案例为 Oracle RAC和 OceanBase[4]。
| 算法类型 | 算法描述 | 应用案例 |
|---|---|---|
| 中心化死锁检测 | 选择一个中心化的死锁检测节点,收集整个系统内的锁等待关系构建WFG并检测死锁 | TiDB[1] |
| 死锁预防策略 | 在死锁产生之前,以Wound-Wait或Wait-Die等策略,悲观地将冲突的事务杀掉 | Google Spanner[2] |
| 路径推动算法 | 节点之间传输并收集局部WFG关系,死锁的产生能够被部分节点检测到 | CockroachDB[3] |
| 边追逐算法 | 依据事务依赖关系向下游节点发送消息,死锁产生的环将通过这些消息被推断出来 | Oracle RAC, OceanBase[4] |
1.2 OceanBase 死锁检测需要的特性
对于OceanBase需要以下三个特性,第一个特性是每个顶点不需要建立整个系统的全局或局部事务等待视图,只需要向事务依赖关系的下游节点发送消息进行死锁检测与消除。第二个特性是一个死锁环路中只有一个顶点检测并消除死锁,避免了死锁中多个事务的回滚。第三个特性是只检测解决真正的死锁问题,不回滚不在死锁关系内的事务。
2 关于 LCL 算法流程的定义
为方便读者的理解,在此仅给出介绍 LCL 算法流程必要的定义,不针对推导证明过程给出详细描述(可通过文章结尾的链接,获取论文全文),定义编号与原文保持一致。
2.1 基础定义
定义Ⅱ.1 (A→B),A→B表示从节点A到节点B的边,物理意义上表示A事务正在等待B事务持有的一些资源。类似的,A(≠B)→B表示A≠B且A→B。
定义Ⅱ.2 (A⇒B),A⇒B表示从节点A到节点B的游走。A⇔B如果A⇒B且B⇒A。
定义Ⅱ.3 (Dist(A, B)),Dist(A, B)代表从节点A到节点B的最短距离。
2.2 环形子图距离
定义 (SCC(A)),SCC(A) 表示WFG中包含A的强连通分量[5]。
定义Ⅱ.6 (USG(scc)),USG(scc)=(VS, ES) 表示强连通分量 scc 的上游子图,其中VS={X∈WFG: X⇒A,A∈scc},ES= {X→T : X∈VS and Y∈VS and X→Y∈WFG }。
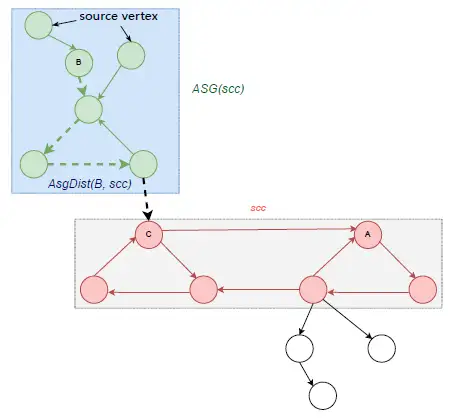
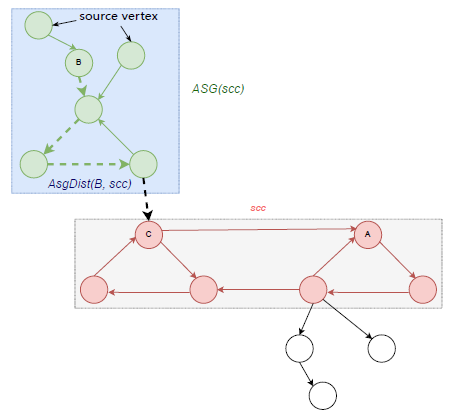
定义Ⅱ.7 (ASG(scc)),ASG(scc)=(VS, ES) 表示强连通分量 scc 的环形子图,其中VS={X∈WFG: X∈USG(scc) and X ∉ scc},ES={X→Y: X∈VS and Y∈ VS and X→Y∈WFG }。
定义Ⅱ.8 (AsgDist(A, scc)),AsgDist(A, scc)=max{m: Exist m distinct vertices Cm(=A), Cm-1, … ,C1 in ASG(scc) and a vertices C0 ∈ scc such that Cm(=A) → Cm-1 → … → C1 → C0 } 表示强连通分量 scc 的环形子图中节点 A 到 scc 的距离。
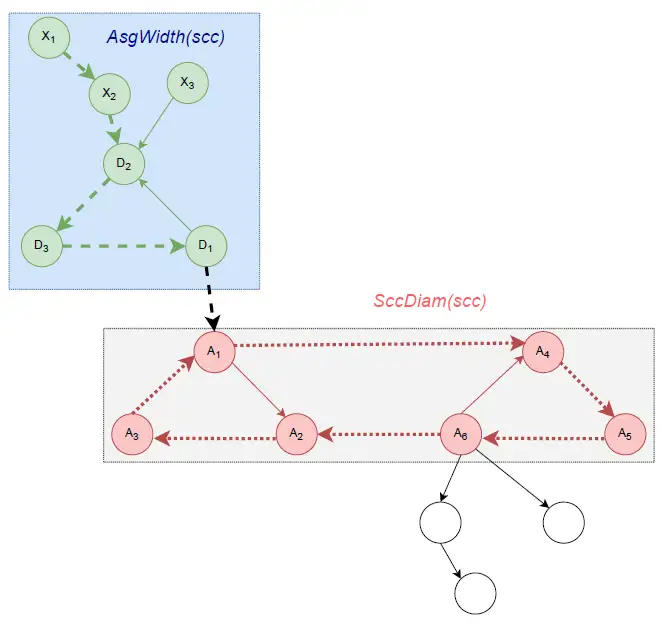
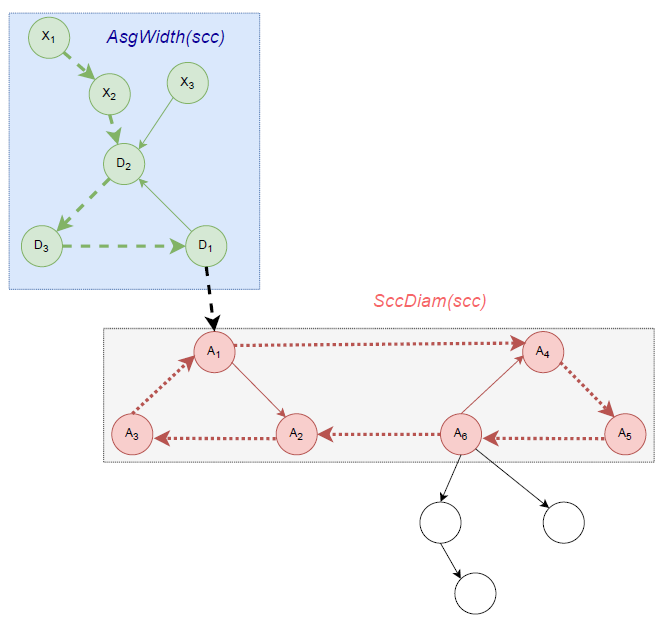
定义Ⅲ.1 (AsgWidth(scc)),AsgWidth(scc):=max{AsgDist(X, scc): X∈USG(scc)} 表示强连通分量 环形子图的宽度。
定义Ⅲ.8 (SccDiam(scc)),SccDiam(scc):=max{Dist(X, Y): X∈scc and Y∈scc} 表示强连通分量scc的直径。
2.3 LCL 算法中的概念及其定义
定义Ⅲ.2/4 (<PrAP,PrID>),PrID 和 PrAP 分别是每个顶点的私有的常量编号和优先级。死锁中具有最大 <PrAP,PrID>的顶点将被杀掉来消除死锁。
定义Ⅲ.3/5 (<PuAP,PuID>),PuID 和 PuAP 是非常量的编号和优先级,初值分别为 PrID 和 PrAP。
定义Ⅲ.6 (LCLV),LCLV 是初始值为零的顶点的锁链长度值。通常 A.LCLV=m 意味着从存在某个顶点到A有一段长度为m的游走。
定义Ⅲ.7 (max{S.LCLV}),S是 WFG 的一个子集,max{S.LCLV}:=max{X.LCLV: X is a vertex in S}。 max{S.<PuAP, PuID>} 和 max{S.<PrAP, PrID>} 的含义类似。
定义Ⅲ.9(LCL繁殖阶段),繁殖阶段在A(≠B)→B上的推演定义为:A.<PuAP, PuID>=A.<PrAP, PrID>, B.<PuAP, PuID>=B.<PrAP, PrID>,B.LCLV=max(B.LCLV, A.LCLV+1)。
定义Ⅲ.10(LCL扩散阶段),扩散阶段在A(≠B)→B上的推演定义为:B.LCLV=max(B.LCLV,A.LCLV),如果 B.LCLV==A.LCLV,那么 B.<PuAP, PuID>=max(B.<PuAP, PuID>, A.<PuAP, PuID>)。
LCL 繁殖与扩散阶段至少在 WFG 中的每条边都推演过一次,且每个边上的确切推演次数和顺序没有强制的要求。
3 什么是 LCL 算法
我们提出了一种分布式死锁检测算法,该算法被归类为边追踪方法。该算法基于锁链长度值,该值对事务访问所需资源的依赖关系进行建模,分为三个阶段:繁殖阶段、扩散阶段和检测阶段。
在每个阶段中,如果事务A 触发检测事件,则 A 将其 LCLV,<PuAP,PuID> 和 PrID 发送到其所有直接下游节点。 A 的所有直接下游顶点收到 A 的消息后,根据对应的阶段,执行相应的 LCL 操作,并像 A 一样通知自己的直接下游顶点。ASG(scc) 中任何 LCLV 最多在 AsgWidth(scc) 轮推演之后传播到 scc,之后 ASG(scc) 中顶点的 LCLV 不再增加。如图2 所示,A1→A2→A3→A1 是 scc 中的一个循环,如果不限制繁殖过程的时间,循环上顶点的 LCLV 可以无限增大,所以 LCL 算法里面会设置时间上限。
3.1 LCL 繁殖阶段
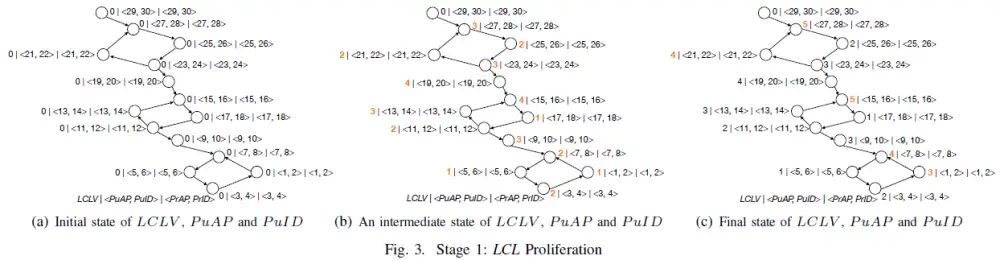
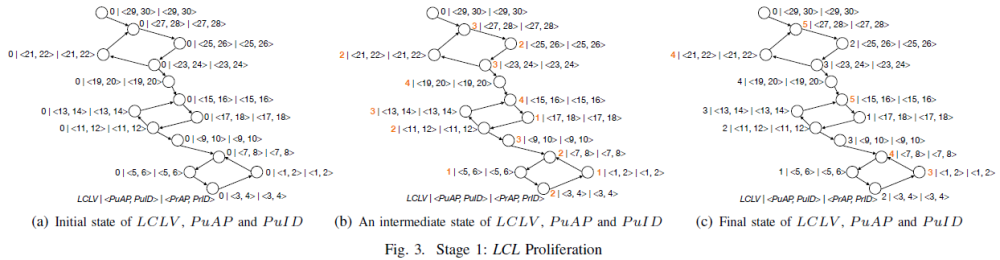
繁殖阶段设置的持续时间保证 max(AsgWidth(scc), 1) 轮繁殖阶段推演,时间复杂度 (NxM1),其中N为 WFG 中的有向边数,M1为 AsgWidth(scc),即 scc 环形子图的宽度。图3(a)展示了繁殖阶段初始状态下每个节点的 LCLV 和<PuAP,PuID>,图3(b)展示了推演过程中每个节点的状态,每条边上的推演顺序没有强制的要求,图3(c)展示了繁殖阶段结束之后每个节点的状态。
3.2 LCL扩散阶段
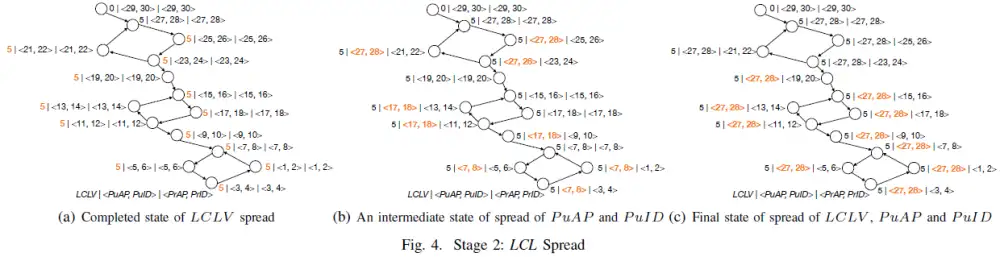
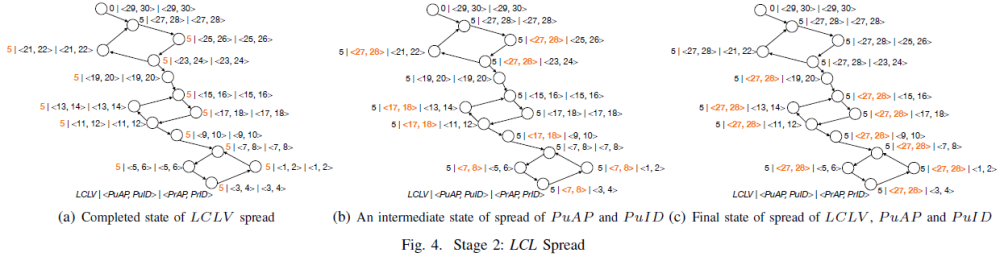
扩散阶段设置的持续时间保证 2×SccDiam(scc) 轮扩散阶段推演,时间复杂度为 O(NxM2),其中 N 为 WFG 中的有向边数,M2为 SccDiam(scc),即 scc 的直径。图4(a)展示了扩散阶段传播 LCLV 的结果,图4(b)展示了扩散阶段传播 PuAP 和 PuID 的中间状态,图4(c)展示了扩散阶段结束后每个节点的状态。
3.3 LCL检测阶段
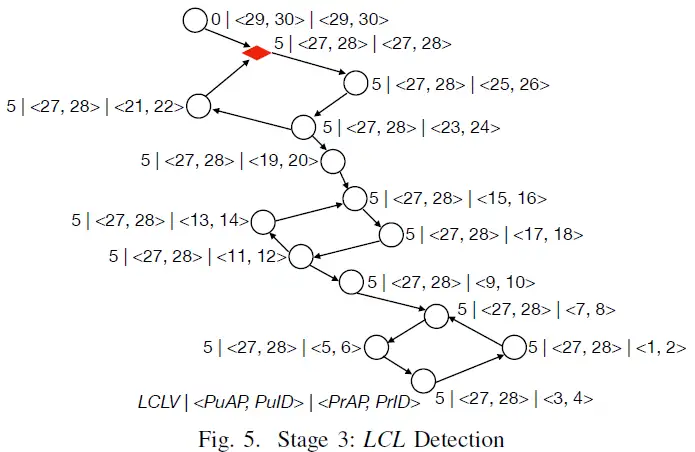
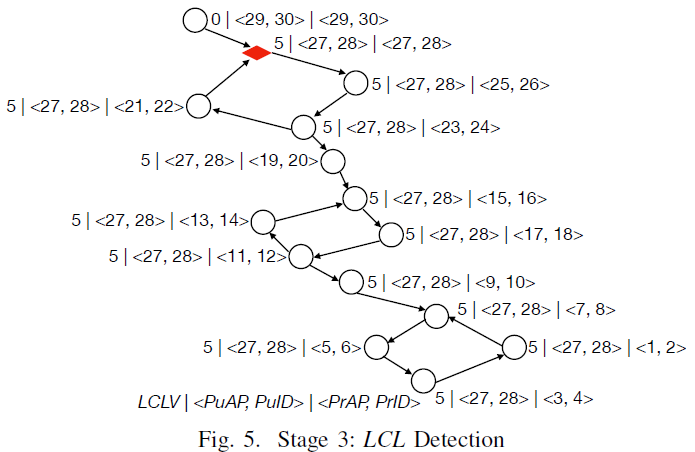
LCL 检测阶段在 A(≠B)→B 上的推演:如果 B.LCLV==A.LCLV 且 B.<PuAP, PuID>==A.<PuAP, PuID> 且 B.<PuAP, PuID>==B.<PrAP, PrID>,则 B 将检测检测到死锁并主动释放资源。繁殖阶段的时间复杂度为 O(N),其中 N 是 WFG 中有向边的数量。图5 展示了系统中检测到死锁的情况。
3.4 LCL算法逻辑证明
定义Ⅳ.2(上游SCC),如果 scc2⊆ASG(scc1),则 scc2 被认为是 scc1 的上游 SCC。
定义Ⅳ.3(最顶层SCC),如果 scc 没有任何上游 SCC,则它被称为最顶层的 SCC。
定理Ⅳ.5,在 WFG中 ,如果存在一个 SCC,那么至少存在一个最顶层的 SCC。
WFG中只要存在死锁就会有 scc,只要存在 scc 就肯定有一个最顶层 scc,详细证明过程见论文附录。
定义Ⅳ.10,在 LCL 繁殖阶段,scc 是WFG中最顶层的 SCC,w=AsgWidth(scc),经过至少 w轮 LCL 繁殖推算,
1)ASG(scc) 中每个顶点的 LCLV 是不变的;
2)∀X∈ASG(scc) 和 ∀Y∈USG(scc) 使得 X(≠Y)→Y,则 X.LCLV < Y.LCLV;
3)max{ASG(scc).LCLV} < max{scc.LCLV} = max{USG(scc).LCLV}。
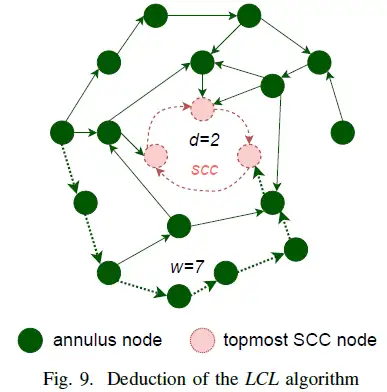
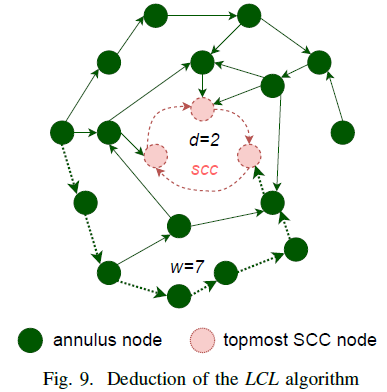
图9 展示了 LCL 的推演流程,ASG 中最外圈的节点需要经过 ASG 中其他节点将 LCLV 传播到 scc 中,最多需要 AsgWidth(scc) 步。在 LCL 繁殖阶段之后,Asg(scc) 中顶点的 LCLV 值不再变化,并且小于它们在 scc 中对应有依赖关系的节点。因此,在 LCL 的传播阶段,Asg(scc) 中的任何节点都不能改变 scc 中任何节点的 <PuAP,PuID>。
定义Ⅳ.11,假设 scc 是 WFG 中最顶层的 SCC,让 w=AsgWidth(scc) 和 d=SccDiam(scc)。在至少 max{w, 1} 轮 LCL 繁殖过程,以及至少 2×d 轮 LCL 扩散过程后,存在唯一的顶点A满足 A(≠B)→B 且 B.LCLV==A.LCLV 且 B.<PuAP,PuID>==A.<PuAP,PuID> 且 B.<PuAP,PuID>==B.<PrAP,PrID>。此外,B是在 scc 中具有最大 <PrAP,PrID> 的顶点。
scc 中具有最大 <PrAP,PrID> 的顶点具有唯一性,且将满足检测要求并解锁最顶层的 scc,所以 LCL 算法至少能保证最顶层的 scc 检测并消除死锁。在最顶层的 scc 中的死锁被打破后,接下来的检测轮次中将检测到其他潜在的死锁。
4 LCL 在 OceanBase 中的实现
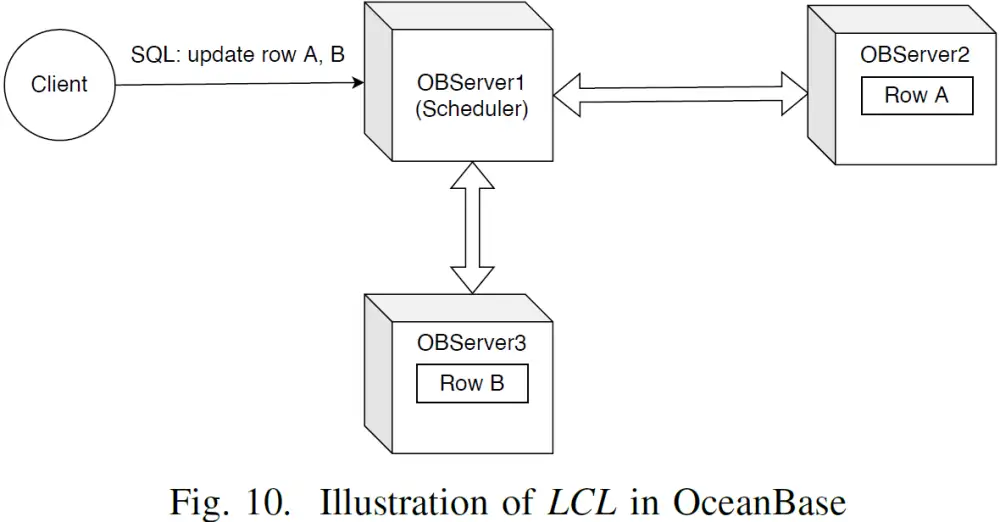
图10 展示了 LCL 在 OceanBase 中的实现,客户端连接集群中的节点 OBServer1 并启动事务,OBServer1 被称为事务协调者。SQL 语句涉及对数据行的修改会被路由到 Paxos Leader 执行。Leader 上的锁冲突可能导致执行失败,事务协调者从失败的子任务中获取信息并建立依赖关系。LCL 的推演过程会周期性地通过依赖关系传递一个特殊的消息,以发现可能的死锁并进行消除。
5 性能测试
5.1 M&M 和 LCL 算法比较
Mitchell 和 Merritt (M&M) 的算法[6]是一种简单且完全分布式的边追踪算法,它提供了检测和解决死锁的方法。OceanBase LCL 算法的灵感来自于M&M算法。M&M 和 LCL 主要差异在于: M&M 假设事务等待单一资源,LCL 对事务可以等待的资源数量没有任何限制。
5.2 事务执行模拟器(TPE)
在模拟事务执行的实验中,每个数据库节点上都会创建具有相同行数的数据表。工作负载由包含两种 SQL 的事务组成,1)需要申请锁资源的更新操作,占比约 50%,2)不需要申请锁资源的查询请求,占比约 50%。每个事务中 SQL 的数量服从指数分布或正态分布,每个 SQL 申请资源的数量也服从指数分布或正态分布。在整个测试流程中,TPE 将持续生成事务,执行事务,以及提交事务。具体实现过程中,所有事务都包含在一个全局数组中,私有编号是数组索引,私有优先级由每个数据库节点上的自增整数列生成,类似于事务的开始时间戳。
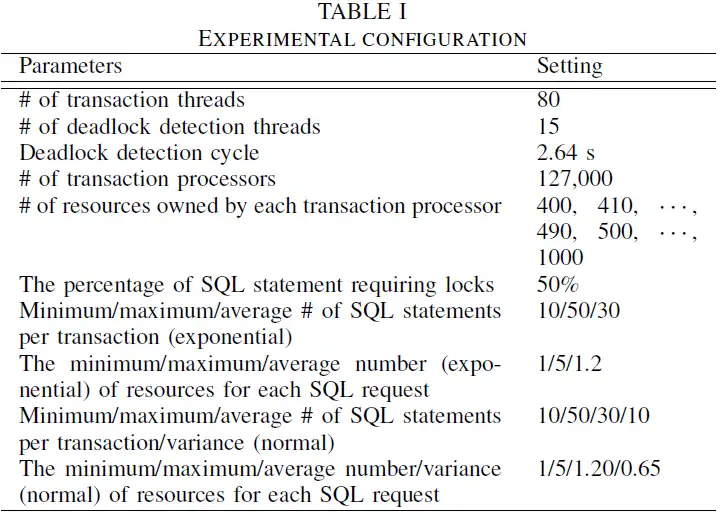
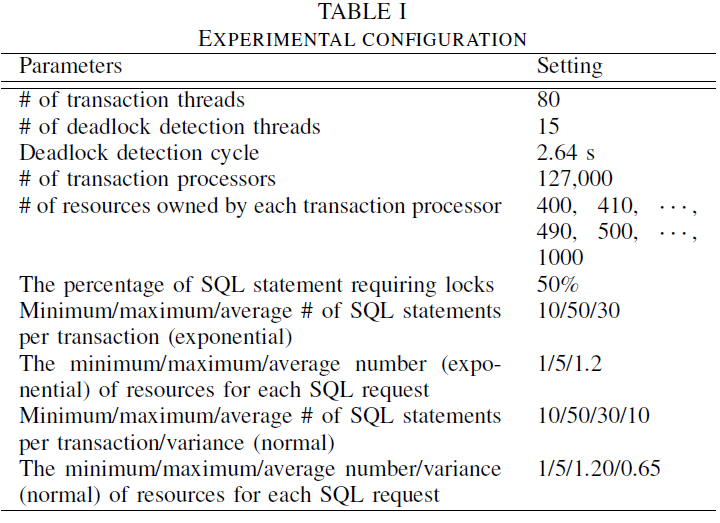
5.3 TPE 实验配置
LCL 算法配置:每轮 LCL 推演过程持续 2,640ms,其中 LCL 繁殖过程 1,200ms,LCL 扩散过程 1,200ms,LCL 检测过程 240ms。每次仿真实验运行 300s,时间结束后不再产生新的事务,但是已生成的事务将执行知道提交或者回滚。
5.4 TPE 实验结果
在 SQL 和资源都是指数分布以及每个表包含 400,000行的情况下,检测到的死锁和提交的事务随着时间推进呈线性增长。LCL 是一种多出度算法,在死锁检测方面比单出度 M&M 更有效,比 M&M 产生的死锁数量更少。LCL 运行在多出度的事务处理系统中,事务并行执行的能力,比运行在单出度系统的 M&M 具有更高的吞吐量。
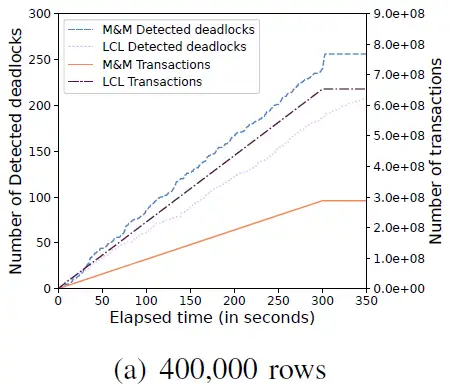
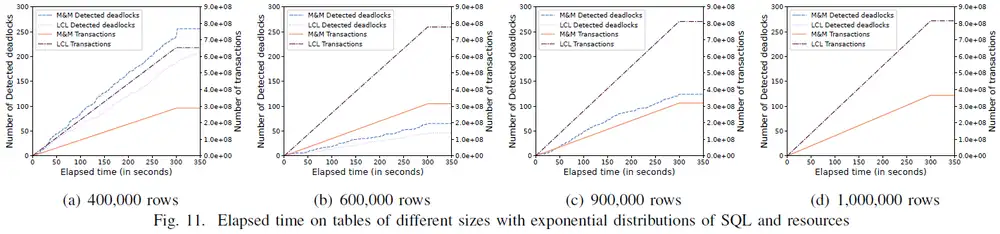
图11 展示了不断增加每个表中行数的情况下,LCL 和 M&M 在检测到死锁数量和事务完成数量的变化,随着行数的增加(从400,000,600,000,900,000到1,000,000行),行锁冲突发生的数量减少,进而死锁的数量减少,并且提交的事务数量增加。
在论文中还有其他三组实验,第二组是 SQL 呈指数分布和资源呈正态分布,第三组是 SQL 呈正态分布,资源呈指数分布,最后一组是 SQL 和资源都呈正态分布。
5.5 在 OceanBase 上的实验验证
1)OceanBase 集群:实验中的OceanBase集群包括 9台服务器,每台服务器都配备 Intel(R) Xeon(R) Platinum 8269CY CPU @ 2.50GHz,256 GB内存和千兆以太网。
2)资源及工作负载:每个节点上表的行数相同,从2000到6000不等。SQL的分布与TPE实验中相同。
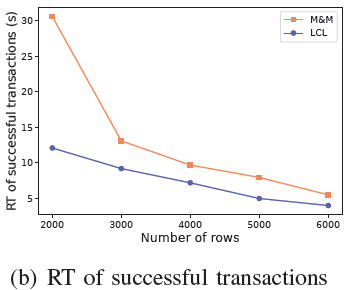
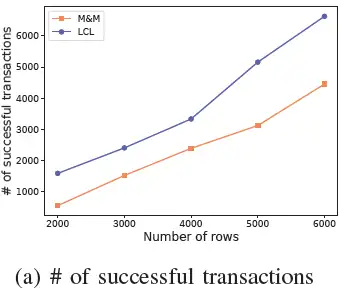
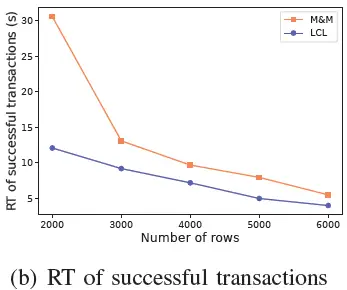
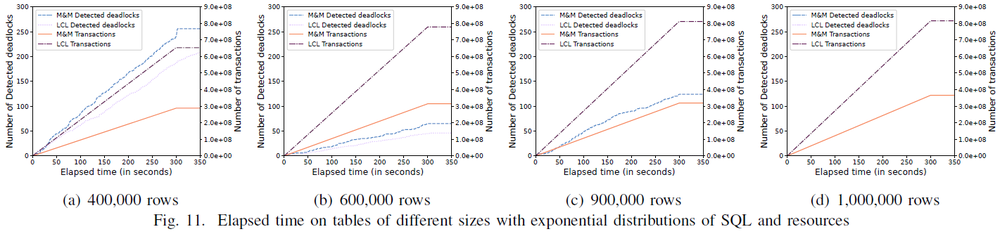
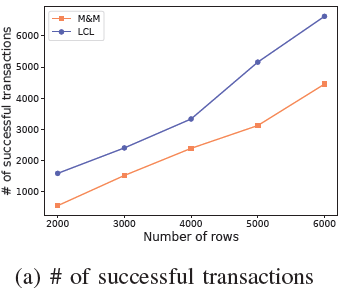
3)SQL和资源呈指数分布:LCL 允许事务同时申请多个资源,在解除死锁并释放多个资源后,事务很快就能成功执行。M&M 在事务执行过程中会阻塞在一条申请资源的 SQL 上,整体上会遇到更多的死锁,因此 LCL 在成功事务的数量上比 M&M 多40%以上。
在没有锁冲突的情况下单个事务的执行时间应该在 100ms以内,由于锁冲突较强,每个事务的响应时间(RT)普遍较高。M&M 只检测一个出度,可能发生死锁没有检测到的情况,事务的超时结束造成其他等待事务的延迟较高。LCL 检测所有出度并有效地解除死锁,在延迟方面好于 M&M。
1 研究背景
1.1 死锁检测与消除
分布式环境中的死锁检测比集中式环境中的死锁检测更具挑战性,因为每一个顶点只有整个系统视图的一部分,且 SQL 在并行执行的过程中同时访问数据表的多个部分,每个部分都可能被其他事务锁所阻塞,从而引起一个事务等待多个锁的情况。如表1 所示,当前的死锁检测与消除算法主要有四种:
- 集中式死锁检测,基本思想是选择一个中心节点作为检测器,收集所有节点的锁等待关系,生成全局锁等待图(WFG),应用案例为TiDB[1]。这种方法的缺点是典型应用的锁等待关系通常较为简单,整合所有局部 WFG的开销较大;
- 死锁预防策略,基本思想是在死锁发生之前通过 Wound-Wait,Wait-Die 等策略有选择地杀死事务,应用案例为Google Spanner[2]。这种方法的缺点是大量不会导致死锁的事务被杀掉,用户无法接受;
- 路径推动算法,基本思想是在每个顶点构建局部WFG,每个顶点将其本地WFG发送到多个相邻节点,并重复此过程。直到某个顶点有足够的视图来宣布死锁,应用案例为 CockroachDB[3]。这种方法的缺点是多个顶点会检测到同一个死锁,每个顶点都试图通过杀死一些事务来消除死锁,这可能具有多杀性;
- 边追逐算法,基本思想就是沿着事务 WFG 的边传播具有特殊意义的消息,死锁产生的环路关系最终将导致消息返回到它的发起者处,从而提示死锁的存在,应用案例为 Oracle RAC和 OceanBase[4]。
| 算法类型 | 算法描述 | 应用案例 |
|---|---|---|
| 中心化死锁检测 | 选择一个中心化的死锁检测节点,收集整个系统内的锁等待关系构建WFG并检测死锁 | TiDB[1] |
| 死锁预防策略 | 在死锁产生之前,以Wound-Wait或Wait-Die等策略,悲观地将冲突的事务杀掉 | Google Spanner[2] |
| 路径推动算法 | 节点之间传输并收集局部WFG关系,死锁的产生能够被部分节点检测到 | CockroachDB[3] |
| 边追逐算法 | 依据事务依赖关系向下游节点发送消息,死锁产生的环将通过这些消息被推断出来 | Oracle RAC, OceanBase[4] |
1.2 OceanBase 死锁检测需要的特性
对于OceanBase需要以下三个特性,第一个特性是每个顶点不需要建立整个系统的全局或局部事务等待视图,只需要向事务依赖关系的下游节点发送消息进行死锁检测与消除。第二个特性是一个死锁环路中只有一个顶点检测并消除死锁,避免了死锁中多个事务的回滚。第三个特性是只检测解决真正的死锁问题,不回滚不在死锁关系内的事务。
2 关于 LCL 算法流程的定义
为方便读者的理解,在此仅给出介绍 LCL 算法流程必要的定义,不针对推导证明过程给出详细描述(可通过文章结尾的链接,获取论文全文),定义编号与原文保持一致。
2.1 基础定义
定义Ⅱ.1 (A→B),A→B表示从节点A到节点B的边,物理意义上表示A事务正在等待B事务持有的一些资源。类似的,A(≠B)→B表示A≠B且A→B。
定义Ⅱ.2 (A⇒B),A⇒B表示从节点A到节点B的游走。A⇔B如果A⇒B且B⇒A。
定义Ⅱ.3 (Dist(A, B)),Dist(A, B)代表从节点A到节点B的最短距离。
2.2 环形子图距离
定义 (SCC(A)),SCC(A) 表示WFG中包含A的强连通分量[5]。
定义Ⅱ.6 (USG(scc)),USG(scc)=(VS, ES) 表示强连通分量 scc 的上游子图,其中VS={X∈WFG: X⇒A,A∈scc},ES= {X→T : X∈VS and Y∈VS and X→Y∈WFG }。
定义Ⅱ.7 (ASG(scc)),ASG(scc)=(VS, ES) 表示强连通分量 scc 的环形子图,其中VS={X∈WFG: X∈USG(scc) and X ∉ scc},ES={X→Y: X∈VS and Y∈ VS and X→Y∈WFG }。
定义Ⅱ.8 (AsgDist(A, scc)),AsgDist(A, scc)=max{m: Exist m distinct vertices Cm(=A), Cm-1, … ,C1 in ASG(scc) and a vertices C0 ∈ scc such that Cm(=A) → Cm-1 → … → C1 → C0 } 表示强连通分量 scc 的环形子图中节点 A 到 scc 的距离。
定义Ⅲ.1 (AsgWidth(scc)),AsgWidth(scc):=max{AsgDist(X, scc): X∈USG(scc)} 表示强连通分量 环形子图的宽度。
定义Ⅲ.8 (SccDiam(scc)),SccDiam(scc):=max{Dist(X, Y): X∈scc and Y∈scc} 表示强连通分量scc的直径。
2.3 LCL 算法中的概念及其定义
定义Ⅲ.2/4 (<PrAP,PrID>),PrID 和 PrAP 分别是每个顶点的私有的常量编号和优先级。死锁中具有最大 <PrAP,PrID>的顶点将被杀掉来消除死锁。
定义Ⅲ.3/5 (<PuAP,PuID>),PuID 和 PuAP 是非常量的编号和优先级,初值分别为 PrID 和 PrAP。
定义Ⅲ.6 (LCLV),LCLV 是初始值为零的顶点的锁链长度值。通常 A.LCLV=m 意味着从存在某个顶点到A有一段长度为m的游走。
定义Ⅲ.7 (max{S.LCLV}),S是 WFG 的一个子集,max{S.LCLV}:=max{X.LCLV: X is a vertex in S}。 max{S.<PuAP, PuID>} 和 max{S.<PrAP, PrID>} 的含义类似。
定义Ⅲ.9(LCL繁殖阶段),繁殖阶段在A(≠B)→B上的推演定义为:A.<PuAP, PuID>=A.<PrAP, PrID>, B.<PuAP, PuID>=B.<PrAP, PrID>,B.LCLV=max(B.LCLV, A.LCLV+1)。
定义Ⅲ.10(LCL扩散阶段),扩散阶段在A(≠B)→B上的推演定义为:B.LCLV=max(B.LCLV,A.LCLV),如果 B.LCLV==A.LCLV,那么 B.<PuAP, PuID>=max(B.<PuAP, PuID>, A.<PuAP, PuID>)。
LCL 繁殖与扩散阶段至少在 WFG 中的每条边都推演过一次,且每个边上的确切推演次数和顺序没有强制的要求。
3 什么是 LCL 算法
我们提出了一种分布式死锁检测算法,该算法被归类为边追踪方法。该算法基于锁链长度值,该值对事务访问所需资源的依赖关系进行建模,分为三个阶段:繁殖阶段、扩散阶段和检测阶段。
在每个阶段中,如果事务A 触发检测事件,则 A 将其 LCLV,<PuAP,PuID> 和 PrID 发送到其所有直接下游节点。 A 的所有直接下游顶点收到 A 的消息后,根据对应的阶段,执行相应的 LCL 操作,并像 A 一样通知自己的直接下游顶点。ASG(scc) 中任何 LCLV 最多在 AsgWidth(scc) 轮推演之后传播到 scc,之后 ASG(scc) 中顶点的 LCLV 不再增加。如图2 所示,A1→A2→A3→A1 是 scc 中的一个循环,如果不限制繁殖过程的时间,循环上顶点的 LCLV 可以无限增大,所以 LCL 算法里面会设置时间上限。
3.1 LCL 繁殖阶段
繁殖阶段设置的持续时间保证 max(AsgWidth(scc), 1) 轮繁殖阶段推演,时间复杂度 (NxM1),其中N为 WFG 中的有向边数,M1为 AsgWidth(scc),即 scc 环形子图的宽度。图3(a)展示了繁殖阶段初始状态下每个节点的 LCLV 和<PuAP,PuID>,图3(b)展示了推演过程中每个节点的状态,每条边上的推演顺序没有强制的要求,图3(c)展示了繁殖阶段结束之后每个节点的状态。
3.2 LCL扩散阶段
扩散阶段设置的持续时间保证 2×SccDiam(scc) 轮扩散阶段推演,时间复杂度为 O(NxM2),其中 N 为 WFG 中的有向边数,M2为 SccDiam(scc),即 scc 的直径。图4(a)展示了扩散阶段传播 LCLV 的结果,图4(b)展示了扩散阶段传播 PuAP 和 PuID 的中间状态,图4(c)展示了扩散阶段结束后每个节点的状态。
3.3 LCL检测阶段
LCL 检测阶段在 A(≠B)→B 上的推演:如果 B.LCLV==A.LCLV 且 B.<PuAP, PuID>==A.<PuAP, PuID> 且 B.<PuAP, PuID>==B.<PrAP, PrID>,则 B 将检测检测到死锁并主动释放资源。繁殖阶段的时间复杂度为 O(N),其中 N 是 WFG 中有向边的数量。图5 展示了系统中检测到死锁的情况。
3.4 LCL算法逻辑证明
定义Ⅳ.2(上游SCC),如果 scc2⊆ASG(scc1),则 scc2 被认为是 scc1 的上游 SCC。
定义Ⅳ.3(最顶层SCC),如果 scc 没有任何上游 SCC,则它被称为最顶层的 SCC。
定理Ⅳ.5,在 WFG中 ,如果存在一个 SCC,那么至少存在一个最顶层的 SCC。
WFG中只要存在死锁就会有 scc,只要存在 scc 就肯定有一个最顶层 scc,详细证明过程见论文附录。
定义Ⅳ.10,在 LCL 繁殖阶段,scc 是WFG中最顶层的 SCC,w=AsgWidth(scc),经过至少 w轮 LCL 繁殖推算,
1)ASG(scc) 中每个顶点的 LCLV 是不变的;
2)∀X∈ASG(scc) 和 ∀Y∈USG(scc) 使得 X(≠Y)→Y,则 X.LCLV < Y.LCLV;
3)max{ASG(scc).LCLV} < max{scc.LCLV} = max{USG(scc).LCLV}。
图9 展示了 LCL 的推演流程,ASG 中最外圈的节点需要经过 ASG 中其他节点将 LCLV 传播到 scc 中,最多需要 AsgWidth(scc) 步。在 LCL 繁殖阶段之后,Asg(scc) 中顶点的 LCLV 值不再变化,并且小于它们在 scc 中对应有依赖关系的节点。因此,在 LCL 的传播阶段,Asg(scc) 中的任何节点都不能改变 scc 中任何节点的 <PuAP,PuID>。
定义Ⅳ.11,假设 scc 是 WFG 中最顶层的 SCC,让 w=AsgWidth(scc) 和 d=SccDiam(scc)。在至少 max{w, 1} 轮 LCL 繁殖过程,以及至少 2×d 轮 LCL 扩散过程后,存在唯一的顶点A满足 A(≠B)→B 且 B.LCLV==A.LCLV 且 B.<PuAP,PuID>==A.<PuAP,PuID> 且 B.<PuAP,PuID>==B.<PrAP,PrID>。此外,B是在 scc 中具有最大 <PrAP,PrID> 的顶点。
scc 中具有最大 <PrAP,PrID> 的顶点具有唯一性,且将满足检测要求并解锁最顶层的 scc,所以 LCL 算法至少能保证最顶层的 scc 检测并消除死锁。在最顶层的 scc 中的死锁被打破后,接下来的检测轮次中将检测到其他潜在的死锁。
4 LCL 在 OceanBase 中的实现
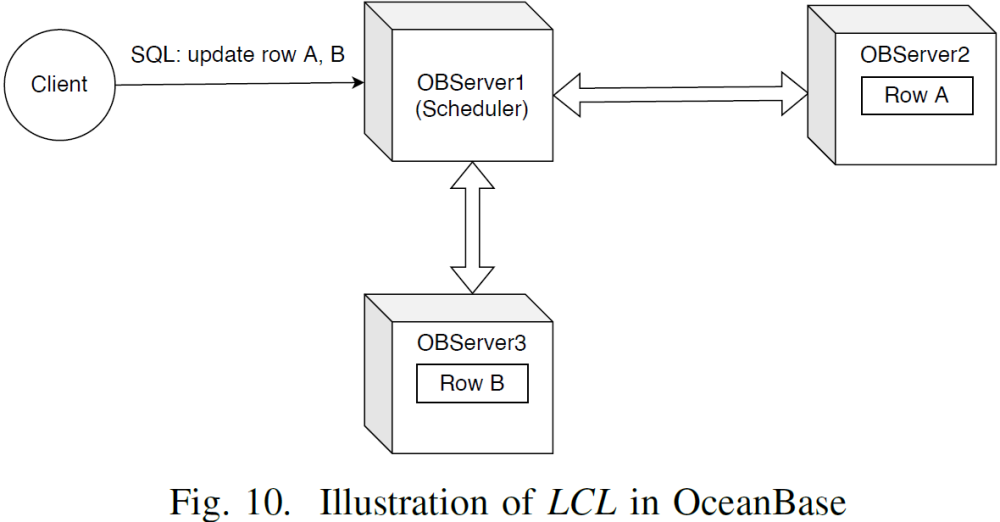
图10 展示了 LCL 在 OceanBase 中的实现,客户端连接集群中的节点 OBServer1 并启动事务,OBServer1 被称为事务协调者。SQL 语句涉及对数据行的修改会被路由到 Paxos Leader 执行。Leader 上的锁冲突可能导致执行失败,事务协调者从失败的子任务中获取信息并建立依赖关系。LCL 的推演过程会周期性地通过依赖关系传递一个特殊的消息,以发现可能的死锁并进行消除。
5 性能测试
5.1 M&M 和 LCL 算法比较
Mitchell 和 Merritt (M&M) 的算法[6]是一种简单且完全分布式的边追踪算法,它提供了检测和解决死锁的方法。OceanBase LCL 算法的灵感来自于M&M算法。M&M 和 LCL 主要差异在于: M&M 假设事务等待单一资源,LCL 对事务可以等待的资源数量没有任何限制。
5.2 事务执行模拟器(TPE)
在模拟事务执行的实验中,每个数据库节点上都会创建具有相同行数的数据表。工作负载由包含两种 SQL 的事务组成,1)需要申请锁资源的更新操作,占比约 50%,2)不需要申请锁资源的查询请求,占比约 50%。每个事务中 SQL 的数量服从指数分布或正态分布,每个 SQL 申请资源的数量也服从指数分布或正态分布。在整个测试流程中,TPE 将持续生成事务,执行事务,以及提交事务。具体实现过程中,所有事务都包含在一个全局数组中,私有编号是数组索引,私有优先级由每个数据库节点上的自增整数列生成,类似于事务的开始时间戳。
5.3 TPE 实验配置
LCL 算法配置:每轮 LCL 推演过程持续 2,640ms,其中 LCL 繁殖过程 1,200ms,LCL 扩散过程 1,200ms,LCL 检测过程 240ms。每次仿真实验运行 300s,时间结束后不再产生新的事务,但是已生成的事务将执行知道提交或者回滚。
5.4 TPE 实验结果
在 SQL 和资源都是指数分布以及每个表包含 400,000行的情况下,检测到的死锁和提交的事务随着时间推进呈线性增长。LCL 是一种多出度算法,在死锁检测方面比单出度 M&M 更有效,比 M&M 产生的死锁数量更少。LCL 运行在多出度的事务处理系统中,事务并行执行的能力,比运行在单出度系统的 M&M 具有更高的吞吐量。
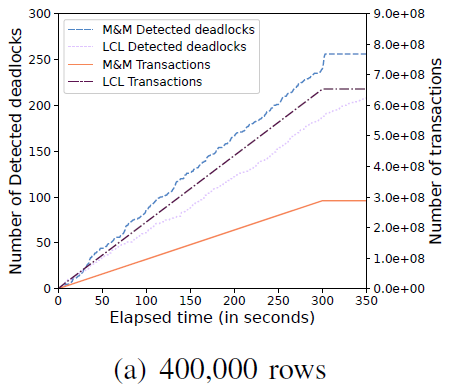
图11 展示了不断增加每个表中行数的情况下,LCL 和 M&M 在检测到死锁数量和事务完成数量的变化,随着行数的增加(从400,000,600,000,900,000到1,000,000行),行锁冲突发生的数量减少,进而死锁的数量减少,并且提交的事务数量增加。
在论文中还有其他三组实验,第二组是 SQL 呈指数分布和资源呈正态分布,第三组是 SQL 呈正态分布,资源呈指数分布,最后一组是 SQL 和资源都呈正态分布。
5.5 在 OceanBase 上的实验验证
1)OceanBase 集群:实验中的OceanBase集群包括 9台服务器,每台服务器都配备 Intel(R) Xeon(R) Platinum 8269CY CPU @ 2.50GHz,256 GB内存和千兆以太网。
2)资源及工作负载:每个节点上表的行数相同,从2000到6000不等。SQL的分布与TPE实验中相同。
3)SQL和资源呈指数分布:LCL 允许事务同时申请多个资源,在解除死锁并释放多个资源后,事务很快就能成功执行。M&M 在事务执行过程中会阻塞在一条申请资源的 SQL 上,整体上会遇到更多的死锁,因此 LCL 在成功事务的数量上比 M&M 多40%以上。
在没有锁冲突的情况下单个事务的执行时间应该在 100ms以内,由于锁冲突较强,每个事务的响应时间(RT)普遍较高。M&M 只检测一个出度,可能发生死锁没有检测到的情况,事务的超时结束造成其他等待事务的延迟较高。LCL 检测所有出度并有效地解除死锁,在延迟方面好于 M&M。