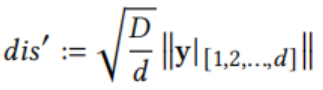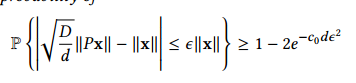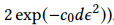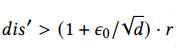论文分享
本篇论文来自于 SIGMOD 2023,介绍了一种可靠和有效的距离比较操作的高维近似最近邻搜索。主要工作1.提出一种随机算法 ADSampling; 2.基于 ADSampling ,开发了两种算法特定的技术作为插件来增强现有的 AKNN 算法。
论文背景

提出问题:
在高维空间中,几乎所有 AKNN 算法的时间消耗都由距离比较操作(DCOs)所占据。对于每个操作,它扫描一个对象的全部维度,因此在维度上运行的时间是线性的。
解决方法:
提出了一种随机算法,名为 ADSampling,它在大多数距离比较操作(DCOs)中运行时间是对数级别,并且具有高概率成功。特点概括起来便是1. 缩短比较时间;2. 成功率高。
论文主要工作:
(1)提出一种随机算法 ADSampling;
(2)基于 ADSampling,我们开发了两种算法特定的技术作为插件来增强现有的AKNN算法。
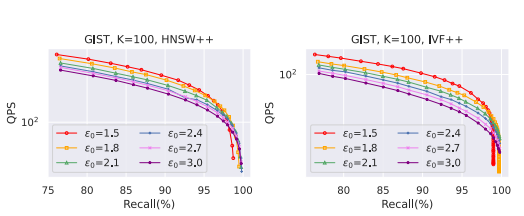
其中,两种特定技术为:HNSW++和 IVF++。
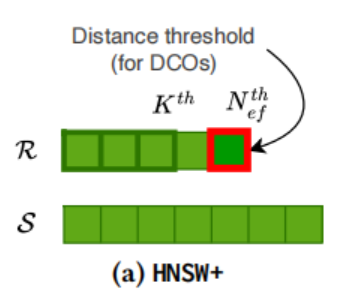
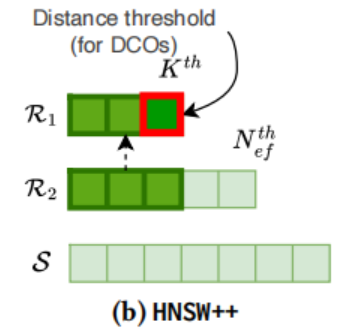
HNSW++ 是基于 HNSW 算法的改进,通过使用更好的近似距离和更高效的候选生成策略来提高搜索速度。
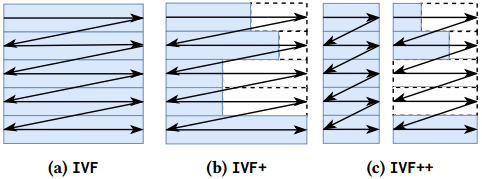
IVF++ 是基于 IVF 算法的改进,通过重新组织数据布局和调整维度顺序来提高缓存友好性,从而减少内存访问开销,提高搜索速度。
传统方法:
1、FDScanning:计算对象的距离(从查询点),然后将计算的距离与阈值进行比较。(需要扫描对象的全部维度来执行操作)
2、PDScanning:增量扫描原始向量的维度,并在基于部分扫描的𝑑维度的距离(如下图公式)大于距离阈值𝑟时终止该过程。
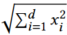
ADSampling 核心:
将对象投影到具有不同维度的空间中,并基于投影向量进行比较操作(DCOs)以提高效率。
原理:对于远离查询的负对象来说,将它们投影到维数更少的空间就足以进行可靠的比较操作(DCOs); 而对于靠近查询的负对象,它们应该被投影到具有更多维数的空间中以进行可靠的比较操作(DCOs)。
实现步骤:
(1)通过随机正交变换对对象进行预处理。(注:这一步仅是随机地旋转对象而不扭曲它们的距离。)
(2)在查询阶段处理不同对象的比较操作(DCOs)时,它会对其转换后的向量进行不同维度的采样。
注:ADSampling 根据查询期间对象的 DCO 自适应地决定每个对象要采样的维度数量,而不是在索引阶段预设一个确定的数量(这需要具有专业知识,实践中难以设置)

补充

索引阶段:
我们首先用 NumPy 库生成一个随机正交变换矩阵,存储它并将变换应用到所有数据向量。然后我们将转换后的向量(AKNN, AKNN* 和 AKNN** 的原始向量)输入到现有的 AKNN 算法中。
对于 HNSW、HNSW+、HNSW++ 和 HNSW*(注意它们具有相同的图结构),我们的实现基于 hnswlib
对于 IVF、IVF+、IVF++、IVF* 和 IVF**(注意它们具有相同的聚类结构),我们的 K-means 聚类实现基于 Faiss 库
查询阶段:
所有算法都是用 c++ 实现的。
对于一个新的查询,我们首先使用特征库[25]转换查询向量,以便在运行 AKNN+ 和 AKNN++ 算法时进行快速矩阵乘法(对于 AKNN, AKNN* 和 AKNN**,它们不涉及转换)。
然后我们将向量输入 AKNN, AKNN+, AKNN++, AKNN* 和 AKNN** 算法。
时间成分分析:
应用 ADSampling 需要随机转换数据和查询向量的额外成本。具体来说,转换数据向量的成本位于索引阶段,并且可以由同一数据库上的所有后续查询摊销。查询向量的转换在查询阶段进行,当出现查询时,查询的代价可以由回答相同查询所涉及的所有 dco 分摊。
为了简单起见,我们将这一步(又称为 Johnson-Lindenstrauss 变换)实现为矩阵乘法运算,它需要 𝑂(𝐷^2) 时间。我们注意到,使用高级算法[19]可以在更短的时间内执行这一步,例如,使用 Kac 's Walk 需要 𝑂(𝐷log𝐷) 时间。

— 参考文献 —
[1]Yu A. Malkov and D. A. Yashunin. 2020. Efficient and Robust Approximate Nearest Neighbor Search Using Hierarchical Navigable Small World Graphs. IEEE Transactions on Pattern Analysis and Machine Intelligence 42, 4 (2020), 824-836. https://doi.org/10.1109/TPAMI.2018.2889473
[2]Herve Jegou, Matthijs Douze, and Cordelia Schmid. 2010. Product quantization for nearest neighbor search. IEEE transactions on pattern analysis and machine intelligence 33, 1 (2010), 117–128.
向量检索实验室
微信号:VectorSearch
扫码关注 了解更多