论文分享
本次分享内容包含了回顾并重新审视图索引的设计原则和代价分析,介绍图索引的前沿学术进展 HVS,总结当前树结构与图结构结合的索引方案,并对未来的发展和优化方向提出思考。
接下来看看由复旦大学计算机专业博士研究生王泽宇带来的基于图的向量索引结构回顾与前沿进展都有哪些精彩内容吧。

文字稿近万字(嗯~怎么不算呢),干货多多,记得准备好水杯哦!

背景介绍
VectorSearch
基于图的高维向量索引凭借其优越的查询性能已成为当前学术界和产业界公认的最优向量检索解决方案。然而,人们对于图索引结构的理解和分析尚在探索当中。目前基于图的向量检索有许多的应用场景,最常见的是在商品推荐、以图搜图和科学研究(蛋白质结构预测)中。

这里举一个 chatGPT 利用向量检索的场景。之前有不少人提出 chatGPT 在检索文献的时候存在提供虚假的文献的问题。前几天发布的插件式 chatGPT 就有一个专门的 Retrieval Plugin 模块专门用于检索专业文献来解决这个问题。这个插件做了一个语义分解,把一个大问题拆分成了若干个小问题,然后在小问题里面检测出一些筛选条件,在语料库里面依次查询。


Retrieval Plugin 插件的基本工作逻辑是这样的:
把我们提供的语料库利用 OpenAI 的 embedding 技术去做一次嵌入,把得到的结果放到向量数据库里;当用户提问时,就将用户的问题进行处理,然后放到向量数据库中进行 query。
目前市场上向量数据库有6种选型:Mivuls、pinecone、Qdrant、Weaviate、Redis 和 Zilliz,而这6种数据库的核心数据结构均为近邻图索引—— HNSW 。其中最重要的两个性能指标就是查询的准确性和效率。由此引出了接下来要介绍的近邻图索引。

回顾近邻图索引设计
VectorSearch
近邻图索引是近年来被广泛使用的一种向量索引方式。它的基本思想是将向量表示为点,向量的邻近性表示为边,以此构成一个图,然后利用图的结构来加速近邻搜索。这个部分会给大家介绍一下图索引预备知识。
设计原则
问题定义:在大量等长向量中找出距离给定向量最近的 top-K 个向量,距离一般定义为欧氏距离。
如图,图索引的每个节点就是一个向量,边表示两个节点存在近邻关系,图中边的长度表示向量之间的距离。

而这个图索引的设计原则是这样的:
1、导航特性(small-world phenomenon)
(1)边的长度服从指数分布 ,即边越长数量越少;
(2)长边负责快速导航
(3)短边负责高精度搜索
2、裁边策略(边的多样性)
保留多方向的邻居
查询方式
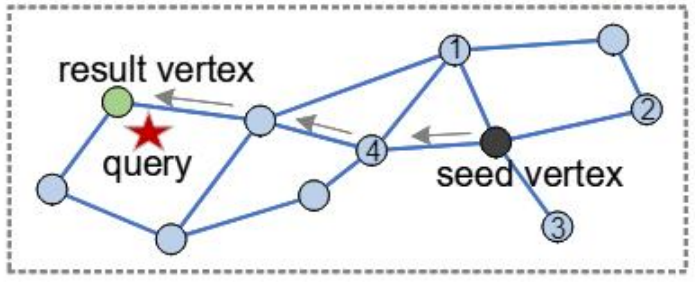
Best First Search:从某一/几个入口点开始,探测每一个邻居,维护探测过的所有点的距离(保存在优先级队列中),每次选择与query最近的点继续路由。
注意:并非一定是沿着单方向的路线靠近 query。若不甚“走偏” ,即邻居不是最近的结果有可能选择别的路径,就可以从新的方向继续路由搜索。
限制优先级队列的长度,直到队列中没有能提供更近距离的点了,算法中止。
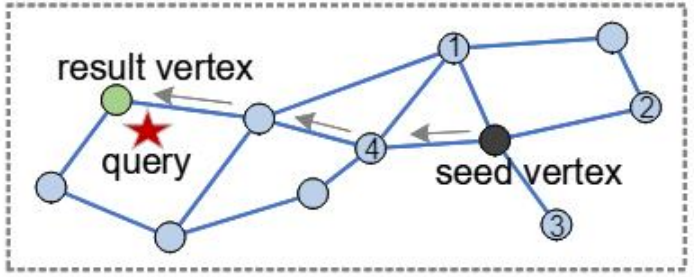
设计思路
在设计时边并非越多越好,图索引的查询复杂度为 O(Mpd) ,其中 M 为最大邻居个数,p 为搜索路径长度,d 为向量维度,也就是说每次查询要和 M 个邻居进行距离计算,则 M 越小越好,即保持连通性的情况下边裁掉越多越好。
那么设计思路可以从性质良好的基本几何图入手,然后去做近似,目前常用 Voroni 图。Voroni 和 K-means 聚类算法是有相似之处,但是这里是把图上每一个点都当成聚类中心来看待,即图上每一条边都对应两个点连线的垂直平分线。

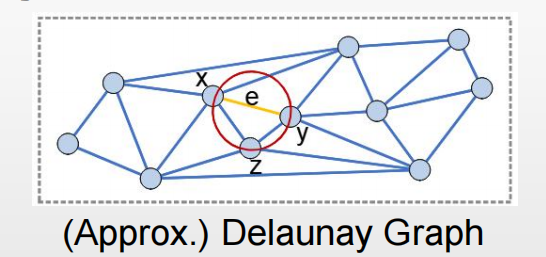
如果把 Voroni 图的相邻两个点用边连接起来就形成了 Delaunay 图,这和我们在用的图索引有些相似了。Delaunay 图的性质很好,用贪心算法可以保证得到精确而非近似的 1-NN,但是构建成本很高,一般会用近似的算法代替。
更进一步的为了限制边的数量,会引入 RNG 的剪枝规则,会把靠近同方向且距离很近的边裁掉,比如下图中的黄线,算法认为 xy 和 xz 这两条边的方向离得很近,而且长度也差不多,如果从 x 走到 y 也可以通过 x 走到 z 再走到 y 实现,就会把这样的边裁掉。

构建方法
最早的近邻图索引就是 NSW,通过近似查询的方式随机排列插入,每次随机从数据库里面选一个点,然后在已有的图上做一次 Best-First-Search,插入时间越早越趋向于生成长边,边的长度分布近似为指数分布。
但是人们发现 NSW 会存在一些 hub 节点,会导致它的最大邻居个数变得很大,很大程度上会影响时间复杂度。后来 HNSW 对此做了两个比较重要的优化,一个是做了层次化,将可能的 hub 节点优先挑出来放到上层去做导航,这样在做下层路由的时候就可以把邻居节点的个数变得小一点;另一个就是引进了 RNG 剪枝和反向边补充。
反向边怎么理解呢?就是我们要为插入的一个点找邻居其实就是找以前的点,或者说找已经插入的点来当它的充边邻居,那么用以前插入的点指向新插入的点,这个就是反向边。由于这两点优化,HNSW 对于邻居数量(M)的要求就大大降低了,整体查询性能和 NSW 相比得到了质的提升。

进一步思考
HNSW 自从2018年发布之后就得到了十分广泛的应用,引起了很多学者的研究和分析。首先是对层次化的必要性的思考。
arXiv’19[5] 上的一组实验将 HNSW 上层去掉,只保留最底层,发现检索性能没有受到太大的影响。

WSDM’22[6] 的一组实验发现 HNSW 的访问频率存在“二八定律”,即访问次数少的边占据图的大多数,最底层依旧含有 hub 节点,侧面验证了 arXiv‘19 的实验结论。

第二是对裁边规则的必要性的思考。
ArXiv’19[5] 的另一组实验根据裁边规则进行了对比试验,将无裁边只维近邻关系(图中黑线)和有反向边补充及 RNG 裁边(图中紫线)进行了对比,可以发现裁边规则对性能提升影响很大。

MDM’22[7] 的另一组实验则进一步增加了反向边的补充,也获得了小幅的性能提升。
在某种程度上也佐证了裁边规则才是 HNSW 性能提升的要点所在。

下面思考图结构唯一性的问题。
改变索引的插入顺序,即将原先的数据集重新排列后再构建索引,看看重新构建出来是什么样子。如下图,横轴是第一次构建的时候这批 query 最小搜索部署,纵轴是第二次的部署,可以看出对于同一个 query 难度变化的影响是非常大的,根本没有按照x=y这条线部署。最后测下来整体的平均性能是比较稳定的,也就是说这个索引结构不是唯一的,用别的结构也可以达到同样的索引效果。

最后思考一下 HSNW 查询复杂度方面的问题。
在最初发布 HNSW 的文章中提到, HNSW 的时间复杂度是 O(logn) 的,但是实现这个时间复杂度是有前置条件的。第一条就是需要是精确 delaunay 图,这已经和实际情况相差甚远。
第二个是在推导过程中,将每层的搜索复杂度解释为常量,但是,按照之前的结论,将上层结构去除对于搜索复杂度的影响是很小的,那么这是不是意味着其实整体的搜索复杂度是个常量呢?这很显然是存在疑点的。
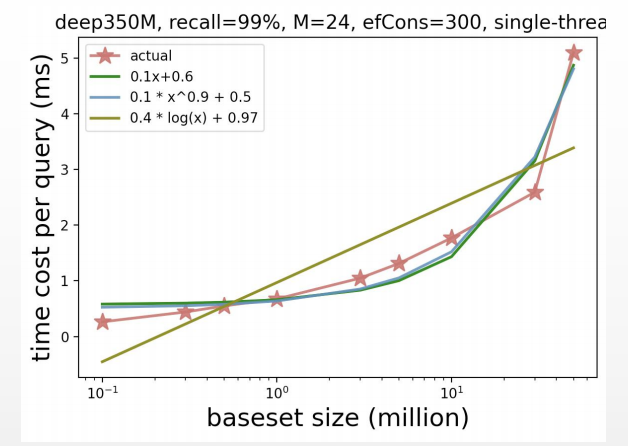
王博士所在的实验室对这个问题进行了实验,发现数据的数量级小于千万级别时复杂度较为符合 logn 的,但是超过千万级别之后用幂次函数的拟合会更吻合。
前沿近邻图索引解决方案介绍:HVS
VectorSearch
为什么会提出 HVS?
在图索引的搜索路径中,路径长度和每跳距离计算次数(去重后的邻居个数)共同构成搜索的时间开销。
在搜索的早期阶段,由于只是想要找到一个路由的方向,不需要去和每个邻居都做一次距离计算,论文作者想要将这一部分时间开销节约掉,基于这个动机提出了 HVS。
基本的思路就是可通过由粗到细的层次化的空间分割将 query 点快速路由到结果附近的区域当中,然后在此区域利用图索引找出高精度的 kNN。相当于是给 HNSW 找了一个很好的入口点,这个入口点已经落在了 kNN 的周围,这就取代了 HNSW 上层的作用。
回顾 PQ 算法
在介绍 HVS 之前,先对 PQ 做一下回顾,因为 HVS 的上层和 PQ 的关联是很大的。

我们用一个例子来理解这个过程。这里有一个六维的原始向量,将它分成三段,即 m=3;然后在每段向量上做 K-means 聚类,因为每个库里面有很多向量,同样的放到第一段会有很多子向量,将这些子向量去做一个 K-means 聚类,聚类完之后我们把每个子向量规约到最近的聚类中心,这里聚类中心有4个,即 L=4,我们假设最近的聚类中心是[1.0,1.9],然后呢我们用二进制数对聚类中心进行编码,因为这里是有四个聚类中心,所以是用两位的二进制数进行编码,[1.0,1.9]的编码是11。

我们进行一个基本的分析,每一段有 L 种编码,m 段可以产生 L^m 种编码,这就在高维找到了 L^m 个聚类中心,相当于将整个高维空间进行了一次分割,这样我们就得到了一个子码书,即 PQ 中聚类中心的编码表。每个子码书里面我们限定一共有 L 个子码字,也就是 K-means 时的聚类中心。
多级乘积量化算法介绍
接下来介绍 HVS 提供的多级乘积量化算法,这个算法的目的是为了构建均匀的空间分区,因为无论是 K-means 还是一个多段的乘积量化得到的空间分区没办法保证最后得到的分区结果是均匀的,而多级乘积量化算法很大程度上可以解决这个问题,它使每一个点都可以落在密度差不多的区域当中,可以达到一个从“等宽量化”到“等深量化”的进步,不会产生很严重的数据倾斜问题。
核心思路就是自底向上构建分区。首先在最低层构建充分稠密的 Voronoi 图,就是做一次 L 和 m 都比较大的一个 PQ,然后逐层向上抽取聚类中心,文中的术语叫做 seed point ,将这些生成的聚类中心每次抽取一些到上层,这样上层聚类中心的数量就会逐层递减。像图中这样我们固定每一层的子码字个数为2,从1到 T 层的分段数为(2,4,8,……,2^T),聚类中心个数为(2^2,2^4,2^8,……,2^2T),这个是 HVS 算法的第一个特点,分区密度自上而下是按照指数递增的(图中红色区域为最上层)。
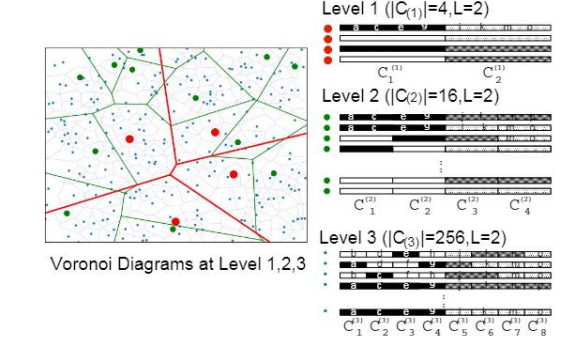
这也产生了一个问题,如何基于底层的稠密分区构造上层稀疏分区?想法是
1、最好在已有的聚类中心中选择,一方面是子码书已经构建出来了,另一方面在做路由和查询的时候距离计算也可以大范围简化,可以很好的避免每次都要和不同的子码书进行距离计算,带来的计算量较大的问题。
2、将分段减少,比如最底层是 m 段,那么往上一层就是 m/2 段,然后两两匹配分段及其对应的子码书。
3、每一对子码书都会产生 L^2 个子码字(由笛卡尔积得来),如图中从 level 3 到 level 2 的这个过程,可以看到 level 2 第一段里面只有 ac 纯白和 bd 纯黑两种子码字,组合起来有4种选择:ac、ad、bc 和 bd。Level 2 到level 3 的过程中抛弃了其中两种,也就是 ad 和 bc(黑色白色和白色黑色)。
这里就产生了第二个特点,上层的 seed point(聚类中心) 都是取自下层的,这会对后面的查询起到一个非常大的帮助。至于如何进行两两匹配,这里不具体展开,有兴趣的朋友可以看看原版论文。
基于密度的数据分配策略
HVS 的另一个贡献就是提出了基于密度的数据分配策略,这个策略的目的是在层次化分区的空间中放置数据,解决数据分布倾斜问题。上一段讲了如何寻找聚类中心,现在我们来介绍一下如何将数据点放到对应的区域中。
核心思路是自上而下分配数据点,顶层包含所有数据,下层数据是上层数据的子集,越到上层越稀疏。具体方法是在上层的分区中,某个点周围过于“稠密”,就会被放置入下层以细粒度区分,因为下一层的区域会更细一些,将稠密的区域切割开,来保证做到等深量化的效果。
如何判断是否过于稠密?会有一个具体公式进行量化,这里就不具体说明了,主要思想是对于每个点,找到当前层的第 k 个 NN 的位置,和第 k 个 NN 的距离过近的点会落入下层。这样每次筛选一部分点进入下层,下层到上层点的数量进行一个指数下降,就可以达到一个指数分布。这也是 HVS 的第三个特点:数据基数指数递减(自上而下)。
HVS 整体结构
HVS 整体分为两个部分,前一部分为 HVS,后一部分为 HNSW 的第0层,如下图所示

代表点(representative):我们通过层次化 PQ 得到的每一个 Voronoi cell(图层)中和 seed point 最近的数据点;
层内连接(point-point):层内连接(point-point):除第一层外,每一层的有效 seed point 之间会按照HNSW相同的构图方法进行连接。有效的 seed point 是指 seed point 所在的 Voronoi cell 是含有数据点的,因为所在cell如果没有数据,所以对它继续进行查询是没有意义的;
跨层连接(cell-point):分成三种情况,
如果当前 cell 中的所有点都中止了,即当前所有的点都处在比较稀疏的区域,则此 cell 直接连向 base layer(HNSW 的第0层) 中的代表点,例如上图中的虚线1;
如果存在未中止的点,即周围比较稠密的点,那么找到距离 seed point 最近的未中止的点,则此 cell 连向下一层包含该点的 cell 的 seed point,例如上图中虚线2;
top layer 的点因为比较少,所以会直接在 secondlayer 中寻找精确的 k0 -NN 连接,例如上图中虚线3。
在 HVS 的多层之间只有这两种连接方式,查询的时候只能按照已经连好的边往下走。
HVS 查询方法
查询分三步:
1、首先在 top layer 找到精确 top-1;
2、此后通过跨层边到达 second layer,在层内做标准贪心搜索,找到一批 seed points 和对应的 Voronoi cells;
3、如仍未中止则继续钻入下层搜索,否则就找到了 base layer 的一个入口点。
最终我们在 base layer 找到了一批距离 kNN 更近的入口点,然后进行标准的 HNSW 搜索就可以了。因为 HVS 有一个比较复杂的训练过程,在索引训练和构建方面的性能有时会比 HNSW 稍慢一些,但在查询性能上可以表现出很稳定的提升。
树图结合的索引方案综述
VectorSearch
树图结合型索引是一种常用的向量索引方法,它将近邻图和树索引结合起来,能够有效地加速近邻搜索。
下面介绍目前已有的两个树图结合的索引解决方案。
方案综述
第一个方案是发表在 SPANN[12] (NeurIPS’21) 上的一篇论文,背景是解决大规模磁盘向量索引问题,核心思路在于通过平衡 K-means 树对数据进行聚类,在内存对聚类中心建图进行导航,加速定位邻近聚类。这样在结果上磁盘索引的性能是优于 diskANN 的。

第二个方案是 Elpis[13] (VLDB’23) ,背景是解决大规模内存向量索引问题,基本方法是基于 SOTA 时序索引树 Hercules ,这是一个专门解决时间序列问题的索引解决方案,因为针对的问题是一样的,只有在数据类型上有些不同,所以可以直接引用。它和 K-means 树以及 HVS 中 PQ 起到的作用是一样的,可以做到初步数据分区,在每个叶子节点上建立 HNSW 图索引。结果:构建开销和内存开销显著降低,十亿级数据集上性能有明显提升。

现有问题与未来展望
VectorSearch
接下来是王泽宇博士对他今天进行一些分享的总结以及对未来研究方向的一个思考。
第一点是更清晰的机理分析和更多的性能优化设计。
图索引的作用机理尚不明晰,设计上的考量多为启发式,缺少形式化验证和对查询的保障,时间复杂度问题尚未完全解决。树图结合式索引已初步体现出优势一个可能的思路是:远距离导航由空间分割树或 PQ 负责,而将图索引改造成专为局部邻近区域(neighborhood)提供高精度搜索。
第二点是未来可以做的更丰富的应用场景:
多模态场景:异构分布的数据集
在线场境:高效动态插入和删除
混合查询:标量向量混合、多向量查询等
第一条多模态场景,比如说刚才在最开始的 motivate 阶段提到过一个多模态的场景,包括一些异构分布的数据集,数据集里面的内容可能是文字、文档,也有可能是图片,当接收的 query 也有可能是不同的类型的,那最终得到的就是这个输入的分布,可能 data set 和 query set 的这个数据分布,可能差距很多。
第二条在线场景,保持一个高效的动态插入和删除,就是在数据集偏大的情况下,持续地去做插入和删除,它的复杂度是比较高的,并不是一个常量。那这种情况下其实就对真正的生产环境中做出了一个要求,就是不能把图建得非常大,可能建到小图左右就要考虑转入线下了。
第三条混合查询,包括标量向量的混合查询。ChatGPT 工作的逻辑里面,也会从中提取一些 filter 出来,就是标量上的一些查询条件,比如时间、日期、国家等,可能混合查询其实也是未来工作需要举的一个点。还有就是像上次王梦召博士提出的多向量查询的视角:以多个向量的方式描述一个对象,会得到一个更精确的一个结果,这个目前也是没有得到完全解决的一个问题。
这里放一个上次王梦召博士分享的内容,感兴趣的小伙伴可以看看。
Q&A
接下来是大家在直播活动中提到的问题,看看是否能解答你的疑问。

Q:这篇文章的核心思想是什么样的?它对目前的这个图索引算法有什么贡献吗?
A:这篇文章在查询性能上做出了一个很稳定的性能提升,在实验里面测试了不少数据集,都做出了一个比较稳定的效果。从技术贡献方面看,一个是多级的乘积量化算法,一个是基于密度的数据分配,用以替换这个 HNSW 的上层。
Q:这些都是达到了一个 SOTA 的效果是吗?
A:对的,像 HVS 这一篇,主要测试的是小数据集,在百万级数据上,做出一些稳定的性能提升其实是不太容易的。这篇文章整体的效果还是很不错的。我们后面额外提到几个树图结合的方法,它有不同的一些点,像 SPANN 专注于磁盘性能,Elpis 专注的是内存大数据集。
Q:有没有计划说对那种树图结合怎么能够适配流式插入这种场景?不知道在工程实现上,或者在算法上有没有一些想法?
A:首先说今天讲的 HVS 这一篇论文,它已经支持了在线的构建,是可以做线上的流式插入,就是单条向量插进来是可以的。包括 PQ 算法本身,其实也有很多 online PQ 的变种,就是在线算法去更新这个 PQ 的一些论文出来。论文对于这方面的评测方面会比较少,Elpis 就是一个以插入的方式进行构建的,所以它自然也是适合流式插入。目前从学术界的角度来说,大家对它的一个重视程度,可能就是设计出来一个接口,然后表示可以支持动态数据集,但是就没有把它把这个指标当做一个很重要的性能评估来做,这一点我觉得可能和产业界是有一些区分的。
Q:按照树图结合型索引的方式,和我在一个顶层套一个类似于 IVF, IMI 之类,底层用 HNSW 有什么优势?
A:第一各方面来说像 Faiss 的这种 IVF PQ 或者是 IVF ADC 类似的实现方式,确实会有一点像这种树图结合,只不过是实现得比较初级。那按照往常的评测结果,是比不过 HNSW 。Elpis 这篇文章,它最终的实验结果是在大数据集上能比 HNSW 能做得更好,也就间接证明了就是它可能会比 IVFADC 这些方法会更好一些。从原理上讲,Elpis的一个优势是整体分区比较均匀,构建开销比较小,它的分区质量也是比较高的,在实际查询时,Elpis提供的导航性比IVF更好。
Q:树图结合型索引优化的方式是要通过树结构分区以节省图索引的查询路径长度,那树索引的深度与这个查询路径的缩短是否存在一个权衡?
A:肯定是存在这种权衡的,用树索引把 HNSW 的上层结构替换掉,就是要看这个上层结构够不够好。那么今天讲解的 HVS 索引,它的优势就是上层的路由非常快,每次距离计算都不需要真实地计算,只需要查表即可。所以说这个上层结构代价极小,能达到优化的效果。
好啦,本期内容到此结束,点击阅读原文跳转到直播回放,关注回复【加入社区】进群获取完整课件哦。
参考文献
[1] https://openai.com/blog/chatgpt-plugins
[2] https://platform.openai.com/docs/guides/embeddings
[3] Malkov, Y. et al. 2014. Approximate nearest neighbor algorithm based on navigable small world graphs. Information Systems. 45, (2014), 61–68.
[4] Malkov, Y.A. and Yashunin, D.A. 2017. Efficient and Robust Approximate Nearest Neighbor Search Using Hierarchical Navigable Small World Graphs. IEEE Transactions on Pattern Analysis and Machine Intelligence. 42, 4 (2017), 824–836.
[5] Lin, P.-C. and Zhao, W.-L. 2019. Graph based Nearest Neighbor Search: Promises and Failures. arXiv. (2019).
[6] Candan, K.S. et al. 2022. GraSP: Optimizing Graph-based Nearest Neighbor Search with Subgraph Sampling and Pruning. Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining. (2022)
[7]Liu, Jun, et al. "Optimizing Graph-based Approximate Nearest Neighbor Search: Stronger and Smarter." 2022 23rd IEEE International Conference on Mobile Data Management (MDM). IEEE, 2022.
[8] Maier, D. et al. 2020. Improving Approximate Nearest Neighbor Search through Learned Adaptive Early Termination. Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data. (2020),
[9] Yang, K. et al. 2021. Tao: A Learning Framework for Adaptive Nearest Neighbor Search using Static Features Only. arXiv. (2021).
[10] Zhang, P. et al. 2022. Learning-based query optimization for multi-probe approximate nearest neighbor search. The VLDB Journal. (2022), 1–23.
[11] Lu, K. et al. 2022. HVS: hierarchical graph structure based on voronoi diagrams for solving approximate nearest neighbor search. Proceedings of the VLDB Endowment. 15, 2 (Dec. 2022), 246–258.
[12] Chen, Qi, et al. "Spann: Highly-efficient billion-scale approximate nearest neighborhood search." Advances in Neural Information Processing Systems 34 (2021): 5199-5212.
[13] Echihabi, K. et al. 2023. Elpis: Graph-Based Similarity Search for Scalable Data Science. VLDB, (Mar. 2023), 2369–2372.
看到这里的你不妨点亮赞和在看留下你的足迹吧~
向量检索实验室
微信号:VectorSearch
扫码关注 了解更多








