【导读】本文分享内容及图片来自HVS:Hierarchical Graph Structure Based on Voronoi Diagrams for Solving Approximate Nearest Neighbor Search,该篇论文是发表在 VLDB2022 的一篇工作,主要思路是在于融合 HNSW 和 PQ 的特性,进一步提升 ANNS 算法的性能。本文会从图索引、量化索引、HVS 的设计、与其他混合型索引的对比这几个方面介绍该篇工作。
Graph Based
01
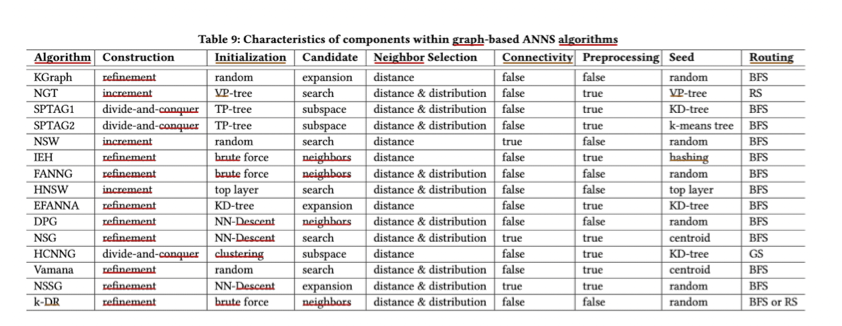
由上图可以看出,大多数图索引的寻路(Routing)阶段都是 BFS 的方法。该方法可以概括为维护一个优先队列,通过节点之间的邻居关系不断迭代,逼近目标节点。那么可以定义搜索阶段的时间复杂度是 O(yvd),y 代表搜索路径长度,v 代表平均节点出度,d 代表向量维度。HNSW、NSG 都是在降低其中的 y 和 v。这带来的一定的缺点就是不改变原始数据维度导致距离计算复杂度高,且占用大量内存。
Quantization Based
02
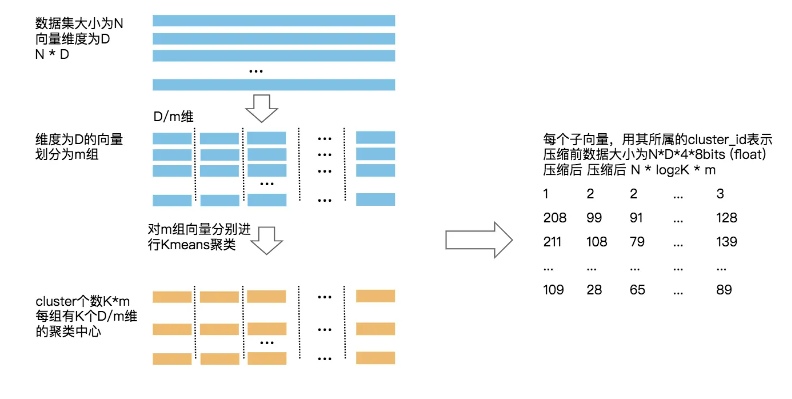
PQ:通过降低向量维度,减少距离计算的时间消耗,但存在精度天花板,量化一定会带来精度损耗。
两阶段搜索 IVF-PQ:
1. 逐渐逼近目标区域(粗聚类+ PQ 扩界召回)
2.在候选区域内通过原始向量进行距离计算并完成召回
综上,在图索引领域是否可以存在优秀的二阶段搜索算法?
HVS结构
03
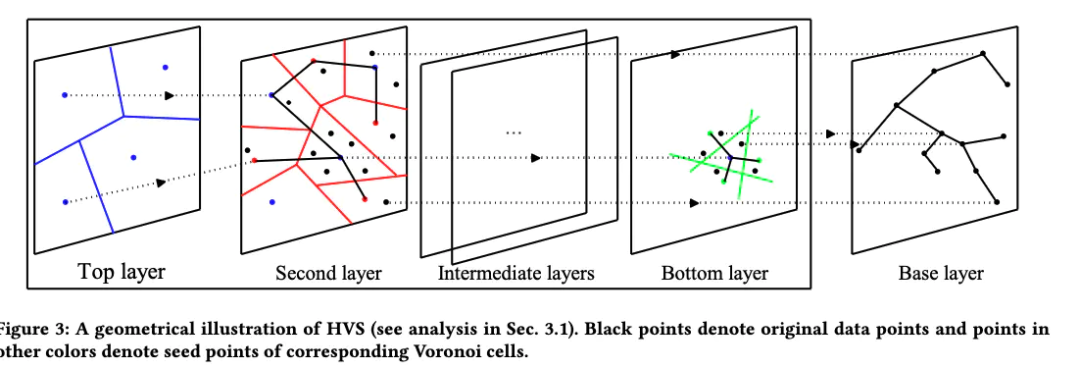
HVS的主要结构分成三部分:
第一部分:
top layer,这一层没有边,只有一些 node,但不是数据集中的点;由计算得到的4个聚类中心构成。
第二部分:
从 second layer 到 bottom layer 这些中间层,有一些 node,node 之间有边相连(以 HNSW 的方式连边),每个 node 会对应一个真实数据点作为代表;
首先在第T层 (bottom layer) 做一下 PCA-OPQ,结果需要保留一个旋转矩阵,和2的T次方个 codebooks。
其中,需要注意的是,第一部分和第二部分的图中 node 不是数据集中的点,具体来说:
在 bottom layer,会做一次 PQ,PQ 的聚类中心就是图中的 node;这一次 PQ 选的段数会很多(即 codebook 个数很多),之后上层图通过将两段合一不断将 codebooks 个数减半来让图中的node个数向上层快速衰退。通过这种方法保证了上层的 node 一定属于下层,正因为此才可以将多层的 PQ 图之间构建连接。这种多层结构在每层中虽然形如 PQ,但实质上只有 bottom layer 的结果是根据PQ结果生成的。
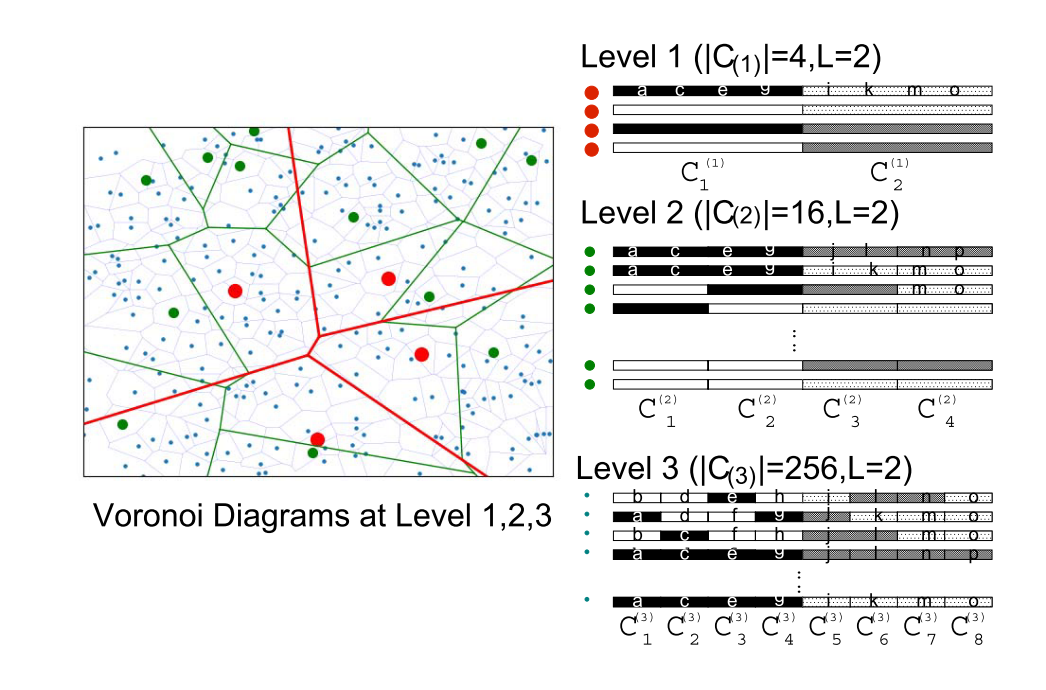
第三部分:
base layer,就是 HNSW 第零层,每个 node 都是真实数据点。与 hnsw 的0层完全相同。
从 top layer 到 base layer,从上往下会有一些跨层的边,只有这些边能负责跨层的路由。第一部分和第二部分在查询时负责找 base layer 的入口点。
vector search
在自底向上生成多层PQ图的过程中有两个问题
Part.1
如何两两配对 codebook?
作者使用互信息来评价一对 codebook,其中f函数代表 x 在C上的密度,定义为数据集中点落在 x 的 cell 里的比例,比例越高密度越大。作者认为 PQ 能更好处理熵值大的数据,因此就选择互信息大的了。由于找一个全局最优的组合很困难,是一个 NP-hard 的问题,所以也就贪婪算法了,每个 codebook 找一个局部最优的而已。
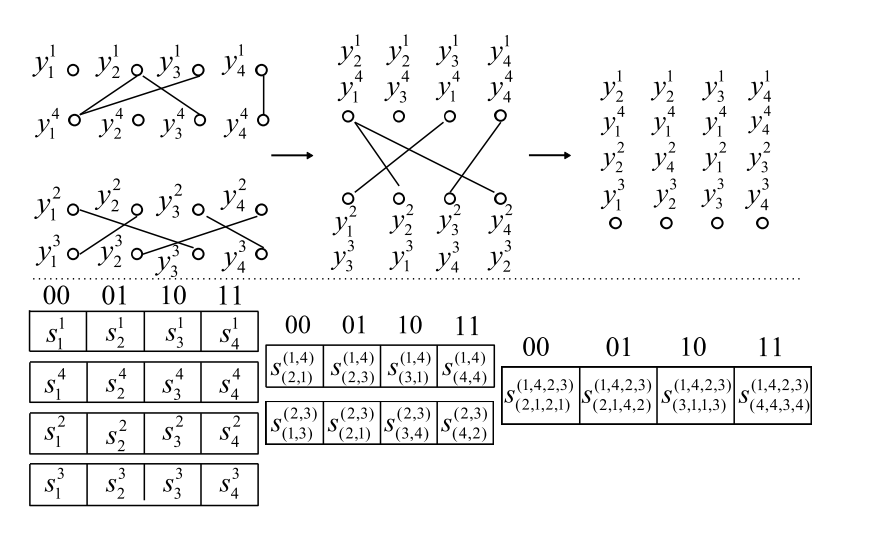
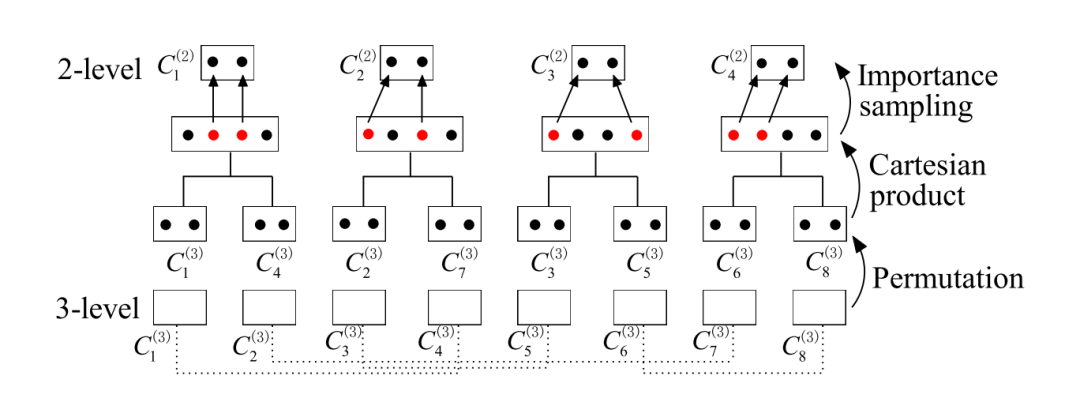
Part.2
如何选择 L 个 codewords ?
合并两个 codebooks 需要从多个 codewords 中选择L个最合适的。作者将这个 codewords 做了个带权 K-means,然后把聚类中心移动到最近的 codewords 即可。如果有重复,就再用一个“重要性采样技术”去生成剩下的几个。
HVS 与其他索引对比
04
无论什么类型的索引,在近似最近邻检索任务上,本质上我们都是在做召回率和花销之间的平衡。这个花销包括时间开销、内存开销等。
在 HNSW 中,一个多层结构的所有非0层都在做一件任务,即是给0层选一个更优秀的 entry point。使得在0层可以更快更准的逼近目标节点。
所以算法设计层面中这两者更偏向于 recall,但由于小世界图模型的可导航性质(由启发式选边策略带来的高速公路)和多层结构导致了最终的 time cost 也小于 PQ。缺陷是内存消耗过大。
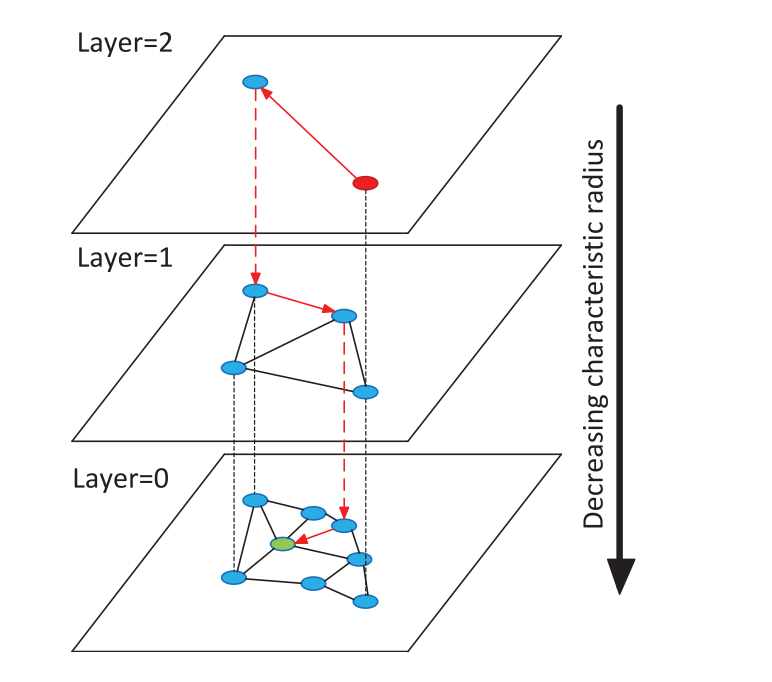
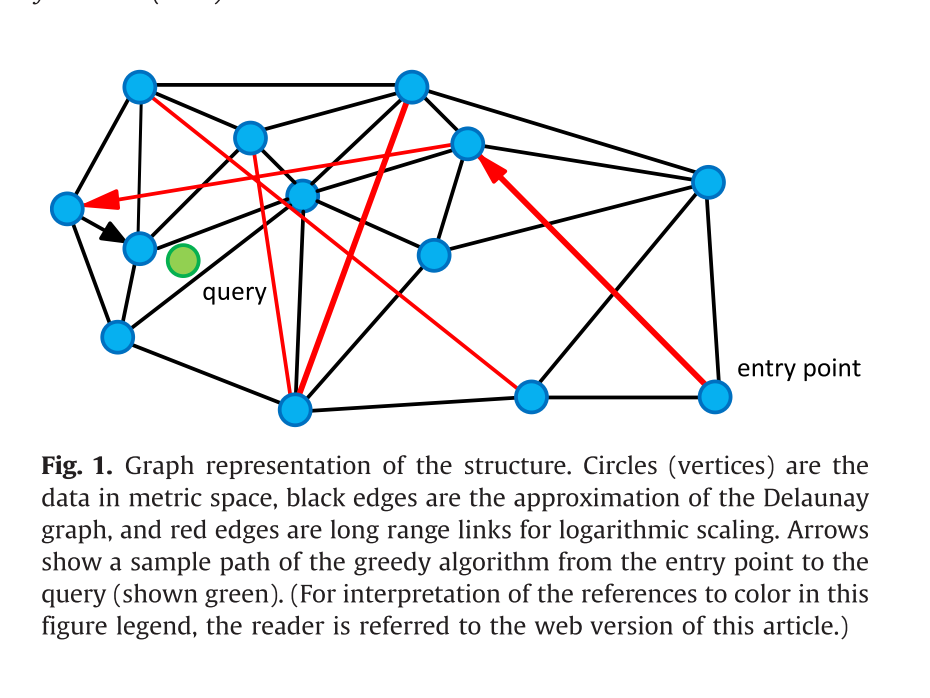
而在 HNSW 的前身 NSW 上,他的 entry point 的选择是一个随机节点或者可以选择一个出度最高的节点。正因为如此,HVS 的作者做出了一定的改进,在两者之间取中间且发挥了 PQ 的量化优势,代替了 HNSW 的非0层。这一点也导致了 HVS 虽然形如 HNSW 但本质上不同的点在于从算法设计上,HVS 更偏向于效率和开销。
目前,在混合型索引还有一种比较简单的方法一般称为 IVF-HNSW-PQ。这种方法同样是一种两阶段的搜索方法。
1. HNSW 使用所有聚类中心进行构图
2. 返回 n 个簇,在簇中使用 PQ 进行召回
这种方法的优势在于:
1. 使用了两阶段的方案
2. 聚类中心数量相对完整数据量较少,极大的节省了内存消耗
但有一个很明显的缺点,即同为两阶段搜索,在第一阶段使用了精度高的算法、在第二阶段使用了有精度损失的方案。而 HVS 的设计使得第二阶段使用图搜索的方式极大地规避了第一阶段的量化损失。
实验部分
05
1
内存消耗:
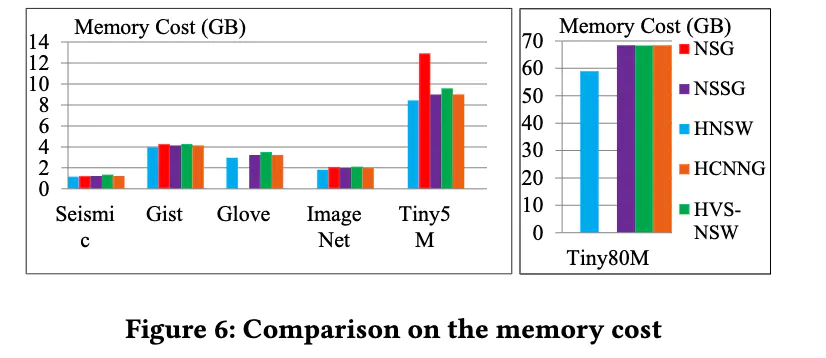
NSG 和 NSSG 的出度很大,因此内存占用量比 HNSW 还要高。HVS-NSW 的内存消耗高于 HNSW。作者认为是 seed points 更多,且每个 seed points 还会关联真实数据节点。
2
时间开销:
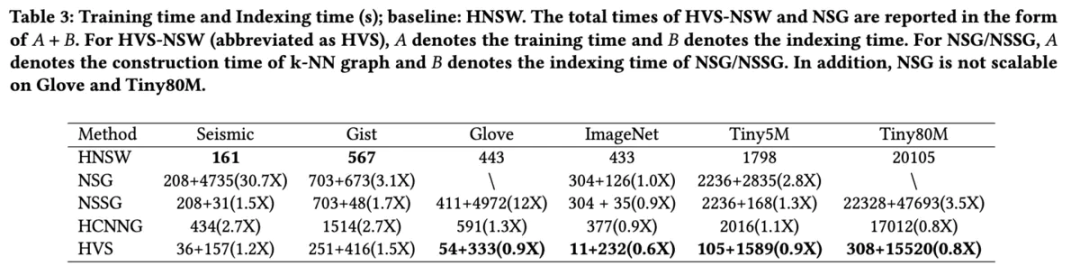
HVS 构建速度较快,原因是它的 efconstruction 比 HNSW 选的要小(500 v.s. 1024),能选的比较小的原因是上层图质量比较高。而上层图的构建速度上,作者认为得益于 distance book 可以构建地比较快,HVS 的上层构建也比较快。
3
召回率:
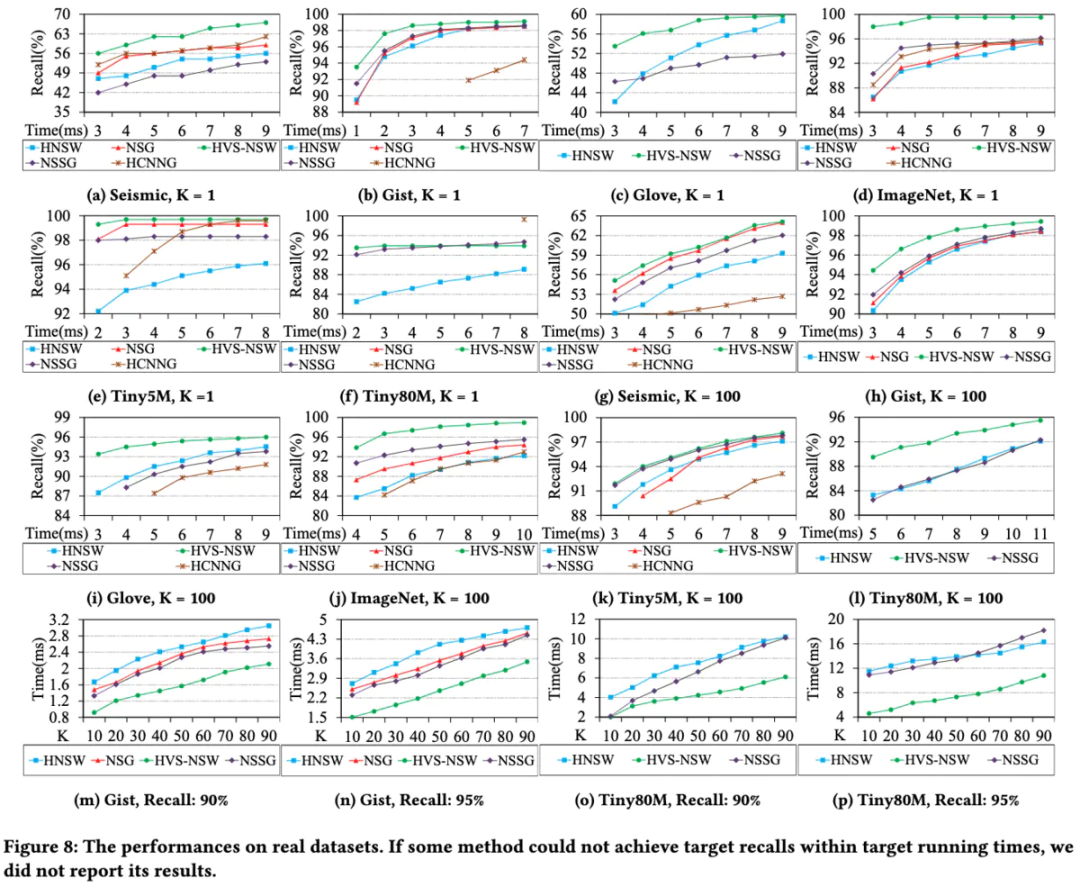
召回率方面,在控制相同召回率的情况下,HVS 的搜索时间是更小的。且在有些数据集下精度上限对比于HNSW也会有明显的提升。
总结
1. 代替了 HNSW 顶层的寻找 entry point 的过程。
2. 动态分区的思路,更像是为数据密度更高的簇划分更多的区域。
3. 二阶段的搜索,充分融合了两算法的优势,弥补了量化的精度损失
对于实验部分,或许应该验证不同方法选择出的 HNSW 最终在底层图上的平均搜索路径长度。







