ICLR 2020: Learning Space Partitions for Nearest Neighbor Search

向量检索实验室 2022-11-04

215

【导读】在分布式场景下，分区型索引在数据分配上起到至关重要的作用。本文介绍选自 ICLR 2020 的一篇论文 Learning Space Partitions for Nearest Neighbor Search，结合平衡图划分与监督分类器技术，构建基于学习的分区型索引。

高效的NNS数据结构

最近邻搜索问题（Nearest Neighbor Search，NNS）一直是数据分析领域的热点问题。随着数据量愈发庞大，传统的详尽搜索方法已经不再适用。因此，当前研究的重心在于如何更高效地寻找近似的最近邻。

影响近邻搜索效率的主要因素就是数据量和数据维度，针对这两个因素，当前的优化的方法大致可以分为两类：

索引（Indexing）：索引的目标是构建一个数据结构，对于一个给定的查询点，它可以返回一个包含近邻的数据子集。可以看出索引意在构造高效的数据访问结构来减少距离计算的次数；
草图（Sketching）：草图的目标是计算数据点的压缩表示，从而削减距离计算的开销。虽然压缩数据会带来不可避免的精度损失，但在实际使用中，往往极少量的精度损失就可以换来跨数量级的压缩效果。

索引与草图分别针对两种因素进行优化。二者也经常被结合使用以提升整体性能，例如：Faiss中的PreTransform类索引支持先对数据进行线性变换降维（如：PCA、ITQ），然后在降维后的数据上构建索引进行查询。

struct IndexPreTransform : Index {
    std::vector<VectorTransform*> chain; // 一组线性变换
    Index* index;                        // 索引
    // ...
}

分区型索引

这篇文章的研究主要关注的就是使用索引技术来加速近邻搜索。其中，索引技术使用到的是基于空间分区的索引。那么什么是基于空间分区的索引呢？我们假设数据集中的所有数据都是高维点的形式，它们都分布在一个数据空间中（如：欧式空间）。空间分区就是将这个数据空间进行划分，可以均匀划分也可以按照一定的规则划分。之后根据这个空间的划分规则将整个数据集拆分为多个子集，这样构造的索引就是基于空间划分的索引。在查询的时候，给定一个查询点，我们先验证查询点属于哪一个数据子集，之后直接将这个子集中的所有点作为候选结果，在其中计算出最近邻。这样，相较于传统的详尽搜索，分区型索引有效地将检索的数据量控制在一个数据子集大小。为了提高精度，也可以同时将邻近的数据子集中的点一起作为获选结果并检索。

基于空间分区的索引方法有很多，如：

局部敏感哈希（LSH）：使用哈希函数将数据点散列到不同的分区中；
基于量化的方法：通过k-means算法实现分区；
基于树的方法：如PCA树，沿主特征向量切分数据空间。

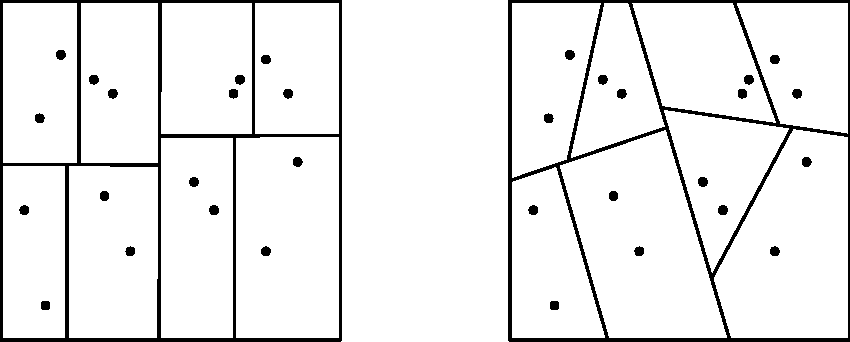
图一基于空间划分的索引

分区型索引的优势

既然文章重点关注分区型索引，那么相较于其他索引方法，分区型索引都有什么值得关注的优势呢？

首先，分区型索引原生就很适合分布式环境。在亿万数据量的场景下，集中式系统已经不能满足性能需求。分布式系统能够联合多个机器实现计算，突破了单机的存储和计算性能瓶颈。通过分区型索引可以将相近的数据派发到不同的机器上计算，例如：向量数据库Milvus的集群版本，采用一致性哈希的索引方法将数据派发到不同的数据节点上。

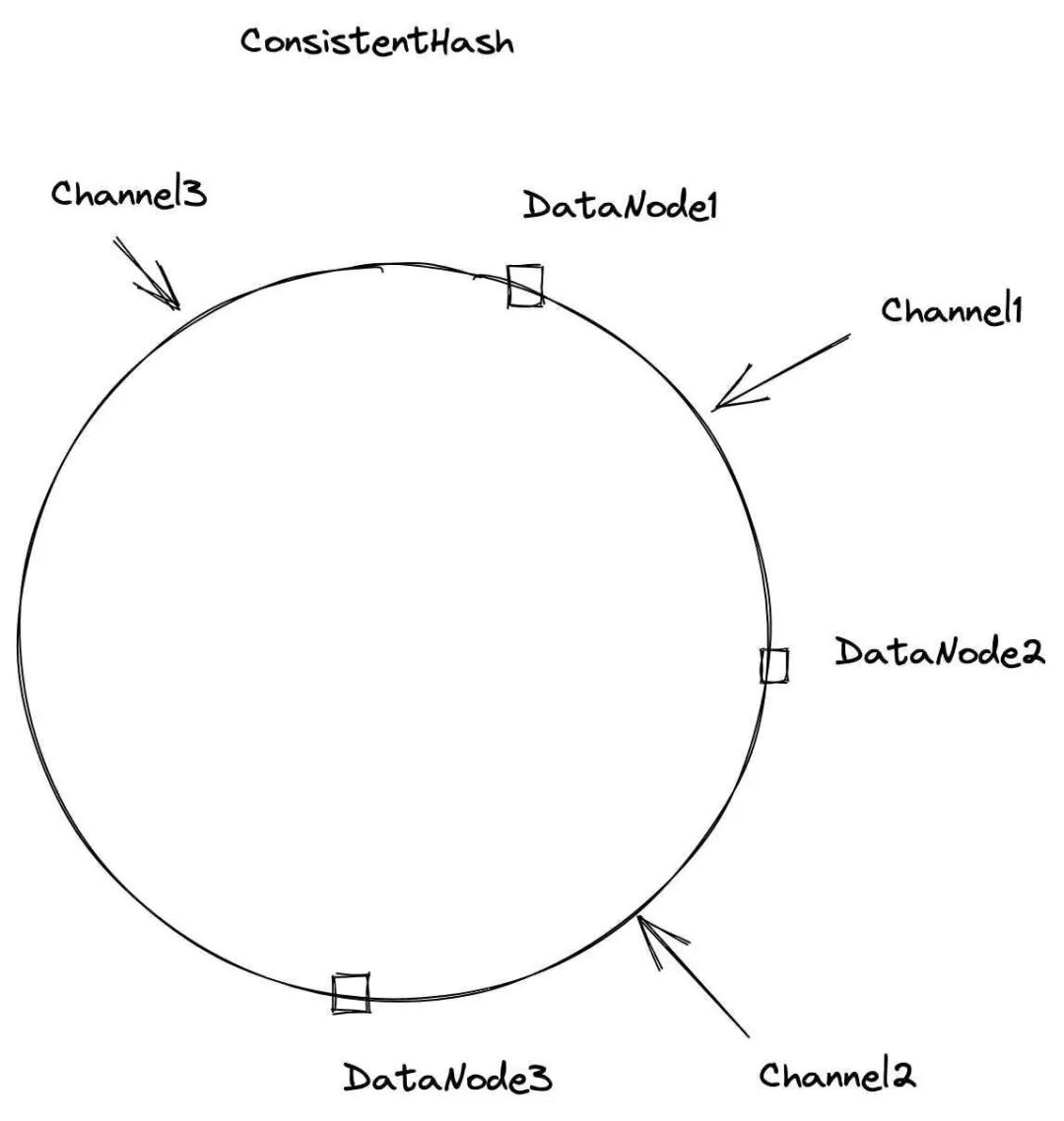
图二 Milvus中的一致性哈希（摘自Milvus官网）

其次，分区型索引特别适合GPU的计算架构。因为GPU的优秀的并行计算能力，越来越多的索引结构都被适配到GPU上实现计算加速。分区型索引因为简单且可预测内存访问模式，很适合与GPU相结合。

最后，分区型索引可以与加密技术结合，实现加密NNS。目前应用广泛的图索引结构在查询时需要多次自使用访问数据集，而分区型索引每次查询只需要访问一次数据集，大大增加了数据的安全性。

基于学习的分区型索引

针对分区型索引，文章提出了一种结合平衡图划分与监督分类器的新型分区索引，Neural LSH。方法由以下三个主要步骤组成：

在原始数据集上构建k-NN图，即每个数据点连接其k个最近邻点的图；
均匀划分k-NN图，使得划分得到的子图节点数量相近，子图之间的边尽可能少；
由第2步得到的划分构建数据点到分区的映射标签，使用标签数据来训练分类器。

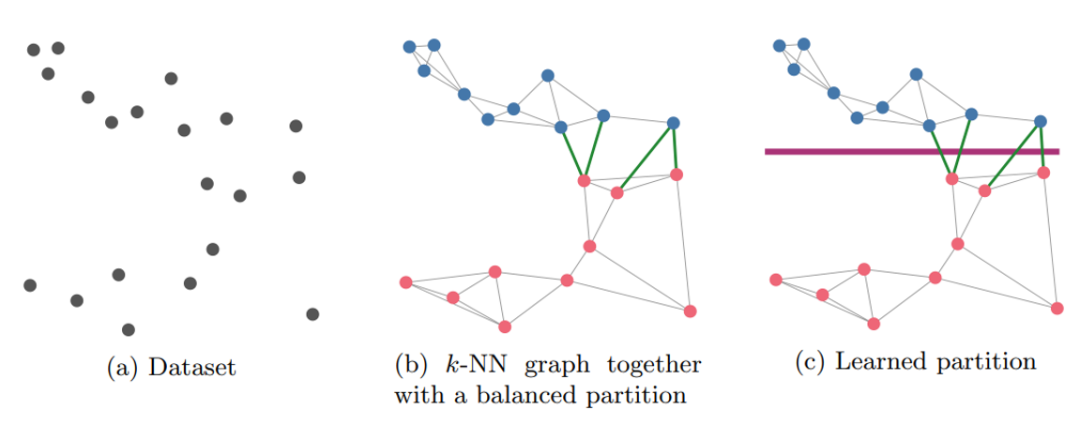图三 Neural LSH 的各个阶段

可以看出Neural LSH的基本思路是使用监督分类器来学习由平衡图划分得到的分区模式。平衡图划分保证了分区的质量，监督分类器保证了索引的效率。

根据以上步骤可以看出，Neural LSH期望构建的分区型索引具有一些特性。首先，平衡，在第2步中得到的划分尽可能地保证了各个数据子集的平衡；其次，局部敏感，使用k-NN捕获数据之间的近邻关系，保证划分后的每个子图中都包含的某个点与其近邻点；最后，简单，分区的描述是紧凑的，并且使用分类器可以高效地计算出数据点的位置。

使用平衡图划分来实现数据分区有平衡和局部敏感的特性，但是仍存在一些问题。在切图的时候，势必会有一些表示近邻关系的边被斩断，导致一些点与其近邻被分配到不同的数据子集当中。

基于平衡图划分实现数据分区

针对以上问题，文章首先证明了对k-NN图进行切分可以保证被斩断的各子图之间的连边是尽可能少的。对于点p，设Dclose为在点p与其近邻点p'组成的边上的随机分布，α表示数据点与其近邻点之间的距离，β表示数据集中任意两点之间的距离。在α远小于β的情况下，使用超平面H对k-NN图进行划分满足下式：

可以看出，在k-NN图上存在平衡划分满足子图之间的连边尽可能少。

分层分区索引

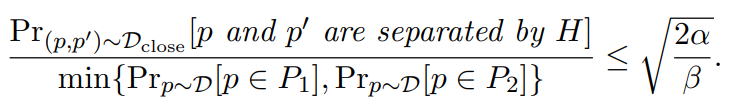
当所需要划分的分区数量m很大时，为了提高分区效率，文章提出以分层的结构构建分类器。也就是说，首先将数据空间划分为m1个分区，然后递归地将每个分区再划分为m2个分区，以此类推。这种分层分区比一次性分区要简单得多。

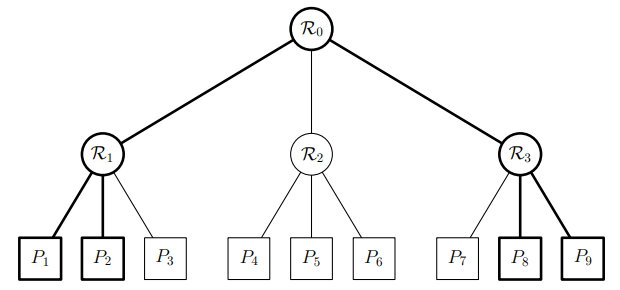
图四分层分区，m1=m2=3

软标签结合多探针搜索分类器训练

其次，对于仍不可避免的一些边被斩断的问题，文章在训练分类器的时候采用了软标签的方式，结合多探针搜索，有效地降低了精度的损失。

给定一个查询点，分类器首先预测得到一个包含查询点的分区，然后在该分区中搜索最近邻。为了达到更高的精度，Neural LSH 的分类器不只预测包含查询点的分区，而是预测一个查询点及其近邻点在各个分区中的分布情况。基于此分布，实施多探针搜索提升精度。

为了能够正确地引导分类器预测到近邻点分布，Neural LSH 为每个数据点都生成的软标签。具体地，设置一个超参数 S ≥ 1 和一个数据点p，点p的软标签就是包括它在内的随机S个近邻点所在分区的分布情况。在训练时，使用预测分布与软标签之间的KL散度作为损失引导模型更新。

实验效果

文章使用KaHIP算法实现平衡图划分，依照分类需求构造分类器。对于多分类问题基于神经网络构建分类器 Neural LSH，对于二分类问题基于回归模型构建分类器 Regression LSH。并且从候选集大小和准确率两个角度评估了方法的性能。其中，候选集大小能够有效评估索引是否高效，更小的候选集代表更少的冗余计算；文章定义准确率为真实k近邻在候选集中的占比，能够有效评估分区是否优质。

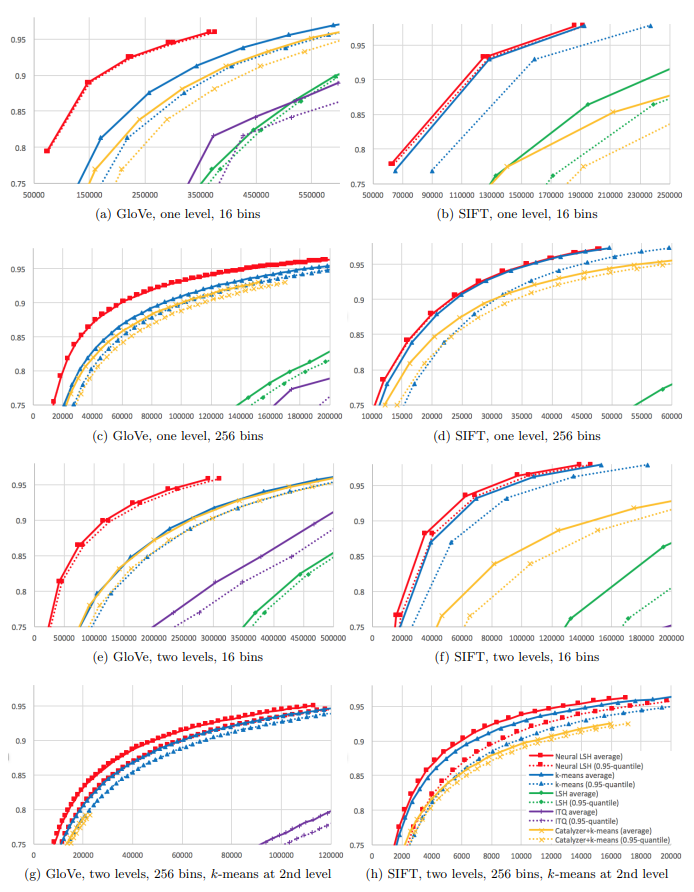图五 Neural LSH 性能评估

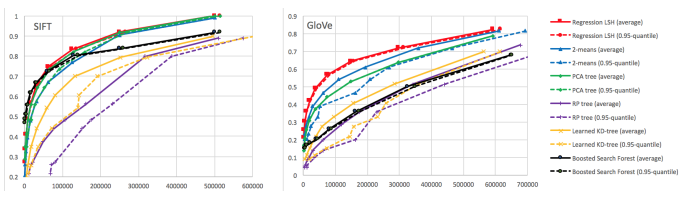图六 Regression LSH 性能评估

从实验结果可以看出，无论是单层还是双层，多分类还是二分类，Neural(Regression) LSH 的性能都要优于基准算法，总是能获取更优质的分区。足见，以k-NN图引导近邻分区是有效的。

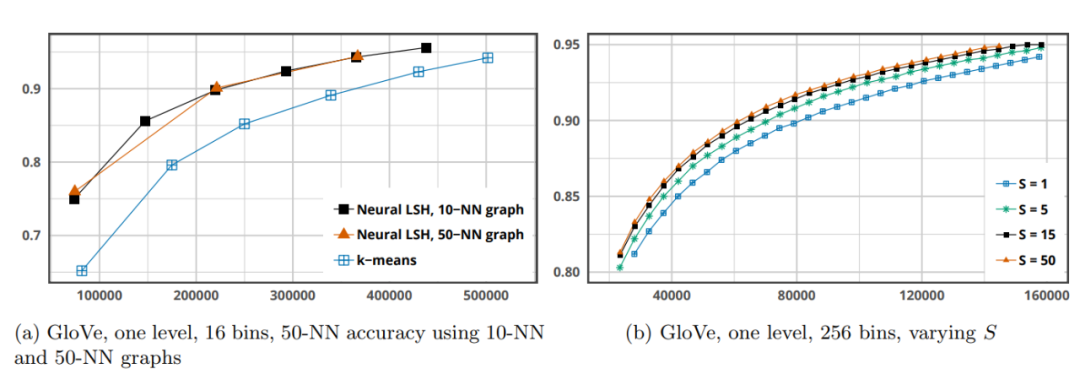图七参数实验

此外，文章也对一些重要的参数对模型的影响做了评估。首先，对于k-NN图的k值选择上，可以看出相较于k-means(k=50)算法，Neural LSH 明显性能更强，分区质量更好。并且k=10和k=50两种情况对Nueral LSH 性能的影响并不明显。其次，对于生成软标签依赖的超参数S，随着S的增大，可以看出模型的性能有较为明显的提升。多探针搜索是有效提升索引准确率的

总结

分区型索引作为一种高效的NNS数据结构，相较于其他索引方法，更适合新型的计算架构，如：分布式、GPU并行等。Neural LSH 利用平衡图划分与监督分类器技术有效地获取了优质的近邻分区以及高效的数据分配。这是一个使用机器学习方法加速索引计算的新鲜尝试。然而，学习型索引仍然面临很多挑战。k-NN图的构建与平衡划分都是时间开销庞大的工程，面对亿万规模数据集时仍需改进。监督分类器的延展性、泛化性能仍有待检验。

参考资料：

[1] Dong, Yihe et al. “Learning Space Partitions for Nearest Neighbor Search.” ICLR (2020).

[2] Johnson, Jeff et al. “Billion-Scale Similarity Search with GPUs.” IEEE Transactions on Big Data 7 (2021): 535-547.

[3] Wang, Mengzhao et al. “A Comprehensive Survey and Experimental Comparison of Graph-Based Approximate Nearest Neighbor Search.” Proc. VLDB Endow. 14 (2021): 1964-1978.

向量检索实验室

微信号：VectorSearch

扫码关注了解更多

分类器大数据 lsh 数据库分区

文章转载自向量检索实验室，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

ICLR 2020: Learning Space Partitions for Nearest Neighbor Search

向量检索实验室

评论