1 摘要
这篇文章于八月份被VLDB接收,作者团队由上交、达摩院组成。文章的完整标题是Learning-based query optimization for multi-probe approximate nearest neighbor search。从这个标题中我们可以看出本篇主要围绕以下几个方面进行展开。
Learning-based 基于学习的方法 query optimazation 针对查询阶段的优化方案 multi-probe ANNS 适用于多探针ANNS算法
那么,在本篇文章中我们会重点关注如何解决以下的几个问题:
如何学习到过往的query中的经验,即如何利用好先验知识 针对数据如何分区是否有更优的方案 多探针方案中的参数如何选择
2 背景知识
2.1 多探针ANNS算法
前面的文章中我们已经介绍过什么是ANNS算法了,那这篇文章提及的多探针ANNS算法是指通常我们会将全量的向量数据使用例如聚类等方法进行分区。多探针即在所有分区中执行检索并收集生成最终的kNNs。这种方法有很多应用,例如在基于磁盘的数据库系统中,每个分区都保存为单独的文件或磁盘块。这种系统在人脸识别场景或其他相似item的检索中十分常见。同时,分区的方案可以与量化结合,以实现基于GPU的高吞吐量ANNS算法。多探针ANNS算法通常分为以下两种。
one-level approaches
将完整的原始向量存储在每个分区中。而检索算法通过启发式的方案选择M个分区,在选中的分区中执行暴力穷举的检索。例如Faiss中的IVF-Flat索引就是典型的one-level approaches方案。
two-level approaches
一般基于图索引的分布式分区检索方法都是使用two-level approaches方法。依然将数据分为多个分区。不同的是,为每个分区构建图索引。例如NSG中,将数据集随机拆分成多个分区,为每个分区构建NSG索引以支撑分布式ANNS。ADBV中选择了使用Kmeans聚类对数据集进行分区,并通过计算query与各个聚类中心的距离进行筛选分区。在选择的M个分区中,分别的执行ANNS算法返回c个候选邻居。最终归并每个分区返回的c个候选邻居,生成最终的kNNs。
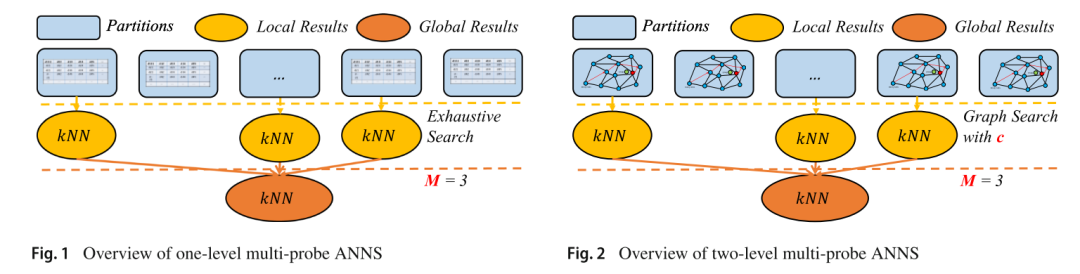
综上,我们可以看出,在多探针的方案中,影响效率的因素有两个。
更优的数据分区方案 如何选择分区以及two-level方案中每个分区要返回的候选邻居个数c如何设定
因素2中,M和c的选择是较为关键的。目前的方案中,通常选择固定的M、c。但很显然这并不灵活。
举一个例子,假设将数据集划分为512个分区,为每个分区建立图索引。某query的top 10节点中,有8个节点在分区1中,2个节点在分区2中。在这种情况下,找到top 10 的最有效的方法是仅搜索这两个分区且在分区1中返回更多的结果,在分区2中返回较少的结果。
如果在这个过程中,我们选择了固定的M、c分别为50,20。很显然造成了大量的时间开销。
2.2 0-1背包问题

给定多个物品,每种物品都有自己的重量和价值,在限定的总重量/总容量内,选择其中若干个,设计选择方案使得物品的总价值最高。用表达式进行定义则如下。
通常我们使用动态规划来解决0-1背包问题。
for (int i = 1; i <= N; i++) {
for (int w = 1; w <= W; w++) {
if (w - wt[i-1] < 0) {
dp[i][w] = dp[i - 1][w];
} else {
dp[i][w] = max(dp[i - 1][w - wt[i-1]] + val[i-1],dp[i - 1][w]);
}}}
2.3 多项选择背包
在0-1背包的基础上,每种物品都有了类别属性。需要从每类中选择一个物品,使得利润最大化而不超过容量W。
2.4 LR逻辑回归模型
LR逻辑回归模型是二分类的经典模型,是一个被Sigmoid函数归一化后的线性回归模型。输入一个向量后,通过sigmoid(wx+b)预测样本属于正类的可能性。其中w、b是模型的优化参数。
损失函数使用对数损失函数(二分类简化):
2.5 多项逻辑回归模型
将逻辑回归扩展到多分类任务上,将sigmoid函数改为softmax,对于d维向量z,softmax如下定义:
对于一个样例x,共有d个类别,则有d维向量y是x的one-hot标签。
损失函数选择交叉熵:
2.6 多层感知机
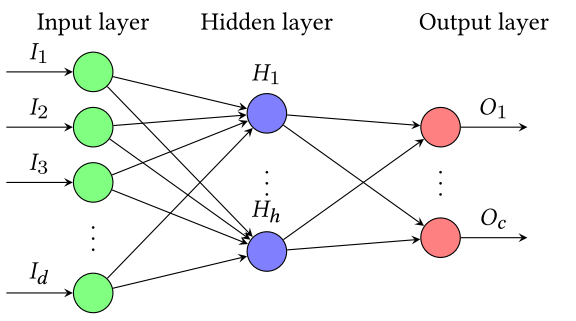
经典的多层感知机包括三层,输入层、隐藏层、输出层。相邻层之间是全连接的。每个神经元节点都会使用激活函数进行激活。采用反向传播的方法进行训练其中的所有权重和偏置。
3 LEQAT
在学习完以上背景知识后,我们就可以来看一下LEQAT的整体架构。为了解决如何学习过往的query的经验和如何优化query查询时所选的c、M两个参数。整个优化器分为两部分。
通过模型学习和估计每个query的KNN分布
基于KNN分布,将查询参数配置问题转换为背包问题进行参数的优化
3.1 kNN分布预测模型
一个优秀的kNN分布预测模型应该满足
准确:预测器必须产生合理准确的预测来帮助我们解决问题。 高效:不能在kNN分布预测阶段承受太大的开销,即推理必须比查询执行快得多。
这里首先介绍一种朴素方法:
给定一个查询q,对于由聚类产生的分区,可以得到q与N个分区的聚类质心之间的距离。
di表示q和聚类质心之间的距离,d表示向量
根据更近的分区,可能包含更多最近邻的已知
使用计算预测的分布
该篇论文中提出了以下learned-based方案:
将数据集的N个分区视为N个类别,并将KNN分布视为标签。将KNN分布估计的任务视为了多分类的任务。即使用LR、多层感知机模型进行训练。将每个query的分区选择问题转换成了多分类问题。特别的是,传统的多分类模型通过最后一层softmax后,生成对应每个类别的概率向量。选择概率大的n个类别作为预测的标签。而这里,得到的概率分布向量整体会保存下来。每个类别即每个分区的概率会被下文中参数优化模块所使用。并非直接将概率高的n个分区作为所选分区。
3.2 背包问题求解
one-level approaches中,我们希望能够选择出包含kNNs最多的几个分区。如果将分区看作背包问题中的货品,而上一步推理得到的概率作为每个分区的权重。即可发现one-level approaches问题似乎和0-1背包问题本质类似。公式推导如下:
bi取值为1、0,代表当前分区选或不选。ni为当前分区内有多少个向量(即如果选择了当前分区,那么需要多少次距离计算) Ki为当前分区内有多少个kNNs(相当于背包问题中每个货品的价值),在query到来的时候,对于算法来说,Ki是未知的。这里会使用第一阶段预测的概率计算出一个近似的Ki值。
令,则得到
=
令,则可推出
令,最终我们将one-level的公式转换为如下
这个式子和前面0-1背包的公式就可以对应起来,后续使用求解背包问题的动态规划方法即可进行该问题的求解。
two-level approaches中,我们也可以将分区看作物品类别,在多项选择背包中,我们会决定每类物品选哪几个,而这里我们需要决定每个分区返回几个结果。故也可以通过类似数学变化将两种问题类比起来。详细的推导过程可以参考原文。
4. 实验
4.1 one-level approaches
实验步骤是,对于每个数据集,通过 K-means 或 CPLSH 将其划分为 16/256/1024 个分区。然后,通过穷举搜索训练集的真实 kNN 分布向量。最后,我们使用 99% 的训练向量来训练 LEQAT 中的 NN 或 LR 模型,剩余的 1% 向量用作提前停止的验证集。该模型在 50 个 epoch 下进行训练,当模型在验证集上的损失在最近 10 个 epoch 中没有减少时,停止训练过程。
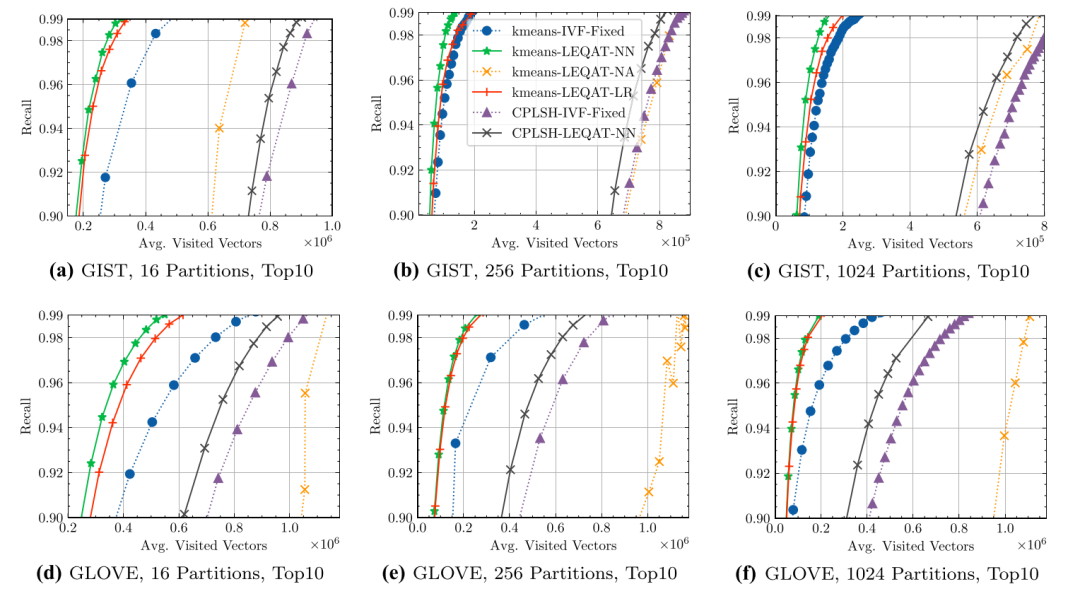
从实验1可以看出,使用LEQAT优化后的查询可以在保证召回率的情况下,减少了访问节点的次数。其中kmeans-LEQAT-NN 都优于其他方法。此外,对于 K-means 和 CPLSH 分区,LEQAT 可以实现更好的效率和准确度平衡。达到相同的召回率时,LEQAT 在 K-means 情况下减少最高 60% 的向量访问次数,在 CPLSH 中减少最高 25% 的向量访问次数。
值得注意的是,kmeans-LEQAT-NA 的性能比 kmeans-LEQAT-NN 差很多,甚至比baseline kmeans-IVF-Fixed 还要差。主要是因为NA模型的kNN分布估计带来的误差误导了dp算法而做出错误的决策。包含许多 kNN 的分区可能会被 dp 错误地丢弃。
4.2 two-level approaches
将 LEQAT 应用于 HNSW 和 SSG,并比较了 LEQAT 与固定配置的性能。使用 X-Clustering 来表示baseline。这里 X 表示图索引的名称,Clustering 意味着我们选择聚类质心最接近查询向量的固定 M 个分区,并为所有分区设置一个固定的 c 配置。同样,使用 XLEQAT 来引用带有图索引 X 的 LEQAT。
将分区号设置为 8、16 和 32,并将这些分区平均分配到 8 台机器上。为这些分区构建了图索引(HNSW 和 SSG),这里根据 HNSW 和 SSG 的原始论文中的建议参数,而无需对其进行微调。此外,我们为每个数据集中的 100 万个训练向量找到前 10 个和前 100 个最近邻,以生成 LEQAT 的 kNN 分布估计器所需的训练输入-输出对。是由 99.9% 召回率的 HNSW-Clustering 完成的。最后,按照上述的相同预处理方法在 LEQAT 中训练 NN 模型。
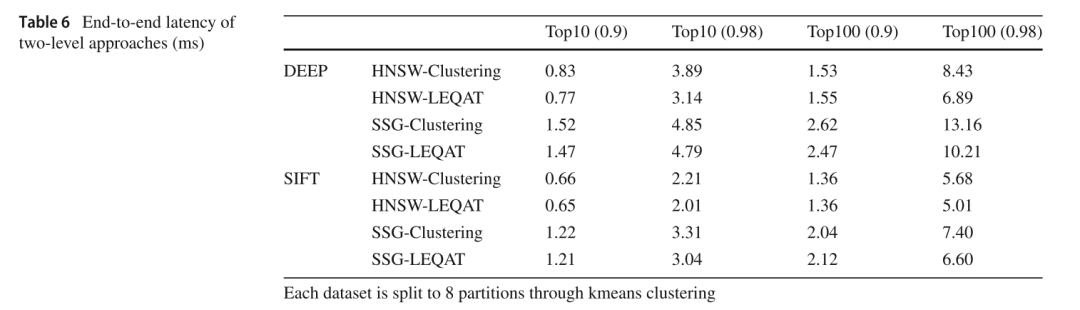
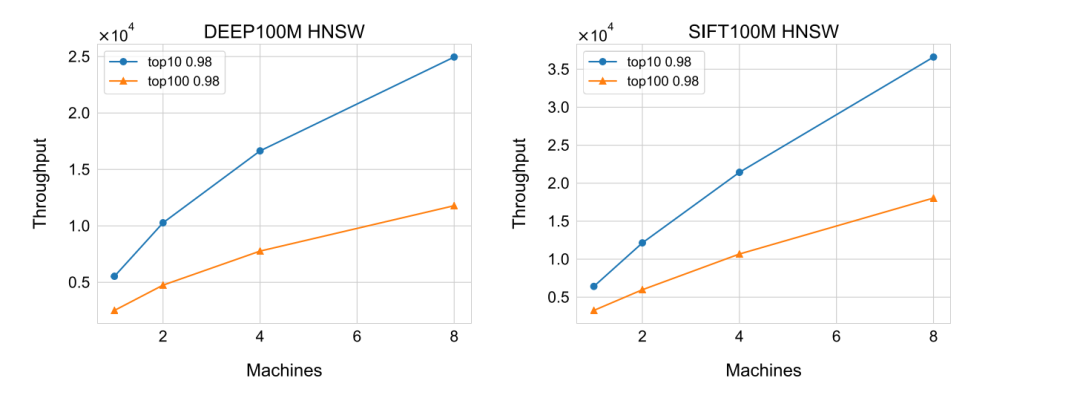
从上表中可以看出,使用优化器的方法还是减少了一定的搜索时间,但效果没有one-level的明显,这是因为多项选择背包的时间复杂度较于0-1背包更高,所以花费在优化器的时间相对较长。故最终结果并没有one-level的那么直观。且对于分布式ANNS而言,延迟主要受耗时最长的分区的影响。吞吐量指标在分布式设置中更为重要。在下图中,可以看出吞吐量提升1.5-3.9倍之间。
5 总结
目前效果较好的多探针 ANNS 解决方案通常将原始数据集分成几个分区,并使用固定配置(c和M)来平衡准确性和效率。然而,本文的实验结果表明,这种固定的配置会导致非最佳的准确性-效率权衡,因为它们没有考虑查询和分区的多样性。在本文中,证明了可以通过利用不同查询的 kNN 分布来优化多探针 ANNS 性能。因此提出了新技术,包括 kNN 分布估计和查询感知搜索配置,以单独确定查询的有效配置。提出的方法大大提高了 SOTA 方法的端到端性能。
向量检索实验室
微信号:VectorSearch
扫码关注 了解更多







