论文分享
今日分享论文MQH: Locality Sensitive Hashing on Multi-level Qantization Errors for Point-to-Hyperplane Distances
本篇论文来自于VLDB2022,提出了一个基于多级量化的可证明的LSH方案来解决点对超平面近邻搜索(P2HNNS)的问题。实验证明这种方法不仅能获得一个对查询结果的概率保证还能使生成的哈希函数有效的修建了错误的点。
Hyperplane超平面
VectorSearch
超平面是n维欧氏空间中余维度等于一的线性子空间,也就是必须是(n-1)维度。这是平面中的直线、空间中的平面之推广(n大于3才被称为“超”平面),是纯粹的数学概念,不是现实的物理概念。因为是子空间,所以超平面一定经过原点。
仿射超平面:仿射超平面是仿射空间中的代数1的仿射子空间。在笛卡尔坐标中,可以用以下形式的单一线性方程来描述这样的超平面(至少有一个ai不是0)仿射超平面用于定义许多机器学习算法中的决策边界,例如线性组合(倾斜)决策树和感知器。本文提到的超平面实际是指仿射超平面。
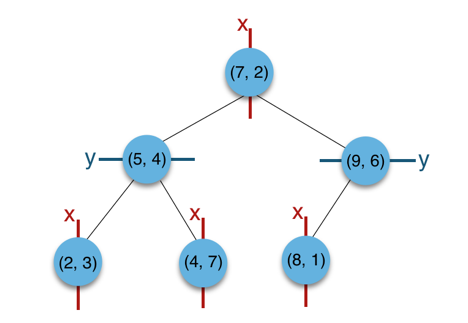
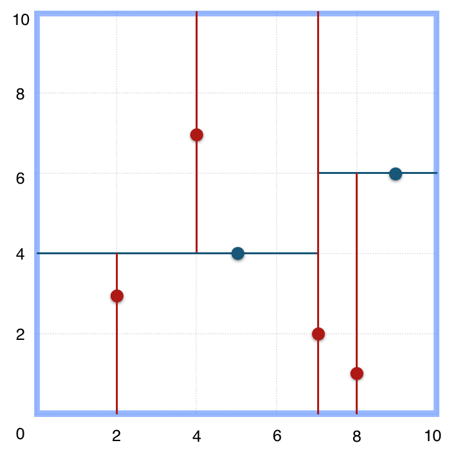
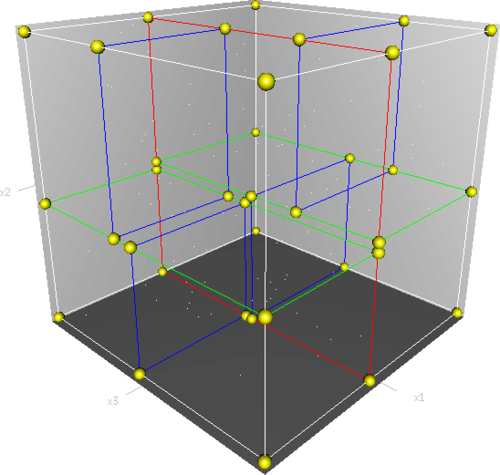
在上图所示的KD树中,我们通常会轮流对x、y轴进行基于仿射超平面的切割。而生成的这种树结构在搜索时类似二分搜索。在三维空间如下图所示。
点到超平面的距离
VectorSearch
如果用
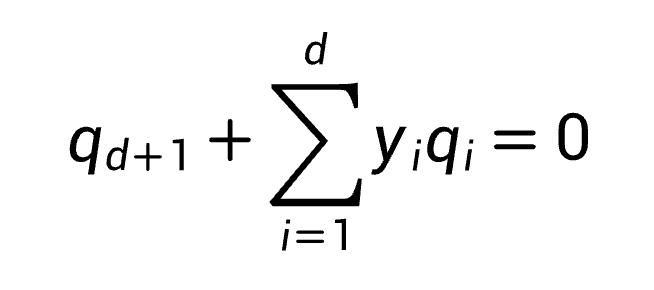
表示超平面,那么最近点xmin可表示为
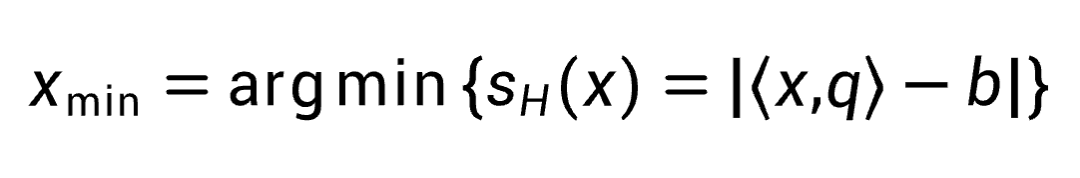
LSH 局部敏感哈希
VectorSearch
LSH的理论依据是将原始数据空间中的两个相邻数据点通过相同的映射或投影变换后,这两个数据点在新的数据空间中仍然相邻的概率很大,而不相邻的数据点被映射到同一个桶的概率很小。
基于这个定义,令 h(x)表示样本x的哈希变换, x与y表示任意两个样本,d(x,y)为x、y之间的距离,d1、d2为两个常量。且d1<d2, p1与p2为介于0与1之间的常量值,若h(x)满足以下两个条件,则称哈希函数h(x)为(d1,d2,="" p1,="" p2)-senstive<="" div="">
1、如果d(x, y) <= d1, 则h(x) = h(y)的概率至少为p1;
2、如果d(x, y) >= d1, 则h(x) = h(y)的概率至多为p2。
通过一个或多个(d1,d2,p1,p2)-senstive 的哈希函数对原始数据集合进行哈希运算,得到一个或者多个哈希表的过程就称为是局部敏感哈希。
MQH结构
VectorSearch
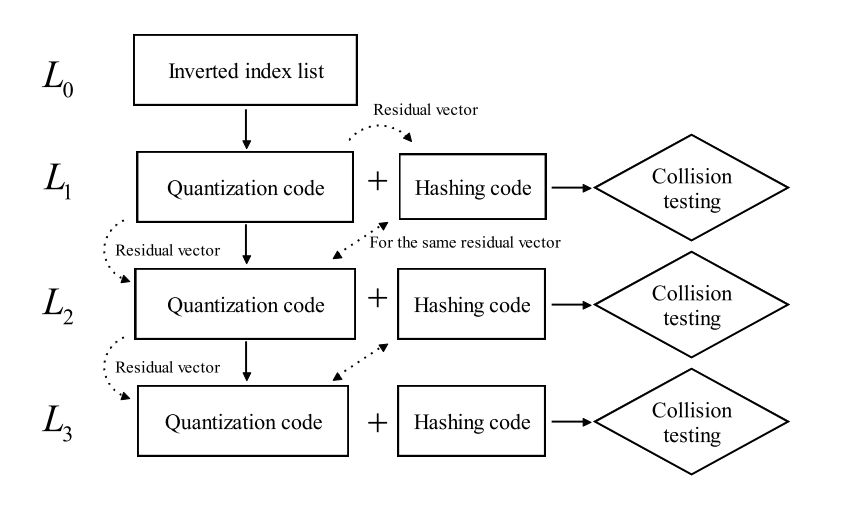
MQH整体基于多级量化和LSH,每一层独立的进行量化(这里不局限量化方法),对量化生成的残差向量进行哈希编码,残差向量同时会作为下一层的量化输入。
训练器中,输入为D - 数据集、L - 层级、M - 每层中码本的个数、 m - 每层LSH中的hash函数个数

在每层的循环中,执行训练量化器、计算量化编码和残差向量、为残差向量进行hash编码。
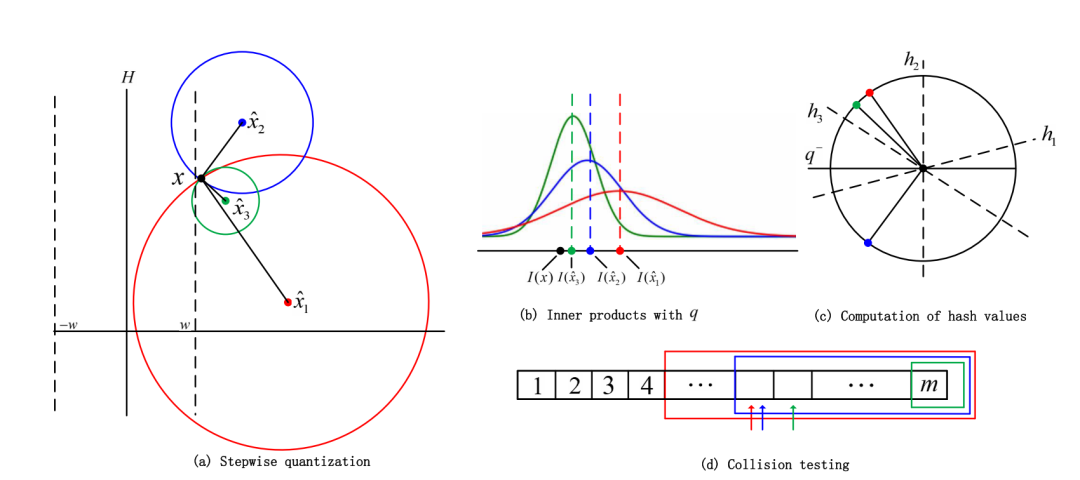
搜索阶段,以(a)中的黑色点x为例,因不在虚线范围内(代表可能是近邻的一个区域),第一层中的量化结果为红色点x1,两者的差值即为残差向量。
根据推导,在第一层中该残差向量与目标平面对应的q向量发生的碰撞次数应该在[5,m]。实际发生碰撞次数也是在该范围内,所以该数据点进入下一层,图中蓝色代表第二层。在第二层中重复搜索过程,在碰撞检测阶段发生碰撞的次数在范围内,在第三层也就是绿色层中,发生的碰撞次数在范围之外,故判定该点为假点。
每一层中的碰撞的范围为[mP0-l0, m],该范围详细的推导见原文第三章。
实验结果
VectorSearch
文章中分别对有无归一化的数据集进行了实验,使用的量化方法为NEQ。对于每个运行时间,MQH的召回率比最先进的基于LSH的方法FH大20%-70%。这表明了建立在量化误差上的散列方案的优越性。
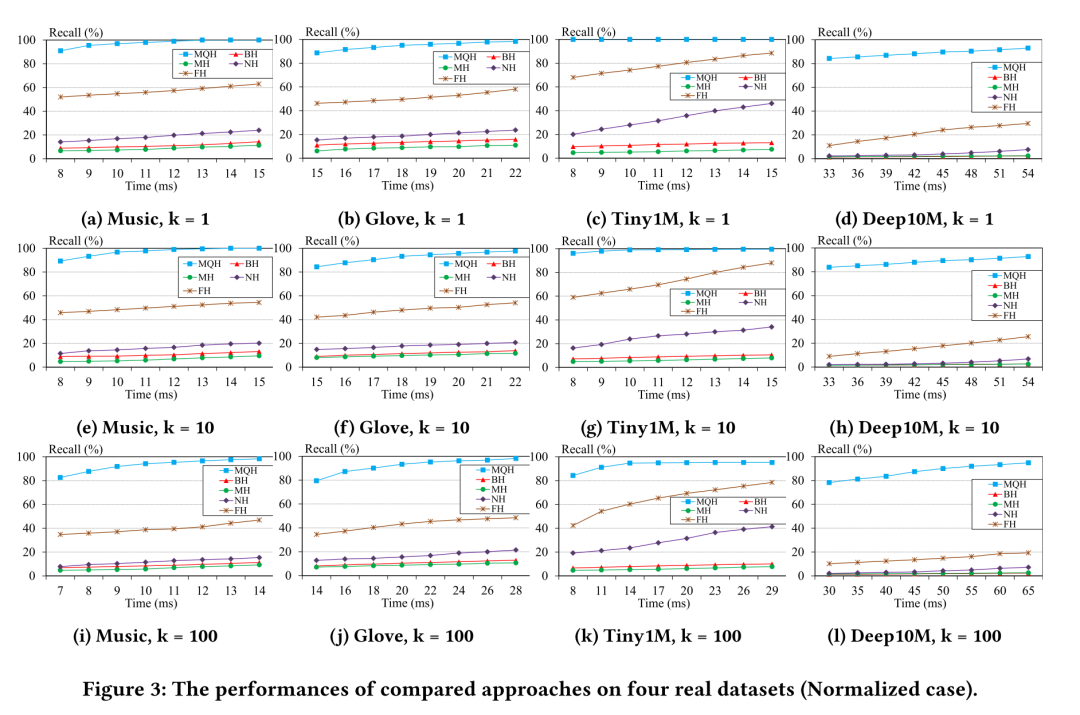
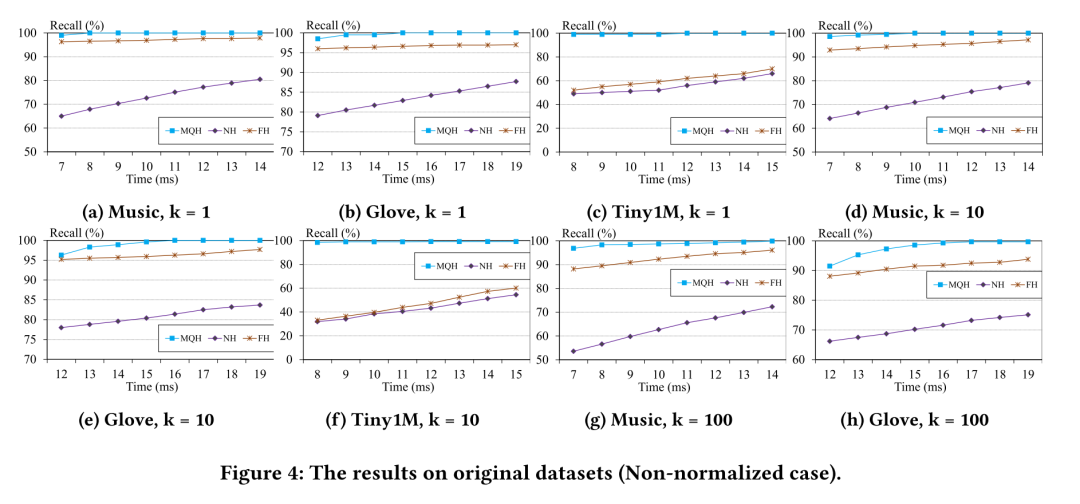
总结
在本文中,为了解决P2HNNS,建立了一个叫做MQH的分层结构。它可以确定当前的残差向量是否适用于散列。理论分析表明,MQH不仅有对查询结果准确率的保证,而且还能自动判断每个点所需的编码长度,以保证 高效率。在真实数据集上的实验证明了MQH的优越性能。
向量检索实验室
微信号:VectorSearch
扫码关注 了解更多







