今日分享论文DiskANN: Fast Accurate Billion-point Nearest Neighbor Search on a Single Node。
该文章提出了一种全新的图索引技术以及一种基于磁盘的近邻搜索方案。SSD足够的情况下,DiskANN仅使用64G内存资源既可以完成十亿规模的近邻检索任务。在16核64G的机器上评估,对于SIFT1B数据集,DiskANN的Recall@1 > 95%,QPS > 5000,平均延时能够控制在3ms以内。
十亿规模近邻搜索现状
对于十亿规模的近邻搜索任务,目前有两类主流方法:
1
倒排索引 + 数据压缩
首先,数据压缩算法(如:PQ)可以显著降低存储索引数据所带来的空间开销,同时还能减少单次距离计算的时间开销;其次,通过倒排索引结构,可以有效地缩减搜索范围,减少距离计算的次数;同时,这类方法能很好地适配GPU等新型计算架构,进一步加速搜索。可见,这类方法在索引尺寸与搜索延时方面都有优势,然而,有损压缩带来的不可避免的信息损失会严重影响搜索的准确性。同样环境下,SIFT1B上,这类索引在GPU上的平均延时在5ms以内,Recall@1仅仅能维持在50%的水平。
2
分布式系统
这类方法通过对数据进行分片,将大规模的搜索任务划分为多个在小数据集上的搜索任务,使用多台机器搭建的分布式系统进行管理。系统分别在每台机器上构建独立的索引,搜索时,主节点合并每台工作节点的搜索结果作为最终结果返回。这类方法不再受限于计算资源的匮乏,所以在每台机器上通常构建HNSW或NSG这类图索引以达到高吞吐、高召回的目的。在淘宝的实际应用中,将20亿128维浮点数据分配到32个分片中分别构建NSG索引,Recall@100约为98%,延时在5ms水平。这类方法的缺点也很明显,成本极高,当数据规模扩展到千亿级别时就需要上千台机器的集群了。
优化搜索半径的图索引:Vamana
文章首先提出了一种全新的图索引Vamana。
1
HNSW和NSG的可优化空间
以数据作为点,数据之间的关系作为边构造出的图索引具有高吞吐、高召回的特点,HNSW和NSG是目前最为流行的两种图索引。
HNSW按顺序将数据点插入图中,每次贪心地在当前图中选择插入点的近邻作为它的邻居节点。这种方式构造图索引效率高并且十分灵活。然而,HNSW在构造时并没有考虑全量数据的关系,只依赖插入顺序贪心构造边会陷入局部最优的困境,从而会产生个别入口点搜索路径极长的不均衡现象。
NSG首先在全量数据上构建KNNG,并且计算全局质心作为搜索的同一入口点。然后,以每个点的搜索路径经过的点作为候选集执行边裁剪以简化图索引。最后,使用深度优先搜索遍历图保证连通性。NSG展示出了比HNSW更优秀的吞吐表现。但是,以KNNG作为基图构造,NSG的索引构造时间开销极大(O(n^2) ),难以应用于大规模场景。
2
Vamana构造方法
如上,HNSW的贪心连边策略会出现局部最优的情况。为此,Vamana首先提出了一个参数可调的边裁剪策略。Vamana的边裁剪策略和NSG相似,同样是搜索路径上的点作为候选集。不同之处在于,Vamana在被裁边的判定上增加了一个可调参数α的干预,对于点p和它的两个近邻点p*、p',若α·d(p*,p')≤d(p,p'),则裁剪掉边<p,p'>。
基于以上的边修剪策略,Vamana的构造流程如下:
1.随机初始化图G,每个点随机指向R个近邻;
2.计算全局质心,找到距离全局质心最近的点作为所有搜索请求的入口点p;
3.基于图G和入口点p对数据集中的每个点执行近邻搜索,将搜索路径上经过的所有点作为候选点集,执行α=1的边修剪策略;
4.调整α>1重复步骤3,再次执行边修剪策略来填充边,提高图G的质量以保证召回率。
下图展示了Vamana的构造过程中,图G发生的变化。第一行中,以α=1执行边裁剪策略,可以观察到图G从密集逐渐稀疏的过程。第二行,以α=1.2 执行边裁剪策略,图G中被填充了一些长边。

3
Vamana的表现
首先,在图索引的质量上,Vamana的结构更优质。如下图,同样基准下,Vamana相较于HNSW和NSG,搜索路径更短、节点度数更小,即搜索时距离计算的次数更少,搜索效率更高。
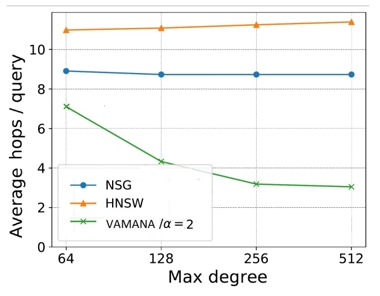
其次,在同样的内存环境下,Vamana的召回率和延时都会优于HNSW和NSG。
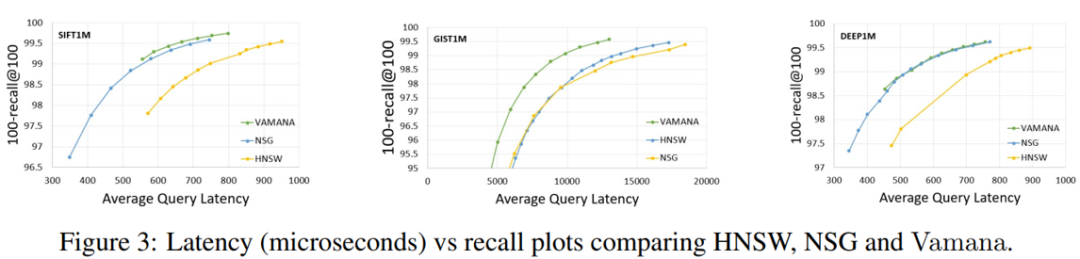
相较于HNSW和NSG,Vamana在以下几点做出了改进:
1.HNSW采用贪心策略插入,并没有像NSG、Vamana一样考虑全局点;
2.NSG和HNSW都没有可调参数α,无法平衡图的度数和直径;
3.NSG和Vamana都使用贪心路径上的点作为候选集,可以有效保证生成长链接边,HNSW会陷入局部最优;
4.NSG以KNNG作为基图,构造开销大。
磁盘近邻搜索方案:DiskANN
Vector retrieval

接下来,文章提出了基于磁盘的索引策略DiskANN。
1
内存资源有限怎么办?
在一台64G内存的机器上执行十亿规模的近邻检索任务首要的难点就是内存严重不足怎么办。如下图,以SIFT1B数据集为例,92G的原始数据大小就已经超过了内存限制,更不要提构建近邻搜索系统了。
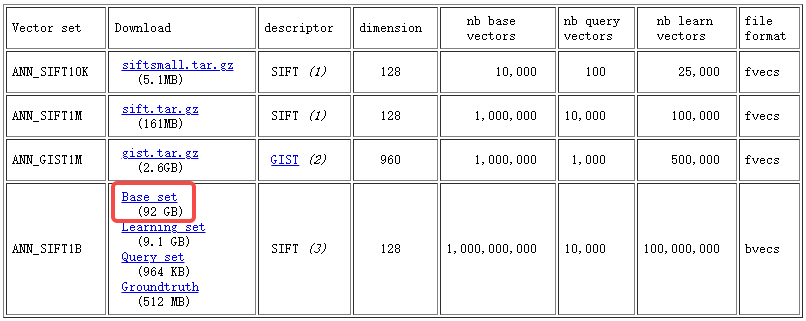
针对内存有限带来的挑战,文章提出了两个具体的问题,并给出了相应的解决方案。
问题一:如何利用有限的内存资源构建十亿规模的索引结构?
内存资源有限的直接影响就是无法一次性加载十亿规模的全量数据进行索引构建任务。既然无法直接构建覆盖全量数据的大型索引,DiskANN采取基于重叠分区合并构建索引的策略,先将全量数据划分为多个小数据集,分别在小数据集上构建索引,然后将小索引合并成大索引,具体流程如下:
1.从全量数据上采样出部分数据,训练k-means聚类,从而将全量数据划分为k个簇。为了保证以簇为单位构建的图索引能够合并起来,DiskANN将每个数据点分配到距离最近的两个簇中;
2.分别在内存中为每个簇构建图索引;
3.依赖簇之间的重叠点将小图索引合并为大图索引。
如下图,实验结果表明,使用合并构建策略构建的索引(R128/Merged)和直接在全量数据上构建的索引(R128)在性能表现上极为接近,这表明合并构建的策略是可行的、有效的。
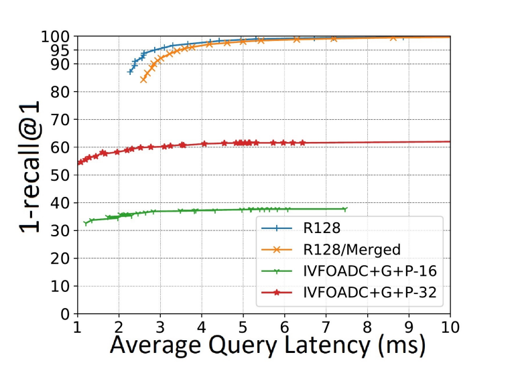
问题二:既然全量数据无法驻留内存,那么如何实现距离计算?
DiskANN使用压缩数据在内存中进行距离计算。使用乘积量化算法(Product Quantization,PQ)对原始数据进行压缩编码,得到一个可以驻留在内存的全量数据的近似距离计算方式。
进一步地,DiskANN在内存中维护PQ索引以便执行距离计算,并且在磁盘中同时保存Vamana图索引和全量的原始数据。其中Vamana在磁盘上以“邻接表”的形式存储,具体地,每个数据点后面都跟随一个长度固定为R的邻居id数组,对于邻居数量不足R的点,在id数组后面以0填充。每个数据点后面跟随的id数组长度固定,更适合磁盘读取。
2
磁盘索引怎么满足毫秒级的延时要求?
对于磁盘索引,吞吐量受限于随机磁盘读取的次数,延迟受限于往返磁盘的次数(一次往返可以包含多次读取)。在web搜索应用中,近邻搜索一般要求达到毫秒级的平均延时,这就要求将随机磁盘读取次数和磁盘往返次数最好都控制在5次以内。
为此,DiskANN提出了两个优化策略:
1.束搜索:为了减少单次查询的磁盘往返次数,对于当前搜索点p,DiskANN一次性从磁盘中读取它的W个邻居,从而减少磁盘访问的次数。W取值越大占用的带宽也就越多,设置时需要根据实际情况加以权衡。
2.热点缓存:为了进一步节省多次查询的磁盘访问次数,DiskANN在内存中申请了一个缓存区,根据查询的分布决定被缓存的节点。一般来说,DiskANN将入口点的C(C ≈ 3)跳邻居都缓存在内存中。
3
DiskANN搜索流程
DiskANN在整个搜索过程中维护搜索队列、结果队列两个队列,值得强调的是搜索队列的长度有限,受超参数控制。首先,使用PQ距离对候选入口点排序并传入搜索队列;然后,对于搜索队列中已经缓存的点,用其原始数据和查询点计算距离并送入结果队列。对于未命中缓存的点,开启异步进程使用束搜索去磁盘中以Vamana索引取回其原始数据表示和邻居列表;将每次取回的邻居列表送入搜索队列,因为搜索队列长度有限,所以依PQ距离近似排序舍弃超出部分;重复以上步骤,直至搜索队列为空,返回结果队列中的top-k作为最终结果。
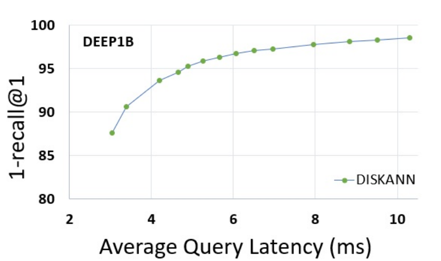
如下图实验结果表明,在DEEP1B数据集上,DiskANN可以在5ms延时下达到95%的召回率表现。
总结
DiskANN以更低的成本获得了与当下流行的解决方案同等的延时水平。以PQ距离做搜索引导,以Vamana索引做精确重排序的设计实现了内存和磁盘的异步调用。束搜索和热点缓存有效地避免了频繁地磁盘读取带来的巨大时间开销。基于重叠区域合并构建图索引更是巧妙地解决了图索引占用空间大,大规模场景下难以在内存中直接构建的尴尬问题。可以说DiskANN是联合内存磁盘构建并使用图索引的一个启发,真是妙啊~
references
[1]Simhadri, Harsha Vardhan et al. “Results of the NeurIPS'21 Challenge on Billion-Scale Approximate Nearest Neighbor Search.” Neural Information Processing Systems (2022).
[2]Malkov, Yu A. and Dmitry A. Yashunin. “Efficient and Robust Approximate Nearest Neighbor Search Using Hierarchical Navigable Small World Graphs.” IEEE Transactions on Pattern Analysis and Machine Intelligence 42 (2016): 824-836.
[3]Fu, Cong et al. “Fast Approximate Nearest Neighbor Search With The Navigating Spreading-out Graph.” Proc. VLDB Endow. 12 (2017): 461-474.
[4]Subramanya, Suhas Jayaram. “DiskANN: Fast Accurate Billion-point Nearest Neighbor Search on a Single Node.” (2019).
[5]Jégou, Hervé et al. “Product Quantization for Nearest Neighbor Search.” IEEE Transactions on Pattern Analysis and Machine Intelligence 33 (2011): 117-128.
向量检索实验室
微信号:VectorSearch
扫码关注 了解更多







