一. 前缀树
1.1 前缀树的定义
前缀树,通俗的说就是讲一个词表,用树的形式组织存储
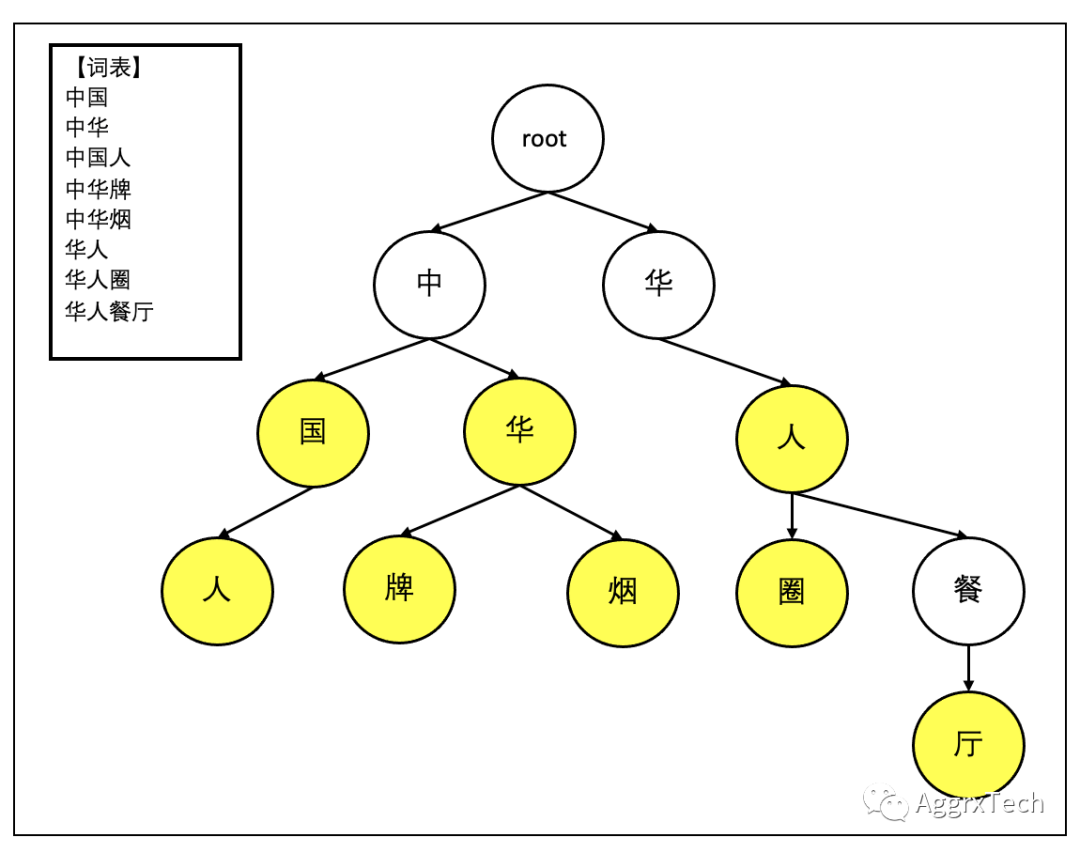
1.2 使用场景
用于匹配出,一段文本中,所有命中词表中关键词的词
例如:
网文的创作者后台
随着作者的输入,动态的标红所有命中关键词的地方
文本工具类应用中,输入自动补全
文本标签提取
在MapReduce或者Spark程序中,提取文本命中的关键词,作为文本标签算法的输入
1.3 查找过程
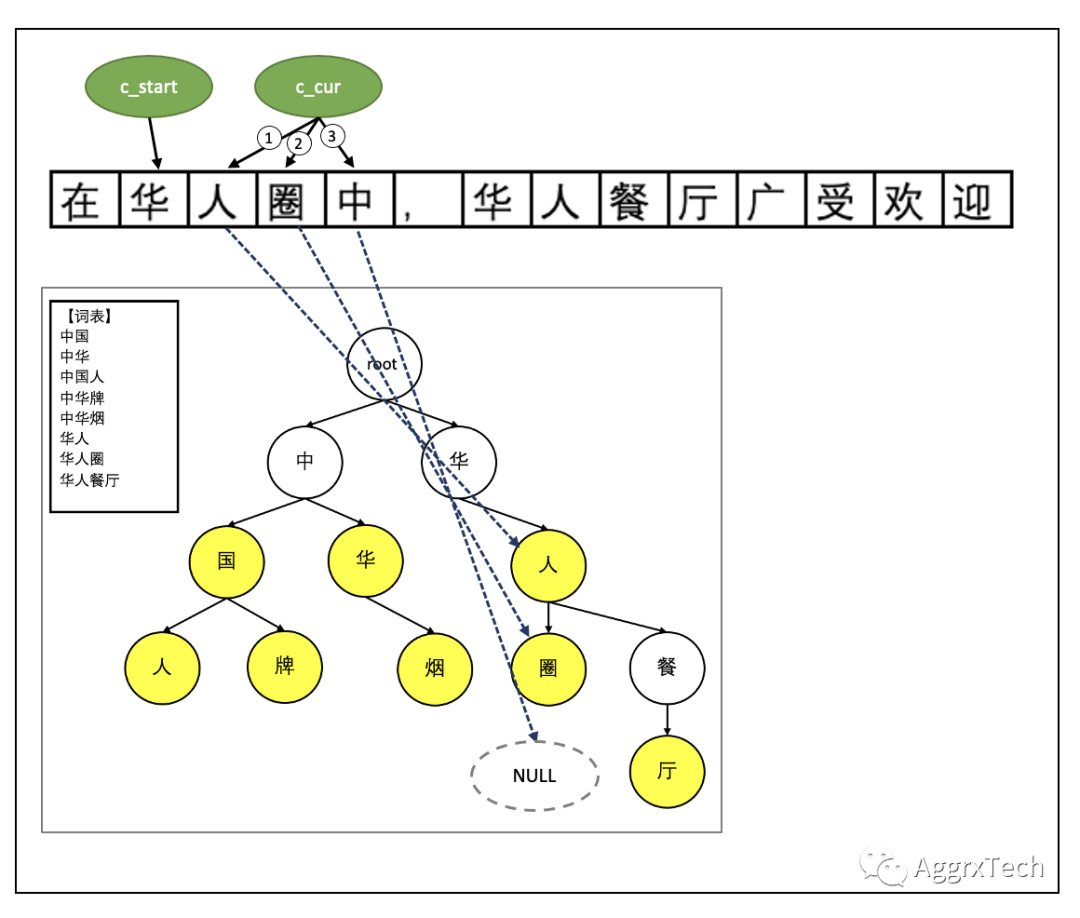
查找过程说明
c_start = 0,指向 "在"
由于"在"不在root节点的子节点中, 跳过
c_start + 1, c_start = 1: 指向 "华"
c_start += 1, c_cur = c_start
"圈" 节点为黄色,此时命中词表中的词: "华人圈"
"人" 节点为黄色,此时命中词表中的词: "华人"
(0): "华" 是root的子节点,c_cur = c_start + 1 (c_cur = 2)
① 人是 "华" 的子节点,c_cur += 1: 指向 "人"
② "圈" 是 "人" 的子节点,c_cur += 1: 指向 "圈"
③ "中" 不是 "圈" 节点的的子节点: 指向null
重复上述过程,知道 c_start >= content.length()
1.4 复杂度分析
- 从content某个位置,查找前缀树的复杂度为常数C(最大为前缀树的深度)
- 备注:词表最长的词的长度,即为前缀树深度
所以有, 时间复杂度为:
- c * O(n) = O(n), n为content长度
然而、上文故意忽略了一个核心查找的复杂度
==> 核心查找: 查找content中, 下一个文字是否是当前前缀树节点的子节点
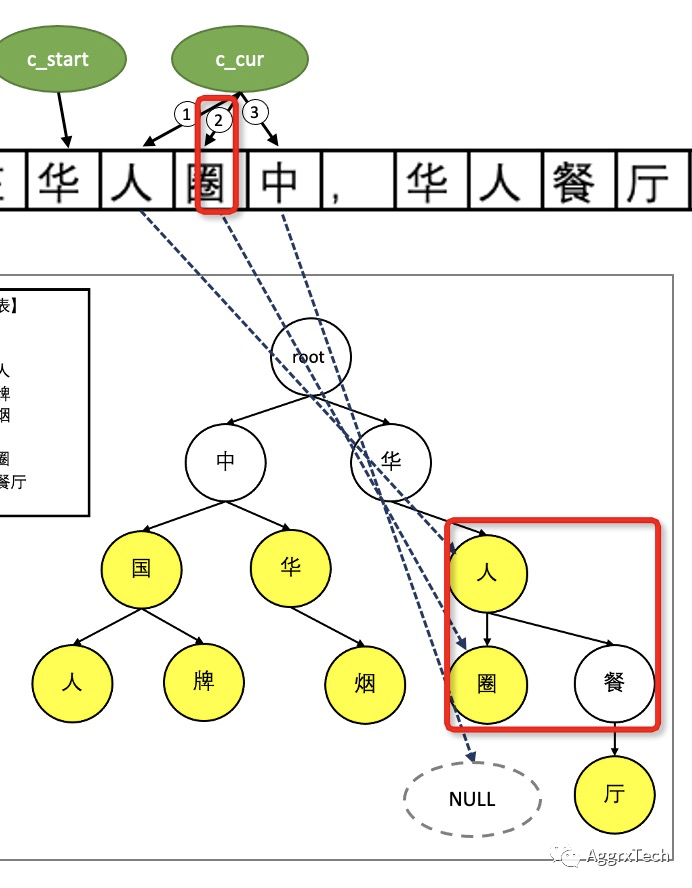
如上图所示,判断 "圈" 是否是 "人" 的子节点,复杂度
取决于子节点(node.children)的存储方式
- 采用List存储:
- 时间复杂度: "平均数(子节点个数)"
- 空间复杂度: 树的节点个数,无额外内存消耗
- 采用Map存储
- 时间复杂度: O(1)
- 空间复杂度:
- Map空间复杂度本身较高
- "随字典key的数量增加,内存消耗很非线性增加"
- 这里不详细展开,Google可以得到很多说明
看上去两种方案都不够优秀,所以,我们来到第二部分
二. Double Array Trie
目标:
找到一种数据结构,实现前缀树的功能,且时间复杂度和空间复杂度都控制在O(n)
4.1 前缀树的本质
前缀树本质
- 树,就是一个有限状态机,每个节点代表一个状态
- 在牺牲内存的方式下(HashMap存储子节点集children),可以实现
- 查找一个“字”,是否是上一个”字“的子状态,时间复杂度O(1)
我们需要的替代方案
- 查找一个文字,是否是上一个文字的子状态,时间复杂度O(1)
- "子状态的存储复杂度为O(n)"
4.2 Double Array Tie 相关定义
定义0: code (Map<Character, Integer> code)
x为一个"字", code[x]为一个整型数, 代表x在编码集中的值
【备注】
- 为了压缩Double Array Tie的空间,code往往不使用标准编码的值
- 参阅下文: "4.3 Double Array Tie的构造"
定义1: base数组 (int[] base)
- 数组的每个格子,代表前缀树中的一个"节点",既上文中说到的"状态"
- base[i]的结构
- base[i].value: 用于状态迁移的计算,参见"定义3"
- base[i].isEndNode: 当前节点,是否是一个词的结尾
- 【备注】有的实现中: base[i].isEndNode: 放入check数组
定义2: index(x)
- x为前缀树中的一个节点,index(x)为x在base数组中的位置
【问题】index(x)的值,如何确定?
- 参见下文"状态迁移方程"和"4.3 Double Array Tie的构造"
定义3: check数组 (int[] check)
- check是一个整数型数组
- check[i]
1. index(x) = i, 代表:
节点x在base数组中,存放在第i个位置
2. x的父节点为y,则满足
check[i] = index(y)
4.3 状态迁移的定义/方程
child为前缀树中的一个节点,如果parent为其父节点,则
- base[index(parent)].value + code(child) = index(child)
- check[index(child)] = index(parent)
利用这个状态迁移方程,"核心查找"的复杂度,变为了O(1)
4.4 查找的图解
4.4.1 图解Double Array Trie
假设已经构造好了Double Array Trie如下图
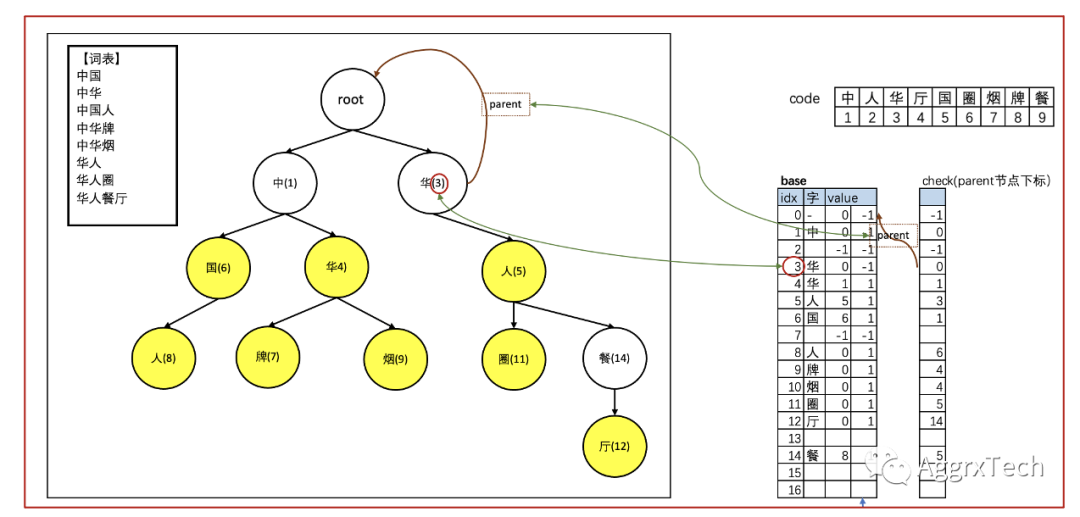
上图绿色箭头代表等价关系
1. 右边红圈的"华", 放在base数组3的位置,是因为满足状态迁移方程
- base[index(parent)].value + code(child) == index(child),既↓
- base[root.value] + code['华'] = 0 + 3 == 3
2. 右边红圈的"华", 通过 check[3] 指向其父节点
3. 补充说明
- 我们可以检查其他节点,均满足上述条件
- base数组中,value为-1表示该位置未使用
查找过程
上图上方红圈为例,"在华人圈"这几个字的查找过程
1. 初始化
cur_parent_idx = index(root) = 0
// cur_content_idx 代表从content的哪个位置开始查找
cur_content_idx = 0
2. "在" 的查找: content.get(cur_content_idx) == '在'
- index('在') = base[cur_parent_idx].value + code['在'] = 0 + 2 = 2
- check[index('在')] = -1 **!=** cur_parent_idx
- [↑↑] 与【状态转移方程冲突】
- 中断当前content位置cur_content_idx的查找
- cur_parent_idx += 1
3. 当前处理content中第二个字"华"
- 1. "华"的查找
- index('华') = base[cur_parent_idx].value + code['华'] = 0 + 3 = 3
- check[index('华')] = check(3) = 0 **==** cur_parent_idx
- [↑↑] 【满足状态转移方程】, cur_parent_idx 设为 index('华') = 3
- 开始查找下一个字 "人"
- 2. "人" 的查找
- index('人') = base[cur_parent_idx].value + code['人'] = 3 + 2 = 5
- check[5] == cur_parent_idx == index('华')
- [↑↑] 【满足状态转移方程】, cur_parent_idx 设为 index('人') = 5
- 3. "圈" 的处理
- 同上,略,符合状态迁移方程,且作输出
- 4. "中" 的处理
- 通上,略,不符合状态迁移方程
- cur_parent_idx+=1, 中断当前content位置查找,跳到1,开始新一轮处理
3. 重复上述过程,直到遍历完成content ()
4.3 Double Array Trie的构造
我们仔细回顾上文中的定义和状态迁移方程,
可以发现,构造过程需要指定两个值
1. 编码表 "code": code(x) = ?
2. base[i].value = ?
构造Double Array Trie, 就是构造这两组数值,目标是:
A. 满足状态迁移方程,实现O(1)时间复杂度的查找
B. base数组中,未使用的位置尽可能的少,以节省内存开销
4.3.1 构造伪代码
网上介绍的算法,个人认为实现比较复杂、且难以理解
在静态加载场景下,'建一颗前缀树的时间成本几乎可以忽略不计',所以,
这里建议先建一颗前缀树
为了代码更短
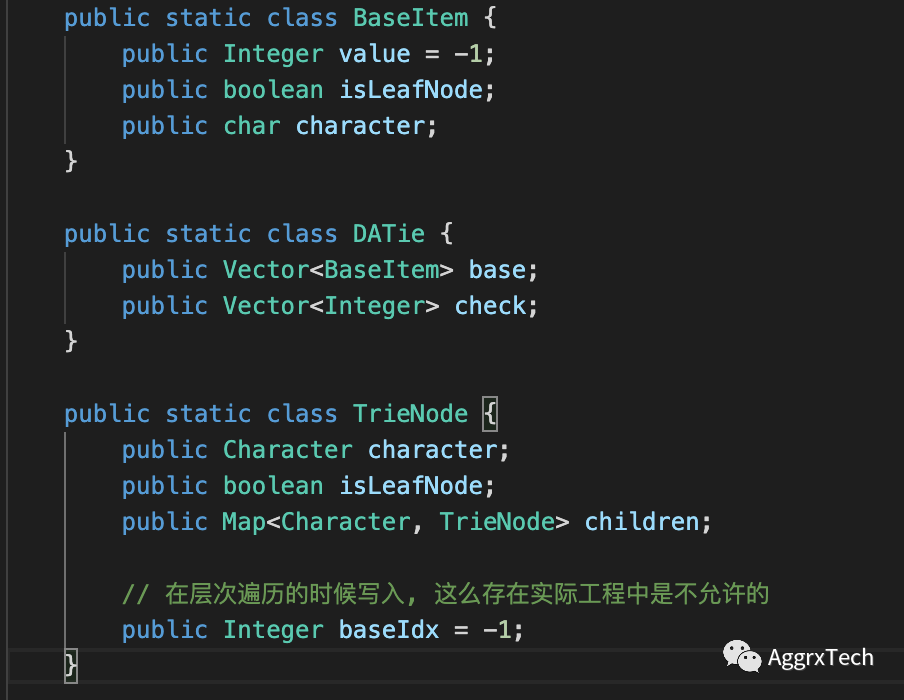
前缀树的构造过程
code初始化过程
base/check的初始化和resize代码
忽略了代码规范
没有使用unicode的方式遍历字符
省略了
前缀树的构造过程
code初始化过程
base/check的初始化和resize代码
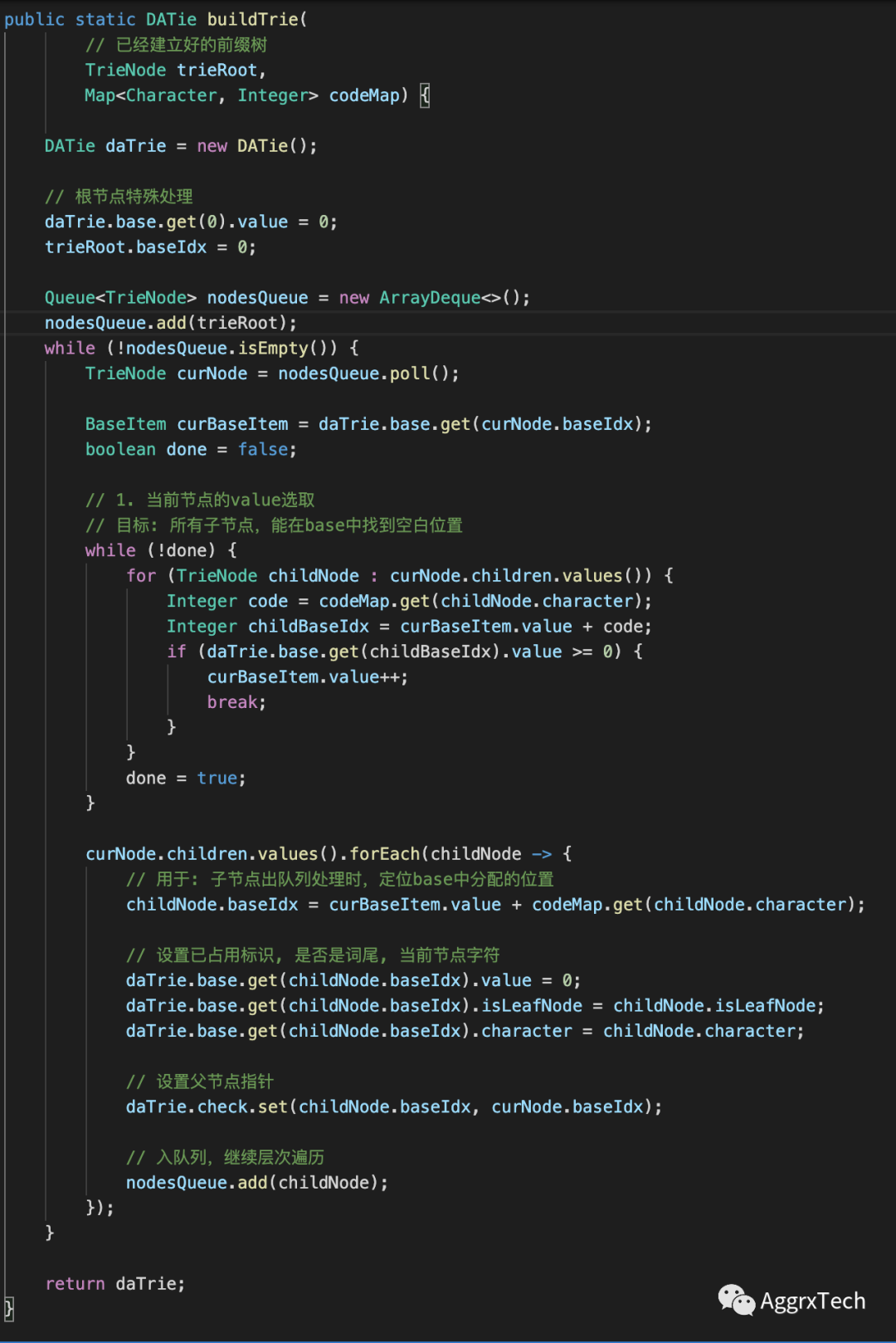
4.3.2 优化
目标:让base和check数组中,空格子尽量的少(未使用的位置)
要达到最优解,是一个NP问题,可以采用贪心的方法得到次优解
相关论证冗长,下次有时间再单独发文给出介绍






