赛题背景理解
纳斯达克股票交易所的每个交易日都会以纳斯达克闭市竞拍活动结束。这个过程确定了交易所上市的证券的官方闭市价格。这些闭市价格对于投资者、分析师和其他市场参与者来说,是评估个别证券和整个市场表现的关键指标。纳斯达克的平均每日成交量中,将近10% 发生在闭市竞拍活动中。提供真实的价格和规模发现,闭市竞拍活动确定了指数基金和其他投资策略的基准定价。
在纳斯达克交易所交易会话的最后十分钟,像Optiver这样的市场做市商会将传统的订单簿交易与价格竞拍数据合并在一起。 整合来自两个来源的信息的能力对于为所有市场参与者提供最佳价格至关重要。
拍卖机制 Auction
在金融市场中,拍卖是一种机制,通过允许多个买家和卖家在受控、监管的环境中直接互动来确定特定资产的价格。有许多不同种类的拍卖,但在这个竞赛中,我们特别关注闭市拍卖的概念。

在闭市拍卖中,订单在预定的时间范围内收集,然后根据竞拍参与者表达的买卖需求在一个由拍卖参与者确定的单一价格上匹配。对于纳斯达克的闭市拍卖,交易所从交易日开始接受订单,并在美东时间下午3:50开始发布拍卖簿的状态,持续10分钟,然后在美东时间下午4点市场闭市时,订单会立即以一个单一价格匹配。
闭市价格的确定方式以能够成交最大数量股票的价格为准。如果竞拍在不同价格水平上有相同数量的成交手数,纳斯达克将使用一种专有算法,该算法考虑了最后成交价格、订单的价格-时间优先级以及不同价格水平上的可用流动性。以能够成交最大数量股票的价格不唯一的情况相当罕见。
Order book 订单簿
订单簿是指一个按价格水平组织的特定证券或金融工具的买入(也称为买盘)和卖出(也称为卖盘)订单的电子列表。
以下是一个在连续(非竞拍)交易中的订单簿的简单示例。我们可以看到,在价格水平为9的地方,有2股的买盘,这意味着市场参与者愿意以9的价格购买2股。类似地,我们可以看到在价格水平为10的地方,有1股的卖盘,这意味着市场参与者愿意以10的价格出售1股。
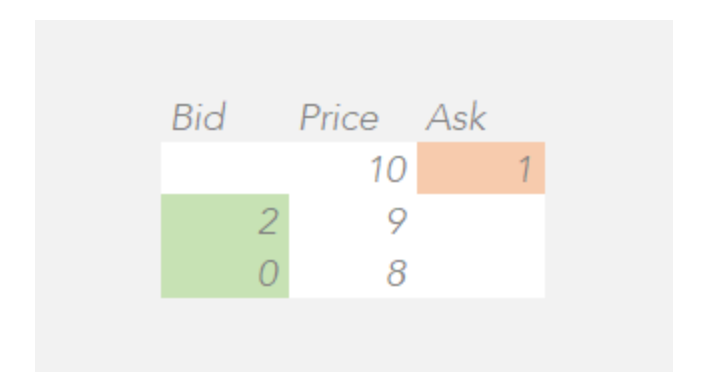
对于这种连续交易的订单簿,最高的买盘价格始终会低于最低的卖盘价格。例如,如果有人以价格为9的价格提交了10股的卖盘,那么将会匹配2股,因为有人愿意以9的价格购买2股。新的最佳卖盘将是以价格9的8股,订单簿的新状态如下所示。
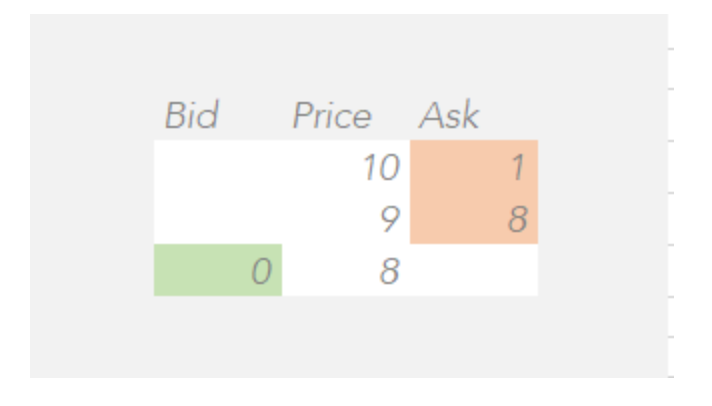
Auction order book 竞拍订单簿
竞拍订单簿与连续交易的订单簿有略微不同的行为方式。在这本书中,订单不会立即匹配,而是在竞拍结束时收集。你可能会注意到,在下面的示例中,与连续交易的订单簿不同,最高买盘不大于最低卖盘。在下面的示例中,这本书被称为“在竞交中”,因为最佳买盘和卖盘重叠。因此,闭市竞拍价格被称为“未交叉价格”,即在交叉中的股票的价格。
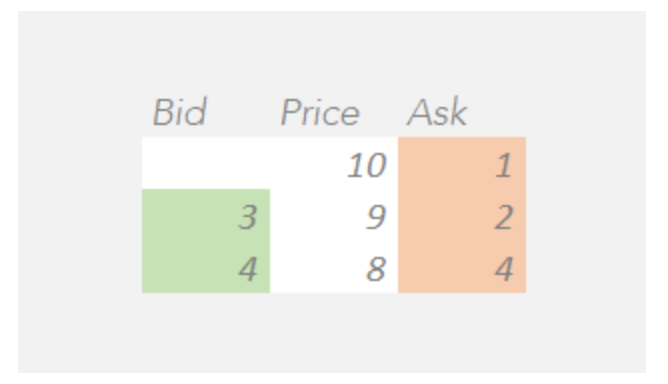
对于上述竞拍订单簿示例,我们可以定义一些关键术语。假设在这种状态下竞拍未交叉,那么:
在价格为10的地方,不会匹配任何手数,因为没有买盘大于或等于10。 在价格为9的地方,将匹配3手,因为有3个买盘大于或等于9,以及6个卖盘小于或等于9。 在价格为8的地方,将匹配4手,因为有7个买盘大于或等于8,以及4个卖盘小于或等于8。
因此,使成交手数最多的价格将是8。因此,我们将描述竞拍订单簿如下:
未交叉价格为8 成交手数为4 不平衡量为买入方向的3手。
术语“不平衡量”指的是未匹配股票的数量。在价格8的未交叉价格下,有7个买盘和4个卖盘可以匹配,因此我们剩下3个未匹配的买盘。由于买盘是购买订单,所以在买入方向上存在3手的不平衡。
术语“远期价格”指的是如果竞拍订单簿在报告时间未交叉时的假设未交叉价格。纳斯达克在闭市交叉前5分钟提供远期价格信息。
Combined book 综合订单簿
将两本订单簿合并可以更准确地反映市场在不同价格水平上的买入和卖出兴趣,有助于更好地发现价格,使市场在竞拍未交叉时达到更准确和公平的均衡价格。
在这里,我们通过汇总所有价格水平上的买入和卖出兴趣,将我们的原始订单簿示例与竞拍订单簿示例合并。
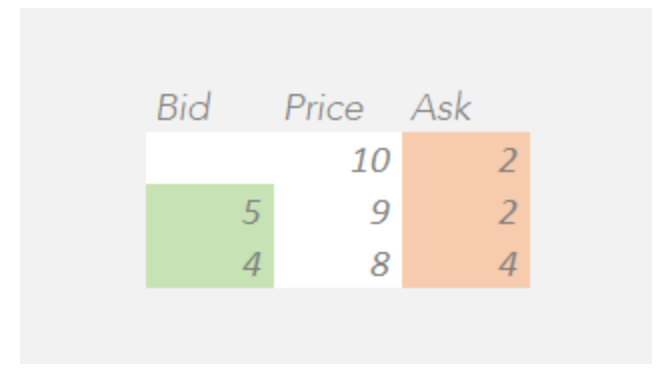
对于这本综合订单簿:
在价格为10的地方,不会匹配任何手数,因为没有买盘大于或等于10。 在价格为9的地方,将匹配5手,因为有5个买盘大于或等于9,以及6个卖盘小于或等于9。 在价格为8的地方,将匹配4手,因为有9个买盘大于或等于8,以及4个卖盘小于或等于8。
因此,使成交手数最多的价格将是9。因此,我们将描述综合订单簿如下:
未交叉价格为9 成交手数为5 不平衡量为卖出方向的1手。
综合订单簿的假设未交叉价格称为“近期价格”。纳斯达克在闭市交叉前5分钟提供近期价格信息。
纳斯达克还提供一个称为“参考价格”的公平价格指示。参考价格的计算如下:
如果近期价格介于最佳买盘和卖盘之间,则参考价格等于近期价格。 如果近期价格大于最佳卖盘,则参考价格等于最佳卖盘。 如果近期价格小于最佳买盘,则参考价格等于最佳买盘。
因此,参考价格是在最佳买盘和卖盘之间限制的近期价格。
赛题数据集
在这个竞赛中,参与者被挑战来预测在10分钟的闭市竞拍期间的短期价格走势。所有的训练数据都包含在一个名为 train.csv
的文件中。
更多数据字段介绍:https://www.kaggle.com/competitions/optiver-trading-at-the-close/data
stock_id
- 股票的唯一标识符。并非每个时间段都存在所有股票ID。date_id
- 日期的唯一标识符。日期ID在所有股票中是顺序的且一致的。imbalance_size
- 在当前参考价格下未匹配的金额(以美元计)。imbalance_buy_sell_flag
- 反映竞拍不平衡方向的指示器。买方不平衡;1 卖方不平衡;-1 无不平衡;0 reference_price
- 最大化已配对股票、最小化不平衡、最小化与买卖中间价的距离的价格顺序。也可以看作是在最佳买盘和卖盘价格之间限制的近期价格。matched_size
- 在当前参考价格下可以匹配的金额(以美元计)。far_price
- 基于竞拍兴趣来最大化匹配股票数量的交叉价格。该计算不包括连续市场订单。near_price
- 基于竞拍和连续市场订单,最大化匹配股票数量的交叉价格。[bid/ask]_price
- 非竞拍订单簿中最具竞争力的买入/卖出水平的价格。[bid/ask]_size
- 非竞拍订单簿中最具竞争力的买入/卖出水平上的美元名义金额。wap
- 非竞拍订单簿中的加权平均价格。
seconds_in_bucket
- 自闭市竞拍开始以来经过的秒数,始终从0开始。target
- 股票的wap未来60秒的变动,减去合成指数未来60秒的变动。合成指数是Optiver为此竞赛构建的纳斯达克上市股票的自定义加权指数。 目标的单位是基点,这是金融市场中常用的测量单位。1个基点的价格变动等于0.01%的价格变动。 在当前观察的时间t,可以定义目标如下:
数据可视化
train = pd.read_csv('/kaggle/input/optiver-trading-at-the-close/train.csv')
train.head()
(
train
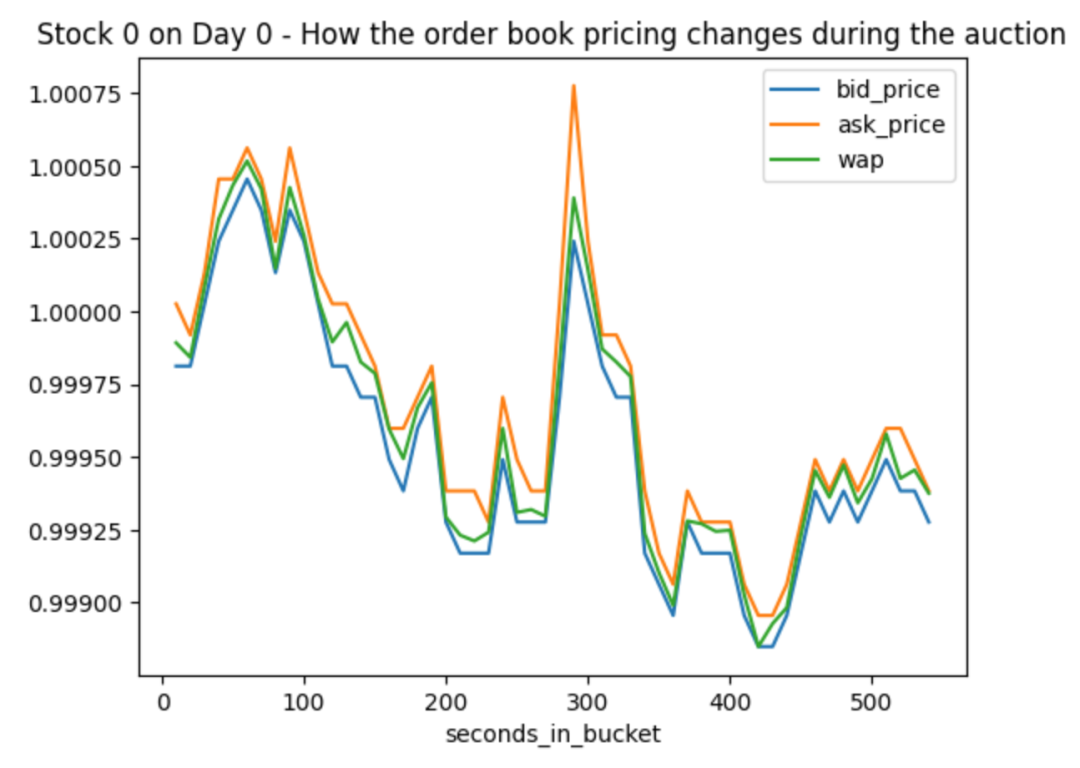
.query('stock_id ==0 & date_id ==0')
[['seconds_in_bucket','bid_price','ask_price', 'wap']]
.replace(0, np.nan)
.set_index('seconds_in_bucket')
.plot(title='Stock 0 on Day 0 - How the order book pricing changes during the auction')
)
(
train
.query('stock_id ==0 & date_id ==0')
[['seconds_in_bucket','near_price','far_price','reference_price']]
.replace(0, np.nan)
.set_index('seconds_in_bucket')
.plot(title = 'Stock 0 on Day 0 - How the auction & combined book pricing changes during the auction')
)
基础baseline
https://www.kaggle.com/code/yuanzhezhou/baseline-lgb-xgb-and-catboost
基础特征工程
import pandas as pd
def generate_features(df):
features = ['seconds_in_bucket', 'imbalance_buy_sell_flag',
'imbalance_size', 'matched_size', 'bid_size', 'ask_size',
'reference_price','far_price', 'near_price', 'ask_price', 'bid_price', 'wap',
'imb_s1', 'imb_s2'
]
df['imb_s1'] = df.eval('(bid_size-ask_size)/(bid_size+ask_size)')
df['imb_s2'] = df.eval('(imbalance_size-matched_size)/(matched_size+imbalance_size)')
prices = ['reference_price','far_price', 'near_price', 'ask_price', 'bid_price', 'wap']
for i,a in enumerate(prices):
for j,b in enumerate(prices):
if i>j:
df[f'{a}_{b}_imb'] = df.eval(f'({a}-{b})/({a}+{b})')
features.append(f'{a}_{b}_imb')
for i,a in enumerate(prices):
for j,b in enumerate(prices):
for k,c in enumerate(prices):
if i>j and j>k:
max_ = df[[a,b,c]].max(axis=1)
min_ = df[[a,b,c]].min(axis=1)
mid_ = df[[a,b,c]].sum(axis=1)-min_-max_
df[f'{a}_{b}_{c}_imb2'] = (max_-mid_)/(mid_-min_)
features.append(f'{a}_{b}_{c}_imb2')
return df[features]
模型训练与验证
def train(model_dict, modelname='lgb'):
if TRAINING:
model = model_dict[modelname]
model.fit(X[index%N_fold!=i], Y[index%N_fold!=i],
eval_set=[(X[index%N_fold==i], Y[index%N_fold==i])],
verbose=10,
early_stopping_rounds=100
)
models.append(model)
joblib.dump(model, './models/{modelname}_{i}.model')
else:
models.append(joblib.load(f'{model_path}/{modelname}_{i}.model'))
return
model_dict = {
'lgb': lgb.LGBMRegressor(objective='regression_l1', n_estimators=500),
'xgb': xgb.XGBRegressor(tree_method='hist', objective='reg:absoluteerror', n_estimators=500),
'cbt': cbt.CatBoostRegressor(objective='MAE', iterations=3000),
}
# 竞赛交流群 邀请函 #
每天大模型、算法竞赛、干货资讯







