2NF
定义6 若R∈1NF,且每一个非主属性完全函数依赖于任何一个候选码,则R∈2NF。
下面举一个不是2NF的例子。
【例1】有关系模式S-L-C(Sno, Sdept, Sloc, Cno, Grade),其中Sloc为学生的住处,
并且每个系的学生住在同一个地方。S-L-C 的码为(Sno, Cno)。则函数依赖有

函数依赖关系如下图所示。
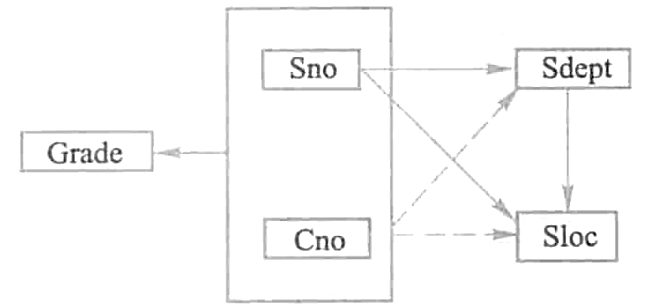
图中用虚线表示部分函数依赖。另外,Sdept还函数确定Sloc,这一点在讨论第二范式时暂不考虑。可以看到非主属性Sdept、Sloc并不完全函数依赖于码。因此S-L-C(Sno, Sdept, Sloc, Cno, Grade)不符合2NF定义,即S-L-C∉2NF。
一个关系模式R不属于2NF,就会产生以下几个问题:
(1)插入异常。假若要插入一个学生Sno=S7,Sdept=PHY,Sloc=BLD2,但该生还未选课,即这个学生无Cno,这样的元组就插不进S-L-C中。因为插入元组时必须给定码值,而这时码值的一部分为空,因而学生的固有信息无法插入。
(2)删除异常。假定某个学生只选一门课,如S4就选了一门课C3,现在C3这门课他也不选了,那么C3这个数据项就要删除。而C3是主属性,删除了C3,整个元组就必须一起删除,使得S4的其他信息也被删除了,从而造成删除异常,即不应删除的信息也删除了。
(3)修改复杂。某个学生从数学系(MA)转到计算机科学系(CS),这本来只需修改此学生元组中的Sdept分量即可,但因为关系模式S-L-C中还含有系的住处Sloc属性,学生转系将同时改变住处,因而还必须修改元组中的Sloc分量。另外,如果这个学生选修了k门课,Sdept、Sloc重复存储了k次,不仅存储冗余度大,而且必须无遗漏地修改k个元组中全部Sdept、Sloc 信息,造成修改的复杂化。
分析上面的例子可以发现问题在于有两类非主属性,一类如Grade,它对码是完全函数依赖;另一类如Sdept、Sloc,它们对码不是完全函数依赖。解决的办法是用投影分解把关系模式S-L-C分解为两个关系模式:SC(Sno, Cno, Grade)和S-L(Sno, Sdept, Sloc)。
关系模式SC与S-L中属性间的函数依赖可以用下图表示如下。
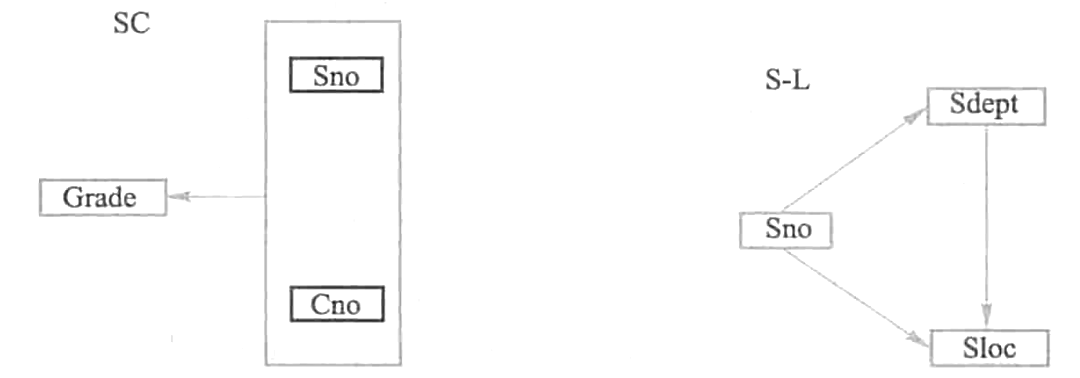
关系模式SC的码为(Sno, Cno),关系模式S-L的码为Sno,这样就使得非主属性对码都是完全函数依赖了。
3NF
定义7 设关系模式R<U,F>∈1NF,若R中不存在这样的码X,属性组Y及非主属性Z(Z⊉Y)使得X→Y,Y→Z成立,Y不依赖于X,则称R<U,F>∈3NF。
由定义7可以证明,若R∈3NF,则每一个非主属性既不传递依赖于码,也不部分依赖于码。也就是说,可以证明如果R属于3NF,则必有R属于2NF。
在上左图中关系模式SC没有传递依赖,而上右图中关系模式S-L存在非主属性对码的传递依赖。在S-L中,由Sno→Sdept(Sno不依赖于Sdept),Sdept→Sloc,可得Sno传递依赖Sloc。因此SC∈3NF,而S-L∉3NF。
一个关系模式R若不是3NF,就会产生与上面2NF相类似的问题。读者可以类
比2NF的反例加以说明。
解决的办法同样是将S-L分解为:S-D (Sno, Sdept)和D-L(Sdept,Sloc)。分解后的关系模式S-D与D-L 中不再存在传递依赖。
BCNF
BCNF(Boyce Codd Normal Form)是由Boyce与Codd提出的,比上述的3NF又进了一步,通常认为BCNF是修正的第三范式,有时也称为扩充的第三范式。
定义8 关系模式R<U,F>∈1NF,若X→Y且Y⊊X时X必含有码,则R<U,F>∈BCNF。
也就是说,关系模式R<U,F>中,若每一个决定因素都包含码,则R<U,F>∈BCNF。
由BCNF的定义可以得到结论,一个满足BCNF的关系模式有:
所有非主属性对每一个码都是完全函数依赖。
所有主属性对每一个不包含它的码也是完全函数依赖。
没有任何属性完全函数依赖于非码的任何一组属性。
由于R∈BCNF,按定义排除了任何属性对码的传递依赖与部分依赖,所以R∈3NF。严格的证明留给读者完成。但是若R∈3NF,R未必属于BCNF。
下面用几个例子说明属于3NF的关系模式有的属于BCNF,但有的不属于BCNF。
【例2】考察关系模式C(Cno, Cname, Pcno),它只有一个码Cno,这里没有任何属性对Cno部分依赖或传递依赖,所以C∈3NF。同时C中Cno是唯一的决定因素,所以C∈BCNF。对于关系模式SC(Sno, Cno, Grade)可作同样分析。
【例3】关系模式S(Sno, Sname, Sdept, Sage),假定Sname也具有唯一性,那么S就有两个码,这两个码都由单个属性组成,彼此不相交。其他属性不存在对码的传递依赖与部分依赖,所以S∈3NF。同时S 中除Sno、Sname 外没有其他决定因素,所以S也属于BCNF。
以下再举几个例子。
【例4】关系模式SJP(S, J, P)中,S是学生,J表示课程,P表示名次。每一个学生选修每门课程的成绩有一定的名次,每门课程中每一名次只有一个学生(即没有并列名次)。
由语义可得到下面的函数依赖:
(S,J)→P,(J,P)→S
所以(S,J)与(J,P)都可以作为候选码。这两个码各由两个属性组成,而且它们是相交的。这个关系模式中显然没有属性对码传递依赖或部分依赖。所以SJP∈3NF,而且除(S,J)与(J,P)以外没有其他决定因素,所以SJP∈BCNF。
【例5】关系模式STJ(S,T,J)中,S表示学生,T表示教师,J表示课程。每一教师只教一门课,每门课有若干教师,某一学生选定某门课,就对应一个固定的教师。由语义可得到如下的函数依赖。
(S,J)→T,(S,T)→J,T→J
函数依赖关系可以用下图表示,这里(S,J)与(S,T)都是候选码。
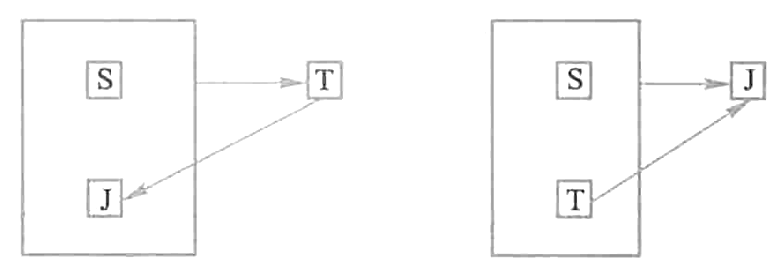
STJ是3NF,因为没有任何非主属性对码传递依赖或部分依赖,但STJ不是BCNF关系,因为T是决定因素,而T不包含码。
对于不是BCNF的关系模式,仍然存在不合适的地方。读者可自己举例指出STJ的不合适之处。非BCNF的关系模式也可以通过分解成为BCNF。例如STJ可分解为ST(S,T)与TJ(T,J),它们都是BCNF。
3NF和BCNF是在函数依赖的条件下对模式分解所能达到的分离程度的测度。一个模式中的关系模式如果都属于BCNF,那么在函数依赖范畴内它已实现了彻底的分离,已消除了插入和删除的异常。3NF的“不彻底”性表现在可能存在主属性对码的部分依赖和传递依赖。









