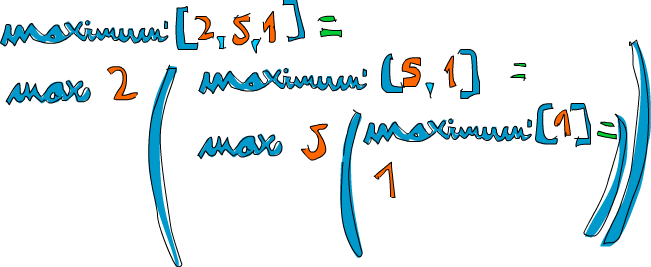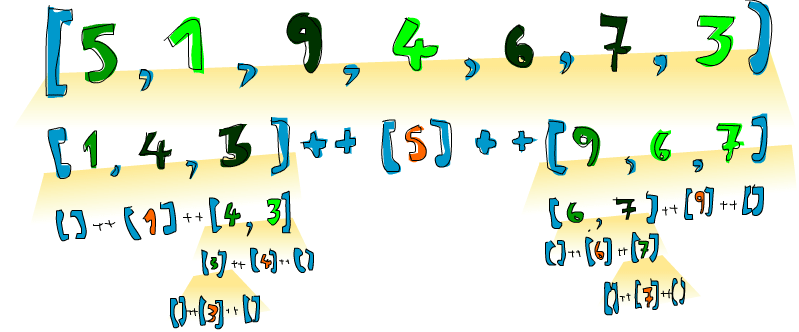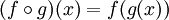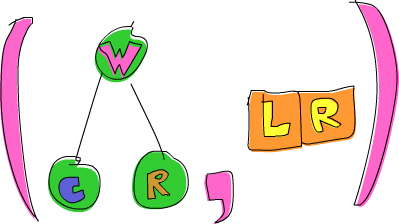Table of Contents
#
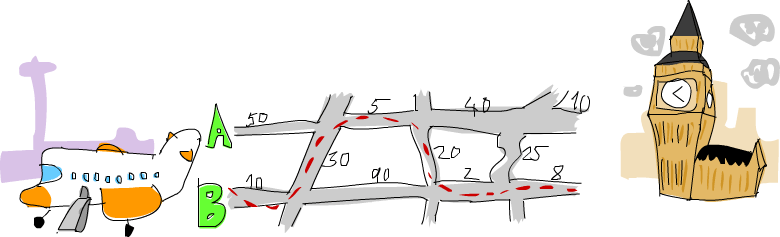
#
#
第 8 章 构造我们自己的 Types 和 Typeclasses
第 11 章 Functors, Applicative Functors 与 Monoids
前言
Haskell 是一种标准化的、通用纯函数式编程语言,有非限定性语义和强静态类型。
介绍
作者通过阅读不同的 Haskell 教学文章,从多个角度出发把这些知识化整为零。这份教学是希望提供更多的机会能让你找到你想要得到的解答。希望能够分享我的学习经验,帮助初学者更快进入状况。
致谢
原文作者:Miran Lipovača
译者:github repo
译者:Fleurer
版本信息
书中演示代码基于以下版本:
语言 | 版本信息 |
Haskell | 2010 |
注意:开发工具版本 GHC,版本6.8.2
1
简介
关于这份教学
欢迎来到 Haskell 趣学指南!会想看这篇文章表示你对学习 Haskell 有很大的兴趣。你来对地方了,来让我简单介绍一下这个教学。
撰写这份教学,一方面是让我自己对 Haskell 更熟练,另一方面是希望能够分享我的学习经验,帮助初学者更快进入状况。网路上已经有无数 Haskell 的教学文件,在我学习的过程中,我并不限于只参考一份来源。我常常阅读不同的教学文章,他们每个都从不同的角度出发。参考这些资源让我能将知识化整为零。这份教学是希望提供更多的机会能让你找到你想要得到的解答。
这份教学主要针对已经有使用命令式程式语言 (imperative programming languages) 写程式经验 (C, C++, Java, Python …) 、却未曾接触过函数式程式语言 (functional programming languages) (Haskell, ML, OCaml …) 的读者。就算没有写程式经验也没关系,会想学 Haskell 的人我相信都是很聪明的。
若在学习中遇到什么地方不懂的,Freenode IRC 上的 #Haskell 频道是提问的绝佳去处。那里的人都很友善,有耐心且能体谅初学者。 (译注: Stackoverflow 上的 #haskell tag 也有很多 Haskell 神人们耐心地回答问题,提供给不习惯用 IRC 的人的另一个选择。)
我经历了不少挫折才学会 Haskell,在初学的时候它看起来是如此奇怪的语言。但有一天我突然开窍了,之后的学习便如鱼得水。我想要表达的是:尽管 Haskell 乍看下如此地诡异,但假如你对程式设计十分有兴趣,他非常值得你学习。学习 Haskell 让你想起你第一次写程式的感觉。非常有趣,而且强迫你 Think different。
#
什么是 Haskell?
Haskell 与其他语言不同,是一门纯粹函数式程式语言 (purely functional programming language)。在一般常见的命令式语言中,要执行操作的话是给电脑一组命令,而状态会随着命令的执行而改变。例如你指派变数 a
的值为 5,而随后做了其它一些事情之后 a 就可能变成的其它值。有控制流程 (control flow),你就可以重复执行操作。然而在纯粹函数式程式语言中,你不是像命令式语言那样命令电脑「要做什么」,而是通过用函数来描述出问题「是什么」,如「阶乘是指从1到某个数的乘积」,「一个串列中数字的和」是指把第一个数字跟剩余数字的和相加。你用宣告函数是什么的形式来写程式。另外,变数 (variable) 一旦被指定,就不可以更改了,你已经说了 a
就是 5,就不能再另说 a 是别的什么数。(译注:其实用 variable 来表达造成字义的 overloading,会让人联想到 imperative languages 中 variable 是代表状态,但在 functional languages 中 variable 是相近于数学中使用的 variable。x=5
代表 x
就是 5,不是说 x
在 5 这个状态。) 所以说,在纯粹函数式程式语言中的函数能做的唯一事情就是利用引数计算结果,不会产生所谓的"副作用 (side effect)" (译注:也就是改变非函数内部的状态,像是 imperative languages 里面动到 global variable 就是 side effect)。一开始会觉得这限制很大,不过这也是他的优点所在:若以同样的参数呼叫同一个函数两次,得到的结果一定是相同。这被称作“引用透明 (Referential Transparency)_” (译注:这就跟数学上函数的使用一样)。如此一来编译器就可以理解程式的行为,你也很容易就能验证一个函数的正确性,继而可以将一些简单的函数组合成更复杂的函数。
Haskell 是惰性 (lazy) 的。也就是说若非特殊指明,函数在真正需要结果以前不会被求值。再加上引用透明,你就可以把程式仅看作是数据的一系列变形。如此一来就有了很多有趣的特性,如无限长度的资料结构。假设你有一个 List: xs = [1,2,3,4,5,6,7,8]
,还有一个函数 doubleMe
,它可以将一个 List 中的所有元素都乘以二,返回一个新的 List。若是在命令式语言中,把一个 List 乘以 8,执行 doubleMe(doubleMe(doubleMe(xs)))
,得遍历三遍 xs
才会得到结果。而在惰性语言中,调用 doubleMe
时并不会立即求值,它会说“嗯嗯,待会儿再做!”。不过一旦要看结果,第一个 doubleMe
就会对第二个说“给我结果,快!”第二个 doubleMe
就会把同样的话传给第三个 doubleMe
,第三个 doubleMe
只能将 1 乘以 2 得 2 后交给第二个,第二个再乘以 2 得 4 交给第一个,最终得到第一个元素 8。也就是说,这一切只需要遍历一次 list 即可,而且仅在你真正需要结果时才会执行。惰性语言中的计算只是一组初始数据和变换公式。
Haskell 是静态类型 (statically typed) 的。当你编译程式时,编译器需要明确哪个是数字,哪个是字串。这就意味着很大一部分错误都可以在编译时被发现,若试图将一个数字和字串相加,编译器就会报错。Haskell 拥有一套强大的类型系统,支持自动类型推导 (type inference)。这一来你就不需要在每段程式码上都标明它的类型,像计算 a=5+4
,你就不需另告诉编译器“ a 是一个数值”,它可以自己推导出来。类型推导可以让你的程式更加简练。假设有个函数是将两个数值相加,你不需要声明其类型,这个函数可以对一切可以相加的值进行计算。
Haskell 采纳了很多高阶程式语言的概念,因而它的程式码优雅且简练。与同层次的命令式语言相比,Haskell 的程式码往往会更短,更短就意味着更容易理解,bug 也就更少。
Haskell 这语言是一群非常聪明的人设计的 (他们每个人都有 PhD 学位)。最初的工作始于 1987 年,一群学者聚在一起想设计一个屌到爆的程式语言。到了 2003 年,他们公开了 Haskell Report,这份报告描述了 Haskell 语言的一个稳定版本。(译注:这份报告是 Haskell 98 标准的修订版,Haskell 98 是在 1999 年公开的,是目前 Haskell 各个编译器实现预设支援的标准。在 2010 年又公开了另一份 Haskell 2010 标准,详情可见穆信成老师所撰写的简介。
#
要使用 Haskell 有哪些要求呢?
一句话版本的答案是:你只需要一个编辑器和一个编译器。在这里我们不会对编辑器多加着墨,你可以用任何你喜欢的编辑器。至于编译器,在这份教学中我们会使用目前最流行的版本:GHC。而安装 GHC 最方便的方法就是去下载 Haskell Platform,他包含了许多现成 Runtime Library 让你方便写程式。(译注:Ubuntu 的使用者有现成的套件可以使用,可以直接 apt-get install Haskell-platform
来安装。但套件的版本有可能比较旧。)
GHC 可以解释执行 Haskell Script (通常是以 .hs
作为结尾),也可以编译。它还有个互动模式,你可以在里面呼叫 Script 里定义的函数,即时得到结果。 对于学习而言,这比每次修改都编译执行要方便的多。想进入互动模式,只要打开控制台输入 ghci
即可。假设你在 myfunctions.hs
里定义了一些函数,在 ghci 中输入 :l myfunctions.hs
,ghci 便会载入 myfunctions.hs
。之后你便可以呼叫你定义的函数。一旦修改了这个 .hs
档案的内容,再次执行 :l myfunctions.hs
或者相同作用的 :r
,都可以重新载入该档案。我自己通常就是在 .hs
档案中定义几个函数,再到 ghci 载入,呼叫看看,再修改再重新载入。这也正是我们往后的基本流程。
2
从零开始
准备好了吗?
准备来开始我们的旅程!如果你就是那种从不看说明书的人,我推荐你还是回头看一下简介的最后一节。那里面讲了这个教学中你需要用到的工具及基本用法。我们首先要做的就是进入 ghc 的互动模式,接着就可以写几个函数体验一下 Haskell 了。打开终端机,输入 ghci
,你会看到下列欢迎讯息:
GHCi, version 6.8.2: http://www.haskell.org/ghc/
:? for help Loading package base ... linking ... done.
Prelude>
恭喜您已经进入了 ghci 了!目前它的命令列提示是 prelude>
,不过它在你装载一些模组之后会变的比较长。为了美观起见,我们会输入指令 :set prompt "ghci> "
把它改成 ghci>
。
首先来看一些简单的运算
ghci> 2 + 15
17
ghci> 49 * 100
4900
ghci> 1892 - 1472
420
ghci> 5 / 2
2.5
ghci>
很简单吧!你也可以在一行中使用多个运算子,他们会按照运算子优先顺序执行计算,而使用括号可以改变执行的优先顺序。
ghci> (50 * 100) - 4999
1
ghci> 50 * 100 - 4999
1
ghci> 50 * (100 - 4999)
-244950
但注意处理负数的时候有个小陷阱:我们执行 5 * -3
会 ghci 会回报错误。所以说,使用负数时最好将其置于括号之中,像 5*(-3)
就不会有问题。
要进行布林代数 (Boolean Algebra) 的演算也是很直觉的。你也许早就会猜,&&
指的是布林代数上的 AND,而 ||
指的是布林代数上的 OR,not
会把 True
变成 False
,False
变成 True
。
ghci> True && False
False
ghci> True && True
True
ghci> False || True
True
ghci> not False
True
ghci> not (True && True)
False
相等性可以这样判定
ghci> 5 == 5
True
ghci> 1 == 0
False
ghci> 5 /= 5
False
ghci> 5 /= 4
True
ghci> "hello" == "hello"
True
那执行 5+"llama"
或者 5==True
会怎样? 如果我们真的试着在 ghci 中跑,会得到下列的错误讯息:
No instance for (Num [Char])
arising from a use of `+' at :1:0-9
Possible fix: add an instance declaration for (Num [Char])
In the expression: 5 + "llama"
In the definition of `it': it = 5 + "llama"
这边 ghci 提示说 "llama"
并不是数值型别,所以它不知道该怎样才能给它加上 5。即便是 “four” 甚至是 “4” 也不可以,Haskell 不拿它当数值。执行 True==5
, ghci 就会提示型别不匹配。+
运算子要求两端都是数值,而 ==
运算子仅对两个可比较的值可用。这就要求他们的型别都必须一致,苹果和橘子就无法做比较。我们会在后面深入地理解型别的概念。Note: 5+4.0
是可以执行的,5 既可以做被看做整数也可以被看做浮点数,但 4.0 则不能被看做整数。
也许你并未察觉,不过从始至终我们一直都在使用函数。*
就是一个将两个数相乘的函数,就像三明治一样,用两个参数将它夹在中央,这被称作中缀函数。而其他大多数不能与数夹在一起的函数则被称作前缀函数。绝大部分函数都是前缀函数,在接下来我们就不多做区别。大多数命令式程式语言中的函数呼叫形式通常就是函数名,括号,由逗号分隔的参数列。而在 Haskell 中,函数呼叫的形式是函数名,空格,空格分隔的参数列。简单举个例子,我们呼叫 Haskell 中最无趣的函数:
ghci> succ 8
9
succ
函数返回一个数的后继 (successor)。而且如你所见,在 Haskell 中是用空格来将函数与参数分隔的。至于呼叫多个参数的函数也很容易,min
和 max
接受两个可比较大小的参数,并返回较大或者较小的那个数。
ghci> min 9 10
9
ghci> min 3.4 3.2
3.2
ghci> max 100 101
101
函数呼叫拥有最高的优先顺序,如下两句是等效的
ghci> succ 9 + max 5 4 + 1
16
ghci> (succ 9) + (max 5 4) + 1
16
若要取 9 乘 10 的后继,succ 9*10
是不行的,程式会先取 9 的后继,然后再乘以 10 得 100。正确的写法应该是 succ(9*10)
,得 91。如果某函数有两个参数,也可以用 `
符号将它括起,以中缀函数的形式呼叫它。
例如取两个整数相除所得商的 div
函数, div 92 10
可得 9,但这种形式不容易理解:究竟是哪个数是除数,哪个数被除?使用中缀函数的形式 92 `div` 10
就更清晰了。
从命令式程式语言走过来的人们往往会觉得函数呼叫与括号密不可分,在 C 中,呼叫函数必加括号,就像 foo()
, bar(1)
,或者 baz(3,"haha")
。而在 Haskell 中,函数的呼叫使用空格,例如 bar (bar 3)
,它并不表示以 bar
和 3 两个参数去呼叫 bar
,而是以 bar 3
所得的结果作为参数去呼叫 bar
。在 C 中,就相当于 bar(bar(3))
。
#
初学者的第一个函数
在前一节中我们简单介绍了函数的呼叫,现在让我们编写我们自己的函数!打开你最喜欢的编辑器,输入如下程式码,它的功能就是将一个数字乘以 2。
doubleMe x = x + x
函数的声明与它的呼叫形式大致相同,都是先函数名,后跟由空格分隔的参数表。但在声明中一定要在 =
后面定义函数的行为。
保存为 baby.hs
或任意名称,然后转至保存的位置,打开 ghci,执行 :l baby.hs
。这样我们的函数就装载成功,可以呼叫了。
ghci> :l baby
[1 of 1] Compiling Main ( baby.hs, interpreted )
Ok, modules loaded: Main.
ghci> doubleMe 9
18
ghci> doubleMe 8.3
16.6
+
运算子对整数和浮点都可用(实际上所有有数字特征的值都可以),所以我们的函数可以处理一切数值。声明一个包含两个参数的函数如下:
doubleUs x y = x*2 + y*2
很简单。将其写成 doubleUs x y = x + x + y + y
也可以。测试一下(记住要保存为 baby.hs
并到 ghci 下边执行 :l baby.hs
)
ghci> doubleUs 4 9
26
ghci> doubleUs 2.3 34.2
73.0
ghci> doubleUs 28 88 + doubleMe 123
478
你可以在其他函数中呼叫你编写的函数,如此一来我们可以将 doubleUs
函数改为:
doubleUs x y = doubleMe x + doubleMe y
这种情形在 Haskell 下边十分常见:编写一些简单的函数,然后将其组合,形成一个较为复杂的函数,这样可以减少重复工作。设想若是哪天有个数学家验证说 2 应该是 3,我们只需要将 doubleMe
改为 x+x+x
即可,由于 doubleUs
呼叫到 doubleMe
,于是整个程式便进入了 2 即是 3 的古怪世界。
Haskell 中的函数并没有顺序,所以先声明 doubleUs
还是先声明 doubleMe
都是同样的。如下,我们编写一个函数,它将小于 100 的数都乘以 2,因为大于 100 的数都已经足够大了!
doubleSmallNumber x = if x > 100
then x
else x*2
接下来介绍 Haskell 的 if
语句。你也许会觉得和其他语言很像,不过存在一些不同。Haskell 中 if
语句的 else
部分是不可省略。在命令式语言中,你可以通过 if
语句来跳过一段程式码,而在 Haskell
中,每个函数和表达式都要返回一个结果。对于这点我觉得将 if
语句置于一行之中会更易理解。Haskell 中的 if
语句的另一个特点就是它其实是个表达式,表达式就是返回一个值的一段程式码:5 是个表达式,它返回 5;4+8
是个表达式;x+y
也是个表达式,它返回 x+y
的结果。正由于 else
是强制的,if
语句一定会返回某个值,所以说 if
语句也是个表达式。如果要给刚刚定义的函数的结果都加上 1,可以如此修改:
doubleSmallNumber' x = (if x > 100 then x else x*2) + 1
若是去掉括号,那就会只在小于 100 的时候加 1。注意函数名最后的那个单引号,它没有任何特殊含义,只是一个函数名的合法字元罢了。通常,我们使用单引号来区分一个稍经修改但差别不大的函数。定义这样的函数也是可以的:
conanO'Brien = "It's a-me, Conan O'Brien!"
在这里有两点需要注意。首先就是我们没有大写 conan
的首字母,因为首字母大写的函数是不允许的,稍后我们将讨论其原因;另外就是这个函数并没有任何参数。没有参数的函数通常被称作“定义”(或者“名字”),一旦定义,conanO'Brien
就与字串 "It's a-me, Conan O'Brien!"
完全等价,且它的值不可以修改。
#
List 入门
在 Haskell 中,List 就像现实世界中的购物单一样重要。它是最常用的资料结构,并且十分强大,灵活地使用它可以解决很多问题。本节我们将对 List,字串和 list comprehension 有个初步了解。 在 Haskell 中,List 是一种单型别的资料结构,可以用来存储多个型别相同的元素。我们可以在里面装一组数字或者一组字元,但不能把字元和数字装在一起。
*Note*: 在 ghci 下,我们可以使用 ``let`` 关键字来定义一个常量。在 ghci 下执行 ``let a=1`` 与在脚本中编写 ``a=1`` 是等价的。
ghci> let lostNumbers = [4,8,15,16,23,48]
ghci> lostNumbers
[4,8,15,16,23,48]
如你所见,一个 List 由方括号括起,其中的元素用逗号分隔开来。若试图写 [1,2,'a',3,'b','c',4]
这样的 List,Haskell 就会报出这几个字元不是数字的错误。字串实际上就是一组字元的 List,"Hello" 只是 ['h','e','l','l','o']
的语法糖而已。所以我们可以使用处理 List 的函数来对字串进行操作。 将两个 List 合并是很常见的操作,这可以通过 ++
运算子实现。
ghci> [1,2,3,4] ++ [9,10,11,12]
[1,2,3,4,9,10,11,12]
ghci> "hello" ++ " " ++ "world"
"hello world"
ghci> ['w','o'] ++ ['o','t']
"woot"
在使用 ++
运算子处理长字串时要格外小心(对长 List 也是同样),Haskell 会遍历整个的 List(++
符号左边的那个)。在处理较短的字串时问题还不大,但要是在一个 5000 万长度的 List 上追加元素,那可得执行好一会儿了。所以说,用 :
运算子往一个 List 前端插入元素会是更好的选择。
ghci> 'A':" SMALL CAT"
"A SMALL CAT"
ghci> 5:[1,2,3,4,5]
[5,1,2,3,4,5]
:
运算子可以连接一个元素到一个 List 或者字串之中,而 ++
运算子则是连接两个 List。若要使用 ++
运算子连接单个元素到一个 List 之中,就用方括号把它括起使之成为单个元素的 List。[1,2,3]
实际上是 1:2:3:[]
的语法糖。[]
表示一个空 List,若要从前端插入 3,它就成了 [3]
, 再插入 2,它就成了 [2,3]
,以此类推。
*Note*: ``[],[[]],[[],[],[]]`` 是不同的。第一个是一个空的 List,第二个是含有一个空 List 的 List,第三个是含有三个空 List 的 List。
若是要按照索引取得 List 中的元素,可以使用 !!
运算子,索引的下标为 0。
ghci> "Steve Buscemi" !! 6
'B'
ghci> [9.4,33.2,96.2,11.2,23.25] !! 1
33.2
但你若是试图在一个只含有 4 个元素的 List 中取它的第 6 个元素,就会报错。要小心!
List 同样也可以用来装 List,甚至是 List 的 List 的 List:
ghci> let b = [[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3]]
ghci> b
[[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3]]
ghci> b ++ [[1,1,1,1]]
[[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3],[1,1,1,1]]
ghci> [6,6,6]:b
[[6,6,6],[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3]]
ghci> b !! 2
[1,2,2,3,4]
List 中的 List 可以是不同长度,但必须得是相同的型别。如不可以在 List 中混合放置字元和数组相同,混合放置数值和字元的 List 也是同样不可以的。当 List 内装有可比较的元素时,使用 >
和 >=
可以比较 List 的大小。它会先比较第一个元素,若它们的值相等,则比较下一个,以此类推。
ghci> [3,2,1] > [2,1,0]
True
ghci> [3,2,1] > [2,10,100]
True
ghci> [3,4,2] > [3,4]
True
ghci> [3,4,2] > [2,4]
True
ghci> [3,4,2] == [3,4,2]
True
还可以对 List 做啥?如下是几个常用的函数:
head 返回一个 List 的头部,也就是 List 的首个元素。
ghci> head [5,4,3,2,1]
5
tail 返回一个 List 的尾部,也就是 List 除去头部之后的部分。
ghci> tail [5,4,3,2,1]
[4,3,2,1]
last 返回一个 List 的最后一个元素。
ghci> last [5,4,3,2,1]
1
init 返回一个 List 除去最后一个元素的部分。
ghci> init [5,4,3,2,1]
[5,4,3,2]
如果我们把 List 想象为一头怪兽,那这就是它的样子:
试一下,若是取一个空 List 的 head
又会怎样?
ghci> head []
*** Exception: Prelude.head: empty list
糟糕,程式直接跳出错误。如果怪兽都不存在的话,那他的头也不会存在。在使用 head
,tail
,last
和 init
时要小心别用到空的 List 上,这个错误不会在编译时被捕获。所以说做些工作以防止从空 List 中取值会是个好的做法。
length 返回一个 List 的长度。
ghci> length [5,4,3,2,1]
5
null 检查一个 List 是否为空。如果是,则返回 True
,否则返回 False
。应当避免使用 xs==[]
之类的语句来判断 List 是否为空,使用 null 会更好。
ghci> null [1,2,3]
False
ghci> null []
True
reverse 将一个 List 反转:
ghci> reverse [5,4,3,2,1]
[1,2,3,4,5]
take 返回一个 List 的前几个元素,看:
ghci> take 3 [5,4,3,2,1]
[5,4,3]
ghci> take 1 [3,9,3]
[3]
ghci> take 5 [1,2]
[1,2]
ghci> take 0 [6,6,6]
[]
如上,若是图取超过 List 长度的元素个数,只能得到原 List。若 take 0
个元素,则会得到一个空 List! drop
与 take
的用法大体相同,它会删除一个 List 中的前几个元素。
ghci> drop 3 [8,4,2,1,5,6]
[1,5,6]
ghci> drop 0 [1,2,3,4]
[1,2,3,4]
ghci> drop 100 [1,2,3,4]
[]
maximum 返回一个 List 中最大的那个元素。minimun
返回最小的。
ghci> minimum [8,4,2,1,5,6]
1
ghci> maximum [1,9,2,3,4]
9
sum 返回一个 List 中所有元素的和。product
返回一个 List 中所有元素的积。
ghci> sum [5,2,1,6,3,2,5,7]
31
ghci> product [6,2,1,2]
24
ghci> product [1,2,5,6,7,9,2,0]
0
elem 判断一个元素是否在包含于一个 List,通常以中缀函数的形式呼叫它。
ghci> 4 `elem` [3,4,5,6]
True
ghci> 10 `elem` [3,4,5,6]
False
这就是几个基本的 List 操作函数,我们会在往后的一节中了解更多的函数。
#
使用 Range
今天如果想得到一个包含 1 到 20 之间所有数的 List,你会怎么做? 我们可以将它们一个一个用键盘打出来,但很明显地这不是一个完美的方案,特别是你追求一个好的程式语言的时候。我们想用的是区间 (Range)。Range 是构造 List 方法之一,而其中的值必须是可枚举的,像 1、2、3、4...字元同样也可以枚举,字母表就是 A..Z
所有字元的枚举。而名字就不可以枚举了,"john"
后面是谁?我不知道。
要得到包含 1 到 20 中所有自然数的 List,只要 [1..20]
即可,这与用手写 [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]
是完全等价的。其实用手写一两个还不是什么大事,但若是手写一个非常长的 List 那就铁定是个笨方法。
ghci> [1..20]
[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]
ghci> ['a'..'z']
"abcdefghijklmnopqrstuvwxyz"
ghci> ['K'..'Z']
"KLMNOPQRSTUVWXYZ"
Range 的特点是他还允许你指定每一步该跨多远。譬如说,今天的问题换成是要得到 1 到 20 间所有的偶数或者 3 的倍数该怎样?
ghci> [2,4..20]
[2,4,6,8,10,12,14,16,18,20]
ghci> [3,6..20]
[3,6,9,12,15,18]
仅需用逗号将前两个元素隔开,再标上上限即可。尽管 Range 很聪明,但它恐怕还满足不了一些人对它的期许。你就不能通过 [1,2,4..100]
这样的语句来获得所有 2 的幂。一方面是因为步长只能标明一次,另一方面就是仅凭前几项,数组的后项是不能确定的。要得到 20 到 1 的 List,[20..1]
是不可以的。必须得 [20,19..1]
。 在 Range 中使用浮点数要格外小心!出于定义的原因,浮点数并不精确。若是使用浮点数的话,你就会得到如下的糟糕结果
ghci> [0.1, 0.3 .. 1]
[0.1,0.3,0.5,0.7,0.8999999999999999,1.0999999999999999]
我的建议就是避免在 Range 中使用浮点数。
你也可以不标明 Range 的上限,从而得到一个无限长度的 List。在后面我们会讲解关于无限 List 的更多细节。取前 24 个 13 的倍数该怎样?恩,你完全可以 [13,26..24*13]
,但有更好的方法: take 24 [13,26..]
。
由于 Haskell 是惰性的,它不会对无限长度的 List 求值,否则会没完没了的。它会等着,看你会从它那儿取多少。在这里它见你只要 24 个元素,便欣然交差。如下是几个生成无限 List 的函数 cycle
接受一个 List 做参数并返回一个无限 List 。如果你只是想看一下它的运算结果而已,它会运行个没完的。所以应该在某处划好范围。
ghci> take 10 (cycle [1,2,3])
[1,2,3,1,2,3,1,2,3,1]
ghci> take 12 (cycle "LOL ")
"LOL LOL LOL "
repeat 接受一个值作参数,并返回一个仅包含该值的无限 List。这与用 cycle
处理单元素 List 差不多。
ghci> take 10 (repeat 5)
[5,5,5,5,5,5,5,5,5,5]
其实,你若只是想得到包含相同元素的 List ,使用 replicate
会更简单,如 replicate 3 10
,得 [10,10,10]
。
#
List Comprehension
学过数学的你对集合的 comprehension (Set Comprehension) 概念一定不会陌生。通过它,可以从既有的集合中按照规则产生一个新集合。前十个偶数的 set comprehension 可以表示为
,竖线左端的部分是输出函数,x
是变数,N
是输入集合。在 Haskell 下,我们可以通过类似 take 10 [2,4..]
的程式码来实现。但若是把简单的乘 2 改成更复杂的函数操作该怎么办呢?用 list comprehension,它与 set comprehension 十分的相似,用它取前十个偶数轻而易举。这个 list comprehension 可以表示为:
ghci> [x*2 | x <- [1..10]]
[2,4,6,8,10,12,14,16,18,20]
如你所见,结果正确。给这个 comprehension 再添个限制条件 (predicate),它与前面的条件由一个逗号分隔。在这里,我们要求只取乘以 2 后大于等于 12 的元素。
ghci> [x*2 | x <- [1..10], x*2 >= 12]
[12,14,16,18,20]
cool,灵了。若是取 50 到 100 间所有除7的余数为 3 的元素该怎么办?简单:
ghci> [ x | x <- [50..100], x `mod` 7 == 3]
[52,59,66,73,80,87,94]
成功!从一个 List 中筛选出符合特定限制条件的操作也可以称为过滤 (flitering)。即取一组数并且按照一定的限制条件过滤它们。再举个例子 吧,假如我们想要一个 comprehension,它能够使 List 中所有大于 10 的奇数变为 "BANG"
,小于 10 的奇数变为 "BOOM"
,其他则统统扔掉。方便重用起见,我们将这个 comprehension 置于一个函数之中。
boomBangs xs = [ if x < 10 then "BOOM!" else "BANG!" | x <- xs, odd x]
这个 comprehension 的最后部分就是限制条件,使用 odd
函数判断是否为奇数:返回 True
,就是奇数,该 List 中的元素才被包含。
ghci> boomBangs [7..13]
["BOOM!","BOOM!","BANG!","BANG!"]
也可以加多个限制条件。若要达到 10 到 20 间所有不等于 13,15 或 19 的数,可以这样:
ghci> [ x | x <- [10..20], x /= 13, x /= 15, x /= 19]
[10,11,12,14,16,17,18,20]
除了多个限制条件之外,从多个 List 中取元素也是可以的。这样的话 comprehension 会把所有的元素组合交付给我们的输出函数。在不过滤的前提 下,取自两个长度为 4 的集合的 comprehension 会产生一个长度为 16 的 List。假设有两个 List,[2,5,10]
和 [8,10,11]
, 要取它们所有组合的积,可以这样:
ghci> [ x*y | x <- [2,5,10], y <- [8,10,11]]
[16,20,22,40,50,55,80,100,110]
意料之中,得到的新 List 长度为 9。若只取乘积大于 50 的结果该如何?
ghci> [ x*y | x <-[2,5,10], y <- [8,10,11], x*y > 50]
[55,80,100,110]
取个包含一组名词和形容词的 List comprehension 吧,写诗的话也许用得着。
ghci> let nouns = ["hobo","frog","pope"]
ghci> let adjectives = ["lazy","grouchy","scheming"]
ghci> [adjective ++ " " ++ noun | adjective <- adjectives, noun <- nouns]
["lazy hobo","lazy frog","lazy pope","grouchy hobo","grouchy frog", "grouchy pope","scheming hobo",
"scheming frog","scheming pope"]
明白!让我们编写自己的 length
函数吧!就叫做 length'
!
length' xs = sum [1 | _ <- xs]
_
表示我们并不关心从 List 中取什么值,与其弄个永远不用的变数,不如直接一个 _
。这个函数将一个 List 中所有元素置换为 1,并且使其相加求和。得到的结果便是我们的 List 长度。友情提示:字串也是 List,完全可以使用 list comprehension 来处理字串。如下是个除去字串中所有非大写字母的函数:
removeNonUppercase st = [ c | c <- st, c `elem` ['A'..'Z']]
测试一下:
ghci> removeNonUppercase "Hahaha! Ahahaha!"
"HA"
ghci> removeNonUppercase "IdontLIKEFROGS"
"ILIKEFROGS"
在这里,限制条件做了所有的工作。它说:只有在 ['A'..'Z']
之间的字元才可以被包含。
若操作含有 List 的 List,使用嵌套的 List comprehension 也是可以的。假设有个包含许多数值的 List 的 List,让我们在不拆开它的前提下除去其中的所有奇数:
ghci> let xxs = [[1,3,5,2,3,1,2,4,5],[1,2,3,4,5,6,7,8,9],[1,2,4,2,1,6,3,1,3,2,3,6]]
ghci> [ [ x | x <- xs, even x ] | xs <- xxs]
[[2,2,4],[2,4,6,8],[2,4,2,6,2,6]]
将 List Comprehension 分成多行也是可以的。若非在 ghci 之下,还是将 List Comprehension 分成多行好,尤其是需要嵌套的时候。
#
Tuple
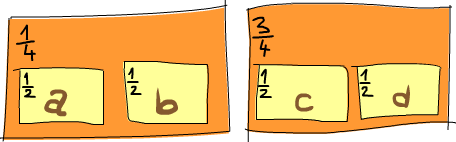
从某种意义上讲,Tuple (元组)很像 List --都是将多个值存入一个个体的容器。但它们却有着本质的不同,一组数字的 List 就是一组数字,它们的型别相同,且不关心其中包含元素的数量。而 Tuple 则要求你对需要组合的数据的数目非常的明确,它的型别取决于其中项的数目与其各自的型别。Tuple 中的项由括号括起,并由逗号隔开。
另外的不同之处就是 Tuple 中的项不必为同一型别,在 Tuple 里可以存入多型别项的组合。
动脑筋,在 Haskell 中表示二维向量该如何?使用 List 是一种方法,它倒也工作良好。若要将一组向量置于一个 List 中来表示平面图形又该怎样?我们可以写类似 [[1,2],[8,11],[4,5]]
的程式码来实现。但问题在于,[[1,2],[8,11,5],[4,5]]
也是同样合法的,因为其中元素的型别都相同。尽管这样并不靠谱,但编译时并不会报错。然而一个长度为 2 的 Tuple (也可以称作序对,Pair) ,是一个独立的类型,这便意味着一个包含一组序对的 List 不能再加入一个三元组,所以说把原先的方括号改为圆括号使用 Tuple 会 更好: [(1,2),(8,11),(4,5)]
。若试图表示这样的图形: [(1,2),(8,11,5),(4,5)]
,就会报出以下的错误:
Couldn't match expected type `(t, t1)'
against inferred type `(t2, t3, t4)'
In the expression: (8, 11, 5)
In the expression: [(1, 2), (8, 11, 5), (4, 5)]
In the definition of `it': it = [(1, 2), (8, 11, 5), (4, 5)]
这告诉我们说程式在试图将序对和三元组置于同一 List 中,而这是不允许的。同样 [(1,2),("one",2)]
这样的 List 也不行,因为 其中的第一个 Tuple 是一对数字,而第二个 Tuple 却成了一个字串和一个数字。Tuple 可以用来储存多个数据,如,我们要表示一个人的名字与年 龄,可以使用这样的 Tuple: ("Christopher", "Walken", 55)
。从这个例子里也可以看出,Tuple 中也可以存储 List。
使用 Tuple 前应当事先明确一条数据中应该由多少个项。每个不同长度的 Tuple 都是独立的型别,所以你就不可以写个函数来给它追加元素。而唯一能做的,就是通过函数来给一个 List 追加序对,三元组或是四元组等内容。
可以有单元素的 List,但 Tuple 不行。想想看,单元素的 Tuple 本身就只有一个值,对我们又有啥意义?不靠谱。
同 List 相同,只要其中的项是可比较的,Tuple 也可以比较大小,只是你不可以像比较不同长度的 List 那样比较不同长度的 Tuple 。如下是两个有用的序对操作函数:
fst 返回一个序对的首项。
ghci> fst (8,11)
8
ghci> fst ("Wow", False)
"Wow"
snd 返回序对的尾项。
ghci> snd (8,11)
11
ghci> snd ("Wow", False)
False
*Note*:这两个函数仅对序对有效,而不能应用于三元组,四元组和五元组之上。稍后,我们将过一遍从 Tuple 中取数据的所有方式。
有个函数很 cool,它就是 zip
。它可以用来生成一组序对 (Pair) 的 List。它取两个 List,然后将它们交叉配对,形成一组序对的 List。它很简单,却很实用,尤其是你需要组合或是遍历两个 List 时。如下是个例子:
ghci> zip [1,2,3,4,5] [5,5,5,5,5]
[(1,5),(2,5),(3,5),(4,5),(5,5)]
ghci> zip [1 .. 5] ["one", "two", "three", "four", "five"]
[(1,"one"),(2,"two"),(3,"three"),(4,"four"),(5,"five")]
它把元素配对并返回一个新的 List。第一个元素配第一个,第二个元素配第二个..以此类推。注意,由于序对中可以含有不同的型别,zip
函数可能会将不同型别的序对组合在一起。若是两个不同长度的 List 会怎么样?
ghci> zip [5,3,2,6,2,7,2,5,4,6,6] ["im","a","turtle"]
[(5,"im"),(3,"a"),(2,"turtle")]
较长的那个会在中间断开,去匹配较短的那个。由于 Haskell 是惰性的,使用 zip
同时处理有限和无限的 List 也是可以的:
ghci> zip [1..] ["apple", "orange", "cherry", "mango"]
[(1,"apple"),(2,"orange"),(3,"cherry"),(4,"mango")]
接下来考虑一个同时应用到 List 和 Tuple 的问题:如何取得所有三边长度皆为整数且小于等于 10,周长为 24 的直角三角形?首先,把所有三遍长度小于等于 10 的三角形都列出来:
ghci> let triangles = [ (a,b,c) | c <- [1..10], b <- [1..10], a <- [1..10] ]
刚才我们是从三个 List 中取值,并且通过输出函数将其组合为一个三元组。只要在 ghci 下边呼叫 triangle,你就会得到所有三边都小于等于 10 的三角形。我们接下来给它添加一个限制条件,令其必须为直角三角形。同时也考虑上 b
边要短于斜边,a
边要短于 b
边情况:
ghci> let rightTriangles = [ (a,b,c) | c <- [1..10], b <- [1..c], a <- [1..b], a^2 + b^2 == c^2]
已经差不多了。最后修改函数,告诉它只要周长为 24 的三角形。
ghci> let rightTriangles' = [ (a,b,c) | c <- [1..10], b <- [1..c], a <- [1..b], a^2 + b^2 == c^2, a+b+c == 24]
ghci> rightTriangles'
[(6,8,10)]
得到正确结果!这便是函数式程式语言的一般思路:先取一个初始的集合并将其变形,执行过滤条件,最终取得正确的结果。
3
Types and Typeclasses
Type
之前我们有说过 Haskell 是 Static Type,这表示在编译时期每个表达式的型别都已经确定下来,这提高了程式码的安全性。若程式码中有让布林值与数字相除的动作,就不会通过编译。这样的好处就是与其让程序在运行时崩溃,不如在编译时就找出可能的错误。Haskell 中所有东西都有型别,因此在编译的时候编译器可以做到很多事情。
与 Java 和 Pascal 不同,Haskell 支持型别推导。写下一个数字,你就没必要另告诉 Haskell 说"它是个数字",它自己能推导出来。这样我们就不必在每个函数或表达式上都标明其型别了。在前面我们只简单涉及一下 Haskell 的型别方面的知识,但是理解这一型别系统对于 Haskell 的学习是至关重要的。
型别是每个表达式都有的某种标签,它标明了这一表达式所属的范畴。例如,表达式 True
是 boolean
型,"hello"
是个字串,等等。
可以使用 ghci 来检测表达式的型别。使用 :t
命令后跟任何可用的表达式,即可得到该表达式的型别,先试一下:
ghci> :t 'a'
'a' :: Char
ghci> :t True
True :: Bool
ghci> :t "HELLO!"
"HELLO!" :: [Char]
ghci> :t (True, 'a')
(True, 'a') :: (Bool, Char)
ghci> :t 4 == 5
4 == 5 :: Bool
可以看出,:t
命令处理一个表达式的输出结果为表达式后跟 ::
及其型别,::
读作"它的型别为"。凡是明确的型别,其首字母必为大写。'a'
, 如它的样子,是 Char
型别,易知是个字元 (character)。True
是 Bool
型别,也靠谱。不过这又是啥,检测 "hello"
得一个 [Char]
这方括号表示一个 List,所以我们可以将其读作"一组字元的 List"。而与 List 不同,每个 Tuple 都是独立的型别,于是 (True,'a')
的型别是 (Bool,Char)
,而 ('a','b','c')
的型别为 (Char,Char,Char)
。4==5
一定回传 False
,所以它的型别为 Bool。
同样,函数也有型别。编写函数时,给它一个明确的型别声明是个好习惯,比较短的函数就不用多此一举了。还记得前面那个过滤大写字母的 List Comprehension 吗?给它加上型别声明便是这个样子:
removeNonUppercase :: [Char] -> [Char]
removeNonUppercase st = [ c | c <- st, c `elem` ['A'..'Z']]
removeNonUppercase
的型别为 [Char]->[Char]
,从它的参数和回传值的型别上可以看出,它将一个字串映射为另一个字串。[Char]
与 String
是等价的,但使用 String
会更清晰:removeNonUppercase :: String -> String
。编译器会自动检测出它的型别,我们还是标明了它的型别声明。要是多个参数的函数该怎样?如下便是一个将三个整数相加的简单函数。
addThree :: Int -> Int -> Int -> Int
addThree x y z = x + y + z
参数之间由 ->
分隔,而与回传值之间并无特殊差异。回传值是最后一项,参数就是前三项。稍后,我们将讲解为何只用 ->
而不是 Int,Int,Int->Int
之类"更好看"的方式来分隔参数。
如果你打算给你编写的函数加上个型别声明却拿不准它的型别是啥,只要先不写型别声明,把函数体写出来,再使用 :t
命令测一下即可。函数也是表达式,所以 :t
对函数也是同样可用的。
如下是几个常见的型别:
Int 表示整数。7 可以是 Int,但 7.2 不可以。Int 是有界的,也就是说它由上限和下限。对 32 位的机器而言,上限一般是 2147483647
,下限是 -2147483648
。
Integer 表示...厄...也是整数,但它是无界的。这就意味着可以用它存放非常非常大的数,我是说非常大。它的效率不如 Int 高。
factorial :: Integer -> Integer
factorial n = product [1..n]
ghci> factorial 50
30414093201713378043612608166064768844377641568960512000000000000
Float 表示单精度的浮点数。
circumference :: Float -> Float
circumference r = 2 * pi * r
ghci> circumference 4.0
25.132742
Double 表示双精度的浮点数。
circumference' :: Double -> Double
circumference' r = 2 * pi * r
ghci> circumference' 4.0
25.132741228718345
Bool 表示布林值,它只有两种值:True
和 False
。
Char 表示一个字元。一个字元由单引号括起,一组字元的 List 即为字串。
Tuple 的型别取决于它的长度及其中项的型别。注意,空 Tuple 同样也是个型别,它只有一种值:()
。
#
Type variables
你觉得 head
函数的型别是啥?它可以取任意型别的 List 的首项,是怎么做到的呢?我们查一下!
ghci> :t head
head :: [a] -> a
嗯! a
是啥?型别吗?想想我们在前面说过,凡是型别其首字母必大写,所以它不会是个型别。它是个型别变数,意味着 a 可以是任意的型别。这一点与其他语言中的泛型 (generic) 很相似,但在 Haskell 中要更为强大。它可以让我们轻而易举地写出型别无关的函数。使用到型别变数的函数被称作"多态函数 ",head
函数的型别声明里标明了它可以取任意型别的 List 并回传其中的第一个元素。
在命名上,型别变数使用多个字元是合法的,不过约定俗成,通常都是使用单个字元,如 a
, b
,c
,d
...
还记得 fst
?我们查一下它的型别:
ghci> :t fst
fst :: (a, b) -> a
可以看到fst
取一个包含两个型别的 Tuple 作参数,并以第一个项的型别作为回传值。这便是 fst
可以处理一个含有两种型别项的 pair 的原因。注意,a
和 b
是不同的型别变数,但它们不一定非得是不同的型别,它只是标明了首项的型别与回传值的型别相同。
#
Typeclasses入门
型别定义行为的介面,如果一个型别属于某 Typeclass,那它必实现了该 Typeclass 所描述的行为。很多从 OOP 走过来的人们往往会把 Typeclass 当成物件导向语言中的 class
而感到疑惑,厄,它们不是一回事。易于理解起见,你可以把它看做是 Java 的 interface。
==
函数的型别声明是怎样的?
ghci> :t (==)
(==) :: (Eq a) => a -> a -> Bool
*Note*: 判断相等的==运算子是函数,``+-*/``之类的运算子也是同样。在预设条件下,它们多为中缀函数。若要检查它的型别,就必须得用括号括起使之作为另一个函数,或者说以首码函数的形式呼叫它。
有意思。在这里我们见到个新东西:=>
符号。它左边的部分叫做型别约束。我们可以这样阅读这段型别声明:"相等函数取两个相同型别的值作为参数并回传一个布林值,而这两个参数的型别同在 Eq 类之中(即型别约束)"
Eq 这一 Typeclass 提供了判断相等性的介面,凡是可比较相等性的型别必属于 Eq
class。
ghci> 5 == 5
True
ghci> 5 /= 5
False
ghci> 'a' == 'a'
True
ghci> "Ho Ho" == "Ho Ho"
True
ghci> 3.432 == 3.432
True
elem
函数的型别为: (Eq a)=>a->[a]->Bool
。这是它在检测值是否存在于一个 List 时使用到了==的缘故。
几个基本的 Typeclass:
Eq 包含可判断相等性的型别。提供实现的函数是 ==
和 /=
。所以,只要一个函数有Eq类的型别限制,那么它就必定在定义中用到了 ==
和 /=
。刚才说了,除函数以外的所有型别都属于 Eq
,所以它们都可以判断相等性。
Ord 包含可比较大小的型别。除了函数以外,我们目前所谈到的所有型别都属于 Ord
类。Ord
包中包含了<, >, <=, >=
之类用于比较大小的函数。compare
函数取两个 Ord
类中的相同型别的值作参数,回传比较的结果。这个结果是如下三种型别之一:GT, LT, EQ
。
ghci> :t (>)
(>) :: (Ord a) => a -> a -> Bool
型别若要成为Ord的成员,必先加入Eq家族。
ghci> "Abrakadabra" < "Zebra"
True
ghci> "Abrakadabra" `compare` "Zebra"
LT
ghci> 5 >= 2
True
ghci> 5 `compare` 3
GT
Show 的成员为可用字串表示的型别。目前为止,除函数以外的所有型别都是 Show
的成员。操作 Show Typeclass,最常用的函数表示 show
。它可以取任一Show的成员型别并将其转为字串。
ghci> show 3
"3"
ghci> show 5.334
"5.334"
ghci> show True
"True"
Read 是与 Show
相反的 Typeclass。read
函数可以将一个字串转为 Read
的某成员型别。
ghci> read "True" || False
True
ghci> read "8.2" + 3.8
12.0
ghci> read "5" - 2
3
ghci> read "[1,2,3,4]" ++ [3]
[1,2,3,4,3]
一切良好,如上的所有型别都属于这一 Typeclass。尝试 read "4"
又会怎样?
ghci> read "4"
< interactive >:1:0:
Ambiguous type variable `a' in the constraint:
`Read a' arising from a use of `read' at <interactive>:1:0-7
Probable fix: add a type signature that fixes these type variable(s)
ghci 跟我们说它搞不清楚我们想要的是什么样的回传值。注意呼叫 read
后跟的那部分,ghci 通过它来辨认其型别。若要一个 boolean
值,他就知道必须得回传一个 Bool
型别的值。但在这里它只知道我们要的型别属于 Read Typeclass,而不能明确到底是哪个。看一下 read
函数的型别声明吧:
ghci> :t read
read :: (Read a) => String -> a
看,它的回传值属于 ReadTypeclass,但我们若用不到这个值,它就永远都不会得知该表达式的型别。所以我们需要在一个表达式后跟::
的型别注释,以明确其型别。如下:
ghci> read "5" :: Int
5
ghci> read "5" :: Float
5.0
ghci> (read "5" :: Float) * 4
20.0
ghci> read "[1,2,3,4]" :: [Int]
[1,2,3,4]
ghci> read "(3, 'a')" :: (Int, Char)
(3, 'a')
编译器可以辨认出大部分表达式的型别,但遇到 read "5"
的时候它就搞不清楚究竟该是 Int 还是 Float 了。只有经过运算,Haskell 才会明确其型别;同时由于 Haskell 是静态的,它还必须得在 编译前搞清楚所有值的型别。所以我们就最好提前给它打声招呼:"嘿,这个表达式应该是这个型别,省的你认不出来!"
Enum 的成员都是连续的型别 -- 也就是可枚举。Enum
类存在的主要好处就在于我们可以在 Range
中用到它的成员型别:每个值都有后继子 (successer) 和前置子 (predecesor),分别可以通过 succ
函数和 pred
函数得到。该 Typeclass 包含的型别有:()
, Bool
, Char
, Ordering
, Int
, Integer
, Float
和 Double
。
ghci> ['a'..'e']
"abcde"
ghci> [LT .. GT]
[LT,EQ,GT]
ghci> [3 .. 5]
[3,4,5]
ghci> succ 'B'
'C'
Bounded 的成员都有一个上限和下限。
ghci> minBound :: Int
-2147483648
ghci> maxBound :: Char
'\1114111'
ghci> maxBound :: Bool
True
ghci> minBound :: Bool
False
minBound
和 maxBound
函数很有趣,它们的型别都是 (Bounded a) => a
。可以说,它们都是多态常量。
如果其中的项都属于 Bounded
Typeclass,那么该 Tuple 也属于 Bounded
ghci> maxBound :: (Bool, Int, Char)
(True,2147483647,'\1114111')
Num 是表示数字的 Typeclass,它的成员型别都具有数字的特征。检查一个数字的型别:
ghci> :t 20
20 :: (Num t) => t
看样子所有的数字都是多态常量,它可以作为所有 Num
Typeclass中的成员型别。以上便是 Num
Typeclass 中包含的所有型别,检测 *
运算子的型别,可以发现它可以处理一切的数字:
ghci> :t (*)
(*) :: (Num a) => a -> a -> a
它只取两个相同型别的参数。所以 (5 :: Int) * (6 :: Integer)
会引发一个型别错误,而 5 * (6 :: Integer)
就不会有问题。
型别只有亲近 Show
和 Eq
,才可以加入 Num
。
Integral 同样是表示数字的 Typeclass。Num
包含所有的数字:实数和整数。而 Integral 仅包含整数,其中的成员型别有 Int
和 Integer
。
Floating 仅包含浮点型别:Float
和 Double
。
有个函数在处理数字时会非常有用,它便是 fromIntegral。其型别声明为: fromIntegral :: (Num b, Integral a) => a -> b
。从中可以看出,它取一个整数做参数并回传一个更加通用的数字,这在同时处理整数和浮点时会尤为有用。举例来说,length
函数的型别声明为:length :: [a] -> Int
,而非更通用的形式,如 length :: (Num b) => [a] -> b
。这应该是历史原因吧,反正我觉得挺蠢。如果取了一个 List 长度的值再给它加 3.2 就会报错,因为这是将浮点数和整数相加。面对这种情况,我们就用 fromIntegral (length [1,2,3,4]) + 3.2
来解决。
注意到,fromIntegral
的型别声明中用到了多个型别约束。如你所见,只要将多个型别约束放到括号里用逗号隔开即可。
4
函数的语法
模式匹配 (Pattern matching)
本章讲的就是 Haskell 那套独特的语法结构,先从模式匹配开始。模式匹配通过检查数据的特定结构来检查其是否匹配,并按模式从中取得数据。
在定义函数时,你可以为不同的模式分别定义函数本身,这就让程式码更加简洁易读。你可以匹配一切数据型别 --- 数字,字元,List,元组,等等。我们弄个简单函数,让它检查我们传给它的数字是不是 7。
lucky :: (Integral a) => a -> String
lucky 7 = "LUCKY NUMBER SEVEN!"
lucky x = "Sorry, you're out of luck, pal!"
在呼叫 lucky
时,模式会从上至下进行检查,一旦有匹配,那对应的函数体就被应用了。这个模式中的唯一匹配是参数为 7,如果不是 7,就转到下一个模式,它匹配一切数值并将其绑定为 x
。这个函数完全可以使用 if
实现,不过我们若要个分辨 1 到 5 中的数字,而无视其它数的函数该怎么办?要是没有模式匹配的话,那可得好大一棵 if-else
树了!
sayMe :: (Integral a) => a -> String
sayMe 1 = "One!"
sayMe 2 = "Two!"
sayMe 3 = "Three!"
sayMe 4 = "Four!"
sayMe 5 = "Five!"
sayMe x = "Not between 1 and 5"
注意下,如果我们把最后匹配一切的那个模式挪到最前,它的结果就全都是 "Not between 1 and 5"
了。因为它自己匹配了一切数字,不给后面的模式留机会。
记得前面实现的那个阶乘函数么?当时是把 n
的阶乘定义成了 product [1..n]
。也可以写出像数学那样的递回实现,先说明 0 的阶乘是 1 ,再说明每个正整数的阶乘都是这个数与它前驱 (predecessor) 对应的阶乘的积。如下便是翻译到 Haskell 的样子:
factorial :: (Integral a) => a -> a
factorial 0 = 1
factorial n = n * factorial (n - 1)
这就是我们定义的第一个递回函数。递回在 Haskell 中十分重要,我们会在后面深入理解。如果拿一个数(如 3)呼叫 factorial
函数,这就是接下来的计算步骤:先计算 3*factorial 2
,factorial 2
等于 2*factorial 1
,也就是 3*(2*(factorial 1))
。factorial 1
等于 1*factorial 0
,好,得 3*(2*(1*factorial 0))
,递回在这里到头了,嗯 --- 我们在万能匹配前面有定义,0 的阶乘是 1。于是最终的结果等于 3*(2*(1*1))
。若是把第二个模式放在前面,它就会捕获包括 0 在内的一切数字,这一来我们的计算就永远都不会停止了。这便是为什么说模式的顺序是如此重要:它总是优先匹配最符合的那个,最后才是那个万能的。
模式匹配也会失败。假如这个函数:
charName :: Char -> String
charName 'a' = "Albert"
charName 'b' = "Broseph"
charName 'c' = "Cecil"
拿个它没有考虑到的字元去呼叫它,你就会看到这个:
ghci> charName 'a'
"Albert"
ghci> charName 'b'
"Broseph"
ghci> charName 'h'
"*** Exception: tut.hs:(53,0)-(55,21): Non-exhaustive patterns in function charName
它告诉我们说,这个模式不够全面。因此,在定义模式时,一定要留一个万能匹配的模式,这样我们的程序就不会为了不可预料的输入而崩溃了。
对 Tuple 同样可以使用模式匹配。写个函数,将二维空间中的向量相加该如何?将它们的 x
项和 y
项分别相加就是了。如果不了解模式匹配,我们很可能会写出这样的程式码:
addVectors :: (Num a) => (a, a) -> (a, a) -> (a, a)
addVectors a b = (fst a + fst b, snd a + snd b)
嗯,可以运行。但有更好的方法,上模式匹配:
addVectors :: (Num a) => (a, a) -> (a, a) -> (a, a)
addVectors (x1, y1) (x2, y2) = (x1 + x2, y1 + y2)
there we go!好多了!注意,它已经是个万能的匹配了。两个 addVector
的型别都是 addVectors:: (Num a) => (a,a) -> (a,a) -> (a,a)
,我们就能够保证,两个参数都是序对 (Pair) 了。
fst
和 snd
可以从序对中取出元素。三元组 (Tripple) 呢?嗯,没现成的函数,得自己动手:
first :: (a, b, c) -> a
first (x, _, _) = x
second :: (a, b, c) -> b
second (_, y, _) = y
third :: (a, b, c) -> c
third (_, _, z) = z
这里的 _
就和 List Comprehension 中一样。表示我们不关心这部分的具体内容。
说到 List Comprehension,我想起来在 List Comprehension 中也能用模式匹配:
ghci> let xs = [(1,3), (4,3), (2,4), (5,3), (5,6), (3,1)]
ghci> [a+b | (a,b) <- xs]
[4,7,6,8,11,4]
一旦模式匹配失败,它就简单挪到下个元素。
对 List 本身也可以使用模式匹配。你可以用 []
或 :
来匹配它。因为 [1,2,3]
本质就是 1:2:3:[]
的语法糖。你也可以使用前一种形式,像 x:xs
这样的模式可以将 List 的头部绑定为 x
,尾部绑定为 xs
。如果这 List 只有一个元素,那么 xs
就是一个空 List。
*Note*:``x:xs`` 这模式的应用非常广泛,尤其是递回函数。不过它只能匹配长度大于等于 1 的 List。
如果你要把 List 的前三个元素都绑定到变数中,可以使用类似 x:y:z:xs
这样的形式。它只能匹配长度大于等于 3 的 List。
我们已经知道了对 List 做模式匹配的方法,就实现个我们自己的 head
函数。
head' :: [a] -> a
head' [] = error "Can't call head on an empty list, dummy!"
head' (x:_) = x
看看管不管用:
ghci> head' [4,5,6]
4
ghci> head' "Hello"
'H'
漂亮!注意下,你若要绑定多个变数(用 _
也是如此),我们必须用括号将其括起。同时注意下我们用的这个 error
函数,它可以生成一个运行时错误,用参数中的字串表示对错误的描述。它会直接导致程序崩溃,因此应谨慎使用。可是对一个空 List 取 head
真的不靠谱哇。
弄个简单函数,让它用非标准的英语给我们展示 List 的前几项。
tell :: (Show a) => [a] -> String
tell [] = "The list is empty"
tell (x:[]) = "The list has one element: " ++ show x
tell (x:y:[]) = "The list has two elements: " ++ show x ++ " and " ++ show y
tell (x:y:_) = "This list is long. The first two elements are: " ++ show x ++ " and " ++ show y
这个函数顾及了空 List,单元素 List,双元素 List 以及较长的 List,所以这个函数很安全。(x:[])
与 (x:y:[])
也可以写作 [x]
和 [x,y]
(有了语法糖,我们不必多加括号)。不过 (x:y:_)
这样的模式就不行了,因为它匹配的 List 长度不固定。
我们曾用 List Comprehension 实现过自己的 length
函数,现在用模式匹配和递回重新实现它:
length' :: (Num b) => [a] -> b
length' [] = 0
length' (_:xs) = 1 + length' xs
这与先前写的那个 factorial
函数很相似。先定义好未知输入的结果 --- 空 List,这也叫作边界条件。再在第二个模式中将这 List 分割为头部和尾部。说,List 的长度就是其尾部的长度加 1。匹配头部用的 _
,因为我们并不关心它的值。同时也应明确,我们顾及了 List 所有可能的模式:第一个模式匹配空 List,第二个匹配任意的非空 List。
看下拿 "ham"
呼叫 length'
会怎样。首先它会检查它是否为空 List。显然不是,于是进入下一模式。它匹配了第二个模式,把它分割为头部和尾部并无视掉头部的值,得长度就是 1+length' "am"
。ok。以此类推,"am"
的 length
就是 1+length' "m"
。好,现在我们有了 1+(1+length' "m")
。length' "m"
即 1+length ""
(也就是 1+length' []
)。根据定义,length' []
等于 0
。最后得 1+(1+(1+0))
。
再实现 sum
。我们知道空 List 的和是 0,就把它定义为一个模式。我们也知道一个 List 的和就是头部加上尾部的和的和。写下来就成了:
sum' :: (Num a) => [a] -> a
sum' [] = 0
sum' (x:xs) = x + sum' xs
还有个东西叫做 as
模式,就是将一个名字和 @
置于模式前,可以在按模式分割什么东西时仍保留对其整体的引用。如这个模式 xs@(x:y:ys)
,它会匹配出与 x:y:ys
对应的东西,同时你也可以方便地通过 xs
得到整个 List,而不必在函数体中重复 x:y:ys
。看下这个 quick and dirty 的例子:
capital :: String -> String
capital "" = "Empty string, whoops!"
capital all@(x:xs) = "The first letter of " ++ all ++ " is " ++ [x]
ghci> capital "Dracula"
"The first letter of Dracula is D"
我们使用 as
模式通常就是为了在较大的模式中保留对整体的引用,从而减少重复性的工作。
还有——你不可以在模式匹配中使用 ++
。若有个模式是 (xs++ys)
,那么这个 List 该从什么地方分开呢?不靠谱吧。而 (xs++[x,y,z])
或只一个 (xs++[x])
或许还能说的过去,不过出于 List 的本质,这样写也是不可以的。
#
什么是 Guards
模式用来检查一个值是否合适并从中取值,而 guard 则用来检查一个值的某项属性是否为真。咋一听有点像是 if
语句,实际上也正是如此。不过处理多个条件分支时 guard 的可读性要高些,并且与模式匹配契合的很好。
在讲解它的语法前,我们先看一个用到 guard 的函数。它会依据你的 BMI 值 (body mass index,身体质量指数)来不同程度地侮辱你。BMI 值即为体重除以身高的平方。如果小于 18.5,就是太瘦;如果在 18.5 到 25 之间,就是正常;25 到 30 之间,超重;如果超过 30,肥胖。这就是那个函数(我们目前暂不为您计算 BMI,它只是直接取一个 BMI 值)。
bmiTell :: (RealFloat a) => a -> String
bmiTell bmi
| bmi <= 18.5 = "You're underweight, you emo, you!"
| bmi <= 25.0 = "You're supposedly normal. Pffft, I bet you're ugly!"
| bmi <= 30.0 = "You're fat! Lose some weight, fatty!"
| otherwise = "You're a whale, congratulations!"
guard 由跟在函数名及参数后面的竖线标志,通常他们都是靠右一个缩进排成一列。一个 guard 就是一个布尔表达式,如果为真,就使用其对应的函数体。如果为假,就送去见下一个 guard,如之继续。如果我们用 24.3 呼叫这个函数,它就会先检查它是否小于等于 18.5,显然不是,于是见下一个 guard。24.3 小于 25.0,因此通过了第二个 guard 的检查,就返回第二个字串。
在这里则是相当的简洁,不过不难想象这在命令式语言中又会是怎样的一棵 if-else 树。由于 if-else 的大树比较杂乱,若是出现问题会很难发现,guard 对此则十分清楚。
最后的那个 guard 往往都是 otherwise
,它的定义就是简单一个 otherwise = True
,捕获一切。这与模式很相像,只是模式检查的是匹配,而它们检查的是布尔表达式 。如果一个函数的所有 guard 都没有通过(而且没有提供 otherwise
作万能匹配),就转入下一模式。这便是 guard 与模式契合的地方。如果始终没有找到合适的 guard 或模式,就会发生一个错误。
当然,guard 可以在含有任意数量参数的函数中使用。省得用户在使用这函数之前每次都自己计算 bmi
。我们修改下这个函数,让它取身高体重为我们计算。
bmiTell :: (RealFloat a) => a -> a -> String
bmiTell weight height
| weight / height ^ 2 <= 18.5 = "You're underweight, you emo, you!"
| weight / height ^ 2 <= 25.0 = "You're supposedly normal. Pffft, I bet you're ugly!"
| weight / height ^ 2 <= 30.0 = "You're fat! Lose some weight, fatty!"
| otherwise = "You're a whale, congratulations!"
你可以测试自己胖不胖。
ghci> bmiTell 85 1.90
"You're supposedly normal. Pffft, I bet you're ugly!"
运行的结果是我不太胖。不过程式却说我很丑。
要注意一点,函数的名字和参数的后面并没有 =
。许多初学者会造成语法错误,就是因为在后面加上了 =
。
另一个简单的例子:写个自己的 max
函数。应该还记得,它是取两个可比较的值,返回较大的那个。
max' :: (Ord a) => a -> a -> a
max' a b
| a > b = a
| otherwise = b
guard 也可以塞在一行里面。但这样会丧失可读性,因此是不被鼓励的。即使是较短的函数也是如此,不过出于展示,我们可以这样重写 max'
:
max' :: (Ord a) => a -> a -> a
max' a b | a > b = a | otherwise = b
这样的写法根本一点都不容易读。
我们再来试试用 guard 实现我们自己的 compare
函数:
myCompare :: (Ord a) => a -> a -> Ordering
a `myCompare` b
| a > b = GT
| a == b = EQ
| otherwise = LT
ghci> 3 `myCompare` 2
GT
*Note*:通过反单引号,我们不仅可以以中缀形式呼叫函数,也可以在定义函数的时候使用它。有时这样会更易读。
#
关键字 Where
前一节中我们写了这个 bmi
计算函数:
bmiTell :: (RealFloat a) => a -> a -> String
bmiTell weight height
| weight / height ^ 2 <= 18.5 = "You're underweight, you emo, you!"
| weight / height ^ 2 <= 25.0 = "You're supposedly normal. Pffft, I bet you're ugly!"
| weight / height ^ 2 <= 30.0 = "You're fat! Lose some weight, fatty!"
| otherwise = "You're a whale, congratulations!"
注意,我们重复了 3 次。我们重复了 3 次。程式设计师的字典里不应该有"重复"这个词。既然发现有重复,那么给它一个名字来代替这三个表达式会更好些。嗯,我们可以这样修改:
bmiTell :: (RealFloat a) => a -> a -> String
bmiTell weight height
| bmi <= 18.5 = "You're underweight, you emo, you!"
| bmi <= 25.0 = "You're supposedly normal. Pffft, I bet you're ugly!"
| bmi <= 30.0 = "You're fat! Lose some weight, fatty!"
| otherwise = "You're a whale, congratulations!"
where bmi = weight / height ^ 2
我们的 where
关键字跟在 guard 后面(最好是与竖线缩进一致),可以定义多个名字和函数。这些名字对每个 guard 都是可见的,这一来就避免了重复。如果我们打算换种方式计算 bmi
,只需进行一次修改就行了。通过命名,我们提升了程式码的可读性,并且由于 bmi
只计算了一次,函数的执行效率也有所提升。我们可以再做下修改:
bmiTell :: (RealFloat a) => a -> a -> String
bmiTell weight height
| bmi <= skinny = "You're underweight, you emo, you!"
| bmi <= normal = "You're supposedly normal. Pffft, I bet you're ugly!"
| bmi <= fat = "You're fat! Lose some weight, fatty!"
| otherwise = "You're a whale, congratulations!"
where bmi = weight / height ^ 2
skinny = 18.5
normal = 25.0
fat = 30.0
函数在 where
绑定中定义的名字只对本函数可见,因此我们不必担心它会污染其他函数的命名空间。注意,其中的名字都是一列垂直排开,如果不这样规范,Haskell 就搞不清楚它们在哪个地方了。
where
绑定不会在多个模式中共享。如果你在一个函数的多个模式中重复用到同一名字,就应该把它置于全局定义之中。
where
绑定也可以使用模式匹配!前面那段程式码可以改成:
...
where bmi = weight / height ^ 2
(skinny, normal, fat) = (18.5, 25.0, 30.0)
我们再搞个简单函数,让它告诉我们姓名的首字母:
initials :: String -> String -> String
initials firstname lastname = [f] ++ ". " ++ [l] ++ "."
where (f:_) = firstname
(l:_) = lastname
我们完全按可以在函数的参数上直接使用模式匹配(这样更短更简洁),在这里只是为了演示在 where
语句中同样可以使用模式匹配:
where
绑定可以定义名字,也可以定义函数。保持健康的程式语言风格,我们搞个计算一组 bmi
的函数:
calcBmis :: (RealFloat a) => [(a, a)] -> [a]
calcBmis xs = [bmi w h | (w, h) <- xs]
where bmi weight height = weight / height ^ 2
这就全了!在这里将 bmi
搞成一个函数,是因为我们不能依据参数直接进行计算,而必须先从传入函数的 List 中取出每个序对并计算对应的值。
where
绑定还可以一层套一层地来使用。 有个常见的写法是,在定义一个函数的时候也写几个辅助函数摆在 where
绑定中。 而每个辅助函数也可以透过 where
拥有各自的辅助函数。
#
关键字 Let
let
绑定与 where
绑定很相似。where
绑定是在函数底部定义名字,对包括所有 guard 在内的整个函数可见。let
绑定则是个表达式,允许你在任何位置定义局部变数,而对不同的 guard 不可见。正如 Haskell 中所有赋值结构一样,let
绑定也可以使用模式匹配。看下它的实际应用!这是个依据半径和高度求圆柱体表面积的函数:
cylinder :: (RealFloat a) => a -> a -> a
cylinder r h =
let sideArea = 2 * pi * r * h
topArea = pi * r ^2
in sideArea + 2 * topArea
let
的格式为 let [bindings] in [expressions]
。在 let
中绑定的名字仅对 in
部分可见。let
里面定义的名字也得对齐到一列。不难看出,这用 where
绑定也可以做到。那么它俩有什么区别呢?看起来无非就是,let
把绑定放在语句前面而 where
放在后面嘛。
不同之处在于,let
绑定本身是个表达式,而 where
绑定则是个语法结构。还记得前面我们讲if语句时提到它是个表达式,因而可以随处安放?
ghci> [if 5 > 3 then "Woo" else "Boo", if 'a' > 'b' then "Foo" else "Bar"]
["Woo", "Bar"]
ghci> 4 * (if 10 > 5 then 10 else 0) + 2
42
用 let
绑定也可以实现:
ghci> 4 * (let a = 9 in a + 1) + 2
42
let
也可以定义局部函数:
ghci> [let square x = x * x in (square 5, square 3, square 2)]
[(25,9,4)]
若要在一行中绑定多个名字,再将它们排成一列显然是不可以的。不过可以用分号将其分开。
ghci> (let a = 100; b = 200; c = 300 in a*b*c, let foo="Hey "; bar = "there!" in foo ++ bar)
(6000000,"Hey there!")
最后那个绑定后面的分号不是必须的,不过加上也没关系。如我们前面所说,你可以在 let
绑定中使用模式匹配。这在从 Tuple 取值之类的操作中很方便。
ghci> (let (a,b,c) = (1,2,3) in a+b+c) * 100
600
你也可以把 let
绑定放到 List Comprehension 中。我们重写下那个计算 bmi
值的函数,用个 let
替换掉原先的 where
。
calcBmis :: (RealFloat a) => [(a, a)] -> [a]
calcBmis xs = [bmi | (w, h) <- xs, let bmi = w / h ^ 2]
List Comprehension 中 let
绑定的样子和限制条件差不多,只不过它做的不是过滤,而是绑定名字。let
中绑定的名字在输出函数及限制条件中都可见。这一来我们就可以让我们的函数只返回胖子的 bmi
值:
calcBmis :: (RealFloat a) => [(a, a)] -> [a]
calcBmis xs = [bmi | (w, h) <- xs, let bmi = w / h ^ 2, bmi >= 25.0]
在 (w, h) <- xs
这里无法使用 bmi
这名字,因为它在 let
绑定的前面。
在 List Comprehension 中我们忽略了 let
绑定的 in
部分,因为名字的可见性已经预先定义好了。不过,把一个 let...in
放到限制条件中也是可以的,这样名字只对这个限制条件可见。在 ghci 中 in
部分也可以省略,名字的定义就在整个交互中可见。
ghci> let zoot x y z = x * y + z
ghci> zoot 3 9 2
29
ghci> let boot x y z = x * y + z in boot 3 4 2
14
ghci> boot
< interactive>:1:0: Not in scope: `boot'
你说既然 let
已经这么好了,还要 where
干嘛呢?嗯,let
是个表达式,定义域限制的相当小,因此不能在多个 guard 中使用。一些朋友更喜欢 where
,因为它是跟在函数体后面,把主函数体距离型别声明近一些会更易读。
#
Case expressions
有命令式程式语言 (C, C++, Java, etc.) 的经验的同学一定会有所了解,很多命令式语言都提供了 case
语句。就是取一个变数,按照对变数的判断选择对应的程式码块。其中可能会存在一个万能匹配以处理未预料的情况。
Haskell 取了这一概念融合其中。如其名,case
表达式就是,嗯,一种表达式。跟 if..else
和 let
一样的表达式。用它可以对变数的不同情况分别求值,还可以使用模式匹配。Hmm,取一个变数,对它模式匹配,执行对应的程式码块。好像在哪儿听过?啊,就是函数定义时参数的模式匹配!好吧,模式匹配本质上不过就是 case
语句的语法糖而已。这两段程式码就是完全等价的:
head' :: [a] -> a
head' [] = error "No head for empty lists!"
head' (x:_) = x
head' :: [a] -> a
head' xs = case xs of [] -> error "No head for empty lists!"
(x:_) -> x
看得出,case表达式的语法十分简单:
case expression of pattern -> result
pattern -> result
pattern -> result
...
expression 匹配合适的模式。 一如预期地,第一个模式若匹配,就执行第一个区块的程式码;否则就接下去比对下一个模式。如果到最后依然没有匹配的模式,就会产生运行时错误。
函数参数的模式匹配只能在定义函数时使用,而 case
表达式可以用在任何地方。例如:
describeList :: [a] -> String
describeList xs = "The list is " ++ case xs of [] -> "empty."
[x] -> "a singleton list."
xs -> "a longer list."
这在表达式中作模式匹配很方便,由于模式匹配本质上就是 case
表达式的语法糖,那么写成这样也是等价的:
describeList :: [a] -> String
describeList xs = "The list is " ++ what xs
where what [] = "empty."
what [x] = "a singleton list."
what xs = "a longer list."
5
递回
你好,递回!
前面的章节中我们简要谈了一下递回。而在本章,我们会深入地了解到它为何在 Haskell 中是如此重要,能够以递回思想写出简洁优雅的程式码。
如果你还不知道什么是递回,就读这个句子。哈哈!开个玩笑而已!递回实际上是定义函数以呼叫自身的方式。在数学定义中,递回随处可见,如斐波那契数列 (fibonacci)。它先是定义两个非递回的数:F(0)=0,F(1)=1
,表示斐波那契数列的前两个数为 0 和 1。然后就是对其他自然数,其斐波那契数就是它前面两个数字的和,即 F(N)=F(N-1)+F(N-2)
。这样一来,F(3)
就是 F(2)+F(1)
,进一步便是 (F(1)+F(0))+F(1)
。已经下探到了前面定义的非递回斐波那契数,可以放心地说 F(3)
就是 2 了。在递回定义中声明的一两个非递回的值(如 F(0)
和 F(1)
) 也可以称作边界条件,这对递回函数的正确求值至关重要。要是前面没有定义 F(0)
和 F(1)
的话,它下探到 0 之后就会进一步到负数,你就永远都得不到结果了。一不留神它就算到了 F(-2000)=F(-2001)+F(-2002)
,并且永远都算不到头!
递回在 Haskell 中非常重要。命令式语言要求你提供求解的步骤,Haskell 则倾向于让你提供问题的描述。这便是 Haskell 没有 while
或 for
循环的原因,递回是我们的替代方案。
#
实作 Maximum
maximum
函数取一组可排序的 List(属于 Ord Typeclass) 做参数,并回传其中的最大值。想想,在命令式风格中这一函数该怎么实现。很可能你会设一个变数来存储当前的最大值,然后用循环遍历该 List,若存在比这个值更大的元素,则修改变数为这一元素的值。到最后,变数的值就是运算结果。唔!描述如此简单的算法还颇费了点口舌呢!
现在看看递回的思路是如何:我们先定下一个边界条件,即处理单个元素的 List 时,回传该元素。如果该 List 的头部大于尾部的最大值,我们就可以假定较长的 List 的最大值就是它的头部。而尾部若存在比它更大的元素,它就是尾部的最大值。就这么简单!现在,我们在 Haskell 中实现它
maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty list"
maximum' [x] = x
maximum' (x:xs)
| x > maxTail = x
| otherwise = maxTail
where maxTail = maximum' xs
如你所见,模式匹配与递回简直就是天造地设!大多数命令式语言中都没有模式匹配,于是你就得造一堆 if-else 来测试边界条件。而在这里,我们仅需要使用模式将其表示出来。第一个模式说,如果该 List 为空,崩溃!就该这样,一个空 List 的最大值能是啥?我不知道。第二个模式也表示一个边缘条件,它说, 如果这个 List 仅包含单个元素,就回传该元素的值。
现在是第三个模式,执行动作的地方。 通过模式匹配,可以取得一个 List 的头部和尾部。这在使用递回处理 List 时是十分常见的。出于习惯,我们用个 where
语句来表示 maxTail
作为该 List 中尾部的最大值,然后检查头部是否大于尾部的最大值。若是,回传头部;若非,回传尾部的最大值。
我们取个 List [2,5,1]
做例子来看看它的工作原理。当呼叫 maximum'
处理它时,前两个模式不会被匹配,而第三个模式匹配了它并将其分为 2
与 [5,1]
。 where
子句再取 [5,1]
的最大值。于是再次与第三个模式匹配,并将 [5,1]
分割为 5
和 [1]
。继续,where
子句取 [1]
的最大值,这时终于到了边缘条件!回传 1
。进一步,将 5
与 [1]
中的最大值做比较,易得 5
,现在我们就得到了 [5,1]
的最大值。再进一步,将 2
与 [5,1]
中的最大值相比较,可得 5
更大,最终得 5
。
改用 max
函数会使程式码更加清晰。如果你还记得,max
函数取两个值做参数并回传其中较大的值。如下便是用 max
函数重写的 maximun'
maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty list"
maximum' [x] = x
maximum' (x:xs) = max x (maximum' xs)
太漂亮了!一个 List 的最大值就是它的首个元素与它尾部中最大值相比较所得的结果,简明扼要。
#
来看几个递回函数
现在我们已经了解了递回的思路,接下来就使用递回来实现几个函数. 先实现下 replicate
函数, 它取一个 Int
值和一个元素做参数, 回传一个包含多个重复元素的 List, 如 replicate 3 5
回传 [5,5,5]
. 考虑一下, 我觉得它的边界条件应该是负数. 如果要 replicate
重复某元素零次, 那就是空 List. 负数也是同样, 不靠谱.
replicate' :: (Num i, Ord i) => i -> a -> [a]
replicate' n x
| n <= 0 = []
| otherwise = x:replicate' (n-1) x
在这里我们使用了 guard 而非模式匹配, 是因为这里做的是布林判断. 如果 n
小于 0 就回传一个空 List, 否则, 回传以 x
作首个元素并后接重复 n-1
次 x
的 List. 最后, (n-1)
的那部分就会令函数抵达边缘条件.
*Note*: Num 不是 Ord 的子集, 表示数字不一定得拘泥于排序, 这就是在做加减法比较时要将 Num 与 Ord 型别约束区别开来的原因.
接下来实现 take
函数, 它可以从一个 List 取出一定数量的元素. 如 take 3 [5,4,3,2,1]
, 得 [5,4,3]
. 若要取零或负数个的话就会得到一个空 List. 同样, 若是从一个空 List中取值, 它会得到一个空 List. 注意, 这儿有两个边界条件, 写出来:
take' :: (Num i, Ord i) => i -> [a] -> [a]
take' n _
| n <= 0 = []
take' _ [] = []
take' n (x:xs) = x : take' (n-1) xs
首个模式辨认若为 0 或负数, 回传空 List. 同时注意这里用了一个 guard 却没有指定 otherwise
部分, 这就表示 n
若大于 0, 会转入下一模式. 第二个模式指明了若试图从一个空 List 中取值, 则回传空 List. 第三个模式将 List 分割为头部和尾部, 然后表明从一个 List 中取多个元素等同于令 x
作头部后接从尾部取 n-1
个元素所得的 List. 假如我们要从 [4,3,2,1]
中取 3 个元素, 试着从纸上写出它的推导过程
reverse
函数简单地反转一个 List, 动脑筋想一下它的边界条件! 该怎样呢? 想想...是空 List! 空 List 的反转结果还是它自己. Okay, 接下来该怎么办? 好的, 你猜的出来. 若将一个 List 分割为头部与尾部, 那它反转的结果就是反转后的尾部与头部相连所得的 List.
reverse' :: [a] -> [a]
reverse' [] = []
reverse' (x:xs) = reverse' xs ++ [x]
继续下去!
Haskell 支持无限 List,所以我们的递回就不必添加边界条件。这样一来,它可以对某值计算个没完, 也可以产生一个无限的资料结构,如无限 List。而无限 List 的好处就在于我们可以在任意位置将它断开.
repeat
函数取一个元素作参数, 回传一个仅包含该元素的无限 List. 它的递回实现简单的很, 看:
repeat' :: a -> [a]
repeat' x = x:repeat' x
呼叫 repeat 3
会得到一个以 3 为头部并无限数量的 3 为尾部的 List, 可以说 repeat 3
运行起来就是 3:repeat 3
, 然后 3:3:3:3
等等. 若执行 repeat 3
, 那它的运算永远都不会停止。而 take 5 (repeat 3)
就可以得到 5 个 3, 与 replicate 5 3
差不多.
zip
取两个 List 作参数并将其捆在一起。zip [1,2,3] [2,3]
回传 [(1,2),(2,3)]
, 它会把较长的 List 从中间断开, 以匹配较短的 List. 用 zip
处理一个 List 与空 List 又会怎样? 嗯, 会得一个空 List, 这便是我们的限制条件, 由于 zip
取两个参数, 所以要有两个边缘条件
zip' :: [a] -> [b] -> [(a,b)]
zip' _ [] = []
zip' [] _ = []
zip' (x:xs) (y:ys) = (x,y):zip' xs ys
前两个模式表示两个 List 中若存在空 List, 则回传空 List. 第三个模式表示将两个 List 捆绑的行为, 即将其头部配对并后跟捆绑的尾部. 用 zip
处理 [1,2,3]
与 ['a','b']
的话, 就会在 [3]
与 []
时触及边界条件, 得到 (1,'a'):(2,'b'):[]
的结果,与 [(1,'a'),(2,'b')]
等价.
再实现一个标准库函数 -- elem
! 它取一个元素与一个 List 作参数, 并检测该元素是否包含于此 List. 而边缘条件就与大多数情况相同, 空 List. 大家都知道空 List 中不包含任何元素, 便不必再做任何判断
elem' :: (Eq a) => a -> [a] -> Bool
elem' a [] = False
elem' a (x:xs)
| a == x = True
| otherwise = a `elem'` xs
这很简单明了。若头部不是该元素, 就检测尾部, 若为空 List 就回传 False
.
#
"快速"排序
假定我们有一个可排序的 List, 其中元素的型别为 Ord Typeclass 的成员. 现在我们要给它排序! 有个排序算法非常的酷, 就是快速排序 (quick sort), 睿智的排序方法. 尽管它在命令式语言中也不过 10 行, 但在 Haskell 下边要更短, 更漂亮, 俨然已经成了 Haskell 的招牌了. 嗯, 我们在这里也实现一下. 或许会显得很俗气, 因为每个人都用它来展示 Haskell 究竟有多优雅!
它的型别声明应为 quicksort :: (Ord a) => [a] -> [a]
, 没啥奇怪的. 边界条件呢? 如料,空 List。排过序的空 List 还是空 List。接下来便是算法的定义:排过序的 List 就是令所有小于等于头部的元素在先(它们已经排过了序), 后跟大于头部的元素(它们同样已经拍过了序)。 注意定义中有两次排序,所以就得递回两次!同时也需要注意算法定义的动词为"是"什么而非"做"这个, "做"那个, 再"做"那个...这便是函数式编程之美!如何才能从 List 中取得比头部小的那些元素呢?List Comprehension。好,动手写出这个函数!
quicksort :: (Ord a) => [a] -> [a]
quicksort [] = []
quicksort (x:xs) =
let smallerSorted = quicksort [a | a <- xs, a <= x]
biggerSorted = quicksort [a | a <- xs, a > x]
in smallerSorted ++ [x] ++ biggerSorted
小小的测试一下, 看看结果是否正确~
ghci> quicksort [10,2,5,3,1,6,7,4,2,3,4,8,9]
[1,2,2,3,3,4,4,5,6,7,8,9,10]
ghci> quicksort "the quick brown fox jumps over the lazy dog"
" abcdeeefghhijklmnoooopqrrsttuuvwxyz"
booyah! 如我所说的一样! 若给 [5,1,9,4,6,7,3]
排序,这个算法就会取出它的头部,即 5。 将其置于分别比它大和比它小的两个 List 中间,得 [1,4,3] ++ [5] ++ [9,6,7]
, 我们便知道了当排序结束之时,5会在第四位,因为有3个数比它小每,也有三个数比它大。好的,接着排 [1,4,3]
与 [9,6,7]
, 结果就出来了!对它们的排序也是使用同样的函数,将它们分成许多小块,最终到达临界条件,即空 List 经排序依然为空,有个插图:
橙色的部分表示已定位并不再移动的元素。从左到右看,便是一个排过序的 List。在这里我们将所有元素与 head
作比较,而实际上就快速排序算法而言,选择任意元素都是可以的。被选择的元素就被称作锚 (pivot
),以方便模式匹配。小于锚的元素都在浅绿的部分,大于锚都在深绿部分,这个黄黄的坡就表示了快速排序的执行方式:
#
用递回来思考
我们已经写了不少递回了,也许你已经发觉了其中的固定模式:先定义一个边界条件,再定义个函数,让它从一堆元素中取一个并做点事情后,把余下的元素重新交给这个函数。 这一模式对 List、Tree 等资料结构都是适用的。例如,sum
函数就是一个 List 头部与其尾部的 sum
的和。一个 List 的积便是该 List 的头与其尾部的积相乘的积,一个 List 的长度就是 1 与其尾部长度的和. 等等
再者就是边界条件。一般而言,边界条件就是为避免程序出错而设置的保护措施,处理 List 时的边界条件大部分都是空 List,而处理 Tree 时的边界条件就是没有子元素的节点。
处理数字时也与之相似。函数一般都得接受一个值并修改它。早些时候我们编写过一个计算 Fibonacci 的函数,它便是某数与它减一的 Fibonacci 数的积。让它乘以零就不行了, Fibonacci 数又都是非负数,边界条件便可以定为 1,即乘法的单位元。 因为任何数乘以 1 的结果还是这个数。而在 sum
中,加法的单位元就是 0。在快速排序中,边界条件和单位元都是空 List,因为任一 List 与空 List 相加的结果依然是原 List。
使用递回来解决问题时应当先考虑递回会在什么样的条件下不可用, 然后再找出它的边界条件和单位元, 考虑参数应该在何时切开(如对 List 使用模式匹配), 以及在何处执行递回.
6
高阶函数
Haskell 中的函数可以作为参数和回传值传来传去,这样的函数就被称作高阶函数。高阶函数可不只是某简单特性而已,它贯穿于 Haskell 的方方面面。要拒绝循环与状态的改变而通过定义问题"是什么"来解决问题,高阶函数必不可少。它们是编码的得力工具。
#
Curried functions
本质上,Haskell 的所有函数都只有一个参数,那么我们先前编那么多含有多个参数的函数又是怎么回事? 呵,小伎俩! 所有多个参数的函数都是 Curried functions。 什么意思呢? 取一个例子最好理解,就拿我们的好朋友 max
函数说事吧。它看起来像是取两个参数,回传较大的那个数。 实际上,执行 max 4 5
时,它会首先回传一个取一个参数的函数,其回传值不是 4 就是该参数,取决于谁大。 然后,以 5 为参数呼叫它,并取得最终结果。 这听着挺绕口的,不过这一概念十分的酷! 如下的两个呼叫是等价的:
ghci> max 4 5
5
ghci> (max 4) 5
5
把空格放到两个东西之间,称作函数呼叫。它有点像个运算符,并拥有最高的优先顺序。 看看 max
函数的型别: max :: (Ord a) => a -> a -> a
。 也可以写作: max :: (Ord a) => a -> (a -> a)
。 可以读作 max
取一个参数 a
,并回传一个函数(就是那个 ->
),这个函数取一个 a
型别的参数,回传一个a。 这便是为何只用箭头来分隔参数和回传值型别。
这样的好处又是如何? 简言之,我们若以不全的参数来呼叫某函数,就可以得到一个不全呼叫的函数。 如果你高兴,构造新函数就可以如此便捷,将其传给另一个函数也是同样方便。
看下这个函数,简单至极:
multThree :: (Num a) => a -> a -> a -> a
multThree x y z = x * y * z
我们若执行 mulThree 3 5 9
或 ((mulThree 3) 5) 9
,它背后是如何运作呢? 首先,按照空格分隔,把 3
交给 mulThree
。 这回传一个回传函数的函数。 然后把 5
交给它,回传一个取一个参数并使之乘以 15
的函数。 最后把 9
交给这一函数,回传 135
。 想想,这个函数的型别也可以写作 multThree :: (Num a) => a -> (a -> (a -> a))
,->
前面的东西就是函数取的参数,后面的东西就是其回传值。所以说,我们的函数取一个 a
,并回传一个型别为 (Num a) => a -> (a -> a)
的函数,类似,这一函数回传一个取一个 a
,回传一个型别为 (Num a) => a -> a
的函数。 而最后的这个函数就只取一个 a
并回传一个 a
,如下:
ghci> let multTwoWithNine = multThree 9
ghci> multTwoWithNine 2 3
54
ghci> let multWithEighteen = multTwoWithNine 2
ghci> multWithEighteen 10
180
前面提到,以不全的参数呼叫函数可以方便地创造新的函数。例如,搞个取一数与 100 比较大小的函数该如何? 大可这样:
compareWithHundred :: (Num a, Ord a) => a -> Ordering
compareWithHundred x = compare 100 x
用 99 呼叫它,就可以得到一个 GT
。 简单。 注意下在等号两边都有 x
。 想想 compare 100
会回传什么?一个取一数与 100 比较的函数。 Wow,这不正是我们想要的? 这样重写:
compareWithHundred :: (Num a, Ord a) => a -> Ordering
compareWithHundred = compare 100
型别声明依然相同,因为 compare 100
回传函数。compare
的型别为 (Ord a) => a -> (a -> Ordering)
,用 100 呼叫它后回传的函数型别为 (Num a, Ord a) => a -> Ordering
,同时由于 100 还是 Num
型别类的实例,所以还得另留一个类约束。
Yo! 你得保证已经弄明白了 Curried functions 与不全呼叫的原理,它们很重要!
中缀函数也可以不全呼叫,用括号把它和一边的参数括在一起就行了。 这回传一个取一参数并将其补到缺少的那一端的函数。 一个简单函数如下:
divideByTen :: (Floating a) => a -> a
divideByTen = (/10)
呼叫 divideByTen 200
就是 (/10) 200
,和 200 / 10
等价。
一个检查字元是否为大写的函数:
isUpperAlphanum :: Char -> Bool
isUpperAlphanum = (`elem` ['A'..'Z'])
唯一的例外就是 -
运算符,按照前面提到的定义,(-4)
理应回传一个并将参数减 4 的函数,而实际上,处于计算上的方便,(-4)
表示负 4
。 若你一定要弄个将参数减 4 的函数,就用 subtract
好了,像这样 (subtract 4)
.
若不用 let
给它命名或传到另一函数中,在 ghci 中直接执行 multThree 3 4
会怎样?
ghci> multThree 3 4
:1:0:
No instance for (Show (t -> t))
arising from a use of `print' at :1:0-12
Possible fix: add an instance declaration for (Show (t -> t))
In the expression: print it
In a 'do' expression: print it
ghci 说,这一表达式回传了一个 a -> a
型别的函数,但它不知道该如何显示它。 函数不是 Show
型别类的实例,所以我们不能得到表示一函数内容的字串。 若在 ghci 中计算 1+1
,它会首先计算得 2
,然后呼叫 show 2
得到该数值的字串表示,即 "2"
,再输出到屏幕.
#
是时候了,来点高阶函数!
Haskell 中的函数可以取另一个函数做参数,也可以回传函数。 举个例子,我们弄个取一个函数并呼叫它两次的函数.
applyTwice :: (a -> a) -> a -> a
applyTwice f x = f (f x)
首先注意这型别声明。 在此之前我们很少用到括号,因为 (->)
是自然的右结合,不过在这里括号是必须的。 它标明了首个参数是个参数与回传值型别都是a的函数,第二个参数与回传值的型别也都是a。 我们可以用 Curried functions 的思路来理解这一函数,不过免得自寻烦恼,我们姑且直接把它看作是取两个参数回传一个值,其首个参数是个型别为 (a->a)
的函数,第二个参数是个 a
。 该函数的型别可以是 (Int->Int)
,也可以是 (String->String)
,但第二个参数必须与之一致。
*Note*: 现在开始我们会直说某函数含有多个参数(除非它真的只有一个参数)。 以简洁之名,我们会说 ``(a->a->a)`` 取两个参数,尽管我们知道它在背后做的手脚.
这个函数是相当的简单,就拿参数 f
当函数,用 x
呼叫它得到的结果再去呼叫它。也就可以这样玩:
ghci> applyTwice (+3) 10
16
ghci> applyTwice (++ " HAHA") "HEY"
"HEY HAHA HAHA"
ghci> applyTwice ("HAHA " ++) "HEY"
"HAHA HAHA HEY"
ghci> applyTwice (multThree 2 2) 9
144
ghci> applyTwice (3:) [1]
[3,3,1]
看,不全呼叫多神奇! 如果有个函数要我们给它传个一元函数,大可以不全呼叫一个函数让它剩一个参数,再把它交出去。
接下来我们用高阶函数的编程思想来实现个标准库中的函数,它就是 zipWith
。 它取一个函数和两个 List 做参数,并把两个 List 交到一起(使相应的元素去呼叫该函数)。 如下就是我们的实现:
zipWith' :: (a -> b -> c) -> [a] -> [b] -> [c]
zipWith' _ [] _ = []
zipWith' _ _ [] = []
zipWith' f (x:xs) (y:ys) = f x y : zipWith' f xs ys
看下这个型别声明,它的首个参数是个函数,取两个参数处理交叉,其型别不必相同,不过相同也没关系。 第二三个参数都是 List,回传值也是个 List。 第一个 List中元素的型别必须是a,因为这个处理交叉的函数的第一个参数是a。 第二个 List 中元素的型别必为 b
,因为这个处理交叉的函数第二个参数的型别是 b
。 回传的 List 中元素型别为 c
。 如果一个函数说取一个型别为 a->b->c
的函数做参数,传给它个 a->a->c
型别的也是可以的,但反过来就不行了。 可以记下,若在使用高阶函数的时候不清楚其型别为何,就先忽略掉它的型别声明,再到 ghci 下用 :t
命令来看下 Haskell 的型别推导.
这函数的行为与普通的 zip
很相似,边界条件也是相同,只不过多了个参数,即处理元素交叉的函数。它关不着边界条件什么事儿,所以我们就只留一个 _
。后一个模式的函数体与 zip
也很像,只不过这里是 f x y
而非 (x,y)
。 只要足够通用,一个简单的高阶函数可以在不同的场合反复使用。 如下便是我们 zipWith'
函数本领的冰山一角:
ghci> zipWith' (+) [4,2,5,6] [2,6,2,3]
[6,8,7,9]
ghci> zipWith' max [6,3,2,1] [7,3,1,5]
[7,3,2,5]
ghci> zipWith' (++) ["foo ","bar ","baz "] ["fighters","hoppers","aldrin"]
["foo fighters","bar hoppers","baz aldrin"]
ghci> zipWith' (*) (replicate 5 2) [1..]
[2,4,6,8,10]
ghci> zipWith' (zipWith' (*)) [[1,2,3],[3,5,6],[2,3,4]] [[3,2,2],[3,4,5],[5,4,3]]
[[3,4,6],[9,20,30],[10,12,12]]
如你所见,一个简单的高阶函数就可以玩出很多花样。命令式语言使用 for
、while
、赋值、状态检测来实现功能,再包起来留个介面,使之像个函数一样呼叫。而函数式语言使用高阶函数来抽象出常见的模式,像成对遍历并处理两个 List 或从中筛掉自己不需要的结果。
接下来实现标准库中的另一个函数 flip
,flip
简单地取一个函数作参数并回传一个相似的函数,只是它们的两个参数倒了个。
flip' :: (a -> b -> c) -> (b -> a -> c)
flip' f = g
where g x y = f y x
从这型别声明中可以看出,它取一个函数,其参数型别分别为 a
和 b
,而它回传的函数的参数型别为 b
和 a
。 由于函数预设都是柯里化的,->
为右结合,这里的第二对括号其实并无必要,(a -> b -> c) -> (b -> a -> c)
与 (a -> b -> c) -> (b -> (a -> c))
等价,也与 (a -> b -> c) -> b -> a -> c
等价。 前面我们写了 g x y = f y x
,既然这样可行,那么 f y x = g x y
不也一样? 这一来我们可以改成更简单的写法:
flip' :: (a -> b -> c) -> b -> a -> c
flip' f y x = f x y
在这里我们就利用了 Curried functions 的优势,只要呼叫 flip' f
而不带 y
和x
,它就会回传一个俩参数倒个的函数。 flip
处理的函数往往都是用来传给其他函数呼叫,于是我们可以发挥 Curried functions 的优势,预先想好发生完全呼叫的情景并处理好回传值.
ghci> flip' zip [1,2,3,4,5] "hello"
[('h',1),('e',2),('l',3),('l',4),('o',5)]
ghci> zipWith (flip' div) [2,2..] [10,8,6,4,2]
[5,4,3,2,1]
#
map 与 filter
map 取一个函数和 List 做参数,遍历该 List 的每个元素来呼叫该函数产生一个新的 List。 看下它的型别声明和实现:
map :: (a -> b) -> [a] -> [b]
map _ [] = []
map f (x:xs) = f x : map f xs
从这型别声明中可以看出,它取一个取 a
回传 b
的函数和一组 a
的 List,并回传一组 b
。 这就是 Haskell 的有趣之处:有时只看型别声明就能对函数的行为猜个大致。map
函数多才多艺,有一百万种用法。如下是其中一小部分:
ghci> map (+3) [1,5,3,1,6]
[4,8,6,4,9]
ghci> map (++ "!") ["BIFF","BANG","POW"]
["BIFF!","BANG!","POW!"]
ghci> map (replicate 3) [3..6]
[[3,3,3],[4,4,4],[5,5,5],[6,6,6]]
ghci> map (map (^2)) [[1,2],[3,4,5,6],[7,8]]
[[1,4],[9,16,25,36],[49,64]]
ghci> map fst [(1,2),(3,5),(6,3),(2,6),(2,5)]
[1,3,6,2,2]
你可能会发现,以上的所有程式码都可以用 List Comprehension 来替代。map (+3) [1,5,3,1,6]
与 [x+3 | x <- [1,5,3,1,6]
完全等价。
filter 函数取一个限制条件和一个 List,回传该 List 中所有符合该条件的元素。它的型别声明及实现大致如下:
filter :: (a -> Bool) -> [a] -> [a]
filter _ [] = []
filter p (x:xs)
| p x = x : filter p xs
| otherwise = filter p xs
很简单。只要 p x
所得的结果为真,就将这一元素加入新 List,否则就无视之。几个使用范例:
ghci> filter (>3) [1,5,3,2,1,6,4,3,2,1]
[5,6,4]
ghci> filter (==3) [1,2,3,4,5]
[3]
ghci> filter even [1..10]
[2,4,6,8,10]
ghci> let notNull x = not (null x) in filter notNull [[1,2,3],[],[3,4,5],[2,2],[],[],[]]
[[1,2,3],[3,4,5],[2,2]]
ghci> filter (`elem` ['a'..'z']) "u LaUgH aT mE BeCaUsE I aM diFfeRent"
"uagameasadifeent"
ghci> filter (`elem` ['A'..'Z']) "i lauGh At You BecAuse u r aLL the Same"
"GAYBALLS"
同样,以上都可以用 List Comprehension 的限制条件来实现。并没有教条规定你必须在什么情况下用 map
和 filter
还是 List Comprehension,选择权归你,看谁舒服用谁就是。 如果有多个限制条件,只能连着套好几个 filter
或用 &&
等逻辑函数的组合之,这时就不如 List comprehension 来得爽了。
还记得上一章的那个 quicksort
函数么? 我们用到了 List Comprehension 来过滤大于或小于锚的元素。 换做 filter
也可以实现,而且更加易读:
quicksort :: (Ord a) => [a] -> [a]
quicksort [] = []
quicksort (x:xs) =
let smallerSorted = quicksort (filter (<=x) xs)
biggerSorted = quicksort (filter (>x) xs)
in smallerSorted ++ [x] ++ biggerSorted
map
和 filter
是每个函数式程序员的面包黄油(呃,map
和 filter
还是 List Comprehension 并不重要)。 想想前面我们如何解决给定周长寻找合适直角三角形的问题的? 在命令式编程中,我们可以套上三个循环逐个测试当前的组合是否满足条件,若满足,就打印到屏幕或其他类似的输出。 而在函数式编程中,这行就都交给 map
和 filter
。 你弄个取一参数的函数,把它交给 map
过一遍 List,再 filter
之找到合适的结果。 感谢 Haskell 的惰性,即便是你多次 map
一个 ``List` 也只会遍历一遍该 List,要找出小于 100000 的数中最大的 3829 的倍数,只需过滤结果所在的 List 就行了.
要找出小于 100000 的 3829 的所有倍数,我们应当过滤一个已知结果所在的 List.
largestDivisible :: (Integral a) => a
largestDivisible = head (filter p [100000,99999..])
where p x = x `mod` 3829 == 0
首先,取一个降序的小于 100000 所有数的 List,然后按照限制条件过滤它。 由于这个 List 是降序的,所以结果 List 中的首个元素就是最大的那个数。惰性再次行动! 由于我们只取这结果 List 的首个元素,所以它并不关心这 List 是有限还是无限的,在找到首个合适的结果处运算就停止了。
接下来,我们就要找出所有小于 10000 的奇数的平方和,得先提下 takeWhile 函数,它取一个限制条件和 List 作参数,然后从头开始遍历这一 List,并回传符合限制条件的元素。 而一旦遇到不符合条件的元素,它就停止了。 如果我们要取出字串 "elephants know how to party"
中的首个单词,可以 takeWhile (/=' ') "elephants know how to party"
,回传 "elephants"
。okay,要求所有小于 10000 的奇数的平方的和,首先就用 (^2)
函数 map
掉这个无限的 List [1..]
。然后过滤之,只取奇数就是了。 在大于 10000 处将它断开,最后前面的所有元素加到一起。 这一切连写函数都不用,在 ghci 下直接搞定.
ghci> sum (takeWhile (<10000) (filter odd (map (^2) [1..])))
166650
不错! 先从几个初始数据(表示所有自然数的无限 List),再 map
它,filter
它,切它,直到它符合我们的要求,再将其加起来。 这用 List comprehension 也是可以的,而哪种方式就全看你的个人口味.
ghci> sum (takeWhile (<10000) [m | m <- [n^2 | n <- [1..]], odd m])
166650
感谢 Haskell 的惰性特质,这一切才得以实现。 我们之所以可以 map
或 filter
一个无限 List,是因为它的操作不会被立即执行,而是拖延一下。只有我们要求 Haskell 交给我们 sum
的结果的时候,sum
函数才会跟 takeWhile
说,它要这些数。takeWhile
就再去要求 filter
和 map
行动起来,并在遇到大于等于 10000 时候停止. 下个问题与 Collatz 序列有关,取一个自然数,若为偶数就除以 2。 若为奇数就乘以 3 再加 1。 再用相同的方式处理所得的结果,得到一组数字构成的的链。它有个性质,无论任何以任何数字开始,最终的结果都会归 1。所以若拿 13 当作起始数,就可以得到这样一个序列 13,40,20,10,5,16,8,4,2,1
。13*3+1
得 40,40 除 2 得 20,如是继续,得到一个 10 个元素的链。
好的,我们想知道的是: 以 1 到 100 之间的所有数作为起始数,会有多少个链的长度大于 15?
chain :: (Integral a) => a -> [a]
chain 1 = [1]
chain n
| even n = n:chain (n `div` 2)
| odd n = n:chain (n*3 + 1)
该链止于 1,这便是边界条件。标准的递归函数:
ghci> chain 10
[10,5,16,8,4,2,1]
ghci> chain 1
[1]
ghci> chain 30
[30,15,46,23,70,35,106,53,160,80,40,20,10,5,16,8,4,2,1]
yay! 貌似工作良好。 现在由这个函数来告诉我们结果:
numLongChains :: Int
numLongChains = length (filter isLong (map chain [1..100]))
where isLong xs = length xs > 15
我们把 chain
函数 map
到 [1..100]
,得到一组链的 List,然后用个限制条件过滤长度大于 15 的链。过滤完毕后就可以得出结果list中的元素个数.
*Note*: 这函数的型别为 ``numLongChains :: Int``。这是由于历史原因,``length`` 回传一个 ``Int`` 而非 ``Num`` 的成员型别,若要得到一个更通用的 ``Num a``,我们可以使用 ``fromIntegral`` 函数来处理所得结果.
用 map
,我们可以写出类似 map (*) [0..]
之类的程式码。 如果只是为了例证 Curried functions 和不全呼叫的函数是真正的值及其原理,那就是你可以把函数传递或把函数装在 List 中(只是你还不能将它们转换为字串)。 迄今为止,我们还只是 map
单参数的函数到 List,如 map (*2) [0..]
可得一组型别为 (Num a) => [a]
的 List,而 map (*) [0..]
也是完全没问题的。*
的型别为 (Num a) => a -> a -> a
,用单个参数呼叫二元函数会回传一个一元函数。如果用 *
来 map
一个 [0..]
的 List,就会得到一组一元函数组成的 List,即 (Num a) => [a->a]
。map (*) [0..]
所得的结果写起来大约就是 [(0*),(1*),(2*)..]
.
ghci> let listOfFuns = map (*) [0..]
ghci> (listOfFuns !! 4) 5
20
取所得 List 的第四个元素可得一函数,与 (*4)
等价。 然后用 5
呼叫它,与 (* 4) 5
或 4*5
都是等价的.
#
lambda
lambda 就是匿名函数。有些时候我们需要传给高阶函数一个函数,而这函数我们只会用这一次,这就弄个特定功能的 lambda。编写 lambda,就写个 \
(因为它看起来像是希腊字母的 lambda -- 如果你斜视的厉害),后面是用空格分隔的参数,->
后面就是函数体。通常我们都是用括号将其括起,要不然它就会占据整个右边部分。
向上 5 英吋左右,你会看到我们在 numLongChain
函数中用 where
语句声明了个 isLong
函数传递给了 filter
。好的,用 lambda 代替它。
numLongChains :: Int
numLongChains = length (filter (\xs -> length xs > 15) (map chain [1..100]))
lambda 是个表达式,因此我们可以任意传递。表达式 (\xs -> length xs > 15)
回传一个函数,它可以告诉我们一个 List 的长度是否大于 15。
不熟悉 Curried functions 与不全呼叫的人们往往会写出很多 lambda,而实际上大部分都是没必要的。例如,表达式 map (+3) [1,6,3,2]
与 map (\x -> x+3) [1,6,3,2]
等价,(+3)
和 (\x -> x+3)
都是给一个数加上 3。不用说,在这种情况下不用 lambda 要清爽的多。
和普通函数一样,lambda 也可以取多个参数。
ghci> zipWith (\a b -> (a * 30 + 3) / b) [5,4,3,2,1] [1,2,3,4,5]
[153.0,61.5,31.0,15.75,6.6]
同普通函数一样,你也可以在 lambda 中使用模式匹配,只是你无法为一个参数设置多个模式,如 []
和 (x:xs)
。lambda 的模式匹配若失败,就会引发一个运行时错误,所以慎用!
ghci> map (\(a,b) -> a + b) [(1,2),(3,5),(6,3),(2,6),(2,5)]
[3,8,9,8,7]
一般情况下,lambda 都是括在括号中,除非我们想要后面的整个语句都作为 lambda 的函数体。很有趣,由于有柯里化,如下的两段是等价的:
addThree :: (Num a) => a -> a -> a -> a
addThree x y z = x + y + z
addThree :: (Num a) => a -> a -> a -> a
addThree = \x -> \y -> \z -> x + y + z
这样的函数声明与函数体中都有 ->
,这一来型别声明的写法就很明白了。当然第一段程式码更易读,不过第二个函数使得柯里化更容易理解。
有些时候用这种语句写还是挺酷的,我觉得这应该是最易读的 flip
函数实现了:
flip' :: (a -> b -> c) -> b -> a -> c
flip' f = \x y -> f y x
尽管这与 flip' f x y = f y x
等价,但它可以更明白地表示出它会产生一个新的函数。flip
常用来处理一个函数,再将回传的新函数传递给 map
或 filter
。所以如此使用 lambda 可以更明确地表现出回传值是个函数,可以用来传递给其他函数作参数。
#
关键字 fold
回到当初我们学习递归的情景。我们会发现处理 List 的许多函数都有固定的模式,通常我们会将边界条件设置为空 List,再引入 (x:xs)
模式,对单个元素和余下的 List 做些事情。这一模式是如此常见,因此 Haskell 引入了一组函数来使之简化,也就是 fold
。它们与map有点像,只是它们回传的是单个值。
一个 fold
取一个二元函数,一个初始值(我喜欢管它叫累加值)和一个需要折叠的 List。这个二元函数有两个参数,即累加值和 List 的首项(或尾项),回传值是新的累加值。然后,以新的累加值和新的 List 首项呼叫该函数,如是继续。到 List 遍历完毕时,只剩下一个累加值,也就是最终的结果。
首先看下 foldl 函数,也叫做左折叠。它从 List 的左端开始折叠,用初始值和 List 的头部呼叫这二元函数,得一新的累加值,并用新的累加值与 List 的下一个元素呼叫二元函数。如是继续。
我们再实现下 sum
,这次用 fold
替代那复杂的递归:
sum' :: (Num a) => [a] -> a
sum' xs = foldl (\acc x -> acc + x) 0 xs
测试下,一二三~
ghci> sum' [3,5,2,1]
11
我们深入看下 fold
的执行过程:\acc x-> acc + x
是个二元函数,0
是初始值,xs
是待折叠的 List。一开始,累加值为 0
,当前项为 3
,呼叫二元函数 0+3
得 3
,作新的累加值。接着来,累加值为 3
,当前项为 5
,得新累加值 8
。再往后,累加值为 8
,当前项为 2
,得新累加值 10
。最后累加值为 10
,当前项为 1
,得 11
。恭喜,你完成了一次折叠 (fold)
!
左边的这个图表示了折叠的执行过程,一步又一步(一天又一天!)。浅棕色的数字都是累加值,你可以从中看出 List 是如何从左端一点点加到累加值上的。唔对对对!如果我们考虑到函数的柯里化,可以写出更简单的实现:
sum' :: (Num a) => [a] -> a
sum' = foldl (+) 0
这个 lambda 函数 (\acc x -> acc + x )
与 (+)
等价。我们可以把 xs
等一应参数省略掉,反正呼叫 foldl (+) 0
会回传一个取 List 作参数的函数。通常,如果你的函数类似 foo a = bar b a
, 大可改为 foo = bar b
。有柯里化嘛。
呼呼,进入右折叠前我们再实现个用到左折叠的函数。大家肯定都知道 elem
是检查某元素是否属于某 List 的函数吧,我就不再提了(唔,刚提了)。用左折叠实现它:
elem' :: (Eq a) => a -> [a] -> Bool
elem' y ys = foldl (\acc x -> if x == y then True else acc) False ys
好好好,这里我们有什么?起始值与累加值都是布尔值。在处理 fold
时,累加值与最终结果的型别总是相同的。如果你不知道怎样对待起始值,那我告诉你,我们先假设它不存在,以 False
开始。我们要是 fold
一个空 List,结果就是 False
。然后我们检查当前元素是否为我们寻找的,如果是,就令累加值为 True
,如果否,就保留原值不变。若 False
,及表明当前元素不是。若 True
,就表明已经找到了。
右折叠 foldr 的行为与左折叠相似,只是累加值是从 List 的右边开始。同样,左折叠的二元函数取累加值作首个参数,当前值为第二个参数(即 \acc x -> ...
),而右折叠的二元函数参数的顺序正好相反(即 \x acc -> ...
)。这倒也正常,毕竟是从右端开始折叠。
累加值可以是任何型别,可以是数值,布尔值,甚至一个新的 List。我们可以用右 fold
实现 map
函数,累加值就是个 List。将 map
处理过的元素一个一个连到一起。很容易想到,起始值就是空 List。
map' :: (a -> b) -> [a] -> [b]
map' f xs = foldr (\x acc -> f x : acc) [] xs
如果我们用 (+3)
来映射 [1,2,3]
,它就会先到达 List 的右端,我们取最后那个元素,也就是 3
来呼叫 (+3)
,得 6
。追加 (:)
到累加值上,6:[]
得 [6]
并成为新的累加值。用 2
呼叫 (+3)
,得 5
,追加到累加值,于是累加值成了 [5,6]
。再对 1
呼叫 (+3)
,并将结果 4 追加到累加值,最终得结果 [4,5,6]
。
当然,我们也完全可以用左折叠来实现它,map' f xs = foldl (\acc x -> acc ++ [f x]) [] xs
就行了。不过问题是,使用 (++)
往 List 后面追加元素的效率要比使用 (:)
低得多。所以在生成新 List 的时候人们一般都是使用右折叠。
反转一个 List,既也可以通过右折叠,也可以通过左折叠。有时甚至不需要管它们的分别,如 sum
函数的左右折叠实现都是十分相似。不过有个大的不同,那就是右折叠可以处理无限长度的资料结构,而左折叠不可以。将无限 List 从中断开执行左折叠是可以的,不过若是向右,就永远到不了头了。
所有遍历 List 中元素并据此回传一个值的操作都可以交给 fold
实现。无论何时需要遍历 List 并回传某值,都可以尝试下 fold
。因此,fold
的地位可以说与 map
和 filter
并驾齐驱,同为函数式编程中最常用的函数之一。
foldl1 与 foldr1 的行为与 foldl
和 foldr
相似,只是你无需明确提供初始值。他们假定 List 的首个(或末尾)元素作为起始值,并从旁边的元素开始折叠。这一来,sum
函数大可这样实现:sum = foldl1 (+)
。这里待折叠的 List 中至少要有一个元素,若使用空 List 就会产生一个运行时错误。不过 foldl
和 foldr
与空 List 相处的就很好。所以在使用 fold
前,应该先想下它会不会遇到空 List,如果不会遇到,大可放心使用 foldr1
和 foldl1
。
为了体会 fold
的威力,我们就用它实现几个库函数:
maximum' :: (Ord a) => [a] -> a
maximum' = foldr1 (\x acc -> if x > acc then x else acc)
reverse' :: [a] -> [a]
reverse' = foldl (\acc x -> x : acc) []
product' :: (Num a) => [a] -> a
product' = foldr1 (*)
filter' :: (a -> Bool) -> [a] -> [a]
filter' p = foldr (\x acc -> if p x then x : acc else acc) []
head' :: [a] -> a
head' = foldr1 (\x _ -> x)
last' :: [a] -> a
last' = foldl1 (\_ x -> x)
仅靠模式匹配就可以实现 head
函数和 last
函数,而且效率也很高。这里只是为了演示,用 fold
的实现方法。我觉得我们这个 reverse'
定义的相当聪明,用一个空 List 做初始值,并向左展开 List,从左追加到累加值,最后得到一个反转的新 List。\acc x -> x : acc
有点像 :
函数,只是参数顺序相反。所以我们可以改成 foldl (flip (:)) []
。
有个理解折叠的思路:假设我们有个二元函数 f
,起始值 z
,如果从右折叠 [3,4,5,6]
,实际上执行的就是 f 3 (f 4 (f 5 (f 6 z)))
。f
会被 List 的尾项和累加值呼叫,所得的结果会作为新的累加值传入下一个呼叫。假设 f
是 (+)
,起始值 z
是 0
,那么就是 3 + (4 + (5 + (6 + 0)))
,或等价的首码形式:(+) 3 ((+) 4 ((+) 5 ((+) 6 0)))
。相似,左折叠一个 List,以 g
为二元函数,z
为累加值,它就与 g (g (g (g z 3) 4) 5) 6
等价。如果用 flip (:)
作二元函数,[]
为累加值(看得出,我们是要反转一个 List),这就与 flip (:) (flip (:) (flip (:) (flip (:) [] 3) 4) 5) 6
等价。显而易见,执行该表达式的结果为 [6,5,4,3]
。
scanl 和 scanr 与 foldl
和 foldr
相似,只是它们会记录下累加值的所有状态到一个 List。也有 scanl1 和 scanr1。
ghci> scanl (+) 0 [3,5,2,1]
[0,3,8,10,11]
ghci> scanr (+) 0 [3,5,2,1]
[11,8,3,1,0]
ghci> scanl1 (\acc x -> if x > acc then x else acc) [3,4,5,3,7,9,2,1]
[3,4,5,5,7,9,9,9]
ghci> scanl (flip (:)) [] [3,2,1]
[[],[3],[2,3],[1,2,3]]
当使用 scanl
时,最终结果就是 List 的最后一个元素。而在 scanr
中则是第一个。
sqrtSums :: Int
sqrtSums = length (takeWhile (<1000) (scanl1 (+) (map sqrt [1..]))) + 1
ghci> sqrtSums
131
ghci> sum (map sqrt [1..131])
1005.0942035344083
ghci> sum (map sqrt [1..130])
993.6486803921487
scan
可以用来跟踪 fold
函数的执行过程。想想这个问题,取所有自然数的平方根的和,寻找在何处超过 1000? 先map sqrt [1..]
,然后用个 fold
来求它们的和。但在这里我们想知道求和的过程,所以使用 scan
,scan
完毕时就可以得到小于 1000 的所有和。所得结果 List 的第一个元素为 1,第二个就是 1+根2,第三个就是 1+根2+根3。若有 x
个和小于 1000,那结果就是 x+1
。
#
有$的函数呼叫
好的,接下来看看 $ 函数。它也叫作函数呼叫符。先看下它的定义:
($) :: (a -> b) -> a -> b
f $ x = f x
什么鬼东西?这没啥意义的操作符?它只是个函数呼叫符罢了?好吧,不全是,但差不多。普通的函数呼叫符有最高的优先顺序,而 $
的优先顺序则最低。用空格的函数呼叫符是左结合的,如 f a b c
与 ((f a) b) c
等价,而 $
则是右结合的。
听着不错。但有什么用?它可以减少我们程式码中括号的数目。试想有这个表达式: sum (map sqrt [1..130])
。由于低优先顺序的 $
,我们可以将其改为 sum $ map sqrt [1..130]
,可以省敲不少键!sqrt 3 + 4 + 9
会怎样?这会得到 9,4 和根3 的和。若要取 (3+4+9)
的平方根,就得 sqrt (3+4+9)
或用 $
:sqrt $ 3+4+9
。因为 $
有最低的优先顺序,所以你可以把$看作是在右面写一对括号的等价形式。
sum (filter (> 10) (map (*2) [2..10]))
该如何?嗯,$
是右结合,f (g (z x))
与 f $ g $ z x
等价。所以我么可以将 sum (filter (> 10) (map (*2) [2..10])
重写为 sum $ filter (> 10) $ map (*2) [2..10]
。
除了减少括号外,$
还可以将数据作为函数使用。例如映射一个函数呼叫符到一组函数组成的 List:
ghci> map ($ 3) [(4+),(10*),(^2),sqrt]
[7.0,30.0,9.0,1.7320508075688772]
#
Function composition
在数学中,函数组合是这样定义的:
,表示组合两个函数成为一个函数。以 x
呼叫这一函数,就与用 x
呼叫 g
再用所得的结果呼叫 f
等价。
Haskell 中的函数组合与之很像,即 . 函数。其定义为:
(.) :: (b -> c) -> (a -> b) -> a -> c
f . g = \x -> f (g x)
注意下这型别声明,f
的参数型别必须与 g
的回传型别相同。所以得到的组合函数的参数型别与 g
相同,回传型别与 f
相同。表达式 negate . (*3)
回传一个求一数字乘以 3 后的负数的函数。
函数组合的用处之一就是生成新函数,并传递给其它函数。当然我们可以用 lambda 实现,但大多数情况下,使用函数组合无疑更清楚。假设我们有一组由数字组成的 List,要将其全部转为负数,很容易就想到应先取其绝对值,再取负数,像这样:
ghci> map (\x -> negate (abs x)) [5,-3,-6,7,-3,2,-19,24]
[-5,-3,-6,-7,-3,-2,-19,-24]
注意下这个 lambda 与那函数组合是多么的相像。用函数组合,我们可以将程式码改为:
ghci> map (negate . abs) [5,-3,-6,7,-3,2,-19,24]
[-5,-3,-6,-7,-3,-2,-19,-24]
漂亮!函数组合是右结合的,我们同时组合多个函数。表达式 f (g (z x))
与 (f . g . z) x
等价。按照这个思路,我们可以将
ghci> map (\xs -> negate (sum (tail xs))) [[1..5],[3..6],[1..7]]
[-14,-15,-27]
改为:
ghci> map (negate . sum . tail) [[1..5],[3..6],[1..7]]
[-14,-15,-27]
不过含多个参数的函数该怎么办?好,我们可以使用不全呼叫使每个函数都只剩下一个参数。sum (replicate 5 (max 6.7 8.9))
可以重写为 (sum . replicate 5 . max 6.7) 8.9
或 sum . replicate 5 . max 6.7 $ 8.9
。在这里会产生一个函数,它取与 max 6.7
同样的参数,并使用结果呼叫 replicate 5
再用 sum
求和。最后用 8.9
呼叫该函数。不过一般你可以这么读,用 8.9 呼叫 max 6.7
,然后使它 replicate 5
,再 sum
之。如果你打算用函数组合来替掉那堆括号,可以先在最靠近参数的函数后面加一个 $
,接着就用 .
组合其所有函数呼叫,而不用管最后那个参数。如果有这样一段程式码:replicate 100 (product (map (*3) (zipWith max [1,2,3,4,5] [4,5,6,7,8])))
,可以改为:replicate 100 . product . map (*3) . zipWith max [1,2,3,4,5] $ [4,5,6,7,8]
。如果表达式以 3 个括号结尾,就表示你可以将其修改为函数组合的形式。
函数组合的另一用途就是定义 point free style (也称作 pointless style) 的函数。就拿我们之前写的函数作例子:
sum' :: (Num a) => [a] -> a
sum' xs = foldl (+) 0 xs
等号的两端都有个 xs
。由于有柯里化 (Currying),我们可以省掉两端的 xs
。foldl (+) 0
回传的就是一个取一 List 作参数的函数,我们把它修改为 sum' = foldl (+) 0
,这就是 point free style。下面这个函数又该如何改成 point free style 呢?
fn x = ceiling (negate (tan (cos (max 50 x))))
像刚才那样简单去掉两端的 x
是不行的,函数定义中 x
的右边还有括号。cos (max 50)
是有错误的,你不能求一个函数的余弦。我们的解决方法就是,使用函数组合。
fn = ceiling . negate . tan . cos . max 50
漂亮!point free style 会令你去思考函数的组合方式,而非数据的传递方式,更加简洁明了。你可以将一组简单的函数组合在一起,使之形成一个复杂的函数。不过函数若过于复杂,再使用 point free style 往往会适得其反,因此构造较长的函数组合链是不被鼓励的(虽然我本人热衷于函数组合)。更好的解决方法,就是使用 let
语句给中间的运算结果绑定一个名字,或者说把问题分解成几个小问题再组合到一起。这样一来我们程式码的读者就可以轻松些,不必要纠结那巨长的函数组合链了。
在 map
和 filter
那节中,我们求了小于 10000 的所有奇数的平方的和。如下就是将其置于一个函数中的样子:
oddSquareSum :: Integer
oddSquareSum = sum (takeWhile (<10000) (filter odd (map (^2) [1..])))
身为函数组合狂人,我可能会这么写:
oddSquareSum :: Integer
oddSquareSum = sum . takeWhile (<10000) . filter odd . map (^2) $ [1..]
不过若是给别人看,我可能就这么写了:
oddSquareSum :: Integer
oddSquareSum =
let oddSquares = filter odd $ map (^2) [1..]
belowLimit = takeWhile (<10000) oddSquares
in sum belowLimit
这段程式码可赢不了程式码花样大赛,不过我们的读者可能会觉得它比函数组合链更好看。
7
模组 (Modules)
装载模组
Haskell 中的模组是含有一组相关的函数,型别和型别类的组合。而 Haskell 程序的本质便是从主模组中引用其它模组并呼叫其中的函数来执行操作。这样可以把程式码分成多块,只要一个模组足够的独立,它里面的函数便可以被不同的程序反复重用。这就让不同的程式码各司其职,提高了程式码的健壮性。
Haskell 的标准库就是一组模组,每个模组都含有一组功能相近或相关的函数和型别。有处理 List 的模组,有处理并发的模组,也有处理复数的模组,等等。目前为止我们谈及的所有函数,型别以及型别类都是 Prelude
模组的一部分,它预设自动装载。在本章,我们看一下几个常用的模组,在开始浏览其中的函数之前,我们先得知道如何装载模组.
在 Haskell中,装载模组的语法为 import
,这必须得在函数的定义之前,所以一般都是将它置于程式码的顶部。无疑,一段程式码中可以装载很多模组,只要将 import
语句分行写开即可。装载 Data.List
试下,它里面有很多实用的 List 处理函数.
执行 import Data.List
,这样一来 Data.List
中包含的所有函数就都进入了全局命名空间。也就是说,你可以在程式码的任意位置呼叫这些函数.Data.List
模组中有个 nub
函数,它可以筛掉一个 List 中的所有重复元素。用点号将 length
和 nub
组合: length . nub
,即可得到一个与 (\xs -> length (nub xs))
等价的函数。
import Data.List
numUniques :: (Eq a) => [a] -> Int
numUniques = length . nub
你也可以在 ghci 中装载模组,若要呼叫 Data.List
中的函数,就这样:
ghci> :m Data.List
若要在 ghci 中装载多个模组,不必多次 :m
命令,一下就可以全部搞定:
ghci> :m Data.List Data.Map Data.Set
而你的程序中若已经有包含的程式码,就不必再用 :m
了.
如果你只用得到某模组的两个函数,大可仅包含它俩。若仅装载 Data.List
模组 nub
和 sort
,就这样:
import Data.List (nub,sort)
也可以只包含除去某函数之外的其它函数,这在避免多个模组中函数的命名冲突很有用。假设我们的程式码中已经有了一个叫做 nub
的函数,而装入 Data.List
模组时就要把它里面的 nub
除掉.
import Data.List hiding (nub)
避免命名冲突还有个方法,便是 qualified import
,Data.Map
模组提供一了一个按键索值的资料结构,它里面有几个和 Prelude
模组重名的函数。如 filter
和 null
,装入 Data.Map
模组之后再呼叫 filter
,Haskell 就不知道它究竟是哪个函数。如下便是解决的方法:
import qualified Data.Map
这样一来,再呼叫 Data.Map
中的 filter
函数,就必须得 Data.Map.filter
,而 filter
依然是为我们熟悉喜爱的样子。但是要在每个函数前面都加 个Data.Map
实在是太烦人了! 那就给它起个别名,让它短些:
import qualified Data.Map as M
好,再呼叫 Data.Map
模组的 filter
函数的话仅需 M.filter
就行了
要浏览所有的标准库模组,参考这个手册。翻阅标准库中的模组和函数是提升个人 Haskell 水平的重要途径。你也可以各个模组的原始码,这对 Haskell 的深入学习及掌握都是大有好处的.
检索函数或搜寻函数位置就用 [http://www.Haskell.org/hoogle/ Hoogle],相当了不起的 Haskell 搜索引擎! 你可以用函数名,模组名甚至型别声明来作为检索的条件.
#
Data.List
显而易见,Data.List
是关于 List 操作的模组,它提供了一组非常有用的 List 处理函数。在前面我们已经见过了其中的几个函数(如 map
和 filter
),这是 Prelude
模组出于方便起见,导出了几个 Data.List
里的函数。因为这几个函数是直接引用自 Data.List
,所以就无需使用 qualified import
。在下面,我们来看看几个以前没见过的函数:
intersperse 取一个元素与 List 作参数,并将该元素置于 List 中每对元素的中间。如下是个例子:
ghci> intersperse '.' "MONKEY"
"M.O.N.K.E.Y"
ghci> intersperse 0 [1,2,3,4,5,6]
[1,0,2,0,3,0,4,0,5,0,6]
intercalate 取两个 List 作参数。它会将第一个 List 交叉插入第二个 List 中间,并返回一个 List.
ghci> intercalate " " ["hey","there","guys"]
"hey there guys"
ghci> intercalate [0,0,0] [[1,2,3],[4,5,6],[7,8,9]]
[1,2,3,0,0,0,4,5,6,0,0,0,7,8,9]
transpose 函数可以反转一组 List 的 List。你若把一组 List 的 List 看作是个 2D 的矩阵,那 transpose
的操作就是将其列为行。
ghci> transpose [[1,2,3],[4,5,6],[7,8,9]]
[[1,4,7],[2,5,8],[3,6,9]]
ghci> transpose ["hey","there","guys"]
["htg","ehu","yey","rs","e"]
假如有两个多项式 3x<sup>2</sup> + 5x + 9
,10x<sup>3</sup> + 9
和 8x<sup>3</sup> + 5x<sup>2</sup> + x - 1
,将其相加,我们可以列三个 List: [0,3,5,9]
,[10,0,0,9]
和 [8,5,1,-1]
来表示。再用如下的方法取得结果.
ghci> map sum $ transpose [[0,3,5,9],[10,0,0,9],[8,5,1,-1]]
[18,8,6,17]
使用 transpose
处理这三个 List 之后,三次幂就到了第一行,二次幂到了第二行,以此类推。在用 sum
函数将其映射,即可得到正确的结果。
foldl' 和 foldl1' 是它们各自惰性实现的严格版本。在用 fold
处理较大的 List 时,经常会遇到堆栈溢出的问题。而这罪魁祸首就是 fold
的惰性: 在执行 fold
时,累加器的值并不会被立即更新,而是做一个"在必要时会取得所需的结果"的承诺。每过一遍累加器,这一行为就重复一次。而所有的这堆"承诺"最终就会塞满你的堆栈。严格的 fold
就不会有这一问题,它们不会作"承诺",而是直接计算中间值的结果并继续执行下去。如果用惰性 fold
时经常遇到溢出错误,就应换用它们的严格版。
concat 把一组 List 连接为一个 List。
ghci> concat ["foo","bar","car"]
"foobarcar"
ghci> concat [[3,4,5],[2,3,4],[2,1,1]]
[3,4,5,2,3,4,2,1,1]
它相当于移除一级嵌套。若要彻底地连接其中的元素,你得 concat
它两次才行.
concatMap 函数与 map
一个 List 之后再 concat
它等价.
ghci> concatMap (replicate 4) [1..3]
[1,1,1,1,2,2,2,2,3,3,3,3]
and 取一组布林值 List 作参数。只有其中的值全为 True
的情况下才会返回 True
。
ghci> and $ map (>4) [5,6,7,8]
True
ghci> and $ map (==4) [4,4,4,3,4]
False
or 与 and
相似,一组布林值 List 中若存在一个 True
它就返回 True
.
ghci> or $ map (==4) [2,3,4,5,6,1]
True
ghci> or $ map (>4) [1,2,3]
False
any 和 all 取一个限制条件和一组布林值 List 作参数,检查是否该 List 的某个元素或每个元素都符合该条件。通常较 map
一个 List 到 and
或 or
而言,使用 any
或 all
会更多些。
ghci> any (==4) [2,3,5,6,1,4]
True
ghci> all (>4) [6,9,10]
True
ghci> all (`elem` ['A'..'Z']) "HEYGUYSwhatsup"
False
ghci> any (`elem` ['A'..'Z']) "HEYGUYSwhatsup"
True
iterate 取一个函数和一个值作参数。它会用该值去呼叫该函数并用所得的结果再次呼叫该函数,产生一个无限的 List.
ghci> take 10 $ iterate (*2) 1
[1,2,4,8,16,32,64,128,256,512]
ghci> take 3 $ iterate (++ "haha") "haha"
["haha","hahahaha","hahahahahaha"]
splitAt 取一个 List 和数值作参数,将该 List 在特定的位置断开。返回一个包含两个 List 的二元组.
ghci> splitAt 3 "heyman"
("hey","man")
ghci> splitAt 100 "heyman"
("heyman","")
ghci> splitAt (-3) "heyman"
("","heyman")
ghci> let (a,b) = splitAt 3 "foobar" in b ++ a
"barfoo"
takeWhile 这一函数十分的实用。它从一个 List 中取元素,一旦遇到不符合条件的某元素就停止.
ghci> takeWhile (>3) [6,5,4,3,2,1,2,3,4,5,4,3,2,1]
[6,5,4]
ghci> takeWhile (/=' ') "This is a sentence"
"This"
如果要求所有三次方小于 1000 的数的和,用 filter
来过滤 map (^3) [1..]
所得结果中所有小于 1000 的数是不行的。因为对无限 List 执行的 filter
永远都不会停止。你已经知道了这个 List 是单增的,但 Haskell 不知道。所以应该这样:
ghci> sum $ takeWhile (<10000) $ map (^3) [1..]
53361
用 (^3)
处理一个无限 List,而一旦出现了大于 10000 的元素这个 List 就被切断了,sum 到一起也就轻而易举.
dropWhile 与此相似,不过它是扔掉符合条件的元素。一旦限制条件返回 False
,它就返回 List 的余下部分。方便实用!
ghci> dropWhile (/=' ') "This is a sentence"
" is a sentence"
ghci> dropWhile (<3) [1,2,2,2,3,4,5,4,3,2,1]
[3,4,5,4,3,2,1]
给一 Tuple
组成的 List,这 Tuple 的首项表示股票价格,第二三四项分别表示年,月,日。我们想知道它是在哪天首次突破 $1000 的!
ghci> let stock = [(994.4,2008,9,1),(995.2,2008,9,2),(999.2,2008,9,3),(1001.4,2008,9,4),(998.3,2008,9,5)]
ghci> head (dropWhile (\(val,y,m,d) -> val < 1000) stock)
(1001.4,2008,9,4)
span 与 takeWhile
有点像,只是它返回两个 List。第一个 List 与同参数呼叫 takeWhile
所得的结果相同,第二个 List 就是原 List 中余下的部分。
ghci> let (fw,rest) = span (/=' ') "This is a sentence" in "First word:" ++ fw ++ ",the rest:" ++ rest
"First word: This,the rest: is a sentence"
span 是在条件首次为 False
时断开 List,而 break
则是在条件首次为 True
时断开 List
。break p
与 span (not . p)
是等价的.
ghci> break (==4) [1,2,3,4,5,6,7]
([1,2,3],[4,5,6,7])
ghci> span (/=4) [1,2,3,4,5,6,7]
([1,2,3],[4,5,6,7])
break 返回的第二个 List 就会以第一个符合条件的元素开头。
sort 可以排序一个 List,因为只有能够作比较的元素才可以被排序,所以这一 List 的元素必须是 Ord 型别类的实例型别。
ghci> sort [8,5,3,2,1,6,4,2]
[1,2,2,3,4,5,6,8]
ghci> sort "This will be sorted soon"
" Tbdeehiillnooorssstw"
group 取一个 List 作参数,并将其中相邻并相等的元素各自归类,组成一个个子 List.
ghci> group [1,1,1,1,2,2,2,2,3,3,2,2,2,5,6,7]
[[1,1,1,1],[2,2,2,2],[3,3],[2,2,2],[5],[6],[7]]
若在 group
一个 List 之前给它排序就可以得到每个元素在该 List 中的出现次数。
ghci> map (\l@(x:xs) -> (x,length l)) . group . sort $ [1,1,1,1,2,2,2,2,3,3,2,2,2,5,6,7]
[(1,4),(2,7),(3,2),(5,1),(6,1),(7,1)]
inits 和 tails 与 init
和 tail
相似,只是它们会递归地呼叫自身直到什么都不剩,看:
ghci> inits "w00t"
["","w","w0","w00","w00t"]
ghci> tails "w00t"
["w00t","00t","0t","t",""]
ghci> let w = "w00t" in zip (inits w) (tails w)
[("","w00t"),("w","00t"),("w0","0t"),("w00","t"),("w00t","")]
我们用 fold
实现一个搜索子 List 的函数:
search :: (Eq a) => [a] -> [a] -> Bool
search needle haystack =
let nlen = length needle
in foldl (\acc x -> if take nlen x == needle then True else acc) False (tails haystack)
首先,对搜索的 List 呼叫 tails
,然后遍历每个 List 来检查它是不是我们想要的.
由此我们便实现了一个类似 isInfixOf 的函数,isInfixOf 从一个 List 中搜索一个子 List,若该 List 包含子 List,则返回 True
.
ghci> "cat" `isInfixOf` "im a cat burglar"
True
ghci> "Cat" `isInfixOf` "im a cat burglar"
False
ghci> "cats" `isInfixOf` "im a cat burglar"
False
isPrefixOf 与 isSuffixOf 分别检查一个 List 是否以某子 List 开头或者结尾.
ghci> "hey" `isPrefixOf` "hey there!"
True
ghci> "hey" `isPrefixOf` "oh hey there!"
False
ghci> "there!" `isSuffixOf` "oh hey there!"
True
ghci> "there!" `isSuffixOf` "oh hey there"
False
elem 与 notElem 检查一个 List 是否包含某元素.
partition 取一个限制条件和 List 作参数,返回两个 List,第一个 List 中包含所有符合条件的元素,而第二个 List 中包含余下的.
ghci> partition (`elem` ['A'..'Z']) "BOBsidneyMORGANeddy"
("BOBMORGAN","sidneyeddy")
ghci> partition (>3) [1,3,5,6,3,2,1,0,3,7]
([5,6,7],[1,3,3,2,1,0,3])
了解这个与 span
和 break
的差异是很重要的.
ghci> span (`elem` ['A'..'Z']) "BOBsidneyMORGANeddy"
("BOB","sidneyMORGANeddy")
span
和 break
会在遇到第一个符合或不符合条件的元素处断开,而 partition
则会遍历整个 List。
find 取一个 List 和限制条件作参数,并返回首个符合该条件的元素,而这个元素是个 Maybe
值。在下章,我们将深入地探讨相关的算法和资料结构,但在这里你只需了解 Maybe
值是 Just something
或 Nothing
就够了。与一个 List 可以为空也可以包含多个元素相似,一个 Maybe
可以为空,也可以是单一元素。同样与 List 类似,一个 Int 型的 List 可以写作 [Int]
,Maybe
有个 Int 型可以写作 Maybe Int
。先试一下 find
函数再说.
ghci> find (>4) [1,2,3,4,5,6]
Just 5
ghci> find (>9) [1,2,3,4,5,6]
Nothing
ghci> :t find
find :: (a -> Bool) -> [a] -> Maybe a
注意一下 find
的型别,它的返回结果为 Maybe a
,这与 [a]
的写法有点像,只是 Maybe
型的值只能为空或者单一元素,而 List 可以为空,一个元素,也可以是多个元素.
想想前面那段找股票的程式码,head (dropWhile (\(val,y,m,d) -> val < 1000) stock)
。但 head
并不安全! 如果我们的股票没涨过 $1000 会怎样? dropWhile
会返回一个空 List,而对空 List 取 head
就会引发一个错误。把它改成 find (\(val,y,m,d) -> val > 1000) stock
就安全多啦,若存在合适的结果就得到它, 像 Just (1001.4,2008,9,4)
,若不存在合适的元素(即我们的股票没有涨到过 $1000),就会得到一个 Nothing
.
elemIndex 与 elem
相似,只是它返回的不是布林值,它只是'可能' (Maybe)返回我们找的元素的索引,若这一元素不存在,就返回 Nothing
。
ghci> :t elemIndex
elemIndex :: (Eq a) => a -> [a] -> Maybe Int
ghci> 4 `elemIndex` [1,2,3,4,5,6]
Just 3
ghci> 10 `elemIndex` [1,2,3,4,5,6]
Nothing
elemIndices 与 elemIndex
相似,只不过它返回的是 List,就不需要 Maybe
了。因为不存在用空 List 就可以表示,这就与 Nothing
相似了.
ghci> ' ' `elemIndices` "Where are the spaces?"
[5,9,13]
findIndex 与 find
相似,但它返回的是可能存在的首个符合该条件元素的索引。findIndices 会返回所有符合条件的索引.
ghci> findIndex (==4) [5,3,2,1,6,4]
Just 5
ghci> findIndex (==7) [5,3,2,1,6,4]
Nothing
ghci> findIndices (`elem` ['A'..'Z']) "Where Are The Caps?"
[0,6,10,14]
在前面,我们讲过了 zip
和 zipWith
,它们只能将两个 List 组到一个二元组数或二参函数中,但若要组三个 List 该怎么办? 好说~ 有 zip3
,zip4
...,和 zipWith3
, zipWith4
...直到 7。这看起来像是个 hack,但工作良好。连着组 8 个 List 的情况很少遇到。还有个聪明办法可以组起无限多个 List,但限于我们目前的水平,就先不谈了.
ghci> zipWith3 (\x y z -> x + y + z) [1,2,3] [4,5,2,2] [2,2,3]
[7,9,8]
ghci> zip4 [2,3,3] [2,2,2] [5,5,3] [2,2,2]
[(2,2,5,2),(3,2,5,2),(3,2,3,2)]
与普通的 zip
操作相似,以返回的 List 中长度最短的那个为准.
在处理来自档案或其它地方的输入时,lines 会非常有用。它取一个字串作参数。并返回由其中的每一行组成的 List.
ghci> lines "first line\nsecond line\nthird line"
["first line","second line","third line"]
'\n'
表示unix下的换行符,在 Haskell 的字元中,反斜杠表示特殊字元.
unlines 是 lines
的反函数,它取一组字串的 List,并将其通过 '\n'
合并到一块.
ghci> unlines ["first line","second line","third line"]
"first line\nsecond line\nthird line\n"
words 和 unwords 可以把一个字串分为一组单词或执行相反的操作,很有用.
ghci> words "hey these are the words in this sentence"
["hey","these","are","the","words","in","this","sentence"]
ghci> words "hey these are the words in this\nsentence"
["hey","these","are","the","words","in","this","sentence"]
ghci> unwords ["hey","there","mate"]
"hey there mate"
我们前面讲到了 nub,它可以将一个 List 中的重复元素全部筛掉,使该 List 的每个元素都如雪花般独一无二,'nub' 的含义就是'一小块'或'一部分',用在这里觉得很古怪。我觉得,在函数的命名上应该用更确切的词语,而避免使用老掉牙的过时词汇.
ghci> nub [1,2,3,4,3,2,1,2,3,4,3,2,1]
[1,2,3,4]
ghci> nub "Lots of words and stuff"
"Lots fwrdanu"
delete 取一个元素和 List 作参数,会删掉该 List 中首次出现的这一元素.
ghci> delete 'h' "hey there ghang!"
"ey there ghang!"
ghci> delete 'h' . delete 'h' $ "hey there ghang!"
"ey tere ghang!"
ghci> delete 'h' . delete 'h' . delete 'h' $ "hey there ghang!"
"ey tere gang!"
\ 表示 List 的差集操作,这与集合的差集很相似,它会从左边 List 中的元素扣除存在于右边 List 中的元素一次.
ghci> [1..10] \\ [2,5,9]
[1,3,4,6,7,8,10]
ghci> "Im a big baby" \\ "big"
"Im a baby"
union 与集合的并集也是很相似,它返回两个 List 的并集,即遍历第二个 List 若存在某元素不属于第一个 List,则追加到第一个 List。看,第二个 List 中的重复元素就都没了!
ghci> "hey man" `union` "man what's up"
"hey manwt'sup"
ghci> [1..7] `union` [5..10]
[1,2,3,4,5,6,7,8,9,10]
intersection 相当于集合的交集。它返回两个 List 的相同部分.
ghci> [1..7] `intersect` [5..10]
[5,6,7]
insert 可以将一个元素插入一个可排序的 List,并将其置于首个大于等于它的元素之前,如果使用 insert
来给一个排过序的 List 插入元素,返回的结果依然是排序的.
ghci> insert 4 [1,2,3,5,6,7]
[1,2,3,4,5,6,7]
ghci> insert 'g' $ ['a'..'f'] ++ ['h'..'z']
"abcdefghijklmnopqrstuvwxyz"
ghci> insert 3 [1,2,4,3,2,1]
[1,2,3,4,3,2,1]
length
,take
,drop
,splitAt
,!!
和 replicate
之类的函数有个共同点。那就是它们的参数中都有个 Int 值(或者返回Int值),我觉得使用 Intergal 或 Num 型别类会更好,但出于历史原因,修改这些会破坏掉许多既有的程式码。在 Data.List
中包含了更通用的替代版,如: genericLength,genericTake,genericDrop,genericSplitAt,genericIndex
和 genericReplicate
。length
的型别声明为 length :: [a] -> Int
,而我们若要像这样求它的平均值,let xs = [1..6] in sum xs / length xs
,就会得到一个型别错误,因为 /
运算符不能对 Int 型使用! 而 genericLength
的型别声明则为 genericLength :: (Num a) => [b] -> a
,Num 既可以是整数又可以是浮点数,let xs = [1..6] in sum xs / genericLength xs
这样再求平均数就不会有问题了.
nub
, delete
, union
, intsect
和 group
函数也有各自的通用替代版 nubBy
,deleteBy
,unionBy
,intersectBy
和 groupBy
,它们的区别就是前一组函数使用 (==)
来测试是否相等,而带 By
的那组则取一个函数作参数来判定相等性,group
就与 groupBy (==)
等价.
假如有个记录某函数在每秒的值的 List,而我们要按照它小于零或者大于零的交界处将其分为一组子 List。如果用 group
,它只能将相邻并相等的元素组到一起,而在这里我们的标准是它们是否互为相反数。groupBy
登场! 它取一个含两个参数的函数作为参数来判定相等性.
ghci> let values = [-4.3,-2.4,-1.2,0.4,2.3,5.9,10.5,29.1,5.3,-2.4,-14.5,2.9,2.3]
ghci> groupBy (\x y -> (x > 0) == (y > 0)) values
[[-4.3,-2.4,-1.2],[0.4,2.3,5.9,10.5,29.1,5.3],[-2.4,-14.5],[2.9,2.3]]
这样一来我们就可以很清楚地看出哪部分是正数,哪部分是负数,这个判断相等性的函数会在两个元素同时大于零或同时小于零时返回 True
。也可以写作 \x y -> (x > 0) && (y > 0) || (x <= 0) && (y <= 0)
。但我觉得第一个写法的可读性更高。Data.Function
中还有个 on
函数可以让它的表达更清晰,其定义如下:
on :: (b -> b -> c) -> (a -> b) -> a -> a -> c
f `on` g = \x y -> f (g x) (g y)
执行 (==) `on` (> 0)
得到的函数就与 \x y -> (x > 0) == (y > 0)
基本等价。on
与带 By
的函数在一起会非常好用,你可以这样写:
ghci> groupBy ((==) `on` (> 0)) values
[[-4.3,-2.4,-1.2],[0.4,2.3,5.9,10.5,29.1,5.3],[-2.4,-14.5],[2.9,2.3]]
可读性很高! 你可以大声念出来: 按照元素是否大于零,给它分类!
同样,sort
,insert
,maximum
和 min
都有各自的通用版本。如 groupBy
类似,sortBy,insertBy,maximumBy 和 minimumBy 都取一个函数来比较两个元素的大小。像 sortBy
的型别声明为: sortBy :: (a -> a -> Ordering) -> [a] -> [a]
。前面提过,Ordering
型别可以有三个值,LT
,EQ
和 GT
。compare
取两个 Ord
型别类的元素作参数,所以 sort
与 sortBy compare
等价.
List 是可以比较大小的,且比较的依据就是其中元素的大小。如果按照其子 List 的长度为标准当如何? 很好,你可能已经猜到了,sortBy
函数.
ghci> let xs = [[5,4,5,4,4],[1,2,3],[3,5,4,3],[],[2],[2,2]]
ghci> sortBy (compare `on` length) xs
[[],[2],[2,2],[1,2,3],[3,5,4,3],[5,4,5,4,4]]
太绝了! compare `on` length
,乖乖,这简直就是英文! 如果你搞不清楚 on
在这里的原理,就可以认为它与 \x y -> length x `compare` length y
等价。通常,与带 By
的函数打交道时,若要判断相等性,则 (==) `on` something
。若要判定大小,则 compare `on` something
.
#
Data.Char
如其名,Data.Char
模组包含了一组用于处理字元的函数。由于字串的本质就是一组字元的 List,所以往往会在 filter
或是 map
字串时用到它.
Data.Char
模组中含有一系列用于判定字元范围的函数,如下:
isControl 判断一个字元是否是控制字元。 isSpace 判断一个字元是否是空格字元,包括空格,tab,换行符等. isLower 判断一个字元是否为小写. isUper 判断一个字元是否为大写。 isAlpha 判断一个字元是否为字母. isAlphaNum 判断一个字元是否为字母或数字. isPrint 判断一个字元是否是可打印的. isDigit 判断一个字元是否为数字. isOctDigit 判断一个字元是否为八进制数字. isHexDigit 判断一个字元是否为十六进制数字. isLetter 判断一个字元是否为字母. isMark 判断是否为 unicode 注音字元,你如果是法国人就会经常用到的. isNumber 判断一个字元是否为数字. isPunctuation 判断一个字元是否为标点符号. isSymbol判断一个字元是否为货币符号. isSeperater 判断一个字元是否为 unicode 空格或分隔符. isAscii 判断一个字元是否在 unicode 字母表的前 128 位。 isLatin1 判断一个字元是否在 unicode 字母表的前 256 位. isAsciiUpper 判断一个字元是否为大写的 ascii 字元. isAsciiLower 判断一个字元是否为小写的 ascii 字元.
以上所有判断函数的型别声明皆为 Char -> Bool
,用到它们的绝大多数情况都无非就是过滤字串或类似操作。假设我们在写个程序,它需要一个由字元和数字组成的用户名。要实现对用户名的检验,我们可以结合使用 Data.List
模组的 all
函数与 Data.Char
的判断函数.
ghci> all isAlphaNum "bobby283"
True
ghci> all isAlphaNum "eddy the fish!"
False
Kewl~ 免得你忘记,all
函数取一个判断函数和一个 List 做参数,若该 List 的所有元素都符合条件,就返回 True
.
也可以使用 isSpace
来实现 Data.List
的 words
函数.
ghci> words "hey guys its me"
["hey","guys","its","me"]
ghci> groupBy ((==) `on` isSpace) "hey guys its me"
["hey"," ","guys"," ","its"," ","me"]
ghci>
Hmm,不错,有点 words
的样子了。只是还有空格在里面,恩,该怎么办? 我知道,用 filter
滤掉它们!
ghci> filter (not . any isSpace) . groupBy ((==) `on` isSpace) $ "hey guys its me"
["hey","guys","its","me"]
啊哈.
Data.Char
中也含有与 Ordering
相似的型别。Ordering
可以有三个值,LT
,GT
和 EQ
。这就是个枚举,它表示了两个元素作比较可能的结果. GeneralCategory
型别也是个枚举,它表示了一个字元可能所在的分类。而得到一个字元所在分类的主要方法就是使用 generalCategory
函数.它的型别为: generalCategory :: Char -> GeneralCategory
。那 31 个分类就不在此一一列出了,试下这个函数先:
ghci> generalCategory ' '
Space
ghci> generalCategory 'A'
UppercaseLetter
ghci> generalCategory 'a'
LowercaseLetter
ghci> generalCategory '.'
OtherPunctuation
ghci> generalCategory '9'
DecimalNumber
ghci> map generalCategory " \t\nA9?|"
[Space,Control,Control,UppercaseLetter,DecimalNumber,OtherPunctuation,MathSymbol]
由于 GeneralCategory
型别是 Eq
型别类的一部分,使用类似 generalCategory c == Space
的程式码也是可以的.
toUpper 将一个字元转为大写字母,若该字元不是小写字母,就按原值返回. toLower 将一个字元转为小写字母,若该字元不是大写字母,就按原值返回. toTitle 将一个字元转为 title-case,对大多数字元而言,title-case 就是大写. digitToInt 将一个字元转为 Int 值,而这一字元必须得在 '1'..'9','a'..'f'
或'A'..'F'
的范围之内.
ghci> map digitToInt "34538"
[3,4,5,3,8]
ghci> map digitToInt "FF85AB"
[15,15,8,5,10,11]
intToDigit
是 digitToInt
的反函数。它取一个 0
到 15
的 Int
值作参数,并返回一个小写的字元.
ghci> intToDigit 15
'f'
ghci> intToDigit 5
'5'
ord 与 char 函数可以将字元与其对应的数字相互转换.
ghci> ord 'a'
97
ghci> chr 97
'a'
ghci> map ord "abcdefgh"
[97,98,99,100,101,102,103,104]
两个字元的 ord
值之差就是它们在 unicode 字元表上的距离.
Caesar ciphar 是加密的基础算法,它将消息中的每个字元都按照特定的字母表进行替换。它的实现非常简单,我们这里就先不管字母表了.
encode :: Int -> String -> String
encode shift msg =
let ords = map ord msg
shifted = map (+ shift) ords
in map chr shifted
先将一个字串转为一组数字,然后给它加上某数,再转回去。如果你是标准的组合牛仔,大可将函数写为: map (chr . (+ shift) . ord) msg
。试一下它的效果:
ghci> encode 3 "Heeeeey"
"Khhhhh|"
ghci> encode 4 "Heeeeey"
"Liiiii}"
ghci> encode 1 "abcd"
"bcde"
ghci> encode 5 "Marry Christmas! Ho ho ho!"
"Rfww~%Hmwnxyrfx&%Mt%mt%mt&"
不错。再简单地将它转成一组数字,减去某数后再转回来就是解密了.
decode :: Int -> String -> String
decode shift msg = encode (negate shift) msg
ghci> encode 3 "Im a little teapot"
"Lp#d#olwwoh#whdsrw"
ghci> decode 3 "Lp#d#olwwoh#whdsrw"
"Im a little teapot"
ghci> decode 5 . encode 5 $ "This is a sentence"
"This is a sentence"
#
Data.Map
关联列表(也叫做字典)是按照键值对排列而没有特定顺序的一种 List。例如,我们用关联列表储存电话号码,号码就是值,人名就是键。我们并不关心它们的存储顺序,只要能按人名得到正确的号码就好.在 Haskell 中表示关联列表的最简单方法就是弄一个二元组的 List,而这二元组就首项为键,后项为值。如下便是个表示电话号码的关联列表:
phoneBook = [("betty","555-2938") ,
("bonnie","452-2928") ,
("patsy","493-2928") ,
("lucille","205-2928") ,
("wendy","939-8282") ,
("penny","853-2492") ]
不理这貌似古怪的缩进,它就是一组二元组的 List 而已。话说对关联列表最常见的操作就是按键索值,我们就写个函数来实现它。
findKey :: (Eq k) => k -> [(k,v)] -> v
findKey key xs = snd . head . filter (\(k,v) -> key == k) $ xs
简洁漂亮。这个函数取一个键和 List 做参数,过滤这一 List 仅保留键匹配的项,并返回首个键值对。但若该关联列表中不存在这个键那会怎样? 哼,那就会在试图从空 List 中取 head
时引发一个运行时错误。无论如何也不能让程序就这么轻易地崩溃吧,所以就应该用 Maybe
型别。如果没找到相应的键,就返回 Nothing
。而找到了就返回 Just something
。而这 something
就是键对应的值。
findKey :: (Eq k) => k -> [(k,v)] -> Maybe v
findKey key [] = Nothing
findKey key ((k,v):xs) =
if key == k then
Just v
else
findKey key xs
看这型别声明,它取一个可判断相等性的键和一个关联列表做参数,可能 (Maybe) 得到一个值。听起来不错.这便是个标准的处理 List 的递归函数,边界条件,分割 List,递归呼叫,都有了 -- 经典的 fold
模式。 看看用 fold
怎样实现吧。
findKey :: (Eq k) => k -> [(k,v)] -> Maybe v
findKey key = foldr (\(k,v) acc -> if key == k then Just v else acc) Nothing
*Note*: 通常,使用 ``fold`` 来替代类似的递归函数会更好些。用 ``fold`` 的程式码让人一目了然,而看明白递归则得多花点脑子。
ghci> findKey "penny" phoneBook
Just "853-2492"
ghci> findKey "betty" phoneBook
Just "555-2938"
ghci> findKey "wilma" phoneBook
Nothing
如魔咒般灵验! 只要我们有这姑娘的号码就 Just
可以得到,否则就是 Nothing
. 方才我们实现的函数便是 Data.List
模组的 lookup
,如果要按键去寻找相应的值,它就必须得遍历整个 List,直到找到为止。而 Data.Map
模组提供了更高效的方式(通过树实现),并提供了一组好用的函数。从现在开始,我们扔掉关联列表,改用map.由于Data.Map
中的一些函数与Prelude和Data.List
模组存在命名冲突,所以我们使用 qualified import
。import qualified Data.Map as Map
在程式码中加上这句,并 load
到 ghci 中.继续前进,看看 Data.Map
是如何的一座宝库! 如下便是其中函数的一瞥:
fromList 取一个关联列表,返回一个与之等价的 Map。
ghci> Map.fromList [("betty","555-2938"),("bonnie","452-2928"),("lucille","205-2928")]
fromList [("betty","555-2938"),("bonnie","452-2928"),("lucille","205-2928")]
ghci> Map.fromList [(1,2),(3,4),(3,2),(5,5)]
fromList [(1,2),(3,2),(5,5)]
若其中存在重复的键,就将其忽略。如下即 fromList
的型别声明。
Map.fromList :: (Ord k) => [(k,v)] -> Map.Map k v
这表示它取一组键值对的 List,并返回一个将 k
映射为 v
的 map
。注意一下,当使用普通的关联列表时,只需要键的可判断相等性就行了。而在这里,它还必须得是可排序的。这在 Data.Map
模组中是强制的。因为它会按照某顺序将其组织在一棵树中.在处理键值对时,只要键的型别属于 Ord
型别类,就应该尽量使用Data.Map
.empty
返回一个空 map
.
ghci> Map.empty
fromList []
insert 取一个键,一个值和一个 map
做参数,给这个 map
插入新的键值对,并返回一个新的 map
。
ghci> Map.empty
fromList []
ghci> Map.insert 3 100 Map.empty
fromList [(3,100)]
ghci> Map.insert 5 600 (Map.insert 4 200 ( Map.insert 3 100 Map.empty))
fromList [(3,100),(4,200),(5,600)]
ghci> Map.insert 5 600 . Map.insert 4 200 . Map.insert 3 100 $ Map.empty
fromList [(3,100),(4,200),(5,600)]
通过 empty
,insert
与 fold
,我们可以编写出自己的 fromList
。
fromList' :: (Ord k) => [(k,v)] -> Map.Map k v
fromList' = foldr (\(k,v) acc -> Map.insert k v acc) Map.empty
简洁明了的 fold
! 从一个空的 map
开始,然后从右折叠,随着遍历不断地往 map
中插入新的键值对.
null 检查一个 map
是否为空.
ghci> Map.null Map.empty
True
ghci> Map.null $ Map.fromList [(2,3),(5,5)]
False
size 返回一个 map
的大小。
ghci> Map.size Map.empty
0
ghci> Map.size $ Map.fromList [(2,4),(3,3),(4,2),(5,4),(6,4)]
5
singleton 取一个键值对做参数,并返回一个只含有一个映射的 map
.
ghci> Map.singleton 3 9
fromList [(3,9)]
ghci> Map.insert 5 9 $ Map.singleton 3 9
fromList [(3,9),(5,9)]
lookup 与 Data.List
的 lookup
很像,只是它的作用对象是 map
,如果它找到键对应的值。就返回 Just something
,否则返回 Nothing
。
member 是个判断函数,它取一个键与 map
做参数,并返回该键是否存在于该 map
。
ghci> Map.member 3 $ Map.fromList [(3,6),(4,3),(6,9)]
True
ghci> Map.member 3 $ Map.fromList [(2,5),(4,5)]
False
map 与 filter 与其对应的 List
版本很相似:
ghci> Map.map (*100) $ Map.fromList [(1,1),(2,4),(3,9)]
fromList [(1,100),(2,400),(3,900)]
ghci> Map.filter isUpper $ Map.fromList [(1,'a'),(2,'A'),(3,'b'),(4,'B')]
fromList [(2,'A'),(4,'B')]
toList
是 fromList
的反函数。
ghci> Map.toList . Map.insert 9 2 $ Map.singleton 4 3
[(4,3),(9,2)]
keys 与 elems 各自返回一组由键或值组成的 List,keys
与 map fst . Map.toList
等价,elems
与 map snd . Map.toList
等价. fromListWith
是个很酷的小函数,它与 fromList
很像,只是它不会直接忽略掉重复键,而是交给一个函数来处理它们。假设一个姑娘可以有多个号码,而我们有个像这样的关联列表:
phoneBook =
[("betty","555-2938")
,("betty","342-2492")
,("bonnie","452-2928")
,("patsy","493-2928")
,("patsy","943-2929")
,("patsy","827-9162")
,("lucille","205-2928")
,("wendy","939-8282")
,("penny","853-2492")
,("penny","555-2111")
]
如果用 fromList
来生成 map
,我们会丢掉许多号码! 如下才是正确的做法:
phoneBookToMap :: (Ord k) => [(k, String)] -> Map.Map k String
phoneBookToMap xs = Map.fromListWith (\number1 number2 -> number1 ++ ", " ++ number2) xs
ghci> Map.lookup "patsy" $ phoneBookToMap phoneBook
"827-9162, 943-2929, 493-2928"
ghci> Map.lookup "wendy" $ phoneBookToMap phoneBook
"939-8282"
ghci> Map.lookup "betty" $ phoneBookToMap phoneBook
"342-2492,555-2938"
一旦出现重复键,这个函数会将不同的值组在一起,同样,也可以预设地将每个值放到一个单元素的 List 中,再用 ++
将他们都连接在一起。
phoneBookToMap :: (Ord k) => [(k,a)] -> Map.Map k [a]
phoneBookToMap xs = Map.fromListWith (++) $ map (\(k,v) -> (k,[v])) xs
ghci> Map.lookup "patsy" $ phoneBookToMap phoneBook
["827-9162","943-2929","493-2928"]
很简洁! 它还有别的玩法,例如在遇到重复元素时,单选最大的那个值.
ghci> Map.fromListWith max [(2,3),(2,5),(2,100),(3,29),(3,22),(3,11),(4,22),(4,15)]
fromList [(2,100),(3,29),(4,22)]
或是将相同键的值都加在一起.
ghci> Map.fromListWith (+) [(2,3),(2,5),(2,100),(3,29),(3,22),(3,11),(4,22),(4,15)]
fromList [(2,108),(3,62),(4,37)]
insertWith 之于 insert
,恰如 fromListWith
之于 fromList
。它会将一个键值对插入一个 map
之中,而该 map
若已经包含这个键,就问问这个函数该怎么办。
ghci> Map.insertWith (+) 3 100 $ Map.fromList [(3,4),(5,103),(6,339)]
fromList [(3,104),(5,103),(6,339)]
Data.Map
里面还有不少函数,[http://www.haskell.org/ghc/docs/latest/html/libraries/containers/Data-Map.html 这个文档]中的列表就很全了.
#
Data.Set
Data.Set
模组提供了对数学中集合的处理。集合既像 List 也像 Map
: 它里面的每个元素都是唯一的,且内部的数据由一棵树来组织(这和 Data.Map
模组的 map
很像),必须得是可排序的。同样是插入,删除,判断从属关系之类的操作,使用集合要比 List 快得多。对一个集合而言,最常见的操作莫过于并集,判断从属或是将集合转为 List.
由于 Data.Set
模组与 Prelude
模组和 Data.List
模组中存在大量的命名冲突,所以我们使用 qualified import
将 import
语句至于程式码之中:
import qualified Data.Set as Set
然后在 ghci 中装载
假定我们有两个字串,要找出同时存在于两个字串的字元
text1 = "I just had an anime dream. Anime... Reality... Are they so different?"
text2 = "The old man left his garbage can out and now his trash is all over my lawn!"
fromList 函数同你想的一样,它取一个 List 作参数并将其转为一个集合
ghci> let set1 = Set.fromList text1
ghci> let set2 = Set.fromList text2
ghci> set1
fromList " .?AIRadefhijlmnorstuy"
ghci> set2
fromList " !Tabcdefghilmnorstuvwy"
如你所见,所有的元素都被排了序。而且每个元素都是唯一的。现在我们取它的交集看看它们共同包含的元素:
ghci> Set.intersection set1 set2
fromList " adefhilmnorstuy"
使用 difference
函数可以得到存在于第一个集合但不在第二个集合的元素
ghci> Set.difference set1 set2
fromList ".?AIRj"
ghci> Set.difference set2 set1
fromList "!Tbcgvw"
也可以使用 union
得到两个集合的并集
ghci> Set.union set1 set2
fromList " !.?AIRTabcdefghijlmnorstuvwy"
null
,size
,member
,empty
,singleton
,insert
,delete
这几个函数就跟你想的差不多啦
ghci> Set.null Set.empty
True
ghci> Set.null $ Set.fromList [3,4,5,5,4,3]
False
ghci> Set.size $ Set.fromList [3,4,5,3,4,5]
3
ghci> Set.singleton 9
fromList [9]
ghci> Set.insert 4 $ Set.fromList [9,3,8,1]
fromList [1,3,4,8,9]
ghci> Set.insert 8 $ Set.fromList [5..10]
fromList [5,6,7,8,9,10]
ghci> Set.delete 4 $ Set.fromList [3,4,5,4,3,4,5]
fromList [3,5]
也可以判断子集与真子集,如果集合 A 中的元素都属于集合 B,那么 A 就是 B 的子集, 如果 A 中的元素都属于 B 且 B 的元素比 A 多,那 A 就是 B 的真子集
ghci> Set.fromList [2,3,4] `Set.isSubsetOf` Set.fromList [1,2,3,4,5]
True
ghci> Set.fromList [1,2,3,4,5] `Set.isSubsetOf` Set.fromList [1,2,3,4,5]
True
ghci> Set.fromList [1,2,3,4,5] `Set.isProperSubsetOf` Set.fromList [1,2,3,4,5]
False
ghci> Set.fromList [2,3,4,8] `Set.isSubsetOf` Set.fromList [1,2,3,4,5]
False
对集合也可以执行 map
和 filter
:
ghci> Set.filter odd $ Set.fromList [3,4,5,6,7,2,3,4]
fromList [3,5,7]
ghci> Set.map (+1) $ Set.fromList [3,4,5,6,7,2,3,4]
fromList [3,4,5,6,7,8]
集合有一常见用途,那就是先 fromList
删掉重复元素后再 toList
转回去。尽管 Data.List
模组的 nub
函数完全可以完成这一工作,但在对付大 List 时则会明显的力不从心。使用集合则会快很多,nub
函数只需 List 中的元素属于 Eq
型别类就行了,而若要使用集合,它必须得属于 Ord
型别类
ghci> let setNub xs = Set.toList $ Set.fromList xs
ghci> setNub "HEY WHATS CRACKALACKIN"
" ACEHIKLNRSTWY"
ghci> nub "HEY WHATS CRACKALACKIN"
"HEY WATSCRKLIN"
在处理较大的 List 时,setNub
要比 nub
快,但也可以从中看出,nub
保留了 List 中元素的原有顺序,而 setNub
不。
#
建立自己的模组
我们已经见识过了几个很酷的模组,但怎样才能构造自己的模组呢? 几乎所有的编程语言都允许你将程式码分成多个档案,Haskell 也不例外。在编程时,将功能相近的函数和型别至于同一模组中会是个很好的习惯。这样一来,你就可以轻松地一个 import
来重用其中的函数.
接下来我们将构造一个由计算机几何图形体积和面积组成的模组,先从新建一个 Geometry.hs
的档案开始.
在模组的开头定义模组的名称,如果档案名叫做 Geometry.hs
那它的名字就得是 Geometry
。在声明出它含有的函数名之后就可以编写函数的实现啦,就这样写:
module Geometry
( sphereVolume
,sphereArea
,cubeVolume
,cubeArea
,cuboidArea
,cuboidVolume
) where
如你所见,我们提供了对球体,立方体和立方体的面积和体积的解法。继续进发,定义函数体:
module Geometry
( sphereVolume
,sphereArea
,cubeVolume
,cubeArea
,cuboidArea
,cuboidVolume
) where
sphereVolume :: Float -> Float
sphereVolume radius = (4.0 / 3.0) * pi * (radius ^ 3)
sphereArea :: Float -> Float
sphereArea radius = 4 * pi * (radius ^ 2)
cubeVolume :: Float -> Float
cubeVolume side = cuboidVolume side side side
cubeArea :: Float -> Float
cubeArea side = cuboidArea side side side
cuboidVolume :: Float -> Float -> Float -> Float
cuboidVolume a b c = rectangleArea a b * c
cuboidArea :: Float -> Float -> Float -> Float
cuboidArea a b c = rectangleArea a b * 2 + rectangleArea a c * 2 + rectangleArea c b * 2
rectangleArea :: Float -> Float -> Float
rectangleArea a b = a * b
标准的几何公式。有几个地方需要注意一下,由于立方体只是长方体的特殊形式,所以在求它面积和体积的时候我们就将它当作是边长相等的长方体。在这里还定义了一个 helper
函数,rectangleArea
它可以通过长方体的两条边计算出长方体的面积。它仅仅是简单的相乘而已,份量不大。但请注意我们可以在这一模组中呼叫这个函数,而它不会被导出! 因为我们这个模组只与三维图形打交道.
当构造一个模组的时候,我们通常只会导出那些行为相近的函数,而其内部的实现则是隐蔽的。如果有人用到了 Geometry
模组,就不需要关心它的内部实现是如何。我们作为编写者,完全可以随意修改这些函数甚至将其删掉,没有人会注意到里面的变动,因为我们并不把它们导出.
要使用我们的模组,只需:
import Geometry
将 Geometry.hs
档案至于用到它的程序档案的同一目录之下.
模组也可以按照分层的结构来组织,每个模组都可以含有多个子模组。而子模组还可以有自己的子模组。我们可以把 Geometry
分成三个子模组,而一个模组对应各自的图形对象.
首先,建立一个 Geometry
档案夹,注意首字母要大写,在里面新建三个档案
如下就是各个档案的内容:
sphere.hs
module Geometry.Sphere
( volume
,area
) where
volume :: Float -> Float
volume radius = (4.0 / 3.0) * pi * (radius ^ 3)
area :: Float -> Float
area radius = 4 * pi * (radius ^ 2)
cuboid.hs
module Geometry.Cuboid
( volume
,area
) where
volume :: Float -> Float -> Float -> Float
volume a b c = rectangleArea a b * c
area :: Float -> Float -> Float -> Float
area a b c = rectangleArea a b * 2 + rectangleArea a c * 2 + rectangleArea c b * 2
rectangleArea :: Float -> Float -> Float
rectangleArea a b = a * b
cube.hs
module Geometry.Cube
( volume
,area
) where
import qualified Geometry.Cuboid as Cuboid
volume :: Float -> Float
volume side = Cuboid.volume side side side
area :: Float -> Float
area side = Cuboid.area side side side
好的! 先是 Geometry.Sphere
。注意,我们将它置于 Geometry
档案夹之中并将它的名字定为 Geometry.Sphere
。对 Cuboid 也是同样,也注意下,在三个模组中我们定义了许多名称相同的函数,因为所在模组不同,所以不会产生命名冲突。若要在 Geometry.Cube
使用 Geometry.Cuboid
中的函数,就不能直接 import Geometry.Cuboid
,而必须得 qualified import
。因为它们中间的函数名完全相同.
import Geometry.Sphere
然后,呼叫 area
和 volume
,就可以得到球体的面积和体积,而若要用到两个或更多此类模组,就必须得 qualified import
来避免重名。所以就得这样写:
import qualified Geometry.Sphere as Sphere
import qualified Geometry.Cuboid as Cuboid
import qualified Geometry.Cube as Cube
然后就可以呼叫 Sphere.area
,Sphere.volume
,Cuboid.area
了,而每个函数都只计算其对应物体的面积和体积.
以后你若发现自己的程式码体积庞大且函数众多,就应该试着找找目的相近的函数能否装入各自的模组,也方便日后的重用.
8
构造我们自己的 Types 和 Typeclasses
Algebraic Data Types 入门
在前面的章节中,我们谈了一些 Haskell 内建的型别和 Typeclass。而在本章中,我们将学习构造型别和 Typeclass 的方法。
我们已经见识过许多型别,如 Bool
、Int
、Char
、Maybe
等等,不过在 Haskell 中该如何构造自己的型别呢?好问题,一种方法是使用 data 关键字。首先我们来看看 Bool
在标准函式库中的定义:
data Bool = False | True
data 表示我们要定义一个新的型别。=
的左端标明型别的名称即 Bool
,=
的右端就是值构造子 (Value Constructor),它们明确了该型别可能的值。|
读作"或",所以可以这样阅读该声明:Bool
型别的值可以是 True
或 False
。型别名和值构造子的首字母必大写。
相似,我们可以假想 Int
型别的声明:
data Int = -2147483648 | -2147483647 | ... | -1 | 0 | 1 | 2 | ... | 2147483647
头尾两个值构造子分别表示了 Int
型别的最小值和最大值,注意到真正的型别宣告不是长这个样子的,这样写只是为了便于理解。我们用省略号表示中间省略的一大段数字。
我们想想 Haskell 中图形的表示方法。表示圆可以用一个 Tuple,如 (43.1,55.0,10.4)
,前两项表示圆心的位置,末项表示半径。听着不错,不过三维向量或其它什么东西也可能是这种形式!更好的方法就是自己构造一个表示图形的型别。假定图形可以是圆 (Circle) 或长方形 (Rectangle):
data Shape = Circle Float Float Float | Rectangle Float Float Float Float
这是啥,想想?Circle
的值构造子有三个项,都是 Float。可见我们在定义值构造子时,可以在后面跟几个型别表示它包含值的型别。在这里,前两项表示圆心的坐标,尾项表示半径。Rectangle
的值构造子取四个 Float
项,前两项表示其左上角的坐标,后两项表示右下角的坐标。
谈到「项」 (field),其实应为「参数」 (parameters)。值构造子的本质是个函数,可以返回一个型别的值。我们看下这两个值构造子的型别声明:
ghci> :t Circle
Circle :: Float -> Float -> Float -> Shape
ghci> :t Rectangle
Rectangle :: Float -> Float -> Float -> Float -> Shape
Cool,这么说值构造子就跟普通函数并无二致啰,谁想得到?我们写个函数计算图形面积:
surface :: Shape -> Float
surface (Circle _ _ r) = pi * r ^ 2
surface (Rectangle x1 y1 x2 y2) = (abs $ x2 - x1) * (abs $ y2 - y1)
值得一提的是,它的型别声明表示了该函数取一个 Shape
值并返回一个 Float
值。写 Circle -> Float
是不可以的,因为 Circle
并非型别,真正的型别应该是 Shape
。这与不能写True->False
的道理是一样的。再就是,我们使用的模式匹配针对的都是值构造子。之前我们匹配过 []
、False
或 5
,它们都是不包含参数的值构造子。
我们只关心圆的半径,因此不需理会表示坐标的前两项:
ghci> surface $ Circle 10 20 10
314.15927
ghci> surface $ Rectangle 0 0 100 100
10000.0
Yay,it works!不过我们若尝试输出 Circle 10 20
到控制台,就会得到一个错误。这是因为 Haskell 还不知道该型别的字元串表示方法。想想,当我们往控制台输出值的时候,Haskell 会先呼叫 show
函数得到这个值的字元串表示才会输出。因此要让我们的 Shape
型别成为 Show 型别类的成员。可以这样修改:
data Shape = Circle Float Float Float | Rectangle Float Float Float Float deriving (Show)
先不去深究 deriving(派生),可以先这样理解:若在 data
声明的后面加上 deriving (Show)
,那 Haskell 就会自动将该型别至于 Show
型别类之中。好了,由于值构造子是个函数,因此我们可以拿它交给 map
,拿它不全呼叫,以及普通函数能做的一切。
ghci> Circle 10 20 5
Circle 10.0 20.0 5.0
ghci> Rectangle 50 230 60 90
Rectangle 50.0 230.0 60.0 90.0
我们若要取一组不同半径的同心圆,可以这样:
ghci> map (Circle 10 20) [4,5,6,6]
[Circle 10.0 20.0 4.0,Circle 10.0 20.0 5.0,Circle 10.0 20.0 6.0,Circle 10.0 20.0 6.0]
我们的型别还可以更好。增加加一个表示二维空间中点的型别,可以让我们的 Shape
更加容易理解:
data Point = Point Float Float deriving (Show)
data Shape = Circle Point Float | Rectangle Point Point deriving (Show)
注意下 Point
的定义,它的型别与值构造子用了相同的名字。没啥特殊含义,实际上,在一个型别含有唯一值构造子时这种重名是很常见的。好的,如今我们的 Circle
含有两个项,一个是 Point
型别,一个是 Float
型别,好作区分。Rectangle
也是同样,我们得修改 surface
函数以适应型别定义的变动。
surface :: Shape -> Float
surface (Circle _ r) = pi * r ^ 2
surface (Rectangle (Point x1 y1) (Point x2 y2)) = (abs $ x2 - x1) * (abs $ y2 - y1)
唯一需要修改的地方就是模式。在 Circle
的模式中,我们无视了整个 Point
。而在 Rectangle
的模式中,我们用了一个嵌套的模式来取得 Point
中的项。若出于某原因而需要整个 Point
,那么直接匹配就是了。
ghci> surface (Rectangle (Point 0 0) (Point 100 100))
10000.0
ghci> surface (Circle (Point 0 0) 24)
1809.5574
表示移动一个图形的函数该怎么写?它应当取一个 Shape
和表示位移的两个数,返回一个位于新位置的图形。
nudge :: Shape -> Float -> Float -> Shape
nudge (Circle (Point x y) r) a b = Circle (Point (x+a) (y+b)) r
nudge (Rectangle (Point x1 y1) (Point x2 y2)) a b = Rectangle (Point (x1+a) (y1+b)) (Point (x2+a) (y2+b))
简洁明了。我们再给这一 Shape
的点加上位移的量。
ghci> nudge (Circle (Point 34 34) 10) 5 10
Circle (Point 39.0 44.0) 10.0
如果不想直接处理 Point
,我们可以搞个辅助函数 (auxilliary function),初始从原点创建图形,再移动它们。
baseCircle :: Float -> Shape
baseCircle r = Circle (Point 0 0) r
baseRect :: Float -> Float -> Shape
baseRect width height = Rectangle (Point 0 0) (Point width height)
ghci> nudge (baseRect 40 100) 60 23
Rectangle (Point 60.0 23.0) (Point 100.0 123.0)
毫无疑问,你可以把你的数据型别导出到模组中。只要把你的型别与要导出的函数写到一起就是了。再在后面跟个括号,列出要导出的值构造子,用逗号隔开。如要导出所有的值构造子,那就写个..。
若要将这里定义的所有函数和型别都导出到一个模组中,可以这样:
module Shapes
( Point(..)
, Shape(..)
, surface
, nudge
, baseCircle
, baseRect
) where
一个 Shape
(..),我们就导出了 Shape
的所有值构造子。这一来无论谁导入我们的模组,都可以用 Rectangle
和 Circle
值构造子来构造 Shape
了。这与写 Shape(Rectangle,Circle)
等价。
我们可以选择不导出任何 Shape
的值构造子,这一来使用我们模组的人就只能用辅助函数 baseCircle
和 baseRect
来得到 Shape
了。Data.Map
就是这一套,没有 Map.Map [(1,2),(3,4)]
,因为它没有导出任何一个值构造子。但你可以用,像 Map.fromList
这样的辅助函数得到 map
。应该记住,值构造子只是函数而已,如果不导出它们,就拒绝了使用我们模组的人呼叫它们。但可以使用其他返回该型别的函数,来取得这一型别的值。
不导出数据型别的值构造子隐藏了他们的内部实现,令型别的抽象度更高。同时,我们模组的使用者也就无法使用该值构造子进行模式匹配了。
#
Record Syntax
OK,我们需要一个数据型别来描述一个人,得包含他的姓、名、年龄、身高、体重、电话号码以及最爱的冰激淋。我不知你的想法,不过我觉得要了解一个人,这些资料就够了。就这样,实现出来!
data Person = Person String String Int Float String String deriving (Show)
O~Kay,第一项是名,第二项是姓,第三项是年龄,等等。我们造一个人:
ghci> let guy = Person "Buddy" "Finklestein" 43 184.2 "526-2928" "Chocolate"
ghci> guy
Person "Buddy" "Finklestein" 43 184.2 "526-2928" "Chocolate"
貌似很酷,就是难读了点儿。弄个函数得人的某项资料又该如何?如姓的函数,名的函数,等等。好吧,我们只能这样:
firstName :: Person -> String
firstName (Person firstname _ _ _ _ _) = firstname
lastName :: Person -> String
lastName (Person _ lastname _ _ _ _) = lastname
age :: Person -> Int
age (Person _ _ age _ _ _) = age
height :: Person -> Float
height (Person _ _ _ height _ _) = height
phoneNumber :: Person -> String
phoneNumber (Person _ _ _ _ number _) = number
flavor :: Person -> String
flavor (Person _ _ _ _ _ flavor) = flavor
唔,我可不愿写这样的程式码!虽然 it works,但也太无聊了哇。
ghci> let guy = Person "Buddy" "Finklestein" 43 184.2 "526-2928" "Chocolate"
ghci> firstName guy
"Buddy"
ghci> height guy
184.2
ghci> flavor guy
"Chocolate"
你可能会说,一定有更好的方法!呃,抱歉,没有。
开个玩笑,其实有的,哈哈哈~Haskell 的发明者都是天才,早就料到了此类情形。他们引入了一个特殊的型别,也就是刚才提到的更好的方法 -- Record Syntax。
data Person = Person { firstName :: String
, lastName :: String
, age :: Int
, height :: Float
, phoneNumber :: String
, flavor :: String
} deriving (Show)
与原先让那些项一个挨一个的空格隔开不同,这里用了花括号 {}
。先写出项的名字,如 firstName
,后跟两个冒号(也叫 Paamayim Nekudotayim,哈哈~(译者不知道什么意思~囧)),标明其型别,返回的数据型别仍与以前相同。这样的好处就是,可以用函数从中直接按项取值。通过 Record Syntax,Haskell 就自动生成了这些函数:firstName
, lastName
, age
, height
, phoneNumber
和 flavor
。
ghci> :t flavor
flavor :: Person -> String
ghci> :t firstName
firstName :: Person -> String
还有个好处,就是若派生 (deriving) 到 Show
型别类,它的显示是不同的。假如我们有个型别表示一辆车,要包含生产商、型号以及出场年份:
data Car = Car String String Int deriving (Show)
ghci> Car "Ford" "Mustang" 1967
Car "Ford" "Mustang" 1967
若用 Record Syntax,就可以得到像这样的新车:
data Car = Car {company :: String, model :: String, year :: Int} deriving (Show)
ghci> Car {company="Ford", model="Mustang", year=1967}
Car {company = "Ford", model = "Mustang", year = 1967}
这一来在造车时我们就不必关心各项的顺序了。
表示三维向量之类简单数据,Vector = Vector Int Int Int
就足够明白了。但一个值构造子中若含有很多个项且不易区分,如一个人或者一辆车啥的,就应该使用 Record Syntax。
#
Type parameters
值构造子可以取几个参数产生一个新值,如 Car
的构造子是取三个参数返回一个 Car
。与之相似,型别构造子可以取型别作参数,产生新的型别。这咋一听貌似有点深奥,不过实际上并不复杂。如果你对 C++ 的模板有了解,就会看到很多相似的地方。我们看一个熟悉的型别,好对型别参数有个大致印象:
data Maybe a = Nothing | Just a
这里的a就是个型别参数。也正因为有了它,Maybe
就成为了一个型别构造子。在它的值不是 Nothing
时,它的型别构造子可以搞出 Maybe Int
,Maybe String
等等诸多型别。但只一个 Maybe
是不行的,因为它不是型别,而是型别构造子。要成为真正的型别,必须得把它需要的型别参数全部填满。
所以,如果拿 Char
作参数交给 Maybe
,就可以得到一个 Maybe Char
的型别。如,Just 'a'
的型别就是 Maybe Char
。
你可能并未察觉,在遇见 Maybe 之前我们早就接触到型别参数了。它便是 List 型别。这里面有点语法糖,List 型别实际上就是取一个参数来生成一个特定型别,这型别可以是 [Int]
,[Char]
也可以是 [String]
,但不会跟在 []
的后面。
把玩一下 Maybe
!
ghci> Just "Haha"
Just "Haha"
ghci> Just 84
Just 84
ghci> :t Just "Haha"
Just "Haha" :: Maybe [Char]
ghci> :t Just 84
Just 84 :: (Num t) => Maybe t
ghci> :t Nothing
Nothing :: Maybe a
ghci> Just 10 :: Maybe Double
Just 10.0
型别参数很实用。有了它,我们就可以按照我们的需要构造出不同的型别。若执行 :t Just "Haha"
,型别推导引擎就会认出它是个 Maybe [Char]
,由于 Just a
里的 a
是个字元串,那么 Maybe a
里的 a
一定也是个字元串。
注意下,Nothing
的型别为 Maybe a
。它是多态的,若有函数取 Maybe Int
型别的参数,就一概可以传给它一个 Nothing
,因为 Nothing
中不包含任何值。Maybe a
型别可以有 Maybe Int
的行为,正如 5
可以是 Int
也可以是 Double
。与之相似,空 List 的型别是 [a]
,可以与一切 List 打交道。因此,我们可以 [1,2,3]++[]
,也可以 ["ha","ha,","ha"]++[]
。
型别参数有很多好处,但前提是用对了地方才行。一般都是不关心型别里面的内容,如 Maybe a
。一个型别的行为若有点像是容器,那么使用型别参数会是个不错的选择。我们完全可以把我们的Car
型别从
data Car = Car { company :: String
, model :: String
, year :: Int
} deriving (Show)
改成:
data Car a b c = Car { company :: a
, model :: b
, year :: c
} deriving (Show)
但是,这样我们又得到了什么好处?回答很可能是,一无所得。因为我们只定义了处理 Car String String Int
型别的函数,像以前,我们还可以弄个简单函数来描述车的属性。
tellCar :: Car -> String
tellCar (Car {company = c, model = m, year = y}) = "This " ++ c ++ " " ++ m ++ " was made in " ++ show y
ghci> let stang = Car {company="Ford", model="Mustang", year=1967}
ghci> tellCar stang
"This Ford Mustang was made in 1967"
可爱的小函数!它的型别声明得很漂亮,而且工作良好。好,如果改成 Car a b c
又会怎样?
tellCar :: (Show a) => Car String String a -> String
tellCar (Car {company = c, model = m, year = y}) = "This " ++ c ++ " " ++ m ++ " was made in " ++ show y
我们只能强制性地给这个函数安一个 (Show a) => Car String String a
的型别约束。看得出来,这要繁复得多。而唯一的好处貌似就是,我们可以使用 Show
型别类的 instance
来作 a
的型别。
ghci> tellCar (Car "Ford" "Mustang" 1967)
"This Ford Mustang was made in 1967"
ghci> tellCar (Car "Ford" "Mustang" "nineteen sixty seven")
"This Ford Mustang was made in \"nineteen sixty seven\""
ghci> :t Car "Ford" "Mustang" 1967
Car "Ford" "Mustang" 1967 :: (Num t) => Car [Char] [Char] t
ghci> :t Car "Ford" "Mustang" "nineteen sixty seven"
Car "Ford" "Mustang" "nineteen sixty seven" :: Car [Char] [Char] [Char]
其实在现实生活中,使用 Car String String Int
在大多数情况下已经满够了。所以给 Car
型别加型别参数貌似并没有什么必要。通常我们都是都是在一个型别中包含的型别并不影响它的行为时才引入型别参数。一组什么东西组成的 List 就是一个 List,它不关心里面东西的型别是啥,然而总是工作良好。若取一组数字的和,我们可以在后面的函数体中明确是一组数字的 List。Maybe 与之相似,它表示可以有什么东西可以没有,而不必关心这东西是啥。
我们之前还遇见过一个型别参数的应用,就是 Data.Map
中的 Map k v
。 k
表示 Map 中键的型别,v
表示值的型别。这是个好例子,Map 中型别参数的使用允许我们能够用一个型别索引另一个型别,只要键的型别在 Ord
型别类就行。如果叫我们自己定义一个 Map 型别,可以在 data
声明中加上一个型别类的约束。
data (Ord k) => Map k v = ...
然而 Haskell 中有一个严格的约定,那就是永远不要在 data
声明中添加型别约束。为啥?嗯,因为这样没好处,反而得写更多不必要的型别约束。Map k v
要是有 Ord k
的约束,那就相当于假定每个 Map 的相关函数都认为 k
是可排序的。若不给数据型别加约束,我们就不必给那些不关心键是否可排序的函数另加约束了。这类函数的一个例子就是 toList
,它只是把一个 Map 转换为关联 List 罢了,型别声明为 toList :: Map k v -> [(k, v)]
。要是加上型别约束,就只能是 toList :: (Ord k) =>Map k a -> [(k,v)]
,明显没必要嘛。
所以说,永远不要在 data
声明中加型别约束 --- 即便看起来没问题。免得在函数声明中写出过多无谓的型别约束。
我们实现个表示三维向量的型别,再给它加几个处理函数。我么那就给它个型别参数,虽然大多数情况都是数值型,不过这一来它就支持了多种数值型别。
data Vector a = Vector a a a deriving (Show)
vplus :: (Num t) => Vector t -> Vector t -> Vector t
(Vector i j k) `vplus` (Vector l m n) = Vector (i+l) (j+m) (k+n)
vectMult :: (Num t) => Vector t -> t -> Vector t
(Vector i j k) `vectMult` m = Vector (i*m) (j*m) (k*m)
scalarMult :: (Num t) => Vector t -> Vector t -> t
(Vector i j k) `scalarMult` (Vector l m n) = i*l + j*m + k*n
vplus
用来相加两个向量,即将其所有对应的项相加。scalarMult
用来求两个向量的标量积,vectMult
求一个向量和一个标量的积。这些函数可以处理 Vector Int
,Vector Integer
,Vector Float
等等型别,只要 Vector a
里的这个 a
在 Num
型别类中就行。同样,如果你看下这些函数的型别声明就会发现,它们只能处理相同型别的向量,其中包含的数字型别必须与另一个向量一致。注意,我们并没有在 data
声明中添加 Num
的类约束。反正无论怎么着都是给函数加约束。
再度重申,型别构造子和值构造子的区分是相当重要的。在声明数据型别时,等号=左端的那个是型别构造子,右端的(中间可能有|分隔)都是值构造子。拿 Vector t t t -> Vector t t t -> t
作函数的型别就会产生一个错误,因为在型别声明中只能写型别,而 Vector
的型别构造子只有个参数,它的值构造子才是有三个。我们就慢慢耍:
ghci> Vector 3 5 8 `vplus` Vector 9 2 8
Vector 12 7 16
ghci> Vector 3 5 8 `vplus` Vector 9 2 8 `vplus` Vector 0 2 3
Vector 12 9 19
ghci> Vector 3 9 7 `vectMult` 10
Vector 30 90 70
ghci> Vector 4 9 5 `scalarMult` Vector 9.0 2.0 4.0
74.0
ghci> Vector 2 9 3 `vectMult` (Vector 4 9 5 `scalarMult` Vector 9 2 4)
Vector 148 666 222
#
Derived instances
在 [types-and-type-classes.html#Typeclasses入门 Typeclass 101] 那一节里面,我们了解了 Typeclass 的基础内容。里面提到,型别类就是定义了某些行为的介面。例如,Int 型别是 Eq
型别类的一个 instance,Eq
类就定义了判定相等性的行为。Int 值可以判断相等性,所以 Int 就是 Eq
型别类的成员。它的真正威力体现在作为 Eq
介面的函数中,即 ==
和 /=
。只要一个型别是 Eq
型别类的成员,我们就可以使用 ==
函数来处理这一型别。这便是为何 4==4
和 "foo"/="bar"
这样的表达式都需要作型别检查。
我们也曾提到,人们很容易把型别类与 Java,Python,C++ 等语言的类混淆。很多人对此都倍感不解,在原先那些语言中,类就像是蓝图,我们可以根据它来创造对象、保存状态并执行操作。而型别类更像是介面,我们不是靠它构造数据,而是给既有的数据型别描述行为。什么东西若可以判定相等性,我们就可以让它成为 Eq
型别类的 instance。什么东西若可以比较大小,那就可以让它成为 Ord
型别类的 instance。
在下一节,我们将看一下如何手工实现型别类中定义函数来构造 instance。现在呢,我们先了解下 Haskell 是如何自动生成这几个型别类的 instance,Eq
, Ord
, Enum
, Bounded
, Show
, Read
。只要我们在构造型别时在后面加个 deriving
(派生)关键字,Haskell 就可以自动地给我们的型别加上这些行为。
看这个数据型别:
data Person = Person { firstName :: String
, lastName :: String
, age :: Int
}
这描述了一个人。我们先假定世界上没有重名重姓又同龄的人存在,好,假如有两个 record,有没有可能是描述同一个人呢?当然可能,我么可以判定姓名年龄的相等性,来判断它俩是否相等。这一来,让这个型别成为 Eq
的成员就很靠谱了。直接 derive 这个 instance:
data Person = Person { firstName :: String
, lastName :: String
, age :: Int
} deriving (Eq)
在一个型别 derive 为 Eq
的 instance 后,就可以直接使用 ==
或 /=
来判断它们的相等性了。Haskell 会先看下这两个值的值构造子是否一致(这里只是单值构造子),再用 ==
来检查其中的所有数据(必须都是 Eq
的成员)是否一致。在这里只有 String
和 Int,所以是没有问题的。测试下我们的 Eqinstance:
ghci> let mikeD = Person {firstName = "Michael", lastName = "Diamond", age = 43}
ghci> let adRock = Person {firstName = "Adam", lastName = "Horovitz", age = 41}
ghci> let mca = Person {firstName = "Adam", lastName = "Yauch", age = 44}
ghci> mca == adRock
False
ghci> mikeD == adRock
False
ghci> mikeD == mikeD
True
ghci> mikeD == Person {firstName = "Michael", lastName = "Diamond", age = 43}
True
自然,Person
如今已经成为了 Eq
的成员,我们就可以将其应用于所有在型别声明中用到 Eq
类约束的函数了,如 elem
。
ghci> let beastieBoys = [mca, adRock, mikeD]
ghci> mikeD `elem` beastieBoys
True
Show
和 Read
型别类处理可与字元串相互转换的东西。同 Eq
相似,如果一个型别的构造子含有参数,那所有参数的型别必须都得属于 Show
或 Read
才能让该型别成为其 instance。就让我们的 Person
也成为 Read
和 Show
的一员吧。
data Person = Person { firstName :: String
, lastName :: String
, age :: Int
} deriving (Eq, Show, Read)
然后就可以输出一个 Person
到控制台了。
ghci> let mikeD = Person {firstName = "Michael", lastName = "Diamond", age = 43}
ghci> mikeD
Person {firstName = "Michael", lastName = "Diamond", age = 43}
ghci> "mikeD is: " ++ show mikeD
"mikeD is: Person {firstName = \"Michael\", lastName = \"Diamond\", age = 43}"
如果我们还没让 Person
型别作为 Show
的成员就尝试输出它,Haskell 就会向我们抱怨,说它不知道该怎么把它表示成一个字元串。不过现在既然已经 derive 成为了 Show
的一个 instance,它就知道了。
Read
几乎就是与 Show
相对的型别类,show
是将一个值转换成字元串,而 read
则是将一个字元串转成某型别的值。还记得,使用 read
函数时我们必须得用型别注释注明想要的型别,否则 Haskell 就不会知道如何转换。
ghci> read "Person {firstName =\"Michael\", lastName =\"Diamond\", age = 43}" :: Person
Person {firstName = "Michael", lastName = "Diamond", age = 43}
如果我们 read
的结果会在后面用到参与计算,Haskell 就可以推导出是一个 Person 的行为,不加注释也是可以的。
ghci> read "Person {firstName =\"Michael\", lastName =\"Diamond\", age = 43}" == mikeD
True
也可以 read
带参数的型别,但必须填满所有的参数。因此 read "Just 't'" :: Maybe a
是不可以的,read "Just 't'" :: Maybe Char
才对。
很容易想象 Ord
型别类 derive instance 的行为。首先,判断两个值构造子是否一致,如果是,再判断它们的参数,前提是它们的参数都得是 Ord
的 instance。Bool
型别可以有两种值,False
和 True
。为了了解在比较中程序的行为,我们可以这样想象:
data Bool = False | True deriving (Ord)
由于值构造子 False
安排在 True
的前面,我们可以认为 True
比 False
大。
ghci> True `compare` False
GT
ghci> True > False
True
ghci> True < False
False
在 Maybe a
数据型别中,值构造子 Nothing
在 Just
值构造子前面,所以一个 Nothing
总要比 Just something
的值小。即便这个 something
是 -100000000
也是如此。
ghci> Nothing < Just 100
True
ghci> Nothing > Just (-49999)
False
ghci> Just 3 `compare` Just 2
GT
ghci> Just 100 > Just 50
True
不过类似 Just (*3) > Just (*2)
之类的程式码是不可以的。因为 (*3)
和 (*2)
都是函数,而函数不是 Ord
类的成员。
作枚举,使用数字型别就能轻易做到。不过使用 Enum
和 Bounded
型别类会更好,看下这个型别:
data Day = Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday
所有的值构造子都是 nullary
的(也就是没有参数),每个东西都有前置子和后继子,我们可以让它成为 Enum
型别类的成员。同样,每个东西都有可能的最小值和最大值,我们也可以让它成为 Bounded
型别类的成员。在这里,我们就同时将它搞成其它可 derive型别类的 instance。再看看我们能拿它做啥:
data Day = Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday
deriving (Eq, Ord, Show, Read, Bounded, Enum)
由于它是 Show
和 Read
型别类的成员,我们可以将这个型别的值与字元串相互转换。
ghci> Wednesday
Wednesday
ghci> show Wednesday
"Wednesday"
ghci> read "Saturday" :: Day
Saturday
由于它是 Eq
与 Ord
的成员,因此我们可以拿 Day
作比较。
ghci> Saturday == Sunday
False
ghci> Saturday == Saturday
True
ghci> Saturday > Friday
True
ghci> Monday `compare` Wednesday
LT
它也是 Bounded
的成员,因此有最早和最晚的一天。
ghci> minBound :: Day
Monday
ghci> maxBound :: Day
Sunday
它也是 Enum
的 instance,可以得到前一天和后一天,并且可以对此使用 List 的区间。
ghci> succ Monday
Tuesday
ghci> pred Saturday
Friday
ghci> [Thursday .. Sunday]
[Thursday,Friday,Saturday,Sunday]
ghci> [minBound .. maxBound] :: [Day]
[Monday,Tuesday,Wednesday,Thursday,Friday,Saturday,Sunday]
那是相当的棒。
#
Type synonyms
在前面我们提到在写型别名的时候,[Char]
和 String
等价,可以互换。这就是由型别别名实现的。型别别名实际上什么也没做,只是给型别提供了不同的名字,让我们的程式码更容易理解。这就是 [Char]
的别名 String
的由来。
type String = [Char]
我们已经介绍过了 type
关键字,这个关键字有一定误导性,它并不是用来创造新类(这是 data
关键字做的事情),而是给一个既有型别提供一个别名。
如果我们随便搞个函数 toUpperString
或其他什么名字,将一个字元串变成大写,可以用这样的型别声明 toUpperString :: [Char] -> [Char]
, 也可以这样 toUpperString :: String -> String
,二者在本质上是完全相同的。后者要更易读些。
在前面 Data.Map
那部分,我们用了一个关联 List
来表示 phoneBook
,之后才改成的 Map。我们已经发现了,一个关联 List 就是一组键值对组成的 List。再看下我们 phoneBook
的样子:
phoneBook :: [(String,String)]
phoneBook =
[("betty","555-2938")
,("bonnie","452-2928")
,("patsy","493-2928")
,("lucille","205-2928")
,("wendy","939-8282")
,("penny","853-2492")
]
可以看出,phoneBook
的型别就是 [(String,String)]
,这表示一个关联 List 仅是 String 到 String 的映射关系。我们就弄个型别别名,好让它型别声明中能够表达更多资讯。
type PhoneBook = [(String,String)]
现在我们 phoneBook
的型别声明就可以是 phoneBook :: PhoneBook
了。再给字元串加上别名:
type PhoneNumber = String
type Name = String
type PhoneBook = [(Name,PhoneNumber)]
Haskell 程序员给 String 加别名是为了让函数中字元串的表达方式及用途更加明确。
好的,我们实现了一个函数,它可以取一名字和号码检查它是否存在于电话本。现在可以给它加一个相当好看明了的型别声明:
inPhoneBook :: Name -> PhoneNumber -> PhoneBook -> Bool
inPhoneBook name pnumber pbook = (name,pnumber) `elem` pbook
如果不用型别别名,我们函数的型别声明就只能是 String -> String -> [(String ,String)] -> Bool
了。在这里使用型别别名是为了让型别声明更加易读,但你也不必拘泥于它。引入型别别名的动机既非单纯表示我们函数中的既有型别,也不是为了替换掉那些重复率高的长名字型别(如 [(String,String)]
),而是为了让型别对事物的描述更加明确。
型别别名也是可以有参数的,如果你想搞个型别来表示关联 List,但依然要它保持通用,好让它可以使用任意型别作 key
和 value
,我们可以这样:
type AssocList k v = [(k,v)]
好的,现在一个从关联 List 中按键索值的函数型别可以定义为 (Eq k) => k -> AssocList k v -> Maybe v. AssocList i
。AssocList
是个取两个型别做参数生成一个具体型别的型别构造子,如 Assoc Int String
等等。
*Fronzie 说*:Hey!当我提到具体型别,那我就是说它是完全呼叫的,就像 ``Map Int String``。要不就是多态函数中的 ``[a]`` 或 ``(Ord a) => Maybe a`` 之类。有时我和孩子们会说 "Maybe 型别",但我们的意思并不是按字面来,傻瓜都知道 ``Maybe`` 是型别构造子嘛。只要用一个明确的型别呼叫 ``Maybe``,如 ``Maybe String`` 可得一个具体型别。你知道,只有具体型别才可以储存值。
我们可以用不全呼叫来得到新的函数,同样也可以使用不全呼叫得到新的型别构造子。同函数一样,用不全的型别参数呼叫型别构造子就可以得到一个不全呼叫的型别构造子,如果我们要一个表示从整数到某东西间映射关系的型别,我们可以这样:
type IntMap v = Map Int v
也可以这样:
type IntMap = Map Int
无论怎样,IntMap
的型别构造子都是取一个参数,而它就是这整数指向的型别。
Oh yeah,如果要你去实现它,很可能会用个 qualified import
来导入 Data.Map
。这时,型别构造子前面必须得加上模组名。所以应该写个 type IntMap = Map.Map Int
你得保证真正弄明白了型别构造子和值构造子的区别。我们有了个叫 IntMap
或者 AssocList
的别名并不意味着我们可以执行类似 AssocList [(1,2),(4,5),(7,9)]
的程式码,而是可以用不同的名字来表示原先的 List,就像 [(1,2),(4,5),(7,9)] :: AssocList Int Int
让它里面的型别都是 Int。而像处理普通的 Tuple 构成的那种 List 处理它也是可以的。型别别名(型别依然不变),只可以在 Haskell 的型别部分中使用,像定义新型别或型别声明或型别注释中跟在::后面的部分。
另一个很酷的二参型别就是 Either a b
了,它大约是这样定义的:
data Either a b = Left a | Right b deriving (Eq, Ord, Read, Show)
它有两个值构造子。如果用了 Left
,那它内容的型别就是 a
;用了 Right
,那它内容的型别就是 b
。我们可以用它来将可能是两种型别的值封装起来,从里面取值时就同时提供 Left
和 Right
的模式匹配。
ghci> Right 20
Right 20
ghci> Left "w00t"
Left "w00t"
ghci> :t Right 'a'
Right 'a' :: Either a Char
ghci> :t Left True
Left True :: Either Bool b
到现在为止,Maybe
是最常见的表示可能失败的计算的型别了。但有时 Maybe
也并不是十分的好用,因为 Nothing
中包含的信息还是太少。要是我们不关心函数失败的原因,它还是不错的。就像 Data.Map
的 lookup
只有在搜寻的项不在 Map 时才会失败,对此我们一清二楚。但我们若想知道函数失败的原因,那还得使用 Either a b
,用 a
来表示可能的错误的型别,用 b
来表示一个成功运算的型别。从现在开始,错误一律用 Left
值构造子,而结果一律用 Right
。
一个例子:有个学校提供了不少壁橱,好给学生们地方放他们的 Gun'N'Rose 海报。每个壁橱都有个密码,哪个学生想用个壁橱,就告诉管理员壁橱的号码,管理员就会告诉他壁橱的密码。但如果这个壁橱已经让别人用了,管理员就不能告诉他密码了,得换一个壁橱。我们就用 Data.Map
的一个 Map 来表示这些壁橱,把一个号码映射到一个表示壁橱占用情况及密码的 Tuple 里。
import qualified Data.Map as Map
data LockerState = Taken | Free deriving (Show, Eq)
type Code = String
type LockerMap = Map.Map Int (LockerState, Code)
很简单,我们引入了一个新的型别来表示壁橱的占用情况。并为壁橱密码及按号码找壁橱的 Map 分别设置了一个别名。好,现在我们实现这个按号码找壁橱的函数,就用 Either String Code
型别表示我们的结果,因为 lookup
可能会以两种原因失败。橱子已经让别人用了或者压根就没有这个橱子。如果 lookup
失败,就用字元串表明失败的原因。
lockerLookup :: Int -> LockerMap -> Either String Code
lockerLookup lockerNumber map =
case Map.lookup lockerNumber map of
Nothing -> Left $ "Locker number " ++ show lockerNumber ++ " doesn't exist!"
Just (state, code) -> if state /= Taken
then Right code
else Left $ "Locker " ++ show lockerNumber ++ " is already taken!"
我们在这里个 Map 中执行一次普通的 lookup
,如果得到一个 Nothing
,就返回一个 Left String
的值,告诉他压根就没这个号码的橱子。如果找到了,就再检查下,看这橱子是不是已经让别人用了,如果是,就返回个 Left String
说它已经让别人用了。否则就返回个 Right Code
的值,通过它来告诉学生壁橱的密码。它实际上就是个 Right String
,我们引入了个型别别名让它这型别声明更好看。
如下是个 Map 的例子:
lockers :: LockerMap
lockers = Map.fromList
[(100,(Taken,"ZD39I"))
,(101,(Free,"JAH3I"))
,(103,(Free,"IQSA9"))
,(105,(Free,"QOTSA"))
,(109,(Taken,"893JJ"))
,(110,(Taken,"99292"))
]
现在从里面 lookup
某个橱子号..
ghci> lockerLookup 101 lockers
Right "JAH3I"
ghci> lockerLookup 100 lockers
Left "Locker 100 is already taken!"
ghci> lockerLookup 102 lockers
Left "Locker number 102 doesn't exist!"
ghci> lockerLookup 110 lockers
Left "Locker 110 is already taken!"
ghci> lockerLookup 105 lockers
Right "QOTSA"
我们完全可以用 Maybe a
来表示它的结果,但这样一来我们就对得不到密码的原因不得而知了。而在这里,我们的新型别可以告诉我们失败的原因。
#
Recursive data structures (递回地定义资料结构)
如我们先前看到的,一个 algebraic data type 的构造子可以有好几个 field,其中每个 field 都必须有具体的型态。有了那个概念,我们能定义一个型态,其中他的构造子的 field 的型态是他自己。这样我们可以递回地定义下去,某个型态的值便可能包含同样型态的值,进一步下去他还可以再包含同样型态的值。
考虑一下 List: [5]
。他其实是 5:[]
的语法糖。在 :
的左边是一个普通值,而在右边是一串 List。只是在这个案例中是空的 List。再考虑 [4,5]
。他可以看作 4:(5:[])
。看看第一个 :
,我们看到他也有一个元素在左边,一串 List 5:[]
在右边。同样的道理 3:(4:(5:6:[]))
也是这样。
我们可以说一个 List 的定义是要码是空的 List 或是一个元素,后面用 :
接了另一串 List。
我们用 algebraic data type 来实作我们自己的 List!
data List a = Empty | Cons a (List a) deriving (Show, Read, Eq, Ord)
这读起来好像我们前一段提及的定义。他要码是空的 List,或是一个元素跟一串 List 的结合。如果你被搞混了,看看用 record syntax 定义的可能比较清楚。
data List a = Empty | Cons { listHead :: a, listTail :: List a} deriving (Show, Read, Eq, Ord)
你可能也对这边的 Cons
构造子不太清楚。cons
其实就是指 :
。对 List 而言,:
其实是一个构造子,他接受一个值跟另一串 List 来构造一个 List。现在我们可以使用我们新定义的 List 型态。换句话说,他有两个 field,其中一个 field 具有型态 a
,另一个有型态 [a]
。
ghci> Empty
Empty
ghci> 5 `Cons` Empty
Cons 5 Empty
ghci> 4 `Cons` (5 `Cons` Empty)
Cons 4 (Cons 5 Empty)
ghci> 3 `Cons` (4 `Cons` (5 `Cons` Empty))
Cons 3 (Cons 4 (Cons 5 Empty))
我们用中缀的方式呼叫 Cons
构造子,这样你可以很清楚地看到他就是 :
。Empty
代表 []
,而 4 `Cons` (5 `Cons` Empty)
就是 4:(5:[])
。
我们可以只用特殊字元来定义函数,这样他们就会自动具有中缀的性质。我们也能同样的手法套用在构造子上,毕竟他们不过是回传型态的函数而已。
infixr 5 :-:
data List a = Empty | a :-: (List a) deriving (Show, Read, Eq, Ord)
首先我们留意新的语法结构:fixity 宣告。当我们定义函数成 operator,我们能同时指定 fixity (但并不是必须的)。fixity 指定了他应该是 left-associative 或是 right-associative,还有他的优先顺序。例如说,*
的 fixity 是 infixl 7 *
,而 +
的 fixity 是 infixl 6
。代表他们都是 left-associative。(4 * 3 * 2)
等于 ((4 * 3) * 2)
。但 *
拥有比 +
更高的优先顺序。所以 5 * 4 + 3
会是 (5 * 4) + 3
。
这样我们就可以写成 a :-: (List a)
而不是 Cons a (List a)
:
ghci> 3 :-: 4 :-: 5 :-: Empty
(:-:) 3 ((:-:) 4 ((:-:) 5 Empty))
ghci> let a = 3 :-: 4 :-: 5 :-: Empty
ghci> 100 :-: a
(:-:) 100 ((:-:) 3 ((:-:) 4 ((:-:) 5 Empty)))
Haskell 在宣告 deriving Show
的时候,他会仍视构造子为前缀函数,因此必须要用括号括起来。
我们在来写个函数来把两个 List 连起来。一般 ++
在操作普通 List 的时候是这样的:
infixr 5 ++
(++) :: [a] -> [a] -> [a]
[] ++ ys = ys
(x:xs) ++ ys = x : (xs ++ ys)
我们把他偷过来用在我们的 List 上,把函数命名成 .++
:
infixr 5 .++
(.++) :: List a -> List a -> List a
Empty .++ ys = ys
(x :-: xs) .++ ys = x :-: (xs .++ ys)
来看看他如何运作:
ghci> let a = 3 :-: 4 :-: 5 :-: Empty
ghci> let b = 6 :-: 7 :-: Empty
ghci> a .++ b
(:-:) 3 ((:-:) 4 ((:-:) 5 ((:-:) 6 ((:-:) 7 Empty))))
如果我们想要的话,我们可以定义其他操作我们list的函数。
注意到我们是如何利用 (x :-: xs)
做模式匹配的。他运作的原理实际上就是利用到构造子。我们可以利用 :-:
做模式匹配原因就是他是构造子,同样的 :
也是构造子所以可以用他做匹配。[]
也是同样道理。由于模式匹配是用构造子来作的,所以我们才能对像 8
, 'a'
之类的做模式匹配。他们是数值与字元的构造子。
接下来我们要实作二元搜寻树 (binary search tree)。如果你对二元搜寻树不太清楚,我们来快速地解释一遍。他的结构是每个节点指向两个其他节点,一个在左边一个在右边。在左边节点的元素会比这个节点的元素要小。在右边的话则比较大。每个节点最多可以有两棵子树。而我们知道譬如说一棵包含 5 的节点的左子树,里面所有的元素都会小于 5。而节点的右子树里面的元素都会大于 5。如果我们想找找看 8是不是在我们的树里面,我们就从 5 那个节点找起,由于 8 比 5 要大,很自然地就会往右搜寻。接着我们走到 7,又由于 8 比 7 要大,所以我们再往右走。我们在三步就找到了我们要的元素。如果这不是棵树而是 List 的话,那就会需要花到七步才能找到 8。
Data.Set
跟 Data.Map
中的 set
和 Map 都是用树来实现的,只是他们是用平衡二元搜寻树而不是随意的二元搜寻树。不过这边我们就只先写一棵普通的二元搜寻树就好了。
这边我们来定义一棵树的结构:他不是一棵空的树就是带有值并含有两棵子树。听起来非常符合 algebraic data type 的结构!
data Tree a = EmptyTree | Node a (Tree a) (Tree a) deriving (Show, Read, Eq)
我们不太想手动来建棵二元搜寻树,所以我们要来写一个函数,他接受一棵树还有一个元素,把这个元素安插到这棵二元搜寻树中。当拿这个元素跟树的节点比较结果比较小的话,我们就往左走,如果比较大,就往右走。重复这个动作直到我们走到一棵空的树。一旦碰到空的树的话,我们就把元素插入节点。
在 C 语言中,我们是用修改指标的方式来达成这件事。但在 Haskell 中,我们没办法修改我们的树。所以我们在决定要往左或往右走的时候就做一棵新的子树,走到最后要安插节点的时候也是做一棵新的树。因此我们插入函数的型态会是 a -> Tree a -> Tree a
。他接受一个元素跟一棵树,并回传一棵包含了新元素的新的树。这看起来很没效率的样子,但别担心,惰性的特性可以让我们不用担心这个。
来看下列两个函数。第一个做了一个单节点的树,而第二个插入一个元素到一棵树中。
singleton :: a -> Tree a
singleton x = Node x EmptyTree EmptyTree
treeInsert :: (Ord a) => a -> Tree a -> Tree a
treeInsert x EmptyTree = singleton x
treeInsert x (Node a left right)
| x == a = Node x left right
| x < a = Node a (treeInsert x left) right
| x > a = Node a left (treeInsert x right)
singleton
函数只是一个做一个含有两棵空子树的节点的函数的别名。在插入的操作中,我们先为终端条件定义了一个模式匹配。如果我们走到了一棵空的子树,这表示我们到达了我们想要的地方,我们便建造一棵空的单元素的树来放在那个位置。如果我们还没走到一棵空的树来插入我们的元素。那就必须要做一些检查来往下走。如果我们要安插的元素跟 root 所含有的元素相等,那就直接回传这棵树。如果安插的元素比较小,就回传一棵新的树。这棵树的 root 跟原来的相同,右子树也相同,只差在我们要安插新的元素到左子树中。如果安插的元素反而比较大,那整个过程就相反。
接下来,我们要写一个函数来检查某个元素是否已经在这棵树中。首先我们定义终端条件。如果我们已经走到一棵空的树,那这个元素一定不在这棵树中。这跟我们搜寻 List 的情形是一致的。如果我们要在空的 List 中搜寻某一元素,那就代表他不在这个 List 里面。假设我们现在搜寻一棵非空的树,而且 root 中的元素刚好就是我们要的,那就找到了。那如果不是呢?我们就要利用在 root 节点左边的元素都比 root 小的这个性质。如果我们的元素比 root 小,那就往左子树中找。如果比较大,那就往右子树中找。
treeElem :: (Ord a) => a -> Tree a -> Bool
treeElem x EmptyTree = False
treeElem x (Node a left right)
| x == a = True
| x < a = treeElem x left
| x > a = treeElem x right
我们要作的就是把之前段落所描述的事转换成程式码。首先我们不想手动一个个来创造一棵树。我们想用一个 fold
来从一个 List 创造一棵树。要知道走遍一个 List 并回传某种值的操作都可以用 fold
来实现。我们先从一棵空的树开始,然后从右边走过 List的 每一个元素,一个一个丢到树里面。
ghci> let nums = [8,6,4,1,7,3,5]
ghci> let numsTree = foldr treeInsert EmptyTree nums
ghci> numsTree
Node 5 (Node 3 (Node 1 EmptyTree EmptyTree) (Node 4 EmptyTree EmptyTree)) (Node 7 (Node 6 EmptyTree EmptyTree) (Node 8 EmptyTree EmptyTree))
在 foldr
中,treeInsert
是做 folding 操作的函数,而 EmptyTree
是起始的 accumulator,nums
则是要被走遍的 List。
当我们想把我们的树印出来的时候,印出来的形式会不太容易读。但如果我们能有结构地印出来呢?我们知道 root 是 5,他有两棵子树,其中一个的 root 是 3 另一个则是 7。
ghci> 8 `treeElem` numsTree
True
ghci> 100 `treeElem` numsTree
False
ghci> 1 `treeElem` numsTree
True
ghci> 10 `treeElem` numsTree
False
检查元素是否属于某棵树的函数现在能正常运作了!
你可以看到 algebraic data structures 是非常有力的概念。我们可以使用这个结构来构造出布林值,周一到周五的概念,甚至还有二元树。
#
Typeclasses 的第二堂课
到目前为止我们学到了一些 Haskell 中的标准 typeclass,也学到了某些已经定义为他们 instance 的型别。我们知道如何让我们自己定义的型别自动被 Haskell 所推导成标准 typeclass 的 instance。在这个章节中,我们会学到如何构造我们自己的 typeclass,并且如何构造这些 typeclass 的 type instance。
来快速复习一下什么是 typeclass: typeclass 就像是 interface。一个 typeclass 定义了一些行为(像是比较相不相等,比较大小顺序,能否穷举)而我们会把希望满足这些性质的型别定义成这些 typeclass 的 instance。typeclass 的行为是由定义的函数来描述。并写出对应的实作。当我们把一个型别定义成某个 typeclass 的 instance,就表示我们可以对那个型别使用 typeclass 中定义的函数。
Typeclass 跟 Java 或 Python 中的 class 一点关系也没有。这个概念让很多人混淆,所以我希望你先忘掉所有在命令式语言中学到有关 class 的所有东西。
例如说,Eq
这个 typeclass 是描述可以比较相等的事物。他定义了 ==
跟 /=
两个函数。如果我们有一个型别 Car
,而且对他们做相等比较是有意义的,那把 Car
作成是 Eq
的一个 instance 是非常合理的。
这边来看看在 Prelude
之中 Eq
是怎么被定义的。
class Eq a where
(==) :: a -> a -> Bool
(/=) :: a -> a -> Bool
x == y = not (x /= y)
x /= y = not (x == y)
我们在这边看到了一些奇怪的语法跟关键字。别担心,你一下子就会了解他们的。首先,我们看到 class Eq a where
,那代表我们定义了一个新的 typeclass 叫做 Eq
。a
是一个型别变数,他代表 a
是任何我们在定义 instance 时的型别。他不一定要叫做 a
。他也不一定非要一个字母不可,只要他是小写就好。然后我们又定义了几个函数。我们并不一定要实作函数的本体,不过必须要写出函数的型别宣告。
如果我们写成 class Eq equatable where
还有 (==) :: equatable -> equatable -> Bool
这样的形式,对一些人可能比较容易理解。
总之我们实作了 Eq
中需要定义的函数本体,只是我们定义他的方式是用交互递回的形式。我们描述两个 Eq
的 instance 要相等,那他们就不能不一样,而他们如果不一样,那他们就是不相等。我们其实不必这样写,但很快你会看到这其实是有用的。
如果我们说 class Eq a where
然后定义 (==) :: a -> a -> Bool
,那我们之后检查函数的型别时会发现他的型别是 (Eq a) => a -> a -> Bool
。
当我们有了 class 以后,可以用来做些什么呢?说实话,不多。不过一旦我们为它写一些 instance,就会有些好功能。来看看下面这个型别:
data TrafficLight = Red | Yellow | Green
这里定义了红绿灯的状态。请注意这个型别并不是任何 class 的 instance,虽然可以透过 derive 让它成为 Eq
或 Show
的 instance,但我们打算手工打造。下面展示了如何让一个型别成为 Eq
的 instance:
instance Eq TrafficLight where
Red == Red = True
Green == Green = True
Yellow == Yellow = True
_ == _ = False
我们使用了 instance
这个关键字。class 是用来定义新的 typeclass,而 instance 是用来说明我们要定义某个 typeclass 的 instance。当我们要定义 Eq
,我们会写 class Eq a where
,其中 a
代表任何型态。我们可以从 instance 的写法:instance Eq TrafficLight where
看出来。我们会把 a
换成实际的型别。
由于 ==
是用 /=
来定义的,同样的 /=
也是用 ==
来定义。所以我们只需要在 instance 定义中复写其中一个就好了。我们这样叫做定义了一个 minimal complete definition。这是说能让型别符合 class 行为所最小需要实作的函数数量。而 Eq
的 minimal complete definition 需要 ==
或 /=
其中一个。而如果 Eq
是这样定义的:
class Eq a where
(==) :: a -> a -> Bool
(/=) :: a -> a -> Bool
当我们定义 instance 的时候必须要两个函数都实作,因为 Haskell 并不知道这两个函数是怎么关联在一起的。所以 minimal complete definition 在这边是 ==
跟 /=
。
你可以看到我们是用模式匹配来实作 ==
。由于不相等的情况比较多,所以我们只写出相等的,最后再用一个 case
接住说你不在前面相等的 case
的话,那就是不相等。
我们再来写 Show
的 instance。要满足 Show
的 minimal complete definition,我们必须实作 show
函数,他接受一个值并把他转成字串。
instance Show TrafficLight where
show Red = "Red light"
show Yellow = "Yellow light"
show Green = "Green light"
再一次地,我们用模式匹配来完成我们的任务。我们来看看他是如何运作的。
ghci> Red == Red
True
ghci> Red == Yellow
False
ghci> Red `elem` [Red, Yellow, Green]
True
ghci> [Red, Yellow, Green]
[Red light,Yellow light,Green light]
如果我们用 derive
来自动产生 Eq
的话,效果是一样的。不过用 derive
来产生 show
的话,他会把值构造子转换成字串。但我们这边要的不太一样,我们希望印出像 "Red light"
这样的字串,所以我们就必须手动来写出 instance。
你也可以把 typeclass 定义成其他 typeclass 的 subclass。像是 Num
的 class 宣告就有点冗长,但我们先看个雏型。
class (Eq a) => Num a where
...
正如我们先前提到的,我们可以在很多地方加上 class constraints。这不过就是在 class Num a where
中的 a
上,加上他必须要是 Eq
的 instance 的限制。这基本上就是在说我们在定义一个型别为 Num
之前,必须先为他定义 Eq
的 instance。在某个型别可以被视作 Number
之前,必须先能被比较相不相等其实是蛮合理的。这就是 subclass 在做的事:帮 class declaration 加上限制。也就是说当我们定义 typeclass 中的函数本体时,我们可以预设 a
是属于 Eq
,因此能使用 ==
。
但像是 Maybe
或是 List 是如何被定义成 typeclass 的 instance 呢?Maybe
的特别之处在于他跟 TrafficLight
不一样,他不是一个具体的型别。他是一个型别构造子,接受一个型别参数(像是 Char
之类的)而构造出一个具体的型别(像是 Maybe Char
)。让我们再回顾一下 Eq
这个 typeclass:
class Eq a where
(==) :: a -> a -> Bool
(/=) :: a -> a -> Bool
x == y = not (x /= y)
x /= y = not (x == y)
从型别宣告来看,可以看到 a
必须是一个具体型别,因为所有在函数中的型别都必须是具体型别。(你没办法写一个函数,他的型别是 a -> Maybe
,但你可以写一个函数,他的型别是 a -> Maybe a
,或是 Maybe Int -> Maybe String
) 这就是为什么我们不能写成像这样:
instance Eq Maybe where
...
instance Eq (Maybe m) where
Just x == Just y = x == y
Nothing == Nothing = True
_ == _ = False
这就好像在说我们要把 Maybe something
这种东西全部都做成 Eq
的 instance。我们的确可以写成 (Maybe something)
,但我们通常是只用一个字母,这样比较像是 Haskell 的风格。(Maybe m)
这边则取代了 a
在 class Eq a where
的位置。尽管 Maybe
不是一个具体的型别。Maybe m
却是。指定一个型别参数(在这边是小写的 m
),我们说我们想要所有像是 Maybe m
的都成为 Eq
的 instance。
不过这仍然有一个问题。你能看出来吗? 我们用 ==
来比较 Maybe
包含的东西,但我们并没有任何保证说 Maybe
装的东西可以是 Eq
。这就是为什么我们需要修改我们的 instance 定义:
instance (Eq m) => Eq (Maybe m) where
Just x == Just y = x == y
Nothing == Nothing = True
_ == _ = False
这边我们必须要加上限制。在这个 instance 的宣告中,我们希望所有 Maybe m
形式的型别都属于 Eq
,但只有当 m
也属于 Eq
的时候。这也是 Haskell 在 derive 的时候做的事。
在大部份情形下,在 typeclass 宣告中的 class constraints 都是要让一个 typeclass 成为另一个 typeclass 的 subclass。而在 instance 宣告中的 class constraint 则是要表达型别的要求限制。举里来说,我们要求 Maybe
的内容物也要属于 Eq
。
当定义 instance 的时候,如果你需要提供具体型别(像是在 a -> a -> Bool
中的 a
),那你必须要加上括号跟型别参数来构造一个具体型别。
要知道你在定义 instance 的时候,型别参数会被取代。class Eq a where
中的 a
会被取代成真实的型别。所以试着想像把型别放进型别宣告中。(==) :: Maybe -> Maybe -> Bool
并非合法。但 (==) :: (Eq m) => Maybe m -> Maybe m -> Bool
则是。这是不论我们要定义什么,通用的型别宣告都是 (==) :: (Eq a) => a -> a -> Bool
还有一件事要确认。如果你想看看一个 typeclass 有定义哪些 instance。可以在 ghci 中输入 :info YourTypeClass
。所以输入 :info Num
会告诉你这个 typeclass 定义了哪些函数,还有哪些型别属于这个 typeclass。:info
也可以查询型别跟型别构造子的资讯。如果你输入 :info Maybe
。他会显示 Maybe
所属的所有 typeclass。:info
也能告诉你函数的型别宣告。
#
yes-no typeclass
在 Javascript 或是其他弱型别的程式语言,你能在 if expression 中摆上任何东西。举例来说,你可以做像下列的事: if (0) alert("YEAH!") else alert("NO!")
, if ("") alert ("YEAH!") else alert("NO!")
, if (false) alert("YEAH") else alert("NO!)
等等, 而上述所有的片段执行后都会跳出 NO!
。如果你写 if ("WHAT") alert ("YEAH") else alert("NO!")
,他会跳出 YEAH!
,因为 Javascript 认为非空字串会是 true。
尽管使用 Bool
来表达布林的语意是比较好的作法。为了有趣起见,我们来试试看模仿 Javascript 的行为。我们先从 typeclass 宣告开始看:
class YesNo a where
yesno :: a -> Bool
YesNo
typeclass 定义了一个函数。这个函数接受一个可以判断为真否的型别的值。而从我们写 a
的位置,可以看出来 a
必须是一个具体型别。
接下来我们来定义一些 instance。对于数字,我们会假设任何非零的数字都会被当作 true
,而 0 则当作 false
。
instance YesNo Int where
yesno 0 = False
yesno _ = True
空的 List (包含字串)代表 false
,而非空的 List 则代表 true
。
instance YesNo [a] where
yesno [] = False
yesno _ = True
留意到我们加了一个型别参数 a
来让整个 List 是一个具体型别,不过我们并没有对包涵在 List 中的元素的型别做任何额外假设。我们还剩下 Bool
可以被作为真假值,要定义他们也很容易:
instance YesNo Bool where
yesno = id
你说 id
是什么?他不过是标准函式库中的一个函数,他接受一个参数并回传相同的东西。
我们也让 Maybe a
成为 YesNo
的 instance。
instance YesNo (Maybe a) where
yesno (Just _) = True
yesno Nothing = False
由于我们不必对 Maybe
的内容做任何假设,因此并不需要 class constraint。我们只要定义遇到 Just
包装过的值就代表 true,而 Nothing
则代表 false。这里还是得写出 (Maybe a)
而不是只有 Maybe
,毕竟 Maybe -> Bool
的函式并不存在(因为 Maybe
并不是具体型别),而 Maybe a -> Bool
看起来就合理多了。现在有了这个定义,Maybe something
型式的型别都属于 YesNo
了,不论 something
是什么。
之前我们定义了 Tree a
,那代表一个二元搜寻树。我们可以说一棵空的树是 false
,而非空的树则是 true
。
instance YesNo (Tree a) where
yesno EmptyTree = False
yesno _ = True
而一个红绿灯可以代表 yes or no 吗?当然可以。如果他是红灯,那你就会停下来,如果他是绿灯,那你就能走。但如果是黄灯呢?只能说我通常会闯黄灯。
instance YesNo TrafficLight where
yesno Red = False
yesno _ = True
现在我们定义了许多 instance,来试着跑跑看!
ghci> yesno $ length []
False
ghci> yesno "haha"
True
ghci> yesno ""
False
ghci> yesno $ Just 0
True
ghci> yesno True
True
ghci> yesno EmptyTree
False
ghci> yesno []
False
ghci> yesno [0,0,0]
True
ghci> :t yesno
yesno :: (YesNo a) => a -> Bool
很好,统统是我们预期的结果。我们来写一个函数来模仿 if statement 的行为,但他是运作在 YesNo
的型别上。
yesnoIf :: (YesNo y) => y -> a -> a -> a
yesnoIf yesnoVal yesResult noResult =
if yesno yesnoVal then yesResult else noResult
很直觉吧!他接受一个 yes or no 的值还有两个部份,如果值是代表 "yes",那第一个部份就会被执行,而如果值是 "no",那第二个部份就会执行。
ghci> yesnoIf [] "YEAH!" "NO!"
"NO!"
ghci> yesnoIf [2,3,4] "YEAH!" "NO!"
"YEAH!"
ghci> yesnoIf True "YEAH!" "NO!"
"YEAH!"
ghci> yesnoIf (Just 500) "YEAH!" "NO!"
"YEAH!"
ghci> yesnoIf Nothing "YEAH!" "NO!"
"NO!"
#
Functor typeclass
到目前为止我们看过了许多在标准函式库中的 typeclass。我们操作过 Ord
,代表可以被排序的东西。我们也操作过 Eq
,代表可以被比较相等性的事物。也看过 Show
,代表可以被印成字串来表示的东西。至于 Read
则是我们可以把字串转换成型别的动作。不过现在我们要来看一下 Functor
这个 typeclass,基本上就代表可以被 map over 的事物。听到这个词你可能会联想到 List,因为 map over list 在 Haskell 中是很常见的操作。你没想错,List 的确是属于 Functor
这个 typeclass。
来看看他的实作会是了解 Functor
的最佳方式:
class Functor f where
fmap :: (a -> b) -> f a -> f b
我们看到他定义了一个函数 fmap
,而且并没有提供一个预设的实作。fmap
的型别蛮有趣的。到目前为止的我们看过的 typeclass 中的型别变数都是具体型别。就像是 (==) :: (Eq a) => a -> a -> Bool
中的 a
一样。但现在碰到的 f
并不是一个具体型别(一个像是 Int
, Bool
或 Maybe String
的型别),而是接受一个型别参数的型别构造子。如果要快速回顾的话可以看一下 Maybe Int
是一个具体型别,而 Maybe
是一个型别构造子,可接受一个型别作为参数。总之,我们知道 fmap
接受一个函数,这个函数从一个型别映射到另一个型别,还接受一个 functor 装有原始的型别,然后会回传一个 functor 装有映射后的型别。
如果听不太懂也没关系。当我们看几个范例之后会比较好懂。不过这边 fmap
的型别宣告让我们想起类似的东西,就是 map :: (a -> b) -> [a] -> [b]
。
他接受一个函数,这函数把一个型别的东西映射成另一个。还有一串装有某个型别的 List 变成装有另一个型别的 List。到这边听起来实在太像 functor 了。实际上,map
就是针对 List 的 fmap
。来看看 List 是如何被定义成 Functor
的 instance 的。
instance Functor [] where
fmap = map
注意到我们不是写成 instance Functor [a] where
,因为从 fmap :: (a -> b) -> f a -> f b
可以知道 f
是一个型别构造子,他接受一个型别。而 [a]
则已经是一个具体型别(一个拥有某个型别的 List),其中 []
是一个型别构造子,能接受某个型别而构造出像 [Int]
、[String]
甚至是 [[String]]
的具体型别。
对于 List,fmap
只不过是 map
,对 List 操作的时候他们都是一样的。
map :: (a -> b) -> [a] -> [b]
ghci> fmap (*2) [1..3]
[2,4,6]
ghci> map (*2) [1..3]
[2,4,6]
至于当我们对空的 List 操作 map
或 fmap
呢?我们会得到一个空的 List。他把一个型别为 [a]
的空的 List 转成型别为 [b]
的空的 List。
可以当作盒子的型别可能就是一个 functor。你可以把 List 想做是一个拥有无限小隔间的盒子。他们可能全部都是空的,已也可能有一部份是满的其他是空的。所以作为一个盒子会具有什么性质呢?例如说 Maybe a
。他表现得像盒子在于他可能什么东西都没有,就是 Nothing
,或是可以装有一个东西,像是 "HAHA"
,在这边就是 Just "HAHA"
。可以看到 Maybe
作为一个 functor 的定义:
instance Functor Maybe where
fmap f (Just x) = Just (f x)
fmap f Nothing = Nothing
注意到我们是写 instance Functor Maybe where
而不是 instance Functor (Maybe m) where
,就像我们在写 YesNo
时的 Maybe
一样。Functor
要的是一个接受一个型别参数的型别构造子而不是一个具体型别。如果你把 f
代换成 Maybe
。fmap
就会像 (a -> b) -> Maybe a -> Maybe b
。但如果你把 f
代换成 (Maybe m)
,那他就会像 (a -> b) -> Maybe m a -> Maybe m b
,这看起来并不合理,因为 Maybe
只接受一个型别参数。
总之,fmap
的实作是很简单的。如果一个空值是 Nothing
,那他就会回传 Nothing
。如果我们 map over 一个空的盒子,我们就会得到一个空的盒子。就像我们 map over 一个空的 List,那我们就会得到一个空的 List。如果他不是一个空值,而是包在 Just
中的某个值,那我们就会套用在包在 Just
中的值。
ghci> fmap (++ " HEY GUYS IM INSIDE THE JUST") (Just "Something serious.")
Just "Something serious. HEY GUYS IM INSIDE THE JUST"
ghci> fmap (++ " HEY GUYS IM INSIDE THE JUST") Nothing
Nothing
ghci> fmap (*2) (Just 200)
Just 400
ghci> fmap (*2) Nothing
Nothing
另外 Tree a
的型别也可以被 map over 且被定义成 Functor
的一个 instance。他可以被想成是一个盒子,而 Tree
的型别构造子也刚好接受单一一个型别参数。如果你把 fmap
看作是一个特别为 Tree
写的函数,他的型别宣告会长得像这样 (a -> b) -> Tree a -> Tree b
。不过我们在这边会用到递回。map over 一棵空的树会得到一棵空的树。map over 一棵非空的树会得到一棵被函数映射过的树,他的 root 会先被映射,然后左右子树都分别递回地被函数映射。
instance Functor Tree where
fmap f EmptyTree = EmptyTree
fmap f (Node x leftsub rightsub) =
Node (f x) (fmap f leftsub) (fmap f rightsub)
ghci> fmap (*2) EmptyTree
EmptyTree
ghci> fmap (*4) (foldr treeInsert EmptyTree [5,7,3,2,1,7])
Node 28 (Node 4 EmptyTree (Node 8 EmptyTree (Node 12 EmptyTree (Node 20 EmptyTree EmptyTree)))) EmptyTree
那 Either a b
又如何?他可以是一个 functor 吗?Functor
限制型别构造子只能接受一个型别参数,但 Either
却接受两个。聪明的你会想到我可以 partial apply Either
,先喂给他一个参数,并把另一个参数当作 free parameter。来看看 Either a
在标准函式库中是如何被定义的:
instance Functor (Either a) where
fmap f (Right x) = Right (f x)
fmap f (Left x) = Left x
我们在这边做了些什么?你可以看到我们把 Either a
定义成一个 instance,而不是 Either
。那是因为 Either a
是一个接受单一型别参数的型别构造子,而 Either
则接受两个。如果 fmap
是针对 Either a
,那他的型别宣告就会像是 (b -> c) -> Either a b -> Either a c
,他又等价于 (b -> c) -> (Either a) b -> (Either a) c
。在实作中,我们碰到一个 Right
的时候会做 map
,但在碰到 Left
的时候却不这样做,为什么呢?如果我们回头看看 Either a b
是怎么定义的:
data Either a b = Left a | Right b
如果我们希望对他们两个都做 map
的动作,那 a
跟 b
必须要是相同的型别。也就是说,如果我们的函数是接受一个字串然后回传另一个字串,而且 b
是字串,a
是数字,这样的情形是不可行的。而且从观察 fmap
的型别也可以知道,当他运作在 Either
上的时候,第一个型别参数必须固定,而第二个则可以改变,而其中第一个参数正好就是 Left
用的。
我们持续用盒子的比喻也仍然贴切,我们可以把 Left
想做是空的盒子在他旁边写上错误讯息,说明为什么他是空的。
在 Data.Map
中的 Map 也可以被定义成 functor,像是 Map k v
的情况下,fmap
可以用 v -> v'
这样一个函数来 map over Map k v
,并回传 Map k v'
。
注意到 '
在这边并没有特别的意思,他只是用来表示他跟另一个东西有点像,只有一点点差别而已。
你可以自己试试看把 Map k
变成 Functor
的一个 instance。
看过了 Functor
这个 typeclass,我们知道 typeclass 可以拿来代表高阶的概念。我们也练习过不少 partially applying type 跟定义 instance。在下几章中,我们也会看到 functor 必须要遵守的定律。
还有一件事就是 functor 应该要遵守一些定律,这样他们的一些性质才能被保证。如果我们用 fmap (+1)
来 map over [1,2,3,4]
,我们会期望结果会是 [2,3,4,5]
而不是反过来变成 [5,4,3,2]
。如果我们使用 fmap (\a -> a)
来 map over 一个 list,我们会期待拿回相同的结果。例如说,如果我们给 Tree
定义了错误的 functor instance,对 tree 使用 fmap
可能会导致二元搜寻树的性质丧失,也就是在 root 左边的节点不再比 root 小,在 root 右边的节点不再比 root 大。我们在下面几章会多谈 functor laws。
#
Kind
型别构造子接受其他型别作为他的参数,来构造出一个具体型别。这样的行为会让我们想到函数,也是接受一个值当作参数,并回传另一个值。我们也看过型别构造子可以 partially apply (Either String
是一个型别构造子,他接受一个型别来构造出一个具体型别,就像 Either String Int
)。这些都是函数能办到的事。在这个章节中,对于型别如何被套用到型别构造子上,我们会来看一下正式的定义。就像我们之前是用函数的型别来定义出函数是如何套用值的。如果你看不懂的话,你可以跳过这一章,这不会影响你后续的阅读。然而如果你搞懂的话,你会对于型别系统有更进一步的了解。
像是 3
,"YEAH"
或是 takeWhile
的值他们都有自己的型别(函数也是值的一种,我们可以把他们传来传去)型别是一个标签,值会把他带着,这样我们就可以推测出他的性质。但型别也有他们自己的标签,叫做 kind。kind 是型别的型别。虽然听起来有点玄妙,不过他的确是个有趣的概念。
那kind可以拿来做什么呢?我们可以在 ghci 中用 :k
来得知一个型别的 kind。
ghci> :k Int
Int :: *
一个星星代表的是什么意思?一个 *
代表这个型别是具体型别。一个具体型别是没有任何型别参数,而值只能属于具体型别。而 *
的读法叫做 star 或是 type。
我们再看看 Maybe
的 kind:
ghci> :k Maybe
Maybe :: * -> *
Maybe
的型别构造子接受一个具体型别(像是 Int
)然后回传一个具体型别,像是 Maybe Int
。这就是 kind 告诉我们的资讯。就像 Int -> Int
代表这个函数接受 Int
并回传一个 Int
。* -> *
代表这个型别构造子接受一个具体型别并回传一个具体型别。我们再来对 Maybe
套用型别参数后再看看他的 kind 是什么:
ghci> :k Maybe Int
Maybe Int :: *
正如我们预期的。我们对 Maybe
套用了型别参数后会得到一个具体型别(这就是 * -> *
的意思)这跟 :t isUpper
还有 :t isUpper 'A'
的差别有点类似。isUpper
的型别是 Char -> Bool
而 isUpper 'A'
的型别是 Bool
。而这两种型别,都是 *
的 kind。
我们对一个型别使用 :k
来得到他的 kind。就像我们对型别使用 :t
来得到的他的型别一样。就像我们先前说的,型别是值的标签,而 kind 是型别的标签。
我们再来看看其他的 kind
ghci> :k Either
Either :: * -> * -> *
这告诉我们 Either
接受两个具体型别作为参数,并构造出一个具体型别。他看起来也像是一个接受两个参数并回传值的函数型别。型别构造子是可以做 curry 的,所以我们也能 partially apply。
ghci> :k Either String
Either String :: * -> *
ghci> :k Either String Int
Either String Int :: *
当我们希望定义 Either
成为 Functor
的 instance 的时候,我们必须先 partial apply,因为 Functor
预期有一个型别参数,但 Either
却有两个。也就是说,Functor
希望型别的 kind 是 * -> *
,而我们必须先 partial apply Either
来得到 kind * -> *
,而不是最开始的 * -> * -> *
。我们再来看看 Functor
的定义
class Functor f where
fmap :: (a -> b) -> f a -> f b
我们看到 f
型别变数是接受一个具体型别且构造出一个具体型别的型别。 知道他构造出具体型别是因为是作为函数参数的型别。 从那里我们可以推测出一个型别要是属于 Functor
必须是 * -> *
kind。
现在我们来练习一下。来看看下面这个新定义的 typeclass。
class Tofu t where
tofu :: j a -> t a j
这看起来很怪。我们干嘛要为这个奇怪的 typeclass 定义 instance?我们可以来看看他的 kind 是什么?由于 j a
被当作 tofu
这个函数的参数的型别,所以 j a
一定是 *
kind。我们假设 a
是 *
kind,那 j
就会是 * -> *
的 kind。我们看到 t
由于是函数的回传值,一定是接受两个型别参数的型别。而知道 a
是 *
,j
是 * -> *
,我们可以推测出 t
是* -> (* -> *) -> *
。也就是说他接受一个具体型别 a
,一个接受单一参数的型别构造子 j
,然后产生出一个具体型别。
我们再来定义出一个型别具有 * -> (* -> *) -> *
的 kind,下面是一种定义的方法:
data Frank a b = Frank {frankField :: b a} deriving (Show)
我们怎么知道这个型别具有 * -> (* -> *) -> *
的 kind 呢?ADT 中的栏位是要来塞值的,所以他们必须是 *
kind。我们假设 a
是 *
,那 b
就是接受一个型别参数的 kind * -> *
。现在我们知道 a
跟 b
的 kind 了,而他们又是 Frank
的型别参数,所以我们知道 Frank
会有 * -> (* -> *) -> *
的 kind。第一个 *
代表 a
,而 (* -> *)
代表 b
。我们构造些 Frank
的值并检查他们的型别吧:
ghci> :t Frank {frankField = Just "HAHA"}
Frank {frankField = Just "HAHA"} :: Frank [Char] Maybe
ghci> :t Frank {frankField = Node 'a' EmptyTree EmptyTree}
Frank {frankField = Node 'a' EmptyTree EmptyTree} :: Frank Char Tree
ghci> :t Frank {frankField = "YES"}
Frank {frankField = "YES"} :: Frank Char []
由于 frankField
具有 a b
的型别。他的值必定有一个类似的型别。他们可能是 Just "HAHA"
,也就有 Maybe [Char]
的型别,或是他们可能是 ['Y','E','S']
,他的型别是 [Char]
。(如果我们是用自己定义的 List 型别的话,那就会是 List Char
)。我们看到 Frank
值的型别对应到 Frank
的 kind。[Char]
具有 *
的 kind,而 Maybe
则是 * -> *
。由于结果必须是个值,也就是他必须要是具体型别,因使他必须 fully applied,因此每个 Frank blah blaah
的值都会是 *
的 kind。
要把 Frank
定义成 Tofu
的 instance 也是很简单。我们看到 tofu
接受 j a
(例如 Maybe Int
)并回传 t a j
。所以我们将 Frank
代入 t
,就得到 Frank Int Maybe
。
instance Tofu Frank where
tofu x = Frank x
ghci> tofu (Just 'a') :: Frank Char Maybe
Frank {frankField = Just 'a'}
ghci> tofu ["HELLO"] :: Frank [Char] []
Frank {frankField = ["HELLO"]}
这并不是很有用,但让我们做了不少型别的练习。再来看看下面的型别:
data Barry t k p = Barry { yabba :: p, dabba :: t k }
我们想要把他定义成 Functor
的 instance。Functor
希望是 * -> *
的型别,但 Barry
并不是那种 kind。那 Barry
的 kind 是什么呢?我们可以看到他接受三个型别参数,所以会是 something -> something -> something -> *
。p
是一个具体型别因此是 *
。至于 k
,我们假设他是 *
,所以 t
会是 * -> *
。现在我们把这些代入 something
,所以 kind 就变成 (* -> *) -> * -> * -> *
。我们用 ghci 来检查一下。
ghci> :k Barry
Barry :: (* -> *) -> * -> * -> *
我们猜对了!现在要把这个型别定义成 Functor
,我们必须先 partially apply 头两个型别参数,这样我们就会是 * -> *
的 kind。这代表 instance 定义会是 instance Functor (Barry a b) where
。如果我们看 fmap
针对 Barry
的型别,也就是把 f
代换成 Barry c d
,那就会是 fmap :: (a -> b) -> Barry c d a -> Barry c d b
。第三个 Barry
的型别参数是对于任何型别,所以我们并不牵扯进他。
instance Functor (Barry a b) where
fmap f (Barry {yabba = x, dabba = y}) = Barry {yabba = f x, dabba = y}
我们把 f
map 到第一个栏位。
在这一个章节中,我们看到型别参数是怎么运作的,以及正如我们用型别来定义出函数的参数,我们也用 kind 是来定义他。我们看到函数跟型别构造子有许多彼此相像的地方。然而他们是两个完全不同的东西。当我们在写一般实用的 Haskell 程式时,你几乎不会碰到需要动到 kind 的东西,也不需要动脑去推敲 kind。通常你只需要在定义 instance 时 partially apply 你自己的 * -> *
或是 *
型别,但知道背后运作的原理也是很好的。知道型别本身也有自己的型别也是很有趣的。如果你实在不懂这边讲的东西,也可以继续阅读下去。但如果你能理解,那你就会理解 Haskell 型别系统的一大部份。
9
输入与输出
我们已经说明了 Haskell 是一个纯粹函数式语言。虽说在命令式语言中我们习惯给电脑执行一连串指令,在函数式语言中我们是用定义东西的方式进行。在 Haskell 中,一个函数不能改变状态,像是改变一个变数的内容。(当一个函数会改变状态,我们说这函数是有副作用的。)在 Haskell 中函数唯一可以做的事是根据我们给定的参数来算出结果。如果我们用同样的参数呼叫两次同一个函数,它会回传相同的结果。尽管这从命令式语言的角度来看是蛮大的限制,我们已经看过它可以达成多么酷的效果。在一个命令式语言中,程式语言没办法给你任何保证在一个简单如打印出几个数字的函数不会同时烧掉你的房子,绑架你的狗并刮伤你车子的烤漆。例如,当我们要建立一棵二元树的时候,我们并不插入一个节点来改变原有的树。由于我们无法改变状态,我们的函数实际上回传了一棵新的二元树。
函数无法改变状态的好处是它让我们促进了我们理解程式的容易度,但同时也造成了一个问题。假如说一个函数无法改变现实世界的状态,那它要如何打印出它所计算的结果?毕竟要告诉我们结果的话,它必须要改变输出装置的状态(譬如说萤幕),然后从萤幕传达到我们的脑,并改变我们心智的状态。
不要太早下结论,Haskell 实际上设计了一个非常聪明的系统来处理有副作用的函数,它漂亮地将我们的程式区分成纯粹跟非纯粹两部分。非纯粹的部分负责跟键盘还有萤幕沟通。有了这区分的机制,在跟外界沟通的同时,我们还是能够有效运用纯粹所带来的好处,像是惰性求值、容错性跟模组性。
#
Hello, world!
到目前为止我们都是将函数载入 GHCi 中来测试,像是标准函式库中的一些函式。但现在我们要做些不一样的,写一个真实跟世界互动的 Haskell 程式。当然不例外,我们会来写个 "hello world"。
现在,我们把下一行打到你熟悉的编辑器中
main = putStrLn "hello, world"
我们定义了一个 main
,并在里面以 "hello, world"
为参数呼叫了 putStrLn
。看起来没什么大不了,但不久你就会发现它的奥妙。把这程式存成 helloworld.hs
。
现在我们将做一件之前没做过的事:编译你的程式。打开你的终端并切换到包含 helloworld.hs
的目录,并输入下列指令。
$ ghc --make helloworld
[1 of 1] Compiling Main ( helloworld.hs, hellowowlrd.o )
Linking helloworld ...
顺利的话你就会得到如上的讯息,接着你便可以执行你的程式 ./helloworld
$ ./helloworld
hello, world
这就是我们第一个编译成功并打印出字串到萤幕的程式。很简单吧。
让我们来看一下我们究竟做了些什么,首先来看一下 putStrLn
函数的型态:
ghci> :t putStrLn
putStrLn :: String -> IO ()
ghci> :t putStrLn "hello, world"
putStrLn "hello, world" :: IO ()
我们可以这么解读 putStrLn
的型态:putStrLn
接受一个字串并回传一个 I/O action,这 I/O action 包含了 ()
的型态。(即空的 tuple,或者是 unit 型态)。一个 I/O action 是一个会造成副作用的动作,常是指读取输入或输出到萤幕,同时也代表会回传某些值。在萤幕打印出几个字串并没有什么有意义的回传值可言,所以这边用一个 ()
来代表。
那究竟 I/O action 会在什么时候被触发呢?这就是 main
的功用所在。一个 I/O action 会在我们把它绑定到 main
这个名字并且执行程式的时候触发。
把整个程式限制在只能有一个 I/O action 看似是个极大的限制。这就是为什么我们需要 do 表示法来将所有 I/O action 绑成一个。来看看下面这个例子。
main = do
putStrLn "Hello, what's your name?"
name <- getLine
putStrLn ("Hey " ++ name ++ ", you rock!")
新的语法,有趣吧!它看起来就像一个命令式的程式。如果你编译并执行它,它便会照你预期的方式执行。我们写了一个 do 并且接着一连串指令,就像写个命令式程式一般,每一步都是一个 I/O action。将所有 I/O action 用 do 绑在一起变成了一个大的 I/O action。这个大的 I/O action 的型态是 IO ()
,这完全是由最后一个 I/O action 所决定的。
这就是为什么 main
的型态永远都是 main :: IO something
,其中 something
是某个具体的型态。按照惯例,我们通常不会把 main
的型态在程式中写出来。
另一个有趣的事情是第三行 name <- getLine
。它看起来像是从输入读取一行并存到一个变数 name
之中。真的是这样吗?我们来看看 getLine
的型态吧
ghci> :t getLine
getLine :: IO String
我们可以看到 getLine
是一个回传 String
的 I/O action。因为它会等使用者输入某些字串,这很合理。那 name <- getLine
又是如何?你能这样解读它:执行一个 I/O action getLine
并将它的结果绑定到 name
这个名字。getLine
的型态是 IO String
,所以 name
的型态会是 String
。你能把 I/O action 想成是一个长了脚的盒子,它会跑到真实世界中替你做某些事,像是在墙壁上涂鸦,然后带回来某些资料。一旦它带了某些资料给你,打开盒子的唯一办法就是用 <-
。而且如果我们要从 I/O action 拿出某些资料,就一定同时要在另一个 I/O action 中。这就是 Haskell 如何漂亮地分开纯粹跟不纯粹的程式的方法。getLine
在这样的意义下是不纯粹的,因为执行两次的时候它没办法保证会回传一样的值。这也是为什么它需要在一个 IO
的型态建构子中,那样我们才能在 I/O action 中取出资料。而且任何一段程式一旦依赖着 I/O 资料的话,那段程式也会被视为 I/O code。
但这不表示我们不能在纯粹的程式码中使用 I/O action 回传的资料。只要我们绑定它到一个名字,我们便可以暂时地使用它。像在 name <- getLine
中 name
不过是一个普通字串,代表在盒子中的内容。我们能将这个普通的字串传给一个极度复杂的函数,并回传你一生会有多少财富。像是这样:
main = do
putStrLn "Hello, what's your name?"
name <- getLine
putStrLn $ "Read this carefully, because this is your future: " ++ tellFortune name
tellFortune
并不知道任何 I/O 有关的事,它的型态只不过是 String -> String
。
再来看看这段程式码吧,他是合法的吗?
nameTag = "Hello, my name is " ++ getLine
如果你回答不是,恭喜你。如果你说是,你答错了。这么做不对的理由是 ++
要求两个参数都必须是串列。他左边的参数是 String
,也就是 [Char]
。然而 getLine
的型态是 IO String
。你不能串接一个字串跟 I/O action。我们必须先把 String
的值从 I/O action 中取出,而唯一可行的方法就是在 I/O action 中使用 name <- getLine
。如果我们需要处理一些非纯粹的资料,那我们就要在非纯粹的环境中做。所以我们最好把 I/O 的部分缩减到最小的比例。
每个 I/O action 都有一个值封装在里面。这也是为什么我们之前的程式可以这么写:
main = do
foo <- putStrLn "Hello, what's your name?"
name <- getLine
putStrLn ("Hey " ++ name ++ ", you rock!")
然而,foo
只会有一个 ()
的值,所以绑定到 foo
这个名字似乎是多余的。另外注意到我们并没有绑定最后一行的 putStrLn
给任何名字。那是因为在一个 do block 中,最后一个 action 不能绑定任何名字。我们在之后讲解 Monad 的时候会说明为什么。现在你可以先想成 do block 会自动从最后一个 action 取出值并绑定给他的结果。
除了最后一行之外,其他在 do 中没有绑定名字的其实也可以写成绑定的形式。所以 putStrLn "BLAH"
可以写成 _ <- putStrLn "BLAH"
。但这没什么实际的意义,所以我们宁愿写成 putStrLn something
。
初学者有时候会想错
name = getLine
以为这行会读取输入并给他绑定一个名字叫 name
但其实只是把 getLine
这个 I/O action 指定一个名字叫 name
罢了。记住,要从一个 I/O action 中取出值,你必须要在另一个 I/O action 中将他用 <-
绑定给一个名字。
I/O actions 只会在绑定给 main
的时候或是在另一个用 do 串起来的 I/O action 才会执行。你可以用 do 来串接 I/O actions,再用 do 来串接这些串接起来的 I/O actions。不过只有最外面的 I/O action 被指定给 main 才会触发执行。
喔对,其实还有另外一个情况。就是在 GHCi 中输入一个 I/O action 并按下 Enter 键,那也会被执行
ghci> putStrLn "HEEY"
HEEY
就算我们只是在 GHCi 中打几个数字或是呼叫一个函数,按下 Enter 就会计算它并呼叫 show
,再用 putStrLn
将字串打印出在终端上。
还记得 let binding 吗?如果不记得,回去温习一下这个章节。它们的形式是 let bindings in expression
,其中 bindings
是 expression 中的名字、expression
则是被运用到这些名字的算式。我们也提到了 list comprehensions 中,in
的部份不是必需的。你能够在 do blocks 中使用 let bindings 如同在 list comprehensions 中使用它们一样,像这样:
import Data.Char
main = do
putStrLn "What's your first name?"
firstName <- getLine
putStrLn "What's your last name?"
lastName <- getLine
let bigFirstName = map toUpper firstName
bigLastName = map toUpper lastName
putStrLn $ "hey " ++ bigFirstName ++ " " ++ bigLastName ++ ", how are you?"
注意我们是怎么编排在 do block 中的 I/O actions,也注意到我们是怎么编排 let 跟其中的名字的,由于对齐在 Haskell 中并不会被无视,这么编排才是好的习惯。我们的程式用 map toUpper firstName
将 "John"
转成大写的 "JOHN"
,并将大写的结果绑定到一个名字上,之后在输出的时候参考到了这个名字。
你也许会问究竟什么时候要用 <-
,什么时候用 let bindings?记住,<-
是用来运算 I/O actions 并将他的结果绑定到名称。而 map toUpper firstName
并不是一个 I/O action。他只是一个纯粹的 expression。所以总结来说,当你要绑定 I/O actions 的结果时用 <-
,而对于纯粹的 expression 使用 let bindings。对于错误的 let firstName = getLine
,我们只不过是把 getLine
这个 I/O actions 给了一个不同的名字罢了。最后还是要用 <-
将结果取出。
现在我们来写一个会一行一行不断地读取输入,并将读进来的字反过来输出到萤幕上的程式。程式会在输入空白行的时候停止。
main = do
line <- getLine
if null line
then return ()
else do
putStrLn $ reverseWords line
main
reverseWords :: String -> String
reverseWords = unwords . map reverse . words
在分析这段程式前,你可以执行看看来感受一下程式的运行。
首先,我们来看一下 reverseWords
。他不过是一个普通的函数,假如接受了个字串 "hey there man"
,他会先呼叫 words
来产生一个字的串列 ["hey", "there", "man"]
。然后用 reverse
来 map 整个串列,得到 ["yeh", "ereht", "nam"]
,接着用 unwords
来得到最终的结果 "yeh ereht nam"
。这些用函数合成来简洁的表达。如果没有用函数合成,那就会写成丑丑的样子 reverseWords st = unwords (map reverse (words st))
那 main
又是怎么一回事呢?首先,我们用 getLine
从终端读取了一行,并把这行输入取名叫 line
。然后接着一个条件式 expression。记住,在 Haskell 中 if 永远要伴随一个 else,这样每个 expression 才会有值。当 if 的条件是 true (也就是输入了一个空白行),我们便执行一个 I/O action,如果 if 的条件是 false,那 else 底下的 I/O action 被执行。这也就是说当 if 在一个 I/O do block 中的时候,长的样子是 if condition then I/O action else I/O action
。
我们首先来看一下在 else 中发生了什么事。由于我们在 else 中只能有一个 I/O action,所以我们用 do 来将两个 I/O actions 绑成一个,你可以写成这样:
else (do
putStrLn $ reverseWords line
main)
这样可以明显看到整个 do block 可以看作一个 I/O action,只是比较丑。但总之,在 do block 里面,我们依序呼叫了 getLine
以及 reverseWords
,在那之后,我们递回呼叫了 main
。由于 main 也是一个 I/O action,所以这不会造成任何问题。呼叫 main
也就代表我们回到程式的起点。
那假如 null line
的结果是 true 呢?也就是说 then 的区块被执行。我们看一下区块里面有 then return ()
。如果你是从 C、Java 或 Python 过来的,你可能会认为 return
不过是作一样的事情便跳过这一段。但很重要的: return
在 Hakell 里面的意义跟其他语言的 return
完全不同!他们有相同的样貌,造成了许多人搞错,但确实他们是不一样的。在命令式语言中,return
通常结束 method 或 subroutine 的执行,并且回传某个值给呼叫者。在 Haskell 中,他的意义则是利用某个 pure value 造出 I/O action。用之前盒子的比喻来说,就是将一个 value 装进箱子里面。产生出的 I/O action 并没有作任何事,只不过将 value 包起来而已。所以在 I/O 的情况下来说,return "haha"
的型态是 IO String
。将 pure value 包成 I/O action 有什么实质意义呢?为什么要弄成 IO
包起来的值?这是因为我们一定要在 else 中摆上某些 I/O action,所以我们才用 return ()
做了一个没作什么事情的 I/O action。
在 I/O do block 中放一个 return
并不会结束执行。像下面这个程式会执行到底。
main = do
return ()
return "HAHAHA"
line <- getLine
return "BLAH BLAH BLAH"
return 4
putStrLn line
所有在程式中的 return
都是将 value 包成 I/O actions,而且由于我们没有将他们绑定名称,所以这些结果都被忽略。我们能用 <-
与 return
来达到绑定名称的目的。
main = do
a <- return "hell"
b <- return "yeah!"
putStrLn $ a ++ " " ++ b
可以看到 return
与 <-
作用相反。return
把 value 装进盒子中,而 <-
将 value 从盒子拿出来,并绑定一个名称。不过这么做是有些多余,因为你可以用 let bindings 来绑定
main = do
let a = "hell"
b = "yeah"
putStrLn $ a ++ " " ++ b
在 I/O do block 中需要 return
的原因大致上有两个:一个是我们需要一个什么事都不做的 I/O action,或是我们不希望这个 do block 形成的 I/O action 的结果值是这个 block 中的最后一个 I/O action,我们希望有一个不同的结果值,所以我们用 return
来作一个 I/O action 包了我们想要的结果放在 do block 的最后。
在我们接下去讲档案之前,让我们来看看有哪些实用的函数可以处理 I/O。
putStr
跟 putStrLn
几乎一模一样,都是接受一个字串当作参数,并回传一个 I/O action 打印出字串到终端上,只差在 putStrLn
会换行而 putStr
不会罢了。
main = do putStr "Hey, "
putStr "I'm "
putStrLn "Andy!"
$ runhaskell putstr_test.hs
Hey, I'm Andy!
他的 type signature 是 putStr :: String -> IO ()
,所以是一个包在 I/O action 中的 unit。也就是空值,没有办法绑定他。
putChar
接受一个字元,并回传一个 I/O action 将他打印到终端上。
main = do putChar 't'
putChar 'e'
putChar 'h'
$ runhaskell putchar_test.hs
teh
putStr
实际上就是 putChar
递回定义出来的。putStr
的边界条件是空字串,所以假设我们打印一个空字串,那他只是回传一个什么都不做的 I/O action,像 return ()
。如果打印的不是空字串,那就先用 putChar
打印出字串的第一个字元,然后再用 putStr
打印出字串剩下部份。
putStr :: String -> IO ()
putStr [] = return ()
putStr (x:xs) = do
putChar x
putStr xs
看看我们如何在 I/O 中使用递回,就像我们在 pure code 中所做的一样。先定义一个边界条件,然后再思考剩下如何作。
print
接受任何是 Show
typeclass 的 instance 的型态的值,这代表我们知道如何用字串表示他,呼叫 show
来将值变成字串然后将其输出到终端上。基本上,他就是 putStrLn . show
。首先呼叫 show
然后把结果喂给 putStrLn
,回传一个 I/O action 打印出我们的值。
main = do print True
print 2
print "haha"
print 3.2
print [3,4,3]
$ runhaskell print_test.hs
True
2
"haha"
3.2
[3,4,3]
就像你看到的,这是个很方便的函数。还记得我们提到 I/O actions 只有在 main
中才会被执行以及在 GHCI 中运算的事情吗?当我们用键盘打了些值,像 3
或 [1,2,3]
并按下 Enter,GHCI 实际上就是用了 print
来将这些值输出到终端。
ghci> 3
3
ghci> print 3
3
ghci> map (++"!") ["hey","ho","woo"]
["hey!","ho!","woo!"]
ghci> print (map (++"!") ["hey", "ho", "woo"])
["hey!","ho!","woo!"]
当我们需要打印出字串,我们会用 putStrLn
,因为我们不想要周围有引号,但对于输出值来说,print
才是最常用的。
getChar
是一个从输入读进一个字元的 I/O action,因此他的 type signature 是 getChar :: IO Char
,代表一个 I/O action 的结果是 Char
。注意由于缓冲区的关系,只有当 Enter 被按下的时候才会触发读取字元的行为。
main = do
c <- getChar
if c /= ' '
then do
putChar c
main
else return ()
这程式看起来像是读取一个字元并检查他是否为一个空白。如果是的话便停止,如果不是的话便打印到终端上并重复之前的行为。在某种程度上来说也不能说错,只是结果不如你预期而已。来看看结果吧。
$ runhaskell getchar_test.hs
hello sir
hello
上面的第二行是输入。我们输入了 hello sir
并按下了 Enter。由于缓冲区的关系,程式是在我们按了 Enter 后才执行而不是在某个输入字元的时候。一旦我们按下了 Enter,那他就把我们直到目前输入的一次做完。
when
这函数可以在 Control.Monad
中找到他 (你必须 import Contorl.Monad
才能使用他)。他在一个 do block 中看起来就像一个控制流程的 statement,但实际上他的确是一个普通的函数。他接受一个 boolean 值跟一个 I/O action。如果 boolean 值是 True
,便回传我们传给他的 I/O action。如果 boolean 值是 False
,便回传 return ()
,即什么都不做的 I/O action。我们接下来用 when
来改写我们之前的程式。
import Control.Monad
main = do
c <- getChar
when (c /= ' ') $ do
putChar c
main
就像你看到的,他可以将 if something then do some I/O action else return ()
这样的模式封装起来。
sequence
接受一串 I/O action,并回传一个会依序执行他们的 I/O action。运算的结果是包在一个 I/O action 的一连串 I/O action 的运算结果。他的 type signature 是 sequence :: [IO a] -> IO [a]
main = do
a <- getLine
b <- getLine
c <- getLine
print [a,b,c]
其实可以写成
main = do
rs <- sequence [getLine, getLine, getLine]
print rs
所以 sequence [getLine, getLine, getLine]
作成了一个执行 getLine
三次的 I/O action。如果我们对他绑定一个名字,结果便是这串结果的串列。也就是说,三个使用者输入的东西组成的串列。
一个常见的使用方式是我们将 print
或 putStrLn
之类的函数 map 到串列上。map print [1,2,3,4]
这个动作并不会产生一个 I/O action,而是一串 I/O action,就像是 [print 1, print 2, print 3, print 4]
。如果我们将一串 I/O action 变成一个 I/O action,我们必须用 sequence
ghci> sequence (map print [1,2,3,4,5])
1
2
3
4
5
[(),(),(),(),()]
那 [(),(),(),(),()]
是怎么回事?当我们在 GHCI 中运算 I/O action,他会被执行并把结果打印出来,唯一例外是结果是 ()
的时候不会被打印出。这也是为什么 putStrLn "hehe"
在 GHCI 中只会打印出 hehe
(因为 putStrLn "hehe"
的结果是 ()
)。但当我们使用 getLine
时,由于 getLine
的型态是 IO String
,所以结果会被打印出来。
由于对一个串列 map 一个回传 I/O action 的函数,然后再 sequence 他这个动作太常用了。所以有一些函数在函式库中 mapM
跟 mapM_
。mapM
接受一个函数跟一个串列,将对串列用函数 map 然后 sequence 结果。mapM_
也作同样的事,只是他把运算的结果丢掉而已。在我们不关心 I/O action 结果的情况下,mapM_
是最常被使用的。
ghci> mapM print [1,2,3]
1
2
3
[(),(),()]
ghci> mapM_ print [1,2,3]
1
2
3
forever
接受一个 I/O action 并回传一个永远作同一件事的 I/O action。你可以在 Control.Monad
中找到他。下面的程式会不断地要使用者输入些东西,并把输入的东西转成大写输出到萤幕上。
import Control.Monad
import Data.Char
main = forever $ do
putStr "Give me some input: "
l <- getLine
putStrLn $ map toUpper l
在 Control.Monad
中的 forM
跟 mapM
的作用一样,只是参数的顺序相反而已。第一个参数是串列,而第二个则是函数。这有什么用?在一些有趣的情况下还是有用的:
import Control.Monad
main = do
colors <- forM [1,2,3,4] (\a -> do
putStrLn $ "Which color do you associate with the number " ++ show a ++ "?"
color <- getLine
return color)
putStrLn "The colors that you associate with 1, 2, 3 and 4 are: "
mapM putStrLn colors
(\a -> do ...)
是接受一个数字并回传一个 I/O action 的函数。我们必须用括号括住他,不然 lambda 会贪心 match 的策略会把最后两个 I/O action 也算进去。注意我们在 do block 里面 return color
。我们那么作是让 do block 的结果是我们选的颜色。实际上我们并不需那么作,因为 getLine
已经达到我们的目的。先 color <- getLine
再 return color
只不过是把值取出再包起来,其实是跟 getLine
效果相当。forM
产生一个 I/O action,我们把结果绑定到 colors
这名称。colors
是一个普通包含字串的串列。最后,我们用 mapM putStrLn colors
打印出所有颜色。
你可以把 forM
的意思想成将串列中的每个元素作成一个 I/O action。至于每个 I/O action 实际作什么就要看原本的元素是什么。然后,执行这些 I/O action 并将结果绑定到某个名称上。或是直接将结果忽略掉。
$ runhaskell from_test.hs
Which color do you associate with the number 1?
white
Which color do you associate with the number 2?
blue
Which color do you associate with the number 3?
red
Which color do you associate with the number 4?
orange
The colors that you associate with 1, 2, 3 and 4 are:
white
blue
red
orange
其实我们也不是一定要用到 forM
,只是用了 forM
程式会比较容易理解。正常来讲是我们需要在 map 跟 sequence 的时候定义 I/O action 的时候使用 forM
,同样地,我们也可以将最后一行写成 forM colors putStrLn
。
在这一节,我们学会了输入与输出的基础。我们也了解了什么是 I/O action,他们是如何帮助我们达成输入与输出的目的。这边重复一遍,I/O action 跟其他 Haskell 中的 value 没有两样。我们能够把他当参数传给函式,或是函式回传 I/O action。他们特别之处在于当他们是写在 main
里面或 GHCI 里面的时候,他们会被执行,也就是实际输出到你萤幕或输出音效的时候。每个 I/O action 也能包着一个从真实世界拿回来的值。
不要把像是 putStrLn
的函式想成接受字串并输出到萤幕。要想成一个函式接受字串并回传一个 I/O action。当 I/O action 被执行的时候,会漂亮地打印出你想要的东西。
#
档案与字符流
getChar
是一个读取单一字元的 I/O action。getLine
是一个读取一行的 I/O action。这是两个非常直觉的函式,多数程式语言也有类似这两个函式的 statement 或 function。但现在我们来看看 getContents。getContents
是一个从标准输入读取直到 end-of-file 字元的 I/O action。他的型态是 getContents :: IO String
。最酷的是 getContents
是惰性 I/O (Lazy I/O)。当我们写了 foo <- getContents
,他并不会马上读取所有输入,将他们存在 memory 里面。他只有当你真的需要输入资料的时候才会读取。
当我们需要重导一个程式的输出到另一个程式的输入时,getContents
非常有用。假设我们有下面一个文字档:
I'm a lil' teapot
What's with that airplane food, huh?
It's so small, tasteless
还记得我们介绍 forever
时写的小程式吗?会把所有输入的东西转成大写的那一个。为了防止你忘记了,这边再重复一遍。
import Control.Monad
import Data.Char
main = forever $ do
putStr "Give me some input: "
l <- getLine
putStrLn $ map toUpper l
将我们的程式存成 capslocker.hs
然后编译他。然后用 Unix 的 Pipe 将文字档喂给我们的程式。我们使用的是 GNU 的 cat,会将指定的档案输出到萤幕。
$ ghc --make capslocker
[1 of 1] Compiling Main ( capslocker.hs, capslocker.o )
Linking capslocker ...
$ cat haiku.txt
I'm a lil' teapot
What's with that airplane food, huh?
It's so small, tasteless
$ cat haiku.txt | ./capslocker
I'M A LIL' TEAPOT
WHAT'S WITH THAT AIRPLANE FOOD, HUH?
IT'S SO SMALL, TASTELESS
capslocker <stdin>: hGetLine: end of file
就如你看到的,我们是用 |
这符号来将某个程式的输出 piping 到另一个程式的输入。我们做的事相当于 run 我们的 capslocker,然后将 haiku 的内容用键盘打到终端上,最后再按 Ctrl-D 来代表 end-of-file。这就像执行 cat haiku.txt 后大喊,嘿,不要把内容打印到终端上,把内容塞到 capslocker!
我们用 forever
在做的事基本上就是将输入经过转换后变成输出。用 getContents
的话可以让我们的程式更加精炼。
import Data.Char
main = do
contents <- getContents
putStr (map toUpper contents)
我们将 getContents
取回的字串绑定到 contents
。然后用 toUpper
map 到整个字串后打印到终端上。记住字串基本上就是一串惰性的串列 (list),同时 getContents
也是惰性 I/O,他不会一口气读入内容然后将内容存在记忆体中。实际上,他会一行一行读入并输出大写的版本,这是因为输出才是真的需要输入的资料的时候。
$ cat haiku.txt | ./capslocker
I'M A LIL' TEAPOT
WHAT'S WITH THAT AIRPLAN FOOD, HUH?
IT'S SO SMALL, TASTELESS
很好,程式运作正常。假如我们执行 capslocker 然后自己打几行字呢?
$ ./capslocker
hey ho
HEY HO
lets go
LETS GO
按下 Ctrl-D 来离开环境。就像你看到的,程式是一行一行将我们的输入打印出来。当 getContent
的结果被绑定到 contents
的时候,他不是被表示成在记忆体中的一个字串,反而比较像是他有一天会是字串的一个承诺。当我们将 toUpper
map 到 contents
的时候,便也是一个函数被承诺将会被 map 到内容上。最后 putStr
则要求先前的承诺说,给我一行大写的字串吧。实际上还没有任何一行被取出,所以便跟 contents
说,不如从终端那边取出些字串吧。这才是 getContents
真正从终端读入一行并把这一行交给程式的时候。程式便将这一行用 toUpper
处理并交给 putStr
,putStr
则打印出他。之后 putStr
再说:我需要下一行。整个步骤便再重复一次,直到读到 end-of-file 为止。
接着我们来写个程式,读取输入,并只打印出少于十个字元的行。
main = do
contents <- getContents
putStr (shortLinesOnly contents)
shortLinesOnly :: String -> String
shortLinesOnly input =
let allLines = lines input
shortLines = filter (\line -> length line < 10) allLines
result = unlines shortLines
in result
我们把 I/O 部份的程式码弄得很短。由于程式的行为是接某些输入,作些处理然后输出。我们可以把他想成读取输入,呼叫一个函数,然后把函数的结果输出。
shortLinesOnly
的行为是这样:拿到一个字串,像是 "short\nlooooooooooooooong\nshort again"
。这字串有三行,前后两行比较短,中间一行很常。他用 lines
把字串分成 ["short", "looooooooooooooong", "short again"]
,并把结果绑定成 allLines
。然后过滤这些字串,只有少于十个字元的留下,["short", "short again"]
,最后用 unlines
把这些字串用换行接起来,形成 "short\nshort again"
i'm short
so am i
i am a loooooooooong line!!!
yeah i'm long so what hahahaha!!!!!!
short line
loooooooooooooooooooooooooooong
short
$ ghc --make shortlinesonly
[1 of 1] Compiling Main ( shortlinesonly.hs, shortlinesonly.o )
Linking shortlinesonly ...
$ cat shortlines.txt | ./shortlinesonly
i'm short
so am i
short
我们把 shortlines.txt 的内容经由 pipe 送给 shortlinesonly,结果就如你看到,我们只有得到比较短的行。
从输入那一些字串,经由一些转换然后输出这样的模式实在太常用了。常用到甚至建立了一个函数叫 interact。interact
接受一个 String -> String
的函数,并回传一个 I/O action。那个 I/O action 会读取一些输入,呼叫提供的函数,然后把函数的结果打印出来。所以我们的程式可以改写成这样。
main = interact shortLinesOnly
shortLinesOnly :: String -> String
shortLinesOnly input =
let allLines = lines input
shortLines = filter (\line -> length line < 10) allLines
result = unlines shortLines
in result
我们甚至可以再让程式码更短一些,像这样
main = interact $ unlines . filter ((<10) . length) . lines
看吧,我们让程式缩到只剩一行了,很酷吧!
能应用 interact
的情况有几种,像是从输入 pipe 读进一些内容,然后丢出一些结果的程式;或是从使用者获取一行一行的输入,然后丢回根据那一行运算的结果,再拿取另一行。这两者的差别主要是取决于使用者使用他们的方式。
我们再来写另一个程式,它不断地读取一行行并告诉我们那一行字串是不是一个回文字串 (palindrome)。我们当然可以用 getLine
读取一行然后再呼叫 main
作同样的事。不过同样的事情可以用 interact
更简洁地达成。当使用 interact
的时候,想像你是将输入经有某些转换成输出。在这个情况当中,我们要将每一行输入转换成 "palindrome"
或 "not a palindrome"
。所以我们必须写一个函数将 "elephant\nABCBA\nwhatever"
转换成 not a palindrome\npalindrome\nnot a palindrome"
。来动手吧!
respondPalindromes contents = unlines (map (\xs ->
if isPalindrome xs then "palindrome" else "not a palindrome") (lines contents))
where isPalindrome xs = xs == reverse xs
再来将程式改写成 point-free 的形式
respondPalindromes = unlines . map (\xs ->
if isPalindrome xs then "palindrome" else "not a palindrome") . lines
where isPalindrome xs = xs == reverse xs
很直觉吧!首先将 "elephant\nABCBA\nwhatever"
变成 ["elephant", "ABCBA", "whatever"]
然后将一个 lambda 函数 map 它,["not a palindrome", "palindrome", "not a palindrome"]
然后用 unlines
变成一行字串。接着
main = interact respondPalindromes
来测试一下吧。
$ runhaskell palindrome.hs
hehe
not a palindrome
ABCBA
palindrome
cookie
not a palindrome
即使我们的程式是把一大把字串转换成另一个,其实他表现得好像我们是一行一行做的。这是因为 Haskell 是惰性的,程式想要打印出第一行结果时,他必须要先有第一行输入。所以一旦我们给了第一行输入,他便打印出第一行结果。我们用 end-of-line 字元来结束程式。
我们也可以用 pipe 的方式将输入喂给程式。假设我们有这样一个档案。
dogaroo
radar
rotor
madam
将他存为 words.txt
,将他喂给程式后得到的结果
$ cat words.txt | runhaskell palindromes.hs
not a palindrome
palindrome
palindrome
palindrome
再一次地提醒,我们得到的结果跟我们自己一个一个字打进输入的内容是一样的。我们看不到 palindrome.hs
输入的内容是因为内容来自于档案。
你应该大致了解 Lazy I/O 是如何运作,并能善用他的优点。他可以从输入转换成输出的角度方向思考。由于 Lazy I/O,没有输入在被用到之前是真的被读入。
到目前为止,我们的示范都是从终端读取某些东西或是打印出某些东西到终端。但如果我们想要读写档案呢?其实从某个角度来说我们已经作过这件事了。我们可以把读写终端想成读写档案。只是把档案命名成 stdout
跟 stdin
而已。他们分别代表标准输出跟标准输入。我们即将看到的读写档案跟读写终端并没什么不同。
首先来写一个程式,他会开启一个叫 girlfriend.txt 的档案,档案里面有 Avril Lavigne 的畅销名曲 Girlfriend,并将内容打印到终端上。接下来是 girlfriend.txt 的内容。
Hey! Hey! You! You!
I don't like your girlfriend!
No way! No way!
I think you need a new one!
这则是我们的主程式。
import System.IO
main = do
handle <- openFile "girlfriend.txt" ReadMode
contents <- hGetContents handle
putStr contents
hClose handle
执行他后得到的结果。
$ runhaskell girlfriend.hs
Hey! Hey! You! You!
I don't like your girlfriend!
No way! No way!
I think you need a new one!
我们来一行行看一下程式。我们的程式用 do 把好几个 I/O action 绑在一起。在 do block 的第一行,我们注意到有一个新的函数叫 openFile。他的 type signature 是 openFile :: FilePath -> IOMode -> IO Handle
。他说了 openFile
接受一个档案路径跟一个 IOMode
,并回传一个 I/O action,他会打开一个档案并把档案关联到一个 handle。
FilePath
不过是 String
的 type synonym。
type FilePath = String
IOMode
则是一个定义如下的型态
data IOMode = ReadMode | WriteMode | AppendMode | ReadWriteMode
就像我们之前定义的型态,分别代表一个星期的七天。这个型态代表了我们想对打开的档案做什么。很简单吧。留意到我们的型态是 IOMode
而不是 IO Mode
。IO Mode
代表的是一个 I/O action 包含了一个型态为 Mode
的值,但 IOMode
不过是一个阳春的 enumeration。
最后,他回传一个 I/O action 会将指定的档案用指定的模式打开。如果我们将 I/O action 绑定到某个东西,我们会得到一个 Handle
。型态为 Handle
的值代表我们的档案在哪里。有了 handle 我们才知道要从哪个档案读取内容。想读取档案但不将档案绑定到 handle 上这样做是很蠢的。所以,我们将一个 handle 绑定到 handle
。
接着一行,我们看到一个叫 hGetContents 的函数。他接了一个 Handle
,所以他知道要从哪个档案读取内容并回传一个 IO String
。一个包含了档案内容的 I/O action。这函数跟 getContents
差不多。唯一的差别是 getContents
会自动从标准输入读取内容(也就是终端),而 hGetContents
接了一个 file handle,这 file handle 告诉他读取哪个档案。除此之外,他们都是一样的。就像 getContents
,hGetContents
不会把档案一次都拉到记忆体中,而是有必要才会读取。这非常酷,因为我们把 contents
当作是整个档案般用,但他实际上不在记忆体中。就算这是个很大的档案,hGetContents
也不会塞爆你的记忆体,而是只有必要的时候才会读取。
要留意档案的 handle 还有档案的内容两个概念的差异,在我们的程式中他们分别被绑定到 handle
跟 contents
两个名字。handle 是我们拿来区分档案的依据。如果你把整个档案系统想成一本厚厚的书,每个档案分别是其中的一个章节,handle 就像是书签一般标记了你现在正在阅读(或写入)哪一个章节,而内容则是章节本身。
我们使用 putStr contents
打印出内容到标准输出,然后我们用了 hClose。他接受一个 handle 然后回传一个关掉档案的 I/O action。在用了 openFile
之后,你必须自己把档案关掉。
要达到我们目的的另一种方式是使用 withFile,他的 type signature 是 withFile :: FilePath -> IOMode -> (Handle -> IO a) -> IO a
。他接受一个档案路径,一个 IOMode
以及一个函数,这函数则接受一个 handle 跟一个 I/O action。withFile
最后回传一个会打开档案,对档案作某件事然后关掉档案的 I/O action。处理的结果是包在最后的 I/O action 中,这结果跟我们给的函数的回传是相同的。这听起来有些复杂,但其实很简单,特别是我们有 lambda,来看看我们用 withFile
改写前面程式的一个范例:
import System.IO
main = do
withFile "girlfriend.txt" ReadMode (\handle -> do
contents <- hGetContents handle
putStr contents)
正如你看到的,程式跟之前的看起来很像。(\handle -> ... )
是一个接受 handle 并回传 I/O action 的函数,他通常都是用 lambda 来表示。我们需要一个回传 I/O action 的函数的理由而不是一个本身作处理并关掉档案的 I/O action,是因为这样一来那个 I/O action 不会知道他是对哪个档案在做处理。用 withFile
的话,withFile
会打开档案并把 handle 传给我们给他的函数,之后他则拿到一个 I/O action,然后作成一个我们描述的 I/O action,最后关上档案。例如我们可以这样自己作一个 withFile
:
withFile' :: FilePath -> IOMode -> (Handle -> IO a) -> IO a
withFile' path mode f = do
handle <- openFile path mode
result <- f handle
hClose handle
return result
我们知道要回传的是一个 I/O action,所以我们先放一个 do。首先我们打开档案,得到一个 handle。然后我们 apply handle
到我们的函数,并得到一个做事的 I/O action。我们绑定那个 I/O action 到 result
这个名字,关上 handle 并 return result
。return
的作用把从 f
得到的结果包在 I/O action 中,这样一来 I/O action 中就包含了 f handle
得到的结果。如果 f handle
回传一个从标准输入读去数行并写到档案然后回传读入的行数的 I/O action,在 withFile'
的情形中,最后的 I/O action 就会包含读入的行数。
就像 hGetContents
对应 getContents
一样,只不过是针对某个档案。我们也有 hGetLine、hPutStr、hPutStrLn、hGetChar 等等。他们分别是少了 h 的那些函数的对应。只不过他们要多拿一个 handle 当参数,并且是针对特定档案而不是标准输出或标准输入。像是 putStrLn
是一个接受一个字串并回传一个打印出加了换行字元的字串的 I/O action 的函数。hPutStrLn
接受一个 handle 跟一个字串,回传一个打印出加了换行字元的字串到档案的 I/O action。以此类推,hGetLine
接受一个 handle 然后回传一个从档案读取一行的 I/O action。
读取档案并对他们的字串内容作些处理实在太常见了,常见到我们有三个函数来更进一步简化我们的工作。
readFile 的 type signature 是 readFile :: FilePath -> IO String
。记住,FilePath
不过是 String
的一个别名。readFile
接受一个档案路径,回传一个惰性读取我们档案的 I/O action。然后将档案的内容绑定到某个字串。他比起先 openFile
,绑定 handle,然后 hGetContents
要好用多了。这边是一个用 readFile
改写之前例子的范例:
import System.IO
main = do
contents <- readFile "girlfriend.txt"
putStr contents
由于我们拿不到 handle,所以我们也无法关掉他。这件事 Haskell 的 readFile
在背后帮我们做了。
writeFile 的型态是 writefile :: FilePath -> String -> IO ()
。他接受一个档案路径,以及一个要写到档案中的字串,并回传一个写入动作的 I/O action。如果这个档案已经存在了,他会先把档案内容都砍了再写入。下面示范了如何把 girlfriend.txt 的内容转成大写然后写入到 girlfriendcaps.txt 中
import System.IO
import Data.Char
main = do
contents <- readFile "girlfriend.txt"
writeFile "girlfriendcaps.txt" (map toUpper contents)
$ runhaskell girlfriendtocaps.hs
$ cat girlfriendcaps.txt
HEY! HEY! YOU! YOU!
I DON'T LIKE YOUR GIRLFRIEND!
NO WAY! NO WAY!
I THINK YOU NEED A NEW ONE!
appendFile 的型态很像 writeFile
,只是 appendFile
并不会在档案存在时把档案内容砍掉而是接在后面。
假设我们有一个档案叫 todo.txt``,里面每一行是一件要做的事情。现在我们写一个程式,从标准输入接受一行将他加到我们的 to-do list 中。
import System.IO
main = do
todoItem <- getLine
appendFile "todo.txt" (todoItem ++ "\n")
$ runhaskell appendtodo.hs
Iron the dishes
$ runhaskell appendtodo.hs
Dust the dog
$ runhaskell appendtodo.hs
Take salad out of the oven
$ cat todo.txt
Iron the dishes
Dust the dog
Take salad out of the oven
由于 getLine
回传的值不会有换行字元,我们需要在每一行最后加上 "\n"
。
还有一件事,我们提到 contents <- hGetContents handle
是惰性 I/O,不会将档案一次都读到记忆体中。 所以像这样写的话:
main = do
withFile "something.txt" ReadMode (\handle -> do
contents <- hGetContents handle
putStr contents)
实际上像是用一个 pipe 把档案弄到标准输出。正如你可以把 list 想成 stream 一样,你也可以把档案想成 stream。他会每次读一行然后打印到终端上。你也许会问这个 pipe 究竟一次可以塞多少东西,读去硬碟的频率究竟是多少?对于文字档而言,预设的 buffer 通常是 line-buffering。这代表一次被读进来的大小是一行。这也是为什么在这个 case 我们是一行一行处理。对于 binary file 而言,预设的 buffer 是 block-buffering。这代表我们是一个 chunk 一个 chunk 去读得。而一个 chunk 的大小是根据作业系统不同而不同。
你能用 hSetBuffering
来控制 buffer 的行为。他接受一个 handle 跟一个 BufferMode
,回传一个会设定 buffer 行为的 I/O action。BufferMode
是一个 enumeration 型态,他可能的值有:NoBuffering
, LineBuffering
或 BlockBuffering (Maybe Int)
。其中 Maybe Int
是表示一个 chunck 有几个 byte。如果他的值是 Nothing
,则作业系统会帮你决定 chunk 的大小。NoBuffering
代表我们一次读一个 character。一般来说 NoBuffering
的表现很差,因为他存取硬碟的频率很高。
接下来是我们把之前的范例改写成用 2048 bytes 的 chunk 读取,而不是一行一行读。
main = do
withFile "something.txt" ReadMode (\handle -> do
hSetBuffering handle $ BlockBuffering (Just 2048)
contents <- hGetContents handle
putStr contents)
用更大的 chunk 来读取对于减少存取硬碟的次数是有帮助的,特别是我们的档案其实是透过网路来存取。
我们也可以使用 hFlush,他接受一个 handle 并回传一个会 flush buffer 到档案的 I/O action。当我们使用 line-buffering 的时候,buffer 在每一行都会被 flush 到档案。当我们使用 block-buffering 的时候,是在我们读每一个 chunk 作 flush 的动作。flush 也会发生在关闭 handle 的时候。这代表当我们碰到换行字元的时候,读或写的动作都会停止并回报手边的资料。但我们能使用 hFlush
来强迫回报所有已经在 buffer 中的资料。经过 flushing 之后,资料也就能被其他程式看见。
把 block-buffering 的读取想成这样:你的马桶会在水箱有一加仑的水的时候自动冲水。所以你不断灌水进去直到一加仑,马桶就会自动冲水,在水里面的资料也就会被看到。但你也可以手动地按下冲水钮来冲水。他会让现有的水被冲走。冲水这个动作就是 hFlush
这个名字的含意。
我们已经写了一个将 item 加进 to-do list 里面的程式,现在我们想加进移除 item 的功能。我先把程式码贴上然后讲解他。我们会使用一些新面孔像是 System.Directory
以及 System.IO
里面的函数。
来看一下我们包含移除功能的程式:
import System.IO
import System.Directory
import Data.List
main = do
handle <- openFile "todo.txt" ReadMode
(tempName, tempHandle) <- openTempFile "." "temp"
contents <- hGetContents handle
let todoTasks = lines contents
numberedTasks = zipWith (\n line -> show n ++ " - " ++ line) [0..] todoTasks
putStrLn "These are your TO-DO items:"
putStr $ unlines numberedTasks
putStrLn "Which one do you want to delete?"
numberString <- getLine
let number = read numberString
newTodoItems = delete (todoTasks !! number) todoTasks
hPutStr tempHandle $ unlines newTodoItems
hClose handle
hClose tempHandle
removeFile "todo.txt"
renameFile tempName "todo.txt"
一开始,我们用 read mode 打开 todo.txt,并把他绑定到 handle
。
接着,我们使用了一个之前没用过在 System.IO
中的函数 openTempFile。他的名字浅显易懂。他接受一个暂存的资料夹跟一个样板档案名,然后打开一个暂存档。我们使用 "."
当作我们的暂存资料夹,因为 .
在几乎任何作业系统中都代表了现在所在的资料夹。我们使用 "temp"
当作我们暂存档的样板名,他代表暂存档的名字会是 temp 接上某串随机字串。他回传一个创建暂存档的 I/O action,然后那个 I/O action 的结果是一个 pair:暂存档的名字跟一个 handle。我们当然可以随便开启一个 todo2.txt 这种名字的档案。但使用 openTempFile
会是比较好的作法,这样你不会不小心覆写任何档案。
我们不用 getCurrentDirectory
的来拿到现在所在资料夹而用 "."
的原因是 .
在 unix-like 系统跟 Windows 中都表示现在的资料夹。
然后,我们绑定 todo.txt 的内容成 contents
。把字串断成一串字串,每个字串代表一行。todoTasks
就变成 ["Iron the dishes", "Dust the dog", "Take salad out of the oven"]
。我们用一个会把 3 跟 "hey"
变成 "3 - hey"
的函数,然后从 0 开始把这个串列 zip 起来。所以 numberedTasks
就是 ["0 - Iron the dishes", "1 - Dust the dog" ...
。我们用 unlines
把这个串列变成一行,然后打印到终端上。注意我们也有另一种作法,就是用 mapM putStrLn numberedTasks
。
我们问使用者他们想要删除哪一个并且等着他们输入一个数字。假设他们想要删除 1 号,那代表 Dust the dog
,所以他们输入 1
。于是 numberString
就代表 "1"
。由于我们想要一个数字,而不是一个字串,所以我们用对 1
使用 read
,并且绑定到 number
。
还记得在 Data.List
中的 delete
跟 !!
吗?!!
回传某个 index 的元素,而 delete
删除在串列中第一个发现的元素,然后回传一个新的没有那个元素的串列。(todoTasks !! number)
(number 代表 1
) 回传 "Dust the dog"
。我们把 todoTasks
去掉第一个 "Dust the dog"
后的串列绑定到 newTodoItems
,然后用 unlines
变成一行然后写到我们所打开的暂存档。旧有的档案并没有变动,而暂存档包含砍掉那一行后的所有内容。
在我们关掉原始档跟暂存档之后我们用 removeFile 来移除原本的档案。他接受一个档案路径并且删除档案。删除旧得 todo.txt 之后,我们用 renameFile 来将暂存档重新命名成 todo.txt。特别留意 removeFile
跟 renameFile
(两个都在 System.Directory
中)接受的是档案路径,而不是 handle。
这就是我们要的,实际上我们可以用更少行写出同样的程式,但我们很小心地避免覆写任何档案,并询问作业系统我们可以把暂存档摆在哪?让我们来执行看看。
$ runhaskell deletetodo.hs
These are your TO-DO items:
0 - Iron the dishes
1 - Dust the dog
2 - Take salad out of the oven
Which one do you want to delete?
1
$ cat todo.txt
Iron the dishes
Take salad out of the oven
$ runhaskell deletetodo.hs
These are your TO-DO items:
0 - Iron the dishes
1 - Take salad out of the oven
Which one do you want to delete?
0
$ cat todo.txt
Take salad out of the oven
#
命令列引数
如果你想要写一个在终端里运行的程式,处理命令列引数是不可或缺的。幸运的是,利用 Haskell 的 Standard Libary 能让我们有效地处理命令列引数。
在之前的章节中,我们写了一个能将 to-do item 加进或移除 to-do list 的一个程式。但我们的写法有两个问题。第一个是我们把放 to-do list 的档案名称给写死了。我们擅自决定使用者不会有很多个 to-do lists,就把档案命名为 todo.txt。
一种解决的方法是每次都询问使用者他们想将他们的 to-do list 放进哪个档案。我们在使用者要删除的时候也采用这种方式。这是一种可以运作的方式,但不太能被接受,因为他需要使用者运行程式,等待程式询问才能回答。这被称为互动式的程式,但讨厌的地方在当你想要自动化执行程式的时候,好比说写成 script,这会让你的 script 写起来比较困难。
这也是为什么有时候让使用者在执行的时候就告诉程式他们要什么会比较好,而不是让程式去问使用者要什么。比较好的方式是让使用者透过命令列引数告诉程式他们想要什么。
在 System.Environment
模组当中有两个很酷的 I/O actions,一个是 getArgs,他的 type 是 getArgs :: IO [String]
,他是一个拿取命令列引数的 I/O action,并把结果放在包含的一个串列中。getProgName 的型态是 getProgName :: IO String
,他则是一个 I/O action 包含了程式的名称。
我们来看一个展现他们功能的程式。
import System.Environment
import Data.List
main = do
args <- getArgs
progName <- getProgName
putStrLn "The arguments are:"
mapM putStrLn args
putStrLn "The program name is:"
putStrLn progName
我们将 getArgs
跟 progName
分别绑定到 args
跟 progName
。我们打印出 The arguments are:
以及在 args
中的每个引数。最后,我们打印出程式的名字。我们把程式编译成 arg-test
。
$ ./arg-test first second w00t "multi word arg"
The arguments are:
first
second
w00t
multi word arg
The program name is:
arg-test
知道了这些函数现在你能写几个很酷的命令列程式。在之前的章节,我们写了一个程式来加入待作事项,也写了另一个程式删除事项。现在我们要把两个程式合起来,他会根据命令列引数来决定该做的事情。我们也会让程式可以处理不同的档案,而不是只有 todo.txt
我们叫这程式 todo,他会作三件事:
# 检视待作事项
# 加入待作事项
# 删除待作事项
我们暂不考虑不合法的输入这件事。
我们的程式要像这样运作:假如我们要加入 Find the magic sword of power
,则我们会打 todo add todo.txt "Find the magic sword of power"
。要检视事项我们则会打 todo view todo.txt
,如果要移除事项二则会打 todo remove todo.txt 2
我们先作一个分发的 association list。他会把命令列引数当作 key,而对应的处理函数当作 value。这些函数的型态都是 [String] -> IO ()
。他们会接受命令列引数的串列并回传对应的检视,加入以及删除的 I/O action。
import System.Environment
import System.Directory
import System.IO
import Data.List
dispatch :: [(String, [String] -> IO ())]
dispatch = [ ("add", add)
, ("view", view)
, ("remove", remove)
]
我们定义了 main
,add
,view
跟 remove
,就从 main
开始讲吧:
main = do
(command:args) <- getArgs
let (Just action) = lookup command dispatch
action args
首先,我们取出引数并把他们绑定到 (command:args)
。如果你还记得 pattern matching,这么做会把第一个引数绑定到 command
,把其他的绑定到 args
。如果我们像这样执行程式 todo add todo.txt "Spank the monkey"
,command
会变成 "add"
,而 args
会变成 ["todo.txt", "Spank the monkey"]
。
在下一行,我们在一个分派的串列中寻到我们的指令是哪个。由于 "add"
指向 add
,我们的结果便是 Just add
。我们再度使用了 pattern matching 来把我们的函数从 Maybe
中取出。但如果我们想要的指令不在分派的串列中呢?那样 lookup 就会回传 Nothing
,但我们这边并不特别处理失败的情况,所以 pattern matching 会失败然后我们的程式就会当掉。
最后,我们用剩下的引数呼叫 action
这个函数。他会还传一个加入 item,显示所有 items 或者删除 item 的 I/O action。由于这个 I/O action 是在 main
的 do block 中,他最后会被执行。如果我们的 action
函数是 add
,他就会被喂 args
然后回传一个加入 Spank the monkey
到 todo.txt 中的 I/O action。
我们剩下要做的就是实作 add
,view
跟 remove
,我们从 add
开始:
add :: [String] -> IO ()
add [fileName, todoItem] = appendFile fileName (todoItem ++ "\n")
如果我们这样执行程式 todo add todo.txt "Spank the monkey"
,则 "add"
会被绑定到 command
,而 ["todo.txt", "Spank the monkey"]
会被带到从 dispatch list 中拿到的函数。
由于我们不处理不合法的输入,我们只针对这两项作 pattern matching,然后回传一个附加一行到档案末尾的 I/O action。
接着,我们来实作检视串列。如果我们想要检视所有 items,我们会 todo view todo.txt
。所以 command
会是 "view"
,而 args
会是 ["todo.txt"]
。
view :: [String] -> IO ()
view [fileName] = do
contents <- readFile fileName
let todoTasks = lines contents
numberedTasks = zipWith (\n line -> show n ++ " - " ++ line) [0..] todoTasks
putStr $ unlines numberedTasks
这跟我们之前删除档案的程式差不多,只是我们是在显示内容而已,
最后,我们要来实作 remove
。他基本上跟之前写的只有删除功能的程式很像,所以如果你不知道删除是怎么做的,可以去看之前的解释。主要的差别是我们不写死 todo.txt,而是从参数取得。我们也不会提示使用者要删除哪一号的 item,而是从参数取得。
remove :: [String] -> IO ()
remove [fileName, numberString] = do
handle <- openFile fileName ReadMode
(tempName, tempHandle) <- openTempFile "." "temp"
contents <- hGetContents handle
let number = read numberString
todoTasks = lines contents
newTodoItems = delete (todoTasks !! number) todoTasks
hPutStr tempHandle $ unlines newTodoItems
hClose handle
hClose tempHandle
removeFile fileName
renameFile tempName fileName
我们打开 fileName
的档案以及一个暂存。删除使用者要我们删的那一行后,把档案内容写到暂存档。砍掉原本的档案然后把暂存档重新命名成 fileName
。
来看看完整的程式。
import System.Environment
import System.Directory
import System.IO
import Data.List
dispatch :: [(String, [String] -> IO ())]
dispatch = [ ("add", add)
, ("view", view)
, ("remove", remove)
]
main = do
(command:args) <- getArgs
let (Just action) = lookup command dispatch
action args
add :: [String] -> IO ()
add [fileName, todoItem] = appendFile fileName (todoItem ++ "\n")
view :: [String] -> IO ()
view [fileName] = do
contents <- readFile fileName
let todoTasks = lines contents
numberedTasks = zipWith (\n line -> show n ++ " - " ++ line) [0..] todoTasks
putStr $ unlines numberedTasks
remove :: [String] -> IO ()
remove [fileName, numberString] = do
handle <- openFile fileName ReadMode
(tempName, tempHandle) <- openTempFile "." "temp"
contents <- hGetContents handle
let number = read numberString
todoTasks = lines contents
newTodoItems = delete (todoTasks !! number) todoTasks
hPutStr tempHandle $ unlines newTodoItems
hClose handle
hClose tempHandle
removeFile fileName
renameFile tempName fileName
总结我们的程式:我们做了一个 dispatch association,将指令对应到一些会接受命令列引数并回传 I/O action 的函数。我们知道使用者下了什么命令,并根据那个命令从 dispatch list 取出对影的函数。我们用剩下的命令列引数呼叫哪些函数而得到一些作相对应事情的 I/O action。然后便执行那些 I/O action。
在其他程式语言,我们可能会用一个大的 switch case 来实作,但使用高阶函数让我们可以要 dispatch list 给我们要的函数,并要那些函数给我们适当的 I/O action。
让我们看看执行结果。
$ ./todo view todo.txt
0 - Iron the dishes
1 - Dust the dog
2 - Take salad out of the oven
$ ./todo add todo.txt "Pick up children from drycleaners"
$ ./todo view todo.txt
0 - Iron the dishes
1 - Dust the dog
2 - Take salad out of the oven
3 - Pick up children from drycleaners
$ ./todo remove todo.txt 2
$ ./todo view todo.txt
0 - Iron the dishes
1 - Dust the dog
2 - Pick up children from drycleaners
要再另外加新的选项也是很容易。只要在 dispatch list 加入新的会作你要的事情函数。你可以试试实作一个 bump
函数,接受一个档案跟一个 task number,他会回传一个把那个 task 搬到 to-do list 顶端的 I/O action。
对于不合法的输入你也可以让程式结束地漂亮一点。(例如使用者输入了 todo UP YOURS HAHAHAHA
)可以作一个回报错误的 I/O action (例如 ``errorExist :: IO ())检查有没有不合法的输入,如果有便执行这个回报错误的 I/O action。我们之后会谈另一个可能,就是用 exception。
#
乱数
在许多情况下,你写程式会需要些随机的资料。或许你在制作一个游戏,在游戏中你需要掷骰子。或是你需要测试程式的测试资料。精准一点地说,我们需要 pseudo-random 的资料,我们知道真正的随机资料好比是一只猴子拿着起司跟奶油骑在单轮车上,任何事情都会发生。在这个章节,我们要看看如何让 Haskell 产生些 pseudo-random 的资料。
在大多数其他的程式语言中,会给你一些函数能让你拿到些随机乱数。每呼叫一次他就会拿到一个不同的数字。那在 Haskell 中是如何?要记住 Haskell 是一个纯粹函数式语言。代表任何东西都具有 referential transparency。那代表你喂给一个函数相同的参数,不管怎么呼叫都是回传相同的结果。这很新奇的原因是因为他让我们理解程式的方式不同,而且可以让我们延迟计算,直到我们真正需要他。如果我呼叫一个函数,我可以确定他不会乱来。我真正在乎的是他的结果。然而,这会造成在乱数的情况有点复杂。如果我有一个函数像这样:
randomNumber :: (Num a) => a
randomNumber = 4
由于他永远回传 4
,所以对于乱数的情形而言是没什么意义。就算 4 这个结果是掷骰子来的也没有意义。
其他的程式语言是怎么产生乱数的呢?他们可能随便拿取一些电脑的资讯,像是现在的时间,你怎么移动你的滑鼠,以及周围的声音。根据这些算出一个数值让他看起来好像随机的。那些要素算出来的结果可能在每个时间都不同,所以你会拿到不同的随机数字。
所以说在 Haskell 中,假如我们能作一个函数,他会接受一个具随机性的参数,然后根据那些资讯还传一个数值。
在 System.Random
模组中。他包含所有满足我们需求的函数。让我们先来看其中一个,就是 random。他的型态是 random :: (RandomGen g, Random a) => g -> (a, g)
。哇,出现了新的 typeclass。RandomGen typeclass 是指那些可以当作乱源的型态。而Random typeclass 则是可以装乱数的型态。一个布林值可以是随机值,不是 True
就是 False
。一个整数可以是随机的好多不同值。那你会问,函数可以是一个随机值吗?我不这么认为。如果我们试着翻译 random
的型态宣告,大概会是这样:他接受一个 random generator (乱源所在),然后回传一个随机值以及一个新的 random generator。为什么他要回传一个新的 random generator 呢?就是下面我们要讲的。
要使用 random
函数, 我们必须要了解 random generator。 在 System.Random
中有一个很酷的型态,叫做 StdGen, 他是 RandomGen
的一个 instance。 我们可以自己手动作一个 StdGen
也可以告诉系统给我们一个现成的。
要自己做一个 random generator,要使用 mkStdGen 这个函数。他的型态是 mkStdGen :: Int -> StdGen
。他接受一个整数,然后根据这个整数会给一个 random generator。让我们来试一下 random
以及 mkStdGen
,用他们产生一个乱数吧。
ghci> random (mkStdGen 100)
<interactive>:1:0:
Ambiguous type variable `a' in the constraint:
`Random a' arising from a use of `random' at <interactive>:1:0-20
Probable fix: add a type signature that fixes these type variable(s) `
这是什么?由于 random
函数会回传 Random
typeclass 中任何一种型态,所以我们必须告诉 Haskell 我们是要哪一种型态。不要忘了我们是回传 random value 跟 random generator 的一个 pair
ghci> random (mkStdGen 100) :: (Int, StdGen)
(-1352021624,651872571 1655838864)
我们终于有了一个看起来像乱数的数字。tuple 的第一个部份是我们的乱数,而第二个部份是一个新的 random generator 的文字表示。如果我们用相同的 random generator 再呼叫 random
一遍呢?
ghci> random (mkStdGen 100) :: (Int, StdGen)
(-1352021624,651872571 1655838864)
不易外地我们得到相同的结果。所以我们试试用不同的 random generator 作为我们的参数。
ghci> random (mkStdGen 949494) :: (Int, StdGen)
(539963926,466647808 1655838864)
很好,我们拿到了不同的数字。我们可以用不同的型态标志来拿到不同型态的乱数
ghci> random (mkStdGen 949488) :: (Float, StdGen)
(0.8938442,1597344447 1655838864)
ghci> random (mkStdGen 949488) :: (Bool, StdGen)
(False,1485632275 40692)
ghci> random (mkStdGen 949488) :: (Integer, StdGen)
(1691547873,1597344447 1655838864)
让我们写一个模拟丢三次铜板的函数。假如 random
不同时回传一个乱数以及一个新的 random generator,我们就必须让这函数接受三个 random generators 让他们每个回传一个掷铜板的结果。但那样听起来怪怪的,加入一个 generator 可以产生一个型态是 Int
的乱数,他应该可以产生掷三次铜板的结果(总共才八个组合)。这就是 random
为什么要回传一个新的 generator 的关键了。
我们将一个铜板表示成 Bool
。True
代表反面,False
代表正面。
threeCoins :: StdGen -> (Bool, Bool, Bool)
threeCoins gen =
let (firstCoin, newGen) = random gen
(secondCoin, newGen') = random newGen
(thirdCoin, newGen') = random newGen'
in (firstCoin, secondCoin, thirdCoin) )
我们用我们拿来当参数的 generator 呼叫 random
并得到一个掷铜板的结果跟一个新的 generator。然后我们再用新的 generator 呼叫他一遍,来得到第二个掷铜板的结果。对于第三个掷铜板的结果也是如法炮制。如果我们一直都用同样的 generator,那所有的结果都会是相同的值。也就是不是 (False, False, False)
就是 (True, True, True)
。
ghci> threeCoins (mkStdGen 21)
(True,True,True)
ghci> threeCoins (mkStdGen 22)
(True,False,True)
ghci> threeCoins (mkStdGen 943)
(True,False,True)
ghci> threeCoins (mkStdGen 944)
(True,True,True)
留意我们不需要写 random gen :: (Bool, StdGen)
。那是因为我们已经在函数的型态宣告那边就表明我们要的是布林。而 Haskell 可以推敲出我们要的是布林值。
假如我们要的是掷四次?甚至五次呢?有一个函数叫 randoms,他接受一个 generator 并回传一个无穷序列。
ghci> take 5 $ randoms (mkStdGen 11) :: [Int]
[-1807975507,545074951,-1015194702,-1622477312,-502893664]
ghci> take 5 $ randoms (mkStdGen 11) :: [Bool]
[True,True,True,True,False]
ghci> take 5 $ randoms (mkStdGen 11) :: [Float]
[7.904789e-2,0.62691015,0.26363158,0.12223756,0.38291094]
为什么 randoms
不另外多回传一个新的 generator 呢?我们可以这样地实作 randoms
randoms' :: (RandomGen g, Random a) => g -> [a]
randoms' gen = let (value, newGen) = random gen in value:randoms' newGen
一个递回的定义。我们由现在的 generator 拿到一个乱数跟一个新的 generator,然后制作一个 list,list 的第一个值是那个乱数,而 list 的其余部份是根据新的 generator 产生出的其余乱数们。由于我们可能产生出无限的乱数,所以不可能回传一个新的 generator。
我们可以写一个函数,他会回传有限个乱数跟一个新的 generator
finiteRandoms :: (RandomGen g, Random a, Num n) => n -> g -> ([a], g)
finiteRandoms 0 gen = ([], gen)
finiteRandoms n gen =
let (value, newGen) = random gen
(restOfList, finalGen) = finiteRandoms (n-1) newGen
in (value:restOfList, finalGen)
又是一个递回的定义。我们说如果我们要 0 个乱数,我们便回传一个空的 list 跟原本给我们的 generator。对于其他数量的乱数,我们先拿一个乱数跟一个新的 generator。这一个乱数便是 list 的第一个数字。然后 list 中剩下的便是 n-1 个由新的 generator 产生出的乱数。然后我们回传整个 list 跟最后一个产生完 n-1 个乱数后 generator。
如果我们要的是在某个范围内的乱数呢?现在拿到的乱数要不是太大就是太小。如果我们想要的是骰子上的数字呢?randomR 能满足我们的需求。他的型态是 randomR :: (RandomGen g, Random a) :: (a, a) -> g -> (a, g)
,代表他有点类似 random
。只不过他的第一个参数是一对数目,定义了最后产生乱数的上界以及下界。
ghci> randomR (1,6) (mkStdGen 359353)
(6,1494289578 40692)
ghci> randomR (1,6) (mkStdGen 35935335)
(3,1250031057 40692)
另外也有一个 randomRs 的函数,他会产生一连串在给定范围内的乱数:
ghci> take 10 $ randomRs ('a','z') (mkStdGen 3) :: [Char]
"ndkxbvmomg"
这结果看起来像是一个安全性很好的密码。
你会问你自己,这一单元跟 I/O 有关系吗?到现在为止还没出现任何跟 I/O 有关的东西。到现在为止我们都是手动地做我们的 random generator。但那样的问题是,程式永远都会回传同样的乱数。这在真实世界中的程式是不能接受的。这也是为什么 System.Random
要提供 getStdGen 这个 I/O action,他的型态是 IO StdGen
。当你的程式执行时,他会跟系统要一个 random generator,并存成一个 global generator。getStdGen
会替你拿那个 global random generator 并把他绑定到某个名称上。
这里有一个简单的产生随机字串的程式。
import System.Random
main = do
gen <- getStdGen
putStr $ take 20 (randomRs ('a','z') gen)
$ runhaskell random_string.hs
pybphhzzhuepknbykxhe
$ runhaskell random_string.hs
eiqgcxykivpudlsvvjpg
$ runhaskell random_string.hs
nzdceoconysdgcyqjruo
$ runhaskell random_string.hs
bakzhnnuzrkgvesqplrx
要当心当我们连续两次呼叫 getStdGent
的时候,实际上都会回传同样的 global generator。像这样:
import System.Random
main = do
gen <- getStdGen
putStrLn $ take 20 (randomRs ('a','z') gen)
gen2 <- getStdGen
putStr $ take 20 (randomRs ('a','z') gen2)
你会打印出两次同样的字串。要能得到两个不同的字串是建立一个无限的 stream,然后拿前 20 个字当作第一个字串,拿下 20 个字当作第二个字串。要这么做,我们需要在 Data.List
中的 splitAt
函数。他会把一个 list 根据给定的 index 切成一个 tuple,tuple 的第一部份就是切断的前半,第二个部份就是切断的后半。
import System.Random
import Data.List
main = do
gen <- getStdGen
let randomChars = randomRs ('a','z') gen
(first20, rest) = splitAt 20 randomChars
(second20, _) = splitAt 20 rest
putStrLn first20
putStr second20
另一种方法是用 newStdGen 这个 I/O action,他会把现有的 random generator 分成两个新的 generators。然后会把其中一个指定成 global generator,并回传另一个。
import System.Random
main = do
gen <- getStdGen
putStrLn $ take 20 (randomRs ('a','z') gen)
gen' <- newStdGen
putStr $ take 20 (randomRs ('a','z') gen')
当我们绑定 newStdGen
的时候我们不只是会拿到一个新的 generator,global generator 也会被重新指定。所以再呼叫一次 getStdGen
并绑定到某个名称的话,我们就会拿到跟 gen
不一样的 generator。
这边有一个小程式会让使用者猜数字:
import System.Random
import Control.Monad(when)
main = do
gen <- getStdGen
askForNumber gen
askForNumber :: StdGen -> IO ()
askForNumber gen = do
let (randNumber, newGen) = randomR (1,10) gen :: (Int, StdGen)
putStr "Which number in the range from 1 to 10 am I thinking of? "
numberString <- getLine
when (not $ null numberString) $ do
let number = read numberString
if randNumber == number
then putStrLn "You are correct!"
else putStrLn $ "Sorry, it was " ++ show randNumber
askForNumber newGen
我们写了一个 askForNumber
的函数,他接受一个 random generator 并回传一个问使用者要数字并回答是否正确的 I/O action。在那个函数里面,我们先根据从参数拿到的 generator 产生一个乱数以及一个新的 generator,分别叫他们为 randomNumber
跟 newGen
。假设那个产生的数字是 7
。则我们要求使用者猜我们握有的数字是什么。我们用 getLine
来将结果绑定到 numberString
上。当使用者输入 7
,numberString
就会是 "7"
。接下来,我们用 when
来检查使用者输入的是否是空字串。如果是,那一个空的 I/O action return ()
就会被回传。基本上就等于是结束程式的意思。如果不是,那 I/O action 就会被执行。我们用 read
来把 numberString
转成一个数字,所以 number
便会是 7
。
如果使用者给我们一些 ``read`` 没办法读取的输入(像是 ``"haha"``),我们的程式便会当掉并打印出错误讯息。 如果你不希望你的程式当掉,就用 **reads**,当读取失败的时候他会回传一个空的 list。当成功的时候他就回传一个 tuple,第一个部份是我们想要的数字,第二个部份是读取失败的字串。
我们检查如果输入的数字跟我们随机产生的数字一样,便提示使用者恰当的讯息。然后再递回地呼叫 askForNumber
,只是会拿到一个新的 generator。就像之前的 generator 一样,他会给我们一个新的 I/O action。
main
的组成很简单,就是由拿取一个 random generator 跟呼叫 askForNumber
组成罢了。
来看看我们的程式:
$ runhaskell guess_the_number.hs
Which number in the range from 1 to 10 am I thinking of? 4
Sorry, it was 3
Which number in the range from 1 to 10 am I thinking of? 10
You are correct!
Which number in the range from 1 to 10 am I thinking of? 2
Sorry, it was 4
Which number in the range from 1 to 10 am I thinking of? 5
Sorry, it was 10
Which number in the range from 1 to 10 am I thinking of?
用另一种方式写的话像这样:
import System.Random
import Control.Monad(when)
main = do
gen <- getStdGen
let (randNumber, _) = randomR (1,10) gen :: (Int, StdGen)
putStr "Which number in the range from 1 to 10 am I thinking of? "
numberString <- getLine
when (not $ null numberString) $ do
let number = read numberString
if randNumber == number
then putStrLn "You are correct!"
else putStrLn $ "Sorry, it was " ++ show randNumber
newStdGen
main
他非常类似我们之前的版本,只是不是递回地呼叫,而是把所有的工作都在 main
里面做掉。在告诉使用者他们猜得是否正确之后,便更新 global generator 然后再一次呼叫 main
。两种策略都是有效但我比较喜欢第一种方式。因为他在 main
里面做的事比较少,并提供我们一个可以重复使用的函数。
#
Bytestrings
List 是一种有用又酷的资料结构。到目前为止,我们几乎无处不使用他。有好几个函数是专门处理 List 的,而 Haskell 惰性的性质又让我们可以用 filter 跟 map 来替换其他语言中的 for loop 跟 while loop。也由于 evaluation 只会发生在需要的时候,像 infinite list 也对于 Haskell 不成问题(甚至是 infinite list of infinite list)。这也是为什么 list 能被用来表达 stream,像是读取标准输入或是读取档案。我们可以打开档案然后读取内容成字串,即便实际上我们是需要的时候才会真正取读取。
然而,用字串来处理档案有一个缺点:就是他很慢。就像你所知道的,String
是一个 [Char]
的 type synonym。Char
没有一个固定的大小,因为他可能由好几个 byte 组成,好比说 Unicode。再加上 list 是惰性的。如果你有一个 list 像 [1,2,3,4]
,他只会在需要的时候被 evaluate。所以整个 list 其实比较像是一个"保证"你会有一个 list。要记住 [1,2,3,4]
不过是 1:2:3:4:[]
的一个 syntactic sugar。当 list 的第一个元素被 evaluated 的时候,剩余的部份 2:3:4:[]
一样也只是一个"保证"你会有一个 list,以此类推。以此类推。以此类推。所以你可以想像成 list 是保证在你需要的时候会给你第一个元素,以及保证你会有剩下的部份当你还需要更多的时候。其实不难说服你这样做并不是一个最有效率的作法。
这样额外的负担在大多数时候不会造成困扰,但当我们要读取一个很大的档案的时候就是个问题了。这也是为什么 Haskell 要有 bytestrings
。Bytestrings 有点像 list,但他每一个元素都是一个 byte (8 bits),而且他们惰性的程度也是不同。
Bytestrings 有两种:strict 跟 lazy。Strict bytestrings 放在 Data.ByteString
,他们把惰性的性质完全拿掉。不会有所谓任何的「保证」,一个 strict bytestring 就代表一连串的 bytes。因此你不会有一个无限长的 strict bytestrings。如果你 evaluate 第一个 byte,你就必须 evalute 整个 bytestring。这么做的优点是他会比较少 overhaed,因为他没有 "Thunk"(也就是用 Haskell 术语来说的「保证」)。缺点就是他可能会快速消耗你的记忆体,因为你把他们一次都读进了记忆体。
另一种 bytestring 是放在 Data.ByteString.Lazy
中。他们具有惰性,但又不像 list 那么极端。就像我们之前说的,List 的 thunk 个数是跟 list 中有几个元素一模一样。这也是为什么他们速度没办法满足一些特殊需求。Lazy bytestrings 则用另一种作法,他们被存在 chunks 中(不要跟 Thunk 搞混),每一个 chunk 的大小是 64K。所以如果你 evaluate lazy bytestring 中的 byte,则前 64K 会被 evaluated。在那个 chunck 之后,就是一些「保证」会有剩余的 chunk。lazy bytestrings 有点像装了一堆大小为 64K 的 strict bytestrings 的 list。当你用 lazy bytestring 处理一个档案的时候,他是一个 chunk 一个 chunk 去读。这很棒是因为他不会让我们一下使用大量的记忆体,而且 64K 有很高的可能性能够装进你 CPU 的 L2 Cache。
如果你大概看过 Data.ByteString.Lazy
的文件,你会看到到他有一堆函数的名称跟 Data.List
中的函数名称相同,只是出现的 type signature 是 ByteString
而不是 [a]
,是 Word8
而不是 a
。同样名称的函数基本上表现的行为跟 list 中的差不多。因为名称是一样的,所以必须用 qualified import 才不会在装载进 GHCI 的时候造成冲突。
import qualified Data.ByteString.Lazy as B
import qualified Data.ByteString as S
B
中有 lazy bytestrings 跟对应的函数,而 S
中则有 strict 的版本。大多数时候我们是用 lazy 的版本。
pack 函数的 type signature 是 pack :: [Word8] -> ByteString
。代表他接受一串型态为 Word8
的 bytes,并回传一个 ByteString
。你能想像一个 lazy 的 list,要让他稍微不 lazy 一些,所以让他对于 64K lazy。
那 Word8
型态又是怎么一回事?。他就像 Int
,只是他的范围比较小,介于 0-255 之间。他代表一个 8-bit 的数字。就像 Int
一样,他是属于 Num
这个 typeclass。例如我们知道 5
是 polymorphic 的,他能够表现成任何数值型态。其实 Word8
他也能表示。
ghci> B.pack [99,97,110]
Chunk "can" Empty
ghci> B.pack [98..120]
Chunk "bcdefghijklmnopqrstuvwx" Empty
正如你看到的,你其实不必特别在意 Word8
,因为型态系统会选择正确的型态。如果你试着用比较大的数字,像是 336
。那对于 Word8
他就会变成 80
。
我们把一些数值打包成 ByteString
,使他们可以塞进一个 chunk 里面。Empty
之于 ByteString
就像 []
之于 list 一样。
unpack 是 pack
的相反,他把一个 bytestring 变成一个 byte list。
fromChunks 接受一串 strict 的 bytestrings 并把他变成一串 lazy bytestring。toChunks 接受一个 lazy bytestrings 并将他变成一串 strict bytestrings。
ghci> B.fromChunks [S.pack [40,41,42], S.pack [43,44,45], S.pack [46,47,48]]
Chunk "()*" (Chunk "+,-" (Chunk "./0" Empty))
如果你有很多小的 strict bytestrings 而且不想先将他们 join 起来(会耗损 memory)这样的作法是不错的。
bytestring 版本的 :
叫做 cons。他接受一个 byte 跟一个 bytestring,并把这个 byte 放到 bytestring 的前端。他是 lazy 的操作,即使 bytestring 的第一个 chunk 不是满的,他也会新增一个 chunk。这也是为什么当你要插入很多 bytes 的时候最好用 strict 版本的 cons
,也就是 cons'。
ghci> B.cons 85 $ B.pack [80,81,82,84]
Chunk "U" (Chunk "PQRT" Empty)
ghci> B.cons' 85 $ B.pack [80,81,82,84]
Chunk "UPQRT" Empty
ghci> foldr B.cons B.empty [50..60]
Chunk "2" (Chunk "3" (Chunk "4" (Chunk "5" (Chunk "6" (Chunk "7" (Chunk "8" (Chunk "9" (Chunk ":" (Chunk ";" (Chunk "<"
Empty))))))))))
ghci> foldr B.cons' B.empty [50..60]
Chunk "23456789:;<" Empty
你可以看到 empty 制造了一个空的 bytestring。也注意到 cons
跟 cons'
的差异了吗?有了 foldr
,我们逐步地把一串数字从右边开始,一个个放到 bytestring 的前头。当我们用 cons
,我们则得到一个 byte 一个 chunk 的结果,并不是我们要的。
bytestring 模组有一大票很像 Data.List
中的函数。包括了 head
,tail
,init
,null
,length
,map
,reverse
,foldl
,foldr
,concat
,takeWhile
,filter
,等等。
他也有表现得跟 System.IO
中一样的函数,只有 Strings
被换成了 ByteString
而已。像是 System.IO
中的 readFile
,他的型态是 readFile :: FilePath -> IO String
,而 bytestring 模组中的 readFile 则是 readFile :: FilePath -> IO ByteString
。小心,如果你用了 strict bytestring 来读取一个档案,他会把档案内容都读进记忆体中。而使用 lazy bytestring,他则会读取 chunks。
让我们来写一个简单的程式,他从命令列接受两个档案名,然后拷贝第一个档案内容成第二个档案。虽然 System.Directory
中已经有一个函数叫 copyFile
,但我们想要实作自己的版本。
import System.Environment
import qualified Data.ByteString.Lazy as B
main = do
(fileName1:fileName2:_) <- getArgs
copyFile fileName1 fileName2
copyFile :: FilePath -> FilePath -> IO ()
copyFile source dest = do
contents <- B.readFile source
B.writeFile dest contents
我们写了自己的函数,他接受两个 FilePath
(记住 FilePath
不过是 String
的同义词。)并回传一个 I/O action,他会用 bytestring 拷贝第一个档案至另一个。在 main
函数中,我们做的只是拿到命令列引数然后呼叫那个函数来拿到一个 I/O action。
$ runhaskell bytestringcopy.hs something.txt ../../something.txt
就算我们不用 bytestring 来写,程式最后也会长得像这样。差别在于我们会用 B.readFile
跟 B.writeFile
而不是 readFile
跟 writeFile
。有很大的可能性,就是你只要 import 档案并在函数前加上 qualified 模组名,就可以把一个用正常 String 的程式改成用 ByteString。也有可能你是要反过来做,但那也不难。
当你需要更好的效能来读取许多资料,尝试用 bytestring,有很大的机会你会用很小的力气改进很多效能。我通常用正常 String 来写程式,然后在效能不好的时候把他们改成 ByteString。
#
Exceptions (例外)
所有的程式语言都有要处理失败的情形。这就是人生。不同的语言有不同的处理方式。在 C 里面,我们通常用非正常范围的回传值(像是 -1
或 null)来回传错误。Java 跟 C#则倾向于使用 exception 来处理失败的情况。当一个 exception 被丢出的时候,控制流程就会跳到我们做一些清理动作的地方,做完清理后 exception 被重新丢出,这样一些处理错误的程式码可以完成他们的工作。
Haskell 有一个很棒的型态系统。Algebraic data types 允许像是 Maybe
或 Either
这种型态,我们能用这些型态来代表一些可能有或没有的结果。在 C 里面,在失败的时候回传 -1
是很常见的事。但他只对写程式的人有意义。如果我们不小心,我们有可能把这些错误码当作正常值来处理,便造成一些混乱。Haskell 的型态系统赋予我们更安全的环境。一个 a -> Maybe b
的函数指出了他会产生一个包含 b
的 Just
,或是回传 Nothing
。这型态跟 a -> b
是不同的,如果我们试着将两个函数混用,compiler 便会警告我们。
尽管有表达力够强的型态来辅助失败的情形,Haskell 仍然支持 exception,因为 exception 在 I/O 的 contexts 下是比较合理的。在处理 I/O 的时候会有一堆奇奇怪怪的事情发生,环境是很不能被信赖的。像是打开档案。档案有可能被 lock 起来,也有可能档案被移除了,或是整个硬碟都被拔掉。所以直接跳到处理错误的程式码是很合理的。
我们了解到 I/O code 会丢出 exception 是件合理的事。至于 pure code 呢?其实他也能丢出 Exception。想想看 div
跟 head
两个案例。他们的型态是 (Integral a) => a -> a -> a
以及 [a] -> a
。Maybe
跟 Either
都没有在他们的回传型态中,但他们都有可能失败。div
有可能除以零,而 head
有可能你传给他一个空的 list。
ghci> 4 `div` 0
*** Exception: divide by zero
ghci> head []
*** Exception: Prelude.head: empty list
pure code 能丢出 Exception,但 Exception 只能在 I/O section 中被接到(也就是在 main
的 do block 中)这是因为在 pure code 中你不知道什么东西什么时候会被 evaluate。因为 lazy 特性的缘故,程式没有一个特定的执行顺序,但 I/O code 有。
先前我们谈过为什么在 I/O 部份的程式要越少越好。程式的逻辑部份尽量都放在 pure 的部份,因为 pure 的特性就是他们的结果只会根据函数的参数不同而改变。当思考 pure function 的时候,你只需要考虑他回传什么,因为除此之外他不会有任何副作用。这会让事情简单许多。尽管 I/O 的部份是难以避免的(像是打开档案之类),但最好是把 I/O 部份降到最低。Pure functions 预设是 lazy,那代表我们不知道他什么时候会被 evaluate,不过我们也不该知道。然而,一旦 pure functions 需要丢出 Exception,他们何时被 evaluate 就很重要了。那是因为我们只有在 I/O 的部份才能接到 Exception。这很糟糕,因为我们说过希望 I/O 的部份越少越好。但如果我们不接 Exception,我们的程式就会当掉。这问题有解决办法吗?答案是不要在 pure code 里面使用 Exception。利用 Haskell 的型态系统,尽量使用 Either
或 Maybe
之类的型态来表示可能失败的计算。
这也是为什么我们要来看看怎么使用 I/O Excetion。I/O Exception 是当我们在 main
里面跟外界沟通失败而丢出的 Exception。例如我们尝试打开一个档案,结果发现他已经被删掉或是其他状况。来看看一个尝试打开命令列引数所指定档案名称,并计算里面有多少行的程式。
import System.Environment
import System.IO
main = do (fileName:_) <- getArgs
contents <- readFile fileName
putStrLn $ "The file has " ++ show (length (lines contents)) ++ " lines!"
一个很简单的程式。我们使用 getArgs
I/O action,并绑定第一个 string 到 fileName
。然后我们绑定档案内容到 contents
。最后,我们用 lines
来取得 line 的 list,并计算 list 的长度,并用 show
来转换数字成 string。他如我们想像的工作,但当我们给的档案名称不存在的时候呢?
$ runhaskell linecount.hs i_dont_exist.txt
linecount.hs: i_dont_exist.txt: openFile: does not exist (No such file or directory)
GHC 丢了错误讯息给我们,告诉我们档案不存在。然后程式就挂掉了。假如我们希望打印出比较好一些的错误讯息呢?一种方式就是在打开档案前检查他存不存在。用 System.Directory
中的 doesFileExist。
import System.Environment
import System.IO
import System.Directory
main = do (fileName:_) <- getArgs
fileExists <- doesFileExist fileName
if fileExists
then do contents <- readFile fileName
putStrLn $ "The file has " ++ show (length (lines contents)) ++ " lines!"
else do putStrLn "The file doesn't exist!"
由于 doesFileExist
的型态是 doesFileExist :: FilePath -> IO Bool
,所以我们要写成 fileExists <- doesFileExist fileName
。那代表他回传含有一个布林值告诉我们档案存不存在的 I/O action。doesFileExist
是不能直接在 if expression 中使用的。
另一个解法是使用 Exception。在这个情境下使用 Exception 是没问题的。档案不存在这个 Exception 是在 I/O 中被丢出,所以在 I/O 中接起来也没什么不对。
要这样使用 Exception,我们必须使用 System.IO.Error
中的 catch 函数。他的型态是 catch :: IO a -> (IOError -> IO a) -> IO a
。他接受两个参数,第一个是一个 I/O action。像是他可以接受一个打开档案的 I/O action。第二个是 handler。如果第一个参数的 I/O action 丢出了 Exception,则他会被传给 handler,他会决定要作些什么。所以整个 I/O action 的结果不是如预期中做完第一个参数的 I/O action,就是 handler 处理的结果。
如果你对其他语言像是 Java, Python 中 try-catch 的形式很熟,那 catch
其实跟他们很像。第一个参数就是其他语言中的 try block。第二个参数就是其他语言中的 catch block。其中 handler 只有在 exception 被丢出时才会被执行。
handler 接受一个 IOError
型态的值,他代表的是一个 I/O exception 已经发生了。他也带有一些 exception 本身的资讯。至于这型态在语言中使如何被实作则是要看编译器。这代表我们没办法用 pattern matching 的方式来检视 IOError
。就像我们不能用 pattern matching 来检视 IO something
的内容。但我们能用一些 predicate 来检视他们。
我们来看看一个展示 catch
的程式
import System.Environment
import System.IO
import System.IO.Error
main = toTry `catch` handler
toTry :: IO ()
toTry = do (fileName:_) <- getArgs
contents <- readFile fileName
putStrLn $ "The file has " ++ show (length (lines contents)) ++ " lines!"
handler :: IOError -> IO ()
handler e = putStrLn "Whoops, had some trouble!"
首先你看到我们可以在关键字周围加上 backticks 来把 catch
当作 infix function 用,因为他刚好接受两个参数。这样使用让可读性变好。toTry `catch` handler
跟 catch toTry handler
是一模一样的。toTry
是一个 I/O action,而 handler
接受一个 IOError
,并回传一个当 exception 发生时被执行的 I/O action。
来看看执行的结果。
$ runhaskell count_lines.hs i_exist.txt
The file has 3 lines!
$ runhaskell count_lines.hs i_dont_exist.txt
Whoops, had some trouble!
在 handler 里面我们并没有检查我们拿到的是什么样的 IOError
,我们只是打印出 "Whoops, had some trouble!"
。接住任何种类的 Exception 就跟其他语言一样,在 Haskell 中也不是一个好的习惯。假如其他种类的 Exception 发生了,好比说我们送一个中断指令,而我们没有接到的话会发生什么事?这就是为什么我们要做跟其他语言一样的事:就是检查我们拿到的是什么样的 Exception。如果说是我们要的 Exception,那就做对应的处理。如果不是,我们再重新丢出 Exception。我们把我们的程式这样修改,只接住档案不存在的 Exception。
import System.Environment
import System.IO
import System.IO.Error
main = toTry `catch` handler
toTry :: IO ()
toTry = do (fileName:_) <- getArgs
contents <- readFile fileName
putStrLn $ "The file has " ++ show (length (lines contents)) ++ " lines!"
handler :: IOError -> IO ()
handler e
| isDoesNotExistError e = putStrLn "The file doesn't exist!"
| otherwise = ioError e
除了 handler 以外其他东西都没变,我们只接住我们想要的 I/O exception。这边使用了 System.IO.Error
中的函数 isDoesNotExistError 跟 ioError。isDoesNotExistError
是一个运作在 IOError
上的 predicate ,他代表他接受一个 IOError
然后回传 True
或 False
,他的型态是 isDoesNotExistError :: IOError -> Bool
。我们用他来判断是否这个错误是档案不存在所造成的。我们这边使用 guard,但其实也可以用 if else。如果 exception 不是由于档案不存在所造成的,我们就用 ioEroror
重新丢出接到的 exception。他的型态是 ioError :: IOException -> IO a
,所以他接受一个 IOError
然后产生一个会丢出 exception 的 I/O action。那个 I/O action 的型态是 IO a
,但他其实不会产生任何结果,所以他可以被当作是 IO anything
。
所以有可能在 toTry
里面丢出的 exception 并不是档案不存在造成的,而 toTry `catch` handler
会接住再丢出来,很酷吧。
程式里面有好几个运作在 IOError
上的 I/O action,当其中一个没有被 evaluate 成 True
时,就会掉到下一个 guard。这些 predicate 分别为:
* **isAlreadyExistsError**
* **isDoesNotExistError**
* **isFullError**
* **isEOFError**
* **isIllegalOperation**
* **isPermissionError**
* **isUserError**
大部分的意思都是显而易见的。当我们用了 userError 来丢出 exception 的时候,isUserError
被 evaluate 成 True
。例如说,你可以写 ioError $ userError "remote computer unplugged!"
,尽管用 Either
或 Maybe
来表示可能的错误会比自己丢出 exception 更好。
所以你可能写一个像这样的 handler
handler :: IOError -> IO ()
handler e
| isDoesNotExistError e = putStrLn "The file doesn't exist!"
| isFullError e = freeSomeSpace
| isIllegalOperation e = notifyCops
| otherwise = ioError e
其中 notifyCops
跟 freeSomeSpace
是一些你定义的 I/O action。如果 exception 不是你要的,记得要把他们重新丢出,不然你的程式可能只会安静地当掉。
System.IO.Error
也提供了一些能询问 exception 性质的函数,像是哪些 handle 造成错误,或哪些档案名造成错误。这些函数都是 ioe
当开头。而且你可以在文件中看到一整串详细资料。假设我们想要打印出造成错误的档案名。我们不能直接打印出从 getArgs
那边拿到的 fileName
,因为只有 IOError
被传进 handler 中,而 handler 并不知道其他事情。一个函数只依赖于他所被呼叫时的参数。这也是为什么我们会用 ioeGetFileName 这函数,他的型态是 ioeGetFileName :: IOError -> Maybe FilePath
。他接受一个 IOError
并回传一个 FilePath
(他是 String
的同义词。)基本上他做的事就是从 IOError
中抽出档案路径。我们来修改一下我们的程式。
import System.Environment
import System.IO
import System.IO.Error
main = toTry `catch` handler
toTry :: IO ()
toTry = do (fileName:_) <- getArgs
contents <- readFile fileName
putStrLn $ "The file has " ++ show (length (lines contents)) ++ " lines!"
handler :: IOError -> IO ()
handler e
| isDoesNotExistError e =
case ioeGetFileName e of Just path -> putStrLn $ "Whoops! File does not exist at: " ++ path
Nothing -> putStrLn "Whoops! File does not exist at unknown location!"
| otherwise = ioError e
在 isDoesNotExistError
是 True
的 guard 里面,我们在 case expression 中用 e
来呼叫 ioeGetFileName
,然后用 pattern matching 拆出 Maybe
中的值。当你想要用 pattern matching 却又不想要写一个新的函数的时候,case expression 是你的好朋友。
你不想只用一个 catch
来接你 I/O part 中的所有 exception。你可以只在特定地方用 catch
接 exception,或你可以用不同的 handler。像这样:
main = do toTry `catch` handler1
thenTryThis `catch` handler2
launchRockets
这边 toTry
使用 handler1
当作 handler,而 thenTryThis
用了 handler2
。launchRockets
并不是 catch
的参数,所以如果有任何一个 exception 被丢出都会让我们的程式当掉,除非 launchRockets
使用 catch
来处理 exception。当然 toTry
,thenTryThis
跟 launchRockets
都是 I/O actions,而且被 do syntax 绑在一起。这很像其他语言中的 try-catch blocks,你可以把一小段程式用 try-catch 包住,你可以自己调整该包多少进去。
现在你知道如何处理 I/O exception 了。我们并没有提到如何从 pure code 中丢出 exception,这是因为正如我们先前提到的,Haskell 提供了更好的办法来处理错误。就算是在可能会失败的 I/O action 中,我也倾向用 IO (Either a b)
,代表他们是 I/O action,但当他们被执行,他们结果的型态是 Either a b
,意思是不是 Left a
就是 Right b
。
10
函数式地思考来解决问题
在这一章中,我们会检视几个有趣的问题,并尝试用函数式的方式来漂亮地解决他们。我们并不会介绍新的概念,我们只是练习我们刚学到的写程式的技巧。每一节都会探讨不同的问题。会先描述问题,然后用最好的方式解决他。
#
运算逆波兰表示法(Reverse Polish notation form)
我们在学校学习数学的时候,我们多半都是用中置(infix)的方式来写数学式。例如说,我们会写 10 - (4 + 3) * 2
。+
, *
, -
是中置运算子(infix operators)。在 Haskell 中就像是 +
或 elem
一样。这种写法对于人类来说很容易阅读与理解,但缺点是我们必须用括号来描述运算的优先顺序。
逆波兰表示法是另外一种数学式的描述方法。乍看之下显得怪异,但他其实很容易理解并使用。因为我们不需要括弧来描述,也很容易放进计算机里面运算。尽管现在的计算机都是用中置的方式让你输入,有些人仍坚持用 RPN 的计算机。前述的算式如果表达成 RPN 的话会是 10 4 3 + 2 * -
。我们要如何计算他的结果呢?可以想想堆叠,基本上你是从左向右阅读算式。每当碰到一个数值,就把他堆上堆叠。当我们碰到一个运算子。就把两个数值从堆叠上拿下来,用运算子运算两个数值然后把结果推回堆叠中。当你消耗完整个算式的时候,而且假设你的算式是合法的,那你就应该只剩一个数值在堆叠中,
我们再接着看 10 4 3 + 2 * -
。首先我们把 10
推到堆叠上,所以堆叠现在是 10
。下一个接着的输入是 4
,我们也把他推上堆叠。堆叠的状态便变成 10, 4
。接着也对下一个输入 3
做同样的事,所以堆叠变成 10, 4, 3
。然后便碰到了第一个运算子 +
。我们把堆叠最上层的两个数值取下来(所以堆叠变成 10
)把两个数值加起来然后推回堆叠上。堆叠的状态便变成 10, 7
。我们再把输入 2
推上堆叠,堆叠变成 10, 7, 2
。我们又碰到另一个运算子,所以把 7
跟 2
取下,把他们相乘起来然后推回堆叠上。7
跟 2
相乘的结果是 14
,所以堆叠的状态是 10, 14
。最后我们碰到了 -
。我们把 10
跟 14
取下,将他们相减然后推回堆叠上。所以现在堆叠的状态变成 -4
。而我们已经把所有数值跟运算子的消耗完了,所以 -4
便是我们的结果。
现在我们知道我们如何手算 RPN 运算式了,接下来可以思考一下我们写一个 Haskell 的函数,当他接到一个 RPN 运算式,像是 "10 4 3 + 2 * -"
时,他可以给出结果。
这个函数的型别会是什么样呢?我们希望他接受一个字串当作参数,并产出一个数值作为结果。所以应该会是 solveRPN :: (Num a) => String -> a
。
小建议:在你去实作函数之前,先想一下你会怎么宣告这个函数的型别能够帮助你厘清问题。在 Haskell 中由于我们有够强的型别系统,光从函数的宣告就可以得到许多资讯。
当我们要实作一个问题的解法时,你可以先动手一步一步解看看,尝试从里面得到一些灵感。我们这边把每一个用空白隔开的数值或运算子都当作独立的一项。所以把 "10 4 3 + 2 * -"
这样一个字串断成一串 list ["10","4","3","+","2","*","-"]
应该会有帮助。
接下来我们要如何应用这个断好的 list 呢?我们从左至右来走一遍,并保存一个工作用的堆叠。这样有让你想到些什么可以用的吗?没错,在 folds
的那一章里面,我们提到基本上当你需要从左至右或由右至左走过一遍 list 的时候并产生些结果的时候。我们都能用 fold 来实作他。
在这个 case 中由于我们是从左边走到右边,所以我们采取 left fold。accumulator 则是选用堆叠,而 fold 的结果也会是一个堆叠,只是里面只有一个元素而已。
另外要多考虑一件事是我们用什么来代表我们的堆叠?我们可以用 list 来代替,list 的 head 就可以当作是堆叠的顶端。毕竟要把一个元素加到 list 的 head 要比加到最后要有效率多。所以如果我们有一个堆叠,里面有 10, 4, 3
,那我们可以用 [3,4,10]
来代表他。
现在我们有了足够的资讯来写出我们的函数。他会接受一个字串 "10 4 3 + 2 * -"
,随即用 words
来断成 list ["10","4","3","+","2","*","-"]
。接下来我们做一个 left fold 来产生出只有一个元素的堆叠,也就是 [-4]
。我们把这个元素从 list 取出便是最后的结果。
来看看我们的实作:
import Data.List
solveRPN :: (Num a) => String -> a
solveRPN expression = head (foldl foldingFunction [] (words expression))
where foldingFunction stack item = ...
我们接受一个运算式并把他断成一串 List。然后我们用一个 folding 函数来 fold 这串 list。注意到我们用 []
来当作起始的 accumulator。这个 accumulator 就是我们的堆叠,所以 []
代表一个空的堆叠。在运算之后我们得到一个只有一个元素的堆叠,我们呼叫 head
来取出他并用 read
来转换他。
所以我们现在只缺一个接受堆叠的 folding 函数,像是可以接受 [4,10]
跟 "3"
,然后得到 [3,4,10]
。如果是 [4,10]
跟 "*"
,那就会得到 [40]
。但在实作之前,我们先把我们的函数改写成 point-free style,这样可以省下许多括号。
import Data.List
solveRPN :: (Num a) => String -> a
solveRPN = head . foldl foldingFunction [] . words
where foldingFunction stack item = ...
看起来好多了。我们的 folding 函数会接受一个堆叠、新的项,并回传一个新的堆叠。我们使用模式匹配的方式来取出堆叠最上层的元素,然后对 "*"
跟 "-"
做匹配。
solveRPN :: (Num a, Read a) => String -> a
solveRPN = head . foldl foldingFunction [] . words
where foldingFunction (x:y:ys) "*" = (x * y):ys
foldingFunction (x:y:ys) "+" = (x + y):ys
foldingFunction (x:y:ys) "-" = (y - x):ys
foldingFunction xs numberString = read numberString:xs
我们用展开成四个模式匹配。模式会从第一个开始尝试匹配。所以 folding 函数会看看目前的项是否是 "*"
。如果是,那就会将 [3,4,9,3]
的头两个元素绑定到 x
,y
两个名称。所以 x
会是 3
而 y
等于 4
。ys
便会是 [9,3]
。他会回传一个 list,只差在 x
跟 y
相乘的结果为第一个元素。也就是说会把最上层两个元素取出,相乘后再放回去。如果第一个元素不是 "*"
,那模式匹配就会比对到 "+"
,以此类推。
如果项并未匹配到任何一个运算子,那我们就会假设这个字串是一个数值。如果他是一个数值,我们会用 read
来把字串转换成数值。并把这个数值推到堆叠上。
另外注意到我们加了 Read a
这像 class constraint,毕竟我们要使用到 read
来转换成数值。所以我们必须要宣告成他要属于 Num
跟 Read
两种 typeclass。(譬如说 Int
,Float
等)
我们是从左至右走过 ["2","3","+"]
。一开始堆叠的状态是 []
。首先他会用 []
跟 "2"
来喂给 folding 函数。由于此项并不是一个运算子。他会用 read
读取后加到 []
的开头。所以堆叠的状态变成 [2]
。接下来就是用 [2]
跟 ["3"]
来喂给 folding 函数,而得到 [3,2]
。最后再用 [3,2]
跟 "+"
来呼叫 folding 函数。这会堆叠顶端的两个数值,加起来后推回堆叠。最后堆叠变成 [5]
,这就是我们回传的数值。
我们来试试看我们新写的函数:
ghci> solveRPN "10 4 3 + 2 * -"
-4
ghci> solveRPN "2 3 +"
5
ghci> solveRPN "90 34 12 33 55 66 + * - +"
-3947
ghci> solveRPN "90 34 12 33 55 66 + * - + -"
4037
ghci> solveRPN "90 34 12 33 55 66 + * - + -"
4037
ghci> solveRPN "90 3 -"
87
看起来运作良好。这个函数有一个特色就是他很容易改写来支持额外的运算子。他们也不一定要是二元运算子。例如说我们可以写一个运算子叫做 "log"
,他会从堆叠取出一个数值算出他的 log 后推回堆叠。我们也可以用三元运算子来从堆叠取出三个数值,并把结果放回堆叠。甚至是像是 "sum"
这样的运算子,取出所有数值并把他们的和推回堆叠。
我们来改写一下我们的函数让他多支援几个运算子。为了简单起见,我们改写宣告让他回传 Float
型别。
import Data.List
solveRPN :: String -> Float
solveRPN = head . foldl foldingFunction [] . words
where foldingFunction (x:y:ys) "*" = (x * y):ys
foldingFunction (x:y:ys) "+" = (x + y):ys
foldingFunction (x:y:ys) "-" = (y - x):ys
foldingFunction (x:y:ys) "/" = (y / x):ys
foldingFunction (x:y:ys) "^" = (y ** x):ys
foldingFunction (x:xs) "ln" = log x:xs
foldingFunction xs "sum" = [sum xs]
foldingFunction xs numberString = read numberString:xs
看起来不错,没有疑问地 /
是除法而 **
是取 exponential。至于 log 运算子,我们只需要模式匹配一个元素,毕竟 log 只需要一个元素。而 sum 运算子,我们只回传一个仅有一个元素的堆叠,包含了所有元素的和。
ghci> solveRPN "2.7 ln"
0.9932518
ghci> solveRPN "10 10 10 10 sum 4 /"
10.0
ghci> solveRPN "10 10 10 10 10 sum 4 /"
12.5
ghci> solveRPN "10 2 ^"
100.0
由于 read
知道如何转换浮点数,我们也可在运算适中使用他。
ghci> solveRPN "43.2425 0.5 ^"
6.575903
有这样一个容易拓展到浮点数而且动到的程式码又在十行以内的函数,我想是非常棒的。
有一件事要留意的是这个函数对于错误处理并不好。当我们碰到非法输入的时候,他就会直接当掉。之后我们碰到 Monad 的时候我们会写一个容错的版本,他的型别会是 solveRPN :: String -> Maybe Float
。当然我们现在也可以写一个,不过那会有点麻烦,因为会有一大堆检查 Nothing
的动作。如果你希望挑战的话,也可以尽管尝试。(提示:你可以用 reads
来看看一次 read 是否会成功)
#
路径规划
我们接下来的问题是:你的飞机刚刚降落在英格兰的希思罗机场。你接下来有一个会议,你租了一台车希望尽速从机场前往伦敦市中心。
从希思罗机场到伦敦有两条主要道路,他们中间有很多小路连接彼此。如果你要走小路的话都会花掉一定的时间。你的问题就是要选一条最佳路径让你可以尽快前往伦敦。你从图的最左边出发,中间可能穿越小路来前往右边。
你可以从图中看到,从希思罗机场到伦敦在这个路径配置下的最短路径是先选主要道路 B,经由小路到 A 之后,再走一小段,转到 B 之后继续往前走。如果采取这个路径的话,会花去 75 分钟。如果选其他道路的话,就会花更多时间。
我们任务就是要写一个程式,他接受道路配置的输入,然后印出对应的最短路径。我们的输入看起来像是这样:
50
10
30
5
90
20
40
2
25
10
8
0
我们在心中可以把输入的数值三个三个看作一组。每一组由道路 A,道路 B,还有交叉的小路组成。而要能够这样组成,我们必须让最后有一条虚拟的交叉小路,只需要走 0 分钟就可以穿越他。因为我们并不会在意在伦敦里面开车的成本,毕竟我们已经到达伦敦了。
正如我们在解 RPN 计算机的问题的时候,我们是用三步骤来解题:
- 首先忘掉 Haskell,想想我们自己是怎么一步步解题的。
- 想想如何在 Haskell 中表达我们的资料。
- 在 Haskell 中要如何对这些资料做运算来产生出解答。
在介绍 RPN 计算机的章节中,我们首先自己用人脑计算表达式,在心中维持一个堆叠然后一项一项处理。我们决定用一个字串来表达我们的表达式。最后,我们用 left fold 来走过我们这一串 list,并算出结果。
究竟我们要怎么用手算出从希思罗机场到伦敦的最短路径呢?我们可以观察整章图片,猜测哪一条是最短路径然后希望我们有猜对。这样的作法对于很小的输入可以成功,但如果我们的路径超过 10000 组呢?这样我们不知道我们的解法是不是最佳解,我们只能说可能是。
所以那并不是一个好作法。这边有一张简化过后的图。
你能想出来到道路 A 上第一个交叉点的最短路径吗?(标记成 A1 的点)这太容易了。我们只要看看从道路 A 出发或是从道路 B 出发穿越至道路 A 两种作法哪种比较短就好。很明显的,从道路 B 出发的比较短,只要花费 40 分钟,然而从道路 A 则要花费 50 分钟。那到交叉点 B1 呢?同样的作法可以看出从道路 B 出发只要花费 10 分钟,远比从道路 A 出发然后穿越小路要花费少,后者要花费 80 分钟!
现在我们知道要到达 A1 的最短路径是经由 B 然后邹小路到达,共花费 40。而我们知道要达到 B1 的最短路径则是直接走 B,花费 10。这样的知识有办法帮助我们得知到下一个交叉点的最短路径吗?可以的。
我们来看看到达 A2 的最短路径是什么。要到达 A2,我们必须要从 A1 走到 A2 或是从 B1 走小路。由于我们知道到达 A1 跟 B1 的成本,我们可以很容易的想出到达 A2 的最佳路径。到达 A1 要花费 40,而从 A1 到 A2 需要 5。所以 B, C, A
总共要 45。而要到达 B1 只要 10,但需要额外花费 110 分钟来到达 B2 然后走小路到达 A2。所以最佳路径就是 B, C, A
。同样地到达 B2 最好的方式就是走 A1 然后走小路。
也许你会问如果先在 B1 跨到道路 A 然后走到 A2 的情况呢?我们已经考虑过了从 B1 到 A1 的情况,所以我们不需要再把他考虑进去。
现在我们有了至 A2 跟 B2 的最佳路径,我们可以一直重复这个过程直到最右边。一旦我们到达了 A4 跟 B4,那其中比较短的就是我们的最佳路径了。
基本上对于第二组而言,我们只是不断地重复之前的步骤,只是我们考虑进在前面的最佳路径而已。当然我们也可以说在第一步就考虑进了前面的最佳路径,只是他们都是 0 而已。
总结一下。要得到从希思罗机场到伦敦的最短路径。我们首先看看到达下一个道路 A 上的交叉点的最短路径。共有两种选择的路径,一是直接从道路 A 出发然后走到交叉点,要不然就是从道路 B 出发,走到第一个交叉点然后走小路。得到结果后记住结果。接着再用同样的方法来得到走到道路 B 上下一个交叉点的最短路径,并也记住结果。然后我们看看要走到再下一个道路 A 上的交叉点,究竟是从这个道路 A 上的交叉点往前走,或是从对应的道路 B 上的交叉点往前走再走到对面,两种选择哪种比较好。记下比较好的选择,然后也对对应的道路 B 上的交叉点做一次这个过程。做完全部组之后就到达最右边。一旦到达最右边,最佳的选择就是我们的最短路径了。
基本上当我们到达最右边的时候,我们记下了最后停在道路 A 的最短路径跟最后停在道路 B 的最短路径。其中比较短的是我们真正的最短路径。现在我们已经知道怎么用手算出答案。如果你有闲工夫,你可以拿纸笔对于任何一组道路配置算出他的最短路径。
接下来的问题是,我们要如何用 Haskell 的型别来代表这里的道路配置呢?一种方式就是把起始点跟交叉点都当作图的节点,并连到其他的交叉点。如果我们想像其实起点也有一条长度为 1 的虚拟道路连接彼此,那每个交叉点或是节点就都连接对面的节点了。同时他们也连到下一个交叉点。唯一的例外是最后一个节点,他们只连接到对面。
data Node = Node Road Road | EndNode Road
data Road = Road Int Node
一个节点要码是一个普通的节点,他包含有通往下一个交叉点的路径资讯,还有往对面道路的资讯。或是一个终端点,只包含往对面节点的道路资讯。一条道路包含他多长,还有他指向哪里。例如说,道路 A 的第一个部份就可写成 Road 50 a1
。其中 a1
是 Node x y
这样一个节点。而 x
跟 y
则分别指向 B1 跟 A2。
另一种方式就是用 Maybe
来代表往下一个交叉点走的路。每个节点有指到对面节点的路径部份,但只有不是终端节点的节点才有指向下一个交叉点的路。
data Node = Node Road (Maybe Road)
data Road = Road Int Node
这些是用 Haskell 来代表道路系统的方式,而我们也能靠他们来解决问题。但也许我们可以想出更简单的模型?如果我们想想之前手算的方式,我们每次检查都只有检查三条路径的长度而已。在道路 A 的部份,跟在道路 B 的部份,还有接触两个部份并将他们连接起来的部份。当我们观察到 A1 跟 B1 的最短路径时,我们只考虑第一组的三个部份,他们分别花费 50, 10 跟 30。所以道路系统可以用四组来表示:50, 10, 30
,5, 90, 20
,40, 2, 25
跟 10, 8, 0
。
让我们资料型别越简单越好,不过这样已经是极限了。
data Section = Section { getA :: Int, getB :: Int, getC :: Int } deriving (Show)
type RoadSystem = [Section]
这样很完美,而且对于我们的实作也有帮助。Section
是一个 algebraic data type,包含三个整数,分别代表三个不同部份的道路长。我们也定义了型别同义字,说 RoadSystem
代表包含 section 的 list。
当然我们也可以用一个 tuple ``(Int, Int, Int)`` 来代表一个 section。使用 tuple 对于一些简单的情况是比较方便,但对于比较复杂的情况定义自己的 algebraic data type 会比较好。他让型别系统获得比较多的资讯。``(Int, Int, Int)`` 毕竟也可能被使用在定义三维空间中的一个向量,只用 tuple 让我们可能把这两种情形混杂起来使用。如果我们用 ``Section`` 跟 ``Vector`` 的话就不会不小心搞混了。
从希思罗机场到伦敦的道路系统便可以这样表示:
heathrowToLondon :: RoadSystem
heathrowToLondon = [Section 50 10 30, Section 5 90 20, Section 40 2 25, Section 10 8 0]
我们现在要做的就是用 Haskell 实作我们先前的解法。所以我们应该怎样宣告我们计算最短路径函数的型别呢?他应该接受一个道路系统作为参数,然后回传一个路径。我们会用一个 list 来代表我们的路径。我们定义了 Label
来表示 A
, B
或 C
。并且也定义一个同义词 Path
:
data Label = A | B | C deriving (Show)
type Path = [(Label, Int)]
而我们的函数 optimalPath
应该要有 optimalPath :: RoadSystem -> Path
这样的型别。如果被喂给 heathrowToLondon
这样的道路系统,他应该要回传下列的路径:
[(B,10),(C,30),(A,5),(C,20),(B,2),(B,8)]
我们接下来就从左至右来走一遍 list,并沿路上记下 A 的最佳路径跟 B 的最佳路径。我们会 accumulate 我们的最佳路径。这听起来有没有很熟悉?没错!就是 left fold。
当我们手动做解答的时候,有一个步骤是我们不断重复的。就是检查现有 A 跟 B 的最佳路径以及目前的 section,产生出新的 A 跟 B 的最佳路径。举例来说,最开始我们的最佳路径是 []
跟 []
。我们看过 Section 50 10 30
后就得到新的到 A1 的最佳路径为 [(B,10),(C,30)]
,而到 B1 的最佳路径是 [(B,10)]
。如果你们把这个步骤看作是一个函数,他接受一对路径跟一个 section,并产生出新的一对路径。所以型别是 (Path, Path) -> Section -> (Path, Path)
。我们接下来继续实作这个函数。
提示:把 ``(Path, Path) -> Section -> (Path, Path)`` 当作 left fold 用的二元函数,fold 要求的型态是 ``a -> b -> a``。
roadStep :: (Path, Path) -> Section -> (Path, Path)
roadStep (pathA, pathB) (Section a b c) =
let priceA = sum $ map snd pathA
priceB = sum $ map snd pathB
forwardPriceToA = priceA + a
crossPriceToA = priceB + b + c
forwardPriceToB = priceB + b
crossPriceToB = priceA + a + c
newPathToA = if forwardPriceToA <= crossPriceToA
then (A,a):pathA
else (C,c):(B,b):pathB
newPathToB = if forwardPriceToB <= crossPriceToB
then (B,b):pathB
else (C,c):(A,a):pathA
in (newPathToA, newPathToB)
上面的程式究竟写了些什么?首先他根据先前 A 的最佳解计算出道路 A 的最佳解,之后也如法炮制计算 B 的最佳解。使用 sum $ map snd pathA
,所以如果 pathA
是 [(A,100),(C,20)]
。priceA
就是 120
。forwardPriceToA
就会是我们要付的成本。如果我们是从先前在 A 上的交叉点前往。那他就会等于我们至先前交叉点的最佳解加上目前 section 中 A 的部份。crossPriceToA
则是我们从先前在 B 上的交叉点前往 A 所要付出的代价。他是先前 B 的最佳解加上 section 中 B 的部份加上 C 的长。同样地方式也可以决定 forwardPriceToB
跟 crossPriceToB
。
现在我们知道了到 A 跟 B 的最佳路径,我们需要根据这些资讯来构造到 A 跟 B 的整体路径。如果直接走到 A 耗费较少的话,我们就把 newPathToA
设定成 (A,a):pathA
。这样做的事就是把 Label
A
跟 section 的长度 a
接到最佳路径的前面。要记得 A
是一个 label,而 a
的型别是 Int
。我们为什么要接在前面而不是 pathA ++ [(A,a)]
呢?因为接在 list 的前面比起接在后端要有效率多了。不过这样产生出来的 list 就会相反。但要把 list 再反过来并不难。如果先走到 B 再穿越小路走到 A 比较短的话,那 newPathToA
就会包含这样走的路线。同样的道理也可以套用在 newPathToB
上。
最后我们回传 newPathToA
跟 newPathToB
这一对结果。
我们把 heathrowToLondon
的第一个 section 喂给我们的函数。由于他是第一个 section,所以到 A 跟 B 的最佳路径就是一对空的 list。
ghci> roadStep ([], []) (head heathrowToLondon)
([(C,30),(B,10)],[(B,10)])
要记住包含的路径是反过来的,要从右边往左边读。所以到 A 的最佳路径可以解读成从 B 出发,然后穿越到道路 A。而 B 的最佳路径则是直接从 B 出发走到下一个交叉点。
优化小技巧:当我们写 ``priceA = sum $ map snd pathA`` 的时候。我们是在计算每步的成本。如果我们实作 ``roadStep`` 成 ``(Path, Path, Int, Int) -> Section -> (Path, Path, Int, Int)`` 的话就可以不必那么做。其中的整数型别代表 A 跟 B 上的最小成本。
现在我们有了一个函数他接受一对路径跟一个 section,并产生新的最佳路径。我们可以用一个 left fold 来做。我们用 ([],[])
跟第一个 section 来喂给 roadStep
并得到一对最佳路径。然后他又被喂给这个新得到的最佳路径跟下一个 section。以此类推。当我们走过全部的 section 的时候,我们就会得到一对最佳路径,而其中比较短的那个就是解答。有了这样的想法,我们便可以实作 optimalPath
。
optimalPath :: RoadSystem -> Path
optimalPath roadSystem =
let (bestAPath, bestBPath) = foldl roadStep ([],[]) roadSystem
in if sum (map snd bestAPath) <= sum (map snd bestBPath)
then reverse bestAPath
else reverse bestBPath
我们对 roadSystem
做 left fold。而用的起始 accumulator 是一对空的路径。fold 的结果也是一对路径,我们用模式匹配的方式来把路径从结果取出。然后我们检查哪一个路径比较短便回传他。而且在回传之前也顺便把整个结果反过来。因为我们先前提到的我们是用接在前头的方式来构造结果的。
我们来测试一下吧!
ghci> optimalPath heathrowToLondon
[(B,10),(C,30),(A,5),(C,20),(B,2),(B,8),(C,0)]
这正是我们应该得到的结果!不过跟我们预期的结果仍有点差异,在最后有一步 (C,0)
,那代表我们已经在伦敦了仍然跨越小路。不过由于他的成本是 0,所以依然可以算做正确的结果。
我们找出最佳路径的函数,现在要做的只需要从标准输入读取文字形式道路系统,并把他转成 RoadSystem
,然后用 optimalPath
来把他跑一遍就好了。
首先,我们写一个函数,他接受一串 list 并把他切成同样大小的 group。我们命名他为 groupOf
。当参数是 [1..10]
时,groupOf 3
应该回传 [[1,2,3],[4,5,6],[7,8,9],[10]]
。
groupsOf :: Int -> [a] -> [[a]]
groupsOf 0 _ = undefined
groupsOf _ [] = []
groupsOf n xs = take n xs : groupsOf n (drop n xs)
一个标准的递回函数。对于 xs
等于 [1..10]
且 n
等于 3
,这可以写成 [1,2,3] : groupsOf 3 [4,5,6,7,8,9,10]
。当这个递回结束的时候,我们的 list 就三个三个分好组。而下列是我们的 main
函数,他从标准输入读取资料,构造 RoadSystem
并印出最短路径。
import Data.List
main = do
contents <- getContents
let threes = groupsOf 3 (map read $ lines contents)
roadSystem = map (\[a,b,c] -> Section a b c) threes
path = optimalPath roadSystem
pathString = concat $ map (show . fst) path
pathPrice = sum $ map snd path
putStrLn $ "The best path to take is: " ++ pathString
putStrLn $ "The price is: " ++ show pathPrice
首先,我们从标准输入获取所有的资料。然后我们呼叫 lines
来把 "50\n10\n30\n...
转换成 ["50","10","30"..
,然后我们 map read
来把这些转成包含数值的 list。我们呼叫 groupsOf 3
来把 list 的 list,其中子 list 长度为 3。我们接着对这个 list 来 map 一个 lambda (\[a,b,c] -> Section a b c)
。正如你看到的,这个 lambda 接受一个长度为 3 的 list 然后把他变成 Section。所以 roadSystem
现在就是我们的道路配置,而且是正确的型别 RoadSystem
。我们呼叫 optimalPath
而得到一个路径跟对应的代价,之后再印出来。
我们将下列文字存成档案。
50
10
30
5
90
20
40
2
25
10
8
0
存成一个叫 paths.txt
的档案然后喂给我们的程式。
$ cat paths.txt | runhaskell heathrow.hs
The best path to take is: BCACBBC
The price is: 75
执行成功!你可以用你对 Data.Random
的了解来产生一个比较大的路径配置,然后你可以把产生的乱数资料喂给你的程式。如果你碰到堆叠溢出,试试看用 foldl'
而不要用 foldl
。foldl'
是 strict 的可以减少记忆体消耗。
11
Functors, Applicative Functors 与 Monoids
Haskell 的一些特色,像是纯粹性,高阶函数,algebraic data types,typeclasses,这些让我们可以从更高的角度来看到 polymorphism 这件事。不像 OOP 当中需要从庞大的型态阶层来思考。我们只需要看看手边的型态的行为,将他们跟适当地 typeclass 对应起来就可以了。像 Int
的行为跟很多东西很像。好比说他可以比较相不相等,可以从大到小排列,也可以将他们一一穷举出来。
Typeclass 的运用是很随意的。我们可以定义自己的资料型态,然后描述他可以怎样被操作,跟 typeclass 关联起来便定义了他的行为。由于 Haskell 强大的型态系统,这让我们只要读函数的型态宣告就可以知道很多资讯。typeclass 可以定义得很抽象很 general。我们之前有看过 typeclass 定义了可以比较两个东西是否相等,或是定义了可以比较两个东西的大小。这些是既抽象但又描述简洁的行为,但我们不会认为他们有什么特别之处,因为我们时常碰到他们。最近我们看过了 functor,基本上他们是一群可以被 map over 的物件。这是其中一个例子能够抽象但又漂亮地描述行为。在这一章中,我们会详加阐述 functors,并会提到比较强一些的版本,也就是 applicative functors。我们也会提到 monoids。
#
温习 Functors
我们已经在之前的章节提到 functors。如果你还没读那个章节,也许你应该先去看看。或是你直接假装你已经读过了。
来快速复习一下:Functors 是可以被 map over 的物件,像是 lists,Maybe
,trees 等等。在 Haskell 中我们是用 Functor
这个 typeclass 来描述他。这个 typeclass 只有一个 method,叫做 fmap
,他的型态是 fmap :: (a -> b) -> f a -> f b
。这型态说明了如果给我一个从 a
映到 b
的函数,以及一个装了 a
的盒子,我会回给你一个装了 b
的盒子。就好像用这个函数将每个元素都转成 b
一样
*给一点建议*。这盒子的比喻尝试让你抓到些 functors 是如何运作的感觉。在之后我们也会用相同的比喻来比喻 applicative functors 跟 monads。在多数情况下这种比喻是恰当的,但不要过度引申,有些 functors 是不适用这个比喻的。一个比较正确的形容是 functors 是一个计算语境(computational context)。这个语境可能是这个 computation 可能带有值,或是有可能会失败(像 ``Maybe`` 跟 ``Either a``),或是他可能有多个值(像 lists),等等。
如果一个 type constructor 要是 Functor
的 instance,那他的 kind 必须是 * -> *
,这代表他必须刚好接受一个 type 当作 type parameter。像是 Maybe
可以是 Functor 的一个 instance,因为他接受一个 type parameter,来做成像是 Maybe Int
,或是 Maybe String
。如果一个 type constructor 接受两个参数,像是 Either
,我们必须给他两个 type parameter。所以我们不能这样写:instance Functor Either where
,但我们可以写 instance Functor (Either a) where
,如果我们把 fmap
限缩成只是 Either a
的,那他的型态就是 fmap :: (b -> c) -> Either a b -> Either a c
。就像你看到的,Either a
的是固定的一部分,因为 Either a
只恰好接受一个 type parameter,但 Either
则要接受两个 type parameters。这样 fmap 的型态变成 fmap :: (b -> c) -> Either b -> Either c
,这不太合理。
我们知道有许多型态都是 Functor
的 instance,像是 []
,Maybe
,Either a
以及我们自己写的 Tree
。我们也看到了如何用一个函数 map 他们。在这一章节,我们再多举两个例子,也就是 IO
跟 (->) r
。
如果一个值的型态是 IO String
,他代表的是一个会被计算成 String 结果的 I/O action。我们可以用 do syntax 来把结果绑定到某个名称。我们之前把 I/O action 比喻做长了脚的盒子,会到真实世界帮我们取一些值回来。我们可以检视他们取了什么值,但一旦看过,我们必须要把值放回盒子中。用这个比喻,IO
的行为就像是一个 functor。
我们来看看 IO
是怎么样的一个 Functor
instance。当我们 fmap
用一个 function 来 map over I/O action 时,我们会想要拿回一个装着已经用 function 映射过值的 I/O action。
instance Functor IO where
fmap f action = do
result <- action
return (f result)
对一个 I/O action 做 map over 动作的结果仍会是一个 I/O action,所以我们才用 do syntax 来把两个 I/O action 黏成一个。在 fmap
的实作中,我们先执行了原本传进的 I/O action,并把结果绑定成 result
。然后我们写了 return (f result)
。return
就如你所知道的,是一个只会回传包了你传给他东西的 I/O action。还有一个 do block 的回传值一定是他最后一个 I/O action 的回传值。这也是为什么我们需要 return。其实他只是回传包了 f result
的 I/O action。
我们可以再多实验一下来找到些感觉。来看看这段 code:
main = do line <- getLine
let line' = reverse line
putStrLn $ "You said " ++ line' ++ " backwards!"
putStrLn $ "Yes, you really said" ++ line' ++ " backwards!"
这程式要求使用者输入一行文字,然后印出一行反过来的。 我们可以用 fmap
来改写:
main = do line <- fmap reverse getLine
putStrLn $ "You said " ++ line ++ " backwards!"
putStrLn $ "Yes, you really said" ++ line ++ " backwards!"
就像我们用 fmap
reverse
来 map over Just "blah"
会得到 Just "halb"
,我们也可以 fmap
reverse
来 map over getLine
。getLine
是一个 I/O action,他的 type 是 IO String
,而用 reverse
来 map over 他会回传一个取回一个字串并 reverse
他的 I/O action。就像我们 apply 一个 function 到一个 Maybe
一样,我们也可以 apply 一个 function 到一个 IO
,只是这个 IO
会跑去外面拿回某些值。然后我们把结果用 <-
绑定到某个名称,而这个名称绑定的值是已经 reverse
过了。
而 fmap (++"!") getLine
这个 I/O action 表现得就像 getLine
,只是他的结果多了一个 "!"
在最后。
如果我们限缩 fmap
到 IO
型态上,那 fmap 的型态是 fmap :: (a -> b) -> IO a -> IO b
。fmap
接受一个函数跟一个 I/O action,并回传一个 I/O action 包含了已经 apply 过 function 的结果。
如果你曾经注意到你想要将一个 I/O action 绑定到一个名称上,只是为了要 apply 一个 function。你可以考虑使用 fmap
,那会更漂亮地表达这件事。或者你想要对 functor 中的资料做 transformation,你可以先将你要用的 function 写在 top level,或是把他作成一个 lambda function,甚至用 function composition。
import Data.Char
import Data.List
main = do line <- fmap (intersperse '-' . reverse . map toUpper) getLine
putStrLn line
$ runhaskell fmapping_io.hs
hello there
E-R-E-H-T- -O-L-L-E-H
正如你想的,intersperse '-' . reverse . map toUpper
合成了一个 function,他接受一个字串,将他转成大写,然后反过来,再用 intersperse '-'
安插'-'。他是比较漂亮版本的 (\xs -> intersperse '-' (reverse (map toUpper xs)))
。
另一个 Functor
的案例是 (->) r
,只是我们先前没有注意到。你可能会困惑到底 (->) r
究竟代表什么?一个 r -> a
的型态可以写成 (->) r a
,就像是 2 + 3
可以写成 (+) 2 3
一样。我们可以从一个不同的角度来看待 (->) r a
,他其实只是一个接受两个参数的 type constructor,好比 Either
。但记住我们说过 Functor
只能接受一个 type constructor。这也是为什么 (->)
不是 Functor
的一个 instance,但 (->) r
则是。如果程式的语法允许的话,你也可以将 (->) r
写成 (r ->)
。就如 (2+)
代表的其实是 (+) 2
。至于细节是如何呢?我们可以看看 Control.Monad.Instances
。
我们通常说一个接受任何东西以及回传随便一个东西的函数型态是 ``a -> b``。``r -> a`` 是同样意思,只是把符号代换了一下。
instance Functor ((->) r) where
fmap f g = (\x -> f (g x))
如果语法允许的话,他可以被写成
instance Functor (r ->) where
fmap f g = (\x -> f (g x))
但其实是不允许的,所以我们必须写成第一种的样子。
首先我们来看看 fmap
的型态。他的型态是 fmap :: (a -> b) -> f a -> f b
。我们把所有的 f
在心里代换成 (->) r
。则 fmap
的型态就变成 fmap :: (a -> b) -> ((->) r a) -> ((->) r b)
。接着我们把 (->) r a
跟 (->) r b
换成 r -> a
跟 r -> b
。则我们得到 fmap :: (a -> b) -> (r -> a) -> (r -> b)
。
从上面的结果看到将一个 function map over 一个 function 会得到另一个 function,就如 map over 一个 function 到 Maybe
会得到一个 Maybe
,而 map over 一个 function 到一个 list 会得到一个 list。而 fmap :: (a -> b) -> (r -> a) -> (r -> b)
告诉我们什么?他接受一个从 a
到 b
的 function,跟一个从 r
到 a
的 function,并回传一个从 r
到 b
的 function。这根本就是 function composition。把 r -> a
的输出接到 a -> b
的输入,的确是 function composition 在做的事。如果你再仔细看看 instance 的定义,会发现真的就是一个 function composition。
instance Functor ((->) r) where
fmap = (.)
这很明显就是把 fmap
当 composition 在用。可以用 :m + Control.Monad.Instances
把模组装载进来,并做一些尝试。
ghci> :t fmap (*3) (+100)
fmap (*3) (+100) :: (Num a) => a -> a
ghci> fmap (*3) (+100) 1
303
ghci> (*3) `fmap` (+100) $ 1
303
ghci> (*3) . (+100) $ 1
303
ghci> fmap (show . (*3)) (*100) 1
"300"
我们呼叫 fmap
的方式是 infix 的方式,这跟 .
很像。在第二行,我们把 (*3)
map over 到 (+100)
上,这会回传一个先把输入值 (+100)
再 (*3)
的 function,我们再用 1
去呼叫他。
到这边为止盒子的比喻还适用吗?如果你硬是要解释的话还是解释得通。当我们将 fmap (+3)
map over Just 3
的时候,对于 Maybe
我们很容易把他想成是装了值的盒子,我们只是对盒子里面的值 (+3)
。但对于 fmap (*3) (+100)
呢?你可以把 (+100)
想成是一个装了值的盒子。有点像把 I/O action 想成长了脚的盒子一样。对 (+100)
使用 fmap (*3)
会产生另一个表现得像 (+100)
的 function。只是在算出值之前,会再多计算 (*3)
。这样我们可以看出来 fmap
表现得就像 .
一样。
fmap
等同于 function composition 这件事对我们来说并不是很实用,但至少是一个有趣的观点。这也让我们打开视野,看到盒子的比喻不是那么恰当,functors 其实比较像 computation。function 被 map over 到一个 computation 会产生经由那个 function 映射过后的 computation。
在我们继续看 fmap
该遵守的规则之前,我们再看一次 fmap
的型态,他是 fmap :: (a -> b) -> f a -> f b
。很明显我们是在讨论 Functor,所以为了简洁,我们就不写 (Functor f) =>
的部份。当我们在学 curry 的时候,我们说过 Haskell 的 function 实际上只接受一个参数。一个型态是 a -> b -> c
的函数实际上是接受 a
然后回传 b -> c
,而 b -> c
实际上接受一个 b
然后回传一个 c
。如果我们用比较少的参数呼叫一个函数,他就会回传一个函数需要接受剩下的参数。所以 a -> b -> c
可以写成 a -> (b -> c)
。这样 curry 可以明显一些。
同样的,我们可以不要把 fmap
想成是一个接受 function 跟 functor 并回传一个 function 的 function。而是想成一个接受 function 并回传一个新的 function 的 function,回传的 function 接受一个 functor 并回传一个 functor。他接受 a -> b
并回传 f a -> f b
。这动作叫做 lifting。我们用 GHCI 的 :t
来做的实验。
ghci> :t fmap (*2)
fmap (*2) :: (Num a, Functor f) => f a -> f a
ghci> :t fmap (replicate 3)
fmap (replicate 3) :: (Functor f) => f a -> f [a]
fmap (*2)
接受一个 functor f
,并回传一个基于数字的 functor。那个 functor 可以是 list,可以是 Maybe
,可以是 Either String
。fmap (replicate 3)
可以接受一个基于任何型态的 functor,并回传一个基于 list 的 functor。
当我们提到 functor over numbers 的时候,你可以想像他是一个 functor 包含有许多数字在里面。前面一种说法其实比较正确,但后面一种说法比较容易让人理解。
这样的观察在我们只有绑定一个部份套用的函数,像是 fmap (++"!")
,的时候会显得更清楚,
你可以把 fmap
想做是一个函数,他接受另一个函数跟一个 functor,然后把函数对 functor 每一个元素做映射,或你可以想做他是一个函数,他接受一个函数并把他 lift 到可以在 functors 上面操作。两种想法都是正确的,而且在 Haskell 中是等价。
fmap (replicate 3) :: (Functor f) => f a -> f [a]
这样的型态代表这个函数可以运作在任何 functor 上。至于确切的行为则要看究竟我们操作的是什么样的 functor。如果我们是用 fmap (replicate 3)
对一个 list 操作,那我们会选择 fmap
针对 list 的实作,也就是只是一个 map
。如果我们是碰到 Maybe a
。那他在碰到 Just
型态的时候,会对里面的值套用 replicate 3
。而碰到 Nothing
的时候就回传 Nothing
。
ghci> fmap (replicate 3) [1,2,3,4]
[[1,1,1],[2,2,2],[3,3,3],[4,4,4]]
ghci> fmap (replicate 3) (Just 4)
Just [4,4,4]
ghci> fmap (replicate 3) (Right "blah")
Right ["blah","blah","blah"]
ghci> fmap (replicate 3) Nothing
Nothing
ghci> fmap (replicate 3) (Left "foo")
Left "foo"
接下来我们来看看 functor laws。一个东西要成为 functor,必须要遵守某些定律。不管任何一个 functor 都被要求具有某些性质。他们必须是能被 map over 的。对他们呼叫 fmap
应该是要用一个函数 map 每一个元素,不多做任何事情。这些行为都被 functor laws 所描述。对于 Functor
的 instance 来说,总共两条定律应该被遵守。不过他们不会在 Haskell 中自动被检查,所以你必须自己确认这些条件。
functor law 的第一条说明,如果我们对 functor 做 map id
,那得到的新的 functor 应该要跟原来的一样。如果写得正式一点,他代表 fmap id = id
。基本上他就是说对 functor 呼叫 fmap id
,应该等同于对 functor 呼叫 id
一样。毕竟 id
只是 identity function,他只会把参数照原样丢出。他也可以被写成 \x -> x
。如果我们对 functor 的概念就是可以被 map over 的物件,那 fmap id = id
的性就显而易见。
我们来看看这个定律的几个案例:
ghci> fmap id (Just 3)
Just 3
ghci> id (Just 3)
Just 3
ghci> fmap id [1..5]
[1,2,3,4,5]
ghci> id [1..5]
[1,2,3,4,5]
ghci> fmap id []
[]
ghci> fmap id Nothing
Nothing
如果我们看看 Maybe
的 fmap
的实作,我们不难发现第一定律为何被遵守。
instance Functor Maybe where
fmap f (Just x) = Just (f x)
fmap f Nothing = Nothing
我们可以想像在 f
的位置摆上 id
。我们看到 fmap id
拿到 Just x
的时候,结果只不过是 Just (id x)
,而 id
有只回传他拿到的东西,所以可以知道 Just (id x)
等价于 Just x
。所以说我们可以知道对 Maybe
中的 Just
用 id
去做 map over 的动作,会拿回一样的值。
而将 id
map over Nothing
会拿回 Nothing
并不稀奇。所以从这两个 fmap
的实作,我们可以看到的确 fmap id = id
有被遵守。
第二定律描述说先将两个函数合成并将结果 map over 一个 functor 的结果,应该跟先将第一个函数 map over 一个 functor,再将第二个函数 map over 那个 functor 的结果是一样的。正式地写下来的话就是 fmap (f . g) = fmap f . fmap g
。或是用另外一种写法,对于任何一个 functor F,下面这个式子应该要被遵守:fmap (f . g) F = fmap f (fmap g F)
。
如果我们能够证明某个型别遵守两个定律,那我们就可以保证他跟其他 functor 对于映射方面都拥有相同的性质。我们知道如果对他用 fmap
,我们知道不会有除了 mapping 以外的事会发生,而他就仅仅会表现成某个可以被 map over 的东西。也就是一个 functor。你可以再仔细检视 fmap
对于某些型别的实作来了解第二定律。正如我们先前对 Maybe
检视第一定律一般。
如果你需要的话,我们能在这边演练一下 Maybe
是如何遵守第二定律的。首先 fmap (f . g)
来 map over Nothing
的话,我们会得到 Nothing
。因为用任何函数来 fmap
Nothing
的话都会回传 Nothing
。如果我们 fmap f (fmap g Nothing)
,我们会得到 Nothing
。可以看到当面对 Nothing
的时候,Maybe
很显然是遵守第二定律的。 那对于 Just something
呢?如果我们使用 fmap (f . g) (Just x)
的话,从实作的程式码中我可以看到 Just ((f . g ) x)
,也就是 Just (f (g x))
。如果我们使用 fmap f (fmap g (Just x))
的话我们可以从实作知道 fmap g (Just x)
会是 Just (g x)
。fmap f (fmap g (Just x))
跟 fmap f (Just (g x))
相等。而从实作上这又会相等于 Just (f (g x))
。
如果你不太理解这边的说明,别担心。只要确定你了解什么是函数合成就好。在多数的情况下你可以直觉地对应到这些型别表现得就像 containers 或函数一样。或是也可以换种方法,只要多尝试对型别中不同的值做操作你就可以看看型别是否有遵守定律。
我们来看一些经典的例子。这些型别建构子虽然是 Functor
的 instance,但实际上他们并不是 functor,因为他们并不遵守这些定律。我们来看看其中一个型别。
data CMaybe a = CNothing | CJust Int a deriving (Show)
C 这边代表的是计数器。他是一种看起来像是 Maybe a
的型别,只差在 Just
包含了两个 field 而不是一个。在 CJust
中的第一个 field 是 Int
,他是扮演计数器用的。而第二个 field 则为型别 a
,他是从型别参数来的,而他确切的型别当然会依据我们选定的 CMaybe a
而定。我们来对他作些操作来获得些操作上的直觉吧。
ghci> CNothing
CNothing
ghci> CJust 0 "haha"
CJust 0 "haha"
ghci> :t CNothing
CNothing :: CMaybe a
ghci> :t CJust 0 "haha"
CJust 0 "haha" :: CMaybe [Char]
ghci> CJust 100 [1,2,3]
CJust 100 [1,2,3]
如果我们使用 CNothing
,就代表不含有 field。如果我们用的是 CJust
,那第一个 field 是整数,而第二个 field 可以为任何型别。我们来定义一个 Functor
的 instance,这样每次我们使用 fmap
的时候,函数会被套用在第二个 field,而第一个 field 会被加一。
instance Functor CMaybe where
fmap f CNothing = CNothing
fmap f (CJust counter x) = CJust (counter+1) (f x)
这种定义方式有点像是 Maybe
的定义方式,只差在当我们使用 fmap
的时候,如果碰到的不是空值,那我们不只会套用函数,还会把计数器加一。我们可以来看一些范例操作。
ghci> fmap (++"ha") (CJust 0 "ho")
CJust 1 "hoha"
ghci> fmap (++"he") (fmap (++"ha") (CJust 0 "ho"))
CJust 2 "hohahe"
ghci> fmap (++"blah") CNothing
CNothing
这些会遵守 functor laws 吗?要知道有不遵守的情形,只要找到一个反例就好了。
ghci> fmap id (CJust 0 "haha")
CJust 1 "haha"
ghci> id (CJust 0 "haha")
CJust 0 "haha"
我们知道 functor law 的第一定律描述当我们用 id
来 map over 一个 functor 的时候,他的结果应该跟只对 functor 呼叫 id
的结果一样。但我们可以看到这个例子中,这对于 CMaybe
并不遵守。尽管他的确是 Functor
typeclass 的一个 instace。但他并不遵守 functor law 因此不是一个 functor。如果有人使用我们的 CMaybe
型别,把他当作 functor 用,那他就会期待 functor laws 会被遵守。但 CMaybe
并没办法满足,便会造成错误的程式。当我们使用一个 functor 的时候,函数合成跟 map over 的先后顺序不应该有影响。但对于 CMaybe
他是有影响的,因为他纪录了被 map over 的次数。如果我们希望 CMaybe
遵守 functor law,我们必须要让 Int
栏位在做 fmap
的时候维持不变。
乍看之下 functor laws 看起来不是很必要,也容易让人搞不懂,但我们知道如果一个型别遵守 functor laws,那我们就能对他作些基本的假设。如果遵守了 functor laws,我们知道对他做 fmap
不会做多余的事情,只是用一个函数做映射而已。这让写出来的程式码足够抽象也容易扩展。因为我们可以用定律来推论型别的行为。
所有在标准函式库中的 Functor
的 instance 都遵守这些定律,但你可以自己检查一遍。下一次你定义一个型别为 Functor
的 instance 的时候,花点时间确认他确实遵守 functor laws。一旦你操作过足够多的 functors 时,你就会获得直觉,知道他们会有什么样的性质跟行为。而且 functor laws 也会觉得显而易见。但就算没有这些直觉,你仍然可以一行一行地来找看看有没有反例让这些定律失效。
我们可以把 functor 看作输出具有 context 的值。例如说 Just 3
就是输出 3
,但他又带有一个可能没有值的 context。[1,2,3]
输出三个值,1
,2
跟 3
,同时也带有可能有多个值或没有值的 context。(+3)
则会带有一个依赖于参数的 context。
如果你把 functor 想做是输出值这件事,那你可以把 map over 一个 functor 这件事想成在 functor 输出的后面再多加一层转换。当我们做 fmap (+3) [1,2,3]
的时候,我们是把 (+3)
接到 [1,2,3]
后面,所以当我们检视任何一个 list 的输出的时候,(+3)
也会被套用在上面。另一个例子是对函数做 map over。当我们做 fmap (+3) (*3)
,我们是把 (+3)
这个转换套用在 (*3)
后面。这样想的话会很自然就会把 fmap
跟函数合成关联起来(fmap (+3) (*3)
等价于 (+3) . (*3)
,也等价于 \x -> ((x*3)+3)
),毕竟我们是接受一个函数 (*3)
然后套用 (+3)
转换。最后的结果仍然是一个函数,只是当我们喂给他一个数字的时候,他会先乘上三然后做转换加上三。这基本上就是函数合成在做的事。
#
Applicative functors
在这个章节中,我们会学到 applicative functors,也就是加强版的 functors,在 Haskell 中是用在 Control.Applicative
中的 Applicative
这个 typeclass 来定义的。
你还记得 Haskell 中函数预设就是 Curried 的,那代表接受多个参数的函数实际上是接受一个参数然后回传一个接受剩余参数的函数,以此类推。如果一个函数的型别是 a -> b -> c
,我们通常会说这个函数接受两个参数并回传 c
,但他实际上是接受 a
并回传一个 b -> c
的函数。这也是为什么我们可以用 (f x) y
的方式呼叫 f x y
。这个机制让我们可以 partially apply 一个函数,可以用比较少的参数呼叫他们。可以做成一个函数再喂给其他函数。
到目前为止,当我们要对 functor map over 一个函数的时候,我们用的函数都是只接受一个参数的。但如果我们要 map 一个接受两个参数的函数呢?我们来看几个具体的例子。如果我们有 Just 3
然后我们做 fmap (*) (Just 3)
,那我们会获得什么样的结果?从 Maybe
对 Functor
的 instance 实作来看,我们知道如果他是 Just something
,他会对在 Just
中的 something
做映射。因此当 fmap (*) (Just 3)
会得到 Just ((*) 3)
,也可以写做 Just (* 3)
。我们得到了一个包在 Just
中的函数。
ghci> :t fmap (++) (Just "hey")
fmap (++) (Just "hey") :: Maybe ([Char] -> [Char])
ghci> :t fmap compare (Just 'a')
fmap compare (Just 'a') :: Maybe (Char -> Ordering)
ghci> :t fmap compare "A LIST OF CHARS"
fmap compare "A LIST OF CHARS" :: [Char -> Ordering]
ghci> :t fmap (\x y z -> x + y / z) [3,4,5,6]
fmap (\x y z -> x + y / z) [3,4,5,6] :: (Fractional a) => [a -> a -> a]
如果我们 map compare
到一个包含许多字元的 list 呢?他的型别是 (Ord a) => a -> a -> Ordering
,我们会得到包含许多 Char -> Ordering
型别函数的 list,因为 compare
被 partially apply 到 list 中的字元。他不是包含许多 (Ord a) => a -> Ordering
的函数,因为第一个 a
碰到的型别是 Char
,所以第二个 a
也必须是 Char
。
我们看到如何用一个多参数的函数来 map functor,我们会得到一个包含了函数的 functor。那现在我们能对这个包含了函数的 functor 做什么呢?我们能用一个吃这些函数的函数来 map over 这个 functor,这些在 functor 中的函数都会被当作参数丢给我们的函数。
ghci> let a = fmap (*) [1,2,3,4]
ghci> :t a
a :: [Integer -> Integer]
ghci> fmap (\f -> f 9) a
[9,18,27,36]
但如果我们的有一个 functor 里面是 Just (3 *)
还有另一个 functor 里面是 Just 5
,但我们想要把第一个 Just (3 *)
map over Just 5
呢?如果是普通的 functor,那就没救了。因为他们只允许 map 一个普通的函数。即使我们用 \f -> f 9
来 map 一个装了很多函数的 functor,我们也是使用了普通的函数。我们是无法单纯用 fmap
来把包在一个 functor 的函数 map 另一个包在 functor 中的值。我们能用模式匹配 Just
来把函数从里面抽出来,然后再 map Just 5
,但我们是希望有一个一般化的作法,对任何 functor 都有效。
我们来看看 Applicative
这个 typeclass。他位在 Control.Applicative
中,在其中定义了两个函数 pure
跟 <*>
。他并没有提供预设的实作,如果我们想使用他必须要为他们 applicative functor 的实作。typeclass 定义如下:
class (Functor f) => Applicative f where
pure :: a -> f a
(<*>) :: f (a -> b) -> f a -> f b
这简简单单的三行可以让我们学到不少。首先来看第一行。他开启了 Applicative
的定义,并加上 class contraint。描述了一个型别构造子要是 Applicative
,他必须也是 Functor
。这就是为什么我们说一个型别构造子属于 Applicative
的话,他也会是 Functor
,因此我们能对他使用 fmap
。
第一个定义的是 pure
。他的型别宣告是 pure :: a -> f a
。f
代表 applicative functor 的 instance。由于 Haskell 有一个优秀的型别系统,其中函数又是将一些参数映射成结果,我们可以从型别宣告中读出许多讯息。pure
应该要接受一个值,然后回传一个包含那个值的 applicative functor。我们这边是用盒子来作比喻,即使有一些比喻不完全符合现实的情况。尽管这样,a -> f a
仍有许多丰富的资讯,他确实告诉我们他会接受一个值并回传一个 applicative functor,里面装有结果。
对于 pure
比较好的说法是把一个普通值放到一个预设的 context 下,一个最小的 context 但仍然包含这个值。
<*>
也非常有趣。他的型别是 f (a -> b) -> f a -> f b
。这有让你联想到什么吗?没错!就是 fmap :: (a -> b) -> f a -> f b
。他有点像加强版的 fmap
。然而 fmap
接受一个函数跟一个 functor,然后套用 functor 之中的函数。<*>
则是接受一个装有函数的 functor 跟另一个 functor,然后取出第一个 functor 中的函数将他对第二个 functor 中的值做 map。
我们来看看 Maybe
的 Applicative
实作:
instance Applicative Maybe where
pure = Just
Nothing <*> _ = Nothing
(Just f) <*> something = fmap f something
从 class 的定义我们可以看到 f
作为 applicative functor 会接受一个具体型别当作参数,所以我们是写成 instance Applicative Maybe where
而不是写成 instance Applicative (Maybe a) where
。
首先看到 pure
。他只不过是接受一个东西然后包成 applicative functor。我们写成 pure = Just
是因为 Just
不过就是一个普通函数。我们其实也可以写成 pure x = Just x
。
接着我们定义了 <*>
。我们无法从 Nothing
中抽出一个函数,因为 Nothing
并不包含一个函数。所以我们说如果我们要尝试从 Nothing
中取出一个函数,结果必定是 Nothing
。如果你看看 Applicative
的定义,你会看到他有 Functor
的限制,他代表 <*>
的两个参数都会是 functors。如果第一个参数不是 Nothing
,而是一个装了函数的 Just
,而且我们希望将这个函数对第二个参数做 map。这个也考虑到第二个参数是 Nothing
的情况,因为 fmap
任何一个函数至 Nothing
会回传 Nothing
。
对于 Maybe
而言,如果左边是 Just
,那 <*>
会从其中抽出了一个函数来 map 右边的值。如果有任何一个参数是 Nothing
。那结果便是 Nothing
。
来试试看吧!
ghci> Just (+3) <*> Just 9
Just 12
ghci> pure (+3) <*> Just 10
Just 13
ghci> pure (+3) <*> Just 9
Just 12
ghci> Just (++"hahah") <*> Nothing
Nothing
ghci> Nothing <*> Just "woot"
Nothing
我们看到 pure (+3)
跟 Just (+3)
在这个 case 下是一样的。如果你是在 applicative context 底下跟 Maybe
打交道的话请用 pure
,要不然就用 Just
。前四个输入展示了函数是如何被取出并做 map 的动作,但在这个 case 底下,他们同样也可以用 unwrap 函数来 map over functors。最后一行比较有趣,因为我们试着从 Nothing
取出函数并将他 map 到某个值。结果当然是 Nothing
。
对于普通的 functors,你可以用一个函数 map over 一个 functors,但你可能没办法拿到结果。而 applicative functors 则让你可以用单一一个函数操作好几个 functors。看看下面一段程式码:
ghci> pure (+) <*> Just 3 <*> Just 5
Just 8
ghci> pure (+) <*> Just 3 <*> Nothing
Nothing
ghci> pure (+) <*> Nothing <*> Just 5
Nothing
究竟我们写了些什么?我们来一步步看一下。<*>
是 left-associative,也就是说 pure (+) <*> Just 3 <*> Just 5
可以写成 (pure (+) <*> Just 3) <*> Just 5
。首先 +
是摆在一个 functor 中,在这边刚好他是一个 Maybe
。所以首先,我们有 pure (+)
,他等价于 Just (+)
。接下来由于 partial application 的关系,Just (+) <*> Just 3
等价于 Just (3+)
。把一个 3
喂给 +
形成另一个只接受一个参数的函数,他的效果等于加上 3。最后 Just (3+) <*> Just 5
被运算,其结果是 Just 8
。
这样很棒吧!用 applicative style 的方式来使用 applicative functors。像是 pure f <*> x <*> y <*> ...
就让我们可以拿一个接受多个参数的函数,而且这些参数不一定是被包在 functor 中。就这样来套用在多个在 functor context 的值。这个函数可以吃任意多的参数,毕竟 <*>
只是做 partial application 而已。
如果我们考虑到 pure f <*> x
等于 fmap f x
的话,这样的用法就更方便了。这是 applicative laws 的其中一条。我们稍后会更仔细地检视这条定律。现在我们先依直觉来使用他。就像我们先前所说的,pure
把一个值放进一个预设的 context 中。如果我们要把一个函数放在一个预设的 context,然后把他取出并套用在放在另一个 applicative functor 的值。我们会做的事就是把函数 map over 那个 applicative functor。但我们不会写成 pure f <*> x <*> y <*> ...
,而是写成 fmap f x <*> y <*> ...
。这也是为什么 Control.Applicative
会 export 一个函数 <$>
,他基本上就是中缀版的 fmap
。他是这么被定义的:
(<$>) :: (Functor f) => (a -> b) -> f a -> f b
f <$> x = fmap f x
要记住型别变数跟参数的名字还有值绑定的名称不冲突。``f`` 在函数的型别宣告中是型别变数,说明 ``f`` 应该要满足 ``Functor`` typeclass 的条件。而在函数本体中的 ``f`` 则表示一个函数,我们将他 map over x。我们同样用 ``f`` 来表示他们并代表他们是相同的东西。
<$>
的使用显示了 applicative style 的好处。如果我们想要将 f
套用三个 applicative functor。我们可以写成 f <$> x <*> y <*> z
。如果参数不是 applicative functor 而是普通值的话。我们则写成 f x y z
。
我们再仔细看看他是如何运作的。我们有一个 Just "johntra"
跟 Just "volta"
这样的值,我们希望将他们结合成一个 String
,并且包含在 Maybe
中。我们会这样做:
ghci> (++) <$> Just "johntra" <*> Just "volta"
Just "johntravolta"
可以将上面的跟下面这行比较一下:
ghci> (++) "johntra" "volta"
"johntravolta"
可以将一个普通的函数套用在 applicative functor 上真不错。只要稍微写一些 <$>
跟 <*>
就可以把函数变成 applicative style,可以操作 applicatives 并回传 applicatives。
总之当我们在做 (++) <$> Just "johntra" <*> Just "volta"
时,首先我们将 (++)
map over 到 Just "johntra"
,然后产生 Just ("johntra"++)
,其中 (++)
的型别为 (++) :: [a] -> [a] -> [a]
,Just ("johntra"++)
的型别为 Maybe ([Char] -> [Char])
。注意到 (++)
是如何吃掉第一个参数,以及我们是怎么决定 a
是 Char
的。当我们做 Just ("johntra"++) <*> Just "volta"
,他接受一个包在 Just
中的函数,然后 map over Just "volta"
,产生了 Just "johntravolta"
。如果两个值中有任意一个为 Nothing
,那整个结果就会是 Nothing
。
到目前为止我们只有用 Maybe
当作我们的案例,你可能也会想说 applicative functor 差不多就等于 Maybe
。不过其实有许多其他 Applicative
的 instance。我们来看看有哪些。
List 也是 applicative functor。很惊讶吗?来看看我们是怎么定义 []
为 Applicative
的 instance 的。
instance Applicative [] where
pure x = [x]
fs <*> xs = [f x | f <- fs, x <- xs]
早先我们说过 pure
是把一个值放进预设的 context 中。换种说法就是一个会产生那个值的最小 context。而对 list 而言最小 context 就是 []
,但由于空的 list 并不包含一个值,所以我们没办法把他当作 pure
。这也是为什么 pure
其实是接受一个值然后回传一个包含单元素的 list。同样的,Maybe
的最小 context 是 Nothing
,但他其实表示的是没有值。所以 pure
其实是被实作成 Just
的。
ghci> pure "Hey" :: [String]
["Hey"]
ghci> pure "Hey" :: Maybe String
Just "Hey"
至于 <*>
呢?如果我们假定 <*>
的型别是限制在 list 上的话,我们会得到 (<*>) :: [a -> b] -> [a] -> [b]
。他是用 list comprehension 来实作的。<*>
必须要从左边的参数取出函数,将他 map over 右边的参数。但左边的 list 有可能不包含任何函数,也可能包含一个函数,甚至是多个函数。而右边的 list 有可能包含多个值。这也是为什么我们用 list comprehension 的方式来从两个 list 取值。我们要对左右任意的组合都做套用的动作。而得到的结果就会是左右两者任意组合的结果。
ghci> [(*0),(+100),(^2)] <*> [1,2,3]
[0,0,0,101,102,103,1,4,9]
左边的 list 包含三个函数,而右边的 list 有三个值。所以结果会是有九个元素的 list。在左边 list 中的每一个函数都被套用到右边的值。如果我们今天在 list 中的函数是接收两个参数的,我们也可以套用到两个 list 上。
ghci> [(+),(*)] <*> [1,2] <*> [3,4]
[4,5,5,6,3,4,6,8]
由于 <*>
是 left-associative,也就是说 [(+),(*)] <*> [1,2]
会先运作,产生 [(1+),(2+),(1*),(2*)]
。由于左边的每一个函数都套用至右边的每一个值。也就产生 [(1+),(2+),(1*),(2*)] <*> [3,4]
,其便是最终结果。
list 的 applicative style 是相当有趣的:
ghci> (++) <$> ["ha","heh","hmm"] <*> ["?","!","."]
["ha?","ha!","ha.","heh?","heh!","heh.","hmm?","hmm!","hmm."]
看看我们是如何将一个接受两个字串参数的函数套用到两个 applicative functor 上的,只要用适当的 applicative 运算子就可以达成。
你可以将 list 看作是一个 non-deterministic 的计算。而对于像 100
或是 "what"
这样的值则是 deterministic 的计算,只会有一个结果。而 [1,2,3]
则可以看作是没有确定究竟是哪一种结果。所以他代表的是所有可能的结果。当你在做 (+) <$> [1,2,3] <*> [4,5,6]
,你可以想做是把两个 non-deterministic 的计算做 +
,只是他会产生另一个 non-deterministic 的计算,而且结果更加不确定。
Applicative style 对于 list 而言是一个取代 list comprehension 的好方式。在第二章中,我们想要看到 [2,5,10]
跟 [8,10,11]
相乘的结果,所以我们这样做:
ghci> [ x*y | x <- [2,5,10], y <- [8,10,11]]
[16,20,22,40,50,55,80,100,110]
我们只是从两个 list 中取出元素,并将一个函数套用在任何元素的组合上。这也可以用 applicative style 的方式来写:
ghci> (*) <$> [2,5,10] <*> [8,10,11]
[16,20,22,40,50,55,80,100,110]
这写法对我来说比较清楚。可以清楚表达我们是要对两个 non-deterministic 的计算做 *
。如果我们想要所有相乘大于 50 可能的计算结果,我们会这样写:
ghci> filter (>50) $ (*) <$> [2,5,10] <*> [8,10,11]
[55,80,100,110]
很容易看到 pure f <*> xs
等价于 fmap f xs
。而 pure f
就是 [f]
,而且 [f] <*> xs
可将左边的每个函数套用至右边的每个值。但左边其实只有一个函数,所以他做起来就像是 mapping。
另一个我们已经看过的 Applicative
的 instance 是 IO
,来看看他是怎么实作的:
instance Applicative IO where
pure = return
a <*> b = do
f <- a
x <- b
return (f x)
由于 pure
是把一个值放进最小的 context 中,所以将 return
定义成 pure
是很合理的。因为 return
也是做同样的事情。他做了一个不做任何事情的 I/O action,他可以产生某些值来作为结果,但他实际上并没有做任何 I/O 的动作,例如说印出结果到终端或是档案。
如果 <*>
被限定在 IO
上操作的话,他的型别会是 (<*>) :: IO (a -> b) -> IO a -> IO b
。他接受一个产生函数的 I/O action,还有另一个 I/O action,并从以上两者创造一个新的 I/O action,也就是把第二个参数喂给第一个参数。而得到回传的结果,然后放到新的 I/O action 中。我们用 do 的语法来实作他。你还记得的话 do 就是把好几个 I/O action 黏在一起,变成一个大的 I/O action。
而对于 Maybe
跟 []
而言,我们可以把 <*>
想做是从左边的参数取出一个函数,然后套用到右边的参数上。至于 IO
,这种取出的类比方式仍然适用,但我们必须多加一个 sequencing 的概念,因为我们是从两个 I/O action 中取值,也是在 sequencing,把他们黏成一个。我们从第一个 I/O action 中取值,但要取出 I/O action 的结果,他必须要先被执行过。
考虑下面这个范例:
myAction :: IO String
myAction = do
a <- getLine
b <- getLine
return $ a ++ b
这是一个提示使用者输入两行并产生将两行输入串接在一起结果的一个 I/O action。我们先把两个 getLine
黏在一起,然后用一个 return
,这是因为我们想要这个黏成的 I/O action 包含 a ++ b
的结果。我们也可以用 applicative style 的方式来描述:
myAction :: IO String
myAction = (++) <$> getLine <*> getLine
我们先前的作法是将两个 I/O action 的结果喂给函数。还记得 getLine
的型别是 getLine :: IO String
。当我们对 applicative functor 使用 <*>
的时候,结果也会是 applicative functor。
如果我们再使用盒子的类比,我们可以把 getLine
想做是一个去真实世界中拿取字串的盒子。而 (++) <$> getLine <*> getLine
会创造一个比较大的盒子,这个大盒子会派两个盒子去终端拿取字串,并把结果串接起来放进自己的盒子中。
(++) <$> getLine <*> getLine
的型别是 IO String
,他代表这个表达式式一个再普通不过的 I/O action,他里面也装着某种值。这也是为什么我们可以这样写:
main = do
a <- (++) <$> getLine <*> getLine
putStrLn $ "The two lines concatenated turn out to be: " ++ a
如果你发现你是在做 binding I/O action 的动作,而且在 binding 之后还呼叫一些函数,最后用 return
来将结果包起来。 那你可以考虑使用 applicative style,这样可以更简洁。
另一个 Applicative
的 instance 是 (->) r
。虽然他们通常是用在 code golf 的情况,但他们还是十分有趣的例子。所以我们还是来看一下他们是怎么被实作的。
如果你忘记 ``(->) r`` 的意思,回去翻翻前一章节我们介绍 ``(->) r`` 作为一个 functor 的范例。
instance Applicative ((->) r) where
pure x = (\_ -> x)
f <*> g = \x -> f x (g x)
当我们用 pure
将一个值包成 applicative functor 的时候,他产生的结果永远都会是那个值。也就是最小的 context。那也是为什么对于 function 的 pure
实作来讲,他就是接受一个值,然后造一个函数永远回传那个值,不管他被喂了什么参数。如果你限定 pure
的型别至 (->) r
上,他就会是 pure :: a -> (r -> a)
。
ghci> (pure 3) "blah"
3
由于 currying 的关系,函数套用是 left-associative,所以我们忽略掉括弧。
ghci> pure 3 "blah"
3
而 <*>
的实作是比较不容易了解的,我们最好看一下怎么用 applicative style 的方式来使用作为 applicative functor 的 function。
ghci> :t (+) <$> (+3) <*> (*100)
(+) <$> (+3) <*> (*100) :: (Num a) => a -> a
ghci> (+) <$> (+3) <*> (*100) $ 5
508
将两个 applicative functor 喂给 <*>
可以产生一个新的 applicative functor,所以如果我们丢给他两个函数,我们能得到一个新的函数。所以是怎么一回事呢?当我们做 (+) <$> (+3) <*> (*100)
,我们是在实作一个函数,他会将 (+3)
跟 (*100)
的结果再套用 +
。要看一个实际的范例的话,可以看一下 (+) <$> (+3) <*> (*100) $ 5
首先 5
被丢给 (+3)
跟 (*100)
,产生 8
跟 500
。然后 +
被套用到 8
跟 500
,得到 508
。
ghci> (\x y z -> [x,y,z]) <$> (+3) <*> (*2) <*> (/2) $ 5
[8.0,10.0,2.5]
这边也一样。我们创建了一个函数,他会呼叫 \x y z -> [x,y,z]
,而丢的参数是 (+3)
, (*2)
跟 (/2)
。5
被丢给以上三个函数,然后他们结果又接到 \x y z -> [x, y, z]
。
你可以将函数想做是装着最终结果的盒子,所以 k <$> f <*> g
会制造一个函数,他会将 f
跟 g
的结果丢给 k
。当我们做 (+) <$> Just 3 <*> Just 5
,我们是用 +
套用在一些可能有或可能没有的值上,所以结果也会是可能有或没有。当我们做 (+) <$> (+10) <*> (+5)
,我们是将 +
套用在 (+10)
跟 (+5)
的结果上,而结果也会是一个函数,当被喂给一个参数的时候会产生结果。
我们通常不会将函数当作 applicative 用,不过仍然值得当作练习。对于 (->) r
怎么定义成 Applicative
的并不是真的那么重要,所以如果你不是很懂的话也没关系。这只是让你获得一些操作上的直觉罢了。
一个我们之前还没碰过的 Applicative
的 instance 是 ZipList
,他是包含在 Control.Applicative
中。
对于 list 要作为一个 applicative functor 可以有多种方式。我们已经介绍过其中一种。如果套用 <*>
,左边是许多函数,而右边是许多值,那结果会是函数套用到值的所有组合。如果我们做 [(+3),(*2)] <*> [1,2]
。那 (+3)
会先套用至 1
跟 2
。接着 (*2)
套用至 1
跟 2
。而得到 [4,5,2,4]
。
然而 [(+3),(*2)] <*> [1,2]
也可以这样运作:把左边第一个函数套用至右边第一个值,接着左边第二个函数套用右边第二个值,以此类推。这样得到的会是 [4,4]
。或是 [1 + 3, 2 * 2]
。
由于一个型别不能对同一个 typeclass 定义两个 instance,所以才会定义了 ZipList a
,他只有一个构造子 ZipList
,他只包含一个栏位,他的型别是 list。
instance Applicative ZipList where
pure x = ZipList (repeat x)
ZipList fs <*> ZipList xs = ZipList (zipWith (\f x -> f x) fs xs)
<*>
做的就是我们之前说的。他将第一个函数套用至第一个值,第二个函数套用第二个值。这也是 zipWith (\f x -> f x) fs xs
做的事。由于 zipWith
的特性,所以结果会跟 list 中比较短的那个一样长。
pure
也值得我们讨论一下。他接受一个值,把他重复地放进一个 list 中。pure "haha"
就会是 ZipList (["haha","haha","haha"...
。这可能会造成些混淆,毕竟我们说过 pure
是把一个值放进一个最小的 context 中。而你会想说无限长的 list 不可能会是一个最小的 context。但对于 zip list 来说这是很合理的,因为他必须在 list 的每个位置都有值。这也遵守了 pure f <*> xs
必须要等价于 fmap f xs
的特性。如果 pure 3
只是回传 ZipList [3]
,那 pure (*2) <*> ZipList [1,5,10]
就只会算出 ZipList [2]
,因为两个 zip list 算出结果的长度会是比较短的那个的长度。如果我们 zip 一个有限长的 list 以及一个无限长的 list,那结果的长会是有限长的 list 的长度。
那 zip list 是怎么用 applicative style 操作的呢?我们来看看,ZipList a
型别并没有定义成 Show
的 instance,所以我们必须用 getZipList
函数来从 zip list 取出一个普通的 list。
ghci> getZipList $ (+) <$> ZipList [1,2,3] <*> ZipList [100,100,100]
[101,102,103]
ghci> getZipList $ (+) <$> ZipList [1,2,3] <*> ZipList [100,100..]
[101,102,103]
ghci> getZipList $ max <$> ZipList [1,2,3,4,5,3] <*> ZipList [5,3,1,2]
[5,3,3,4]
ghci> getZipList $ (,,) <$> ZipList "dog" <*> ZipList "cat" <*> ZipList "rat"
[('d','c','r'),('o','a','a'),('g','t','t')]
``(,,)`` 函数跟 ``\x y z -> (x,y,z)`` 是等价的,而 ``(,)`` 跟 ``\x y -> (x,y)`` 是等价的。
除了 zipWith
,标准函式库中也有 zipWith3
, zipWith4
之类的函数,最多支援到 7。zipWith
接受一个接受两个参数的函数,并把两个 list zip 起来。zipWith3
则接受一个接受三个参数的函数,然后把三个 list zip 起来。以此类推。用 applicative style 的方式来操作 zip list 的话,我们就不需要对每个数量的 list 都定义一个独立的 zip 函数来 zip 他们。我们只需要用 applicative style 的方式来把任意数量的 list zip 起来就可以了。
Control.Applicative
定义了一个函数叫做 liftA2
,他的型别是 liftA2 :: (Applicative f) => (a -> b -> c) -> f a -> f b -> f c
。他定义如下:
liftA2 :: (Applicative f) => (a -> b -> c) -> f a -> f b -> f c
liftA2 f a b = f <$> a <*> b
并没有太难理解的东西,他不过就是对两个 applicatives 套用函数而已,而不用我们刚刚熟悉的 applicative style。我们提及他的理由只是要展示为什么 applicative functors 比起一般的普通 functor 要强。如果只是普通的 functor 的话,我们只能将一个函数 map over 这个 functor。但有了 applicative functor,我们可以对好多个 functor 套用一个函数。看看这个函数的型别,他会是 (a -> b -> c) -> (f a -> f b -> f c)
。当我们从这样的角度来看他的话,我们可以说 liftA2
接受一个普通的二元函数,并将他升级成一个函数可以运作在两个 functor 之上。
另外一个有趣的概念是,我们可以接受两个 applicative functor 并把他们结合成一个 applicative functor,这个新的将这两个 applicative functor 装在 list 中。举例来说,我们现在有 Just 3
跟 Just 4
。我们假设后者是一个只包含单元素的 list。
ghci> fmap (\x -> [x]) (Just 4)
Just [4]
所以假设我们有 Just 3
跟 Just [4]
。我们有怎么得到 Just [3,4]
呢?很简单。
ghci> liftA2 (:) (Just 3) (Just [4])
Just [3,4]
ghci> (:) <$> Just 3 <*> Just [4]
Just [3,4]
还记得 :
是一个函数,他接受一个元素跟一个 list,并回传一个新的 list,其中那个元素已经接在前面。现在我们有了 Just [3,4]
,我们能够将他跟 Just 2
绑在一起变成 Just [2,3,4]
吗?当然可以。我们可以将任意数量的 applicative 绑在一起变成一个 applicative,里面包含一个装有结果的 list。我们试着实作一个函数,他接受一串装有 applicative 的 list,然后回传一个 applicative 里面有一个装有结果的 list。我们称呼他为 sequenceA
。
sequenceA :: (Applicative f) => [f a] -> f [a]
sequenceA [] = pure []
sequenceA (x:xs) = (:) <$> x <*> sequenceA xs
居然用到了递回!首先我们来看一下他的型别。他将一串 applicative 的 list 转换成一个 applicative 装有一个 list。从这个资讯我们可以推测出边界条件。如果我们要将一个空的 list 变成一个装有 list 的 applicative。我们只要把这个空的 list 放进一个预设的 context。现在来看一下我们怎么用递回的。如果们有一个可以分成头跟尾的 list(x
是一个 applicative 而 xs
是一串 applicatve),我们可以对尾巴呼叫 sequenceA
,便会得到一个装有 list 的 applicative。然后我们只要将在 x
中的值把他接到装有 list 的 applicative 前面就可以了。
所以如果我们做 sequenceA [Just 1, Just 2]
,也就是 (:) <$> Just 1 <*> sequenceA [Just 2]
。那会等价于 (:) <$> Just 1 <*> ((:) <$> Just 2 <*> sequenceA [])
。我们知道 sequenceA []
算出来会是 Just []
,所以运算式就变成 (:) <$> Just 1 <*> ((:) <$> Just 2 <*> Just [])
,也就是 (:) <$> Just 1 <*> Just [2]
,算出来就是 Just [1,2]
。
另一种实作 sequenceA
的方式是用 fold。要记得几乎任何需要走遍整个 list 并 accumulate 成一个结果的都可以用 fold 来实作。
sequenceA :: (Applicative f) => [f a] -> f [a]
sequenceA = foldr (liftA2 (:)) (pure [])
我们从右往左走,并且起始的 accumulator 是用 pure []
。我们是用 liftA2 (:)
来结合 accumulator 跟 list 中最后的元素,而得到一个 applicative,里面装有一个单一元素的一个 list。然后我们再用 liftA2 (:)
来结合 accumulator 跟最后一个元素,直到我们只剩下 accumulator 为止,而得到一个 applicative,里面装有所有结果。
我们来试试看套用在不同 applicative 上。
ghci> sequenceA [Just 3, Just 2, Just 1]
Just [3,2,1]
ghci> sequenceA [Just 3, Nothing, Just 1]
Nothing
ghci> sequenceA [(+3),(+2),(+1)] 3
[6,5,4]
ghci> sequenceA [[1,2,3],[4,5,6]]
[[1,4],[1,5],[1,6],[2,4],[2,5],[2,6],[3,4],[3,5],[3,6]]
ghci> sequenceA [[1,2,3],[4,5,6],[3,4,4],[]]
[]
很酷吧。当我们套用在 Maybe
上时,sequenceA
创造一个新的 Maybe
,他包含了一个 list 装有所有结果。如果其中一个值是 Nothing
,那整个结果就会是 Nothing
。如果你有一串 Maybe
型别的值,但你只在乎当结果不包含任何 Nothing
的情况,这样的特性就很方便。
当套用在函数时,sequenceA
接受装有一堆函数的 list,并回传一个回传 list 的函数。在我们的范例中,我们写了一个函数,他只接受一个数值作为参数,他会把他套用至 list 中的每一个函数,并回传一个包含结果的 list。sequenceA [(+3),(+2),(+1)] 3
会将 3
喂给 (+3)
, (+2)
跟 (+1)
,然后将所有结果装在一个 list 中。
而 (+) <$> (+3) <*> (*2)
会创见一个接受单一参数的一函数,将他同时喂给 (+3)
跟 (*2)
,然后呼叫 +
来将两者加起来。同样的道理,sequenceA [(+3),(*2)]
是制造一个接受单一参数的函数,他会将他喂给所有包含在 list 中的函数。但他最后不是呼叫 +
,而是呼叫 :
跟 pure []
来把结果接成一个 list,得到最后的结果。
当我们有一串函数,我们想要将相同的输入都喂给他们并检视结果的时候,sequenceA
非常好用。例如说,我们手上有一个数值,但不知道他是否满足一串 predicate。一种实作的方式是像这样:
ghci> map (\f -> f 7) [(>4),(<10),odd]
[True,True,True]
ghci> and $ map (\f -> f 7) [(>4),(<10),odd]
True
记住 and
接受一串布林值,并只有在全部都是 True
的时候才回传 True
。 另一种实作方式是用 sequenceA
:
ghci> sequenceA [(>4),(<10),odd] 7
[True,True,True]
ghci> and $ sequenceA [(>4),(<10),odd] 7
True
sequenceA [(>4),(<10),odd]
接受一个函数,他接受一个数值并将他喂给所有的 predicate,包含 [(>4),(<10),odd]
。然后回传一串布林值。他将一个型别为 (Num a) => [a -> Bool]
的 list 变成一个型别为 (Num a) => a -> [Bool]
的函数,很酷吧。
由于 list 要求里面元素的型别要一致,所以包含在 list 中的所有函数都是同样型别。你不能创造一个像是 [ord, (+3)]
这样的 list,因为 ord
接受一个字元并回传一个数值,然而 (+3)
接受一个数值并回传一个数值。
当跟 []
一起使用的时候,sequenceA
接受一串 list,并回传另一串 list。他实际上是创建一个包含所有可能组合的 list。为了方便说明,我们比较一下使用 sequenceA
跟 list comprehension 的差异:
ghci> sequenceA [[1,2,3],[4,5,6]]
[[1,4],[1,5],[1,6],[2,4],[2,5],[2,6],[3,4],[3,5],[3,6]]
ghci> [[x,y] | x <- [1,2,3], y <- [4,5,6]]
[[1,4],[1,5],[1,6],[2,4],[2,5],[2,6],[3,4],[3,5],[3,6]]
ghci> sequenceA [[1,2],[3,4]]
[[1,3],[1,4],[2,3],[2,4]]
ghci> [[x,y] | x <- [1,2], y <- [3,4]]
[[1,3],[1,4],[2,3],[2,4]]
ghci> sequenceA [[1,2],[3,4],[5,6]]
[[1,3,5],[1,3,6],[1,4,5],[1,4,6],[2,3,5],[2,3,6],[2,4,5],[2,4,6]]
ghci> [[x,y,z] | x <- [1,2], y <- [3,4], z <- [5,6]]
[[1,3,5],[1,3,6],[1,4,5],[1,4,6],[2,3,5],[2,3,6],[2,4,5],[2,4,6]]
这可能有点难以理解,但如果你多做点尝试,你会比较能看出来些眉目。假设我们在做 sequenceA [[1,2],[3,4]]
。要知道这是怎么回事,我们首先用 sequenceA
的定义 sequenceA (x:xs) = (:) <$> x <*> sequenceA xs
还有边界条件 sequenceA [] = pure []
来看看。你不需要实际计算,但他可以帮助你理解 sequenceA
是怎么运作在一串 list 上,毕竟这有点复杂。
# 我们从 ``sequenceA [[1,2],[3,4]]`` 开始
# 那可以被计算成 ``(:) <$> [1,2] <*> sequenceA [[3,4]]``
# 计算内层的 ``sequenceA``,会得到 ``(:) <$> [1,2] <*> ((:) <$> [3,4] <*> sequenceA [])``
# 我们碰到了边界条件,所以会是 ``(:) <$> [1,2] <*> ((:) <$> [3,4] <*> [[]])``
# 现在我们计算 ``(:) <$> [3,4] <*> [[]] `` 的部份,我们会对左边 list 中的每一个值 (也就是 ``3`` 跟 ``4``) 跟右边的每一个值 (只有 ``[]``)套用 ``:``,而得到 ``[3:[], 4:[]]``,也就是 ``[[3],[4]]``。所以我们有 ``(:) <$> [1,2] <*> [[3],[4]]``
# 而对于左边的每一个值(``1`` 跟 ``2``)以及右边可能的值(``[3]`` 跟 ``[4]``)我们套用 ``:`` 而得到 ``[1:[3], 1:[4], 2:[3], 2:[4]]``,他等于 ``[[1,3],[1,4],[2,3],[2,4]]``
计算 (+) <$> [1,2] <*> [4,5,6]
会得到一个 non-deterministic 的结果 x + y
,其中 x
代表 [1,2]
中的每一个值,而 y
代表 [4,5,6]
中的每一个值。我们用 list 来表示每一种可能的情形。同样的,当我们在做 sequence [[1,2],[3,4],[5,6],[7,8]]
,他的结果会是 non-deterministic 的 [x,y,z,w]
,其中 x
代表 [1,2]
中的每一个值,而 y
代表 [3,4]
中的每一个值。以此类推。我们用 list 代表 non-deterministic 的计算,每一个元素都是一个可能的情形。这也是为什么会用到 list of list。
当使用在 I/O action 上的时候,sequenceA
跟 sequence
是等价的。他接受一串 I/O action 并回传一个 I/O action,这个 I/O action 会计算 list 中的每一个 I/O action,并把结果放在一个 list 中。要将型别为 [IO a]
的值转换成 IO [a]
的值,也就是会产生一串 list 的一个 I/O action,那这些 I/O action 必须要一个一个地被计算,毕竟对于这些 I/O action 你没办法不计算就得到结果。
ghci> sequenceA [getLine, getLine, getLine]
heyh
ho
woo
["heyh","ho","woo"]
就像普通的函数一样,applicative functors 也遵循一些定律。其中最重要的一个是我们之前提过的 pure f <*> x = fmap f x
。你可以证明一些我们之前介绍过的 applicative functor 遵守这个定律当作练习。其他的 functors law 有:
# ``pure id <*> v = v``
# ``pure (.) <*> u <*> v <*> w = u <*> (v <*> w)``
# ``pure f <*> pure x = pure (f x)``
# ``u <*> pure y = pure ($ y) <*> u``
我们不会一项一项地细看,那样会花费很大的篇幅而且对读者来说很无聊,但如果你有兴趣,你可以针对某些 instance 看看他们会不会遵守。
结论就是 applicative functor 不只是有趣而且实用, 他允许我们结合不同种类的计算,像是 I/O 计算,non-deterministic 的计算,有可能失败的计算等等。而使用 <$>
跟 <*>
我们可以将普通的函数来运作在任意数量的 applicative functors 上。
#
关键字"newtype"
到目前为止,我们已经看过了如何用 data
关键字定义自己的 algebraic data type。我们也学习到了如何用 type
来定义 type synonyms。在这个章节中,我们会看一下如何使用 newtype
来从一个现有的型别中定义出新的型别,并说明我们为什么会想要那么做。
在之前的章节中,我们了解到其实 list 有很多种方式可以被视为一种 applicative functor。一中方式是定义 <*>
将左边的每一个值跟右边的每一个值组合,而得到各种组合的结果。
ghci> [(+1),(*100),(*5)] <*> [1,2,3]
[2,3,4,100,200,300,5,10,15]
第二种方式是将 <*>
定义成将左边的第一个函数套用至右边的第一个值,然后将左边第二个函数套用至右边第二个值。以此类推。最终,这表现得有点像将两个 list 用一个拉链拉起来一样。但由于 list 已经被定义成 Applicaitive
的 instance 了,所以我们要怎么要让 list 可以被定义成第二种方式呢?如果你还记得我们说过我们是有很好的理由定义了 ZipList a
,其中他里面只包含一个值构造子跟只包含一个栏位。其实他的理由就是要让 ZipList
定义成用拉链的方式来表现 applicative 行为。我们只不过用 ZipList
这个构造子将他包起来,然后用 getZipList
来解开来。
ghci> getZipList $ ZipList [(+1),(*100),(*5)] <*> ZipList [1,2,3]
[2,200,15]
所以这跟 newtype 这个关键字有什么关系呢?想想看我们是怎么宣告我们的 ZipList a
的,一种方式是像这样:
data ZipList a = ZipList [a]
也就是一个只有一个值构造子的型别而且那个构造子里面只有一个栏位。我们也可以用 record syntax 来定义一个解开的函数:
data ZipList a = ZipList { getZipList :: [a] }
这样听起来不错。这样我们就有两种方式来让一个型别来表现一个 typeclass,我们可以用 data
关键字来把一个型别包在另一个里面,然后再将他定义成第二种表现方式。
而在 Haskell 中 newtype
正是为了这种情形,我们想将一个型别包在另一个型别中。在实际的函式库中 ZipList a
是这样定义了:
newtype ZipList a = ZipList { getZipList :: [a] }
这边我们不用 data
关键字反而是用 newtype
关键字。这是为什么呢?第一个理由是 newtype
比较快速。如果你用 data
关键字来包一个型别的话,在你执行的时候会有一些包起来跟解开来的成本。但如果你用 newtype
的话,Haskell 会知道你只是要将一个现有的型别包成一个新的型别,你想要内部运作完全一样但只是要一个全新的型别而已。有了这个概念,Haskell 可以将包裹跟解开来的成本都去除掉。
那为什么我们不是一直使用 newtype
呢?当你用 newtype
来制作一个新的型别时,你只能定义单一一个值构造子,而且那个构造子只能有一个栏位。但使用 data
的话,你可以让那个型别有好几个值构造子,并且每个构造子可以有零个或多个栏位。
data Profession = Fighter | Archer | Accountant
data Race = Human | Elf | Orc | Goblin
data PlayerCharacter = PlayerCharacter Race Profession
当使用 newtype
的时候,你是被限制只能用一个值构造子跟单一栏位。
对于 newtype
我们也能使用 deriving
关键字。我们可以 derive 像是 Eq
, Ord
, Enum
, Bounded
, Show
跟 Read
的 instance。如果我们想要对新的型别做 derive,那原本的型别必须已经在那个 typeclass 中。这样很合理,毕竟 newtype
就是要将现有的型别包起来。如果我们按照下面的方式定义的话,我们就能对我们的型别做印出以及比较相等性的操作:
newtype CharList = CharList { getCharList :: [Char] } deriving (Eq, Show)
我们来跑跑看:
ghci> CharList "this will be shown!"
CharList {getCharList = "this will be shown!"}
ghci> CharList "benny" == CharList "benny"
True
ghci> CharList "benny" == CharList "oisters"
False
对于这个 newtype
,他的值构造子有下列型别:
CharList :: [Char] -> CharList
他接受一个 [Char]
的值,例如 "my sharona"
并回传一个 CharList
的值。从上面我们使用 CharList
的值构造子的范例中,我们可以看到的确是这样。相反地,getCharList
具有下列的型别。
getCharList :: CharList -> [Char]
他接受一个 CharList
的值并将他转成 [Char]
。你可以将这个想成包装跟解开的动作,但你也可以将他想成从一个型别转成另一个型别。
#
Using newtype to make type class instances
有好几次我们想要让我们的型别属于某个 typeclass,但型别变数并没有符合我们想要的。要把 Maybe
定义成 Functor
的 instance 很容易,因为 Functor
这个 typeclass 被定义如下:
class Functor f where
fmap :: (a -> b) -> f a -> f b
我们先定义如下:
instance Functor Maybe where
然后我们实作 fmap
。当所有的型别变数被填上时,由于 Maybe
取代了 Functor
中 f
的位置,所以如果我们看看 fmap
运作在 Maybe
上时是什么样,他会像这样:
fmap :: (a -> b) -> Maybe a -> Maybe b
看起来不错吧?现在我们想要 tuple 成为 Functor
的一个 instance,所以当我们用 fmap
来 map over 一个 tuple 时,他会先套用到 tuple 中的第一个元素。这样当我们做 fmap (+3) (1,1)
会得到 (4,1)
。不过要定义出这样的 instance 有些困难。对于 Maybe
,我们只要写 instance Functor Maybe where
,这是因为对于只吃一个参数的型别构造子我们很容易定义成 Functor
的 instance。但对于 (a,b)
这样的就没办法。要绕过这样的困境,我们可以用 newtype
来重新定义我们的 tuple,这样第二个型别参数就代表了 tuple 中的第一个元素部份。
newtype Pair b a = Pair { getPair :: (a,b) }
现在我们可以将他定义成 Functor
的 instance,所以函数被 map over tuple 中的第一个部份。
instance Functor (Pair c) where
fmap f (Pair (x,y)) = Pair (f x, y)
正如你看到的,我们可以对 newtype 定义的型别做模式匹配。我们用模式匹配来拿到底层的 tuple,然后我们将 f
来套用至 tuple 的第一个部份,然后我们用 Pair
这个值构造子来将 tuple 转换成 Pair b a
。如果我们问 fmap
的型别究竟是什么,他会是:
fmap :: (a -> b) -> Pair c a -> Pair c b
我们说过 instance Functor (Pair c) where
跟 Pair c
取代了 Functor
中 f
的位置:
class Functor f where
fmap :: (a -> b) -> f a -> f b
如果我们将一个 tuple 转换成 Pair b a
,我们可以用 fmap
来 map over 第一个部份。
ghci> getPair $ fmap (*100) (Pair (2,3))
(200,3)
ghci> getPair $ fmap reverse (Pair ("london calling", 3))
("gnillac nodnol",3)
#
On newtype laziness
我们提到 newtype
一般来讲比 data
来得有效率。newtype
能做的唯一一件事就是将现有的型别包成新的型别。这样 Haskell 在内部就能将新的型别的值用旧的方式来操作。只是要记住他们还是不同的型别。这代表 newtype
并不只是有效率,他也具备 lazy 的特性。我们来说明一下这是什么意思。
就像我们之前说得,Haskell 预设是具备 lazy 的特性,这代表只有当我们要将函数的结果印出来的时候计算才会发生。或者说,只有当我们真的需要结果的时候计算才会发生。在 Haskell 中 undefined
代表会造成错误的计算。如果我们试着计算他,也就是将他印到终端中,Haskell 会丢出错误。
ghci> undefined
*** Exception: Prelude.undefined
然而,如果我们做一个 list,其中包含一些 undefined
的值,但却要求一个不是 undefined
的 head,那一切都会顺利地被计算,因为 Haskell 并不需要 list 中其他元素来得到结果。我们仅仅需要看到第一个元素而已。
ghci> head [3,4,5,undefined,2,undefined]
3
现在们考虑下面的型别:
data CoolBool = CoolBool { getCoolBool :: Bool }
这是一个用 data
关键字定义的 algebraic data type。他有一个值建构子并只有一个型别为 Bool
的栏位。我们写一个函数来对 CoolBool
做模式匹配,并回传一个 "hello"
的值。他并不会管 CoolBool
中装的究竟是 True
或 False
。
helloMe :: CoolBool -> String
helloMe (CoolBool _) = "hello"
这次我们不喂给这个函数一个普通的 CoolBool
,而是丢给他一个 undefined
。
ghci> helloMe undefined
"*** Exception: Prelude.undefined "
结果收到了一个 Exception。是什么造成这个 Exception 的呢?用 data
定义的型别可以有好几个值构造子(尽管 CoolBool
只有一个)所以当我们要看看喂给函数的值是否是 (CoolBool _)
的形式,Haskell 会需要做一些基本的计算来看看是哪个值构造子被用到。但当我们计算 undefined
的时候,就算是一点也会丢出 Exception。
我们不用 data
来定义 CoolBool
而用 newtype
:
newtype CoolBool = CoolBool { getCoolBool :: Bool }
我们不用修改 helloMe
函数,因为对于模式匹配使用 newtype
或 data
都是一样。我们再来将 undefined
喂给 helloMe
。
ghci> helloMe undefined
"hello"
居然正常运作!为什么呢?正如我们说过得,当我们使用 newtype
的时候,Haskell 内部可以将新的型别用旧的型别来表示。他不必加入另一层 box 来包住旧有的型别。他只要注意他是不同的型别就好了。而且 Haskell 会知道 newtype
定义的型别一定只会有一个构造子,他不必计算喂给函数的值就能确定他是 (CoolBool _)
的形式,因为 newtype
只有一个可能的值跟单一栏位!
这样行为的差异可能没什么关系,但实际上他非常重要。因为他让我们认知到尽管从撰写程式的观点来看没什么差异,但他们的确是两种不同的机制。尽管 data
可以让你从无到有定义型别,newtype
是从一个现有的型别做出来的。对 newtype
做模式匹配并不是像从盒子中取出东西,他比较像是将一个型别转换成另一个型别。
#
type vs newtype vs data
到目前为止,你也许对于 type
,data
跟 newtype
之间的差异还不是很了解,让我们快速复习一遍。
type
关键字是让我们定义 type synonyms。他代表我们只是要给一个现有的型别另一个名字,假设我们这样做:
type IntList = [Int]
这样做可以允许我们用 IntList
的名称来指称 [Int]
。我们可以交换地使用他们。但我们并不会因此有一个 IntList
的值构造子。因为 [Int]
跟 IntList
只是两种指称同一个型别的方式。我们在指称的时候用哪一个并无所谓。
ghci> ([1,2,3] :: IntList) ++ ([1,2,3] :: [Int])
[1,2,3,1,2,3]
当我们想要让 type signature 更清楚一些,给予我们更了解函数的 context 的时候,我们会定义 type synonyms。举例来说,当我们用一个型别为 [(String,String)]
的 association list 来代表一个电话簿的时候,我们可以定义一个 PhoneBook
的 type synonym,这样 type signature 会比较容易读。
newtype
关键字将现有的型别包成一个新的型别,大部分是为了要让他们可以是特定 typeclass 的 instance 而这样做。当我们使用 newtype
来包裹一个现有的型别时,这个型别跟原有的型别是分开的。如果我们将下面的型别用 newtype
定义:
newtype CharList = CharList { getCharList :: [Char] }
我们不能用 ++
来将 CharList
跟 [Char]
接在一起。我们也不能用 ++
来将两个 CharList
接在一起,因为 ++
只能套用在 list 上,而 CharList
并不是 list,尽管你会说他包含一个 list。但我们可以将两个 CharList
转成 list,将他们 ++
然后再转回 CharList
。
当我们在 newtype
宣告中使用 record syntax 的时候,我们会得到将新的型别转成旧的型别的函数,也就是我们 newtype
的值构造子,以及一个函数将他的栏位取出。新的型别并不会被自动定义成原有型别所属的 typeclass 的一个 instance,所以我们必须自己来 derive 他们。
实际上你可以将 newtype
想成是只能定义一个构造子跟一个栏位的 data
宣告。如果你碰到这种情形,可以考虑使用 newtype
。
使用 data
关键字是为了定义自己的型别。他们可以在 algebraic data type 中放任意数量的构造子跟栏位。可以定义的东西从 list, Maybe
到 tree。
如果你只是希望你的 type signature 看起来比较干净,你可以只需要 type synonym。如果你想要将现有的型别包起来并定义成一个 type class 的 instance,你可以尝试使用 newtype。如果你想要定义完全新的型别,那你应该使用 data
关键字。
#
Monoids
Haskell 中 typeclass 是用来表示一个型别之间共有的行为,是一种 interface。我们介绍过 Eq
,他定义型别是否可以比较相等性,以及 Ord
,他表示可以被排序的型别。还介绍了更有趣的像是 Functor
跟 Applicative
。
当我们定义一个型别时,我们会想说他应该要支援的行为。也就是表现的行为是什么,并且要让他属于哪些 typeclass。如果希望他可以比较相等与否,那我们就应该定义他成为 Eq
的一个 instance。如果我们想要看看型别是否是一种 functor,我们可以定义他是 Functor
的一个 instance。以此类推。
考虑 *
是一个将两个数值相乘的一个函数。如果我们将一个数值乘上 1
,那就会得到自身的数值。我们实际上是做 1 * x
或 x * 1
并没有差别。结果永远会是 x
。同样的,++
是一个接受两个参数并回传新的值的一个函数。只是他不是相乘而是将两个 list 接在一起。而类似 *
,他也有一个特定的值,当他跟其他值使用 ++
时会得到同样的值。那个值就是空的 list []
。
ghci> 4 * 1
4
ghci> 1 * 9
9
ghci> [1,2,3] ++ []
[1,2,3]
ghci> [] ++ [0.5, 2.5]
[0.5,2.5]
看起来 *
之于 1
跟 ++
之于 []
有类似的性质:
# 函数同样接受两个参数
# 参数跟回传值是同样的型别
# 同样存在某些值当套用二元函数时并不会改变其他值
关于这两种操作还有另一个比较难察觉的性质就是,当我们对这个二元函数对三个以上的值操作并化简,函数套用的顺序并不会影响到结果。不论是 (3 * 4) * 5
或是 3 * (4 * 5)
,两种方式都会得到 60
。而 ++
也是相同的。
ghci> (3 * 2) * (8 * 5)
240
ghci> 3 * (2 * (8 * 5))
240
ghci> "la" ++ ("di" ++ "da")
"ladida"
ghci> ("la" ++ "di") ++ "da"
"ladida"
我们称呼这样的性质为结合律(associativity)。*
遵守结合律,++
也是。但 -
就不遵守。(5 - 3) - 4
跟 5 - (3 - 4)
得到的结果是不同的。
注意到这些性质并具体地写下来,就可以得到 monoid。一个 monoid 是你有一个遵守结合律的二元函数还有一个可以相对于那个函数作为 identity 的值。当某个值相对于一个函数是一个 identity,他表示当我们将这个值丢给函数时,结果永远会是另外一边的那个值本身。1
是相对于 *
的 identity,而 []
是相对于 ++
的 identity。在 Haskell 中还有许多其他的 monoid,这也是为什么我们定义了 Monoid
这个 typeclass。他描述了表现成 monoid 的那些型别。我们来看看这个 typeclass 是怎么被定义的:
class Monoid m where
mempty :: m
mappend :: m -> m -> m
mconcat :: [m] -> m
mconcat = foldr mappend mempty
Monoid
typeclass 被定义在 import Data.Monoid
中。我们来花些时间好好了解他。
首先我们看到只有具体型别才能定义成 Monoid
的 instance。由于在 typeclass 定义中的 m
并不接受任何型别参数。这跟 Functor
以及 Applicative
不同,他们要求他们的 instance 必须是一个接受单一型别参数的型别构造子。
第一个函数是 mempty
,由于他不接受任何参数,所以他并不是一个函数,而是一个 polymorphic 的常数。有点像是 Bounded
中的 minBound
一样。mempty
表示一个特定 monoid 的 identity。
再来我们看到 mappend
,你可能已经猜到,他是一个接受两个相同型别的值的二元函数,并回传同样的型别。不过要注意的是他的名字不太符合他真正的意思,他的名字隐含了我们要将两个东西接在一起。尽管在 list 的情况下 ++
的确将两个 list 接起来,但 *
则否。他只不过将两个数值做相乘。当我们再看到其他 Monoid
的 instance 时,我们会看到他们大部分都没有接起来的做,所以不要用接起来的概念来想像 mappend
,只要想像他们是接受两个 monoid 的值并回传另外一个就好了。
在 typeclass 定义中的最后一个函数是 mconcat
。他接受一串 monoid 值,并将他们用 mappend
简化成单一的值。他有一个预设的实作,就是从 mempty
作为起始值,然后用 mappend
来 fold。由于对于大部分的 instance 预设的实作就没什么问题,我们不会想要实作自己的 mconcat
。当我们定义一个型别属于 Monoid
的时候,多半实作 mempty
跟 mappend
就可以了。而 mconcat
就是因为对于一些 instance,有可能有比较有效率的方式来实作 mconcat
。不过大多数情况都不需要。
在我们继续接下去看几个 Monoid
的例子前,我们来看一下 monoid law。我们提过必须有一个值作为 identity 以及一个遵守结合律的二元函数当作前提。我们是可以定义一个 Monoid
的 instance 却不遵守这些定律的,但这样写出来的 instance 就没有用了,因为我们在使用 Monoid
的时候都是依靠这些定律才可以称作实质上的 monoid。所以我们必须确保他们遵守:
# ``mempty `mappend` x = x``
# ``x `mappend` mempty = x``
# ``(x `mappend` y) `mappend` z = x `mappend` (y `mappend` z)``
前两个描述了 mempty
相对于 mappend
必须要表现成 identity。而第三个定律说了 mappend
必须要遵守结合律。也就是说我们做 mappend
顺序并不重要。Haskell 不会自己检查这些定律是否有被遵守。所以你必须自己小心地检查他们。
#
Lists are monoids
没错,list 是一种 monoid。正如我们先前看到的,++
跟空的 list []
共同形成了一个 monoid。他的 instance 很简单:
instance Monoid [a] where
mempty = []
mappend = (++)
list 是 Monoid
typeclass 的一个 instance,这跟他们装的元素的型别无关。注意到我们写 instance Monoid [a]
而非 instance Monoid []
,这是因为 Monoid
要求 instance 必须是具体型别。
我们试着跑跑看,得到我们预期中的结果:
ghci> [1,2,3] `mappend` [4,5,6]
[1,2,3,4,5,6]
ghci> ("one" `mappend` "two") `mappend` "tree"
"onetwotree"
ghci> "one" `mappend` ("two" `mappend` "tree")
"onetwotree"
ghci> "one" `mappend` "two" `mappend` "tree"
"onetwotree"
ghci> "pang" `mappend` mempty
"pang"
ghci> mconcat [[1,2],[3,6],[9]]
[1,2,3,6,9]
ghci> mempty :: [a]
[]
注意到最后一行我们明白地标记出型别。这是因为如果只些 mempty
的话,GHCi 不会知道他是哪一个 instance 的 mempty
,所以我们必须清楚说出他是 list instance 的 mempty。我们可以使用一般化的型别 [a]
,因为空的 list 可以看作是属于任何型别。
由于 mconcat
有一个预设的实作,我们将某个型别定义成 Monoid
的型别时就可以自动地得到预设的实作。但对于 list 而言,mconcat
其实就是 concat
。他接受一个装有 list 的 list,并把他用 ++
来扁平化他。
list 的 instance 也遵守 monoid law。当我们有好几个 list 并且用 mappend
来把他们串起来,先后顺序并不是很重要,因为他们都是接在最后面。而且空的 list 也表现得如 identity 一样。注意到 monoid 并不要求 a `mappend` b
等于 b `mappend` a
。在 list 的情况下,他们明显不相等。
ghci> "one" `mappend` "two"
"onetwo"
ghci> "two" `mappend` "one"
"twoone"
这样并没有关系。3 * 5
跟 5 * 3
会相等只不过是乘法的性质而已,但没有保证所有 monoid 都要遵守。
#
Product and Sum
我们已经描述过将数值表现成一种 monoid 的方式。只要将 *
当作二元函数而 1
当作 identity 就好了。而且这不是唯一一种方式,另一种方式是将 +
作为二元函数而 0
作为 identity。
ghci> 0 + 4
4
ghci> 5 + 0
5
ghci> (1 + 3) + 5
9
ghci> 1 + (3 + 5)
9
他也遵守 monoid law,因为将 0 加上其他数值,都会是另外一者。而且加法也遵守结合律。所以现在我们有两种方式来将数值表现成 monoid,那要选哪一个呢?其实我们不必要强迫定下来,还记得当同一种型别有好几种表现成某个 typeclass 的方式时,我们可以用 newtype
来包裹现有的型别,然后再定义新的 instance。这样就行了。
Data.Monoid
这个模组汇出了两种型别,Product
跟 Sum
。Product
定义如下:
newtype Product a = Product { getProduct :: a }
deriving (Eq, Ord, Read, Show, Bounded)
简单易懂,就是一个单一型别参数的 newtype
,并 derive 一些性质。他的 Monoid
的 instance 长得像这样:
instance Num a => Monoid (Product a) where
mempty = Product 1
Product x `mappend` Product y = Product (x * y)
mempty
只不过是将 1
包在 Product
中。mappend
则对 Product
的构造子做模式匹配,将两个取出的数值相乘后再将结果放回去。就如你看到的,typeclass 定义前面有 Num a
的条件限制。所以他代表 Product a
对于所有属于 Num
的 a
是一个 Monoid
。要将 Product a
作为一个 monoid 使用,我们需要用 newtype 来做包裹跟解开的动作。
ghci> getProduct $ Product 3 `mappend` Product 9
27
ghci> getProduct $ Product 3 `mappend` mempty
3
ghci> getProduct $ Product 3 `mappend` Product 4 `mappend` Product 2
24
ghci> getProduct . mconcat . map Product $ [3,4,2]
24
这当作 Monoid
的一个演练还不错,但并不会有人觉得这会比 3 * 9
跟 3 * 1
这种方式来做乘法要好。但我们稍后会说明尽管像这种显而易见的定义还是有他方便的地方。
Sum
跟 Product
定义的方式类似,我们也可以用类似的方式操作:
ghci> getSum $ Sum 2 `mappend` Sum 9
11
ghci> getSum $ mempty `mappend` Sum 3
3
ghci> getSum . mconcat . map Sum $ [1,2,3]
6
#
Any and ALL
另一种可以有两种表示成 monoid 方式的型别是 Bool
。第一种方式是将 ||
当作二元函数,而 False
作为 identity。这样的意思是只要有任何一个参数是 True
他就回传 True
,否则回传 False
。所以如果我们使用 False
作为 identity,他会在跟 False
做 OR 时回传 False
,跟 True
做 OR 时回传 True
。Any
这个 newtype 是 Monoid
的一个 instance,并定义如下:
newtype Any = Any { getAny :: Bool }
deriving (Eq, Ord, Read, Show, Bounded)
他的 instance 长得像这样:
instance Monoid Any where
mempty = Any False
Any x `mappend` Any y = Any (x || y)
他叫做 Any
的理由是 x `mappend` y
当有任何一个是 True
时就会是 True
。就算是更多个用 mappend
串起来的 Any
,他也会在任何一个是 True
回传 True
。
ghci> getAny $ Any True `mappend` Any False
True
ghci> getAny $ mempty `mappend` Any True
True
ghci> getAny . mconcat . map Any $ [False, False, False, True]
True
ghci> getAny $ mempty `mappend` mempty
False
另一种 Bool
表现成 Monoid
的方式是用 &&
作为二元函数,而 True
作为 identity。只有当所有都是 True
的时候才会回传 True
。下面是他的 newtype 定义:
newtype All = All { getAll :: Bool }
deriving (Eq, Ord, Read, Show, Bounded)
而这是他的 instance:
instance Monoid All where
mempty = All True
All x `mappend` All y = All (x && y)
当我们用 mappend
来串起 All
型别的值时,结果只有当所有 mappend
的值是 True
时才会是 True
:
ghci> getAll $ mempty `mappend` All True
True
ghci> getAll $ mempty `mappend` All False
False
ghci> getAll . mconcat . map All $ [True, True, True]
True
ghci> getAll . mconcat . map All $ [True, True, False]
False
就如乘法跟加法一样,我们通常宁愿用二元函数来操作他们也不会用 newtype 来将他们包起来。不会将他们包成 Any
或 All
然后用 mappend
,mempty
或 mconcat
来操作。通常使用 or
跟 and
,他们接受一串 Bool
,并只有当任意一个或是所有都是 True
的时候才回传 True
。
#
The Ordering monoid
还记得 Ordering
型别吗?他是比较运算之后得到的结果,包含三个值:LT
,EQ
跟 GT
,分别代表小于,等于跟大于:
ghci> 1 `compare` 2
LT
ghci> 2 `compare` 2
EQ
ghci> 3 `compare` 2
GT
针对 list,数值跟布林值而言,要找出 monoid 的行为只要去检视已经定义的函数,然后看看有没有展现出 monoid 的特性就可以了,但对于 Ordering
,我们就必须要更仔细一点才能看出来是否是一个 monoid,但其实他的 Monoid
instance 还蛮直觉的:
instance Monoid Ordering where
mempty = EQ
LT `mappend` _ = LT
EQ `mappend` y = y
GT `mappend` _ = GT
这个 instance 定义如下:当我们用 mappend
两个 Ordering
型别的值时,左边的会被保留下来。除非左边的值是 EQ
,那我们就会保留右边的当作结果。而 identity 就是 EQ
。乍看之下有点随便,但实际上他是我们比较两个英文字时所用的方法。我们先比较两个字母是否相等,如果他们不一样,那我们就知道那一个字在字典中会在前面。而如果两个字母相等,那我们就继续比较下一个字母,以此类推。
举例来说,如果我们字典顺序地比较 "ox"
跟 "on"
的话。我们会先比较两个字的首个字母,看看他们是否相等,然后继续比较第二个字母。我们看到 'x'
是比 'n'
要来得大,所以我们就知道如何比较两个字了。而要了解为何 EQ
是 identity,我们可以注意到如果我们在两个字中间的同样位置塞入同样的字母,那他们之间的字典顺序并不会改变。"oix"
仍然比 "oin"
要大。
很重要的一件事是在 Ordering
的 Monoid
定义里 x `mappend` y
并不等于 y `mappend` x
。因为除非第一个参数是 EQ
,不然结果就会是第一个参数。所以 LT `mappend` GT
等于 LT
,然而 GT `mappend` LT
等于 GT
。
ghci> LT `mappend` GT
LT
ghci> GT `mappend` LT
GT
ghci> mempty `mappend` LT
LT
ghci> mempty `mappend` GT
GT
所以这个 monoid 在什么情况下会有用呢?假设你要写一个比较两个字串长度的函数,并回传 Ordering
。而且当字串一样长的时候,我们不直接回传 EQ
,反而继续用字典顺序比较他们。一种实作的方式如下:
lengthCompare :: String -> String -> Ordering
lengthCompare x y = let a = length x `compare` length y
b = x `compare` y
in if a == EQ then b else a
我们称呼比较长度的结果为 a
,而比较字典顺序的结果为 b
,而当长度一样时,我们就回传字典顺序。
如果善用我们 Ordering
是一种 monoid 这项知识,我们可以把我们的函数写得更简单些:
import Data.Monoid
lengthCompare :: String -> String -> Ordering
lengthCompare x y = (length x `compare` length y) `mappend`
(x `compare` y)
我们可以试着跑跑看:
ghci> lengthCompare "zen" "ants"
LT
ghci> lengthCompare "zen" "ant"
GT
要记住当我们使用 mappend
。他在左边不等于 EQ
的情况下都会回传左边的值。相反地则回传右边的值。这也是为什么我们将我们认为比较重要的顺序放在左边的参数。如果我们要继续延展这个函数,要让他们比较母音的顺序,并把这顺序列为第二重要,那我们可以这样修改他:
import Data.Monoid
lengthCompare :: String -> String -> Ordering
lengthCompare x y = (length x `compare` length y) `mappend`
(vowels x `compare` vowels y) `mappend`
(x `compare` y)
where vowels = length . filter (`elem` "aeiou")
我们写了一个辅助函数,他接受一个字串并回传他有多少母音。他是先用 filter 来把字母滤到剩下 "aeiou"
,然后再用 length
计算长度。
ghci> lengthCompare "zen" "anna"
LT
ghci> lengthCompare "zen" "ana"
LT
ghci> lengthCompare "zen" "ann"
GT
在第一个例子中我们看到长度不同所以回传 LT
,明显地 "zen"
要短于 "anna"
。在第二个例子中,长度是一样的,但第二个字串有比较多的母音,所以结果仍然是 LT
。在第三个范例中,两个长度都相等,他们也有相同个数的母音,经由字典顺序比较后得到 "zen"
比较大。
Ordering
的 monoid 允许我们用不同方式比较事物,并将这些顺序也定义了依重要度不同的一个顺序。
#
Maybe the monoid
我们来看一下 Maybe a
是怎样有多种方式来表现成 Monoid
的,并且说明哪些是比较有用的。一种将 Maybe a
当作 monoid 的方式就是他的 a
也是一个 monoid,而我们将 mappend
实作成使用包在 Just
里面的值对应的 mappend
。并且用 Nothing
当作 identity。所以如果我 mappend
两个参数中有一个是 Nothing
。那结果就会是另一边的值。他的 instance 定义如下:
instance Monoid a => Monoid (Maybe a) where
mempty = Nothing
Nothing `mappend` m = m
m `mappend` Nothing = m
Just m1 `mappend` Just m2 = Just (m1 `mappend` m2)
留意到 class constraint。他说明 Maybe a
只有在 a
是 Monoid
的情况下才会是一个 Monoid
。如果我们 mappend
某个东西跟 Nothing
。那结果就会是某个东西。如果我们 mappend
两个 Just
,那 Just
包住的结果就会 mappended
在一起并放回 Just
。我们能这么做是因为 class constraint 保证了在 Just
中的值是 Monoid
。
ghci> Nothing `mappend` Just "andy"
Just "andy"
ghci> Just LT `mappend` Nothing
Just LT
ghci> Just (Sum 3) `mappend` Just (Sum 4)
Just (Sum {getSum = 7})
这当你在处理有可能失败的 monoid 的时候比较有用。有了这个 instance,我们就不必一一去检查他们是否失败,是否是 Nothing
或是 Just
,我们可以直接将他们当作普通的 monoid。
但如果在 Maybe
中的型别不是 Monoid
呢?注意到在先前的 instance 定义中,唯一有依赖于 monoid 限制的情况就是在 mappend
两个 Just
的时候。但如果我们不知道包在 Just
里面的值究竟是不是 monoid,我们根本无法用 mappend
操作他们,所以该怎么办呢?一种方式就是直接丢掉第二个值而留下第一个值。这就是 First a
存在的目的,而这是他的定义:
newtype First a = First { getFirst :: Maybe a }
deriving (Eq, Ord, Read, Show)
我们接受一个 Maybe a
并把他包成 newtype,Monoid
的定义如下:
instance Monoid (First a) where
mempty = First Nothing
First (Just x) `mappend` _ = First (Just x)
First Nothing `mappend` x = x
正如我们说过得,mempty
就是包在 First
中的 Nothing
。如果 mappend
的第一个参数是 Just
,我们就直接忽略第二个参数。如果第一个参数是 Nothing
,那我们就将第二个参数当作结果。并不管他究竟是 Just
或是 Nothing
:
ghci> getFirst $ First (Just 'a') `mappend` First (Just 'b')
Just 'a'
ghci> getFirst $ First Nothing `mappend` First (Just 'b')
Just 'b'
ghci> getFirst $ First (Just 'a') `mappend` First Nothing
Just 'a'
First
在我们有一大串 Maybe
而且想知道他们之中就竟有没有 Just
的时候很有用。可以利用 mconcat
:
ghci> getFirst . mconcat . map First $ [Nothing, Just 9, Just 10]
Just 9
如果我们希望定义一个 Maybe a
的 monoid,让他当 mappend
的两个参数都是 Just
的时候将第二个参数当作结果。Data.Monoid
中有一个现成的 Last a
,他很像是 First a
,只差在 mappend
跟 mconcat
会保留最后一个非 Nothing
的值。
ghci> getLast . mconcat . map Last $ [Nothing, Just 9, Just 10]
Just 10
ghci> getLast $ Last (Just "one") `mappend` Last (Just "two")
Just "two"
#
Using monoids to fold data structures
另一种有趣的 monoid 使用方式就是让他来帮助我们 fold 一些资料结构。到目前为止我们只有 fold list。但 list 并不是唯一一种可以 fold 的资料结构。我们几乎可以 fold 任何一种资料结构。像是 tree 也是一种常见的可以 fold 的资料结构。
由于有太多种资料结构可以 fold 了,所以我们定义了 Foldable
这个 typeclass。就像 Functor
是定义可以 map over 的结构。Foldable
是定义可以 fold 的结构。在 Data.Foldable
中有定义了一些有用的函数,但他们名称跟 Prelude
中的名称冲突。所以最好是用 qualified 的方式 import 他们:
import qualified Foldable as F
为了少打一些字,我们将他们 import qualified 成 F
。所以这个 typeclass 中定义了哪些函数呢?有 foldr
,foldl
,foldr1
跟 foldl1
。你会说我们已经知道这些函数了,他们有什么不一样的地方吗?我们来比较一下 Foldable
中的 foldr
跟 Prelude
中的 foldr
的型别异同:
ghci> :t foldr
foldr :: (a -> b -> b) -> b -> [a] -> b
ghci> :t F.foldr
F.foldr :: (F.Foldable t) => (a -> b -> b) -> b -> t a -> b
尽管 foldr
接受一个 list 并将他 fold 起来,Data.Foldable
中的 foldr
接受任何可以 fold 的型别。并不只是 list。 而两个 foldr
对于 list 的结果是相同的:
ghci> foldr (*) 1 [1,2,3]
6
ghci> F.foldr (*) 1 [1,2,3]
6
那有哪些资料结构支援 fold 呢?首先我们有 Maybe
:
ghci> F.foldl (+) 2 (Just 9)
11
ghci> F.foldr (||) False (Just True)
True
但 fold 一个 Maybe
并没什么新意。毕竟当他是 Just
的时候表现得像是只有单一元素的 list,而当他是 Nothing
的时候就像是空的 list 一样。所以我们来看一些比较复杂的资料结构。
还记得 Making Our Own Types and Typeclass 章节中的树状的资料结构吗?我们是这样定义的:
data Tree a = Empty | Node a (Tree a) (Tree a) deriving (Show, Read, Eq)
我们说一棵树要不就是一棵空的树要不然就是一个包含值的节点,并且还指向另外两棵树。定义他之后,我们将他定义成 Functor
的 instance,因此可以 fmap
他。现在我们要将他定义成 Foldable
的 instance,这样我们就可以 fold 他。要定义成 Foldable
的一种方式就是实作 foldr
。但另一种比较简单的方式就是实作 foldMap
,他也属于 Foldable
typeclass。foldMap
的型别如下:
foldMap :: (Monoid m, Foldable t) => (a -> m) -> t a -> m
第一个参数是一个函数,这个函数接受 foldable 资料结构中包含的元素的型别,并回传一个 monoid。他第二个参数是一个 foldable 的结构,并包含型别 a
的元素。他将第一个函数来 map over 这个 foldable 的结构,因此得到一个包含 monoid 的 foldable 结构。然后用 mappend
来简化这些 monoid,最后得到单一的一个 monoid。这个函数听起来不太容易理解,但我们下面会看到他其实很容易实作。而且好消息是只要实作了这个函数就可以让我们的函数成为 Foldable
。所以我们只要实作某个型别的 foldMap
,我们就可以得到那个型别的 foldr
跟 foldl
。
这就是我们如何定义 Tree
成为 Foldable
的:
instance F.Foldable Tree where
foldMap f Empty = mempty
foldMap f (Node x l r) = F.foldMap f l `mappend`
f x `mappend`
F.foldMap f r
我们是这样思考的:如果我们写一个函数,他接受树中的一个元素并回传一个 monoid,那我们要怎么简化整棵树到只有单一一个 monoid?当我们在对树做 fmap
的时候,我们将那函数套用至节点上,并递回地套用至左子树以及右子树。这边我们不只是 map 一个函数而已,我们还要求要把结果用 mappend
简化成只有单一一个 monoid 值。首先我们考虑树为空的情形,一棵没有值也没有子树的情形。由于没有值我们也没办法将他套用上面转换成 monoid 的函数,所以当树为空的时候,结果应该要是 mempty
。
在非空节点的情形下比较有趣,他包含一个值跟两棵子树。在这种情况下,我们递回地做 foldMap
,用 f
来套用到左子树跟右子树上。要记住我们的 foldMap
只会得到单一的 monoid 值。我们也会套用 f
到节点中的值。这样我们就得到三个 monoid 值,有两个来自简化子树的结果,还有一个是套用 f
到节点中的值的结果。而我们需要将这三个值整合成单一个值。要达成这个目的我们使用 mappend
,而且自然地会想到照左子树,节点值以及右子树的顺序来简化。
注意到我们并不一定要提供一个将普通值转成 monoid 的函数。我们只是把他当作是 foldMap
的参数,我们要决定的只是如何套用那个函数,来把得到的 monoid 们简化成单一结果。
现在我们有树的 Foldable
instance,而 foldr
跟 foldl
也有预设的实作了。考虑下面这棵树:
testTree = Node 5
(Node 3
(Node 1 Empty Empty)
(Node 6 Empty Empty)
)
(Node 9
(Node 8 Empty Empty)
(Node 10 Empty Empty)
)
他的 root 是 5
,而他左边下来分别是 3
,再来是 1
跟 6
。而右边下来是 9
,再来是 8
跟 10
。有了 Foldable
的定义,我们就能像对 list 做 fold 一样对树做 fold:
ghci> F.foldl (+) 0 testTree
42
ghci> F.foldl (*) 1 testTree
64800
foldMap
不只是定义 Foldable
新的 instance 有用。他也对简化我们的结构至单一 monoid 值有用。举例来说,如果我们想要知道我们的树中有没有 3
,我们可以这样做:
ghci> getAny $ F.foldMap (\x -> Any $ x == 3) testTree
True
这边 \x -> Any $ x == 3
是一个接受一个数值并回传一个 monoid 的函数,也就是一个包在 Any
中的 Bool
。foldMap
将这个函数套用至树的每一个节点,并把结果用 mappend
简化成单一 monoid。如果我们这样做:
ghci> getAny $ F.foldMap (\x -> Any $ x > 15) testTree
False
经过套用 lambda 之后我们所有的节点都会是 Any False
。但 mappend
必须要至少吃到一个 True
才能让最后的结果变成 True
。这也是为什么结果会是 False
,因为我们树中所有的值都大于 15
。
我们也能将 foldMap
配合 \x -> [x]
使用来将我们的树转成 list。经过套用那个函数后,所有节点都变成包含单一元素的 list。最后用 mappend
将这些单一元素的 list 转成一个装有全部元素的 list:
ghci> F.foldMap (\x -> [x]) testTree
[1,3,6,5,8,9,10]
这个小技巧并不限于树而已,他可以被套用在任何 Foldable
上。
12
来看看几种 Monad
当我们第一次谈到 Functor 的时候,我们了解到他是一个抽象概念,代表是一种可以被 map over 的值。然后我们再将其概念提升到 Applicative Functor,他代表一种带有 context 的型态,我们可以用函数操作他而且同时还保有他的 context。
在这一章,我们会学到 Monad,基本上他是一种加强版的 Applicative Functor,正如 Applicative Functor 是 Functor 的加强版一样。
我们介绍到 Functor 是因为我们观察到有许多型态都可以被 function 给 map over,了解到这个目的,便抽象化了 Functor
这个 typeclass 出来。但这让我们想问:如果给定一个 a -> b
的函数以及 f a
的型态,我们要如何将函数 map over 这个型态而得到 f b
?我们知道要如何 map over Maybe a
,[a]
以及 IO a
。我们甚至还知道如何用 a -> b
map over r -> a
,并且会得到 r -> b
。要回答这个问题,我们只需要看 fmap
的型态就好了:
fmap :: (Functor f) => (a -> b) -> f a -> f b
然后只要针对 Functor
instance 撰写对应的实作。
之后我们又看到一些可以针对 Functor 改进的地方,例如 a -> b
也被包在一个 Functor value 里面呢?像是 Just (*3)
,我们要如何 apply Just 5
给他?如果我们不要 apply Just 5
而是 Nothing
呢?甚至给定 [(*2),(+4)]
,我们要如何 apply 他们到 [1,2,3]
呢?对于此,我们抽象出 Applicative
typeclass,这就是我们想要问的问题:
(<*>) :: (Applicative f) => f (a -> b) -> f a -> f b
我们也看到我们可以将一个正常的值包在一个资料型态中。例如说我们可以拿一个 1
然后把他包成 Just 1
。或是把他包成 [1]
。也可以是一个 I/O action 会产生一个 1
。这样包装的 function 我们叫他做 pure
。
如我们说得,一个 applicative value 可以被看作一个有附加 context 的值。例如说,'a'
只是一个普通的字元,但 Just 'a'
是一个附加了 context 的字元。他不是 Char
而是 Maybe Char
,这型态告诉我们这个值可能是一个字元,也可能什么都没有。
来看看 Applicative
typeclass 怎样让我们用普通的 function 操作他们,同时还保有 context:
ghci> (*) <$> Just 2 <*> Just 8
Just 16
ghci> (++) <$> Just "klingon" <*> Nothing
Nothing
ghci> (-) <$> [3,4] <*> [1,2,3]
[2,1,0,3,2,1]
所以我们可以视他们为 applicative values,Maybe a
代表可能会失败的 computation,[a]
代表同时有好多结果的 computation (non-deterministic computation),而 IO a
代表会有 side-effects 的 computation。
Monad 是一个从 Applicative functors 很自然的一个演进结果。对于他们我们主要考量的点是:如果你有一个具有 context 的值 m a
,你能如何把他丢进一个只接受普通值 a
的函数中,并回传一个具有 context 的值?也就是说,你如何套用一个型态为 a -> m b
的函数至 m a
?基本上,我们要求的函数是:
(>>=) :: (Monad m) => m a -> (a -> m b) -> m b
如果我们有一个漂亮的值跟一个函数接受普通的值但回传漂亮的值,那我们要如何要把漂亮的值丢进函数中?这就是我们使用 Monad 时所要考量的事情。我们不写成 f a
而写成 m a
是因为 m
代表的是 Monad
,但 monad 不过就是支援 >>=
操作的 applicative functors。>>=
我们称呼他为 bind。
当我们有一个普通值 a
跟一个普通函数 a -> b
,要套用函数是一件很简单的事。但当你在处理具有 context 的值时,就需要多考虑些东西,要如何把漂亮的值喂进函数中,并如何考虑他们的行为,但你将会了解到他们其实不难。
#
动手做做看: Maybe Monad
现在对于什么是 Monad 已经有了些模糊的概念, 我们来看看要如何让这概念更具体一些。
不意外地,Maybe
是一个 Monad, 所以让我们对于他多探讨些,看看是否能跟我们所知的 Monad 概念结合起来。
到这边要确定你了解什么是 Applicatives。如果你知道好几种 ``Applicative`` 的 instance 还有他们代表的意含就更好了,因为 monad 不过就是对 applicative 的概念进行一次升级。
一个 Maybe a
型态的值代表型态为 a
的值而且具备一个可能造成错误的 context。而 Just "dharma"
的值代表他不是一个 "dharma"
的字串就是字串不见时的 Nothing
。如果你把字串当作计算的结果,Nothing
就代表计算失败了。
当我们把 Maybe
视作 functor,我们其实要的是一个 fmap
来把一个函数针对其中的元素做套用。他会对 Just
中的元素进行套用,要不然就是保留 Nothing
的状态,其代表里面根本没有元素。
ghci> fmap (++"!") (Just "wisdom")
Just "wisdom!"
ghci> fmap (++"!") Nothing
Nothing
或者视为一个 applicative functor,他也有类似的作用。只是 applicative 也把函数包了起来。Maybe
作为一个 applicative functor,我们能用 <*>
来套用一个存在 Maybe
中的函数至包在另外一个 Maybe
中的值。他们都必须是包在 Just
来代表值存在,要不然其实就是 Nothing
。当你在想套用函数到值上面的时候,缺少了函数或是值都会造成错误,所以这样做是很合理的。
ghci> Just (+3) <*> Just 3
Just 6
ghci> Nothing <*> Just "greed"
Nothing
ghci> Just ord <*> Nothing
Nothing
当我们用 applicative 的方式套用函数至 Maybe
型态的值时,就跟上面描述的差不多。过程中所有值都必须是 Just
,要不然结果一定会是 Nothing
。
ghci> max <$> Just 3 <*> Just 6
Just 6
ghci> max <$> Just 3 <*> Nothing
Nothing
我们来思考一下要怎么为 Maybe
实作 >>=
。正如我们之前提到的,>>=
接受一个 monadic value,以及一个接受普通值的函数,这函数会回传一个 monadic value。>>=
会帮我们套用这个函数到这个 monadic value。在函数只接受普通值的情况侠,函数是如何作到这件事的呢?要作到这件事,他必须要考虑到 monadic value 的 context。
在这个案例中,>>=
会接受一个 Maybe a
以及一个型态为 a -> Maybe b
的函数。他会套用函数到 Maybe a
。要厘清他怎么作到的,首先我们注意到 Maybe
的 applicative functor 特性。假设我们有一个函数 \x -> Just (x+1)
。他接受一个数字,把他加 1
后再包回 Just
。
ghci> (\x -> Just (x+1)) 1
Just 2
ghci> (\x -> Just (x+1)) 100
Just 101
如果我们喂给函数 1
,他会计算成 Just 2
。如果我们喂给函数 100
,那结果便是 Just 101
。但假如我们喂一个 Maybe
的值给函数呢?如果我们把 Maybe
想成一个 applicative functor,那答案便很清楚。如果我们拿到一个 Just
,就把包在 Just
里面的值喂给函数。如果我们拿到一个 Nothing
,我们就说结果是 Nothing
。
我们呼叫 applyMaybe
而不呼叫 >>=
。他接受 Maybe a
跟一个回传 Maybe b
的函数,并套用函数至 Maybe a
。
applyMaybe :: Maybe a -> (a -> Maybe b) -> Maybe b
applyMaybe Nothing f = Nothing
applyMaybe (Just x) f = f x
我们套用一个 infix 函数,这样 Maybe
的值可以写在左边且函数是在右边:
ghci> Just 3 `applyMaybe` \x -> Just (x+1)
Just 4
ghci> Just "smile" `applyMaybe` \x -> Just (x ++ " :")""
Just "smile :""
ghci> Nothing `applyMaybe` \x -> Just (x+1)
Nothing
ghci> Nothing `applyMaybe` \x -> Just (x ++ " :")")
Nothing
在上述的范例中,我们看到在套用 applyMaybe
的时候,函数是套用在 Just
里面的值。当我们试图套用到 Nothing
,那整个结果便是 Nothing
。假如函数回传 Nothing
呢?
ghci> Just 3 `applyMaybe` \x -> if x > 2 then Just x else Nothing
Just 3
ghci> Just 1 `applyMaybe` \x -> if x > 2 then Just x else Nothing
Nothing
这正是我们期待的结果。如果左边的 monadic value 是 Nothing
,那整个结果就是 Nothing
。如果右边的函数是 Nothing
,那结果也会是 Nothing
。这跟我们之前把 Maybe
当作 applicative 时,过程中有任何一个 Nothing
整个结果就会是 Nothing
一样。
对于 Maybe
而言,我们已经找到一个方法处理漂亮值的方式。我们作到这件事的同时,也保留了 Maybe
代表可能造成错误的计算的意义。
你可能会问,这样的结果有用吗?由于 applicative functors 让我们可以拿一个接受普通值的函数,并让他可以操作具有 context 的值,这样看起来 applicative functors 好像比 monad 强。但我们会看到 monad 也能作到,因为他只是 applicative functors 的升级版。他们同时也能作到 applicative functors 不能作到的事情。
稍候我们会再继续探讨 Maybe
,但我们先来看看 monad 的 type class。
#
Monad type class
正如 functors 有 Functor
这个 type class,而 applicative functors 有一个 Applicative
这个 type class,monad 也有他自己的 type class:Monad
他看起来像这样:
class Monad m where
return :: a -> m a
(>>=) :: m a -> (a -> m b) -> m b
(>>) :: m a -> m b -> m b
x >> y = x >>= \_ -> y
fail :: String -> m a
fail msg = error msg
我们从第一行开始看。他说 class Monad m where
。但我们之前不是提到 monad 是 applicative functors 的加强版吗?不是应该有一个限制说一个型态必须先是一个 applicative functor 才可能是一个 monad 吗?像是 class (Applicative m) = > Monad m where
。他的确应该要有,但当 Haskell 被创造的早期,人们没有想到 applicative functor 适合被放进语言中,所以最后没有这个限制。但的确每个 monad 都是 applicative functor,即使 Monad
并没有这么宣告。
在 Monad
typeclass 中定义的第一个函数是 return
。他其实等价于 pure
,只是名字不同罢了。他的型态是 (Monad m) => a -> m a
。他接受一个普通值并把他放进一个最小的 context 中。也就是说他把普通值包进一个 monad 里面。他跟 Applicative
里面 pure
函数做的事情一样,所以说其实我们已经认识了 return
。我们已经用过 return
来处理一些 I/O。我们用他来做一些假的 I/O,印出一些值。对于 Maybe
来说他就是接受一个普通值然后包进 Just
。
提醒一下:``return`` 跟其他语言中的 ``return`` 是完全不一样的。他并不是结束一个函数的执行,他只不过是把一个普通值包进一个 context 里面。
接下来定义的函数是 bind: >>=
。他就像是函数套用一样,只差在他不接受普通值,他是接受一个 monadic value(也就是具有 context 的值)并且把他喂给一个接受普通值的函数,并回传一个 monadic value。
接下来,我们定义了 >>
。我们不会介绍他,因为他有一个事先定义好的实作,基本上我们在实作 Monad
typeclass 的时候都不会去理他。
最后一个函数是 fail
。我们通常在我们程式中不会具体写出来。他是被 Haskell 用在处理语法错误的情况。我们目前不需要太在意 fail
。
我们知道了 Monad
typeclass 长什么样子,我们来看一下 Maybe
的 Monad
instance。
instance Monad Maybe where
return x = Just x
Nothing >>= f = Nothing
Just x >>= f = f x
fail _ = Nothing
return
跟pure
是等价的。这没什么困难的。我们跟我们在定义Applicative
的时候做一样的事,只是把他用Just
包起来。
>>=
跟我们的applyMaybe
是一样的。当我们将Maybe a
塞给我们的函数,我们保留住context,并且在输入是Nothing
的时候回传Nothing
。毕竟当没有值的时候套用我们的函数是没有意义的。当输入是Just
的时候则套用f
并将他包在Just
里面。
我们可以试着感觉一下Maybe
是怎样表现成Monad的。
ghci> return "WHAT" :: Maybe String
Just "WHAT"
ghci> Just 9 >>= \x -> return (x*10)
Just 90
ghci> Nothing >>= \x -> return (x*10)
Nothing
第一行没什么了不起,我们已经知道 return
就是 pure
而我们又对 Maybe
操作过 pure
了。至于下两行就比较有趣点。
留意我们是如何把 Just 9
喂给 \x -> return (x*10)
。在函数中 x
绑定到 9
。他看起好像我们能不用 pattern matching 的方式就从 Maybe
中抽取出值。但我们并没有丧失掉 Maybe
的 context,当他是 Nothing
的时候,>>=
的结果也会是 Nothing
。
#
走钢索
我们已经知道要如何把 Maybe a
喂进 a -> Maybe b
这样的函数。我们可以看看我们如何重复使用 >>=
来处理多个 Maybe a
的值。
首先来说个小故事。皮尔斯决定要辞掉他的工作改行试着走钢索。他对走钢索蛮在行的,不过仍有个小问题。就是鸟会停在他拿的平衡竿上。他们会飞过来停一小会儿,然后再飞走。这样的情况在两边的鸟的数量一样时并不是个太大的问题。但有时候,所有的鸟都会想要停在同一边,皮尔斯就失去了平衡,就会让他从钢索上掉下去。
我们这边假设两边的鸟差异在三个之内的时候,皮尔斯仍能保持平衡。所以如果是右边有一只,左边有四只的话,那还撑得住。但如果左边有五只,那就会失去平衡。
我们要写个程式来模拟整个情况。我们想看看皮尔斯究竟在好几只鸟来来去去后是否还能撑住。例如说,我们想看看先来了一只鸟停在左边,然后来了四只停在右边,然后左边那只飞走了。之后会是什么情形。
我们用一对整数来代表我们的平衡竿状态。头一个位置代表左边的鸟的数量,第二个位置代表右边的鸟的数量。
type Birds = Int
type Pole = (Birds,Birds)
由于我们用整数来代表有多少只鸟,我们便先来定义 Int
的同义型态,叫做 Birds
。然后我们把 (Birds, Birds)
定义成 Pole
。
接下来,我们定义一个函数他接受一个数字,然后把他放在竿子的左边,还有另外一个函数放在右边。
landLeft :: Birds -> Pole -> Pole
landLeft n (left,right) = (left + n,right)
landRight :: Birds -> Pole -> Pole
landRight n (left,right) = (left,right + n)
我们来试着执行看看:
ghci> landLeft 2 (0,0)
(2,0)
ghci> landRight 1 (1,2)
(1,3)
ghci> landRight (-1) (1,2)
(1,1)
要模拟鸟飞走的话我们只要给定一个负数就好了。 由于这些操作是接受 Pole
并回传 Pole
, 所以我们可以把函数串在一起。
ghci> landLeft 2 (landRight 1 (landLeft 1 (0,0)))
(3,1)
当我们喂 (0,0)
给 landLeft 1
时,我们会得到 (1,0)
。接着我们模拟右边又停了一只鸟,状态就变成 (1,1)
。最后又有两只鸟停在左边,状态变成 (3,1)
。我们这边的写法是先写函数名称,然后再套用参数。但如果先写 pole 再写函数名称会比较清楚,所以我们会想定义一个函数
x -: f = f x
我们能先套用参数然后再写函数名称:
ghci> 100 -: (*3)
300
ghci> True -: not
False
ghci> (0,0) -: landLeft 2
(2,0)
有了这个函数,我们便能写得比较好读一些:
ghci> (0,0) -: landLeft 1 -: landRight 1 -: landLeft 2
(3,1)
这个范例跟先前的范例是等价的,只不过好读许多。很清楚的看出我们是从 (0,0)
开始,然后停了一只在左边,接着右边又有一只,最后左边多了两只。
到目前为止没什么问题,但如果我们要停 10 只在左边呢?
ghci> landLeft 10 (0,3)
(10,3)
你说左边有 10 只右边却只有 3 只?那不是早就应该掉下去了?这个例子太明显了,如果换个比较不明显的例子。
ghci> (0,0) -: landLeft 1 -: landRight 4 -: landLeft (-1) -: landRight (-2)
(0,2)
表面看起来没什么问题,但如果你仔细看的话,有一瞬间是右边有四只,但左边没有鸟。要修正这个错误,我们要重新检视 landLeft
跟 landRight
。我们其实是希望这些函数产生失败的情况。那就是在维持平衡的时候回传新的 pole,但失败的时候告诉我们失败了。这时候 Maybe
就刚刚好是我们要的 context 了。我们用 Maybe
重新写一次:
landLeft :: Birds -> Pole -> Maybe Pole
landLeft n (left,right)
| abs ((left + n) - right) < 4 = Just (left + n, right)
| otherwise = Nothing
landRight :: Birds -> Pole -> Maybe Pole
landRight n (left,right)
| abs (left - (right + n)) < 4 = Just (left, right + n)
| otherwise = Nothing
现在这些函数不回传 Pole
而回传 Maybe Pole
了。他们仍接受鸟的数量跟旧的的 pole,但他们现在会检查是否有太多鸟会造成皮尔斯失去平衡。我们用 guards 来检查是否有差异超过三的情况。如果没有,那就包一个在 Just
中的新的 pole,如果是,那就回传 Nothing
。
再来执行看看:
ghci> landLeft 2 (0,0)
Just (2,0)
ghci> landLeft 10 (0,3)
Nothing
一如预期,当皮尔斯不会掉下去的时候,我们就得到一个包在 Just
中的新 pole。当太多鸟停在同一边的时候,我们就会拿到 Nothing
。这样很棒,但我们却不知道怎么把东西串在一起了。我们不能做 landLeft 1 (landRight 1 (0,0))
,因为当我们对 (0,0)
使用 landRight 1
时,我们不是拿到 Pole
而是拿到 Maybe Pole
。landLeft 1
会拿到 Pole
而不是拿到 Maybe Pole
。
我们需要一种方法可以把拿到的 Maybe Pole
塞到拿 Pole
的函数中,然后回传 Maybe Pole
。而我们有 >>=
,他对 Maybe
做的事就是我们要的
ghci> landRight 1 (0,0) >>= landLeft 2
Just (2,1)
landLeft 2
的型态是 Pole -> Maybe Pole
。我们不能喂给他 Maybe Pole
的东西。而 landRight 1 (0,0)
的结果就是 Maybe Pole
,所以我们用 >>=
来接受一个有 context 的值然后拿给 landLeft 2
。>>=
的确让我们把 Maybe
当作有 context 的值,因为当我们丢 Nothing
给 landLeft 2
的时候,结果会是 Nothing
。
ghci> Nothing >>= landLeft 2
Nothing
这样我们可以把这些新写的用 >>=
串在一起。让 monadic value 可以喂进只吃普通值的函数。
来看看些例子:
ghci> return (0,0) >>= landRight 2 >>= landLeft 2 >>= landRight 2
Just (2,4)
我们最开始用 return
回传一个 pole 并把他包在 Just
里面。我们可以像往常套用 landRight 2
,不过我们不那么做,我们改用 >>=
。Just (0,0)
被喂到 landRight 2
,得到 Just (0,2)
。接着被喂到 landLeft 2
,得到 Just (2,2)
。
还记得我们之前引入失败情况的例子吗?
ghci> (0,0) -: landLeft 1 -: landRight 4 -: landLeft (-1) -: landRight (-2)
(0,2)
之前的例子并不会反应失败的情况。但如果我们用 >>=
的话就可以得到失败的结果。
ghci> return (0,0) >>= landLeft 1 >>= landRight 4 >>= landLeft (-1) >>= landRight (-2)
Nothing
正如预期的,最后的情形代表了失败的情况。我们再进一步看看这是怎么产生的。首先 return
把 (0,0)
放到一个最小的 context 中,得到 Just (0,0)
。然后是 Just (0.0) >>= landLeft 1
。由于 Just (0,0)
是一个 Just
的值。landLeft 1
被套用至 (0,0)
而得到 Just (1,0)
。这反应了我们仍保持在平衡的状态。接着是 Just (1,0) >>= landright 4
而得到了 Just (1,4)
。距离不平衡只有一步之遥了。他又被喂给 landLeft (-1)
,这组合成了 landLeft (-1) (1,4)
。由于失去了平衡,我们变得到了 Nothing
。而我们把 Nothing
喂给 landRight (-2)
,由于他是 Nothing
,也就自动得到了 Nothing
。
如果只把 Maybe
当作 applicative 用的话是没有办法达到我们要的效果的。你试着做一遍就会卡住。因为 applicative functor 并不允许 applicative value 之间有弹性的互动。他们最多就是让我们可以用 applicative style 来传递参数给函数。applicative operators 能拿到他们的结果并把他用 applicative 的方式喂给另一个函数,并把最终的 applicative 值放在一起。但在每一步之间并没有太多允许我们作手脚的机会。而我们的范例需要每一步都倚赖前一步的结果。当每一只鸟降落的时候,我们都会把前一步的结果拿出来看看。好知道结果到底应该成功或失败。
我们也能写出一个函数,完全不管现在究竟有几只鸟停在竿子上,只是要害皮尔斯滑倒。我们可以称呼这个函数叫做 banana
:
banana :: Pole -> Maybe Pole
banana _ = Nothing
现在我们能把香蕉皮串到我们的过程中。他绝对会让遇到的人滑倒。他完全不管前面的状态是什么都会产生失败。
ghci> return (0,0) >>= landLeft 1 >>= banana >>= landRight 1
Nothing
Just (1,0)
被喂给 banana
,而产生了 Nothing
,之后所有的结果便都是 Nothing
了。
要同样表示这种忽略前面的结果,只注重眼前的 monadic value 的情况,其实我们可以用 >>
来表达。
(>>) :: (Monad m) => m a -> m b -> m b
m >> n = m >>= \_ -> n
一般来讲,碰到一个完全忽略前面状态的函数,他就应该只会回传他想回传的值而已。但碰到 Monad,他们的 context 还是必须要被考虑到。来看一下 >>
串接 Maybe
的情况。
ghci> Nothing >> Just 3
Nothing
ghci> Just 3 >> Just 4
Just 4
ghci> Just 3 >> Nothing
Nothing
如果你把 >>
换成 >>= \_ ->
,那就很容易看出他的意思。
我们也可以把 banana
改用 >>
跟 Nothing
来表达:
ghci> return (0,0) >>= landLeft 1 >> Nothing >>= landRight 1
Nothing
我们得到了保证的失败。
我们也可以看看假如我们故意不用把 Maybe
视为有 context 的值的写法。他会长得像这样:
routine :: Maybe Pole
routine = case landLeft 1 (0,0) of
Nothing -> Nothing
Just pole1 -> case landRight 4 pole1 of
Nothing -> Nothing
Just pole2 -> case landLeft 2 pole2 of
Nothing -> Nothing
Just pole3 -> landLeft 1 pole3
左边先停了一只鸟,然后我们停下来检查有没有失败。当失败的时候我们回传 Nothing
。当成功的时候,我们在右边停一只鸟,然后再重复前面做的事情。把这些琐事转换成 >>=
证明了 Maybe
Monad 的力量,可以省去我们不少的时间。
注意到 Maybe
对 >>=
的实作,他其实就是在做碰到 Nothing
就会传 Nothing
,碰到正确值就继续用 Just
传递值。
在这个章节中,我们看过了好几个函数,也见识了用 Maybe
monad 来表示失败的 context 的力量。把普通的函数套用换成了 >>=
,让我们可以轻松地应付可能会失败的情况,并帮我们传递 context。这边的 context 就代表失败的可能性,当我们套用函数到 context 的时候,就代表考虑进了失败的情况。
#
do 表示法
Monad 在 Haskell 中是十分重要的,所以我们还特别为了操作他设置了特别的语法:do
表示法。我们在介绍 I/O 的时候已经用过 do
来把小的 I/O action 串在一起了。其实 do
并不只是可以用在 IO
,他可以用在任何 monad 上。他的原则是简单明了,把 monadic value 串成一串。我们这边来细看 do
是如何使用,以及为什么我们十分倚赖他。
来看一下熟悉的例子:
ghci> Just 3 >>= (\x -> Just (show x ++ "!"))
Just "3!"
你说这没什么了不起,不过就是把 monadic value 喂给一个函数罢了。其中 x
就指定成 3
。也从 monadic value 变成了普通值。那如果我们要在 lambda 中使用 >>=
呢?
ghci> Just 3 >>= (\x -> Just "!" >>= (\y -> Just (show x ++ y)))
Just "3!"
我们嵌一个 >>=
在另外一个 >>=
中。在外层的 lambda,我们把 Just "!"
喂给 \y -> Just (show x ++ y)
。在内层的 lambda,y
被指定成 "!"
。x
仍被指定成 3
,是因为我们是从外层的 lambda 取值的。这些行为让我们回想到下列式子:
ghci> let x = 3; y = "!" in show x ++ y
"3!"
差别在于前述的值是 monadic,具有失败可能性的 context。我们可以把其中任何一步代换成失败的状态:
ghci> Nothing >>= (\x -> Just "!" >>= (\y -> Just (show x ++ y)))
Nothing
ghci> Just 3 >>= (\x -> Nothing >>= (\y -> Just (show x ++ y)))
Nothing
ghci> Just 3 >>= (\x -> Just "!" >>= (\y -> Nothing))
Nothing
第一行中,把 Nothing
喂给一个函数,很自然地会回传 Nothing
。第二行里,我们把 Just 3
喂给一个函数,所以 x
就成了 3
。但我们把 Nothing
喂给内层的 lambda 所有的结果就成了 Nothing
,这也进一步使得外层的 lambda 成了 Nothing
。这就好比我们在 let
expression 中来把值指定给变数一般。只差在我们这边的值是 monadic value。
要再说得更清楚点,我们来把 script 改写成每行都处理一个 Maybe
:
foo :: Maybe String
foo = Just 3 >>= (\x ->
Just "!" >>= (\y ->
Just (show x ++ y)))
为了摆脱这些烦人的 lambda,Haskell 允许我们使用 do
表示法。他让我们可以把先前的程式写成这样:
foo :: Maybe String
foo = do
x <- Just 3
y <- Just "!"
Just (show x ++ y)
这看起来好像让我们不用在每一步都去检查 Maybe
的值究竟是 Just
或 Nothing
。这蛮方便的,如果在任何一个步骤我们取出了 Nothing
。那整个 do
的结果就会是 Nothing
。我们把整个责任都交给 >>=
,他会帮我们处理所有 context 的问题。这边的 do
表示法不过是另外一种语法的形式来串连所有的 monadic value 罢了。
在 do
expression 中,每一行都是一个 monadic value。要检查处理的结果的话,就要使用 <-
。如果我们拿到一个 Maybe String
,并用 <-
来绑定给一个变数,那个变数就会是一个 String
,就像是使用 >>=
来将 monadic value 带给 lambda 一样。至于 do
expression 中的最后一个值,好比说 Just (show x ++ y)
,就不能用 <-
来绑定结果,因为那样的写法当转换成 >>=
的结果时并不合理。他必须要是所有 monadic value 黏起来后的总结果,要考虑到前面所有可能失败的情形。
举例来说,来看看下面这行:
ghci> Just 9 >>= (\x -> Just (x > 8))
Just True
由于 >>=
左边的参数是一个 Just
型态的值,当 lambda 被套用至 9
就会得到 Just True
。如果我们重写整个式子,改用 do
表示法:我们会得到:
marySue :: Maybe Bool
marySue = do
x <- Just 9
Just (x > 8)
如果我们比较这两种写法,就很容易看出为什么整个 monadic value 的结果会是在 do
表示法中最后一个 monadic value 的值。他串连了全面所有的结果。
我们走钢索的模拟程式也可以改用 do
表示法重写。landLeft
跟 landRight
接受一个鸟的数字跟一个竿子来产生一个包在 Just
中新的竿子。而在失败的情况会产生 Nothing
。我们使用 >>=
来串连所有的步骤,每一步都倚赖前一步的结果,而且都带有可能失败的 context。这边有一个范例,先是有两只鸟停在左边,接着有两只鸟停在右边,然后是一只鸟停在左边:
routine :: Maybe Pole
routine = do
start <- return (0,0)
first <- landLeft 2 start
second <- landRight 2 first
landLeft 1 second
我们来看看成功的结果:
ghci> routine
Just (3,2)
当我们要把这些 routine 用具体写出的 >>=
,我们会这样写:return (0,0) >>= landLeft 2
,而有了 do
表示法,每一行都必须是一个 monadic value。所以我们清楚地把前一个 Pole
传给 landLeft
跟 landRight
。如果我们检视我们绑定 Maybe
的变数,start
就是 (0,0)
,而 first
就会是 (2,0)
。
由于 do
表示法是一行一行写,他们会看起来很像是命令式的写法。但实际上他们只是代表序列而已,每一步的值都倚赖前一步的结果,并带着他们的 context 继续下去。
我们再重新来看看如果我们没有善用 Maybe
的 monad 性质的程式:
routine :: Maybe Pole
routine =
case Just (0,0) of
Nothing -> Nothing
Just start -> case landLeft 2 start of
Nothing -> Nothing
Just first -> case landRight 2 first of
Nothing -> Nothing
Just second -> landLeft 1 second
在成功的情形下,Just (0,0)
变成了 start
, 而 landLeft 2 start
的结果成了 first
。
如果我们想在 do
表示法里面对皮尔斯丢出香蕉皮,我们可以这样做:
routine :: Maybe Pole
routine = do
start <- return (0,0)
first <- landLeft 2 start
Nothing
second <- landRight 2 first
landLeft 1 second
当我们在 do
表示法写了一行运算,但没有用到 <-
来绑定值的话,其实实际上就是用了 >>
,他会忽略掉计算的结果。我们只是要让他们有序,而不是要他们的结果,而且他比写成 _ <- Nothing
要来得漂亮的多。
你会问究竟我们何时要使用 do
表示法或是 >>=
,这完全取决于你的习惯。在这个例子由于有每一步都倚赖于前一步结果的特性,所以我们使用 >>=
。如果用 do
表示法,我们就必须清楚写出鸟究竟是停在哪根竿子上,但其实每一次都是前一次的结果。不过他还是让我们了解到怎么使用 do
。
在 do
表示法中,我们其实可以用模式匹配来绑定 monadic value,就好像我们在 let
表达式,跟函数参数中使用模式匹配一样。这边来看一个在 do
表示法中使用模式匹配的范例:
justH :: Maybe Char
justH = do
(x:xs) <- Just "hello"
return x
我们用模式匹配来取得 "hello"
的第一个字元,然后回传结果。所以 justH
计算会得到 Just 'h'
。
如果模式匹配失败怎么办?当定义一个函数的时候,一个模式不匹配就会跳到下一个模式。如果所有都不匹配,那就会造成错误,整个程式就当掉。另一方面,如果在 let
中进行模式匹配失败会直接造成错误。毕竟在 let
表达式的情况下并没有失败就跳下一个的设计。至于在 do
表示法中模式匹配失败的话,那就会呼叫 fail
函数。他定义在 Monad
的 type class 定义猪。他允许在现在的 monad context 底下,失败只会造成失败而不会让整个程式当掉。他预设的实作如下:
fail :: (Monad m) => String -> m a
fail msg = error msg
可见预设的实作的确是让程式挂掉,但在某些考虑到失败的可能性的 Monad(像是 Maybe
)常常会有他们自己的实作。对于 Maybe
,他的实作像是这样:
fail _ = Nothing
他忽略错误讯息,并直接回传 Nothing
。所以当在 do
表示法中的 Maybe
模式匹配失败的时候,整个结果就会是 Nothing
。这种方式比起让程式挂掉要好多了。这边来看一下 Maybe
模式匹配失败的范例:
wopwop :: Maybe Char
wopwop = do
(x:xs) <- Just ""
return x
模式匹配的失败,所以那一行的效果相当于一个 Nothing
。我们来看看执行结果:
ghci> wopwop
Nothing
这样模式匹配的失败只会限制在我们 monad 的 context 中,而不是整个程式的失败。这种处理方式要好多了。
#
List Monad
我们已经了解了 Maybe
可以被看作具有失败可能性 context 的值,也见识到如何用 >>=
来把这些具有失败考量的值传给函数。在这一个章节中,我们要看一下如何利用 list 的 monadic 的性质来写 non-deterministic 的程式。
我们已经讨论过在把 list 当作 applicatives 的时候他们具有 non-deterministic 的性质。像 5
这样一个值是 deterministic 的。他只有一种结果,而且我们清楚的知道他是什么结果。另一方面,像 [3,8,9]
这样的值包含好几种结果,所以我们能把他看作是同时具有好几种结果的值。把 list 当作 applicative functors 展示了这种特性:
ghci> (*) <$> [1,2,3] <*> [10,100,1000]
[10,100,1000,20,200,2000,30,300,3000]
将左边 list 中的元素乘上右边 list 中的元素这样所有的组合全都被放进结果的 list 中。当处理 non-determinism 的时候,这代表我们有好几种选择可以选,我们也会每种选择都试试看,因此最终的结果也会是一个 non-deterministic 的值。只是包含更多不同可能罢了。
non-determinism 这样的 context 可以被漂亮地用 monad 来考虑。所以我们这就来看看 list 的 Monad
instance 的定义:
instance Monad [] where
return x = [x]
xs >>= f = concat (map f xs)
fail _ = []
return
跟 pure
是做同样的事,所以我们应该算已经理解了 return
的部份。他接受一个值,并把他放进一个最小的一个 context 中。换种说法,就是他做了一个只包含一个元素的 list。这样对于我们想要操作普通值的时候很有用,可以直接把他包起来变成 non-deterministic value。
要理解 >>=
在 list monad 的情形下是怎么运作的,让我们先来回归基本。>>=
基本上就是接受一个有 context 的值,把他喂进一个只接受普通值的函数,并回传一个具有 context 的值。如果操作的函数只会回传普通值而不是具有 context 的值,那 >>=
在操作一次后就会失效,因为 context 不见了。让我们来试着把一个 non-deterministic value 塞到一个函数中:
ghci> [3,4,5] >>= \x -> [x,-x]
[3,-3,4,-4,5,-5]
当我们对 Maybe
使用 >>=
,是有考虑到可能失败的 context。在这边 >>=
则是有考虑到 non-determinism。[3,4,5]
是一个 non-deterministic value,我们把他喂给一个回传 non-deterministic value 的函数。那结果也会是 non-deterministic。而且他包含了所有从 [3,4,5]
取值,套用 \x -> [x,-x]
后的结果。这个函数他接受一个数值并产生两个数值,一个原来的数值与取过负号的数值。当我们用 >>=
来把一个 list 喂给这个函数,所有在 list 中的数值都保留了原有的跟取负号过的版本。x
会针对 list 中的每个元素走过一遍。
要看看结果是如何算出来的,只要看看实作就好了。首先我们从 [3,4,5]
开始。然后我们用 lambda 映射过所有元素得到:
[[3,-3],[4,-4],[5,-5]]
lambda 会扫过每个元素,所以我们有一串包含一堆 list 的 list,最后我们在把这些 list 压扁,得到一层的 list。这就是我们得到 non-deterministic value 的过程。
non-determinism 也有考虑到失败的可能性。[]
其实等价于 Nothing
,因为他什么结果也没有。所以失败等同于回传一个空的 list。所有的错误讯息都不用。让我们来看看范例:
ghci> [] >>= \x -> ["bad","mad","rad"]
[]
ghci> [1,2,3] >>= \x -> []
[]
第一行里面,一个空的 list 被丢给 lambda。因为 list 没有任何元素,所以函数收不到任何东西而产生空的 list。这跟把 Nothing
喂给函数一样。第二行中,每一个元素都被喂给函数,但所有元素都被丢掉,而只回传一个空的 list。因为所有的元素都造成了失败,所以整个结果也代表失败。
就像 Maybe
一样,我们可以用 >>=
把他们串起来:
ghci> [1,2] >>= \n -> ['a','b'] >>= \ch -> return (n,ch)
[(1,'a'),(1,'b'),(2,'a'),(2,'b')]
[1,2]
被绑定到 n
而 ['a','b']
被绑定到 ch
。最后我们用 return (n,ch)
来把他放到一个最小的 context 中。在这个案例中,就是把 (n,ch)
放到 list 中,这代表最低程度的 non-determinism。整套结构要表达的意思就是对于 [1,2]
的每个元素,以及 ['a','b']
的每个元素,我们产生一个 tuple,每项分别取自不同的 list。
一般来说,由于 return
接受一个值并放到最小的 context 中,他不会多做什么额外的东西仅仅是展示出结果而已。
当你要处理 non-deterministic value 的时候,你可以把 list 中的每个元素想做计算路线的一个 branch。
这边把先前的表达式用 do
重写:
listOfTuples :: [(Int,Char)]
listOfTuples = do
n <- [1,2]
ch <- ['a','b']
return (n,ch)
这样写可以更清楚看到 n
走过 [1,2]
中的每一个值,而 ch
则取过 ['a','b']
中的每个值。正如 Maybe
一般,我们从 monadic value 中取出普通值然后喂给函数。>>=
会帮我们处理好一切 context 相关的问题,只差在这边的 context 指的是 non-determinism。
使用 do
来对 list 操作让我们回想起之前看过的一些东西。来看看下列的片段:
ghci> [ (n,ch) | n <- [1,2], ch <- ['a','b'] ]
[(1,'a'),(1,'b'),(2,'a'),(2,'b')]
没错,就是 list comprehension。在先前的范例中,n
会走过 [1,2]
的每个元素,而 ch
会走过 ['a','b']
的每个元素。同时我们又把 (n,ch)
放进一个 context 中。这跟 list comprehension 的目的一样,只是我们在 list comprehension 里面不用在最后写一个 return
来得到 (n,ch)
的结果。
实际上,list comprehension 不过是一个语法糖。不论是 list comprehension 或是用 do
表示法来表示,他都会转换成用 >>=
来做计算。
List comprehension 允许我们 filter 我们的结果。举例来说,我们可以只要包含 7
在表示位数里面的数值。
ghci> [ x | x <- [1..50], '7' `elem` show x ]
[7,17,27,37,47]
我们用 show
跟 x
来把数值转成字串,然后检查 '7'
是否包含在字串里面。要看看 filtering 要如何转换成用 list monad 来表达,我们可以考虑使用 guard
函数,还有 MonadPlus
这个 type class。MonadPlus
这个 type class 是用来针对可以同时表现成 monoid 的 monad。下面是他的定义:
class Monad m => MonadPlus m where
mzero :: m a
mplus :: m a -> m a -> m a
mzero
是其实是 Monoid
中 mempty
的同义词,而 mplus
则对应到 mappend
。因为 list 同时是 monoid 跟 monad,他们可以是 MonadPlus
的 instance。
instance MonadPlus [] where
mzero = []
mplus = (++)
对于 list 而言,mzero
代表的是不产生任何结果的 non-deterministic value,也就是失败的结果。而 mplus
则把两个 non-deterministic value 结合成一个。guard
这个函数被定义成下列形式:
guard :: (MonadPlus m) => Bool -> m ()
guard True = return ()
guard False = mzero
这函数接受一个布林值,如果他是 True
就回传一个包在预设 context 中的 ()
。如果他失败就产生 mzero。
ghci> guard (5 > 2) :: Maybe ()
Just ()
ghci> guard (1 > 2) :: Maybe ()
Nothing
ghci> guard (5 > 2) :: [()]
[()]
ghci> guard (1 > 2) :: [()]
[]
看起来蛮有趣的,但用起来如何呢?我们可以用他来过滤 non-deterministic 的计算。
ghci> [1..50] >>= (\x -> guard ('7' `elem` show x) >> return x)
[7,17,27,37,47]
这边的结果跟我们之前 list comprehension 的结果一致。究竟 guard
是如何办到的?我们先看看 guard
跟 >>
是如何互动:
ghci> guard (5 > 2) >> return "cool" :: [String]
["cool"]
ghci> guard (1 > 2) >> return "cool" :: [String]
[]
如果 guard
成功的话,结果就会是一个空的 tuple。接着我们用 >>
来忽略掉空的 tuple,而呈现不同的结果。另一方面,如果 guard
失败的话,后面的 return
也会失败。这是因为用 >>=
把空的 list 喂给函数总是会回传空的 list。基本上 guard
的意思就是:如果一个布林值是 False
那就产生一个失败状态,不然的话就回传一个基本的 ()
。这样计算就可以继续进行。
这边我们把先前的范例用 do
改写:
sevensOnly :: [Int]
sevensOnly = do
x <- [1..50]
guard ('7' `elem` show x)
return x
如果我们不写最后一行 return x
,那整个 list 就会是包含一堆空 tuple 的 list。
把上述范例写成 list comprehension 的话就会像这样:
ghci> [ x | x <- [1..50], '7' `elem` show x ]
[7,17,27,37,47]
所以 list comprehension 的 filtering 基本上跟 guard
是一致的。
#
A knight's quest
这边来看一个可以用 non-determinism 解决的问题。假设你有一个西洋棋盘跟一只西洋棋中的骑士摆在上面。我们希望知道是否这只骑士可以在三步之内移到我们想要的位置。我们只要用一对数值来表示骑士在棋盘上的位置。第一个数值代表棋盘的行,而第二个数值代表棋盘的列。
我们先帮骑士的位置定义一个 type synonym。
type KnightPos = (Int,Int)
假设骑士现在是在 (6,2)
。究竟他能不能够在三步内移动到 (6,1)
呢?你可能会先考虑究竟哪一步是最佳的一步。但不如全部一起考虑吧!要好好利用所谓的 non-determinism。所以我们不是只选择一步,而是选择全部。我们先写一个函数回传所有可能的下一步:
moveKnight :: KnightPos -> [KnightPos]
moveKnight (c,r) = do
(c',r') <- [(c+2,r-1),(c+2,r+1),(c-2,r-1),(c-2,r+1)
,(c+1,r-2),(c+1,r+2),(c-1,r-2),(c-1,r+2)
]
guard (c' `elem` [1..8] && r' `elem` [1..8])
return (c',r')
骑士有可能水平或垂直移动一步或二步,但问题是他们必须要同时水平跟垂直移动。(c',r')
走过 list 中的每一个元素,而 guard
会保证产生的结果会停留在棋盘上。如果没有,那就会产生一个空的 list,表示失败的结果,return (c',r')
也就不会被执行。
这个函数也可以不用 list monad 来写,但我们这边只是写好玩的。下面是一个用 filter
实现的版本:
moveKnight :: KnightPos -> [KnightPos]
moveKnight (c,r) = filter onBoard
[(c+2,r-1),(c+2,r+1),(c-2,r-1),(c-2,r+1)
,(c+1,r-2),(c+1,r+2),(c-1,r-2),(c-1,r+2)
]
where onBoard (c,r) = c `elem` [1..8] && r `elem` [1..8]
两个函数做的都是相同的事,所以选个你喜欢的吧。
ghci> moveKnight (6,2)
[(8,1),(8,3),(4,1),(4,3),(7,4),(5,4)]
ghci> moveKnight (8,1)
[(6,2),(7,3)]
我们接受一个位置然后产生所有可能的移动方式。所以我们有一个 non-deterministic 的下一个位置。我们用 >>=
来喂给 moveKnight
。接下来我们就可以写一个三步内可以达到的所有位置:
in3 :: KnightPos -> [KnightPos]
in3 start = do
first <- moveKnight start
second <- moveKnight first
moveKnight second
如果你传 (6,2)
,得到的 list 会很大,因为会有不同种方式来走到同样的一个位置。我们也可以不用 do
来写:
in3 start = return start >>= moveKnight >>= moveKnight >>= moveKnight
第一次 >>=
给我们移动一步的所有结果,第二次 >>=
给我们移动两步的所有结果,第三次则给我们移动三步的所有结果。
用 return
来把一个值放进预设的 context 然后用 >>=
喂给一个函数其实跟函数呼叫是同样的,只是用不同的写法而已。 接着我们写一个函数接受两个位置,然后可以测试是否可以在三步内从一个位置移到另一个位置:
canReachIn3 :: KnightPos -> KnightPos -> Bool
canReachIn3 start end = end `elem` in3 start
我们产生所有三步的可能位置,然后看看其中一个位置是否在里面。所以我们可以看看是否可以在三步内从 (6,2)
走到 (6,1)
:
ghci> (6,2) `canReachIn3` (6,1)
True
那从 (6,2)
到 (7,3)
呢?
ghci> (6,2) `canReachIn3` (7,3)
False
答案是不行。你可以修改函数改成当可以走到的时候,他还会告诉你实际的步骤。之后你也可以改成不只限定成三步,可以任意步。
#
Monad laws (单子律)
正如 applicative functors 以及 functors,Monad 也有一些要遵守的定律。我们定义一个 Monad
的 instance 并不代表他是一个 monad,只代表他被定义成那个 type class 的 instance。一个型态要是 monad,则必须遵守单子律。这些定律让我们可以对这个型态的行为做一些合理的假设。
Haskell 允许任何型态是任何 type class 的 instance。但他不会检查单子律是否有被遵守,所以如果我们要写一个 Monad
的 instance,那最好我们确定他有遵守单子律。我们可以不用担心标准函式库中的型态是否有遵守单子律。但之后我们定义自己的型态时,我们必须自己检查是否有遵守单子律。不用担心,他们不会很复杂。
#
Left identity
单子律的第一项说当我们接受一个值,将他用 return
放进一个预设的 context 并把他用 >>=
喂进一个函数的结果,应该要跟我们直接做函数呼叫的结果一样。
- retrun x >>= f
应该等于 f x
如果你是把 monadic value 视为把一个值放进最小的 context 中,仅仅是把同样的值放进结果中的话, 那这个定律应该很直觉。因为把这个值放进 context 中然后丢给函数,应该要跟直接把这个值丢给函数做呼叫应该没有差别。
对于 Maybe
monad,return
被定义成 Just
。Maybe
monad 讲的是失败的可能性,如果我们有普通值要把他放进 context 中,那把这个动作当作是计算成功应该是很合理的,毕竟我们都知道那个值是很具体的。这边有些范例:
ghci> return 3 >>= (\x -> Just (x+100000))
Just 100003
ghci> (\x -> Just (x+100000)) 3
Just 100003
对于 list monad 而言,return
是把值放进一个 list 中,变成只有一个元素的 list。>>=
则会走过 list 中的每个元素,并把他们丢给函数做运算,但因为在单一元素的 list 中只有一个值,所以跟直接对那元素做运算是等价的:
ghci> return "WoM" >>= (\x -> [x,x,x])
["WoM","WoM","WoM"]
ghci> (\x -> [x,x,x]) "WoM"
["WoM","WoM","WoM"]
至于 IO
,我们已经知道 return
并不会造成副作用,只不过是在结果中呈现原有值。所以这个定律对于 IO
也是有效的。
#
Right identity
单子律的第二个规则是如果我们有一个 monadic value,而且我们把他用 >>=
喂给 return
,那结果就会是原有的 monadic value。
- m >>= return
会等于 m
这一个可能不像第一定律那么明显,但我们还是来看看为什么会遵守这条。当我们把一个 monadic value 用 >>=
喂给函数,那些函数是接受普通值并回传具有 context 的值。return
也是在他们其中。如果你仔细看他的型态,return
是把一个普通值放进一个最小 context 中。这就表示,对于 Maybe
他并没有造成任何失败的状态,而对于 list 他也没有多加 non-determinism。
ghci> Just "move on up" >>= (\x -> return x)
Just "move on up"
ghci> [1,2,3,4] >>= (\x -> return x)
[1,2,3,4]
ghci> putStrLn "Wah!" >>= (\x -> return x)
Wah!
如果我们仔细检视 list monad 的范例,会发现 >>=
的实作是:
xs >>= f = concat (map f xs)
所以当我们将 [1,2,3,4]
丢给 return
,第一个 return
会把 [1,2,3,4]
映射成 [[1],[2],[3],[4]]
,然后再把这些小 list 串接成我们原有的 list。
Left identity 跟 right identity 是描述 return
的行为。他重要的原因是因为他把普通值转换成具有 context 的值,如果他出错的话会很头大。
#
Associativity
单子律最后一条是说当我们用 >>=
把一串 monadic function 串在一起,他们的先后顺序不应该影响结果:
- (m >>= f) >>= g
跟 m >>= (\x -> f x >>= g)
是相等的
究竟这边说的是什么呢?我们有一个 monadic value m
,以及两个 monadic function f
跟 g
。当我们写下 (m >>= f) >>= g
,代表的是我们把 m
喂给 f
,他的结果是一个 monadic value。然后我们把这个结果喂给 g
。而在 m >>= (\x -> f x >>= g)
中,我们接受一个 monadic value 然后喂给一个函数,这个函数会把 f x
的结果丢给 g
。我们不太容易直接看出两者相同,所以先来看个范例比较好理解。
还记得之前皮尔斯的范例吗?要模拟鸟停在他的平衡竿上,我们把好几个函数串在一起
ghci> return (0,0) >>= landRight 2 >>= landLeft 2 >>= landRight 2
Just (2,4)
从 Just (0,0)
出发,然后把值传给 landRight 2
。他的结果又被绑到下一个 monadic function,以此类推。如果我们用括号清楚标出优先顺序的话会是这样:
ghci> ((return (0,0) >>= landRight 2) >>= landLeft 2) >>= landRight 2
Just (2,4)
我们也可以改写成这样:
return (0,0) >>= (\x ->
landRight 2 x >>= (\y ->
landLeft 2 y >>= (\z ->
landRight 2 z)))
return (0,0)
等价于 Just (0,0)
,当我们把他喂给 lambda,里面的 x
就等于 (0,0)
。landRight
接受一个数值跟 pole,算出来的结果是 Just (0,2)
然后把他喂给另一个 lambda,里面的 y
就变成了 (0,2)
。这样的操作持续下去,直到最后一只鸟降落,而得到 Just (2,4)
的结果,这也是整个操作的总结果。
这些 monadic function 的优先顺序并不重要,重点是他们的意义。从另一个角度来看这个定律:考虑两个函数 f
跟 g
,将两个函数组合起来的定义像是这样:
(.) :: (b -> c) -> (a -> b) -> (a -> c)
f . g = (\x -> f (g x))
如果 g
的型态是 a -> b
且 f
的型态是 b -> c
,我们可以把他们合成一个型态是 a -> c
的新函数。所以中间的参数都有自动带过。现在假设这两个函数是 monadic function,也就是说如果他们的回传值是 monadic function?如果我们有一个函数他的型态是 a -> m b
,我们并不能直接把结果丢给另一个型态为 b -> m c
的函数,因为后者只接受型态为 b
的普通值。然而,我们可以用 >>=
来做到我们想要的事。有了 >>=
,我们可以合成两个 monadic function:
(<=<) :: (Monad m) => (b -> m c) -> (a -> m b) -> (a -> m c)
f <=< g = (\x -> g x >>= f)
所以现在我们可以合成两个 monadic functions:
ghci> let f x = [x,-x]
ghci> let g x = [x*3,x*2]
ghci> let h = f <=< g
ghci> h 3
[9,-9,6,-6]
至于这跟结合律有什么关系呢?当我们把这定律看作是合成的定律,他就只是说了 f <=< (g <=< h)
跟 (f <=< g) <=< h
应该等价。只是他是针对 monad 而已。
如果我们把头两个单子律用 <=<
改写,那 left identity 不过就是说对于每个 monadic function f
,f <=< return
跟 f
是等价,而 right identity 说 return <=< f
跟 f
是等价。
如果看看普通函数的情形,就会发现很像,(f . g) . h
等价于 f . (g . h)
,f . id
跟 f
等价,且 id . f
等价于 f
。
在这一章中,我们检视了 monad 的基本性质,而且也了解了 Maybe
monad 跟 list monad 的运作方式。在下一章,我们会看看其他一些有特色的 monad,我们也会学到如何定义自己的 monad。
13
再来看看更多 Monad
我们已经看过 Monad 是如何接受具有 context 的值,并如何用函数操作他们 还有如何用 >>=
跟 do
来减轻我们对 context 的关注,集中精神在 value 本身。
我们也看过了 Maybe
是如何把值加上一个可能会失败的 context。我们学习到 List Monad 是如何加进多重结果的 context。我们也了解 IO
Monad 如何运作,而且我们在知道什么是 Monad 之前就已经知道他了。
在这个章节,我们会介绍一些其他的 Monad。他们可以把值变成 monadic value,因此可以让我们的程式更简洁清晰。多见识几个 Monad 也可以敏锐我们对 Monad 的直觉。
我们即将要介绍的 Monad 都包含在 mtl
这个套建中。一个 Haskell package 包含了一堆模组。而 mtl
已经包含在 Haskell Platform 中,所以你可能不用另外安装。要检查你有没有这套件,你可以下 ghc-pkg list
。这会列出你已经安装的套件,其中应该包含 mtl
后面接着对应的版号。
#
你所不知道的 Writer Monad 我们已经看过 Maybe
, list 以及 IO
Monad。现在我们要来看看 Writer
Monad。
相对于 Maybe
是加入可能失败的 context,list 是加入 non-deterministic 的 context,Writer
则是加进一个附加值的 context,好比 log 一般。Writer
可以让我们在计算的同时搜集所有 log 纪录,并汇集成一个 log 并附加在结果上。
例如我们想要附加一个 String 好说明我们的值在干么(有可能是为了除错)。想像有一个函数接受一个代表帮派人数的数字,然后会回传值告诉我们这是否算是一个庞大的帮派:
isBigGang :: Int -> Bool
isBigGang x = x > 9
现在我们希望他不只是回传 True
或 False
,我们还希望他能够多回传一个字串代表 log。这很容易,只要多加一个 String
在 Bool
旁边就好了。
isBigGang :: Int -> (Bool, String)
isBigGang x = (x > 9, "Compared gang size to 9.")
我们现在回传了一个 Tuple,第一个元素是原来的布林值,第二个元素是一个 String。现在我们的值有了一个 context。
ghci> isBigGang 3
(False,"Compared gang size to 9.")
ghci> isBigGang 30
(True,"Compared gang size to 9.")
到目前为止都还不错,isBigGang
回传一个值跟他的 context。对于正常的数值来说这样的写法都能运作良好。但如果我们想要把一个已经具有 context 的值,像是 (3, "Smallish gang.")
,喂给 isBigGang
呢?我们又面对了同样的问题:如果我们有一个能接受正常数值并回传一个具有 context 值的 function,那我们要如何喂给他一个具有 context 的值?
当我们在研究 Maybe
monad 的时候,我们写了一个 applyMaybe
。他接受一个 Maybe a
值跟一个 a -> Maybe b
型态的函数,他会把 Maybe a
喂给这个 function,即便这个 function 其实是接受 a
而非 Maybe a
。applyMaybe
有针对这样的 context 做处理,也就是会留意有可能发生的失败情况。但在 a -> Maybe b
里面,我们可以只专心处理正常数值即可。因为 applyMaybe
(之后变成了 >>=
)会帮我们处理需要检查 Nothing
或 Just
的情况。
我们再来写一个接受附加 log 值的函数,也就是 (a, String)
型态的值跟 a -> (b, String)
型态的函数。我们称呼这个函数为 applyLog
。这个函数有的 context 是附加 log 值,而不是一个可能会失败的 context,因此 applyLog
会确保原有的 log 被保留,并附上从函数产生出的新的 log。这边我们来看一下实作:
applyLog :: (a,String) -> (a -> (b,String)) -> (b,String)
applyLog (x,log) f = let (y,newLog) = f x in (y,log ++ newLog)
当我们想把一个具有 context 的值喂给一个函数的时候,我们会尝试把值跟他的 context 分开,然后把值喂给函数再重新接回 context。在 Maybe
monad 的情况,我们检查值是否为 Just x
,如果是,便将 x
喂给函数。而在 log 的情况,我们知道 pair 的其中一个 component 是 log 而另一个是值。所以我们先取出值 x
,将 f
apply 到 x
,便获取 (y,newLog)
,其中 y
是新的值而 newLog
则是新的 log。但如果我们回传 newLog
,旧的 log 便不会包含进去,所以我们要回传的是 (y, log ++ newLog)
。我们用 ++
来把新的 log 接到旧的上面。
来看看 applyLog
运作的情形:
ghci> (3, "Smallish gang.") `applyLog` isBigGang
(False,"Smallish gang.Compared gang size to 9")
ghci> (30, "A freaking platoon.") `applyLog` isBigGang
(True,"A freaking platoon.Compared gang size to 9")
跟之前的结果很像,只差在我们多了伴随产生的 log。再来多看几个例子:
ghci> ("Tobin","Got outlaw name.") `applyLog` (\x -> (length x, "Applied length."))
(5,"Got outlaw name.Applied length.")
ghci> ("Bathcat","Got outlaw name.") `applyLog` (\x -> (length x, "Applied length"))
(7,"Got outlaw name.Applied length")
可以看到在 lambda 里面 x
只是个正常的字串而不是 tuple,且 applyLog
帮我们处理掉附加 log 的动作。
#
Monoids 的好处
请确定你了解什么是 Monoids。
到目前为止 applyLog
接受 (a,String)
型态的值,但为什么 log 一定要是 String
呢?我们使用 ++
来附加新的 log,难道 ++
并不能运作在任何形式的 list,而一定要限制我们在 String
上呢?我们当然可以摆脱 String
,我们可以如下改变他的型态:
applyLog :: (a,[c]) -> (a -> (b,[c])) -> (b,[c])
我们用一个 List 来代表 Log。包含在 List 中的元素型态必须跟原有的 List 跟回传的 List 型态相同,否则我们没办法用 ++
来把他们接起来。
这能够运作在 bytestring 上吗?绝对没问题。只是我们现在的型态只对 List 有效。我们必须要另外做一个 bytestring 版本的 applyLog
。但我们注意到 List 跟 bytestring 都是 monoids。因此他们都是 Monoid
type class 的 instance,那代表他们都有实作 mappend
。对 List 以及 bytestring 而言,mappend
都是拿来串接的。
ghci> [1,2,3] `mappend` [4,5,6]
[1,2,3,4,5,6]
ghci> B.pack [99,104,105] `mappend` B.pack [104,117,97,104,117,97]
Chunk "chi" (Chunk "huahua" Empty)
修改后我们的 applyLog
可以运作在任何 monoid 上。我们必须要修改型态宣告来表示这件事,同时也要在实作中把 ++
改成 mappend
:
applyLog :: (Monoid m) => (a,m) -> (a -> (b,m)) -> (b,m)
applyLog (x,log) f = let (y,newLog) = f x in (y,log `mappend` newLog)
由于现在包含的值可以是任何 monoid,我们不再需要把 tuple 想成包含一个值跟对应的 log,我们可以想成他包含一个值跟一个对应的 monoid。举例来说,可以说我们有一个 tuple 包含一个产品名称跟一个符合 monoid 特性的产品价格。我们可以定义一个 Sum
的 newtype 来保证我们在操作产品的时候也会把价钱跟着加起来。
import Data.Monoid
type Food = String
type Price = Sum Int
addDrink :: Food -> (Food,Price)
addDrink "beans" = ("milk", Sum 25)
addDrink "jerky" = ("whiskey", Sum 99)
addDrink _ = ("beer", Sum 30)
我们用 string 来代表食物,用 newtype
重新定义 nInt
为 Sum
,来追踪总共需要花多少钱。可以注意到我们用 mappend
来操作 Sum
的时候,价钱会被一起加起来。
ghci> Sum 3 `mappend` Sum 9
Sum {getSum = 12}
addDrink
的实作很简单,如果我们想吃豆子,他会回传 "milk"
以及伴随的 Sum 25
,同样的如果我们要吃 "jerky",他就会回传 "whiskey",要吃其他东西的话,就会回传 "beer"。乍看之下这个函数没什么特别,但如果用 applyLog
的话就会有趣些。
ghci> ("beans", Sum 10) `applyLog` addDrink
("milk",Sum {getSum = 35})
ghci> ("jerky", Sum 25) `applyLog` addDrink
("whiskey",Sum {getSum = 124})
ghci> ("dogmeat", Sum 5) `applyLog` addDrink
("beer",Sum {getSum = 35})
牛奶价值 25
美分,但如果我们也吃了价值 10
美分的豆子的话,总共需要付 35
美分。这样很清楚地展示了伴随的值不一定需要是 log,他可以是任何 monoid。至于两个值要如何结合,那要看 monoid 中怎么定义。当我们需要的是 log 的时候,他们是串接,但这个 case 里面,数字是被加起来。
由于 addDrink
回传一个 (Food,Price)
,我们可以再把结果重新喂给 addDrink
,这可以很容易告诉我们总共喝了多少钱:
ghci> ("dogmeat", Sum 5) `applyLog` addDrink `applyLog` addDrink
("beer",Sum {getSum = 65})
将狗食跟 30 美分的啤酒加在一起会得到 ("beer", Sum 35)
。如果我们用 applyLog
将上面的结果再喂给 addDrink
,我们会得到 ("beer", Sum 65)
这样的结果。
#
The Writer type
我们认识了一个附加 monoid 的值其实表现出来的是一个 monad,我们来再来看看其他类似的 Monad
instance。Control.Monad.Writer
这模组含有 Writer w a
的一个型态,里面定义了他 Monad
的 instance,还有一些操作这些值的函数。
首先,我们来看一下型态。要把一个 monoid 附加给一个值,只需要定义一个 tuple 就好了。Writer w a
这型态其实是一个 newtype
wrapper。他的定义很简单:
newtype Writer w a = Writer { runWriter :: (a, w) }
他包在一个 newtype
里面,并且可以是一个 Monad
的 instance,而且这样定义的好处是可以跟单纯 tuple 的型态区分开来。a
这个型态参数代表是包含的值的型态,而 w
则是附加的 monoid 的型态。
他 Monad
instance 的定义如下:
instance (Monoid w) => Monad (Writer w) where
return x = Writer (x, mempty)
(Writer (x,v)) >>= f = let (Writer (y, v')) = f x in Writer (y, v `mappend` v')
首先,我们来看看 >>=
。他的实作基本上就是 applyLog
,只是我们的 tuple 现在是包在一个 Writer
的 newtype
中,我们可以用 pattern matching 的方式把他给 unwrap。我们将 x
喂给 f
。这会回给我们 Writer w a
。接着可以用 let
expression 来做 pattern matching。把结果绑定到 y
这个名字上,然后用 mappend
来结合旧的 monoid 值跟新的 monoid 值。最后把结果跟 monoid 值用 Writer
constructor 包起来,形成我们最后的 Writer
value。
那 return
呢?回想 return
的作用是接受一个值,并回传一个具有意义的最小 context 来装我们的值。那究竟什么样的 context 可以代表我们的 Writer
呢?如果我们希望 monoid 值所造成的影响愈小愈好,那 mempty
是个合理的选择。mempty
是被当作 identity monoid value,像是 ""
或 Sum 0
,或是空的 bytestring。当我们对 mempty
用 mappend
跟其他 monoid 值结合,结果会是其他的 monoid 值。所以如果我们用 return
来做一个 Writer
,然后用 >>=
来喂给其他的函数,那函数回传的便是算出来的 monoid。下面我们试着用 return
搭配不同 context 来回传 3
:
ghci> runWriter (return 3 :: Writer String Int)
(3,"")
ghci> runWriter (return 3 :: Writer (Sum Int) Int)
(3,Sum {getSum = 0})
ghci> runWriter (return 3 :: Writer (Product Int) Int)
(3,Product {getProduct = 1})
因为 Writer
并没有定义成 Show
的 instance,我们必须用 runWriter
来把我们的 Writer
转成正常的 tuple。对于 String
,monoid 的值就是空字串。而对于 Sum
来说则是 0
,因为 0
加上其他任何值都会是对方。而对 Product
来说,则是 1
。
这里的 Writer
instance 并没有定义 fail
,所以如果 pattern matching 失败的话,就会呼叫 error
。
#
Using do notation with Writer
既然我们定义了 Monad
的 instance,我们自然可以用 do
串接 Writer
型态的值。这在我们需要对一群 Writer
型态的值做处理时显得特别方便。就如其他的 monad,我们可以把他们当作具有 context 的值。在现在这个 case 中,所有的 monoid 的值都会用 mappend
来连接起来并得到最后的结果。这边有一个简单的范例,我们用 Writer
来相乘两个数。
import Control.Monad.Writer
logNumber :: Int -> Writer [String] Int
logNumber x = Writer (x, ["Got number: " ++ show x])
multWithLog :: Writer [String] Int
multWithLog = do
a <- logNumber 3
b <- logNumber 5
return (a*b)
logNumber
接受一个数并把这个数做成一个 Writer
。我们再用一串 string 来当作我们的 monoid 值,每一个数都跟着一个只有一个元素的 list,说明我们只有一个数。multWithLog
式一个 Writer
,他将 3
跟 5
相乘并确保相乘的纪录有写进最后的 log 中。我们用 return
来做成 a*b
的结果。我们知道 return
会接受某个值并加上某个最小的 context,我们可以确定他不会多添加额外的 log。如果我们执行程式会得到:
ghci> runWriter multWithLog
(15,["Got number: 3","Got number: 5"])
有时候我们就是想要在某个时间点放进某个 Monoid value。tell
正是我们需要的函数。他实作了 MonadWriter
这个 type class,而且在当 Writer
用的时候也能接受一个 monoid value,好比说 ["This is going on"]
。我们能用他来把我们的 monoid value 接到任何一个 dummy value ()
上来形成一个 Writer。当我们拿到的结果是 ()
的时候,我们不会把他绑定到变数上。来看一个 multWithLog
的范例:
multWithLog :: Writer [String] Int
multWithLog = do
a <- logNumber 3
b <- logNumber 5
tell ["Gonna multiply these two"]
return (a*b)
return (a*b)
是我们的最后一行,还记得在一个 do
中的最后一行代表整个 do
的结果。如果我们把 tell
摆到最后,则 do
的结果则会是 ()
。我们会因此丢掉乘法运算的结果。除此之外,log 的结果是不变的。
ghci> runWriter multWithLog
(15,["Got number: 3","Got number: 5","Gonna multiply these two"])
#
Adding logging to programs 欧几里得算法是找出两个数的最大公因数。Haskell 已经提供了 gcd
的函数,但我们来实作一个具有 log 功能的 gcd:
gcd' :: Int -> Int -> Int
gcd' a b
| b == 0 = a
| otherwise = gcd' b (a `mod` b)
演算法的内容很简单。首先他检查第二个数字是否为零。如果是零,那就回传第一个数字。如果不是,那结果就是第二个数字跟将第一个数字除以第二个数字的余数两个数字的最大公因数。举例来说,如果我们想知道 8 跟 3 的最大公因数,首先可以注意到 3 不是 0。所以我们要求的是 3 跟 2 的最大公因数(8 除以 3 余二)。接下去我可以看到 2 不是 0,所以我们要再找 2 跟 1 的最大公因数。同样的,第二个数不是 0,所以我们再找 1 跟 0 的最大公因数。最后第二个数终于是 0 了,所以我们得到最大公因数是 1。
ghci> gcd' 8 3
1
答案真的是这样。接着我们想加进 context,context 会是一个 monoid value 并且像是一个 log 一样。就像之前的范例,我们用一串 string 来当作我们的 monoid。所以 gcd'
会长成这样:
gcd' :: Int -> Int -> Writer [String] Int
而他的程式码会像这样:
import Control.Monad.Writer
gcd' :: Int -> Int -> Writer [String] Int
gcd' a b
| b == 0 = do
tell ["Finished with " ++ show a]
return a
| otherwise = do
tell [show a ++ " mod " ++ show b ++ " = " ++ show (a `mod` b)]
gcd' b (a `mod` b)
这个函数接受两个 Int
并回传一个 Writer [String] Int
,也就是说是一个有 log context 的 Int
。当 b
等于 0
的时候,我们用一个 do
来组成一个 Writer
的值。我们先用 tell
来写入我们的 log,然后用 return
来当作 do
的结果。当然我们也可以这样写:
Writer (a, ["Finished with " ++ show a])
但我想 do
的表达方式是比较容易阅读的。接下来我们看看当 b
不等于 0
的时候。我们会把 mod
的使用情况写进 log。然后在 do
当中的第二行递回呼叫 gcd'
。gcd'
现在是回传一个 Writer
的型态,所以 gcd' b (a `mod` b)
这样的写法是完全没问题的。
尽管去 trace 这个 gcd'
对于理解十分有帮助,但我想了解整个大概念,把值视为具有 context 是更加有用的。
接着来试试跑我们的 gcd'
,他的结果会是 Writer [String] Int
,如果我们把他从 newtype
中取出来,我们会拿到一个 tuple。tuple 的第一个部份就是我们要的结果:
ghci> fst $ runWriter (gcd' 8 3)
1
至于 log 呢,由于 log 是一连串 string,我们就用 mapM_ putStrLn
来把这些 string 印出来:
ghci> mapM_ putStrLn $ snd $ runWriter (gcd' 8 3)
8 mod 3 = 2
3 mod 2 = 1
2 mod 1 = 0
Finished with 1
把普通的演算法转换成具有 log 是很棒的经验,我们不过是把普通的 value 重写成 Monadic value,剩下的就靠 >>=
跟 Writer
来帮我们处理一切。用这样的方法我们几乎可以对任何函数加上 logging 的功能。我们只要把普通的值换成 Writer
,然后把一般的函数呼叫换成 >>=
(当然也可以用 do
)
#
Inefficient list construction 当制作 Writer
Monad 的时候,要特别注意你是使用哪种 monoid。使用 list 的话效能有时候是没办法接受的。因为 list 是使用 ++
来作为 mappend
的实现。而 ++
在 list 很长的时候是非常慢的。
在之前的 gcd'
中,log 并不会慢是因为 list append 的动作实际上看起来是这样:
a ++ (b ++ (c ++ (d ++ (e ++ f))))
list 是建立的方向是从左到右,当我们先建立左边的部份,而把另一串 list 加到右边的时候效能会不错。但如果我们不小心使用,而让 Writer
monad 实际在操作 list 的时候变成像这样的话。
((((a ++ b) ++ c) ++ d) ++ e) ++ f
这会让我们的操作是 left associative,而不是 right associative。这非常没有效率,因为每次都是把右边的部份加到左边的部份,而左边的部份又必须要从头开始建起。
下面这个函数跟 gcd'
差不多,只是 log 的顺序是相反的。他先纪录剩下的操作,然后纪录现在的步骤。
import Control.Monad.Writer
gcdReverse :: Int -> Int -> Writer [String] Int
gcdReverse a b
| b == 0 = do
tell ["Finished with " ++ show a]
return a
| otherwise = do
result <- gcdReverse b (a `mod` b)
tell [show a ++ " mod " ++ show b ++ " = " ++ show (a `mod` b)]
return result
他先递回呼叫,然后把结果绑定到 result
。然后把目前的动作写到 log,在递回的结果之后。最后呈现的就是完整的 log。
ghci> mapM_ putStrLn $ snd $ runWriter (gcdReverse 8 3)
Finished with 1
2 mod 1 = 0
3 mod 2 = 1
8 mod 3 = 2
这没效率是因为他让 ++
成为 left associative 而不是 right associative。
#
Difference lists
由于 list 在重复 append 的时候显得低效,我们最好能使用一种支援高效 appending 的资料结构。其中一种就是 difference list。difference list 很类似 list,只是他是一个函数。他接受一个 list 并 prepend 另一串 list 到他前面。一个等价于 [1,2,3]
的 difference list 是这样一个函数 \xs -> [1,2,3] ++ xs
。一个等价于 []
的 difference list 则是 \xs -> [] ++ xs
。
Difference list 最酷的地方在于他支援高效的 appending。当我们用 ++
来实现 appending 的时候,他必须要走到左边的 list 的尾端,然后把右边的 list 一个个从这边接上。那 difference list 是怎么作的呢?appending 两个 difference list 就像这样
f `append` g = \xs -> f (g xs)
f
跟 g
这边是两个函数,他们都接受一个 list 并 prepend 另一串 list。举例来说,如果 f
代表 ("dog"++)
(可以写成 \xs -> "dog" ++ xs
)而 g
是 ("meat"++)
,那 f `append` g
就会做成一个新的函数,等价于:
\xs -> "dog" ++ ("meat" ++ xs)
append 两个 difference list 其实就是用一个函数,这函数先喂一个 list 给第一个 difference list,然后再把结果喂给第二个 difference list。
我们可以用一个 newtype
来包起来
newtype DiffList a = DiffList { getDiffList :: [a] -> [a] }
我们包起来的型态是 [a] -> [a]
,因为 difference list 不过就是一个转换一个 list 到另一个 list 的函数。要把普通 list 转换成 difference list 也很容易。
toDiffList :: [a] -> DiffList a
toDiffList xs = DiffList (xs++)
fromDiffList :: DiffList a -> [a]
fromDiffList (DiffList f) = f []
要把一个普通 list 转成 difference list 不过就是照之前定义的,作一个 prepend 另一个 list 的函数。由于 difference list 只是一个 prepend 另一串 list 的一个函数,假如我们要转回来的话,只要喂给他空的 list 就行了。
这边我们给一个 difference list 的 Monoid
定义
instance Monoid (DiffList a) where
mempty = DiffList (\xs -> [] ++ xs)
(DiffList f) `mappend` (DiffList g) = DiffList (\xs -> f (g xs))
我们可以看到 mempty
不过就是 id
,而 mappend
其实是 function composition。
ghci> fromDiffList (toDiffList [1,2,3,4] `mappend` toDiffList [1,2,3])
[1,2,3,4,1,2,3]
现在我们可以用 difference list 来加速我们的 gcdReverse
import Control.Monad.Writer
gcd' :: Int -> Int -> Writer (DiffList String) Int
gcd' a b
| b == 0 = do
tell (toDiffList ["Finished with " ++ show a])
return a
| otherwise = do
result <- gcd' b (a `mod` b)
tell (toDiffList [show a ++ " mod " ++ show b ++ " = " ++ show (a `mod` b)])
return result
我们只要把 monoid 的型态从 [String]
改成 DiffList String
,并在使用 tell
的时候把普通的 list 用 toDiffList
转成 difference list 就可以了。
ghci> mapM_ putStrLn . fromDiffList . snd . runWriter $ gcdReverse 110 34
Finished with 2
8 mod 2 = 0
34 mod 8 = 2
110 mod 34 = 8
我们用 runWriter
来取出 gcdReverse 110 34
的结果,然后用 snd
取出 log,并用 fromDiffList
转回普通的 list 印出来。
#
Comparing Performance
要体会 Difference List 能如何增进效率,考虑一个从某数数到零的 case。我们纪录的时候就像 gcdReverse
一样是反过来记的,所以在 log 中实际上是从零数到某个数。
finalCountDown :: Int -> Writer (DiffList String) ()
finalCountDown 0 = do
tell (toDiffList ["0"])
finalCountDown x = do
finalCountDown (x-1)
tell (toDiffList [show x])
如果我们喂 0
,他就只 log 0。如果喂其他正整数,他会先倒数到 0
然后 append 那些数到 log 中,所以如果我们呼叫 finalCountDown
并喂给他 100
,那 log 的最后一笔就会是 "100"
。
如果你把这个函数 load 进 GHCi 中并喂给他一个比较大的整数 500000
,你会看到他无停滞地从 0
开始数起:
ghci> mapM_ putStrLn . fromDiffList . snd . runWriter $ finalCountDown 500000
0
1
2
但如果我们用普通的 list 而不用 difference list
finalCountDown :: Int -> Writer [String] ()
finalCountDown 0 = do
tell ["0"]
finalCountDown x = do
finalCountDown (x-1)
tell [show x]
并下同样的指令
ghci> mapM_ putStrLn . snd . runWriter $ finalCountDown 500000
我们会看到整个运算卡卡的。
当然这不是一个严谨的测试方法,但足以表显出 difference list 是比较有效率的写法。
#
Reader Monad
在讲 Applicative 的章节中,我们说过了 (->) r
的型态只是 Functor
的一个 instance。要将一个函数 f
map over 一个函数 g
,基本上等价于一个函数,他可以接受原本 g
接受的参数,先套用 g
然后再把其结果丢给 f
。
ghci> let f = (*5)
ghci> let g = (+3)
ghci> (fmap f g) 8
我们已经见识过函数当作 applicative functors 的例子。这样能让我们对函数的结果直接进行操作。
ghci> let f = (+) <$> (*2) <*> (+10)
ghci> f 3
19
(+) <$> (*2) <*> (+10)
代表一个函数,他接受一个数值,分别把这数值交给 (*2)
跟 (+10)
。然后把结果加起来。例如说,如果我们喂 3
给这个函数,他会分别对 3
做 (*2)
跟 (+10)
的动作。而得到 6
跟 13
。然后呼叫 (+)
,而得到 19
。
其实 (->) r
不只是一个 functor 跟一个 applicative functor,他也是一个 monad。就如其他 monadic value 一般,一个函数也可以被想做是包含一个 context 的。这个 context 是说我们期待某个值,他还没出现,但我们知道我们会把他当作函数的参数,呼叫函数来得到结果。
我们已经见识到函数是怎样可以看作 functor 或是 applicative functors 了。再来让我们看看当作 Monad
的一个 instance 时会是什么样子。你可以在 Control.Monad.Instances
里面找到,他看起来像这样:
instance Monad ((->) r) where
return x = \_ -> x
h >>= f = \w -> f (h w) w
我们之前已经看过函数的 pure
实作了,而 return
差不多就是 pure
。他接受一个值并把他放进一个 minimal context 里面。而要让一个函数能够是某个定值的唯一方法就是让他完全忽略他的参数。
而 >>=
的实作看起来有点难以理解,我们可以仔细来看看。当我们使用 >>=
的时候,喂进去的是一个 monadic value,处理他的是一个函数,而吐出来的也是一个 monadic value。在这个情况下,当我们将一个函数喂进一个函数,吐出来的也是一个函数。这就是为什么我们在最外层使用了一个 lambda。在我们目前看过的实作中,>>=
几乎都是用 lambda 将内部跟外部隔开来,然后在内部来使用 f
。这边也是一样的道理。要从一个函数得到一个结果,我们必须喂给他一些东西,这也是为什么我们先用 (h w)
取得结果,然后将他丢给 f
。而 f
回传一个 monadic value,在这边这个 monadic value 也就是一个函数。我们再把 w
喂给他。
如果你还不太懂 >>=
怎么写出来的,不要担心,因为接下来的范例会让你晓得这真的是一个简单的 Monad。我们造一个 do
expression 来使用这个 Monad。
import Control.Monad.Instances
addStuff :: Int -> Int
addStuff = do
a <- (*2)
b <- (+10)
return (a+b)
这跟我们之前写的 applicative expression 差不多,只差在他是运作在 monad 上。一个 do
expression 的结果永远会是一个 monadic vlaue,这个也不例外。而这个 monadic value 其实是一个函数。只是在这边他接受一个数字,然后套用 (*2)
,把结果绑定到 a
上面。而 (+10)
也同用被套用到同样的参数。结果被绑定到 b
上。return
就如其他 monad 一样,只是制作一个简单的 monadic value 而不会作多余的事情。这让整个函数的结果是 a+b
。如果我们试着跑跑看,会得到之前的结果。
ghci> addStuff 3
19
其中 3
会被喂给 (*2)
跟 (+10)
。而且他也会被喂给 return (a+b)
,只是他会忽略掉 3
而永远回传 a+b
正因为如此,function monad 也被称作 reader monad。所有函数都从一个固定的地方读取。要写得更清楚一些,可以把 addStuff
改写如下:
addStuff :: Int -> Int
addStuff x = let
a = (*2) x
b = (+10) x
in a+b
我们见识了把函数视作具有 context 的值很自然的可以表达成 reader monad。只要我们当作我们知道函数会回传什么值就好。他作的就是把所有的函数都黏在一起做成一个大的函数,然后把这个函数的参数都喂给全部组成的函数,这有点取出他们未来的值的意味。实作做完了然后 >>=
就会保证一切都能正常运作。
#
State Monad
Haskell 是一个纯粹的语言,正因为如此,我们的程式是有一堆没办法改变全域状态或变数的函数所组成,他们只会作些处理并回传结果。这样的性质让我们很容易思考我们的程式在干嘛,因为我们不需要担心变数在某一个时间点的值是什么。然而,有一些领域的问题根本上就是依赖于随着时间而改变的状态。虽然我们也可以用 Haskell 写出这样的程式,但有时候写起来蛮痛苦的。这也是为什么 Haskell 要加进 State Monad 这个特性。这让我们在 Haskell 中可以容易地处理状态性的问题,并让其他部份的程式还是保持纯粹性。
当我们处理乱数的时候,我们的函数接受一个 random generator 并回传一个新的乱数跟一个新的 random generator。如果我们需要很多个乱数,我们可以用前一个函数回传的 random generator 继续做下去。当我们要写一个接受 StdGen
的函数并产生丢三个硬币结果的函数,我们会这样写:
threeCoins :: StdGen -> (Bool, Bool, Bool)
threeCoins gen =
let (firstCoin, newGen) = random gen
(secondCoin, newGen') = random newGen
(thirdCoin, newGen''') = random newGen'
in (firstCoin, secondCoin, thirdCoin)
他接受一个 gen
然后用 random gen
产生一个 Bool
型态的值以及新的 generator。要模拟丢第二个硬币的话,便使用新的 generator。在其他语言中,多半除了乱数之外不需要多回传一个 generator。那是因为我们可以对现有的进行修改。但 Haskell 是纯粹的语言,我们没办法那么做,所以我们必须要接受一个状态,产生结果然后回传一个新的状态,然后用新的状态来继续做下去。
一般来讲你应该不会喜欢这么写,在程式中有赤裸裸的状态,但我们又不想放弃 Haskell 的纯粹性质。这就是 State Monad 的好处了,他可以帮我们处理这些琐碎的事情,又让我们保持 Haskell 的纯粹性。
为了深入理解状态性的计算,我们先来看看应该给他们什么样的型态。我们会说一个状态性的计算是一个函数,他接受一个状态,回传一个值跟一个新的状态。写起来会像这样:
s -> (a,s)
s
是状态的型态,而 a
是计算结果的型态。
在其他的语言中,赋值大多是被当作会改变状态的操作。举例来说,当我们在命令式语言写 ``x = 5``,这通常代表的是把 ``5`` 指定给 ``x`` 这变数。而且这边 ``5`` 是一个 expression。
如果你用函数语言的角度去思考,你可以把他想做是一个函数,接受一个状态,并回传结果跟新的状态。那新的状态代表所有已指定的值与新加入的变数。
这种改变状态的计算,除了想做是一个接受状态并回传结果跟新状态的函数外,也可以想做是具有 context 的值。 实际的值是结果。然而要得到结果,我们必须要给一个初始的状态,才能得到结果跟最后的状态。
#
Stack and Stones
考虑现在我们要对一个堆叠的操作建立模型。你可以把东西推上堆叠顶端,或是把东西从顶端拿下来。如果你要的元素是在堆叠的底层的话,你必须要把他上面的东西都拿下来才能拿到他。
我们用一个 list 来代表我们的堆叠。而我们把 list 的头当作堆叠的顶端。为了正确的建立模型,我们要写两个函数:pop
跟 push
。pop
会接受一个堆叠,取下一个元素并回传一个新的堆叠,这个新的堆叠不包含取下的元素。push
会接受一个元素,把他堆到堆叠中,并回传一个新的堆叠,其包含这个新的元素。
type Stack = [Int]
pop :: Stack -> (Int,Stack)
pop (x:xs) = (x,xs)
push :: Int -> Stack -> ((),Stack)
push a xs = ((),a:xs)
我们用 ()
来当作 pushing 的结果,毕竟推上堆叠并不需要什么回传值,他的重点是在改变堆叠。注意到 push
跟 pop
都是改变状态的计算,可以从他们的型态看出来。
我们来写一段程式来模拟一个堆叠的操作。我们接受一个堆叠,把 3
推上去,然后取出两个元素。
stackManip :: Stack -> (Int, Stack)
stackManip stack = let
((),newStack1) = push 3 stack
(a ,newStack2) = pop newStack1
in pop newStack2
我们拿一个 stack
来作 push 3 stack
的动作,其结果是一个 tuple。tuple 的第一个部份是 ()
,而第二个部份是新的堆叠,我们把他命名成 newStack1
。然后我们从 newStack1
上 pop 出一个数字。其结果是我们之前 push 上去的一个数字 a
,然后把这个更新的堆叠叫做 newStack2
。然后我们从 newStack2
上再 pop 出一个数字 b
,并得到 newStack3
。我们回传一个 tuple 跟最终的堆叠。
ghci> stackManip [5,8,2,1]
(5,[8,2,1])
结果就是 5
跟新的堆叠 [8,2,1]
。注意到 stackManip
是一个会改变状态的操作。我们把一堆会改变状态的操作绑在一起操作,有没有觉得很耳熟的感觉。
stackManip
的程式有点冗长,因为我们要写得太详细,必须把状态给每个操作,然后把新的状态再喂给下一个。如果我们可以不要这样作的话,那程式应该会长得像这样:
stackManip = do
push 3
a <- pop
pop
这就是 State Monad 在做的事。有了他,我们便可以免除于要把状态操作写得太明白的窘境。
#
The State Monad
Control.Monad.State
这个模组提供了一个 newtype
包起来的型态。
newtype State s a = State { runState :: s -> (a,s) }
一个 State s a
代表的是一个改变状态的操作,他操纵的状态为型态 s
,而产生的结果是 a
。
我们已经见识过什么是改变状态的操作,以及他们是可以被看成具有 context 的值。接着来看看他们 Monad
的 instance:
instance Monad (State s) where
return x = State $ \s -> (x,s)
(State h) >>= f = State $ \s -> let (a, newState) = h s
(State g) = f a
in g newState
我们先来看看 return
那一行。我们 return
要作的事是接受一个值,并做出一个改变状态的操作,让他永远回传那个值。所以我们才做了一个 lambda 函数,\s -> (x,s)
。我们把 x
当成是结果,并且状态仍然是 s
。这就是 return
要完成的 minimal context。
那 >>=
的实作呢?很明显的把改变状态的操作喂进 >>=
也必须要丢出另一个改变状态的操作。所以我们用 State
这个 newtype
wrapper 来把一个 lambda 函数包住。这个 lambda 会是新的一个改变状态的操作。但里面的内容是什么?首先我们应该要从接受的操作取出结果。由于 lambda 是在一个大的操作中,所以我们可以喂给 h
我们现在的状态,也就是 s
。那会产生 (a, newState)
。到目前为止每次我们在实作 >>=
的时候,我们都会先从 monadic value 中取出结果,然后喂给 f
来得到新的 monadic value。在写 Writer
的时候,我们除了这样作还要确保 context 是用 mappend
把旧的 monoid value 跟新的接起来。在这边我们则是用 f a
得到一个新的操作 g
。现在我们有了新的操作跟新的状态(叫做 newState
),我们就把 newState
喂给 g
。结果便是一个 tuple,里面包含了最后的结果跟最终的状态。
有了 >>=
,我们便可以把两个操作黏在一起,只是第二个被放在一个函数中,专门接受第一个的结果。由于 pop
跟 push
已经是改变状态的操作了,我们可以把他们包在 State
中
import Control.Monad.State
pop :: State Stack Int
pop = State $ \(x:xs) -> (x,xs)
push :: Int -> State Stack ()
push a = State $ \xs -> ((),a:xs)
pop
已经满足我们的条件,而 push
要先接受一个 Int
才会回传我们要的操作。所以我们可以改写先前的范例如下:
import Control.Monad.State
stackManip :: State Stack Int
stackManip = do
push 3
a <- pop
pop
看到我们是怎么把一个 push
跟两个 pop
黏成一个操作吗?当我们将他们从一个 newtype
取出,其实就是需要一个能喂进初始状态的函数:
ghci> runState stackManip [5,8,2,1]
(5,[8,2,1])
我们不须绑定第二个 pop
,因为我们根本不会用到 a
,所以可以写成下面的样子:
stackManip :: State Stack Int
stackManip = do
push 3
pop
pop
再来尝试另外一种方式,先从堆叠上取下一个数字,看看他是不是 5
,如果是的话就把他放回堆叠上,如果不是的话就堆上 3
跟 8
。
stackStuff :: State Stack ()
stackStuff = do
a <- pop
if a == 5
then push 5
else do
push 3
push 8
很直觉吧!我们来看看初始的堆叠的样子。
ghci> runState stackStuff [9,0,2,1,0]
((),[8,3,0,2,1,0])
还记得我们说过 do
的结果会是一个 monadic value,而在 State
monad 的 case,do
也就是一个改变状态的函数。而由于 stackManip
跟 stackStuff
都是改变状态的计算,因此我们可以把他们黏在一起:
moreStack :: State Stack ()
moreStack = do
a <- stackManip
if a == 100
then stackStuff
else return ()
如果 stackManip
的结果是 100
,我们就会跑 stackStuff
,如果不是的话就什么都不做。return ()
不过就是什么是都不做,全部保持原样。
Contorl.Monad.State
提供了一个 MonadState
的 typeclass,他有两个有用的函数,分别是 get
跟 put
。对于 State
来说,get
的实作就像这样:
get = State $ \s -> (s,s)
他只是取出现在的状态除此之外什么也不做。而 put
函数会接受一个状态并取代掉现有的状态。
put newState = State $ \s -> ((),newState)
有了这两个状态,我们便可以看到现在堆叠中有什么,或是把整个堆叠中的元素换掉。
stackyStack :: State Stack ()
stackyStack = do
stackNow <- get
if stackNow == [1,2,3]
then put [8,3,1]
else put [9,2,1]
我们可以看看对于 State
而言,>>=
的型态会是什么:
(>>=) :: State s a -> (a -> State s b) -> State s b
我们可以看到状态的型态都是 s
,而结果从型态 a
变成型态 b
。这代表我们可以把好几个改变状态的计算黏在一起,这些计算的结果可以都不一样,但状态的型态会是一样的。举例来说,对于 Maybe
而言,>>=
的型态会是:
(>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
Maybe
不变是有道理的,但如果用 >>=
来把两种不同的 monad 接起来是没道理的。但对于 state monad 而言,monad 其实是 State s
,所以如果 s
不一样,我们就要用 >>=
来把两个 monad 接起来。
#
随机性与 state monad
在章节的一开始,我们知道了在 Haskell 中要产生乱数的不方便。我们要拿一个产生器,并回传一个乱数跟一个新的产生器。接下来我们还一定要用新的产生器不可。但 State Monad 让我们可以方便一些。
System.Random
中的 random
函数有下列的型态:
random :: (RandomGen g, Random a) => g -> (a, g)
代表他接受一个乱数产生器,并产生一个乱数跟一个新的产生器。很明显他是一个会改变状态的计算,所以我们可以用 newtype
把他包在一个 State
中,然后把他当作 monadic value 来操作。
import System.Random
import Control.Monad.State
randomSt :: (RandomGen g, Random a) => State g a
randomSt = State random
这样我们要丢三个硬币的结果可以改写成这样:
import System.Random
import Control.Monad.State
threeCoins :: State StdGen (Bool,Bool,Bool)
threeCoins = do
a <- randomSt
b <- randomSt
c <- randomSt
return (a,b,c)
threeCoins
是一个改变状态的计算,他接受一个初始的乱数产生器,他会把他喂给 randomSt
,他会产生一个数字跟一个新的产生器,然后会一直传递下去。我们用 return (a,b,c)
来呈现 (a,b,c)
,这样并不会改变最近一个产生器的状态。
ghci> runState threeCoins (mkStdGen 33)
((True,False,True),680029187 2103410263)
要完成像这样要改变状态的任务便因此变得轻松了很多。
#
Error Monad
我们知道 Maybe
是拿来赋予一个值具有可能失败的 context。一个值可能会是 Just something
或是一个 Nothing
。尽管这很有用,但当我们拿到了一个 Nothing
,我们只知道他失败了,但我们没办法塞进一些有用的资讯,告诉我们究竟是在什么样的情况下失败了。
而 Either e a
则能让我们可以加入一个可能会发生错误的 context,还可以增加些有用的讯息,这样能让我们知道究竟是什么东西出错了。一个 Either e a
的值可以是代表正确的 Right
,或是代表错误的 Left
,例如说:
ghci> :t Right 4
Right 4 :: (Num t) => Either a t
ghci> :t Left "out of cheese error"
Left "out of cheese error" :: Either [Char] b
这就像是加强版的 Maybe
,他看起来实在很像一个 monad,毕竟他也可以当作是一个可能会发生错误的 context,只是多了些讯息罢了。
在 Control.Monad.Error
里面有他的 Monad
instance。
instance (Error e) => Monad (Either e) where
return x = Right x
Right x >>= f = f x
Left err >>= f = Left err
fail msg = Left (strMsg msg)
return
就是建立起一个最小的 context,由于我们用 Right
代表正确的结果,所以他把值包在一个 Right
constructor 里面。就像实作 Maybe
时的 return
一样。
>>=
会检查两种可能的情况:也就是 Left
跟 Right
。如果进来的是 Right
,那我们就呼叫 f
,就像我们在写 Just
的时候一样,只是呼叫对应的函数。而在错误的情况下,Left
会被传出来,而且里面保有描述失败的值。
Either e
的 Monad
instance 有一项额外的要求,就是包在 Left
中的型态,也就是 e
,必须是 Error
typeclass 的 instance。Error
这个 typeclass 描述一个可以被当作错误讯息的型态。他定义了 strMsg
这个函数,他接受一个用字串表达的错误。一个明显的范例就是 String
型态,当他是 String
的时候,strMsg
只不过回传他接受到的字串。
ghci> :t strMsg
strMsg :: (Error a) => String -> a
ghci> strMsg "boom!" :: String
"boom!"
但因为我们通常在用 Either
来描述错误的时候,是用 String
来装错误讯息,所以我们也不用担心这一点。当在 do
里面做 pattern match 失败的时候,Left
的值会拿来代表失败。
总之来看看一个范例吧:
ghci> Left "boom" >>= \x -> return (x+1)
Left "boom"
ghci> Right 100 >>= \x -> Left "no way!"
Left "no way!"
当我们用 >>=
来把一个 Left
喂进一个函数,函数的运算会被忽略而直接回传丢进去的 Left
值。当我们喂 Right
值给函数,函数就会被计算而得到结果,但函数还是产生了一个 Left
值。
当我们试着喂一个 Right
值给函数,而且函数也成功地计算,我们却碰到了一个奇怪的 type error。
ghci> Right 3 >>= \x -> return (x + 100)
<interactive>:1:0:
Ambiguous type variable `a' in the constraints:
`Error a' arising from a use of `it' at <interactive>:1:0-33
`Show a' arising from a use of `print' at <interactive>:1:0-33
Probable fix: add a type signature that fixes these type variable(s)
Haskell 警告说他不知道要为 e
选择什么样的型态,尽管我们是要印出 Right
的值。这是因为 Error e
被限制成 Monad
。把 Either
当作 Monad 使用就会碰到这样的错误,你只要明确写出 type signature 就行了:
ghci> Right 3 >>= \x -> return (x + 100) :: Either String Int
Right 103
这样就没问题了。
撇除这个小毛病,把 Either
当 Monad 使用就像使用 Maybe
一样。在前一章中,我们展示了 Maybe
的使用方式。你可以把前一章的范例用 Either
重写当作练习。
#
一些实用的 Moandic functions
在这个章节,我们会看看一些操作 monadic value 的函数。这样的函数通常我们称呼他们为 monadic function。其中有些你是第一次见到,但有些不过是 filter
或 foldl
的变形。让我们来看看吧!
#
liftM
当我们开始学习 Monad 的时候,我们是先学习 functors,他代表可以被 map over 的事物。接着我们学了 functors 的加强版,也就是 applicative functors,他可以对 applicative values 做函数的套用,也可以把一个一般值放到一个预设的 context 中。最后,我们介绍在 applicative functors 上更进一步的 monad,他让这些具有 context 的值可以被喂进一般函数中。
也就是说每一个 monad 都是个 applicative functor,而每一个 applicative functor 也都是一个 functor。Applicative
typeclass 中有加入限制,让每一个 Applicative
都是 Functor
。但 Monad
却没有这样的限制,让每个 Monad
都是 Applicative
。这是因为 Monad
这个 typeclass 是在 Applicative
引入前就存在的缘故。
但即使每个 monad 都是一个 functor,但我们不需要依赖 Functor
的定义。那是因为我们有 liftM
这个函数。他会接受一个函数跟一个 monadic value,然后把函数 map over 那些 monadic value。所以他其实就是 fmap
,以下是他的型态:
liftM :: (Monad m) => (a -> b) -> m a -> m b
而这是 fmap
的型态:
fmap :: (Functor f) => (a -> b) -> f a -> f b
如果 Functor
跟 Monad
的 instance 遵守 functor 跟 monad 的法则(到目前为止我们看过的 monad 都遵守),那这两个函数其实是等价的。这就像 pure
跟 return
其实是同一件事,只是一个在 Applicative
中,而另外一个在 Monad
里面,我们来试试看 liftM
吧:
ghci> liftM (*3) (Just 8)
Just 24
ghci> fmap (*3) (Just 8)
Just 24
ghci> runWriter $ liftM not $ Writer (True, "chickpeas")
(False,"chickpeas")
ghci> runWriter $ fmap not $ Writer (True, "chickpeas")
(False,"chickpeas")
ghci> runState (liftM (+100) pop) [1,2,3,4]
(101,[2,3,4])
ghci> runState (fmap (+100) pop) [1,2,3,4]
(101,[2,3,4])
我们已经知道 fmap
是如何运作在 Maybe
上。而 liftM
又跟 fmap
等价。对于 Writer
型态的值而言,函数只有对他的第一个 component 做处理。而对于改变状态的计算,fmap
跟 liftM
也都是产生另一个改变状态的计算。我们也看过了 (+100)
当作用在 pop
上会产生 (1, [2,3,4])
。
来看看 liftM
是如何被实作的:
liftM :: (Monad m) => (a -> b) -> m a -> m b
liftM f m = m >>= (\x -> return (f x))
或者用 do
来表示得清楚些
liftM :: (Monad m) => (a -> b) -> m a -> m b
liftM f m = do
x <- m
return (f x)
我们喂一个 monadic value m
给函数,我们套用那个函数然后把结果放进一个预设的 context。由于遵守 monad laws,这保证这操作不会改变 context,只会呈现最后的结果。我们可以看到实作中 liftM
也没有用到 Functor
的性质。这代表我们能只用 monad 提供给我们的就实作完 fmap
。这特性让我们可以得到 monad 比 functor 性质要强的结论。
Applicative
让我们可以操作具有 context 的值就像操作一般的值一样。 就像这样:
ghci> (+) <$> Just 3 <*> Just 5
Just 8
ghci> (+) <$> Just 3 <*> Nothing
Nothing
使用 applicative 的特性让事情变得很精简。 <$>
不过就是 fmap
,而 <*>
只是一个具有下列型态的函数:
(<*>) :: (Applicative f) => f (a -> b) -> f a -> f b
他有点像 fmap
,只是函数本身有一个 context。我们必须把他从 context 中抽出,对 f a
做 map over 的东做,然后再放回 context 中。由于在 Haskel 中函数预设都是 curried,我们便能用 <$>
以及 <*>
来让接受多个参数的函数也能接受 applicative 种类的值。
总之 <*>
跟 fmap
很类似,他也能只用 Monad
保证的性质实作出来。ap
这个函数基本上就是 <*>
,只是他是限制在 Monad
上而不是 Applicative
上。这边是他的定义:
ap :: (Monad m) => m (a -> b) -> m a -> m b
ap mf m = do
f <- mf
x <- m
return (f x)
mf
是一个 monadic value,他的结果是一个函数。由于函数跟值都是放在 context 中,假设我们从 context 取出的函数叫 f
,从 context 取出的值叫 x
,我们把 x
喂给 f
然后再把结果放回 context。像这样:
ghci> Just (+3) <*> Just 4
Just 7
ghci> Just (+3) `ap` Just 4
Just 7
ghci> [(+1),(+2),(+3)] <*> [10,11]
[11,12,12,13,13,14]
ghci> [(+1),(+2),(+3)] `ap` [10,11]
[11,12,12,13,13,14]
由于我们能用 Monad
提供的函数实作出 Applicative
的函数,因此我们看到 Monad 有比 applicative 强的性质。事实上,当我们知道一个型态是 monad 的时候,大多数会先定义出 Monad
的 instance,然后才定义 Applicative
的 instance。而且只要把 pure
定义成 return
,<*>
定义成 ap
就行了。同样的,如果你已经有了 Monad
的 instance,你也可以简单的定义出 Functor
,只要把 fmap
定义成 liftM
就行了。
liftA2
是一个方便的函数,他可以把两个 applicative 的值喂给一个函数。他的定义很简单:
liftA2 :: (Applicative f) => (a -> b -> c) -> f a -> f b -> f c
liftA2 f x y = f <$> x <*> y
liftM2
也是做差不多的事情,只是多了 Monad
的限制。在函式库中其实也有 liftM3
,liftM4
跟 liftM5
。
我们看到了 monad 相较于 applicative 跟 functor 有比较强的性质。尽管 moand 有 functor 跟 applicative functor 的性质,但他们不见得有 Functor
跟 Applicative
的 instance 定义。所以我们检视了一些在 monad 中定义,且等价于 functor 或 applicative functor 所具有的函数。
#
The join function
如果一个 monadic value 的结果是另一个 monadic value,也就是其中一个 monadic value 被包在另一个里面,你能够把他们变成一个普通的 monadic value 吗?就好像把他们打平一样。譬如说,我们有 Just (Just 9)
,我们能够把他变成 Just 9
吗?事实上是可以的,这也是 monad 的一个性质。也就是我要看的 join
函数,他的型态是这样:
join :: (Monad m) => m (m a) -> m a
他接受一个包在另一个 monadic value 中的 monadic value,然后会回给我们一个普通的 monadic value。这边有一些 Maybe
的范例:
ghci> join (Just (Just 9))
Just 9
ghci> join (Just Nothing)
Nothing
ghci> join Nothing
Nothing
第一行是一个计算成功的结果包在另一个计算成功的结果,他们应该要能结合成为一个比较大的计算成功的结果。第二行则是一个 Nothing
包在一个 Just
中。我们之前在处理 Maybe
型态的值时,会用 <*>
或 >>=
把他们结合起来。输入必须都是 Just
时结果出来才会是 Just
。如果中间有任何的失败,结果就会是一个失败的结果。而第三行就是这样,我们尝试把失败的结果接合起来,结果也会是一个失败。
要 join
一个 list 也是很简单:
ghci> join [[1,2,3],[4,5,6]]
[1,2,3,4,5,6]
你可以看到,对于 list 而言 join
不过就是 concat
。 而要 join
一个包在 Writer
中的 Writer
, 我们必须用 mappend
:
ghci> runWriter $ join (Writer (Writer (1,"aaa"),"bbb"))
(1,"bbbaaa")
"bbb"
先被加到 monoid 中,接着 "aaa"
被附加上去。你想要检视 Writer
中的值的话,必须先把值写进去才行。
要对 Either
做 join
跟对 Maybe
做 join
是很类似的:
ghci> join (Right (Right 9)) :: Either String Int
Right 9
ghci> join (Right (Left "error")) :: Either String Int
Left "error"
ghci> join (Left "error") :: Either String Int
Left "error"
如果我们对一个包了另外一个改变状态的计算的进行改变状态的计算,要作 join
的动作会让外面的先被计算,然后才是计算里面的:
ghci> runState (join (State $ \s -> (push 10,1:2:s))) [0,0,0]
((),[10,1,2,0,0,0])
这边的 lambda 函数接受一个状态,并把 2
跟 1
放到堆叠中,并把 push 10
当作他的结果。当对整个东西做 join
的时候,他会先把 2
跟 1
放到堆叠上,然后进行 push 10
的计算,因而把 10
放到堆叠的顶端。
join
的实作像是这样:
join :: (Monad m) => m (m a) -> m a
join mm = do
m <- mm
m
因为 mm
的结果会是一个 monadic value,我们单独用 m <- mm
拿取他的结果。这也可以说明 Maybe
只有当外层跟内层的值都是 Just
的时候才会是 Just
。如果把 mm
的值设成 Just (Just 8)
的话,他看起来会是这样:
joinedMaybes :: Maybe Int
joinedMaybes = do
m <- Just (Just 8)
m
最有趣的是对于一个 monadic value 而言,用 >>=
把他喂进一个函数其实等价于对 monad 做 mapping over 的动作,然后用 join
来把值从 nested 的状态变成扁平的状态。也就是说 m >>= f
其实就是 join (fmap f m)
。如果你仔细想想的话其实很明显。>>=
的使用方式是,把一个 monadic value 喂进一个接受普通值的函数,但他却会回传 monadic value。如果我们 map over 一个 monadic value,我们会做成一个 monadic value 包了另外一个 monadic value。例如说,我们现在手上有 Just 9
跟 \x -> Just (x+1)
。如果我们把这个函数 map over Just 9
,我们会得到 Just (Just 10)
事实上 m >>= f
永远等价于 join (fmap f m)
这性质非常有用。如果我们要定义自己的 Monad
instance,要知道怎么把 nested monadic value 变成扁平比起要定义 >>=
是比较容易的一件事。
#
filterM
filter
函数是 Haskell 中不可或缺的要素。他接受一个断言(predicate)跟一个 list 来过滤掉断言为否的部份并回传一个新的 list。他的型态是这样:
filter :: (a -> Bool) -> [a] -> [a]
predicate 能接 list 中的一个元素并回传一个 Bool
型态的值。但如果 Bool
型态其实是一个 monadic value 呢?也就是他有一个 context。例如说除了 True
跟 False
之外还伴随一个 monoid,像是 ["Accepted the number 5"]
,或 ["3 is too small"]
。照前面所学的听起来是没问题,而且产出的 list 也会跟随 context,在这个例子中就是 log。所以如果 Bool
会回传伴随 context 的布林值,我们会认为最终的结果也会具有 context。要不然这些 context 都会在处理过程中遗失。
在 Control.Monad
中的 filterM
函数正是我们所需要的,他的型态如下:
filterM :: (Monad m) => (a -> m Bool) -> [a] -> m [a]
predicate 会回传一个 monadic value,他的结果会是 Bool
型态,由于他是 monadic value,他的 context 有可能会是任何 context,譬如说可能的失败,non-determinism,甚至其他的 context。一旦我们能保证 context 也会被保存在最后的结果中,结果也就是一个 monadic value。
我们来写一个接受 list 然后过滤掉小于 4 的函数。先尝试使用 filter
函数:
ghci> filter (\x -> x < 4) [9,1,5,2,10,3]
[1,2,3]
很简单吧。接着我们在做个 predicate,除了表达 True
或 False
之外,还提供了一个 log。我们会用 Writer
monad 来表达这件事:
keepSmall :: Int -> Writer [String] Bool
keepSmall x
| x < 4 = do
tell ["Keeping " ++ show x]
return True
| otherwise = do
tell [show x ++ " is too large, throwing it away"]
return False
这个函数会回传 Writer [String] Bool
而不是一个单纯的 Bool
。他是一个 monadic predicate。如果扫到的数字小于 4
的话,我们就会回报要保存他,而且回传 return True
。
接着,我们把他跟一个 list 喂给 filterM
。由于 predicate 会回传 Writer
,所以结果仍会是一个 Writer
值。
ghci> fst $ runWriter $ filterM keepSmall [9,1,5,2,10,3]
[1,2,3]
要检查 Writer
的结果,我们想要印出 log 看看里面有什么东西:
ghci> mapM_ putStrLn $ snd $ runWriter $ filterM keepSmall [9,1,5,2,10,3]
9 is too large, throwing it away
Keeping 1
5 is too large, throwing it away
Keeping 2
10 is too large, throwing it away
Keeping 3
提供 monadic predicate 给 filterM
,我们便能够做 filter 的动作,同时还能保有 monadic context。
一个比较炫的技巧是用 filterM
来产生一个 list 的 powerset。一个 powerset 就是一个集合所有子集所形成的集合。如果说我们的 list 是 [1,2,3]
,那他个 powerset 就会是:
[1,2,3]
[1,2]
[1,3]
[1]
[2,3]
[2]
[3]
[]
换句话说,要产生一个 powerset 就是要列出所有要丢掉跟保留的组合。[2,3]
只不过代表我们把 1
给丢掉而已。
我们要依赖 non-determinism 来写我们这产生 powerset 的函数。我们接受一个 list [1,2,3]
然后查看第一个元素,这个例子中是 1
,我们会问:我们要保留他呢?还是丢掉他呢?答案是我们都要做。所以我们会用一个 non-determinism 的 predicate 来过滤我的 list。也就是我们的 powerset
函数:
powerset :: [a] -> [[a]]
powerset xs = filterM (\x -> [True, False]) xs
等等,我们已经写完了吗?没错,就这么简单,我们可以同时丢掉跟保留每个元素。只要我们用 non-deterministic predicate,那结果也就是一个 non-deterministic value,也便是一个 list 的 list。试着跑跑看:
ghci> powerset [1,2,3]
[[1,2,3],[1,2],[1,3],[1],[2,3],[2],[3],[]]
这样的写法需要让你好好想一下,但如果你能接受 list 其实就是 non-deterministic value 的话,那要想通会比较容易一些。
#
foldM
foldl
的 monadic 的版本叫做 foldM
。如果你还有印象的话,foldl
会接受一个 binary 函数,一个起始累加值跟一串 list,他会从左边开始用 binary 函数每次带进一个值来 fold。foldM
也是做同样的事,只是他接受的这个 binary 函数会产生 monadic value。不意外的,他的结果也会是 monadic value。foldl
的型态是:
foldl :: (a -> b -> a) -> a -> [b] -> a
而 foldM
的型态则是:
foldM :: (Monad m) => (a -> b -> m a) -> a -> [b] -> m a
binary 函数的回传值是 monadic,所以结果也会是 monadic。我们来试着把 list 的值用 fold 全部加起来:
ghci> foldl (\acc x -> acc + x) 0 [2,8,3,1]
14
这边起始的累加值是 0
,首先 2
会被加进去,变成 2
。然后 8
被加进去变成 10
,直到我们没有值可以再加,那便是最终的结果。
但如果我们想额外加一个条件,也就是当碰到一个数字大于 9
时候,整个运算就算失败呢?一种合理的修改就是用一个 binary 函数,他会检查现在这个数是否大于 9
,如果是便引发失败,如果不是就继续。由于有失败的可能性,我们便需要这个 binary 函数回传一个 Maybe
,而不是一个普通的值。我们来看看这个函数:
binSmalls :: Int -> Int -> Maybe Int
binSmalls acc x
| x > 9 = Nothing
| otherwise = Just (acc + x)
由于这边的 binary 函数是 monadic function,我们不能用普通的 foldl
,我们必须用 foldM
:
ghci> foldM binSmalls 0 [2,8,3,1]
Just 14
ghci> foldM binSmalls 0 [2,11,3,1]
Nothing
由于这串 list 中有一个数值大于 9
,所以整个结果会是 Nothing
。另外你也可以尝试 fold 一个回传 Writer
的 binary 函数,他会在 fold 的过程中纪录你想纪录的资讯。
#
Making a safe RPN calculator
之前的章节我们实作了一个 RPN 计算机,但我们没有做错误的处理。他只有在输入是合法的时候才会运算正确。假如有东西出错了,整个程式便会当掉。我们在这章看到了要怎样把程式码转换成 monadic 的版本,我们先尝适用 Maybe
monad 来帮我们的 RPN 计算机加上些错误处理。
我们的 RPN 计算机接受一个像 "1 3 + 2 *"
这样的字串,把他断成 word,变成 ["1","3","+","2","*"]
这样。然后用一个 binary 函数,跟一个空的堆叠,从左边开始或是将数值推进堆叠中,或是操作堆叠最上层的两个元素。
以下便是程式的核心部份:
import Data.List
solveRPN :: String -> Double
solveRPN = head . foldl foldingFunction [] . words
我们把输入变成一个字串的 list,从左边开始 fold,当堆叠中只剩下一个元素的时候,他便是我们要的答案。以下是我们的 folding 函数:
foldingFunction :: [Double] -> String -> [Double]
foldingFunction (x:y:ys) "*" = (x * y):ys
foldingFunction (x:y:ys) "+" = (x + y):ys
foldingFunction (x:y:ys) "-" = (y - x):ys
foldingFunction xs numberString = read numberString:xs
这边我们的累加元素是一个堆叠,我们用一个 Double
的 list 来表示他。当我们在做 folding 的过程,如果当前的元素是一个 operator,他会从堆叠上拿下两个元素,用 operator 施行运算然后把结果放回堆叠。如果当前的元素是一个表示成字串的数字,他会把字串转换成数字,并回传一个新的堆叠包含了转换后的数字。
我们首先把我们的 folding 函数加上处理错误的 case,所以他的型态会变成这样:
foldingFunction :: [Double] -> String -> Maybe [Double]
他不是回传一个 Just
的堆叠就是回传 Nothing
。
reads
函数就像 read
一样,差别在于他回传一个 list。在成功读取的情况下 list 中只包含读取的那个元素。如果他失败了,他会回传一个空的 list。除了回传读取的元素,他也回传剩下读取失败的元素。他必须要看完整串输入,我们想把他弄成一个 readMaybe
的函数,好方便我们进行。
readMaybe :: (Read a) => String -> Maybe a
readMaybe st = case reads st of [(x,"")] -> Just x
_ -> Nothing
测试结果如下:
ghci> readMaybe "1" :: Maybe Int
Just 1
ghci> readMaybe "GO TO HELL" :: Maybe Int
Nothing
看起来运作正常。我们再把他变成一个可以处理失败情况的 monadic 函数
foldingFunction :: [Double] -> String -> Maybe [Double]
foldingFunction (x:y:ys) "*" = return ((x * y):ys)
foldingFunction (x:y:ys) "+" = return ((x + y):ys)
foldingFunction (x:y:ys) "-" = return ((y - x):ys)
foldingFunction xs numberString = liftM (:xs) (readMaybe numberString)
前三种 case 跟前面的很像,只差在堆叠现在是包在 Just
里面(我们常常是用 return
来做到这件事,但其实我们也可以用 Just
)。在最后一种情况,我们用 readMaybe numberString
然后我们用 (:xs)
map over 他。所以如果堆叠 xs
是 [1.0,2.0]
且 readMaybe numberString
产生 Just 3.0
,那结果便是 Just [3.0,1.0,2.0]
。如果 readyMaybe numberString
产生 Nothing
那结果便是 Nothing
。我们来试着跑跑看 folding 函数
ghci> foldingFunction [3,2] "*"
Just [6.0]
ghci> foldingFunction [3,2] "-"
Just [-1.0]
ghci> foldingFunction [] "*"
Nothing
ghci> foldingFunction [] "1"
Just [1.0]
ghci> foldingFunction [] "1 wawawawa"
Nothing
看起来正常运作。我们可以用他来写一个新的 solveRPN
。
import Data.List
solveRPN :: String -> Maybe Double
solveRPN st = do
[result] <- foldM foldingFunction [] (words st)
return result
我们仍是接受一个字串把他断成一串 word。然后我们用一个空的堆叠来作 folding 的动作,只差在我们用的是 foldM
而不是 foldl
。foldM
的结果会是 Maybe
,Maybe
里面包含了一个只有一个元素的 list。我们用 do
expression 来取出值,把他绑定到 result
上。当 foldM
回传 Nothing
的时候,整个结果就变成 Nothing
。也特别注意我们有在 do
里面做 pattern match 的动作,所以如果 list 中不是只有一个元素的话,最后结果便会是 Nothing
。最后一行我们用 return result
来展示 RPN 计算的结果,把他包在一个 Maybe
里面。
ghci> solveRPN "1 2 * 4 +"
Just 6.0
ghci> solveRPN "1 2 * 4 + 5 *"
Just 30.0
ghci> solveRPN "1 2 * 4"
Nothing
ghci> solveRPN "1 8 wharglbllargh"
Nothing
第一个例子会失败是因为 list 中不是只有一个元素,所以 do
里面的 pattern matching 失败了。第二个例子会失败是因为 readMaybe
回传了 Nothing
。
#
Composing monadic functions
当我们介绍 monad law 的时候,我们说过 <=<
就像是函数合成一样,只差在一个是作用在普通函数 a -> b
。一个是作用在 monadic 函数 a -> m b
。
ghci> let f = (+1) . (*100)
ghci> f 4
401
ghci> let g = (\x -> return (x+1)) <=< (\x -> return (x*100))
ghci> Just 4 >>= g
Just 401
在这个例子中我们合成了两个普通的函数,并喂给给他 4
。我们也合成了两个 monadic 函数并用 >>=
喂给他 Just 4
。
如果我们在 list 中有一大堆函数,我们可以把他们合成一个巨大的函数。用 id
当作累加的起点,.
当作 binary 函数,用 fold 来作这件事。
ghci> let f = foldr (.) id [(+1),(*100),(+1)]
ghci> f 1
201
f
接受一个数字,然后会帮他加 1
,乘以 100
,再加 1
。我们也可以将 monadic 函数用同样的方式做合成,只是不用 .
而用 <=<
,不用 id
而用 return
。我们不需要 foldM
,由于 <=<
只用 foldr
就足够了。
当我们在之前的章节介绍 list monad 的时候, 我们用他来解决一个骑士是否能在三步内走到另一点的问题。 那个函数叫做 moveKnight
, 他接受一个座标然后回传所有可能的下一步。 然后产生出所有可能三步的移动。
in3 start = return start >>= moveKnight >>= moveKnight >>= moveKnight
要检查我们是否能只用三步从 start
走到 end
,我们用下列函数
canReachIn3 :: KnightPos -> KnightPos -> Bool
canReachIn3 start end = end `elem` in3 start
如果使用 monadic 版本的合成的话,我们也可以做一个类似的 in3
,但我们希望他不只有三步的版本,而希望有任意步的版本。如果你仔细观察 in3
,他只不过用 >>=
跟 moveKnight
把之前所有可能结果喂到下一步。把他一般化,就会像下面的样子:
import Data.List
inMany :: Int -> KnightPos -> [KnightPos]
inMany x start = return start >>= foldr (<=<) return (replicate x moveKnight)
首先我们用 replicate
来做出一个 list,里面有 x
份的 moveKnight
。然后我们把所有函数都合成起来,就会给我们从起点走 x
步内所有可能的的位置。然后我们只需要把起始位置喂给他就好了。
我们也可以一般化我们的 canReachIn3
:
canReachIn :: Int -> KnightPos -> KnightPos -> Bool
canReachIn x start end = end `elem` inMany x start
#
定义自己的 Monad
在这一章节,我们会带你看看究竟一个型态是怎么被辨认,确认是一个 monad 而且正确定义出 Monad
的 instance。我们通常不会为了定义 monad 而定义。比较常发生的是,我们想要针对一个问题建立模型,却稍后发现我们定义的型态其实是一个 Monad,所以就定义一个 Monad
的 instance。
正如我们看到的,list 是被拿来当作 non-deterministic values。对于 [3,5,9]
,我们可以看作是一个 non-deterministic value,我们不能知道究竟是哪一个。当我们把一个 list 用 >>=
喂给一个函数,他就是把一串可能的选择都丢给函数,函数一个个去计算在那种情况下的结果,结果也便是一个 list。
如果我们把 [3,5,9]
看作是 3
,5
,9
各出现一次,但这边没有每一种数字出现的机率。如果我们把 non-deterministic 的值看作是 [3,5,9]
,但 3
出现的机率是 50%,5
跟 9
出现的机率各是 25%呢?我们来试着用 Haskell 描述看看。
如果说 list 中的每一个元素都伴随着他出现的机率。那下面的形式就蛮合理的:
[(3,0.5),(5,0.25),(9,0.25)]
在数学上,机率通常不是用百分比表示,而是用介于 0 跟 1 的实数表示。0 代表不可能会发生,而 1 代表绝对会发生。但浮点数很有可能很快随着运算失去精准度,所以 Haskell 有提供有理数。他的型态是摆在 Data.Ratio
中,叫做 Rational
。要创造出一个 Rational
,我们会把他写成一个分数的形式。分子跟分母用 %
分隔。这边有几个例子:
ghci> 1%4
1 % 4
ghci> 1%2 + 1%2
1 % 1
ghci> 1%3 + 5%4
19 % 12
第一行代表四分之一,第二行代表两个二分之一加起来变成一。而第三行我们把三分之一跟四分之五加起来变成十二分之十九。所以我们来用 Rational
取代浮点数来当作我们的机率值吧。
ghci> [(3,1%2),(5,1%4),(9,1%4)]
[(3,1 % 2),(5,1 % 4),(9,1 % 4)]
所以 3
有二分之一的机会出现,而 5
跟 9
有四分之一的机会出现。
可以看到我们帮 list 加上了一些额外的 context。再我们继续深入之前,我们用一个 newtype
把他包起来,好让我们帮他写 instance。
import Data.Ratio
newtype Prob a = Prob { getProb :: [(a,Rational)] } deriving Show
接着我们想问,这是一个 functor 吗?list 是一个 functor,所以很有可能他也是一个 functor,毕竟我们只是在 list 上多加一些东西而已。在 list 的情况下,我们可以针对每个元素用函数做处理。这边我们也是用函数针对每个元素做处理,只是我们是输出机率值。所以我们就来写个 functor 的 instance 吧。
instance Functor Prob where
fmap f (Prob xs) = Prob $ map (\(x,p) -> (f x,p)) xs
我们可以用 pattern matching 的方式把 newtype
解开来,套用函数 f
之后再包回去。过程中不会动到机率值。
ghci> fmap negate (Prob [(3,1%2),(5,1%4),(9,1%4)])
Prob {getProb = [(-3,1 % 2),(-5,1 % 4),(-9,1 % 4)]}
要注意机率的和永远是 1
。如果我们没有漏掉某种情形的话,没有道理他们加起来的值不为 1
。一个有 75% 机率是正面以及 50% 机率是反面的硬币根本没什么道理。
接着要问一个重要的问题,他是一个 monad 吗?我们知道 list 是一个 monad,所以他很有可能也是一个 monad。首先来想想 return
。他在 list 是怎么运作的?他接受一个普通的值并把他放到一个 list 中变成只有一个元素的 list。那在这边又如何?由于他是一个最小的 context,他也应该是一个元素的 list。那机率值呢?return x
的值永远都是 x
,所以机率值不应该是 0
,而应该是 1
。
至于 >>=
呢?看起来有点复杂,所以我们换种方式来思考,我们知道 m >>= f
会等价于 join (fmap f m)
,所以我们来想要怎么把一串包含 probability list 的 list 弄平。举个例子,考虑一个 list,'a'
跟 'b'
恰出现其中一个的机率为 25%,两个出现的机率相等。而 'c'
跟 'd'
恰出现其中一个的机率为 75%,两个出现的机率也是相等。这边有一个图将情形画出来。
每个字母发生的机率有多高呢?如果我们用四个盒子来代表每个字母,那每个盒子的机率为何?每个盒子的机率是他们所装有的机率值相乘的结果。'a'
的机率是八分之一,'b'
同样也是八分之一。八分之一是因为我们把二分之一跟四分之一相乘得到的结果。而 'c'
发生的机率是八分之三,是因为二分之一乘上四分之三。'd'
同样也是八分之三。如果把所有的机率加起来,就会得到一,符合机率的规则。
来看看怎么用一个 list 表达我们要说明的东西:
thisSituation :: Prob (Prob Char)
thisSituation = Prob
[( Prob [('a',1%2),('b',1%2)] , 1%4 )
,( Prob [('c',1%2),('d',1%2)] , 3%4 )
]
注意到这边的型态是 Prob (Prob Char)
。所以我们要思考的是如何把一串包含机率 list 的 list 打平。如果能成功写出这样的逻辑,>>=
不过就是 join (fmap f m)
,我们便得到了一个 monad。我们这边写了一个 flatten
来做这件事。
flatten :: Prob (Prob a) -> Prob a
flatten (Prob xs) = Prob $ concat $ map multAll xs
where multAll (Prob innerxs,p) = map (\(x,r) -> (x,p*r)) innerxs
multAll
接受一个 tuple,里面包含一个 probability list 跟一个伴随的机率值 p
,所以我们要作的事是把 list 里面的机率值都乘以 p
,并回传一个新的 tuple 包含新的 list 跟新的机率值。我们将 multAll
map over 到我们的 probability list 上,我们就成功地打平了我们的 list。
现在我们就能定义我们的 Monad
instance。
instance Monad Prob where
return x = Prob [(x,1%1)]
m >>= f = flatten (fmap f m)
fail _ = Prob []
由于我们已经把所有苦工的做完了,定义这个 instance 显得格外轻松。我们也定义了 fail
,我们定义他的方式跟定义 list 一样。如果在 do
中发生了失败的 pattern match,那就会呼叫 fail
。
检查我们定义的 instance 是否遵守 monad law 也是很重要的。monad law 的第一个定律是 return x >>= f
应该要等价于 f x
。要写出严格的证明会很麻烦,但我们可以观察到下列事实:首先用 return
做一个最小的 context,然后用 fmap
将一个函数 map over 这个 context,再将他打平。这样做出来的 probability list,每一个机率值都相当于将我们最初放到 minimal context 中的值乘上 1%1
。同样的逻辑,也可以看出 m >>= return
是等价于 m
。第三个定律是 f <=< (g <=< h)
应该要等价于 (f <=< g) <=< h
。我们可以从乘法有结合律的性质,以及 list monad 的特性上推出 probability monad 也符合这个定律。1%2 * (1%3 * 1%5)
等于 (1%2 * 1%3) * 1%5
。
现在我们有了一个 monad,这样有什么好处呢?他可以帮助我们计算机率值。我们可以把机率事件看作是具有 context 的 value,而 probability monad 可以保证机率值能正确地被计算成最终的结果。
好比说我们现在有两个普通的硬币以及一个灌铅的硬币。灌铅的硬币十次中有九次会出现正面,只有一次会出现反面。如果我们一次丢掷这三个硬币,有多大的机会他们都会出现正面呢?让我们先来表达丢掷硬币这件事,分别丢的是灌铅的跟普通的硬币。
data Coin = Heads | Tails deriving (Show, Eq)
coin :: Prob Coin
coin = Prob [(Heads,1%2),(Tails,1%2)]
loadedCoin :: Prob Coin
loadedCoin = Prob [(Heads,1%10),(Tails,9%10)]
最后,来看看掷硬币的函数:
import Data.List (all)
flipThree :: Prob Bool
flipThree = do
a <- coin
b <- coin
c <- loadedCoin
return (all (==Tails) [a,b,c])
试着跑一下的话,我们会看到尽管我们用了不公平的硬币,三个反面的机率还是不高。
ghci> getProb flipThree
[(False,1 % 40),(False,9 % 40),(False,1 % 40),(False,9 % 40),
(False,1 % 40),(False,9 % 40),(False,1 % 40),(True,9 % 40)]
同时出现正面的机率是四十分之九,差不多是 25%的机会。我们的 monad 并没有办法 join 所有都是 False
的情形,也就是所有硬币都是出现反面的情况。不过那不是个严重的问题,可以写个函数来将同样的结果变成一种结果,这就留给读者当作习题。
在这章节中,我们从提出问题到真的写出型态,并确认这个型态是一个 monad,写出他的 instance 并实际操作他。这是个很棒的经验。现在读者们应该对于 monad 有不少的了解才是。
14
Zippers 资料结构
尽管 Haskell 的纯粹性质带来很多好处,但他让一些在非纯粹语言很容易处理的一些事情变得要用另一种方法解决。由于 referential transparency,同样一件事在 Haskell 中是没有分别的。所以如果我们有一个装满 5 的树,而我们希望把其中一个换成 6,那我们必须要知道我们究竟是想改变哪个 5。我们也必须知道我们身处在这棵树的哪里。但在 Haskell 中,每个 5 都长得一样,我们并不能因为他们在记忆体中的位址不同就把他们区分开来。我们也不能改变任何状态,当我们想要改变一棵树的时候,我们实际上是说我们要一棵新的树,只是他长得很像旧的。一种解决方式是记住一条从根节点到现在这个节点的路径。我们可以这样表达:给定一棵树,先往左走,再往右走,再往左走,然后改变你走到的元素。虽然这是可行的,但这非常没有效率。如果我们想接连改变一个在附近的节点,我们必须再从根节点走一次。在这个章节中,我们会看到我们可以集中注意在某个资料结构上,这样让改变资料结构跟遍历的动作非常有效率。
#
来走二元树吧!
我们在生物课中学过,树有非常多种。所以我们来自己发明棵树吧!
data Tree a = Empty | Node a (Tree a) (Tree a) deriving (Show)
这边我们的树不是空的就是有两棵子树。来看看一个范例:
freeTree :: Tree Char
freeTree =
Node 'P'
(Node 'O'
(Node 'L'
(Node 'N' Empty Empty)
(Node 'T' Empty Empty)
)
(Node 'Y'
(Node 'S' Empty Empty)
(Node 'A' Empty Empty)
)
)
(Node 'L'
(Node 'W'
(Node 'C' Empty Empty)
(Node 'R' Empty Empty)
)
(Node 'A'
(Node 'A' Empty Empty)
(Node 'C' Empty Empty)
)
)
画成图的话就是像这样:
注意到 W
这个节点了吗?如果我们想要把他变成 P
。我们会怎么做呢?一种方式是用 pattern match 的方式做,直到我们找到那个节点为止。要先往右走再往左走,再改变元素内容,像是这样:
changeToP :: Tree Char -> Tree Char
changeToP (Node x l (Node y (Node _ m n) r)) = Node x l (Node y (Node 'P' m n) r)
这不只看起来很丑,而且很不容易阅读。这到底是怎么回事?我们使用 pattern match 来拆开我们的树,我们把 root 绑定成 x
,把左子树绑定成 l
。对于右子树我们继续使用 pattern match。直到我们碰到一个子树他的 root 是 'W'
。到此为止我们再重建整棵树,新的树只差在把 'W'
改成了 'P'
。
有没有比较好的作法呢?有一种作法是我们写一个函数,他接受一个树跟一串 list,里面包含有行走整个树时的方向。方向可以是 L
或是 R
,分别代表向左走或向右走。我们只要跟随指令就可以走达指定的位置:
data Direction = L | R deriving (Show)
type Directions = [Direction]
changeToP :: Directions-> Tree Char -> Tree Char
changeToP (L:ds) (Node x l r) = Node x (changeToP ds l) r
changeToP (R:ds) (Node x l r) = Node x l (changeToP ds r)
changeToP [] (Node _ l r) = Node 'P' l r
如果在 list 中的第一个元素是 L
,我们会建构一个左子树变成 'P'
的新树。当我们递回地呼叫 changeToP
,我们只会传给他剩下的部份,因为前面的部份已经看过了。对于 R
的 case 也一样。如果 list 已经消耗完了,那表示我们已经走到我们的目的地,所以我们就回传一个新的树,他的 root 被修改成 'P'
。
要避免印出整棵树,我们要写一个函数告诉我们目的地究竟是什么元素。
elemAt :: Directions -> Tree a -> a
elemAt (L:ds) (Node _ l _) = elemAt ds l
elemAt (R:ds) (Node _ _ r) = elemAt ds r
elemAt [] (Node x _ _) = x
这函数跟 changeToP
很像,只是他不会记下沿路上的资讯,他只会记住目的地是什么。我们把 'W'
变成 'P'
,然后用他来查看。
ghci> let newTree = changeToP [R,L] freeTree
ghci> elemAt [R,L] newTree
'P'
看起来运作正常。在这些函数里面,包含方向的 list 比较像是一种"focus",因为他特别指出了一棵子树。一个像 [R]
这样的 list 是聚焦在 root 的右子树。一个空的 list 代表的是主树本身。
这个技巧看起来酷炫,但却不太有效率,特别是在我们想要重复地改变内容的时候。假如我们有一个非常大的树以及非常长的一串包含方向的 list。我们需要沿着方向从 root 一直走到树的底部。如果我们想要改变一个邻近的元素,我们仍需要从 root 开始走到树的底部。这实在不太令人满意。
在下一个章节,我们会介绍一个比较好的方法,让我们可以有效率地改变我们的 focus。
#
凡走过必留下痕迹
我们需要一个比包含一串方向的 list 更好的聚焦的方法。如果我们能够在从 root 走到指定地点的沿路上撒下些面包屑,来纪录我们的足迹呢?当我们往左走,我们便记住我们选择了左边,当我们往右走,便记住我们选择了右边。
要找个东西来代表我们的面包屑,就用一串 Direction
(他可以是 L
或者是 R
),只是我们叫他 BreadCrumb
而不叫 Direction
。这是因为现在我们把这串 direction 反过来看了:
type Breadcrumbs = [Direction]
这边有一个函数,他接受一棵树跟一些面包屑,并在我们往左走时在 list 的前头加上 L
goLeft :: (Tree a, Breadcrumbs) -> (Tree a, Breadcrumbs)
goLeft (Node _ l _, bs) = (l, L:bs)
我们忽略 root 跟右子树,直接回传左子树以及面包屑,只是在现有的面包屑前面加上 L
。再来看看往右走的函数:
goRight :: (Tree a, Breadcrumbs) -> (Tree a, Breadcrumbs)
goRight (Node _ _ r, bs) = (r, R:bs)
几乎是一模一样。我们再来做一个先往右走再往左走的函数,让他来走我们的 freeTree
ghci> goLeft (goRight (freeTree, []))
(Node 'W' (Node 'C' Empty Empty) (Node 'R' Empty Empty),[L,R])
现在我们有了一棵树,他的 root 是 'W'
,而他的左子树的 root 是 'C'
,右子树的 root 是 'R'
。而由于我们先往右走再往左走,所以面包屑是 [L,R]
。
要再表示得更清楚些,我们能用定义一个 -:
x -: f = f x
他让我们可以将值喂给函数这件事反过来写,先写值,再来是 -:
,最后是函数。所以我们可以写成 (freeTree, []) -: goRight
而不是 goRight (freeTree, [])
。我们便可以把上面的例子改写地更清楚。
ghci> (freeTree, []) -: goRight -: goLeft
(Node 'W' (Node 'C' Empty Empty) (Node 'R' Empty Empty),[L,R])
#
Going back up 如果我们想要往回上走回我们原来的路径呢?根据留下的面包屑,我们知道现在的树是他父亲的左子树,而他的父亲是祖父的右子树。这些资讯并不足够我们往回走。看起来要达到这件事情,我们除了单纯纪录方向之外,还必须把其他的资料都记录下来。在这个案例中,也就是他的父亲以及他的右子树。
一般来说,单单一个面包屑有足够的资讯让我们重建父亲的节点。所以他应该要包含所有我们没有选择的路径的资讯,并且他应该要纪录我们沿路走的方向。同时他不应该包含我们现在锁定的子树。因为那棵子树已经在 tuple 的第一个部份中,如果我们也把他纪录在面包屑里,那就会有重复的资讯。
我们来修改一下我们面包屑的定义,让他包含我们之前丢掉的资讯。我们定义一个新的型态,而不用 Direction
:
data Crumb a = LeftCrumb a (Tree a) | RightCrumb a (Tree a) deriving (Show)
我们用 LeftCrumb
来包含我们没有走的右子树,而不仅仅只写个 L
。我们用 RightCrumb
来包含我们没有走的左子树,而不仅仅只写个 R
。
这些面包屑包含了所有重建树所需要的资讯。他们像是软碟一样存了许多我们的足迹,而不仅仅只是方向而已。
大致上可以把每个面包屑想像成一个树的节点,树的节点有一个洞。当我们往树的更深层走,面包屑携带有我们所有走过得所有资讯,只除了目前我们锁定的子树。他也必须纪录洞在哪里。在 LeftCrumb
的案例中,我们知道我们是向左走,所以我们缺少的便是左子树。
我们也要把 Breadcrumbs
的 type synonym 改掉:
type Breadcrumbs a = [Crumb a]
接着我们修改 goLeft
跟 goRight
来纪录一些我们没走过的路径的资讯。不像我们之前选择忽略他。goLeft
像是这样:
goLeft :: (Tree a, Breadcrumbs a) -> (Tree a, Breadcrumbs a)
goLeft (Node x l r, bs) = (l, LeftCrumb x r:bs)
你可以看到跟之前版本的 goLeft
很像,不只是将 L
推到 list 的最前端,我们还加入 LeftCrumb
来表示我们选择向左走。而且我们在 LeftCrumb
里面塞有我们之前走的节点,以及我们选择不走的右子树的资讯。
要注意这个函数会假设我们锁定的子树并不是 Empty
。一个空的树并没有任何子树,所以如果我们选择在一个空的树中向左走,就会因为我们对 Node
做模式匹配而产生错误。我们没有处理 Empty
的情况。
goRight
也是类似:
goRight :: (Tree a, Breadcrumbs a) -> (Tree a, Breadcrumbs a)
goRight (Node x l r, bs) = (r, RightCrumb x l:bs)
在之前我们只能向左或向右走,现在我们由于纪录了关于父节点的资讯以及我们选择不走的路的资讯,而获得向上走的能力。来看看 goUp
函数:
goUp :: (Tree a, Breadcrumbs a) -> (Tree a, Breadcrumbs a)
goUp (t, LeftCrumb x r:bs) = (Node x t r, bs)
goUp (t, RightCrumb x l:bs) = (Node x l t, bs)
我们锁定了 t
这棵树并检查最新的 Crumb
。如果他是 LeftCrumb
,那我们就建立一棵新的树,其中 t
是他的左子树并用关于我们没走过得右子树的资讯来填写其他 Node
的资讯。由于我们使用了面包屑的资讯来建立父子树,所以新的 list 移除了我们的面包屑。
如果我们已经在树的顶端并使用这个函数的话,他会引发错误。等一会我们会用 Maybe
来表达可能失败的情况。
有了 Tree a
跟 Breadcrumbs a
,我们就有足够的资讯来重建整棵树,并且锁定其中一棵子树。这种方式让我们可以轻松的往上,往左,往右走。这样成对的资料结构我们叫做 Zipper,因为当我们改变锁定的时候,他表现得很像是拉链一样。所以我们便定义一个 type synonym:
type Zipper a = (Tree a, Breadcrumbs a)
我个人是比较倾向于命名成 Focus
,这样可以清楚强调我们是锁定在其中一部分, 至于 Zipper 被更广泛地使用,所以这边仍维持叫他做 Zipper
。
#
Manipulating trees under focus
现在我们具备了移动的能力,我们再来写一个改变元素的函数,他能改变我们目前锁定的子树的 root。
modify :: (a -> a) -> Zipper a -> Zipper a
modify f (Node x l r, bs) = (Node (f x) l r, bs)
modify f (Empty, bs) = (Empty, bs)
如果我们锁定一个节点,我们用 f
改变他的 root。如果我们锁定一棵空的树,那就什么也不做。我们可以移来移去并走到我们想要改变的节点,改变元素后并锁定在那个节点,之后我们可以很方便的移上移下。
ghci> let newFocus = modify (\_ -> 'P') (goRight (goLeft (freeTree,[])))
我们往左走,然后往右走并将 root 取代为 'P'
,用 -:
来表达的话就是:
ghci> let newFocus = (freeTree,[]) -: goLeft -: goRight -: modify (\_ -> 'P')
我们也能往上走并置换节点为 'X'
:
ghci> let newFocus2 = modify (\_ -> 'X') (goUp newFocus)
如果我们用 -:
表达的话:
ghci> let newFocus2 = newFocus -: goUp -: modify (\_ -> 'X')
往上走很简单,毕竟面包屑中含有我们没走过的路径的资讯,只是里面的资讯是相反的,这有点像是要把袜子反过来才能用一样。有了这些资讯,我们就不用再从 root 开始走一遍,我们只要把反过来的树翻过来就好,然后锁定他。
每个节点有两棵子树,即使子树是空的也是视作有树。所以如果我们锁定的是一棵空的子树我们可以做的事就是把他变成非空的,也就是叶节点。
attach :: Tree a -> Zipper a -> Zipper a
attach t (_, bs) = (t, bs)
我们接受一棵树跟一个 zipper,回传一个新的 zipper,锁定的目标被换成了提供的树。我们不只可以用这招把空的树换成新的树,我们也能把现有的子树给换掉。让我们来用一棵树换掉我们 freeTree
的最左边:
ghci> let farLeft = (freeTree,[]) -: goLeft -: goLeft -: goLeft -: goLeft
ghci> let newFocus = farLeft -: attach (Node 'Z' Empty Empty)
newFocus
现在锁定在我们刚刚接上的树上,剩下部份的资讯都放在面包屑里。如果我们用 goUp
走到树的最上层,就会得到跟原来 freeTree
很像的树,只差在最左边多了 'Z'
。
#
I'm going straight to top, oh yeah, up where the air is fresh and clean!
写一个函数走到树的最顶端是很简单的:
topMost :: Zipper a -> Zipper a
topMost (t,[]) = (t,[])
topMost z = topMost (goUp z)
如果我们的面包屑都没了,就表示我们已经在树的 root,我们便回传目前的锁定目标。晡然,我们便往上走来锁定到父节点,然后递回地呼叫 topMost
。我们现在可以在我们的树上四处移动,呼叫 modify
或 attach
进行我们要的修改。我们用 topMost
来锁定到 root,便可以满意地欣赏我们的成果。
#
来看串列
Zippers 几乎可以套用在任何资料结构上,所以听到他可以被套用在 list 上可别太惊讶。毕竟,list 就是树,只是节点只有一个儿子,当我们实作我们自己的 list 的时候,我们定义了下面的型态:
data List a = Empty | Cons a (List a) deriving (Show, Read, Eq, Ord)
跟我们二元树的定义比较,我们就可以看出我们把 list 看作树的原则是正确的。
一串 list 像是 [1,2,3]
可以被写作 1:2:3:[]
。他由 list 的 head1
以及 list 的 tail 2:3:[]
组成。而 2:3:[]
又由 2
跟 3:[]
组成。至于 3:[]
,3
是 head 而 tail 是 []
。
我们来帮 list 做个 zipper。list 改变锁定的方式分为往前跟往后(tree 分为往上,往左跟往右)。在树的情形中,锁定的部份是一棵子树跟留下的面包屑。那究竟对于一个 list 而言一个面包屑是什么?当我们处理二元树的时候,我们说面包屑必须代表 root 的父节点跟其他未走过的子树。他也必须记得我们是往左或往右走。所以必须要有除了锁定的子树以外的所有资讯。
list 比 tree 要简单,所以我们不需要记住我们是往左或往右,因为我们只有一种方式可以往 list 的更深层走。我们也不需要哪些路径我们没有走过的资讯。似乎我们所需要的资讯只有前一个元素。如果我们的 list 是像 [3,4,5]
,而且我们知道前一个元素是 2
,我们可以把 2
摆回 list 的 head,成为 [2,3,4,5]
。
由于一个单一的面包屑只是一个元素,我们不需要把他摆进一个型态里面,就像我们在做 tree zippers 时一样摆进 Crumb
:
type ListZipper a = ([a],[a])
第一个 list 代表现在锁定的 list,而第二个代表面包屑。让我们写一下往前跟往后走的函数:
goForward :: ListZipper a -> ListZipper a
goForward (x:xs, bs) = (xs, x:bs)
goBack :: ListZipper a -> ListZipper a
goBack (xs, b:bs) = (b:xs, bs)
当往前走的时候,我们锁定了 list 的 tail,而把 head 当作是面包屑。当我们往回走,我们把最近的面包屑欻来然后摆到 list 的最前头。
来看看两个函数如何运作:
ghci> let xs = [1,2,3,4]
ghci> goForward (xs,[])
([2,3,4],[1])
ghci> goForward ([2,3,4],[1])
([3,4],[2,1])
ghci> goForward ([3,4],[2,1])
([4],[3,2,1])
ghci> goBack ([4],[3,2,1])
([3,4],[2,1])
我们看到在这个案例中面包屑只不过是一部分反过来的 list。所有我们走过的元素都被丢进面包屑里面,所以要往回走很容易,只要把资讯从面包屑里面捡回来就好。
这样的形式也比较容易看出我们为什么称呼他为 Zipper,因为他真的就像是拉链一般。
如果你正在写一个文字编辑器,那你可以用一个装满字串的 list 来表达每一行文字。你也可以加一个 Zipper 以便知道现在游标移动到那一行。有了 Zipper 你就很容易的可以新增或删除现有的每一行。
#
阳春的档案系统
理解了 Zipper 是如何运作之后,我们来用一棵树来表达一个简单的档案系统,然后用一个 Zipper 来增强他的功能。让我们可以在资料夹间移动,就像我们平常对档案系统的操作一般。
这边我们采用一个比较简化的版本,档案系统只有档案跟资料夹。档案是资料的基本单位,只是他有一个名字。而资料夹就是用来让这些档案比较有结构,并且能包含其他资料夹与档案。所以说档案系统中的元件不是一个档案就是一个资料夹,所以我们便用如下的方法定义型态:
type Name = String
type Data = String
data FSItem = File Name Data | Folder Name [FSItem] deriving (Show)
一个档案是由两个字串组成,代表他的名字跟他的内容。一个资料夹由一个字串跟一个 list 组成,字串代表名字,而 list 是装有的元件,如果 list 是空的,就代表他是一个空的资料夹。
这边是一个装有些档案与资料夹的资料夹:
myDisk :: FSItem
myDisk =
Folder "root"
[ File "goat_yelling_like_man.wmv" "baaaaaa"
, File "pope_time.avi" "god bless"
, Folder "pics"
[ File "ape_throwing_up.jpg" "bleargh"
, File "watermelon_smash.gif" "smash!!"
, File "skull_man(scary).bmp" "Yikes!"
]
, File "dijon_poupon.doc" "best mustard"
, Folder "programs"
[ File "fartwizard.exe" "10gotofart"
, File "owl_bandit.dmg" "mov eax, h00t"
, File "not_a_virus.exe" "really not a virus"
, Folder "source code"
[ File "best_hs_prog.hs" "main = print (fix error)"
, File "random.hs" "main = print 4"
]
]
]
这就是目前我的磁碟的内容。
#
A zipper for our file system
我们有了一个档案系统,我们需要一个 Zipper 来让我们可以四处走动,并且增加、修改或移除档案跟资料夹。就像二元树或 list,我们会用面包屑留下我们未走过路径的资讯。正如我们说的,一个面包屑就像是一个节点,只是他包含所有除了我们现在正锁定的子树的资讯。
在这个案例中,一个面包屑应该要像资料夹一样,只差在他缺少了我们目前锁定的资料夹的资讯。为什么要像资料夹而不是档案呢?因为如果我们锁定了一个档案,我们就没办法往下走了,所以要留下资讯说我们是从一个档案走过来的并没有道理。一个档案就像是一棵空的树一样。
如果我们锁定在资料夹 "root"
,然后锁定在档案 "dijon_poupon.doc"
,那面包屑里的资讯会是什么样子呢?他应该要包含上一层资料夹的名字,以及在这个档案前及之后的所有项目。我们要的就是一个 Name
跟两串 list。借由两串 list 来表达之前跟之后的元素,我们就完全可以知道我们目前锁定在哪。
来看看我们面包屑的型态:
data FSCrumb = FSCrumb Name [FSItem] [FSItem] deriving (Show)
这是我们 Zipper 的 type synonym:
type FSZipper = (FSItem, [FSCrumb])
要往上走是很容易的事。我们只要拿现有的面包屑来组出现有的锁定跟面包屑:
fsUp :: FSZipper -> FSZipper
fsUp (item, FSCrumb name ls rs:bs) = (Folder name (ls ++ [item] ++ rs), bs)
由于我们的面包屑有上一层资料夹的名字,跟资料夹中之前跟之后的元素,要往上走不费吹灰之力。
至于要往更深层走呢?如果我们现在在 "root"
,而我们希望走到 "dijon_poupon.doc"
,那我们会在面包屑中留下 "root"
,在 "dijon_poupon.doc"
之前的元素,以及在他之后的元素。
这边有一个函数,给他一个名字,他会锁定在在现有资料夹中的一个档案:
import Data.List (break)
fsTo :: Name -> FSZipper -> FSZipper
fsTo name (Folder folderName items, bs) =
let (ls, item:rs) = break (nameIs name) items
in (item, FSCrumb folderName ls rs:bs)
nameIs :: Name -> FSItem -> Bool
nameIs name (Folder folderName _) = name == folderName
nameIs name (File fileName _) = name == fileName
fsTo
接受一个 Name
跟 FSZipper
,回传一个新的 FSZipper
锁定在某个档案上。那个档案必须在现在身处的资料夹才行。这函数不会四处找寻这档案,他只会看现在的资料夹。
首先我们用 break
来把身处资料夹中的档案们分成在我们要找的档案前的,跟之后的。如果记性好,break
会接受一个 predicate 跟一个 list,并回传两个 list 组成的 pair。第一个 list 装有 predicate 会回传 False
的元素,而一旦碰到一个元素回传 True
,他就把剩下的所有元素都放进第二个 list 中。我们用了一个辅助函数叫做 nameIs
,他接受一个名字跟一个档案系统的元素,如果名字相符的话他就会回传 True
。
现在 ls
一个包含我们要找的元素之前元素的 list。item
就是我们要找的元素,而 rs
是剩下的部份。有了这些,我们不过就是把 break
传回来的东西当作锁定的目标,来建造一个面包屑来包含所有必须的资讯。
如果我们要找的元素不在资料夹中,那 item:rs
这个模式会符合到一个空的 list,便会造成错误。如果我们现在的锁定不是一个资料夹而是一个档案,我们也会造成一个错误而让程式当掉。
现在我们有能力在我们的档案系统中移上移下,我们就来尝试从 root 走到 "skull_man(scary).bmp"
这个档案吧:
ghci> let newFocus = (myDisk,[]) -: fsTo "pics" -: fsTo "skull_man(scary).bmp"
newFocus
现在是一个锁定在 "skull_man(scary).bmp"
的 Zipper。我们把 zipper 的第一个部份拿出来看看:
ghci> fst newFocus
File "skull_man(scary).bmp" "Yikes!"
我们接着往上移动并锁定在一个邻近的档案 "watermelon_smash.gif"
:
ghci> let newFocus2 = newFocus -: fsUp -: fsTo "watermelon_smash.gif"
ghci> fst newFocus2
File "watermelon_smash.gif" "smash!!"
#
Manipulating our file system
现在我们知道如何遍历我们的档案系统,因此操作也并不是难事。这边便来写个重新命名目前锁定档案或资料夹的函数:
fsRename :: Name -> FSZipper -> FSZipper
fsRename newName (Folder name items, bs) = (Folder newName items, bs)
fsRename newName (File name dat, bs) = (File newName dat, bs)
我们可以重新命名 "pics"
资料夹为 "cspi"
:
ghci> let newFocus = (myDisk,[]) -: fsTo "pics" -: fsRename "cspi" -: fsUp
我们走到 "pics"
这个资料夹,重新命名他然后再往回走。
那写一个新的元素在我们目前的资料夹呢?
fsNewFile :: FSItem -> FSZipper -> FSZipper
fsNewFile item (Folder folderName items, bs) =
(Folder folderName (item:items), bs)
注意这个函数会没办法处理当我们在锁定在一个档案却要新增元素的情况。
现在要在 "pics"
资料夹中加一个档案然后走回 root:
ghci> let newFocus = (myDisk,[]) -: fsTo "pics" -: fsNewFile (File "heh.jpg" "lol") -: fsUp
当我们修改我们的档案系统,他不会真的修改原本的档案系统,而是回传一份新的档案系统。这样我们就可以存取我们旧有的系统(也就是 myDisk
)跟新的系统(newFocus
的第一个部份)使用一个 Zippers,我们就能自动获得版本控制,代表我们能存取到旧的资料结构。这也不仅限于 Zippers,也是由于 Haskell 的资料结构有 immutable 的特性。但有了 Zipper,对于操作会变得更容易,我们可以自由地在资料结构中走动。
#
小心每一步
到目前为止,我们并没有特别留意我们在走动时是否会超出界线。不论资料结构是二元树,List 或档案系统。举例来说,我们的 goLeft
函数接受一个二元树的 Zipper 并锁定到他的左子树:
goLeft :: Zipper a -> Zipper a
goLeft (Node x l r, bs) = (l, LeftCrumb x r:bs)
但如果我们走的树其实是空的树呢?也就是说,如果他不是 Node
而是 Empty
?再这情况,我们会因为模式匹配不到东西而造成 runtime error。我们没有处理空的树的情形,也就是没有子树的情形。到目前为止,我们并没有试着在左子树不存在的情形下锁定左子树。但要走到一棵空的树的左子树并不合理,只是到目前为止我们视而不见而已。
如果我们已经在树的 root 但仍旧试着往上走呢?这种情形也同样会造成错误。。用了 Zipper 让我们每一步都好像是我们的最后一步一样。也就是说每一步都有可能会失败。这让你想起什么吗?没错,就是 Monad。更正确的说是 Maybe
monad,也就是有可能失败的 context。
我们用 Maybe
monad 来加入可能失败的 context。我们要把原本接受 Zipper 的函数都改成 monadic 的版本。首先,我们来处理 goLeft
跟 goRight
。函数的失败有可能反应在他们的结果,这个情况也不利外。所以来看下面的版本:
goLeft :: Zipper a -> Maybe (Zipper a)
goLeft (Node x l r, bs) = Just (l, LeftCrumb x r:bs)
goLeft (Empty, _) = Nothing
goRight :: Zipper a -> Maybe (Zipper a)
goRight (Node x l r, bs) = Just (r, RightCrumb x l:bs)
goRight (Empty, _) = Nothing
然后我们试着在一棵空的树往左走,我们会得到 Nothing
:
ghci> goLeft (Empty, [])
Nothing
ghci> goLeft (Node 'A' Empty Empty, [])
Just (Empty,[LeftCrumb 'A' Empty])
看起来不错。之前的问题是我们在面包屑用完的情形下想往上走,那代表我们已经在树的 root。如果我们不注意的话那 goUp
函数就会丢出错误。
goUp :: Zipper a -> Zipper a
goUp (t, LeftCrumb x r:bs) = (Node x t r, bs)
goUp (t, RightCrumb x l:bs) = (Node x l t, bs)
我们改一改让他可以失败得好看些:
goUp :: Zipper a -> Maybe (Zipper a)
goUp (t, LeftCrumb x r:bs) = Just (Node x t r, bs)
goUp (t, RightCrumb x l:bs) = Just (Node x l t, bs)
goUp (_, []) = Nothing
如果我们有面包屑,那我们就能成功锁定新的节点,如果没有,就造成一个失败。
之前这些函数是接受 Zipper 并回传 Zipper,这代表我们可以这样操作:
gchi> let newFocus = (freeTree,[]) -: goLeft -: goRight
但现在我们不回传 Zipper a
而回传 Maybe (Zipper a)
。所以没办法像上面串起来。我们在之前章节也有类似的问题。他是每次走一步,而他的每一步都有可能失败。
幸运的是我们可以从之前的经验中学习,也就是使用 >>=
,他接受一个有 context 的值(也就是 Maybe (Zipper a)
),会把值喂进函数并保持其他 context 的。所以就像之前的例子,我们把 -:
换成 >>=
。
ghci> let coolTree = Node 1 Empty (Node 3 Empty Empty)
ghci> return (coolTree,[]) >>= goRight
Just (Node 3 Empty Empty,[RightCrumb 1 Empty])
ghci> return (coolTree,[]) >>= goRight >>= goRight
Just (Empty,[RightCrumb 3 Empty,RightCrumb 1 Empty])
ghci> return (coolTree,[]) >>= goRight >>= goRight >>= goRight
Nothing
我们用 return
来把 Zipper 放到一个 Just
里面。然后用 >>=
来喂到 goRight
的函数中。首先我们做了一棵树他的左子树是空的,而右边是有两颗空子树的一个节点。当我们尝试往右走一步,便会得到成功的结果。往右走两步也还可以,只是会锁定在一棵空的子树上。但往右走三步就没办法了,因为我们不能在一棵空子树上往右走,这也是为什么结果会是 Nothing
。
现在我们具备了安全网,能够在出错的时候通知我们。
我们的档案系统仍有许多情况会造成错误,例如试着锁定一个档案,或是不存在的资料夹。剩下的就留作习题。
15
FAQ
#
推荐其它几个 Haskell 读物?
有很多出色的教学,但我得告诉你Real World Haskell出类拔萃。它太棒了。我觉得它可以和这个教程搭配着一起读。这个教程提供几个简单例子好让初学者对那点概念有个简单认识,而 Real World Haskell 真正教给你如何充分地使用它们。
#
我怎么联络到你?
最好的方式是用寄封 email 给我,email 是 bonus at learnyouahaskell dot com。不过有点耐心,我没有 24 小时在电脑旁,所以如果我没有即时地回复你的 email 的话,请多包含。
#
我想要一些习题!
很快就会有了!很多人不断来问我能不能加些习题,我正在赶工呢。
#
关于作者
我的名字是 Miran Lipovača,住在斯洛文尼亚的 Ljubljana。 大部分时间我都闲闲没事,不过当我认真的时候我不是在写程式,绘画,练格斗技,或弹 bass。 我甚至弄了一个讨论 bass 的网站。 我甚至搜集一堆猫头鹰玩偶,有时候我会对他们自言自语。
16
Resource
网路上 Haskell 的资源虽不少,但由于目前社群的人力有限。所以比较没能整理成一套能循序渐进的学习方式。常常会在 Haskell Wiki 上撞到对初学者太过于深入的东西。或是觉得奇怪怎么不断有之前没看过的东西冒出来。造成学习 Haskell 很大的撞墙期。这边译者会渐渐补充一些自己觉得有用的资源,尝试找到一些中阶的教材能够衔接初学跟进阶。
#
Specification - Haskell 98 Report: Haskell 的标准,目前 GHC 如果不用任何 Extension,写出来的程式是符合 Haskell 98 的标准。 - Haskell 2010 Report:,最新的标准,有许多已经实作但要开 Extension 才能用。
#
Tools - Hoogle: Haskell 函数的搜寻引擎,不只可以用函数的名称搜寻,也可以用函数的型态来搜寻。 - Hayoo: 跟 Hoogle 同样功能。 - hdiff: 可以方便查询 package 不同版号之间的差异。 - packdeps: 方便查询 Hackage 上面 package 之间的相依性。
#
Lectures & Articles - Wikibook Haskell: 丰富的 Wikibook 资源 - CS240h: David Mazières 跟 Bryan O'Sullivan 在 Stanford 开的课。 - 本物のプログラマはHaskellを使う: Haskell 专栏 - Write Yourself a Scheme in 48 Hours,Audrey Tang 写的教学,教你如何用 Haskell 写出一个 Scheme。 - 德国大学的 Functional Programming 课程,语言是用 FP (英文授课) - Simon Marlow 讲解 parallel haskell 的投影片 - FLOLAC 2012 - ICFP 2012 - Explanation of Generalized Algebraic Data Types - A Quick Intro to Snap - Logic, Languages, Compilation, and Verification 2012 - Haskell in Halle/Saale - Fast Code Nation
#
Forum - Stackoverflow: 著名 stackoverflow 上的*haskell tag - Reddit
#
Online Judge - H-99: Ninety-Nine Haskell Problems - Project Euler: 已经算非常著名的 Online Judge,可惜只有上传答案。如果问题实在想不出来,Haskell Wiki 上也有参考答案。 - SPOJ: 少数的 Online Judge 系统可以上传 Haskell 的,题目非常丰富。也是练 ACM ICPC 常用的网站。
#
Books - Learn you a Haskell for great good (Japanese Translation) - Real World Haskell - Yesod Book, 讲解如何使用 Yesod Web Framework
#
PL Researchers - 穆信成老师 - 单中杰老师 - Conal Elliott - Edward Yang - Edward Kmett
#
Interesting Projects - Fay Programming Langauge 用 Haskell 语言的子集,直接转译成 Javascript - Leksah: Haskell IDE - Super Manao Bros: 超级玛利欧
#
Taiwan Functional Programming User Group - TW-FPUG on Vimeo - Haskell 进阶运算元件介绍
更多信息请访问