基于树索引的向量检索算法 | 必读论文

本文简要概括了两篇基于树索引的向量检索算法相关的必读论文，具体的细节还需阅读原论文。

论文下载链接：http://s.dic.cool/S/ZemCpbwr

这篇文章主要讨论了在一般度量空间中进行最近邻搜索的数据结构和算法。作者首先介绍了一般度量空间的定义和性质，然后讨论了最近邻搜索的基本概念和应用场景。接下来，作者详细介绍了一些常见的最近邻搜索算法，例如暴力搜索、k-d tree、球树、LSH 等。最后，作者还讨论了一些最近邻搜索算法的优化技巧，例如剪枝、分治、并行计算等。

  本文提出了一种新的基于树的索引数据结构，称为 vp-tree。vp-tree 主要用于解决高维空间中最近邻搜索问题，例如在计算机视觉、语音识别、生物信息学等领域中。vp-tree（Vantage-point tree）是一种度量树，它通过选择空间中的一个位置（“视点”）并将数据点分成两部分来将度量空间中的数据分离：那些比阈值更接近视点的点和那些不是的点。vp-tree 特别适用于将非标准度量空间中的数据划分为度量树。vp-tree 的搜索算法是递归的。在任何给定步骤中，我们都在处理具有视点 v 和阈值距离 t 的树节点。兴趣点 x 将与视点 v 有一定距离。如果该距离 d 小于 t，则使用算法递归地搜索包含比阈值 t 更接近视点 v 的点的节点子树；否则递归到包含比阈值 t 更远离视点 v 的点的节点子树。如果算法的递归使用发现距离 x 的相邻点 n 小于 |t - d|，则无法帮助搜索此节点的其他子树；返回发现的节点 n。否则，还需要递归搜索其他子树。类似的方法也适用于查找 x 的 k 个最近邻居。

初始 vp-tree。

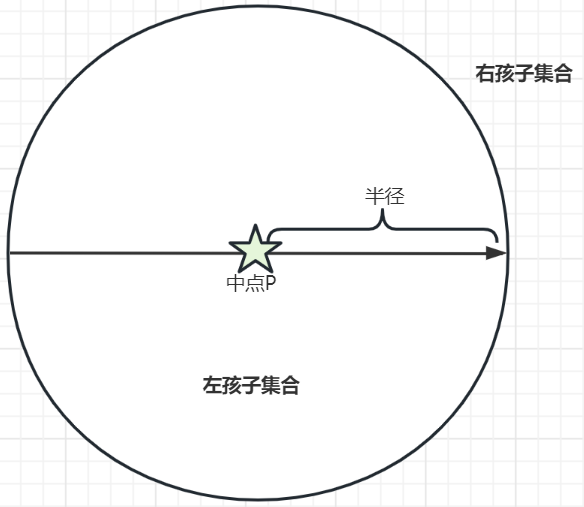
假设我们要找到离目标最近的两个邻居，用红色 X 标记。由于我们还没有点，节点的中心 p 是最接近的候选者，我们将其添加到结果列表中。（以后可能会被撞出来）。同时，我们更新变量 dis，它跟踪结果中最远点的距离。

然后，我们必须决定是先搜索左子还是右子。我们可能最终不得不同时搜索它们，但我们希望在大多数情况下避免这种情况。

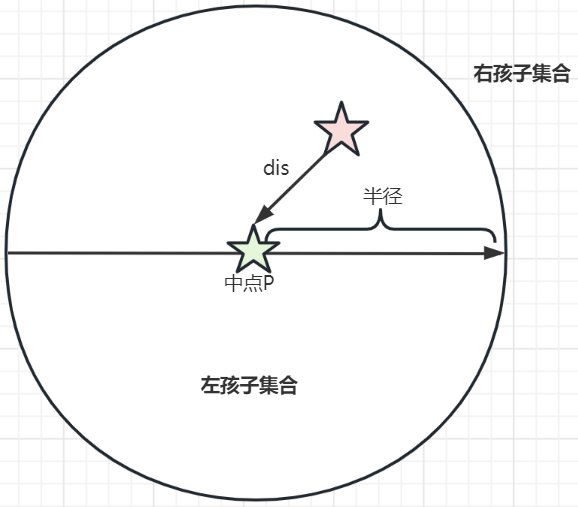
由于目标比其外壳更靠近节点的中心，因此我们首先搜索左子项，其中包含比半径更近的所有点。我们找到蓝点。由于它比 dis 更远，我们更新 dis 值。

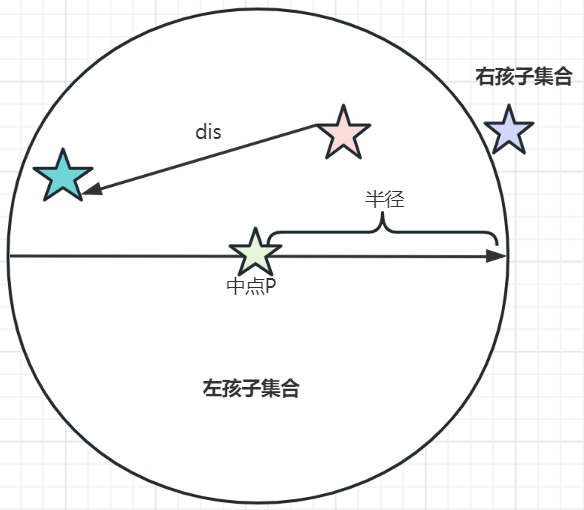
我们需要继续搜索吗？我们知道我们已经考虑了 p 距离半径内的所有点。然而，它比我们发现的最远点更接近外壳。因此，在外壳之外可能会有更近的点。我们确实需要下降到正确的孩子才能找到紫点。

但是，如果我们已经达到了收集 n 个最近点的目标，并且目标点离外壳比我们收集的最远点更远，那么我们就可以停止寻找。这样可以节省大量资金。

论文下载链接：http://s.dic.cool/S/9RpTej4b

这篇论文介绍了一种数据结构，使得 Bregman 散度的最近邻检索更加高效。Bregman 散度是一种广泛使用的不相似性度量，包括KL散度（相对熵）、马氏距离和 Itakura-Saito 散度。这些不相似性度量对于高效的最近邻检索构成了挑战，因为它们通常不是度量，而大多数最近邻数据结构都是为度量而设计的。这个数据结构与流行的度量球树具有相同的基本结构，但是使用 Bregman 散度的凸性质代替了三角不等式。实验表明，与暴力搜索相比，速度提高了几个数量级。

本文提出了一种新的基于树的索引数据结构，称为 bbtrees。这是第一个用于一般布雷格曼散度的神经网络检索数据结构。该数据结构是流行的公制球树。由于这个数据结构是建立在三角形不等式的基础上的，因此对布雷格曼散度的扩展是非平凡的。bbtree 定义了基于 bregman 球的分层空间分解;检索具有树的 NN 需要计算从查询到这些球的 bregman 散度的边界。这种散度可以用一个简单的二分搜索精确地计算出来，这是非常有效的。由于只需要散度的边界，bbtrees 通常可以使用原始函数和对偶函数求值提前停止搜索。

bbtrees的构建

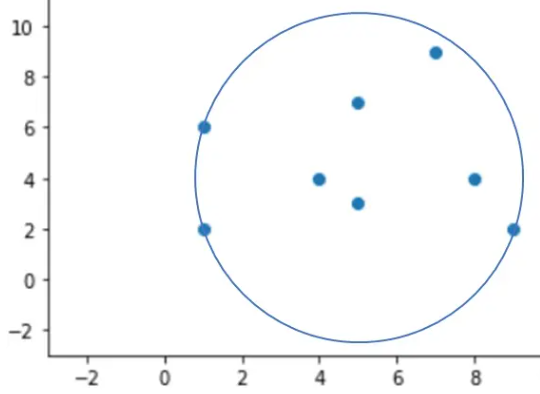
首先建立根节点，找到包含所有样本点的超球体，记录球心位置，作为根节点（超球体可以是最小外接超球体，也可以不是，只需要将符合要求的样本点包含进去即可，当然越小的超球体，在搜索过程中效率越高。

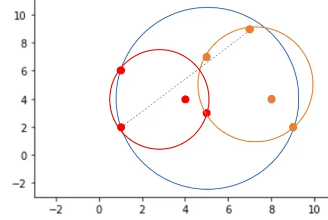
从顶部开始，算法运行 k-means 将点划分为两个簇。同理，找到两个簇包含所有样本点的超球体，记录球心位置，分别做为根节点的左右孩子节点。

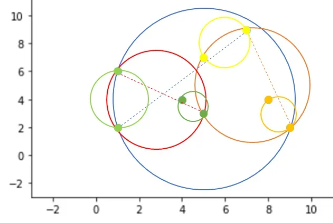
递归上一步骤，可以设定一个阈值 r，当子节点中包含的样本点数量 <= r 时，即可停止对这个子节点的分割。

布雷格散度

我们以欧几里得距离举例，即 n 维空间中的欧几里得距离（1）：

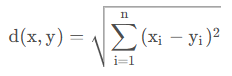
我们将其平方（2）：

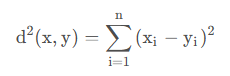
如果我们定义内积为（3）：

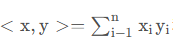
欧式模为（4）：

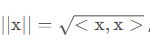
上述（2）式子修改为（5）：

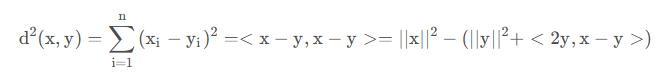
其中2y为y^2的导数，所以公式（5）可修改为式（6）：

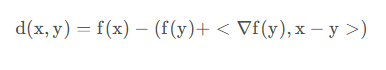
以上就是 Bregman 散度（Bregman Divergence）的定义。

bbtrees 搜索

1.bbtrees 搜索原理：

bbtrees 搜索原理与球树搜索一致，具体可以参考以下链接：

https://zhuanlan.zhihu.com/p/521546068。

2.bbtrees 搜索区别：

首先，树是从根区域向下搜索;在每个节点上，搜索算法选择 df(µ，q)最小的子节点，并暂时忽略兄弟节点。最接近的点是候选 NN;叫它 xc。

公式（1）：

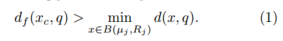
如果(1)成立，则节点 j 及其所有子节点可以被忽略，因为该 NN 无法在该子树中找到。否则，必须探索以 j 为根的子树。该算法很容易调整为返回 k 个最近邻。以此，方式完成了球树搜索的加速。