大家好,我是阿Q。
今天是经典算法的最后一节,一周以来,对这几种经典算法也重新学习了一遍,更加深刻的理解这几种算法。
让我们一起再来巩固一下前面几个:
对发布的这些文章都有各自的pdf版,需要的话,也会发给你的哦~
今日分享:

一、旅行商问题
1.1、问题描述
1.2、解题思路
建模:将问题建模为图,其中每个城市表示图的节点,城市之间的距离表示图的边。 初始化:选择一个起始城市作为出发点,并将其标记为已访问。 分支限界搜索: 从当前城市出发,计算到所有未访问城市的距离,并生成一个候选城市列表。 对候选城市列表按照距离从小到大排序,选择一个距离最小的城市。 将该城市标记为已访问,将其加入当前路径中,并更新路径长度。 生成一个新的TSP子问题,包括未访问的城市,作为下一步的搜索对象。 重复以上步骤,直到所有城市都被访问过一次。 计算当前路径的长度,如果它比已知的最优解更短,更新最优解。 回溯到上一步,继续搜索其他可能的路径。 终止条件:当无法生成更短的路径或者已经搜索完所有可能的路径时,算法终止。返回找到的最短路径。 优化:由于TSP是一个NP困难问题,对于大规模问题,分支限界法可能需要很长时间才能找到最优解。因此,通常需要一些启发式方法来改进算法的性能,例如近似算法或局部搜索算法。
1.3、代码示例
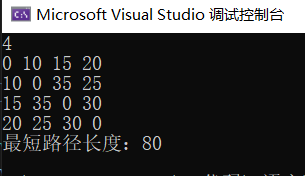
#include <iostream>#include <vector>#include <algorithm>#include <limits>using namespace std;const int INF = numeric_limits<int>::max();int tsp(vector<vector<int>>& graph, vector<bool>& visited, int current, int n, int count, int cost, int& ans) {if (count == n && graph[current][0] != 0) {ans = min(ans, cost + graph[current][0]);return ans;}for (int i = 0; i < n; ++i) {if (!visited[i] && graph[current][i] != 0) {visited[i] = true;tsp(graph, visited, i, n, count + 1, cost + graph[current][i], ans);visited[i] = false;}}return ans;}int main() {int n; // 城市数量cin >> n;vector<vector<int>> graph(n, vector<int>(n));// 输入城市间的距离for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {cin >> graph[i][j];}}vector<bool> visited(n, false);visited[0] = true; // 从第一个城市开始int ans = INF;int result = tsp(graph, visited, 0, n, 1, 0, ans);cout << "最短路径长度:" << result << endl;return 0;}
二、01背包问题
2.1、问题描述
2.2、解题思路
建立节点类:首先,我们需要创建一个节点类,用于表示每个可能的状态。这个节点应该包括以下信息: 当前节点的价值(value) 当前节点的重量(weight) 当前节点的价值上界(upper_bound):这是一个关键的信息,表示在当前节点处,还有多少价值可以被获得。通常,价值上界可以通过将背包容量剩余部分的最大单位价值与当前节点的单位价值相加来估计。 当前节点的层级(level):表示我们在决策树中的哪一层。 初始化根节点:我们从根节点开始,将背包的当前重量和当前价值都初始化为0,层级为0。 创建优先队列:我们使用一个优先队列(通常是最小堆)来存储节点,以便按照价值上界排序。初始时,将根节点加入队列。 循环:进入一个循环,直到队列为空为止。在循环中,我们执行以下步骤: 从队列中取出一个节点。 如果该节点的价值上界小于当前已经找到的最优解的价值,则剪枝,不再继续处理该节点。 否则,考虑两种情况:放入当前物品或不放入。分别创建两个子节点,更新它们的重量、价值和价值上界,并将它们加入队列中。 继续循环。 终止条件:当队列为空时,循环终止。此时,已经找到了最优解,最优解即为已经处理的节点中价值最大的节点。 回溯找到具体物品:从最优节点开始,通过回溯的方式找到具体放入背包的物品,即找到了解。
2.3、代码示例
#include <iostream>#include <vector>#include <queue>using namespace std;// 定义节点结构struct Node {int level; // 当前节点所在层级int value; // 当前节点的价值int weight; // 当前节点的重量int upper_bound; // 当前节点的价值上界// 构造函数Node(int l, int v, int w, int ub) : level(l), value(v), weight(w), upper_bound(ub) {}};// 用于比较节点的仿函数struct CompareNode {bool operator()(const Node& a, const Node& b) {return a.upper_bound < b.upper_bound;}};int knapsack(vector<int>& weights, vector<int>& values, int W) {int n = weights.size();priority_queue<Node, vector<Node>, CompareNode> pq;// 初始化根节点Node root(-1, 0, 0, 0);pq.push(root);int max_value = 0;while (!pq.empty()) {Node current = pq.top();pq.pop();if (current.upper_bound < max_value) {// 当前节点的价值上界小于已知最优解,剪枝continue;}if (current.level == n - 1) {// 已经到达叶子节点if (current.value > max_value) {max_value = current.value;}continue;}// 考虑放入当前物品int next_level = current.level + 1;int next_weight = current.weight + weights[next_level];int next_value = current.value + values[next_level];// 计算价值上界int next_upper_bound = next_value + (W - next_weight) * (values[next_level] (double)weights[next_level]);if (next_weight <= W && next_upper_bound > max_value) {// 创建左子节点,放入当前物品pq.push(Node(next_level, next_value, next_weight, next_upper_bound));}// 不放入当前物品next_weight = current.weight;next_value = current.value;next_upper_bound = next_value + (W - next_weight) * (values[next_level] (double)weights[next_level]);if (next_upper_bound > max_value) {// 创建右子节点,不放入当前物品pq.push(Node(next_level, next_value, next_weight, next_upper_bound));}}return max_value;}int main() {// 物品的重量和价值vector<int> weights = {2, 3, 4, 5};vector<int> values = {3, 4, 5, 6};// 背包的容量int W = 5;int result = knapsack(weights, values, W);cout << "最大价值: " << result << endl;return 0;}

三、图着色问题
3.1、问题描述
3.2、解题思路
问题建模:首先,将图着色问题建模为一个图论问题。给定一个无向图,需要为图的每个节点分配一种颜色,使得相邻的节点具有不同的颜色。这个问题可以看作是在给定的颜色数量下,寻找一个有效的节点着色方案。 数据结构:使用一个领接矩阵来表示图。领接矩阵 adjacency
是一个二维数组,其中adjacency[i][j]
表示节点i
和节点j
之间是否有边相连。另外,使用一个一维数组colors
来存储每个节点的颜色,初始时都设置为0,表示未着色。颜色分配:从一个节点开始,递归地尝试为每个节点分配颜色。对于当前节点 v
,尝试从可用的颜色中选择一个颜色c
,然后检查是否满足以下条件:节点 v
的颜色没有与其相邻的节点重复。如果条件满足,就将节点 v
的颜色设置为c
,然后继续递归地处理下一个节点。如果没有找到有效的颜色,就回溯到前一个节点,并尝试其他颜色,直到找到解决方案或确定没有解决方案。回溯和搜索:使用回溯的方式来搜索可能的解决方案。从第一个节点开始,尝试为其分配颜色,并继续到下一个节点,直到所有节点都被着色。如果在某个节点无法找到合适的颜色,就回溯到上一个节点,尝试其他颜色。通过不断的回溯和尝试,直到找到一个有效的着色方案或确定没有解。 输出结果:一旦找到有效的着色方案,即所有节点都被分配了颜色,就输出这个着色方案,显示每个节点的颜色。 可行性检查:在颜色分配的过程中,需要检查每个节点的颜色是否与相邻节点的颜色冲突。这可以通过检查领接矩阵来实现,确保相邻节点没有相同的颜色。 用户输入:用户需要提供图的描述,包括节点数量、边的连接情况和可用的颜色数量。这些信息将用于构建图和设置问题的参数。
3.3、代码示例
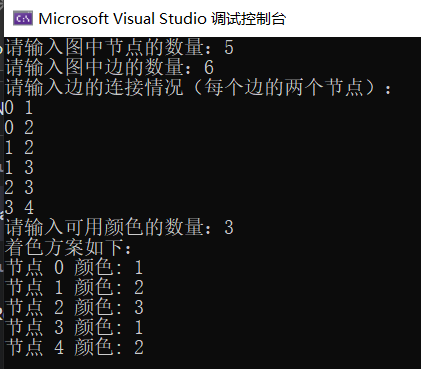
#include <iostream>#include <vector>using namespace std;const int MAX_NODES = 100;class Graph {public:int nodes; // 图中节点的数量int adjacency[MAX_NODES][MAX_NODES]; // 领接矩阵int colors[MAX_NODES]; // 存储节点的颜色Graph(int n) : nodes(n) {for (int i = 0; i < n; ++i) {colors[i] = 0; // 初始化所有节点的颜色为0,表示未着色for (int j = 0; j < n; ++j) {adjacency[i][j] = 0; // 初始化领接矩阵}}}// 添加边void addEdge(int u, int v) {adjacency[u][v] = 1;adjacency[v][u] = 1;}// 检查节点v是否可以被着色为cbool isSafe(int v, int c) {for (int i = 0; i < nodes; ++i) {if (adjacency[v][i] && colors[i] == c) {return false;}}return true;}// 递归函数,尝试着色图的节点bool graphColoringUtil(int m, int v) {if (v == nodes) {// 所有节点都被着色,解决方案找到return true;}for (int c = 1; c <= m; ++c) {if (isSafe(v, c)) {colors[v] = c;if (graphColoringUtil(m, v + 1)) {return true;}colors[v] = 0; // 回溯}}return false;}// 主函数,解决图着色问题bool graphColoring(int m) {if (!graphColoringUtil(m, 0)) {cout << "没有可行的着色方案" << endl;return false;}cout << "着色方案如下:" << endl;for (int i = 0; i < nodes; ++i) {cout << "节点 " << i << " 颜色: " << colors[i] << endl;}return true;}};int main() {int nodes, edges, colors;cout << "请输入图中节点的数量:";cin >> nodes;cout << "请输入图中边的数量:";cin >> edges;Graph graph(nodes);cout << "请输入边的连接情况(每个边的两个节点):" << endl;for (int i = 0; i < edges; ++i) {int u, v;cin >> u >> v;graph.addEdge(u, v);}cout << "请输入可用颜色的数量:";cin >> colors;graph.graphColoring(colors);return 0;}
四、任务分配问题
4.1、问题描述
4.2、解题思路
创建一个大小为n的方阵,用于存储已分配的工作,初始状态下全部置为0,表示未分配。 使用回溯法的分支限界算法来探索所有可能的工作分配方式,同时记录最小成本。 在每个决策节点,选择一个工作者并分配给他一个工作,计算当前的成本,并与当前最小成本进行比较。如果当前成本已经大于最小成本,则可以剪枝,不再继续探索这个分支。 逐步深入,直到找到一种工作分配方式,或者所有分支都被探索完。 最终,最小成本对应的工作分配方式即为问题的解。
4.3、代码示例
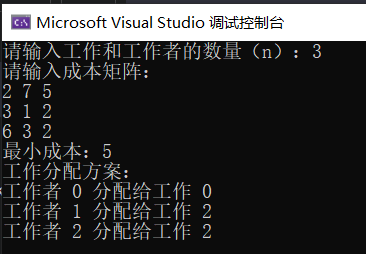
#include <iostream>#include <vector>#include <limits>using namespace std;const int MAX_N = 10; // 最大工作和工作者数量int n; // 工作和工作者的数量int cost[MAX_N][MAX_N]; // 成本矩阵int assignment[MAX_N]; // 存储分配方案bool assigned[MAX_N]; // 记录工作是否已经被分配int minCost = numeric_limits<int>::max(); // 最小成本void backtrack(int worker, int currentCost) {if (worker == n) {// 所有工作都已经分配完,更新最小成本minCost = min(minCost, currentCost);return;}for (int job = 0; job < n; ++job) {if (!assigned[job]) {// 如果工作未分配给工作者if (currentCost + cost[worker][job] < minCost) {// 可行性剪枝:只有当前成本小于最小成本才继续assigned[job] = true;assignment[worker] = job;backtrack(worker + 1, currentCost + cost[worker][job]);assigned[job] = false;}}}}int main() {cout << "请输入工作和工作者的数量(n):";cin >> n;cout << "请输入成本矩阵:" << endl;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {cin >> cost[i][j];}}// 初始化minCost = numeric_limits<int>::max();for (int i = 0; i < n; ++i) {assigned[i] = false;}backtrack(0, 0);cout << "最小成本:" << minCost << endl;cout << "工作分配方案:" << endl;for (int i = 0; i < n; ++i) {cout << "工作者 " << i << " 分配给工作 " << assignment[i] << endl;}return 0;}
五、集合覆盖问题
5.1、问题描述
5.2、解题思路
创建一个结构体 SubsetCoverProblem
来表示集合覆盖问题,包括全集大小n
和子集合的集合subsets
。创建一个函数 estimateCost
来估算节点的代价。代价的估算方法可以是未被覆盖的元素数量,即还需要被覆盖的元素个数。创建一个递归函数 branchAndBound
,该函数将采用深度优先搜索的方式来解决问题。它将接受当前问题的实例和已覆盖的元素集合作为参数。在 branchAndBound
函数中,首先检查是否已经覆盖了全集U
中的所有元素。如果是,表示找到了一个解,可以进行相应的处理(例如输出结果)。否则,计算当前节点的代价,然后选择一个子集进行扩展。选择哪个子集进行扩展可以采用贪心策略,即选择估算代价最小的子集。 递归地调用 branchAndBound
函数,传递新的问题实例和更新的已覆盖元素集合。重复步骤 4-6,直到找到一个解或确定无解为止。
5.3、代码示例
#include <iostream>#include <vector>#include <set>#include <algorithm>using namespace std;struct SubsetCoverProblem {int n; // 全集的大小vector<set<int>> subsets; // 子集合的集合};int estimateCost(const SubsetCoverProblem& problem, const set<int>& covered) {int remainingElements = problem.n - covered.size();return remainingElements;}void branchAndBound(SubsetCoverProblem problem, set<int> covered) {if (covered.size() == problem.n) {// 找到一个解,处理方式可以根据需求进行修改cout << "找到一个解:" << endl;for (const int& subsetIndex : covered) {cout << "选择子集 " << subsetIndex << endl;}return;}// 计算当前节点的代价int nodeCost = estimateCost(problem, covered);// 根据估算的代价排序子集合,选择代价最小的子集进行扩展vector<pair<int, int>> subsetCosts; // 子集索引及对应的代价for (int i = 0; i < problem.subsets.size(); ++i) {if (covered.find(i) == covered.end()) {set<int> newCovered = covered;newCovered.insert(i);int cost = estimateCost(problem, newCovered);subsetCosts.push_back({i, cost});}}sort(subsetCosts.begin(), subsetCosts.end(), [](const pair<int, int>& a, const pair<int, int>& b) {return a.second < b.second;});for (const auto& subsetCost : subsetCosts) {int subsetIndex = subsetCost.first;set<int> newCovered = covered;newCovered.insert(subsetIndex);branchAndBound(problem, newCovered);}}int main() {SubsetCoverProblem problem;// 初始化问题数据结构,包括全集大小 n 和子集合的集合 subsetsset<int> covered; // 初始覆盖集合为空branchAndBound(problem, covered);return 0;}
六、子集合问题
6.1、问题描述
6.2、解题思路
初始化一个队列,将初始节点(空子集和初始索引)放入队列中。 进入循环,直到队列为空: 弹出队列中的节点。 如果节点表示的子集和等于目标值,则找到了一个解,返回“是”。 如果节点表示的子集和小于目标值,可以选择添加下一个元素到子集中。创建两个子节点,一个包含添加元素,一个不包含添加元素。将这两个子节点加入队列。 如果节点表示的子集和大于目标值,表示这个节点无解,舍弃。 如果循环结束时仍然没有找到解,返回“否”。
6.3、代码示例
#include <iostream>#include <vector>#include <queue>using namespace std;// 定义节点结构struct Node {int sum; // 当前子集的和int index; // 当前考虑的数组元素索引vector<int> subset; // 当前子集Node(int s, int i, const vector<int>& ss) : sum(s), index(i), subset(ss) {}};bool subsetSumExists(const vector<int>& nums, int target) {queue<Node> q;vector<int> emptySubset;Node root(0, 0, emptySubset);q.push(root);while (!q.empty()) {Node node = q.front();q.pop();if (node.sum == target) {return true; // 找到一个子集的和等于目标值,返回“是”}if (node.index < nums.size()) {// 考虑下一个元素int nextIndex = node.index + 1;int nextSum = node.sum + nums[node.index];vector<int> nextSubset = node.subset;nextSubset.push_back(nums[node.index]);// 创建包含和不包含下一个元素的两个子节点Node includeNext(nextSum, nextIndex, nextSubset);Node excludeNext(node.sum, nextIndex, node.subset);// 添加子节点到队列q.push(includeNext);q.push(excludeNext);}}return false; // 没有找到解,返回“否”}int main() {vector<int> nums = {2, 4, 7, 10};int target = 13;if (subsetSumExists(nums, target)) {cout << "存在子集的和等于目标值" << endl;} else {cout << "不存在子集的和等于目标值" << endl;}return 0;}

七、最大团问题
7.1、问题描述
7.2、解题思路
初始化一个队列,将初始节点(空子集和初始索引)放入队列中。 进入循环,直到队列为空: 弹出队列中的节点。 如果节点表示的子集是一个团(其中的节点两两相连),则更新当前最大团的大小。 如果节点表示的子集不是团,可以选择添加下一个节点到子集中。创建两个子节点,一个包含添加节点,一个不包含添加节点。将这两个子节点加入队列。 如果循环结束时找到了一个更大的团,更新最大团的大小和团的节点列表。 如果队列为空或者不可能找到比当前最大团更大的团,返回最大团的大小和节点列表。
7.3、代码示例
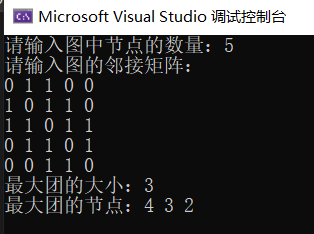
#include <iostream>#include <vector>#include <queue>using namespace std;const int MAX_NODES = 100;// 定义节点结构struct Node {vector<int> clique; // 当前子集中的节点vector<int> candidates; // 剩余可添加的候选节点Node(const vector<int>& c, const vector<int>& cand) : clique(c), candidates(cand) {}};bool isClique(const vector<vector<int>>& graph, const vector<int>& nodes) {for (int i = 0; i < nodes.size(); ++i) {for (int j = i + 1; j < nodes.size(); ++j) {if (graph[nodes[i]][nodes[j]] == 0) {return false; // 存在不相连的节点,不是团}}}return true; // 所有节点两两相连,是团}pair<int, vector<int>> findMaximumClique(const vector<vector<int>>& graph) {int n = graph.size();vector<int> initialClique;vector<int> initialCandidates;for (int i = 0; i < n; ++i) {initialCandidates.push_back(i);}Node initialNode(initialClique, initialCandidates);int maxSize = 0;vector<int> maxClique;queue<Node> q;q.push(initialNode);while (!q.empty()) {Node node = q.front();q.pop();if (node.clique.size() > maxSize) {maxSize = node.clique.size();maxClique = node.clique;}if (!node.candidates.empty()) {int nextNode = node.candidates.back();node.candidates.pop_back();vector<int> newClique = node.clique;newClique.push_back(nextNode);// 检查新子集是否仍然是团if (isClique(graph, newClique)) {vector<int> newCandidates;for (int candidate : node.candidates) {if (graph[nextNode][candidate] == 1) {newCandidates.push_back(candidate);}}Node newNode(newClique, newCandidates);q.push(newNode);}}}return make_pair(maxSize, maxClique);}int main() {int n;cout << "请输入图中节点的数量:";cin >> n;vector<vector<int>> graph(n, vector<int>(n, 0));cout << "请输入图的邻接矩阵:" << endl;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {cin >> graph[i][j];}}pair<int, vector<int>> result = findMaximumClique(graph);cout << "最大团的大小:" << result.first << endl;cout << "最大团的节点:";for (int node : result.second) {cout << node << " ";}cout << endl;return 0;}
八、排列问题
8.1、问题描述
输入:一个包含n个不同元素的集合。 输出:集合的所有不同排列。
8.2、解题思路
创建一个空数组 result
用于存储找到的排列。创建一个大小为n的布尔数组 used
,用于标记元素是否已经被使用。从第一个位置开始,逐个选择元素,并标记为已使用,然后递归地生成剩余元素的排列。 当排列长度达到n时,将该排列添加到 result
中。在递归过程中,可以应用一些限界条件来减少搜索空间,例如剪枝操作。
8.3、代码示例
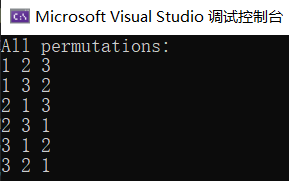
#include <iostream>#include <vector>using namespace std;void backtrack(vector<int>& nums, vector<vector<int>>& result, vector<int>& current, vector<bool>& used) {if (current.size() == nums.size()) {result.push_back(current);return;}for (int i = 0; i < nums.size(); ++i) {if (!used[i]) {current.push_back(nums[i]);used[i] = true;backtrack(nums, result, current, used);used[i] = false;current.pop_back();}}}vector<vector<int>> generatePermutations(vector<int>& nums) {vector<vector<int>> result;vector<int> current;vector<bool> used(nums.size(), false);backtrack(nums, result, current, used);return result;}int main() {vector<int> nums = {1, 2, 3};vector<vector<int>> permutations = generatePermutations(nums);cout << "All permutations:" << endl;for (const vector<int>& perm : permutations) {for (int num : perm) {cout << num << " ";}cout << endl;}return 0;}
九、时间表调度问题
9.1、问题描述
输入:一组待调度的活动或任务,每个活动具有开始时间、结束时间和相关的工作时间或成本。 输出:选择一组活动,使得它们不重叠并且总工作时间最小。
9.2、解题思路
创建一个数组或列表,用于存储已选择的活动。 对所有活动按照结束时间进行排序,以便优先选择结束时间早的活动。 从排好序的活动列表中选择第一个活动,将其加入已选择的列表。 遍历其余的活动,如果下一个活动与已选择的最后一个活动不重叠(即下一个活动的开始时间大于已选择活动的结束时间),则将其加入已选择的列表。 重复上述过程,直到不能再选择活动为止。
9.3、代码示例
#include <iostream>#include <vector>#include <algorithm>using namespace std;struct Activity {int start;int end;};bool compareActivities(const Activity& a, const Activity& b) {return a.end < b.end;}vector<Activity> scheduleActivities(vector<Activity>& activities) {vector<Activity> selectedActivities;// 对活动按结束时间进行排序sort(activities.begin(), activities.end(), compareActivities);// 添加第一个活动到已选择列表selectedActivities.push_back(activities[0]);// 从第二个活动开始遍历for (int i = 1; i < activities.size(); ++i) {// 如果下一个活动的开始时间大于等于已选择活动的结束时间,则选择该活动if (activities[i].start >= selectedActivities.back().end) {selectedActivities.push_back(activities[i]);}}return selectedActivities;}int main() {vector<Activity> activities = {{1, 3},{2, 5},{3, 9},{6, 8},{5, 7},{8, 10}};vector<Activity> selectedActivities = scheduleActivities(activities);cout << "Selected activities:" << endl;for (const Activity& activity : selectedActivities) {cout << "Start: " << activity.start << ", End: " << activity.end << endl;}return 0;}

十、机器调度问题
10.1、问题描述
输入:一组任务,每个任务具有执行时间和需要执行的机器数量。 输出:为每个任务分配机器,以最小化某个目标函数,如总执行时间。
10.2、解题思路
分支限界法思路:
创建一个任务列表,表示未分配的任务。 创建一个机器列表,表示空闲的机器。 创建一个调度方案,用于存储已分配的任务到机器的映射。 创建一个优先队列(或堆)来存储候选解决方案。 初始化调度方案为空,任务列表包含所有任务,机器列表包含所有机器。 将初始节点(无任务分配)加入到优先队列,并计算其目标函数值。 进入循环,直到优先队列为空或者找到最优解决方案为止: 从优先队列中取出一个节点,表示当前的调度方案。 如果调度方案中包含所有任务(所有任务都已分配机器),则计算其目标函数值并更新最优解决方案。 否则,对于每个未分配机器的任务,复制当前调度方案,将该任务分配到一个未分配机器上,并计算新调度方案的目标函数值。 将所有新生成的调度方案加入优先队列。
目标函数:
目标函数的选择取决于问题的具体要求。通常,目标函数可以是总执行时间、总成本、最大负载等。 在分支限界法中,通过选择适当的目标函数来实现问题的最小化或最大化。
10.3、代码示例
#include <iostream>#include <vector>#include <queue>#include <algorithm>using namespace std;struct Task {int executionTime;int requiredMachines;};struct Schedule {vector<int> taskAssignment;vector<int> machineLoad;int makespan; // 目标函数,总执行时间};bool operator>(const Schedule& a, const Schedule& b) {return a.makespan > b.makespan;}int findIdleMachine(const vector<int>& machineLoad) {int minLoad = machineLoad[0];int machineIndex = 0;for (int i = 1; i < machineLoad.size(); ++i) {if (machineLoad[i] < minLoad) {minLoad = machineLoad[i];machineIndex = i;}}return machineIndex;}Schedule branchAndBound(const vector<Task>& tasks, int numMachines) {priority_queue<Schedule, vector<Schedule>, greater<Schedule>> pq;Schedule initialSchedule;initialSchedule.taskAssignment.resize(tasks.size(), -1);initialSchedule.machineLoad.resize(numMachines, 0);initialSchedule.makespan = 0;pq.push(initialSchedule);while (!pq.empty()) {Schedule currentSchedule = pq.top();pq.pop();int taskIndex = -1;for (int i = 0; i < tasks.size(); ++i) {if (currentSchedule.taskAssignment[i] == -1) {taskIndex = i;break;}}if (taskIndex == -1) {// 所有任务都已分配,更新makespanint currentMakespan = *max_element(currentSchedule.machineLoad.begin(), currentSchedule.machineLoad.end());if (currentMakespan < currentSchedule.makespan || currentSchedule.makespan == 0) {currentSchedule.makespan = currentMakespan;}} else {for (int machine = 0; machine < numMachines; ++machine) {Schedule newSchedule = currentSchedule;newSchedule.taskAssignment[taskIndex] = machine;newSchedule.machineLoad[machine] += tasks[taskIndex].executionTime;pq.push(newSchedule);}}}return pq.top();}int main() {vector<Task> tasks = {{2, 2}, {3, 1}, {1, 3}};int numMachines = 2;Schedule optimalSchedule = branchAndBound(tasks, numMachines);cout << "Optimal Schedule:" << endl;for (int i = 0; i < tasks.size(); ++i) {cout << "Task " << i << " assigned to Machine " << optimalSchedule.taskAssignment[i] << endl;}cout << "Total Makespan: " << optimalSchedule.makespan << endl;return 0;}
注:以上代码仅供参考!
这些就是我这一周对经典算法的总结了,希望对大家有帮助。更多的内容请关注公众号,获取其它资料~
文章转载自阿Q正砖,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






