经典算法系列之贪心算法

阿Q正砖 2023-09-07

175

大家好，我是阿Q。

今天该到贪心算法了，改变策略，先说它的基础信息。

基础概念：在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解。

基本思路：

1. 建立数学模型来描述问题。

2. 把求解的问题分成若干个子问题。

3. 对每一子问题求解，得到子问题的局部最优解。

4. 把子问题的解局部最优解合成原来解问题的一个解。

实现框架：

从问题的某一初始解出发；
while （能朝给定总目标前进一步）
{ 
    利用可行的决策，求出可行解的一个解元素；
}
由所有解元素组合成问题的一个可行解；

有了它这些基础信息做开始，我相信你一定对后边的内容感兴趣~

刷题网站相关题目：

455. 分发饼干
376. 摆动序列
53. 最大子数组和
122. 买卖股票的最佳时机 II
55. 跳跃游戏
1005. K 次取反后最大化的数组和
134. 加油站
135. 分发糖果
860. 柠檬水找零
406. 根据身高重建队列
452. 用最少数量的箭引爆气球
435. 无重叠区间

一、最小生成树问题

最小生成树问题是一个经典的组合优化问题，主要用于在一个连通的带权无向图中找到一个树，使得这棵树包含了图中的所有节点，且树上边的权重之和最小。

1.1、问题描述

给定一个带权无向图 G，包含 n 个节点和 m 条边，每条边都有一个权重。您需要找到一个树 T，使得它包含 G 中的所有节点，且树上边的权重之和最小。

1.2、解题思路

Prim算法是一种贪心算法，用于解决最小生成树问题。它从一个起始节点开始，逐步扩展树的规模，每次选择与当前树相连的边中权重最小的边，直到树包含了所有节点为止。下面是Prim算法的详细步骤：

选择一个起始节点作为树的根节点，将其标记为已访问。
初始化一个空的集合，用于存储已选择的边，初始时为空。
重复以下步骤，直到树包含了所有节点：a. 对于树中的每个节点，找到与其相连的边中权重最小的边，且该边连接的节点未被访问。b. 将找到的最小权重边加入已选择的边集合，并将该边连接的节点标记为已访问。
当树包含了所有节点时，Prim算法结束，已选择的边集合即为最小生成树的边集合。

1.3、代码示例


#include <iostream>
#include <vector>
#include <queue>
#include <climits>


using namespace std;


const int INF = INT_MAX; // 无穷大


// 定义带权无向图的邻接矩阵表示
vector<vector<int>> graph;


int prim(int n) {
    vector<int> dist(n, INF);    // 存储节点到最小生成树的最短距离
    vector<bool> inMST(n, false); // 标记节点是否已包含在最小生成树中
    int minCost = 0;             // 最小生成树的总权重


    // 从第一个节点开始构建最小生成树
    dist[0] = 0;


    for (int i = 0; i < n; ++i) {
        int u = -1;


        // 选择距离最小生成树最近的节点
        for (int j = 0; j < n; ++j) {
            if (!inMST[j] && (u == -1 || dist[j] < dist[u])) {
                u = j;
            }
        }


        if (dist[u] == INF) {
            // 无法找到新的节点，说明图不连通
            return -1;
        }


        inMST[u] = true;
        minCost += dist[u];


        // 更新与新节点相邻的节点的距离
        for (int v = 0; v < n; ++v) {
            if (!inMST[v] && graph[u][v] < dist[v]) {
                dist[v] = graph[u][v];
            }
        }
    }


    return minCost;
}


int main() {
    int n, m; // 节点数和边数
    cin >> n >> m;


    // 初始化图的邻接矩阵
    graph.assign(n, vector<int>(n, INF));


    for (int i = 0; i < m; ++i) {
        int u, v, w; // 边的两个节点和权重
        cin >> u >> v >> w;
        // 无向图，更新两个方向的边权
        graph[u][v] = graph[v][u] = w;
    }


    int minCost = prim(n);


    if (minCost == -1) {
        cout << "图不连通，无法构建最小生成树" << endl;
    } else {
        cout << "最小生成树的总权重为：" << minCost << endl;
    }


    return 0;
}

代码中使用邻接矩阵表示图，根据Prim算法的步骤逐步构建最小生成树。

结果输出：

二、单源最短路径问题

单源最短路径问题是一个经典的图论问题，目标是找到从一个源节点到所有其他节点的最短路径。通常使用贪心算法中的Dijkstra算法或动态规划中的Bellman-Ford算法来解决这个问题。

2.1、问题描述

给定一个带权重的有向图，以及一个起始节点，找到从起始节点到图中所有其他节点的最短路径，并计算出每条最短路径的长度。

2.2、解题思路

初始化：创建一个空的集合 visited
用于存储已经找到最短路径的节点，创建一个数组 distance
用于存储从起始节点到每个节点的当前最短路径长度，将所有节点的距离初始化为无穷大，将起始节点的距离初始化为0。
选择当前距离起始节点最近的未访问节点，将其加入 visited
集合中。
对于选定的节点，遍历其所有邻居节点，计算从起始节点经过该节点到达邻居节点的距离，如果该距离小于已知的最短路径长度，则更新该节点的最短路径长度。
重复步骤2和步骤3，直到所有节点都被加入 visited
集合。
最终，distance
数组中存储的就是从起始节点到每个节点的最短路径长度。

2.3、代码示例


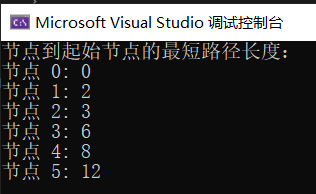
#include <iostream>
#include <vector>
#include <limits>


using namespace std;


const int INF = numeric_limits<int>::max();


int minDistance(const vector<int>& distance, const vector<bool>& visited) {
    int minDist = INF;
    int minIndex = -1;


    for (int i = 0; i < distance.size(); ++i) {
        if (!visited[i] && distance[i] < minDist) {
            minDist = distance[i];
            minIndex = i;
        }
    }


    return minIndex;
}


void dijkstra(const vector<vector<int>>& graph, int start) {
    int n = graph.size();
    vector<int> distance(n, INF);
    vector<bool> visited(n, false);


    distance[start] = 0;


    for (int i = 0; i < n - 1; ++i) {
        int u = minDistance(distance, visited);
        visited[u] = true;


        for (int v = 0; v < n; ++v) {
            if (!visited[v] && graph[u][v] && distance[u] != INF &&
                distance[u] + graph[u][v] < distance[v]) {
                distance[v] = distance[u] + graph[u][v];
            }
        }
    }


    // 输出最短路径长度
    cout << "节点到起始节点的最短路径长度：" << endl;
    for (int i = 0; i < n; ++i) {
        cout << "节点 " << i << ": " << distance[i] << endl;
    }
}


int main() {
    // 定义图的邻接矩阵表示
    vector<vector<int>> graph = {
        {0, 2, 4, 0, 0, 0},
        {0, 0, 1, 7, 0, 0},
        {0, 0, 0, 3, 5, 0},
        {0, 0, 0, 0, 0, 6},
        {0, 0, 0, 0, 0, 0},
        {0, 0, 0, 0, 0, 0}
    };


    int startNode = 0;  // 起始节点


    dijkstra(graph, startNode);


    return 0;
}

结果输出：

三、哈夫曼编码

哈夫曼编码是一种用于数据压缩的编码方法，通过根据字符出现的频率来生成不等长的编码，以实现对数据的高效压缩。在哈夫曼编码中，出现频率高的字符通常具有较短的编码，而出现频率低的字符具有较长的编码。

3.1、问题描述

给定一组字符及其对应的频率，任务是构建一个哈夫曼树，该树的叶节点代表字符，树的每个内部节点都有两个子节点，分别是其下层节点频率之和的字符。最终，生成每个字符的哈夫曼编码。

3.2、解题思路

创建一个包含每个字符及其频率的节点的优先队列（最小堆）。优先队列将根据节点的频率自动排序，因此频率最低的节点将始终位于队列的顶部。
重复以下步骤，直到只剩下一个节点为止：
a. 从优先队列中选择两个频率最低的节点，将它们作为左右子节点创建一个新节点，该节点的频率等于这两个节点的频率之和。
b. 将新节点插入优先队列。
最终，优先队列中将只剩下一个节点，即哈夫曼树的根节点。
遍历哈夫曼树，生成每个字符的编码。从根节点开始，向左走表示0，向右走表示1。每当到达叶节点时，记录下路径，即字符的编码。

3.3、代码示例


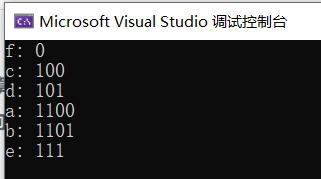
#include <iostream>
#include <queue>
#include <vector>
#include <string>
#include <unordered_map>


using namespace std;


// 定义哈夫曼树节点
struct HuffmanNode {
    char data;
    int freq;
    HuffmanNode* left;
    HuffmanNode* right;


    HuffmanNode(char d, int f) : data(d), freq(f), left(nullptr), right(nullptr) {}
};


// 自定义优先队列比较器
struct CompareNodes {
    bool operator()(HuffmanNode* a, HuffmanNode* b) {
        return a->freq > b->freq;
    }
};


// 生成哈夫曼树
HuffmanNode* buildHuffmanTree(const unordered_map<char, int>& freqMap) {
    priority_queue<HuffmanNode*, vector<HuffmanNode*>, CompareNodes> minHeap;


    // 创建叶节点并将其插入优先队列
    for (const auto& pair : freqMap) {
        HuffmanNode* node = new HuffmanNode(pair.first, pair.second);
        minHeap.push(node);
    }


    // 构建哈夫曼树
    while (minHeap.size() > 1) {
        HuffmanNode* left = minHeap.top();
        minHeap.pop();
        HuffmanNode* right = minHeap.top();
        minHeap.pop();


        // 创建新节点，频率为左右子节点频率之和
        HuffmanNode* newNode = new HuffmanNode('\0', left->freq + right->freq);
        newNode->left = left;
        newNode->right = right;
        minHeap.push(newNode);
    }


    return minHeap.top(); // 返回哈夫曼树的根节点
}


// 生成字符的哈夫曼编码
void generateHuffmanCodes(HuffmanNode* root, const string& code, unordered_map<char, string>& huffmanCodes) {
    if (root == nullptr) {
        return;
    }


    if (root->data != '\0') {
        huffmanCodes[root->data] = code;
    }


    generateHuffmanCodes(root->left, code + "0", huffmanCodes);
    generateHuffmanCodes(root->right, code + "1", huffmanCodes);
}


int main() {
    unordered_map<char, int> freqMap = {
        {'a', 5},
        {'b', 9},
        {'c', 12},
        {'d', 13},
        {'e', 16},
        {'f', 45}
    };


    HuffmanNode* root = buildHuffmanTree(freqMap);


    unordered_map<char, string> huffmanCodes;
    generateHuffmanCodes(root, "", huffmanCodes);


    // 输出字符及其哈夫曼编码
    for (const auto& pair : huffmanCodes) {
        cout << pair.first << ": " << pair.second << endl;
    }


    return 0;
}

结果输出：

四、任务调度问题

4.1、问题描述

任务调度问题是一个经典的计算机科学问题。给定一组任务，每个任务都有一个执行时间和一个截止时间。任务必须在截止时间之前完成。如果任务没有在截止时间之前完成，将会产生惩罚。任务调度问题的目标是找到一个调度方案，以最小化总体惩罚。

4.2、解题思路

首先，将所有任务按照截止时间的先后顺序进行排序。这将使得我们在考虑任务时可以按照截止时间的先后顺序进行处理。
创建一个数组或列表，用于存储已安排的任务。
从排序后的任务列表中选择第一个任务，并将其安排在数组中。
遍历排序后的任务列表，对于每个任务，检查是否可以安排在当前时间之前（即在其截止时间之前）。如果可以安排，则将其加入数组中，并更新当前时间。
继续遍历任务列表，重复步骤4，直到所有任务都被安排或者无法再安排任务为止。
最终，数组中存储的任务顺序即为最优的任务调度方案，总体惩罚也可以计算出来。

4.3、代码示例


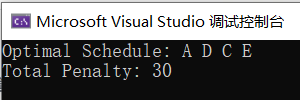
#include <iostream>
#include <vector>
#include <algorithm>


using namespace std;


// 定义任务结构体
struct Task {
    char id;          // 任务标识
    int deadline;     // 截止时间
    int execution;    // 执行时间
};


// 比较函数，用于排序任务
bool compareTasks(const Task& task1, const Task& task2) {
    return task1.deadline < task2.deadline;
}


// 贪心算法解决任务调度问题
void scheduleTasks(vector<Task>& tasks) {
    // 对任务按照截止时间进行排序
    sort(tasks.begin(), tasks.end(), compareTasks);


    int n = tasks.size();  // 任务数量
    vector<char> schedule; // 存储已安排的任务
    int totalPenalty = 0;  // 总体惩罚
    int currentTime = 0;  // 当前时间


    for (int i = 0; i < n; i++) {
        Task& currentTask = tasks[i];


        // 如果当前任务的截止时间小于等于当前时间，可以安排
        if (currentTask.deadline <= currentTime) {
            schedule.push_back(currentTask.id);
            totalPenalty += currentTime - currentTask.deadline;
        }


        currentTime += currentTask.execution;
    }


    // 输出任务调度顺序和总体惩罚
    cout << "Optimal Schedule: ";
    for (char id : schedule) {
        cout << id << " ";
    }
    cout << endl;
    cout << "Total Penalty: " << totalPenalty << endl;
}


int main() {
    vector<Task> tasks = {
        {'A', 2, 5},
        {'B', 1, 3},
        {'C', 4, 2},
        {'D', 2, 7},
        {'E', 5, 4}
    };


    scheduleTasks(tasks);


    return 0;
}

结果输出：

五、零钱找零问题

5.1、问题描述

零钱找零问题是一个常见的问题，也称为硬币找零问题。给定一定面额的硬币，以及一个需要找零的金额，问题是如何用最少数量的硬币来拼凑出这个金额。每种面额的硬币数量是无限的。

5.2、解题思路

首先，准备好一组硬币的面额，按面额从大到小排序。
初始化一个变量 change
用于记录剩余需要找零的金额，初始值为需要找零的总金额。
初始化一个空的数组或列表 result
，用于存储拼凑出的硬币。
从面额最大的硬币开始，尽可能多地使用该硬币，直到无法再使用为止。每次使用一枚硬币，将其加入 result
中，并更新 change
的值为 change - 硬币面额
。
继续尝试下一种面额的硬币，重复步骤4，直到 change
的值变为0。
返回 result
，即拼凑出的硬币组合。

5.3、代码示例


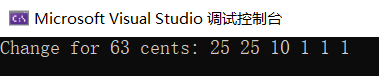
#include <iostream>
#include <vector>


using namespace std;


// 定义硬币面额
vector<int> coins = {25, 10, 5, 1};


// 贪心算法解决零钱找零问题
vector<int> makeChange(int amount) {
    vector<int> result;
    int change = amount;


    for (int i = 0; i < coins.size(); i++) {
        while (change >= coins[i]) {
            result.push_back(coins[i]);
            change -= coins[i];
        }
    }


    return result;
}


int main() {
    int amount = 63;
    vector<int> change = makeChange(amount);


    cout << "Change for " << amount << " cents: ";
    for (int coin : change) {
        cout << coin << " ";
    }
    cout << endl;


    return 0;
}

根据预定义的硬币面额，它找到了一种最优的拼凑方案，以最小数量的硬币来拼凑出指定的金额。你可以根据需要修改硬币面额和需要找零的金额来进行测试。

结果输出：

六、分数背包问题

6.1、问题描述

分数背包问题（Fractional Knapsack Problem）是一个经典的优化问题。在该问题中，给定一组物品，每个物品有一个重量和一个价值，以及一个背包容量。目标是选择一些物品放入背包中，使得这些物品的总重量不超过背包容量，同时总价值最大。与0-1背包问题不同，分数背包问题允许部分物品被放入背包中，而不需要整数数量的物品。

6.2、解题思路

贪心算法的思路是根据每个物品的单位价值（即每单位重量对应的价值）进行排序，然后依次选择单位价值最高的物品放入背包中，直到背包容量用完为止。

以下是解决问题的一般步骤：

对所有物品按照单位价值（价值除以重量）从大到小进行排序。
初始化一个变量 totalValue
用于记录已放入背包的物品的总价值，初始值为0。
初始化一个变量 remainingCapacity
用于记录背包的剩余容量，初始值为背包的总容量。
从排序后的物品列表中，按照单位价值高低依次选择物品放入背包，直到背包容量用完为止。每次选择一个物品后，将其单位价值最大部分放入背包，并更新 totalValue
和 remainingCapacity
。
返回 totalValue
作为最优解。

6.3、代码示例


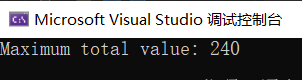
#include <iostream>
#include <vector>
#include <algorithm>


using namespace std;


// 定义物品结构体，包含重量和价值
struct Item {
    int weight;
    int value;
};


// 自定义比较函数，用于按单位价值从大到小排序
bool compareItems(Item item1, Item item2) {
    double ratio1 = static_cast<double>(item1.value)  item1.weight;
    double ratio2 = static_cast<double>(item2.value)  item2.weight;
    return ratio1 > ratio2;
}


// 贪心算法解决分数背包问题
double fractionalKnapsack(vector<Item>& items, int capacity) {
    // 按单位价值排序
    sort(items.begin(), items.end(), compareItems);


    double totalValue = 0.0;
    int remainingCapacity = capacity;


    for (const Item& item : items) {
        if (remainingCapacity >= item.weight) {
            // 放入整个物品
            totalValue += item.value;
            remainingCapacity -= item.weight;
        } else {
            // 放入部分物品
            totalValue += static_cast<double>(remainingCapacity) * (static_cast<double>(item.value)  item.weight);
            break;
        }
    }


    return totalValue;
}


int main() {
    vector<Item> items = {{10, 60}, {20, 100}, {30, 120}};
    int capacity = 50;


    double maxTotalValue = fractionalKnapsack(items, capacity);


    cout << "Maximum total value: " << maxTotalValue << endl;


    return 0;
}

根据预定义的物品列表和背包容量，它找到了一种最优的放置方案，以最大化总价值。

结果输出：

七、作业调度问题

7.1、问题描述

作业调度问题（Job Scheduling Problem）是一个优化问题，通常出现在作业调度、任务调度等领域。在该问题中，有一批作业（或任务）需要在一台机器上依次执行，每个作业都有一个预计的执行时间和一个截止时间。要求找到一种作业的执行顺序，以最大程度地满足作业的截止时间，即最小化延迟时间。

7.2、解题思路

对所有作业按照截止时间从小到大进行排序。
初始化一个变量 currentTime
用于记录当前时间，初始值为0。
初始化一个变量 totalDelay
用于记录总延迟时间，初始值为0。
遍历排序后的作业列表，对于每个作业，计算其延迟时间（即完成时间减去截止时间），并将延迟时间累加到 totalDelay
中。同时更新 currentTime
为作业的完成时间。
返回 totalDelay
作为最优解。

7.3、代码示例


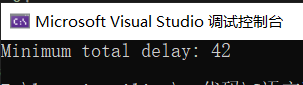
#include <iostream>
#include <vector>
#include <algorithm>


using namespace std;


// 定义作业结构体，包含截止时间和执行时间
struct Job {
    int deadline;
    int executionTime;
};


// 自定义比较函数，用于按截止时间从小到大排序
bool compareJobs(Job job1, Job job2) {
    return job1.deadline < job2.deadline;
}


// 贪心算法解决作业调度问题
int jobScheduling(vector<Job>& jobs) {
    // 按截止时间排序
    sort(jobs.begin(), jobs.end(), compareJobs);


    int currentTime = 0;
    int totalDelay = 0;


    for (const Job& job : jobs) {
        // 计算延迟时间
        int delay = max(0, currentTime + job.executionTime - job.deadline);
        totalDelay += delay;
        currentTime += job.executionTime;
    }


    return totalDelay;
}


int main() {
    vector<Job> jobs = {{2, 5}, {1, 2}, {2, 10}, {3, 7}};


    int minTotalDelay = jobScheduling(jobs);


    cout << "Minimum total delay: " << minTotalDelay << endl;


    return 0;
}

结果输出：

注：以上代码仅供参考！！！

vector 贪心算法最短路径算法背包问题 vector初始化

文章转载自阿Q正砖，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

经典算法系列之贪心算法

一、最小生成树问题

1.1、问题描述

1.2、解题思路

1.3、代码示例

二、单源最短路径问题

2.1、问题描述

2.2、解题思路

2.3、代码示例

三、哈夫曼编码

3.1、问题描述

3.2、解题思路

3.3、代码示例

四、任务调度问题

4.1、问题描述

4.2、解题思路

4.3、代码示例

五、零钱找零问题

5.1、问题描述

5.2、解题思路

5.3、代码示例

六、分数背包问题

6.1、问题描述

6.2、解题思路

6.3、代码示例

七、作业调度问题

7.1、问题描述

7.2、解题思路

7.3、代码示例

评论