经典算法系列之动态规划

阿Q正砖 2023-09-06

157

大家好，我是阿Q。

今天这节就把动态规划的一些经典题目进行一个详细的总结，不论你是在校生还是正在秋招的同学，我相信这个系列一定会对你有非常好的帮助。

通过通俗易懂的文字以及非常详细的代码，一定会让你对动态规划有更深层次的理解。

同样的，比较详细的基础概念直接点这篇：校招生必知必会的几种经典算法

这是今天要输出的总结目录：

一、背包问题

1.1、01背包问题

1.1.1、问题描述

01背包问题是一个经典的组合优化问题。给定一组物品，每个物品有一个重量和一个价值，以及一个固定容量的背包。目标是找到一种装载方式，使得背包中物品的总价值最大化，同时不超过背包的容量。

具体来说，问题可以描述如下：

有 n
个物品，每个物品有一个重量 weight[i]
和一个价值 value[i]
，其中 i
表示物品的索引，取值范围为 0
到 n-1
。
有一个背包，最大容量为 W
。
你需要选择一些物品放入背包中，使得这些物品的总重量不超过背包容量 W
，同时总价值最大。

1.1.2、解题思路

动态规划的思路如下：

创建一个二维数组 dp
，其中 dp[i][w]
表示在考虑前 i
个物品，且背包容量为 w
时的最大总价值。
初始化动态规划数组 dp
，将第一行和第一列都设置为0，因为没有物品或背包容量为0时，最大总价值都是0。
使用递推公式更新 dp
数组：


dp[i][w] = max(dp[i-1][w], dp[i-1][w - weight[i]] + value[i])

最终，dp[n][W]
就是问题的答案，其中 n
表示物品的数量，W
表示背包的容量。

1.1.3、代码示例


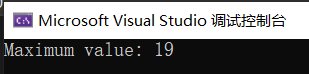
#include <iostream>
#include <vector>


int knapsack(int W, const std::vector<int>& weight, const std::vector<int>& value) {
    int n = weight.size();
    std::vector<std::vector<int>> dp(n + 1, std::vector<int>(W + 1, 0));


    for (int i = 1; i <= n; ++i) {
        for (int w = 1; w <= W; ++w) {
            if (weight[i - 1] <= w) {
                dp[i][w] = std::max(dp[i - 1][w], dp[i - 1][w - weight[i - 1]] + value[i - 1]);
            } else {
                dp[i][w] = dp[i - 1][w];
            }
        }
    }


    return dp[n][W];
}


int main() {
    std::vector<int> weight = {2, 2, 3, 4, 5};
    std::vector<int> value = {3, 4, 5, 8, 10};
    int W = 10;


    int result = knapsack(W, weight, value);
    std::cout << "Maximum value: " << result << std::endl;


    return 0;
}

输入参数包括背包容量 W
，物品的重量和价值分别存储在 weight
和 value
向量中。函数返回问题的最优解，即背包能容纳的最大总价值。

结果输出：

1.2、完全背包问题

1.2.1、问题描述

完全背包问题是背包问题的一种变体，与01背包问题不同，完全背包问题中每个物品可以无限次地选择放入背包中。给定一组物品，每个物品有一个重量和一个价值，以及一个固定容量的背包，目标是找到一种装载方式，使得背包中物品的总价值最大化，同时不超过背包的容量。

具体来说，问题可以描述如下：

有 n
个物品，每个物品有一个重量 weight[i]
和一个价值 value[i]
，其中 i
表示物品的索引，取值范围为 0
到 n-1
。
有一个背包，最大容量为 W
。
每个物品可以选择无限次放入背包中。
你需要选择一些物品放入背包中，使得这些物品的总重量不超过背包容量 W
，同时总价值最大。

1.2.2、解题思路

动态规划的思路如下：

创建一个一维数组 dp
，其中 dp[w]
表示背包容量为 w
时的最大总价值。
初始化动态规划数组 dp
，将所有元素初始化为0。
使用递推公式更新 dp
数组：


dp[w] = max(dp[w], dp[w - weight[i]] + value[i])

最终，dp[W]
就是问题的答案，其中 W
表示背包的容量。

1.2.3、代码示例


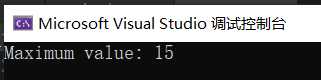
#include <iostream>
#include <vector>


int knapsack(int W, const std::vector<int>& weight, const std::vector<int>& value) {
    int n = weight.size();
    std::vector<int> dp(W + 1, 0);


    for (int w = 1; w <= W; ++w) {
        for (int i = 0; i < n; ++i) {
            if (weight[i] <= w) {
                dp[w] = std::max(dp[w], dp[w - weight[i]] + value[i]);
            }
        }
    }


    return dp[W];
}


int main() {
    std::vector<int> weight = {2, 3, 4, 5};
    std::vector<int> value = {3, 4, 5, 6};
    int W = 10;


    int result = knapsack(W, weight, value);
    std::cout << "Maximum value: " << result << std::endl;


    return 0;
}

输入参数包括背包容量 W
，物品的重量和价值分别存储在 weight
和 value
向量中。函数返回问题的最优解，即背包能容纳的最大总价值。

结果输出：

1.3、多重背包问题

1.3.1、问题描述

多重背包问题是背包问题的一种扩展，与01背包问题和完全背包问题不同，每个物品有一个有限的数量，需要考虑选择多个相同物品放入背包中。给定一组物品，每个物品有一个重量、价值和可用数量，以及一个固定容量的背包，目标是找到一种装载方式，使得背包中物品的总价值最大化，同时不超过背包的容量。

具体来说，问题可以描述如下：

有 n
个物品，每个物品有一个重量 weight[i]
、价值 value[i]
和可用数量 quantity[i]
，其中 i
表示物品的索引，取值范围为 0
到 n-1
。
有一个背包，最大容量为 W
。
每个物品可以选择 0 到 quantity[i]
个放入背包中。
你需要选择一些物品放入背包中，使得这些物品的总重量不超过背包容量 W
，同时总价值最大。

1.3.2、解题思路

要解决多重背包问题，同样使用动态规划方法，但与01背包和完全背包问题不同，需要考虑每个物品的可用数量。

动态规划的思路如下：

创建一个二维数组 dp
，其中 dp[i][w]
表示前 i
个物品放入容量为 w
的背包中的最大总价值。
初始化动态规划数组 dp
，将所有元素初始化为0。
使用递推公式更新 dp
数组：

dp[i][w] = max(dp[i-1][w - k * weight[i]] + k * value[i] | 0 <= k <= quantity[i])

最终，dp[n][W]
就是问题的答案，其中 n
表示物品的数量，W
表示背包的容量。

1.3.3、代码示例


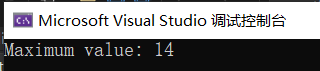
#include <iostream>
#include <vector>


int knapsack(int W, const std::vector<int>& weight, const std::vector<int>& value, const std::vector<int>& quantity) {
    int n = weight.size();
    std::vector<std::vector<int>> dp(n + 1, std::vector<int>(W + 1, 0));


    for (int i = 1; i <= n; ++i) {
        for (int w = 1; w <= W; ++w) {
            for (int k = 0; k <= quantity[i - 1]; ++k) {
                if (k * weight[i - 1] <= w) {
                    dp[i][w] = std::max(dp[i][w], dp[i - 1][w - k * weight[i - 1]] + k * value[i - 1]);
                }
            }
        }
    }


    return dp[n][W];
}


int main() {
    std::vector<int> weight = {2, 3, 4, 5};
    std::vector<int> value = {3, 4, 5, 6};
    std::vector<int> quantity = {2, 3, 1, 4};
    int W = 10;


    int result = knapsack(W, weight, value, quantity);
    std::cout << "Maximum value: " << result << std::endl;


    return 0;
}

输入参数包括背包容量 W
，每个物品的重量、价值和可用数量分别存储在 weight
、value
和 quantity
向量中。函数返回问题的最优解，即背包能容纳的最大总价值。

结果输出：

二、最长公共子序列问题

LeetCode：LCR 095. 最长公共子序列

2.1、问题描述

给定两个字符串s1和s2，找出它们的最长公共子序列的长度。

2.2、解题思路

使用一个二维数组dp，其中dp[i][j]表示s1的前i个字符和s2的前j个字符的最长公共子序列的长度。

以下是解决该问题的一般步骤：

创建一个二维数组dp，其大小为(s1.length() + 1) x (s2.length() + 1)。初始化dp[i][0]和dp[0][j]为0，因为一个空字符串和任何字符串的最长公共子序列长度都是0。
使用双重循环遍历s1和s2的每个字符，如果当前字符相等（s1[i-1] == s2[j-1]），则dp[i][j] = dp[i-1][j-1] + 1，表示在最长公共子序列的基础上加上当前相等的字符。
如果当前字符不相等，取dp[i-1][j]和dp[i][j-1]的较大值，表示选择不同的字符来构建最长公共子序列。
最终，dp[s1.length()][s2.length()]即为s1和s2的最长公共子序列的长度。

2.3、代码示例


#include <iostream>
#include <vector>
#include <string>


using namespace std;


int longestCommonSubsequence(string s1, string s2) {
    int m = s1.length();
    int n = s2.length();
    
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
    
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (s1[i - 1] == s2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    
    return dp[m][n];
}


int main() {
    string s1 = "abcde";
    string s2 = "ace";
    
    int result = longestCommonSubsequence(s1, s2);
    
    cout << "Length of Longest Common Subsequence: " << result << endl;
    
    return 0;
}

结果输出：

三、最短路径问题

最短路径问题是在图论中非常经典的问题，其目标是在一个加权有向图或无向图中找到两个节点之间的最短路径，也就是路径上的边权重之和最小的路径。这个问题在实际应用中有很多场景，如导航系统中的最短路径规划、网络路由中的数据包传输等。

3.1、问题描述

给定一个带权重的有向图或无向图，以及两个节点S和D，找到从节点S到节点D的最短路径，使得路径上的边的权重之和最小。

3.2、解题思路

最短路径问题可以通过多种算法来解决，其中最著名的是Dijkstra算法和Bellman-Ford算法。这里我们介绍Dijkstra算法，它适用于带非负权重的图，且图中不存在负权重的回路。

Dijkstra算法的基本思路如下：

创建一个距离数组dist[]，用于存储从起始节点S到每个节点的最短距离。初始时，将dist[S]设置为0，其他节点的距离初始化为无穷大。
创建一个集合（可以用优先队列实现）Q，用于存储待处理的节点。
将起始节点S加入集合Q中。
重复以下步骤，直到集合Q为空：a. 从集合Q中选择距离dist最小的节点u。b. 对于节点u的每个邻接节点v，计算从S经过u到v的距离d。如果d小于dist[v]，则更新dist[v]为d。c. 将节点u从集合Q中移除。
最终，dist[D]中存储的就是从S到D的最短路径长度。

3.3、代码示例


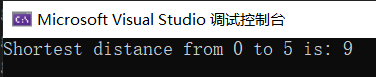
#include <iostream>
#include <vector>
#include <queue>
#include <climits>


using namespace std;


struct Edge {
    int to;
    int weight;
    Edge(int t, int w) : to(t), weight(w) {}
};


vector<vector<Edge>> graph; // 图的邻接表表示
vector<int> dist; // 存储最短距离的数组


void dijkstra(int start) {
    int n = graph.size();
    dist.assign(n, INT_MAX);
    dist[start] = 0;
    
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
    pq.push({0, start});
    
    while (!pq.empty()) {
        int u = pq.top().second;
        int d = pq.top().first;
        pq.pop();
        
        if (d > dist[u]) continue; // 跳过已经处理过的节点
        
        for (const Edge& edge : graph[u]) {
            int v = edge.to;
            int w = edge.weight;
            
            if (dist[u] + w < dist[v]) {
                dist[v] = dist[u] + w;
                pq.push({dist[v], v});
            }
        }
    }
}


int main() {
    // 构建图的邻接表，这里需要根据具体图的情况构建
    // graph[u] 表示节点u的邻接边列表，每个Edge包含目标节点to和权重weight
    int n = 6; // 节点个数
    graph.resize(n);
    
    // 添加边
    graph[0].emplace_back(1, 2);
    graph[0].emplace_back(2, 4);
    graph[1].emplace_back(2, 1);
    graph[1].emplace_back(3, 7);
    graph[2].emplace_back(3, 3);
    graph[2].emplace_back(4, 5);
    graph[3].emplace_back(4, 2);
    graph[4].emplace_back(5, 1);
    
    int start = 0; // 起始节点
    int end = 5;   // 目标节点
    
    dijkstra(start);
    
    if (dist[end] != INT_MAX) {
        cout << "Shortest distance from " << start << " to " << end << " is: " << dist[end] << endl;
    } else {
        cout << "There is no path from " << start << " to " << end << endl;
    }
    
    return 0;
}

注意：这只是一个简单示例，实际应用中需要根据具体问题构建图的邻接表。

结果输出：

四、最长递增子序列问题

4.1、问题描述

最长递增子序列（Longest Increasing Subsequence）是一个经典的问题，其目标是在一个给定的序列中找到最长的子序列，使得子序列中的元素按顺序递增排列。

例如，在序列 [10, 22, 9, 33, 21, 50, 41, 60, 80]
中，最长递增子序列是 [10, 22, 33, 50, 60, 80]
，长度为6。

4.2、解题思路

定义状态：我们定义一个一维数组 dp
，其中 dp[i]
表示以第 i
个元素结尾的最长递增子序列的长度。
初始化状态：初始时，将 dp
数组的所有元素都初始化为1，因为任何一个元素本身也是一个长度为1的递增子序列。
状态转移：我们遍历数组中的每个元素 nums[i]
。对于每个元素 nums[i]
，我们再次遍历其前面的所有元素 nums[j]
（j
从 0 到 i-1
）。如果 nums[i]
大于 nums[j]
，说明 nums[i]
可以接在 nums[j]
后面形成一个递增子序列，此时我们更新 dp[i]
为 dp[j] + 1
，表示以 nums[i]
结尾的递增子序列的长度。
找出最大值：遍历完整个数组后，我们将 dp
数组中的最大值即为最长递增子序列的长度。
返回结果：返回最长递增子序列的长度。

4.3、代码示例

这个算法的核心思想是利用动态规划的方式，逐个元素计算以其结尾的最长递增子序列长度，然后在遍历过程中不断更新 dp
数组，最终找到最大的长度值即可。这个算法的时间复杂度是 O(n^2)，其中 n 是输入数组的长度。


#include <iostream>
#include <vector>


using namespace std;


int lengthOfLIS(vector<int>& nums) {
    int n = nums.size();
    if (n == 0) return 0;
    
    vector<int> dp(n, 1); // 初始化dp数组，所有元素都初始化为1
    
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < i; ++j) {
            if (nums[i] > nums[j]) {
                dp[i] = max(dp[i], dp[j] + 1);
            }
        }
    }
    
    int maxLen = 1;
    for (int i = 0; i < n; ++i) {
        maxLen = max(maxLen, dp[i]);
    }
    
    return maxLen;
}


int main() {
    vector<int> nums = {10, 22, 9, 33, 21, 50, 41, 60, 80};
    
    int lisLength = lengthOfLIS(nums);
    
    cout << "Length of Longest Increasing Subsequence: " << lisLength << endl;
    
    return 0;
}

结果输出：

五、编辑距离问题

5.1、问题描述

编辑距离（Edit Distance），又称Levenshtein距离，是用来衡量两个字符串之间的相似度的指标。它表示将一个字符串转换成另一个字符串所需的最少操作次数，包括插入、删除和替换字符。编辑距离常常用于自然语言处理、拼写纠错、DNA序列匹配等领域。

给定两个字符串 word1
和 word2
，求它们之间的编辑距离。

5.2、解题思路

使用一个二维数组 dp
来存储中间状态，其中 dp[i][j]
表示将 word1
的前 i
个字符转换成 word2
的前 j
个字符所需的最少操作次数。

动态规划的状态转移方程如下：

如果 word1[i-1]
等于 word2[j-1]
，则 dp[i][j] = dp[i-1][j-1]
。这表示当前字符相等，无需进行操作，继承上一个状态的编辑次数。
否则，我们有三种操作选择：

插入（Insert）：dp[i][j] = dp[i][j-1] + 1
，表示在 word1
的第 i
个字符后插入一个字符，使其等于 word2
的第 j
个字符。
删除（Delete）：dp[i][j] = dp[i-1][j] + 1
，表示删除 word1
的第 i
个字符，使其等于 word2
的前 j
个字符。
替换（Replace）：dp[i][j] = dp[i-1][j-1] + 1
，表示将 word1
的第 i
个字符替换成 word2
的第 j
个字符。

最终，dp[word1.size()][word2.size()]
就是所求的编辑距离。

5.3、代码示例


#include <iostream>
#include <vector>
#include <string>
using namespace std;


int minDistance(string word1, string word2) {
    int m = word1.size();
    int n = word2.size();
    
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
    
    for (int i = 1; i <= m; ++i) {
        dp[i][0] = i;
    }
    
    for (int j = 1; j <= n; ++j) {
        dp[0][j] = j;
    }
    
    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j <= n; ++j) {
            if (word1[i - 1] == word2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1];
            } else {
                dp[i][j] = min(dp[i - 1][j], min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
            }
        }
    }
    
    return dp[m][n];
}


int main() {
    string word1, word2;
    cout << "Enter the first word: ";
    cin >> word1;
    cout << "Enter the second word: ";
    cin >> word2;
    
    int distance = minDistance(word1, word2);
    
    cout << "The edit distance between \"" << word1 << "\" and \"" << word2 << "\" is: " << distance << endl;
    
    return 0;
}

结果输出：

六、硬币找零问题

硬币找零问题是一个经典的动态规划问题，其目标是找出一组硬币中最少需要多少枚硬币来凑成给定的金额。

6.1、问题描述

给定一组硬币的面值 coins
和一个目标金额 amount
，请找出凑成目标金额所需的最少硬币数量。如果无法凑成目标金额，则返回 -1。

6.2、解题思路

创建一个长度为 amount + 1
的数组 dp
，并将其初始化为一个较大的数（例如，amount + 1
表示无穷大）。
将 dp[0]
初始化为 0，因为凑成金额为 0 的最少硬币数量为 0。
对于每个金额 i
从 1 到 amount
，遍历硬币面值数组 coins
，对于每个硬币面值 coin
，更新 dp[i]
的值为 min(dp[i], dp[i - coin] + 1)
。
最后，dp[amount]
将包含最少硬币数量的解。如果 dp[amount]
仍然是初始值，表示无法凑成目标金额，返回 -1，否则返回 dp[amount]
。

6.3、代码示例


#include <iostream>
#include <vector>
#include <climits>  For INT_MAX
using namespace std;


int coinChange(vector<int>& coins, int amount) {
    vector<int> dp(amount + 1, INT_MAX);
    dp[0] = 0;


    for (int i = 1; i <= amount; ++i) {
        for (int coin : coins) {
            if (i - coin >= 0 && dp[i - coin] != INT_MAX) {
                dp[i] = min(dp[i], dp[i - coin] + 1);
            }
        }
    }


    return dp[amount] == INT_MAX ? -1 : dp[amount];
}


int main() {
    vector<int> coins = {1, 2, 5};
    int amount;
    cout << "Enter the target amount: ";
    cin >> amount;


    int minCoins = coinChange(coins, amount);


    if (minCoins == -1) {
        cout << "It's not possible to make the target amount with given coins." << endl;
    } else {
        cout << "The minimum number of coins required to make " << amount << " is: " << minCoins << endl;
    }


    return 0;
}

结果输出：

七、矩阵链乘法问题

矩阵链乘法问题是一个经典的动态规划问题，其目标是找到一种最优的顺序来进行一系列矩阵相乘操作，以最小化乘法的总次数。

7.1、问题描述

给定一系列矩阵的维度（如 A1
是 2x3
矩阵， A2
是 3x4
矩阵，等等），找到一个最优的矩阵相乘顺序，以最小化总的乘法次数。如果有多个矩阵相乘的顺序可以达到最小次数，只需找到其中之一即可。

7.2、解题思路

创建一个二维数组 dp
，其中 dp[i][j]
表示从矩阵 i
到矩阵 j
的最小乘法次数。
初始化 dp[i][i]
为 0，因为单个矩阵相乘的次数为 0。
使用一个循环嵌套遍历矩阵链的长度 l
，其中 l
从 2 开始，逐渐增加。外层循环遍历长度 l
，内层循环遍历链的起始位置 i
，通过 i
和 i + l - 1
计算链的终止位置 j
。
对于每个链的起始和终止位置 i
和 j
，遍历中间位置 k
，计算在 i
到 k
和 k + 1
到 j
之间的子链的最小乘法次数，并将结果保存在 dp[i][j]
中。这个过程可以表示为 dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j] + dims[i-1] * dims[k] * dims[j])
，其中 dims
是矩阵维度数组。
最终，dp[1][n-1]
将包含所有矩阵相乘的最小次数，其中 n
是矩阵链的长度。

7.3、代码示例


#include <iostream>
#include <vector>
#include <climits>  For INT_MAX
using namespace std;


int matrixChainMultiplication(vector<int>& dims) {
    int n = dims.size() - 1; // Number of matrices in the chain
    vector<vector<int>> dp(n, vector<int>(n, INT_MAX));


    // Initialize diagonal elements
    for (int i = 0; i < n; ++i) {
        dp[i][i] = 0;
    }


    // Loop over chain lengths
    for (int l = 2; l <= n; ++l) {
        for (int i = 0; i < n - l + 1; ++i) {
            int j = i + l - 1;
            for (int k = i; k < j; ++k) {
                int cost = dp[i][k] + dp[k + 1][j] + dims[i] * dims[k + 1] * dims[j + 1];
                dp[i][j] = min(dp[i][j], cost);
            }
        }
    }


    return dp[0][n - 1];
}


int main() {
    vector<int> dimensions = {2, 3, 4, 5};
    int minMultiplications = matrixChainMultiplication(dimensions);


    cout << "Minimum number of multiplications: " << minMultiplications << endl;


    return 0;
}

结果输出：

八、最长回文子串问题

最长回文子串问题是一个经典的字符串处理问题，目标是找到给定字符串中的最长回文子串。

8.1、问题描述

给定一个字符串，找到该字符串中的一个最长回文子串。回文子串是正着读和反着读都一样的字符串。例如，在字符串 "babad" 中，最长回文子串为 "bab" 或 "aba"。

8.2、解题思路

创建一个二维布尔数组 dp
，其中 dp[i][j]
表示字符串从索引 i
到索引 j
的子串是否是回文子串。初始时，将所有 dp[i][i]
设置为 true
，因为单个字符都是回文。
使用两个指针 i
和 j
，从字符串的末尾开始向前遍历。如果字符 s[i]
和 s[j]
相等且子串 s[i+1:j-1]
也是回文（即 dp[i+1][j-1]
为 true
），则将 dp[i][j]
设置为 true
。
在遍历过程中，记录最长回文子串的起始索引 start
和长度 maxLen
，每当找到更长的回文子串时，更新这些值。
最终，根据 start
和 maxLen
截取字符串 s
的子串，即为最长回文子串。

8.3、代码示例


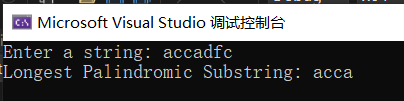
#include <iostream>
#include <string>
#include <vector>
using namespace std;


string longestPalindrome(string s) {
    vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
    int maxlenth = 0;
    int left = 0;
    int right = 0;
    for (int i = s.size() - 1; i >= 0; i--) {
        for (int j = i; j < s.size(); j++) {
            if (s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1])) {
                dp[i][j] = true;
            }
            if (dp[i][j] && j - i + 1 > maxlenth) {
                maxlenth = j - i + 1;
                left = i;
                right = j;
            }
        }
    }
    return s.substr(left, maxlenth);
}


int main() {
        string s;
        cout << "Enter a string: ";
        cin >> s;


        string longestPalindromicSubstring = longestPalindrome(s);
        cout << "Longest Palindromic Substring: " << longestPalindromicSubstring << endl;


        return 0;
}

结果输出：

九、打家劫舍问题

9.1、问题描述

小偷要打劫一个街区，这个街区中的每个房屋都存放着特定金额的钱，而且房屋之间有一条街，相邻的房屋是连续的。如果小偷抢了相邻的两家，就会触发警报系统。问小偷在不触发警报的前提下，最多能够抢劫多少金额的钱。

9.2、解题思路

定义一个一维数组 dp
，dp[i]
表示在前 i
个房屋中可以抢劫的最大金额。

那么，我们可以得到以下状态转移方程：


dp[i] = max(dp[i-2] + nums[i], dp[i-1])

其中，dp[i-2] + nums[i]
表示如果抢劫第 i
家，那么前一家 i-2
家的金额加上当前家的金额就是累计的最大金额；dp[i-1]
表示如果不抢劫第 i
家，那么最大金额就是前 i-1
家的最大金额。

接下来，我们从左到右遍历房屋，计算 dp
数组，最后返回 dp
数组的最后一个元素，即为可以抢劫的最大金额。

9.3、代码示例


#include <iostream>
#include <vector>


using namespace std;


int rob(vector<int>& nums) {
    int n = nums.size();
    if (n == 0) {
        return 0;
    }
    if (n == 1) {
        return nums[0];
    }
    
    vector<int> dp(n, 0);
    dp[0] = nums[0];
    dp[1] = max(nums[0], nums[1]);
    
    for (int i = 2; i < n; ++i) {
        dp[i] = max(dp[i-2] + nums[i], dp[i-1]);
    }
    
    return dp[n-1];
}


int main() {
    vector<int> nums = {2, 7, 9, 3, 1};
    int maxAmount = rob(nums);
    cout << "The maximum amount that can be robbed is: " << maxAmount << endl;
    return 0;
}

结果输出：

十、单词拆分问题

10.1、问题描述

给定一个非空字符串 s
和一个包含非空单词列表的字典 wordDict
，判断 s
是否可以被拆分成一个或多个在字典中出现的单词，且拆分后的单词都在字典中存在。

10.2、解题思路

定义一个一维布尔数组 dp
，其中 dp[i]
表示字符串 s
的前 i
个字符是否可以被拆分成字典中的单词。

接下来，我们从字符串的开头开始遍历，对于每一个位置 i
，我们再从位置 0
到 i
分别判断是否可以拆分成字典中的单词。如果存在一个位置 j
，使得 dp[j]
为 true
，并且子串 s[j:i]
也在字典中，那么 dp[i]
就为 true
。这是因为我们可以将 s[j:i]
划分成一个单词，并且 dp[j]
表示前 j
个字符可以被拆分，所以前 i
个字符也可以被拆分。

最终，dp
数组的最后一个元素 dp[n]
即为是否可以拆分成字典中的单词的结果，其中 n
为字符串 s
的长度。

10.3、代码示例


#include <iostream>
#include <vector>
#include <unordered_set>


using namespace std;


bool wordBreak(string s, vector<string>& wordDict) {
    unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
    int n = s.length();
    vector<bool> dp(n + 1, false);
    dp[0] = true;
    
    for (int i = 1; i <= n; ++i) {
        for (int j = 0; j < i; ++j) {
            if (dp[j] && wordSet.count(s.substr(j, i - j))) {
                dp[i] = true;
                break;
            }
        }
    }
    
    return dp[n];
}


int main() {
    string s = "leetcode";
    vector<string> wordDict = {"leet", "code"};
    bool canBreak = wordBreak(s, wordDict);
    
    if (canBreak) {
        cout << "The string can be segmented into words." << endl;
    } else {
        cout << "The string cannot be segmented into words." << endl;
    }
    
    return 0;
}

结果输出

十一、股票买卖问题

11.1、问题描述

给定一个数组 prices
，其中 prices[i]
是一支股票在第 i
天的价格。你最多可以完成一次交易（买入和卖出一支股票），请计算你能够获得的最大利润。

11.2、解题思路

定义两个状态数组 buy
和 sell
，其中 buy[i]
表示在第 i
天持有股票时的最大利润，sell[i]
表示在第 i
天不持有股票时的最大利润。

初始化时，buy[0]
为 -prices[0]
，表示第一天买入股票，sell[0]
为 0
，表示第一天不做任何操作。

然后，我们从第二天开始遍历数组。对于每一天 i
，有两种操作：

如果在第 i
天买入股票，则 buy[i] = max(buy[i-1], -prices[i])
，表示在前一天持有股票或者在当天买入股票中选择最大利润的情况。
如果在第 i
天卖出股票，则 sell[i] = max(sell[i-1], buy[i-1] + prices[i])
，表示在前一天不持有股票或者在当天卖出股票中选择最大利润的情况。

最终，我们的答案就是 sell[n-1]
，其中 n
是数组的长度。

11.3、代码示例


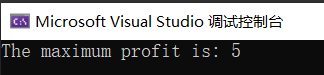
#include <iostream>
#include <vector>


using namespace std;


int maxProfit(vector<int>& prices) {
    int n = prices.size();
    if (n == 0) return 0;
    
    vector<int> buy(n, 0);
    vector<int> sell(n, 0);
    
    buy[0] = -prices[0];
    
    for (int i = 1; i < n; ++i) {
        buy[i] = max(buy[i-1], -prices[i]);
        sell[i] = max(sell[i-1], buy[i-1] + prices[i]);
    }
    
    return sell[n-1];
}


int main() {
    vector<int> prices = {7, 1, 5, 3, 6, 4};
    int maxProfitValue = maxProfit(prices);
    
    cout << "The maximum profit is: " << maxProfitValue << endl;
    
    return 0;
}

结果输出：

vector 动态规划算法背包问题指针初始化 vector初始化

文章转载自阿Q正砖，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

经典算法系列之动态规划

一、背包问题

1.1、01背包问题

1.1.1、问题描述

1.1.2、解题思路

1.1.3、代码示例

1.2、完全背包问题

1.2.1、问题描述

1.2.2、解题思路

1.2.3、代码示例

1.3、多重背包问题

1.3.1、问题描述

1.3.2、解题思路

1.3.3、代码示例

二、最长公共子序列问题

2.1、问题描述

2.2、解题思路

2.3、代码示例

三、最短路径问题

3.1、问题描述

3.2、解题思路

3.3、代码示例

四、最长递增子序列问题

4.1、问题描述

4.2、解题思路

4.3、代码示例

五、编辑距离问题

5.1、问题描述

5.2、解题思路

5.3、代码示例

六、硬币找零问题

6.1、问题描述

6.2、解题思路

6.3、代码示例

七、矩阵链乘法问题

7.1、问题描述

7.2、解题思路

7.3、代码示例

八、最长回文子串问题

8.1、问题描述

8.2、解题思路

8.3、代码示例

九、打家劫舍问题

9.1、问题描述

9.2、解题思路

9.3、代码示例

十、单词拆分问题

10.1、问题描述

10.2、解题思路

10.3、代码示例

十一、股票买卖问题

11.1、问题描述

11.2、解题思路

11.3、代码示例

评论