交替最小二乘(Alternating Least Squares,ALS),是基于矩阵分解的协同过滤算法中的一种, 协同过滤算法分为三类:基于相似性的协同过滤包括基于用户和基于产品的协同过滤;基于矩阵 分解的协同过滤;基于图的协同过滤。其中 ALS 算法是基于矩阵分解的协同过滤算法中的一种典 型算法,是目前协同过滤推荐的核心算法之一,也是基于 spark 计算引擎的协同过滤推荐的核心 算法。
协同过滤推荐,是在信息过滤和信息系统中一项很受欢迎的技术。与传统的基于内容过滤直 接分析内容进行推荐不同,协同过滤分析用户兴趣,在用户群中找到指定用户的相似(兴趣)用 户,综合这些相似用户对某一信息的评价,形成系统对该指定用户对此信息的喜好程度预测。
以美国亚马逊(AMAZON)网上书店为例,亚马逊是个性化推荐系统先驱 (基于协同过滤)。 亚马逊书店提供先进的个性化推荐功能,能为不同兴趣偏好的用户自动推荐尽量符合其兴趣需要 的书籍。亚马逊使用推荐算法对读者曾经购买过的书以及该读者对其他书的评价进行分析后,将 向读者推荐他可能喜欢的新书,只要鼠标点一下,就可以买到该书;亚马逊对顾客购买过的东西 进行自动分析,然后因人而异的提出合适的建议。读者的搜索信息将被再次保存,这样顾客下次来时就能更容易的买到想要的书。
对于 R(m×n)的矩阵,ALS 旨在找到两个低维矩阵 X(m×k)和矩阵 Y(n×k),来近似逼近 R(m
×n),即: ,其中 R(m×n)代表用户对商品的评分矩阵,X(m×k)代表用户对隐含
特征的偏好矩阵,Y(n×k)表示商品所包含隐含特征的矩阵,T 表示矩阵 Y 的转置。实际中,一般
取 k<
为了找到使低秩矩阵 X 和 Y 尽可能地逼近 R,需要最小化下面的平方误差损失函数,得到公
式(1):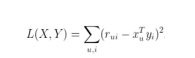
其中 xu(1×k)表示示用户 u 的偏好的隐含特征向量,yi(1×k)表示商品 i 包含的隐含特征向量, rui 表示用户 u 对商品 i 的评分, 向量 xu和 yi的内积 xu Tyi 是用户 u 对商品 i 评分的近似。
损失函数一般需要加入正则化项来避免过拟合等问题,我们使用 L2
2正则化,所以上面的公
式改造为公式(2):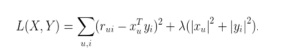
其中λ是正则化项的系数。
到这里,协同过滤就成功转化成了一个优化问题。由于变量 xu 和 yi 耦合到一起,这个问题 并不好求解,所以我们引入了 ALS,也就是说我们可以先固定 Y(例如随机初始化 X),然后利 用公式(2)先求解 X,然后固定 X,再求解 Y,如此交替往复直至收敛,即所谓的交替最小二乘 法算法。






