机器学习之线性代数：向量的投影

在日常生活中，物体在灯光或日光的照射下，在墙面或地面上就会显现出该物体的影子,通过影子能看出物体的外形轮廓，这种现象称为物体在墙面或地面上的投影。

上图向量tB是向量A在向量B的投影，它是向量B的一个纯量倍数，计算出t，就可以求得向量A在向量B上的投影。

可以用A和B的点积来表示t，参见下图：

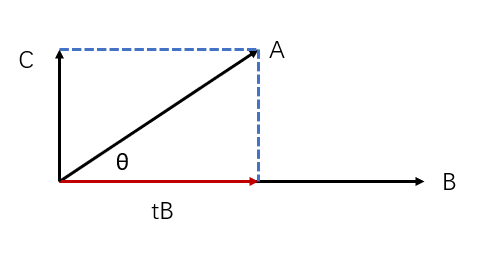
通过上图可知：

tB + C = A

等式两边同时点乘B：

tB*B + C*B = A*B

由于向量C和向量B垂直，所有C*B=0，可得下式：

tB*B = A * B

t为：

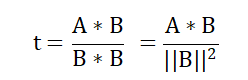
观察上图向量tB和向量A构成的夹角θ，可以得出：

上式也可以表示为：

即两个非零向量的点积等于它们的长度与它们夹角的余弦之积。在机器学习中，经常通过计算两个向量夹角的余弦值，来评估向量的相似度，也称为余弦相似性。例如在文本相似性分析中，需要将文本内容转换为向量空间模型，把对文本内容的处理简化为向量空间中的向量运算，并且它以空间上的相似度表达语义的相似度。

下面给出向量投影的定义：

设A和B为n维空间上两个向量，且B!=0，则向量tB称为A在B上的投影，其中

例1：已知向量A=(1,2,3)，B=(1,2,2)，编写Python程序计算向量A在向量B上的投影。

程序清单

# 导入numpy模块
import  numpy as np
  
# 定义向量A
A = np.array([1,2,3])
# 定义向量B
B = np.array([1,2,2])
  
# 计算t
t = np.dot(A,B)/np.dot(B,B)
# 计算投影tB
tB = t * A
print(tB)

例2：已知向量A=(1,1,2,1,1,0,0)，B=(0,1,2,1,0,1,1)，编写Python程序计算向量A与向量B夹角的余弦值。

程序清单

# 导入numpy模块
import  numpy as np
  
# 定义向量A和B
A = np.array([1,1,2,1,1,0,0])
B = np.array([0,1,2,1,0,1,1])
  
# 计算A和B的点积
AB = np.dot(A,B)
# 计算向量A的模长
mA = np.linalg.norm(A)
# 计算向量B的模长
mB = np.linalg.norm(B)
# 计算向量A和B的相似度
sim = AB/(mA*mB)
print('相似度为%.6f' % (sim))