
论文链接:https://openreview.net/pdf?id=wLFXTAWa5V
文章核心
VectorSearch
本文的核心是介绍了一种新的属性约束 ANNS 框架:NHQ。该方法首先将特征向量和属性结合在一个复合索引中,然后通过考虑特征向量和属性约束来修剪复合索引上的搜索空间,最终直接获得前k个结果。NHQ 框架不仅支持现有的近邻图(PG),并且还支持自定义优化的 PG。此外,论文还设计了两种可导航 PG(NPGs)并讨论了如何在 NHQ 框架中使用这些 NPGs。在10个真实世界数据集上测试表明,本文的方法相对于最先进的属性约束 ANNS 框架和方法的更好的效果、效率和可扩展性。
NHQ
VectorSearch
在介绍 NHQ 之前,先介绍一下 PG(proximity graph)。
PG 的定义:
给定一个对象集 S,我们定义 S 的 PG (a 距离阈值 B)为一个图 G = (V, E),它具有顶点集 V 和边集 E;
1.对于每个顶点 u ∈ V,它都对应一个对象 E ∈ S。
2.对于 V 的任意两个顶点 ui 和 uj,如果 uiuj ∈ E,我们有 δ(ν(ui),ν(uj)) ≤ B,ν(ui) 和 ν(uj) 分别是物体 ui 和 uj 的特征向量。
了解了 PG 的定义之后,我们设 N(ui)为 ui 的邻居集。作者的想法是构建一个同时使用特征向量和属性作为复合索引的 PG,在这个索引当中,u 的邻居可能具有和 u 相同的属性。我们可以用公式1来衡量特征向量之间的距离。
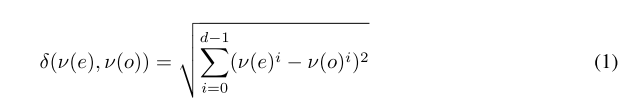
但我们需要量化属性并定义一个距离度量函数。然后,将特征向量距离和属性距离融合为融合距离,对目标进行比较。因此,我们可以直接根据融合距离对特征向量不同或属性不同的顶点进行剪枝。
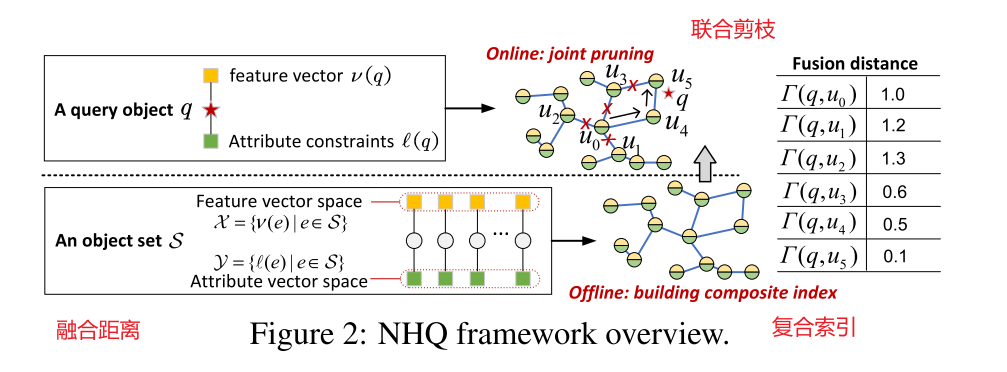
融合距离
给定一个特征向量为 X 的对象集 S,我们可以使用不同的编码方法对每个属于 S 的对象 e 的属性进行编码。顺序编码对于结构化属性的效果很好。我们使用顺序编码 e(.) 来对每个对象 e 得到一个属性向量 l(e) = [l(e)^0,……,l(e)^(m-1)],其中 l(e)^i 为 e.ai's 的编码值(例如:{NeurIPS, NLP} 可以用 l(.) 编码为[1,3])。
然后,我们得到属性向量 Y = {l(e)|e∈S}。我们可以使用公式1来测量 X 中两个特征向量 v(ei) 和 v(ej) 之间的距离,用公式4、5测量 Y 中两个属性向量 l(ei) 和 l(ej) 之间的距离。该距离越小,则属性向量越相似。
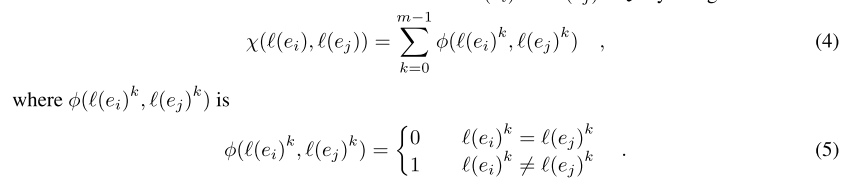
其中,m 表示 l(ei) 的维数,k 表示 l(ei)^k 是第 k 维上的值。
我们可以通过使用公式6将特征向量距离 δ(v(ei),v(ej)) 和属性向量距离 X(l(ei), l(ej)) 融合为对象 ei 和 ej 的单个距离 Г(ei,ej)。
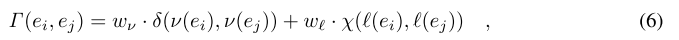
其中 wv 和 wl 是距离权值。
这个距离越小,物体在特征向量和属性上越相似。公式6是一个简单实用的结合两个不同距离的方法。这也使得在现有 PG 之上构建复合索引变得容易,因为我们只需要将距离度量从公式1变为公式6。
例如,如果我们设置 wv=1,wl=0,我们可以得到 Г(ei,ej) = X(l(ei),l(ej)),这与基于特征向量构建 PG 得到的结果相同。设 wv = 0,wl = 1,可以得到 Г(ei,ej) = X(l(ei),l(ej)),与基于属性构造的 PG 相同。由此可见,我们可以通过调整 wv 和 wl 来找到两个距离之间的最佳平衡点。
权重配置
作者发现 wv = 1 和 wl = δ(v(ei),v(ej))/m 对于大多数数据集和算法给出了最好的查询性能。这些权重不依赖于数据集,只依赖于两个对象的特征向量距离 δ(v(ei),v(ej)) 和属性向量维度 m。其思想是用属性距离微调特征向量距离。
例如,如果 ei 和 ej 具有相同的属性,即 X(l(ei),l(ej))=0,我们保持特征向量距离不变(即 Г(ei,ej) = δ(v(ei),v(ej)))。如果 ei 和 ej 有完全不同的属性,即 X(l(ei),l(ej))=m,我们将特征向量距离加倍得到 Г(ei,ej) = 2·δ(v(ei),v(ej))。一般来说,我们有 δ(v(ei), v(ej)) ≤ Γ(ei, ej) ≤ 2·δ(v(ei),v(ej))。
复合索引
作者构建了一个复合索引(见图2,右下)。对于图 G = (V, E),我们令 V = S,此时每个对象 e ∈ S 都是 G 中的顶点 u ∈ V 且 E 为空集。如果 Г(ui, ui) ≤ B',就在 ui 和 uj 两个顶点之间添加一条边 ui,uj ∈ E,,其中 B' 为融合距离的阈值。值得注意的是,复合索引的融合距离范围极小,不会产生额外的空间成本。
联合剪枝
给定一个查询对象 q,我们使用一个复合索引 G 和一个种子集 P(通常从 V 中随机选取)来寻找 top-k 的近似对象。我们遵循以下步骤(见图 2,右上方)
1.初始化。使用访问顶点集 C 来存储搜索扩展的顶点,使用大小为 k 的结果集 R 来存储当前查询结果。最初先把两个集合都设为 P。
2.搜索扩展。我们从 C 中把最小的顶点 ui ∈ Γ(q, ui) 提出来作为下一个访问的顶点,然后添加 N(ui) 到 C 中。
3.查询结果更新。我们用 N(ui) 中更好的顶点来更新 R。对于任意顶点 uj ∈ N(ui) 和一个离 q 最远的顶点 ur ∈ R,如果 Γ(q, uj) < Γ(q, ur),这意味着 uj 在特征向量和属性上都比 ur 更接近 q,我们就用 uj 替换 ur。
重复2、3步骤,直到 R 不变,然后返回 R 作为 top-k 的近似对象。
可导航 PG
VectorSearch
为了形成复合索引,我们可以在 NHQ 中部署一个特定的 PG,并将其原来的距离度量更改为公式6的融合距离。这使 PG 能够有效地处理 属性约束ANNS。然而,目前基于 PG 的综合指标存在一定的局限性,影响了 NHQ 的性能。因此,作者分别对边选择和路由策略进行了优化,设计了两款新的可导航 PG(NPG),以实现在 PG 上的构建和搜索。
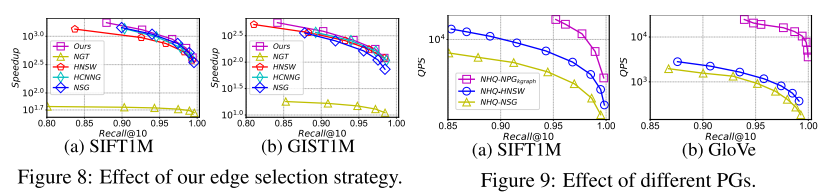
边缘选择
边选择是构建PG索引的关键步骤,它决定了对象集 S 中每个对象 e 的邻居。不同的策略为对象集构建了不同的结构,这影响了对象集的搜索性能。现有的 PG 根据两个因素进行边选择:
D1:两个顶点之间的距离;
D2:所有顶点的分布。
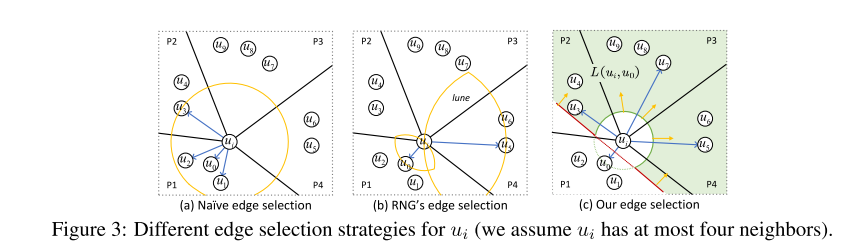
早期的 PG,如 NSW 和 KGraph 只使用 D1,并将每个顶点与其最近的邻居连接(图3(a))。但这会引起冗余计算,降低搜索效率。最近的 PG 也使用 D2 和 RNG 的边缘选择,使邻居的方向多样化。然而,RNG 的边缘选择仍然未能很好地实现邻居的多元化(图3(b))。
作者设计了一种新的利用 D1 和 D2 的边选择策略。它连接 ui 所在每个区域中的一个最近的邻居(图3(c)中的 P1-P4)。
在这里作者定义了着陆区的概念:顶点 ui 及其邻居 uj ∈ N(ui) 的着陆区 L(ui,uj) 是由 H(ui,uj) \ B(ui,δ(v(ui), v(uj))) 定义的区域。这里,H(ui, uj) 是有 ui 的半空间,它被 ui 和 uj 之间连线的垂直平分线 U(ui,uj) 分割。B(ui,δ(v(ui),v(uj))) 是以 ui 为中心半径为 δ(v(ui),v(uj)) 的超球。
如图3(c)所示,在二维空间中,U(ui,u0) 是连接 ui 和 u0 (即红线)的垂直平分线,H(ui,u0) 位于 U(ui, u0) 的上方,B(ui,δ(v(ui),ν(u0))) 是绿圈包围的区域。因此,由 ui 和 u0 组成的着陆区 L(ui,u0) 为绿色阴影区域(即 H(ui,u0) \ B(ui,δ(v(ui),ν(u0))))。
为了找到 ui 没有任何邻居的区域,我们将其所有现有邻居的着陆区域相交(即 uj ∈ N(ui) ∩ L(ui,uj))。然后,我们将该区域内最近的顶点添加到 N(ui) 中,使邻居更加多样化。我们的策略确保 ui 的邻居在 C(ui) 所在的区域是多样化的。这是因为我们每次从不同的区域选取邻居添加到 N(ui)。
我们通过以下步骤得到顶点集 V 中的每个顶点 ui的邻居:
1.候选邻居集获取。我们从 (V\{ui}) 中得到 ui 的 l 个候选邻居的集合,用 C(ui) 表示。我们可以使用随机抽样或一个额外的索引来得到 C(ui) (例如,我们基于 NSW 和 KGraph 得到 C(ui))。需要保证 l ≥ R,其中 R 是 ui 的最大邻居数(即 |N(ui)| < R)。
2.邻居初始化。我们按照到 ui 的距离升序对 C(ui) 中的元素进行排序。我们将 N(ui) 初始化为 ui 在 C(ui) 中的最近候选邻居 ut,并将 ut 从 C(ui) 中移除。
3.邻居更新。我们从 C(ui) 中选择距离 ui 最近的顶点,如果它在 ui 和它现有的邻居形成的着陆区 (即 uj ∈ N(ui) ∩ L(ui,uj)),则将其添加到 N(ui) 中。
我们重复这个过程,直到 C(ui) = 0 或 |N(ui)| = R。取得 C(ui) 该过程的时间复杂度取决于使用的方法,忽略获取C(ui)的时间复杂度,在顶点集 V 上选择边的时间复杂度为 O(l·(R + log(l))·|V |)
路由
路由是在 PG 上进行搜索的一个关键过程,它确定了从开始顶点到匹配查询的结果顶点的路径。路由策略对搜索的效率和准确性都有影响。最近的一项研究根据距离查询对象的距离将路由分为两个阶段:
S1:远阶段;
S2:近阶段。
在本文中采用了随机两阶段路由策略。在 S1 中,我们从 N(ui)随机选择h个邻居(其中 1≤h≤R,R 为最大出度)计算它们到查询对象 q 的距离。这使我们能够快速接近 q 的邻域。在 S2 中,我们遵循类似于贪婪搜索的方法计算 N(ui) 中的邻居到 q 的距离。当 S1 达到一个局部最优值时,就会发生从 S1 到 S2 的转变,即不再更新结果集 R。在 S2 中,我们通过检查访问过的顶点的所有邻居来继续更新 R。当 R 不再接收到任何更新时,搜索终止。
在 S1 中的随机策略并不会降低精度,因为大多数情况下距离查询较远时不需要计算访问顶点的所有邻居到查询的距离,并且可以在 S2 中恢复少量可能丢失的顶点。
我们使用 l1 还有 l2 分别表示 S1 和 S2 中的平均路径长度,路由的时间复杂度为 O((R/h)·l1+ R·l2)。
实验
VectorSearch
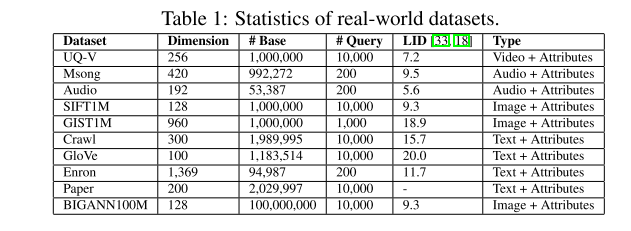
实验使用 C++ 编写的代码,在 g++ 6.5 编译器下进行编译。所有实验在配备 Intel(R) Xeon(R) Gold 6248R CPU(3.00) GHz)和 755G 内存的 Linux 服务器上进行。使用64个线程构建所有索引,而在搜索过程中只使用一个线程,这是相关工作中常见的设置。本研究使用了十个真实世界数据集,包括视频、图像、音频和文本等各种模态。这些数据集在表1中有详细的特征总结。所有实验报告了三次试验的平均结果。
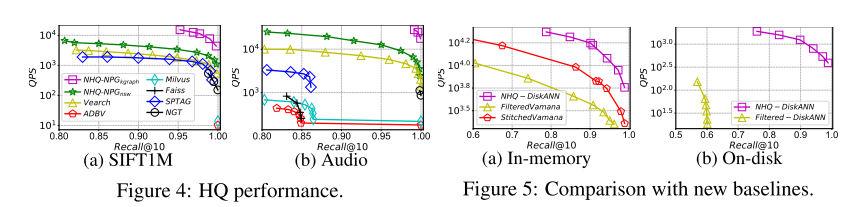
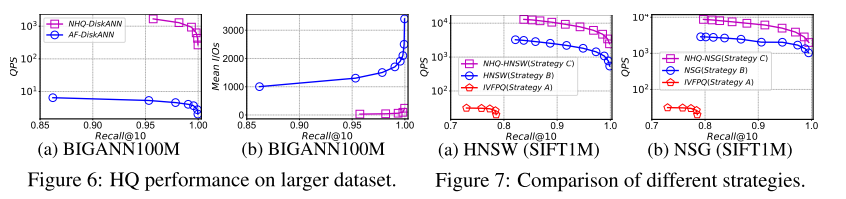
结果显示,在所有数据集上,该方法在 QPS 与 Recall 之间的权衡方面与现有方法相当。例如,当 Recall@10 > 0.99时,NHQ-NPGkgraph 的 QPS 比其他方法高出两到三个数量级。NHQ-DiskANN 在内存和磁盘版本上都优于 Filtered-DiskANN。NHQ-NPGkgraph 在更难的 GloVe 数据集上需要特别其他方法。
向量检索实验室
微信号:VectorSearch
扫码关注 了解更多







