一、技术背景

对于非密码学的开发者来说，同态加密算法是一个比较陌生的词汇，本次我们就来介绍一下同态加密算法的基本概念。

贝格迈思在研发高性能智能数据库AiSQL中，充分运用了全密态数据库的保序加密技术，已实现数据可查询加密，并不断迭代结合同态加密技术，将数据在存储、计算和传输过程中保持加密状态，为数据提供了强大的保护措施，实现了金融级的数据库安全能力。

由于同态加密算法经常与隐私计算联系起来，本次我们将从隐私计算中一个比较常用的技术PSI(Private Set Intersection)说起，串联起密码学及同态加密的常用知识点，希望能让大家对同态加密算法有一个初步的认识。

二、什么是PSI

PSI 即 Private Set Intersection，中文一般叫做隐私求交。其意思是持有数据集合的两方，能够通过计算得到双方集合的交集，但不暴露交集以外的任何信息。

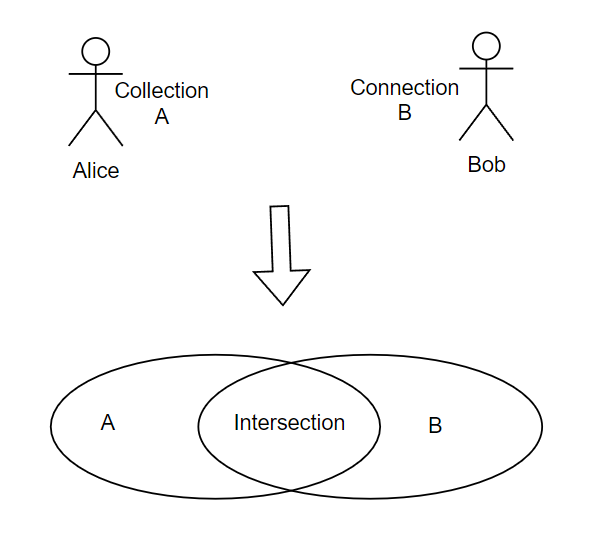
图1 求交集示意图

上图中Alice持有数据集A，Bob持有数据集B。如果Alice想知道Bob的数据集和自己的数据集的交集，传统的方式是Alice将自己的数据集A发送给Bob，然后Bob遍历数据集A，对数据集A中的每个元素，都在自己的数据集B中进行搜索，如果存在则放入交集集合Intersection中；等遍历完数据集A后，Intersection中就存放好了Alice想要的结果，最后Bob将Intersection发送给Alice，就完成了集合A和集合B求交的目的。但是这种传统的方式，只能叫做SI，即Set Intersection；因为在这个过程中，Bob知道了Alice集合中的所有元素，但对Alice而言，自己的数据相当于泄露给了Bob。

而在PSI中，Alice对Bob发起查询请求后，最后只有Alice知道了集合A和集合B之间的交集，Bob对Alice的集合A毫不知情。如果Alice不想将交集的结果共享给Bob，则Bob在这个计算中得不到任何信息；当然Alice也不能知道Bob的集合B的任何信息。在这个过程中，Alice又叫做查询方，Bob又称作数据的提供商。一般来说，数据的提供方提供了PSI的这项服务，可以向查询方进行收费。

三、加密算法简介

PSI能够在参与双方数据集可用不可见的情况下，得到双方数据集的交集，其手段就是加密。加密从其模式上可以分为对称加密和非对称加密。

对称加密又称私钥加密，即使用同一个密钥(私钥)进行加密和解密；AES就是一种常见且著名的对称加密算法；国密算法SM4也是一种对称加密算法。

非对称加密又称公钥加密，即在加密的过程中使用公钥，在解密的过程中使用私钥。这样任何持有公钥的参与方都可以加密数据，但是只有持有私钥的参与方才能解密数据；RSA， 国密算法SM2都是非对称加密算法。

从效率上来讲，对称加密比非对称加密高。但非对称加密因为其更高的安全性，被广泛用于网络通信中，比如HTTPS的认证环节。

这里还需要澄清一点，像一些安全散列算法，比如MD5、SHA1、SHA2、HMAC等，不能算作是加密算法，因为这些算法是不可逆的，它们一般被用在数字签名中。

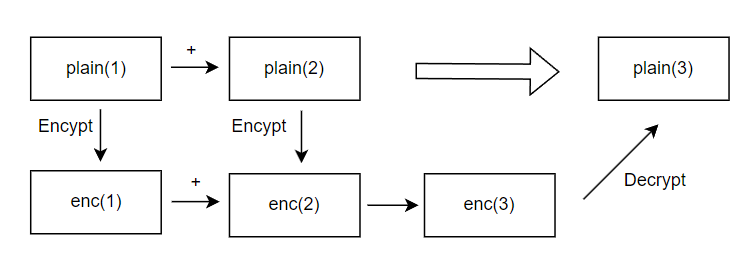
同态加密算法也属于非对称加密。与非同态加密算法不同的是，经过同态加密算法得到的密文，能够进行有限的算数运算(如加法、乘法)。比如，现在我们要计算 1 + 2的结果，先对1加密变成enc(1)，再对2加密变成enc(2)，接着在密文状态下计算enc(1) + enc(2)，(注意，此处非同态加密算法无法进行这个加法运算)，得到了结果enc(result)；这个结果也是密文，最后对enc(result) 进行解密，会得到明文状态的3。这个结果就跟明文状态下计算1 + 2得到的结果一样，这就是这种加密算法为何被叫做同态加密算法的原因。

图2 加法同态示意图

这个例子演示了加法同态。既然有加法同态，那么是不是还有乘法同态呢？这就得看同态加密算法支持的程度了。因为有的同态算法只支持密文间的加法，不支持密文间的乘法；而有的同态算法既支持密文间的加法，也支持密文间的乘法。那么接下来我们看看同态算法有哪些分类。

四、同态算法的分类

根据对加法和乘法的支持程度，同态加密算法可以分为:

1、半同态加密：只支持加法或乘法中的一种运算。

ElGamal加密方案是基于离散对数的公钥加密方案，在其实现上满足乘法同态，其加密运算满足随机性，因此是ISO同态加密国际标准中唯一指定的乘法同态加密算法。

在半同态加密算法中，Paillier算法由于效率较高，安全性证明完备等特点，在众多有同态加密需求的场景中得到了应用，比如PSI，联邦学习等。Paillier算法支持明文和密文之间的加法，明文和密文之间的乘法，密文和密文之间的加法，但不支持密文和密文之间的乘法。因此Paillier算法属于加法同态加密算法，同时也是ISO同态加密国际标准中唯一指定的加法同态加密算法。

另外值得一提的是, 经典的非对称加密算法RSA，在不对明文进行填充的情况下，满足乘法同态特性。但此时的RSA由于在加密过程中没有使用随机因子，因此使用相同密钥加密相同数据会得到相同的结果，所以使用RSA作为乘法同态会存在严重的安全弱点。RSA并非为了同态而设计的，所以在需要使用同态的应用中，不会考虑将RSA作为同态算法。RSA只是恰好满足了乘法同态而已。

2、部分同态加密：可同时支持加法和乘法的运算，但支持的计算次数有限。

部分同态加密算法中，比较有代表性的是BGN算法；这种算法同时支持加法同态和一次乘法同态运算。

3、全同态加密：支持任意次的加法和乘法运算。

全同态算法中，比较著名的算法要属BFV，BGV，CKKS。这些算法从理论上支持任意次的加法和乘法运算，但在工程实现上，只支持有限次的乘法运算。目前只有Concrete的全同态库实现了真正意义上的全同态，但是只支持单比特的加密，因此效率极低。

五、同态算法的优缺点

同态算法的优点：

由于能够在密文上进行运算，使得数据可用而不可见成为可能，因而同态加密算法有着广阔的应用场景。

试想，在拥有海量数据的大厂之间应用联邦学习，由同态加密算法保证各自数据的安全性，使得各方都获得了自己想要的模型，这样数据孤岛问题将得以解决。但对同态算法的应用也带来了很多挑战。

同态算法的主要缺点：

1、密文膨胀

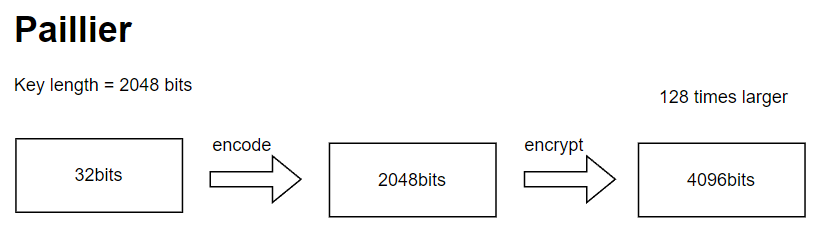
存储一个密文所需的空间比单独存储一个明文要大的多。以Paillier算法为例，对于一个32bits的整形数进行加密，如果密钥长度设为2048bits，加密的过程首先要进行encode，32bits的整形数变成了用2048bits表示的明文；接下来进行加密， 2048bits的明文变成了4096bits的密文。可以看到，密文相对明文的膨胀系数达到了 4096 / 32 = 128 倍。

图3 Paillier算法膨胀系数

2、只支持有限的算数运算

同态加密后的密文，即使是全同态加密算法，也只能支持加法、乘法，无法支持比较操作。如果需要比较两个密文，则需要先做差，再解密，最后进行正负性判定。这使得难以在密文上进行排序。

3、计算速度慢

无论是全同态加密算法，还是半同态加密算法，在计算速度上都比明文要慢上N个数量级。以全同态加密算法来说，在通用芯片上，密文计算相对明文计算要慢10万倍；因此硬件加速非常有必要在同态计算中引入。常用的算力加速设备为GPU与FPGA，FPGA由于其可重构性、高性能、低功耗得到了算力加速厂商的青睐，这也间接带动了芯片产业的发展。可见挑战中也容易出现机会和新的赛道。

4、学习曲线高

软件开发人员和资深的密码研究者，使用有着同样实现的全同态加密算法，大概率会在安全性和计算性能方面有着截然不同的表现。以全同态算法BFV中三个参数配置来进行说明。

plain_modulus、poly_modulus_degree和coeff_modulus需要在使用前由用户配置。

（1）plain_modulus

plain_modulus指明文模数，它的设置与poly_modulus_degress有关(plain_modulus要求是一个质数，且与 1 关于模 2 * poly_modulus_degree同余)，同时它的大小决定了每次进行密文运算所消耗的noise budget的大小，plain_modulus越大，每次计算所消耗的noise budget就越大。这里需要说明的是，noise budget直接决定了一个密文能否被成功解密。每进行一次乘法运算，noise budget会被消耗，连续进行多次乘法，noise budget会被不断消耗，如果一个密文在多次乘法运算后noise budget被消耗完后，这个密文就无法被解密了。是的，即使我们持有正确的私钥，也无法对其进行解密。因此我们希望这个plain_modulus越小越好。

（2）poly_modulus_degree

poly_modulus_degree指明文多项式阶数，是2的整数次幂。它决定了在encode的时候，有多少明文可以被encode到多项式的系数上。后续在密文状态时，可以进行batch操作，这样一次计算可以被应用到多个数据上。这个数值越大，越安全。

（3）coeff_modulus

coeff_modulus 是一组素数，决定了密文的初始noise budget的大小。coeff_modulus越大，密文的初始noise budget越大，后续进行的乘法和加法运算的次数就越多。但coeff_modulus同时还跟密码安全性有关，越大越不安全。因此从计算能力上讲，我们期望coeff_modulus越大越好；但另一方面，从安全性的角度来讲，又希望coeff_modulus越小越好。这就有个折衷。通常如果coeff_modulus增大，需要增大poly_modulus_degree以满足安全性的要求，增大后的poly_modulus_degree又对计算性能有影响。此外plain_modulus因为与poly_modulus_degree相关，因此也需要跟着调整。另外coeff_modulus是一组素数，那么究竟设置多少个合适呢? 可以看到，仅仅三个参数的设置，就已经让我们需要思忖良久，要知道，启动BFV还有很多其他参数需要考虑。

六、同态算法在PSI中的应用

接下来，让我们再看看在PSI中是如何应用同态算法的。基于不同的同态加密算法会有不同的PSI实现，这里我们看看全同态加密算法在PSI中的实现。以下是一个最简单朴素的实现方法: 多项式做差再求积。

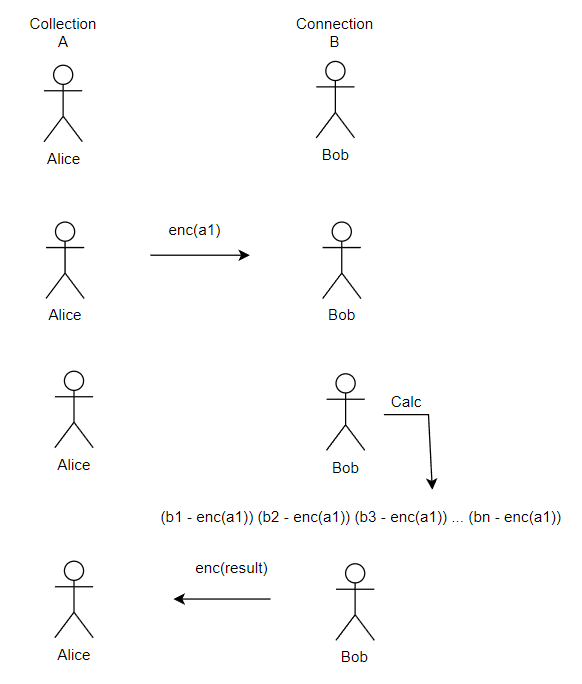
Alice中的集合A，其元素记为(a1， a2， a3， ... ， an)；Bob中的集合B，其元素记为(b1， b2， b3， ... ， bn)。Alice将集合A中的元素加密之后发送给Bob，比如将a1加密之后的结果enc(a1)发送给Bob，Bob用他所有的元素，计算(b1 – enc(a1)) * (b2 – enc(a1)) * (b3 – enc(a1)) * ... * (bn – enc(a1))，然后将得到的结果enc(result)发送给Alice； Alice用她的私钥对enc(result)进行解密，如果是0，就说明a1在B中，如果不为0，就说明a1不在B中。

图4 朴素全同态PSI实现

注意上述过程，Bob进行计算的每一个乘积项(bi – enc(a1))，其中bi是明文。由于是在Bob侧计算的，所以Alice并不知道bi的值是多少； enc(a1)是加密状态的，且私钥在Alice侧， 所以Bob也不知道Alice发送的a1值是多少。最后Bob计算得到了一个结果enc(result)， 由于只有Alice能够解密这个结果，因此Bob此刻并不知道a1是否在B的集合中(除非Alice愿意与Bob分享得到的结果)；Bob将enc(result)的结果发送给Alice后，Alice解密得知a1是否在Bob的集合B中。

当然这只是PSI的一种理论的实现，在工程实际中，会在这个基础上进行很多改良，主要是从安全性、计算速度及传输量上考虑的。

在这个例子中，如果使用半同态加密算法，因为半同态无法计算密文乘法，而这个例子中的每个乘积项都是密文(明文和密文之间进行运算得到的结果会是一个密文)，因此无法进行运算。对于使用半同态的PSI，会有其他实现方式。

七、小结

本文通过隐私计算中的一个常用技术PSI的实现说起，介绍了密码学的相关知识及同态加密算法的现状及使用场景。

同态加密保护了计算过程的安全性，使数据可用不可见成为可能。但同态加密算法不支持大小比较，仅支持有限的算数运算，且运算效率低，使得在数据库中对其进行应用非常困难。

贝格迈思是国际领先的数据智能技术引领者，

数据科技驱动行业应用创新者，研发的高性能智能数据库AiSQL，支持数据可查询加密，在数据处理全过程中对数据进行全密态保护。与传统的加密方式相比，数据可查询加密提供了更高的安全性和隐私性，同时保留了数据的可用性。

贝格迈思将不断探索，持续提升数据库中加密算法的创新应用，欢迎大家的关注与交流！