论文导读 | 因式分解数据库

在传统的关系型数据库中，二维表格形式容易造成信息的冗余。如果我们将数据库中的每条元组看成单项式，一个关系型数据库就可以表示成这些单项式的和。通过对多项式的因式分解就能够得到更加紧凑的表示形式。

例如：下图中的表格，A 的取值有 a1,a2, B的取值有b1,b2，C的取值有c1,c2。不难看出表格中存储的是这些取值的所有组合情况。按照上述思路，我们可以将它用因式分解的表示形式进行表示： 。我们发现，因式分解的表示形式只用了 6 个值就表示了具有 24 个值的二维表格。

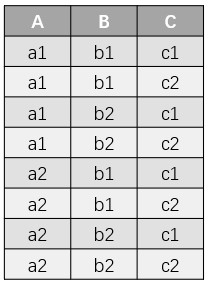
基于这样的思路，牛津大学的Dan Olteanu等人设计了因式分解数据库，尝试利用因式分解的能力来降低关系数据库的冗余从而优化空间和时间复杂度。下图是一个例子，(a) 表示了一个三张表的连接查询，以及它的查询结果。(b) 是这个连接查询超图；（c) 是这个连接查询的一个 d-tree (后文会解释)；(d) 是这个这个连接查询的因式分解的表达式树。

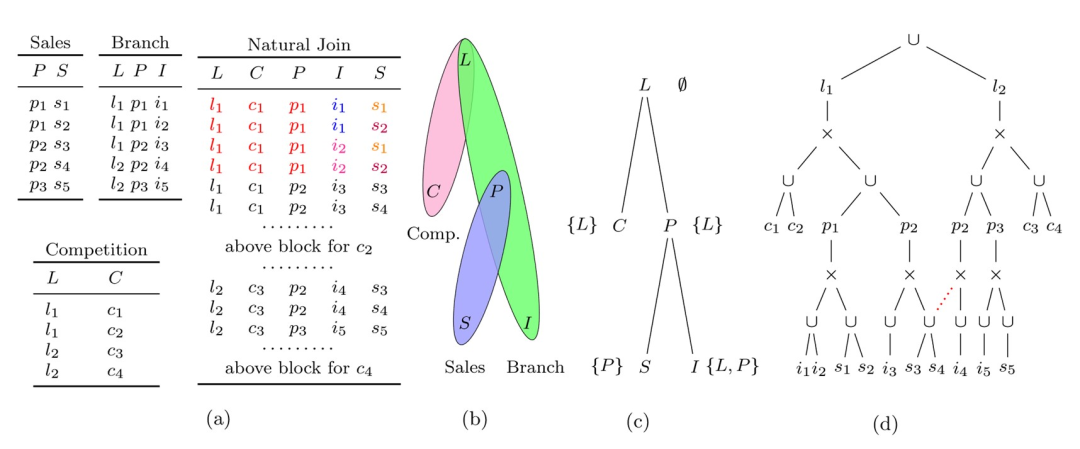
具体问题的问题定义为：给定关系型数据库，对于连接查询（Conjunctive query) 求得它的因式分解表示形式。 由于因式分解表示形式不唯一，因此我们要求结果尽可能紧凑。

其中衡量因式分解表示形式的紧凑程度的指标是 Readability。它表示对于一个因式分解表示，出现最多次数的元组的出现次数。

例如，下图的连接查询，用 1 的表示形式每个元组出现的次数为 1 次，因此它的Readabilty是1。而2的表示形式，R1 出现了两次，因此它的 Readability 是 2。

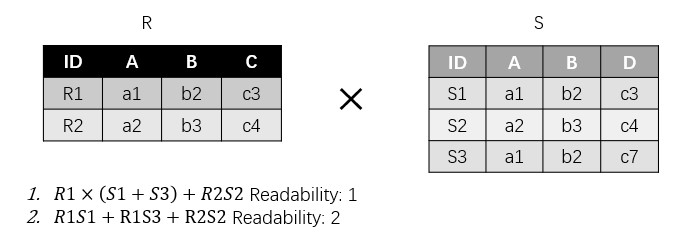
推论：假设数据库的大小是，对于某个连接查询 的结果的因式分解的 Readability 是 ，那么这个因式分解表示形式的大小是 的

F-tree

对于一个连接查询，我们要获得它的因式分解的表示形式，第一步是构建出连接查询的F-tree。它类似于一个连接计划。它需要满足以下条件：

• 叶子节点是关系，内部节点是属性。
• 同一个关系的属性，不能出现在不同的子树中。（即只能是父子或者祖孙关系）

例如：下图是连接查询和它的 F-tree

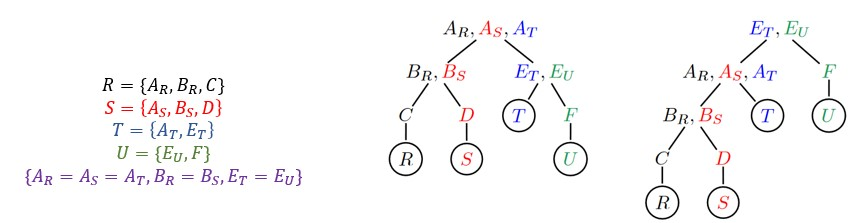
依靠F-tree，我们能够快速求解一个连接查询的因式分解的结果。构建方式类似于前缀树的构建：从树根开始，递归求解。假设我们递归到了 F-tree 的 u 节点，我们依靠 u 节点的祖先节点的取值确定 u 节点的取值，然后再递归到 u 节点的孩子。下图展示了一个连接查询的因式分解的求解过程：

构建一个 F-tree，可以按照以下几个步骤：

1. 选取一个属性作为根节点，把所有的关系删除这个属性
2. 将剩余的属性分成若干组，满足：如果这组包含某个关系的属性，那么这组应该包含这个关系的其他属性
3. 对于每组属性看成一个子问题，递归重复上述步骤。

除此之外，我们还可以通过超图树分解转化成一棵 F-tree. 但是超图树分解是 NPC 问题。

复杂度

对于数据库 ，连接查询 的 分解的 Readability 是  ，其中：

• 表示出现最多的关系出现的次数
• 表示将 分解上所有和 无关的属性取出来，获得的新的查询。因为无关属性决定了 的出现次数，也就是 readability。
• 表示查询 的最优超边分数覆盖。

总结

因式分解的方法不仅对关系型数据库有很大的帮助，而且对基于二维表格表示的数据结构也有很大的启发。目前，因式分解的思路在一些关系型数据库以外的领域有所应用，例如：图查询引擎，机器学习算法加速等。有几个方向我认为可以作为未来的工作：

1. 对于高维数据的因式分解：深度学习的张量都是高维的表示形式，如果能够对高维数据进行因式分解，势必能够有所帮助。
2. 判定二维关系表的冗余程度：因式分解的思路带来的代价是更高的常数，如果数据库的冗余程度较低，因式分解可能适得其反。

参考文献

1. Olteanu, D., & Závodný, J. (2012, March). Factorised representations of query results: size bounds and readability. In Proceedings of the 15th International Conference on Database Theory (pp. 285-298).

2. Olteanu, D., & Závodný, J. (2015). Size bounds for factorised representations of query results. ACM Transactions on Database Systems (TODS), 40(1), 1-44.

3. Olteanu D, Schleich M. Factorized databases[J]. ACM SIGMOD Record, 2016, 45(2): 5-16.

4. Gupta, P., Mhedhbi, A., & Salihoglu, S. (2021). Columnar storage and list-based processing for graph database management systems. arXiv preprint arXiv:2103.02284.

5. Smagulova, A., & Deutsch, A. (2021, June). Vertex-centric Parallel Computation of SQL Queries. In Proceedings of the 2021 International Conference on Management of Data (pp. 1664-1677).