Table of Contents

前言

第 1 章 最快最简单的排序——桶排序

第 2 章 算法 2：邻居好说话：冒泡排序

第 3 章 算法 3：最常用的排序——快速排序

第 4 章 排序总结：小哼买书

第 5 章 算法 4：队列——解密 QQ 号

第 6 章 算法 5：解密回文——栈

第 7 章 算法 6：只有五行的 Floyd 最短路算法

第 8 章 算法 7：Dijkstra 最短路算法

第 9 章 算法 8：巧妙的邻接表（数组实现）

第 10 章 算法 9：开启“树”之旅

第 11 章 算法 10：二叉树

第 12 章 算法 11：堆——神奇的优先队列（上）

前言

在各种算法流行的今天，小编为大家汇总了坐在马桶上看算法系列文章，文章图文并茂，风趣易懂，每天一算法让你轻松走进算法的世界，欢迎大家来学习。

适用人群

本书将繁琐难懂的算法问题，用风趣易懂的方式写出，适合初学者学习

学习前提

在你开始做本文提供的各种类型例子练习之前，你需要对 C++ 语言有一定的了解

致谢：http://blog.51cto.com/zt/595

1

最快最简单的排序——桶排序

在我们生活的这个世界中到处都是被排序过的。站队的时候会按照身高排序，考试的名次需要按照分数排序，网上购物的时候会按照价格排序，电子邮箱中的邮件按照时间排序……总之很多东西都需要排序，可以说排序是无处不在。现在我们举个具体的例子来介绍一下排序算法。

图片 1.1 picture1.1

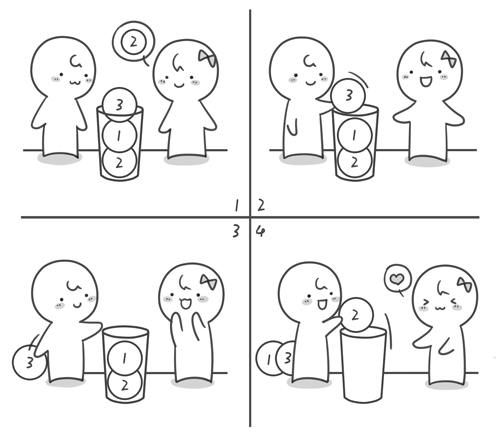
首先出场的我们的主人公小哼，上面这个可爱的娃就是啦。期末考试完了老师要将同学们的分数按照从高到低排序。小哼的班上只有 5 个同学，这 5 个同学分别考了 5 分、3 分、5 分、2 分和 8 分，哎考的真是惨不忍睹（满分是 10 分）。接下来将分数进行从大到小排序，排序后是 8 5 5 3 2。你有没有什么好方法编写一段程序，让计算机随机读入 5 个数然后将这 5 个数从大到小输出？请先想一想，至少想 15 分钟再往下看吧(*^__^*) 。

图片 1.2 picture1.2

我们这里只需借助一个一维数组就可以解决这个问题。请确定你真的仔细想过再往下看哦。

首先我们需要申请一个大小为 11 的数组 int a[11]。OK 现在你已经有了 11 个变量，编号从 a[0]~a[10]。刚开始的时候，我们将 a[0]~a[10]都初始化为 0，表示这些分数还都没有人得过。例如 a[0]等于 0 就表示目前还没有人得过 0 分，同理 a[1]等于 0 就表示目前还没有人得过 1 分……a[10]等于 0 就表示目前还没有人得过 10 分。

图片 1.3 picture1.3

下面开始处理每一个人的分数，第一个人的分数是 5 分，我们就将相对应 a[5]的值在原来的基础增加 1，即将 a[5]的值从 0 改为 1，表示 5 分出现过了一次。

图片 1.4 picture1.4

第二个人的分数是 3 分，我们就把相对应 a[3]的值在原来的基础上增加 1，即将 a[3]的值从 0 改为 1，表示 3 分出现过了一次。

图片 1.5 picture1.5

注意啦！第三个人的分数也是“5 分”，所以a[5]的值需要在此基础上再增加 1，即将 a[5]的值从 1 改为 2。表示 5 分出现过了两次。

图片 1.6 picture1.6

按照刚才的方法处理第四个和第五个人的分数。最终结果就是下面这个图啦。

图片 1.7 picture1.7

你发现没有，a[0]~a[10]中的数值其实就是 0 分到 10 分每个分数出现的次数。接下来，我们只需要将出现过的分数打印出来就可以了，出现几次就打印几次，具体如下。 a[0]为 0，表示“0”没有出现过，不打印。
a[1]为 0，表示“1”没有出现过，不打印。
a[2]为 1，表示“2”出现过 1 次，打印 2。
a[3]为 1，表示“3”出现过 1 次，打印 3。
a[4]为 0，表示“4”没有出现过，不打印。
a[5]为 2，表示“5”出现过 2 次，打印5 5。
a[6]为 0，表示“6”没有出现过，不打印。
a[7]为 0，表示“7”没有出现过，不打印。
a[8]为 1，表示“8”出现过 1 次，打印 8。
a[9]为 0，表示“9”没有出现过，不打印。
a[10]为 0，表示“10”没有出现过，不打印。
最终屏幕输出“2 3 5 5 8”，完整的代码如下。

 
#include <stdio.h>
int main()
{
int a[11],i,j,t;
for(i=0;i<=10;i++)
a[i]=0; //初始化为0
 
for(i=1;i<=5;i++) //循环读入5个数
{
scanf("%d",&t); //把每一个数读到变量t中
a[t]++; //进行计数
}
for(i=0;i<=10;i++) //依次判断a[0]~a[10]
for(j=1;j<=a[i];j++) //出现了几次就打印几次
printf("%d ",i);
getchar();getchar();
//这里的getchar();用来暂停程序，以便查看程序输出的内容
//也可以用system("pause");等来代替
return 0;
}

输入数据为

5 3 5 2 8

仔细观察的同学会发现，刚才实现的是从小到大排序。但是我们要求是从大到小排序，这该怎么办呢？还是先自己想一想再往下看哦。

其实很简单。只需要将 for(i=0;i<=10;i++)改为 for(i=10;i>=0;i--)就 OK 啦，快去试一试吧。

这种排序方法我们暂且叫他“桶排序”。因为其实真正的桶排序要比这个复杂一些，以后再详细讨论，目前此算法已经能够满足我们的需求了。

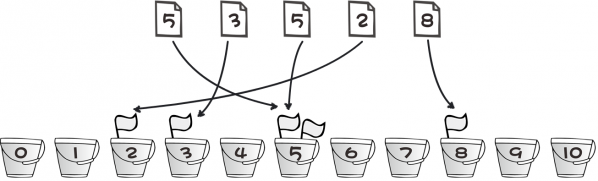
这个算法就好比有 11 个桶，编号从 0~10。每出现一个数，就将对应编号的桶中的放一个小旗子，最后只要数数每个桶中有几个小旗子就 OK 了。例如 2 号桶中有 1 个小旗子，表示 2 出现了一次；3 号桶中有 1 个小旗子，表示 3 出现了一次；5 号桶中有 2 个小旗子，表示 5 出现了两次；8 号桶中有 1 个小旗子，表示 8 出现了一次。

图片 1.8 picture1.8

现在你可以请尝试一下输入 n 个 0~1000 之间的整数，将他们从大到小排序。提醒一下如果需要对数据范围在 0~1000 之间的整数进行排序，我们需要 1001 个桶，来表示 0~1000 之间每一个数出现的次数，这一点一定要注意。另外此处的每一个桶的作用其实就是“标记”每个数出现的次数，因此我喜欢将之前的数组 a 换个更贴切的名字 book（book 这个单词有记录、标记的意思），代码实现如下。

 
#include <stdio.h>
int main()
{
int book[1001],i,j,t,n;
for(i=0;i<=1000;i++)
book[i]=0;
scanf("%d",&n);//输入一个数n，表示接下来有n个数
for(i=1;i<=n;i++)//循环读入n个数，并进行桶排序
{
scanf("%d",&t); //把每一个数读到变量t中
book[t]++; //进行计数，对编号为t的桶放一个小旗子
}
for(i=1000;i>=0;i--) //依次判断编号1000~0的桶
for(j=1;j<=book[i];j++) //出现了几次就将桶的编号打印几次
printf("%d ",i);
getchar();getchar();
return 0;
}

可以输入以下数据进行验证

10
8 100 50 22 15 6 1 1000 999 0

运行结果是

1000 999 100 50 22 15 8 6 1 0

最后来说下时间复杂度的问题。代码中第6行的循环一共循环了 m 次（m 为桶的个数），第 9 行的代码循环了 n 次（n 为待排序数的个数），第 14 和 15 行一共循环了 m+n 次。所以整个排序算法一共执行了 m+n+m+n 次。我们用大写字母 O 来表示时间复杂度，因此该算法的时间复杂度是 O(m+n+m+n)即 O(2*(m+n))。我们在说时间复杂度时候可以忽略较小的常数，最终桶排序的时间复杂度为 O(m+n)。还有一点，在表示时间复杂度的时候，n 和 m 通常用大写字母即 O(M+N)。

这是一个非常快的排序算法。桶排序从 1956 年就开始被使用，该算法的基本思想是由 E.J.Issac R.C.Singleton 提出来。之前说过，其实这并不是真正的桶排序算法，真正的桶排序算法要比这个更加复杂。但是考虑到此处是算法讲解的第一篇，我想还是越简单易懂越好，真正的桶排序留在以后再聊吧。需要说明一点的是：我们目前学习的简化版桶排序算法其本质上还不能算是一个真正意义上的排序算法。为什么呢？例如遇到下面这个例子就没辙了。

现在分别有 5 个人的名字和分数：huhu 5 分、haha 3 分、xixi 5 分、hengheng 2 分和 gaoshou 8 分。请按照分数从高到低，输出他们的名字。即应该输出 gaoshou、huhu、xixi、haha、hengheng。发现问题了没有？如果使用我们刚才简化版的桶排序算法仅仅是把分数进行了排序。最终输出的也仅仅是分数，但没有对人本身进行排序。也就是说，我们现在并不知道排序后的分数原本对应着哪一个人！这该怎么办呢？不要着急请听下回——冒泡排序。

【一周一算法】算法 1：最快最简单的排序——桶排序
http://bbs.ahalei.com/thread-4399-1-1.html

本文出自 “啊哈磊” 博客，请务必保留此出处 http://ahalei.blog.51cto.com/4767671/1362789

2

算法 2：邻居好说话：冒泡排序

简化版的桶排序不仅仅有上一节所遗留的问题，更要命的是：它非常浪费空间！例如需要排序数的范围是 0~2100000000 之间，那你则需要申请 2100000001 个变量，也就是说要写成 int a[2100000001]。因为我们需要用 2100000001 个“桶”来存储 0~2100000000 之间每一个数出现的次数。即便只给你 5 个数进行排序（例如这 5 个数是 1，1912345678，2100000000，18000000 和 912345678），你也仍然需要 2100000001 个“桶”，这真是太浪费了空间了！还有，如果现在需要排序的不再是整数而是一些小数，比如将 5.56789，2.12，1.1，3.123，4.1234 这五个数进行从小大排序又该怎么办呢？现在我们来学习另一种新的排序算法：冒泡排序。它可以很好的解决这两个问题。

冒泡排序的基本思想是：每次比较两个相邻的元素，如果他们的顺序错误就把他们交换过来。

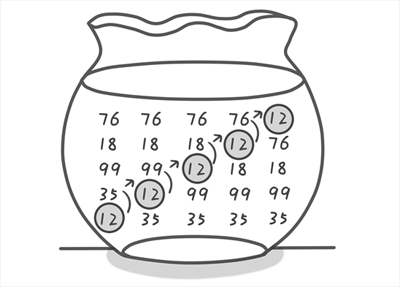
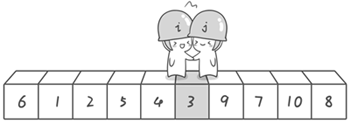
例如我们需要将 12 35 99 18 76 这 5 个数进行从大到小进行排序。既然是从大到小排序也就是说越小的越靠后，你是不是觉得我在说废话，但是这句话很关键(∩_∩)。

首先比较第 1 位和第 2 位的大小，现在第 1 位是 12，第 2 位是 35。发现 12 比 35 要小，因为我们希望越小越靠后嘛，因此需要交换这两个数的位置。交换之后这 5 个数的顺序是 35 12 99 18 76。

按照刚才的方法，继续比较第 2 位和第 3 位的大小，第 2 位是 12，第 3 位是 99。12 比 99 要小，因此需要交换这两个数的位置。交换之后这 5 个数的顺序是 35 99 12 18 76。

根据刚才的规则，继续比较第 3 位和第 4 位的大小，如果第 3 位比第 4 位小，则交换位置。交换之后这 5 个数的顺序是 35 99 18 12 76。

最后，比较第 4 位和第 5 位。4 次比较之后 5 个数的顺序是 35 99 18 76 12。

经过 4 次比较后我们发现最小的一个数已经就位（已经在最后一位，请注意 12 这个数的移动过程），是不是很神奇。现在再来回忆一下刚才比较的过程。每次都是比较相邻的两个数，如果后面的数比前面的数大，则交换这两个数的位置。一直比较下去直到最后两个数比较完毕后，最小的数就在最后一个了。就如同是一个气泡，一步一步往后“翻滚”，直到最后一位。所以这个排序的方法有一个很好听的名字“冒泡排序”。

图片 2.1 picture2.1

说道这里其实我们的排序只将 5 个数中最小的一个归位了。每将一个数归位我们将其称为“一趟”。下面我们将继续重复刚才的过程，将剩下的 4 个数一一归位。

好现在开始“第二趟”，目标是将第 2 小的数归位。首先还是先比较第 1 位和第 2 位，如果第 1 位比第 2 位小，则交换位置。交换之后这 5 个数的顺序是 99 35 18 76 12。接下来你应该都会了，依次比较第 2 位和第 3 位，第 3 位和第 4 位。注意此时已经不需要再比较第 4 位和第 5 位。因为在第一趟结束后已经可以确定第 5 位上放的是最小的了。第二趟结束之后这 5 个数的顺序是 99 35 76 18 12。

“第三趟”也是一样的。第三趟之后这 5 个数的顺序是 99 76 35 18 12。

现在到了最后一趟“第四趟”。有的同学又要问了，这不是已经排好了吗？还要继续？当然，这里纯属巧合，你可以用别的数试一试可能就不是了。你能找出这样的数据样例来吗？请试一试。

“冒泡排序”原理是：每一趟只能确定将一个数归位。即第一趟只能确定将末位上的数（既第 5 位）归位，第二趟只能将倒数第 2 位上的数（既第 4 位）归位，第三趟只能将倒数第 3 位上的数（既第 3 位）归位，而现在前面还有两个位置上的数没有归位，因此我们仍然需要进行“第四趟”。

“第四趟”只需要比较第 1 位和第 2 位的大小。因为后面三个位置上的数归位了，现在第 1 位是 99，第 2 位是 76，无需交换。这 5 个数的顺序不变仍然是 99 76 35 18 12。到此排序完美结束了，5 个数已经有 4 个数归位，那最后一个数也只能放在第 1 位了。

最后我们总结一下：如果有 n 个数进行排序，只需将 n-1 个数归位，也就是说要进行 n-1 趟操作。而“每一趟”都需要从第 1 位开始进行相邻两个数的比较，将较小的一个数放在后面，比较完毕后向后挪一位继续比较下面两个相邻数的大小，重复此步骤，直到最后一个尚未归位的数，已经归位的数则无需再进行比较（已经归位的数你还比较个啥，浪费表情）。

这个算法是不是很强悍。记得我每次拍集体照的时候就总是被别人换来换去的，当时特别烦。不知道发明此算法的人当时的灵感是否来源于此。罗里吧嗦地说了这么多，下面是代码。建议先自己尝试去实现一下看看，再来看我是如何实现的。

 
#include <stdio.h>
int main()
{
int a[100],i,j,t,n;
scanf("%d",&n); //输入一个数n，表示接下来有n个数
for(i=1;i<=n;i++) //循环读入n个数到数组a中
scanf("%d",&a[i]);
//冒泡排序的核心部分
for(i=1;i<=n-1;i++) //n个数排序，只用进行n-1趟
{
for(j=1;j<=n-i;j++) //从第1位开始比较直到最后一个尚未归位的数，想一想为什么到n-i就可以了。
{
if(a[j]<a[j+1]) //比较大小并交换
{ t=a[j]; a[j]=a[j+1]; a[j+1]=t; }
}
}
for(i=1;i<=n;i++) //输出结果
printf("%d ",a[i]);
getchar();getchar();
return 0;
}

可以输入以下数据进行验证

1081005022156110009990

运行结果是

01681522501009991000

将上面代码稍加修改，就可以解决第 1 节遗留的问题，如下。

 
#include <stdio.h>
struct student
{
char name[21];
char score;
};//这里创建了一个结构体用来存储姓名和分数
int main()
{
struct student a[100],t;
int i,j,n;
scanf("%d",&n); //输入一个数n
for(i=1;i<=n;i++) //循环读入n个人名和分数
scanf("%s %d",a[i].name,&a[i].score);
//按分数从高到低进行排序
for(i=1;i<=n-1;i++)
{
for(j=1;j<=n-i;j++)
{
if(a[j].score<a[j+1].score)//对分数进行比较
{ t=a[j]; a[j]=a[j+1]; a[j+1]=t; }
}
}
for(i=1;i<=n;i++)//输出人名
printf("%s\n",a[i].name);
getchar();getchar();
return 0;
}

可以输入以下数据进行验证

5
huhu 5
haha 3
xixi 5
hengheng 2
gaoshou 8

运行结果是

gaoshou
huhu
xixi
haha
hengheng

冒泡排序的核心部分是双重嵌套循环。不难看出冒泡排序的时间复杂度是 O(N2)。这是一个非常高的时间复杂度。冒泡排序早在 1956 年就有人开始研究，之后有很多人都尝试过对冒泡排序进行改进，但结果却令人失望。如 Knuth（Donald E. Knuth 中文名为高德纳，1974 年图灵奖获得者）所说：“冒泡排序除了它迷人的名字和导致了某些有趣的理论问题这一事实之外，似乎没有什么值得推荐的。”你可能要问：那还有没有更好的排序算法呢？请期待下周更新——快速排序。

【一周一算法】算法 2：邻居好说话——冒泡排序
http://bbs.ahalei.com/thread-4400-1-1.html

3

算法 3：最常用的排序——快速排序

上一节的冒泡排序可以说是我们学习第一个真正的排序算法，并且解决了桶排序浪费空间的问题，但在算法的执行效率上却牺牲了很多，它的时间复杂度达到了 O(N2)。假如我们的计算机每秒钟可以运行 10 亿次，那么对 1 亿个数进行排序，桶排序则只需要 0.1 秒，而冒泡排序则需要 1 千万秒，达到 115 天之久，是不是很吓人。那有没有既不浪费空间又可以快一点的排序算法呢？那就是“快速排序”啦！光听这个名字是不是就觉得很高端呢。

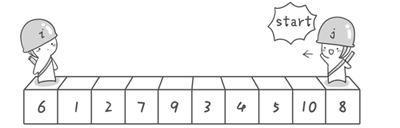
假设我们现在对“6 1 2 7 9 3 4 5 10 8”这个 10 个数进行排序。首先在这个序列中随便找一个数作为基准数（不要被这个名词吓到了，就是一个用来参照的数，待会你就知道它用来做啥的了）。为了方便，就让第一个数 6 作为基准数吧。接下来，需要将这个序列中所有比基准数大的数放在 6 的右边，比基准数小的数放在 6 的左边，类似下面这种排列。

3 1 2 5 4 6 9 7 10 8

在初始状态下，数字 6 在序列的第 1 位。我们的目标是将 6 挪到序列中间的某个位置，假设这个位置是 k。现在就需要寻找这个 k，并且以第 k 位为分界点，左边的数都小于等于 6，右边的数都大于等于 6。想一想，你有办法可以做到这点吗？

给你一个提示吧。请回忆一下冒泡排序，是如何通过“交换”，一步步让每个数归位的。此时你也可以通过“交换”的方法来达到目的。具体是如何一步步交换呢？怎样交换才既方便又节省时间呢？先别急着往下看，拿出笔来，在纸上画画看。我高中时第一次学习冒泡排序算法的时候，就觉得冒泡排序很浪费时间，每次都只能对相邻的两个数进行比较，这显然太不合理了。于是我就想了一个办法，后来才知道原来这就是“快速排序”，请允许我小小的自恋一下(^o^)。

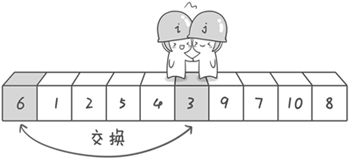
方法其实很简单：分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于 6 的数，再从左往右找一个大于 6 的数，然后交换他们。这里可以用两个变量 i 和 j，分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵 i”和“哨兵 j”。刚开始的时候让哨兵 i 指向序列的最左边（即 i=1），指向数字 6。让哨兵 j 指向序列的最右边（即 j=10），指向数字 8。

图片 3.1 picture3.1

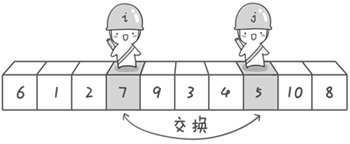
首先哨兵 j 开始出动。因为此处设置的基准数是最左边的数，所以需要让哨兵 j 先出动，这一点非常重要（请自己想一想为什么）。哨兵 j 一步一步地向左挪动（即 j--），直到找到一个小于 6 的数停下来。接下来哨兵 i 再一步一步向右挪动（即 i++），直到找到一个数大于 6 的数停下来。最后哨兵 j 停在了数字 5 面前，哨兵 i 停在了数字 7 面前。

图片 3.2 picture3.2

图片 3.3 picture3.3

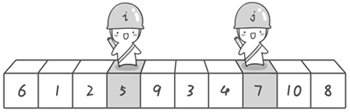
现在交换哨兵 i 和哨兵 j 所指向的元素的值。交换之后的序列如下。

6 1 2 5 9 3 4 7 10 8

图片 3.4 picture3.4

图片 3.5 picture3.5

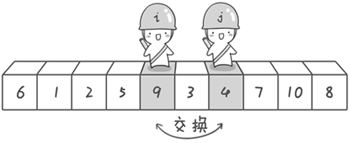
到此，第一次交换结束。接下来开始哨兵 j 继续向左挪动（再友情提醒，每次必须是哨兵 j 先出发）。他发现了 4（比基准数 6 要小，满足要求）之后停了下来。哨兵 i 也继续向右挪动的，他发现了 9（比基准数 6 要大，满足要求）之后停了下来。此时再次进行交换，交换之后的序列如下。

6 1 2 5 4 3 9 7 10 8

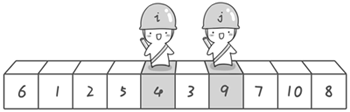
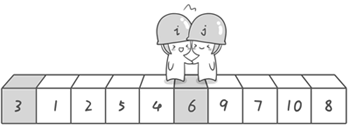
第二次交换结束，“探测”继续。哨兵 j 继续向左挪动，他发现了 3（比基准数 6 要小，满足要求）之后又停了下来。哨兵 i 继续向右移动，糟啦！此时哨兵 i 和哨兵 j 相遇了，哨兵 i 和哨兵 j 都走到 3 面前。说明此时“探测”结束。我们将基准数 6 和 3 进行交换。交换之后的序列如下。

3 1 2 5 4 6 9 7 10 8

图片 3.6 picture3.6

图片 3.7 picture3.7

图片 3.8 picture3.8

到此第一轮“探测”真正结束。此时以基准数 6 为分界点，6 左边的数都小于等于 6，6 右边的数都大于等于 6。回顾一下刚才的过程，其实哨兵 j 的使命就是要找小于基准数的数，而哨兵 i 的使命就是要找大于基准数的数，直到 i 和 j 碰头为止。

OK，解释完毕。现在基准数 6 已经归位，它正好处在序列的第 6 位。此时我们已经将原来的序列，以 6 为分界点拆分成了两个序列，左边的序列是“3 1 2 5 4”，右边的序列是“ 9 7 10 8 ”。接下来还需要分别处理这两个序列。因为 6 左边和右边的序列目前都还是很混乱的。不过不要紧，我们已经掌握了方法，接下来只要模拟刚才的方法分别处理 6 左边和右边的序列即可。现在先来处理 6 左边的序列现吧。

左边的序列是“3 1 2 5 4”。请将这个序列以 3 为基准数进行调整，使得 3 左边的数都小于等于 3，3 右边的数都大于等于 3。好了开始动笔吧。

如果你模拟的没有错，调整完毕之后的序列的顺序应该是。

2 1 3 5 4

OK，现在 3 已经归位。接下来需要处理 3 左边的序列“ 2 1 ”和右边的序列“5 4”。对序列“ 2 1 ”以 2 为基准数进行调整，处理完毕之后的序列为“1 2”，到此 2 已经归位。序列“1”只有一个数，也不需要进行任何处理。至此我们对序列“ 2 1 ”已全部处理完毕，得到序列是“1 2”。序列“5 4”的处理也仿照此方法，最后得到的序列如下。

1 2 3 4 5 6 9 7 10 8

对于序列“9 7 10 8”也模拟刚才的过程，直到不可拆分出新的子序列为止。最终将会得到这样的序列，如下。

1 2 3 4 5 6 7 8 9 10

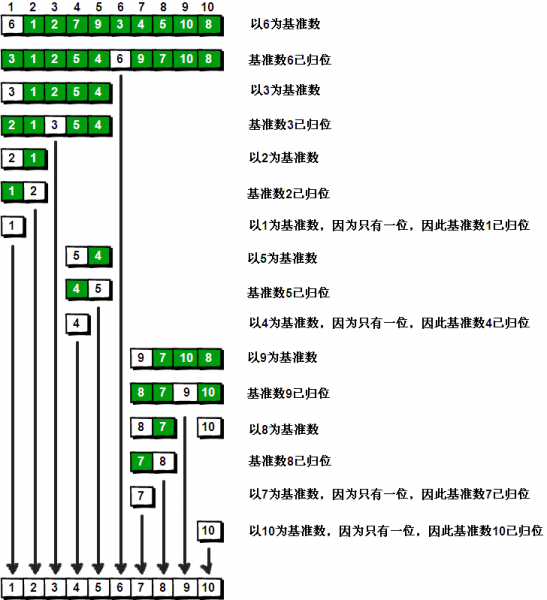
到此，排序完全结束。细心的同学可能已经发现，快速排序的每一轮处理其实就是将这一轮的基准数归位，直到所有的数都归位为止，排序就结束了。下面上个霸气的图来描述下整个算法的处理过程。

图片 3.9 picture3.9

快速排序之所比较快，因为相比冒泡排序，每次交换是跳跃式的。每次排序的时候设置一个基准点，将小于等于基准点的数全部放到基准点的左边，将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换，交换的距离就大的多了。因此总的比较和交换次数就少了，速度自然就提高了。当然在最坏的情况下，仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和冒泡排序是一样的都是 O(N2)，它的平均时间复杂度为 O(NlogN)。其实快速排序是基于一种叫做“二分”的思想。我们后面还会遇到“二分”思想，到时候再聊。先上代码，如下。

 
#include <stdio.h>
int a[101],n;//定义全局变量，这两个变量需要在子函数中使用
void quicksort(int left,int right)
{
int i,j,t,temp;
if(left>right)
return;
 
temp=a[left]; //temp中存的就是基准数
i=left;
j=right;
while(i!=j)
{
//顺序很重要，要先从右边开始找
while(a[j]>=temp && i<j)
j--;
//再找右边的
while(a[i]<=temp && i<j)
i++;
//交换两个数在数组中的位置
if(i<j)
{
t=a[i];
a[i]=a[j];
a[j]=t;
}
}
//最终将基准数归位
a[left]=a[i];
a[i]=temp;
 
quicksort(left,i-1);//继续处理左边的，这里是一个递归的过程
quicksort(i+1,right);//继续处理右边的 ，这里是一个递归的过程
}
int main()
{
int i,j,t;
//读入数据
scanf("%d",&n);
for(i=1;i<=n;i++)
scanf("%d",&a[i]);
quicksort(1,n); //快速排序调用
 
//输出排序后的结果
for(i=1;i<=n;i++)
printf("%d ",a[i]);
getchar();getchar();
return 0;
}

可以输入以下数据进行验证

1061279345108

运行结果是

12345678910

下面是程序执行过程中数组 a 的变化过程，带下划线的数表示的已归位的基准数。

 
1 2 7 9 3 4 5 10 8
1 2 5 4 6 9 7 10 8
1 3 5 4 6 9 7 10 8
2 3 5 4 6 9 7 10 8
2 3 5 4 6 9 7 10 8
2 3 4 5 6 9 7 10 8
2 3 4 5 6 9 7 10 8
2 3 4 5 6 8 7 9 10
2 3 4 5 6 7 8 9 10
2 3 4 5 6 7 8 9 10
2 3 4 5 6 7 8 9 10

快速排序由 C. A. R. Hoare（东尼霍尔，Charles Antony Richard Hoare）在 1960 年提出，之后又有许多人做了进一步的优化。如果你对快速排序感兴趣可以去看看东尼霍尔 1962 年在 Computer Journal 发表的论文“Quicksort”以及《算法导论》的第七章。快速排序算法仅仅是东尼霍尔在计算机领域才能的第一次显露，后来他受到了老板的赏识和重用，公司希望他为新机器设计一个新的高级语言。你要知道当时还没有 PASCAL 或者C语言这些高级的东东。后来东尼霍尔参加了由 Edsger Wybe Dijkstra（1972 年图灵奖得主，这个大神我们后面还会遇到的到时候再细聊）举办的“ALGOL 60”培训班，他觉得自己与其没有把握去设计一个新的语言，还不如对现有的“ALGOL 60”进行改进，使之能在公司的新机器上使用。于是他便设计了“ALGOL 60”的一个子集版本。这个版本在执行效率和可靠性上都在当时“ALGOL 60”的各种版本中首屈一指，因此东尼霍尔受到了国际学术界的重视。后来他在“ALGOL X”的设计中还发明了大家熟知的“case”语句，后来也被各种高级语言广泛采用，比如 PASCAL、C、Java 语言等等。当然，东尼霍尔在计算机领域的贡献还有很多很多，他在 1980 年获得了图灵奖。

【一周一算法】算法 3：最常用的排序——快速排序
http://bbs.ahalei.com/thread-4419-1-1.html

4

排序总结：小哼买书

之前讲了三种常用的经典排序。排序算法还有很多，例如选择排序、计数排序、基数排序、插入排序、归并排序和堆排序等等。堆排序是基于二叉树的排序，以后再说吧。先分享一个超酷的排序算法的视频。

再来看一个具体的例子《小哼买书》来看看三个排序在应用上的区别和局限性。 小哼的学校要建立一个图书角，老师派小哼去找一些同学做调查，看看同学们都喜欢读哪些书。小哼让每个同学写出一个自己最想读的书的 ISBN 号（你知道吗？每本书都有唯一的 ISBN 号，不信话你去找本书翻到背面看看）。当然有一些好书会有很多同学都喜欢，这样就会收集到很多重复的 ISBN 号。小哼需要去掉其中重复的 ISBN 号，即每个 ISBN 号只保留一个，也就说同样的书只买一本（学校真是够抠门的）。然后再把这些 ISBN 号从小到大排序，小哼将按照排序好的 ISBN 号去书店去买书。请你协助小哼完成“去重”与“排序”的工作。

图片 4.1 picturez.1

输入有 2 行，第 1 行为一个正整数，表示有 n 个同学参与调查（n<=100）。第 2 行有 n 个用空格隔开的正整数，为每本图书的 ISBN 号（假设图书的 ISBN 号在 1~1000 之间）。

输出也是 2 行，第 1 行为一个正整数k，表示需要买多少本书。第 2 行为 k 个用空格隔开的正整数，为从小到大已排好序的需要购买的图书 ISBN 号。 例如输入

102040326740208930040015

则输出

8152032406789300400

最后，程序运行的时间限制为：1秒。

解决这个问题的方法大致有两种，第一种方法：先将这 n 个图书的 ISBN 号去重，再进行从小到大排序并输出。第二种方法：先从小到大排序，输出的时候再去重。这两种方法都可以。

先来看第一种方法。通过第一节的学习我们发现桶排序稍加改动正好可以起到去重的效果，因此我们可以使用桶排序的方法来解决此问题。

 
#include <stdio.h>
int main()
{
int a[1001],n,i,t;
for(i=1;i<=1000;i++)
a[i]=0; //初始化
 
scanf("%d",&n); //读入n
for(i=1;i<=n;i++) //循环读入n个图书的ISBN号
{
scanf("%d",&t); //把每一个ISBN号读到变量t中
a[t]=1; //标记出现过的ISBN号
}
 
for(i=1;i<=1000;i++) //依次判断1~1000这个1000个桶
{
if(a[i]==1)//如果这个ISBN号出现过则打印出来
printf("%d ",i);
}
 
getchar();getchar();
return 0;
}

这种方法的时间复杂度是就是桶排序的时间复杂度为 O(N+M)。

第二种方法我们需要先排序再去重。排序我们可以用冒泡排序或者快速排序。

20 40 32 67 40 20 89 300 400 15

将这 10 个数从小到大排序之后为 15 20 20 32 40 40 67 89 300 400。

接下来，要在输出的时候去掉重复的。因为我们已经排好序，因此相同的数都会紧挨在一起。只要在输出的时候，预先判断一下当前这个数 a 与前面一个数 a[i-1]是否相同。如果相同则表示这个数之前已经输出过了，不同再次输出。不同则表示这个数是第一次出现需要，则需要输出这个数。

 
#include <stdio.h>
int main()
{
int a[101],n,i,j,t;
 
scanf("%d",&n); //读入n
for(i=1;i<=n;i++) //循环读入n个图书ISBN号
{
scanf("%d",&a[i]);
}
 
//开始冒泡排序
for(i=1;i<=n-1;i++)
{
for(j=1;j<=n-i;j++)
{
if(a[j]>a[j+1])
{ t=a[j]; a[j]=a[j+1]; a[j+1]=t; }
}
}
printf("%d ",a[1]); //输出第1个数
for(i=2;i<=n;i++) //从2循环到n
{
if( a[i] != a[i-1] ) //如果当前这个数是第一次出现则输出
printf("%d ",a[i]);
}
 
getchar();getchar();
return 0;
}

这种方法的时间复杂度由两部分组成，一部分是冒泡排序时间复杂度是 O(N2)，另一部分是读入和输出都是 O(N)，因此整个算法的时间复杂度是 O(2N+N2)。相对于 N2 来说，2N 可以忽略（我们通常忽略低阶），最终该方法的时间复杂度是 O(N2)。

接下来我们还需要看下数据范围。每个图书 ISBN 号都是 1~1000 之间的整数，并且参加调查的同学人数不超过 100，即 n<=100。之前已经说过，在粗略计算时间复杂度的时候，我们通常认为计算机每秒钟大约运行 10 亿次（当然实际情况要更快）。因此以上两种方法都可以在 1 秒钟内计算出解。如果题目图书 ISBN 号范围不是在 1~1000 之间，而是 -2147483648~2147483647 之间的话，那么第一种方法就不可行了，因为你无法申请出这么大数组来标记每一个 ISBN 号是否出现过。另外如果 n 的范围不是小于等于 100 而是小于等于 10 万，那么第二种方法的排序部分也不能使用冒泡排序。因为题目要求的时间限制是 1 秒，使用冒泡排序对 10 万个数的排序，计算机需要运行 100 亿次，需要 10 秒钟，需要替换为快速排序，快速排序只需要 100000×log2100000≈100000×17≈170 万次，这还不到 0.0017 秒。是不是很神奇，同样的问题使用不同的算法竟然有如此之大的时间差距，这就是算法的魅力！

我们来回顾一下本章三种排序算法的时间复杂度。桶排序是最快的，它的时间复杂度是 O(N+M)；冒泡排序是 O(N2)；快速排序是 O(NlogN)。

【一周一算法】小哼买书
http://bbs.ahalei.com/thread-4443-1-1.html
(出处: 啊哈磊_编程从这里起步)

5

算法 4：队列——解密 QQ 号

新学期开始了，小哈是小哼的新同桌（小哈是个小美女哦~），小哼向小哈询问 QQ 号，小哈当然不会直接告诉小哼啦，原因嘛你懂的。所以小哈给了小哼一串加密过的数字，同时小哈也告诉了小哼解密规则。规则是这样的：首先将第 1 个数删除，紧接着将第 2 个数放到这串数的末尾，再将第 3个数删除并将第 4 个数再放到这串数的末尾，再将第 5 个数删除……直到剩下最后一个数，将最后一个数也删除。按照刚才删除的顺序，把这些删除的数连在一起就是小哈的 QQ 啦。现在你来帮帮小哼吧。小哈给小哼加密过的一串数是“6 3 1 75 8 9 2 4”。

图片 5.1 picture4.1

OK，现在轮到你动手的时候了。快去找出 9 张便签或小纸片，将“6 3 1 75 8 9 2 4”这 9 个数分别写在 9 张便签上，模拟一下解密过程。如果你没有理解错解密规则的话，解密后小哈的 QQ 号应该是“6 1 5 94 7 2 8 3”。

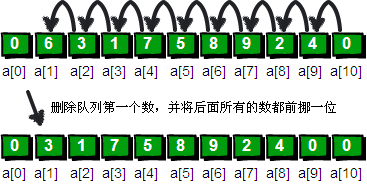
其实解密的过程就像是将这些数“排队”。每次从最前面拿两个，第 1 个扔掉，第 2 个放到尾部。具体过程是这样的：刚开始这串数是“6 3 1 75 8 9 2 4”，首先删除 6 并将 3 放到这串数的末尾，这串数更新为“1 7 5 89 2 4 3”。接下来删除 1 并将 7 放到末尾，即更新为“5 8 9 24 3 7”。再删除 5 并将 8 放到末尾即“9 2 4 3 7 8”，删除 9 并将 2 放到末尾即“4 3 7 8 2”，删除 4 并将 3 放到末尾即“7 8 2 3”，删除 7 并将 8 放到末尾即“2 3 8”，删除 2 并将 3 放到末尾即“8 3”，删除 8 并将 3 放到末尾即“3”，最后删除 3。因此被删除的顺序是“6 1 5 9 4 7 2 8 3”，这就是小哈的 QQ 号码了，你可以加她试试看^_^。

既然现在已经搞清楚了解密法则，不妨自己尝试一下去编程，我相信你一定可以写出来的。

首先需要一个数组来存储这一串数即 intq[101]。并初始化这个数组即 intq[101]={0,6,3,1,7,5,8,9,2,4};（此处初始化是我多写了一个 0，用来填充 q[0]，因为我比较喜欢从 q[1]开始用，对数组初始化不是很理解的同学可以去看下我的上一本书《啊哈 C！思考快你一步》）接下来就是模拟解密的过程了。

解密的第一步是将第一个数删除，你可以想一下如何在数组中删除一个数呢？最简单的方法是将所有后面的数都往前面挪动一位，将前面的数覆盖。就好比我们在排队买票，最前面的人买好离开了，后面所有的人就需要全部向前面走一步，补上之前的空位，但是这样的做法很耗费时间。

图片 5.2 picture4.2

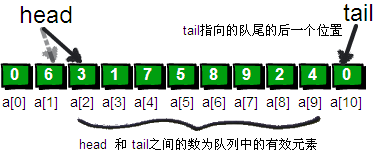
在这里，我将引入两个整型变量 head 和 tail。head 用来记录队列的队首（即第一位），tail 用来记录队列的队尾（即最后一位）的下一个位置。你可能会问为什么 tail 不直接记录队尾，却要记录队尾的下一个位置呢？这是因为当队列当中只剩下一个元素时，队首和队尾重合会带来一些麻烦。我们这里规定队首和队尾重合时，队列为空。

现在有 9 个数，9 个数全部放入队列之后 head=1;tail=10;此时 head 和 tail 之间的数就是目前队列中“有效”的数。如果要删除一个数的话，就将 head++ 就 OK 了，这样仍然可以保持 head 和 tail 之间的数为目前队列中“有效”的数。这样做虽然浪费了一个空间，却节省了大量的时间，这是非常划算的。新增加一个数也很简单，把需要增加的数放到队尾即 q[tail]之后再 tail++ 就欧克啦。

图片 5.3 picture4.3

我们来小结一下，在队首删除一个数的操作是 head++;
在队尾增加一个数（假设这个数是x）的操作是 q[tail]=x;tail++;
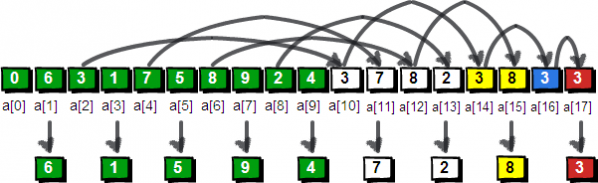
整个解密过程，请看下面这个霸气外漏的图。

图片 5.4 picture4.4

最后的输出就是 6 1 5 94 7 2 8 3，代码实现如下。

 
#include <stdio.h>
int main()
{
int q[102]={0,6,3,1,7,5,8,9,2,4},head,tail;
int i;
//初始化队列
head=1;
tail=10; //队列中已经有9个元素了，tail执向的队尾的后一个位置
while(head<tail) //当队列不为空的时候执行循环
{
//打印队首并将队首出队
printf("%d ",q[head]);
head++;
 
//先将新队首的数添加到队尾
q[tail]=q[head];
tail++;
//再将队首出队
head++;
}
 
getchar();getchar();
return 0;
}

怎么样上面的代码运行成功没有？现在我们再来总结一下队列的概念。队列是一种特殊的线性结构，它只允许在队列的首部（head）进行删除操作称之为“出队”，而在队列的尾部（tail）进行插入操作称之为“入队”。当队列中没有元素时（即 head==tail），称为空队列。在我们的日常生活中有很多情况都符合队列的特性。比如我们之前提到过的买票，每个排队买票的窗口就是一个队列。在这个队列当中，新来的人总是站在队列的最后面，来的越早的人越靠前也就越早能买到票，就是先来的人先服务，我们称为“先进先出”（First InFirst Out，FIFO）原则。

队列将是我们今后学习广度优先搜索以及队列优化的 Bellman-Ford 最短路算法的核心数据结构。所以现在将队列的三个基本元素（一个数组，两个变量）封装为一个结构体类型，如下。

 
struct queue
{
int data[100];//队列的主体，用来存储内容
int head;//队首
int tail;//队尾
};

上面我们定义了一个结构体类型，我们通常将其放在 main 函数的外面，请注意结构体的定义末尾有个;号。struct 是结构体的关键字，queue 是我们为这个结构体起的名字。这个结构体有三个成员分别是：整型数组 data、整型 head 和整型 tail。这样我们就可以把这三个部分放在一起作为一个整体来对待。你可以这么理解：我们定义了一个新的数据类型，这个新类型非常强大，用这个新类型定义出的每一个变量可以同时存储一个整型数组和两个整数。

图片 5.5 picture4.5

有了新的结构体类型，如何定义结构体变量呢？很简单，这与我们之前定义变量的方式是一样，如下。

 
struct queue q;

请注意 struct queue 需要整体使用，不能直接写 queue q;这样我们就定义了一个结构体变量 q。这个结构体变量 q 就可以满足队列的所有操作了。那又该如何访问结构体变量的内部成员呢？可以使用.号，它叫做成员运算符或者点号运算符，如下：

 
q.head=1;
q.tail=1;
scanf("%d",&q.data[q.tail]);

好了，下面这段代码就是使用结构体来实现的队列操作。

 
#include <stdio.h>
struct queue
{
int data[100];//队列的主体，用来存储内容
int head;//队首
int tail;//队尾
};
 
int main()
{
struct queue q;
int i;
//初始化队列
q.head=1;
q.tail=1;
for(i=1;i<=9;i++)
{
//依次向队列插入9个数
scanf("%d",&q.data[q.tail]);
q.tail++;
}
 
while(q.head<q.tail) //当队列不为空的时候执行循环
{
//打印队首并将队首出队
printf("%d ",q.data[q.head]);
q.head++;
 
//先将新队首的数添加到队尾
q.data[q.tail]=q.data[q.head];
q.tail++;
//再将队首出队
q.head++;
}
 
getchar();getchar();
return 0;
}

【一周一算法】解密 QQ 号——队列
http://bbs.ahalei.com/thread-4489-1-1.html
(出处: 啊哈磊_编程从这里起步)

6

算法 5：解密回文——栈

上一节中我们学习了队列，它是一种先进先出的数据结构。还有一种是后进先出的数据结构它叫做栈。栈限定只能在一端进行插入和删除操作。比如说有一个小桶，小桶的直径只能放一个小球，我们现在向小桶内依次放入 2 号、1 号、3 号小球。假如你现在需要拿出 2 号小球，那就必须先将 3 号小球拿出，再拿出 1 号小球，最后才能将 2 号小球拿出来。在刚才取小球的过程中，我们最先放进去的小球最后才能拿出来，而最后放进去的小球却可以最先拿出来。这就是后进先出，也可以称为先进后出。

图片 6.1 picture5.1

我们生活中还有很多这样的例子，比如我们在吃桶装薯片的时候，要想吃掉最后一片，就必须把前面的全部吃完（貌似现在的桶装薯片为了减少分量，在桶里面增加了一个透明的抽屉）；再比如我们浏览网页时候需要退回到之前的某个网页，我们需要一步步的点击后退键。还有手-枪的弹夹，在装子弹的时候，最后装的一发子弹，是被第一个打出去的。栈的实现也很简单，只需要一个一维数组和一个指向栈顶的变量 top 就可以了。我们通过变量 top 来对栈进行插入和删除操作。

这种特殊的数据结构栈究竟有哪些作用呢？我们来看一个例子。“xyzyx”是一个回文字符串，所谓回文字符串就是指正读反读均相同的字符序列，如“席主席”、“记书记”、“aha”和“ahaha”均是回文，但“ahah”不是回文。通过栈这个数据结构我们将很容易判断一个字符串是否为回文。

首先我们需要读取这行字符串，并求出这个字符串的长度。

char a[101]; //101是一个估算值，只需比待读入的字符串长度大即可
int len;
gets(a);
len=strlen(a);

如果一个字符串是回文的话，那么它必须是中间对称，我们需要求这个字符串的 中点，即：

mid=len/2-1;

接下来就轮到栈出场了。

我们先将 mid 之前的部分的字符全部入栈。因为这里的栈是用来存储字符的，所以这里用来实现栈的数组类型是字符数组即 char s[101]; 初始化栈很简单，top=0;就可以了。入栈的操作是 top++;s[top]=x; （假设需要入栈的字符存储暂存在字符变量 x 中）其实可以简写为 s[++top]=x;

现在我们就来将 mid 之前的字符依次全部入栈。这里循环要 0 开始，因为刚才读取字符串使用了 gets()函数，读取的第一个字符存储在 s[0]中，随后一个字符存储在 s[len-1]中。

 
for(i=0;i<=mid;i++)
{
s[++top]=a[i];
}

接下来进入判断回文的关键步骤。将当前栈中的字符依次出栈，看看是否能与 mid 之后的字符一一匹配，如果都能匹配则说明这个字符串是回文字符串，否则这个字符串就不是回文字符串。

 
for(i=mid+1;i<=len-1;i++) //其实这里并不一定是mid+1，需要讨论字符串长度的奇偶性
{
if (a[i]!=s[top])
{
break;
}
top--;
}
if(top==0)
printf("YES");
else
printf("NO");

最后如果 top 的值为 0，就说明栈内所有的字符都被一一匹配了，那么这个字符串就是回文字符串。完整的代码如下。

 
#include <stdio.h>
#include <string.h>
int main()
{
char a[101],s[101];
int i,len,mid,next,top;
 
gets(a); //读入一行字符串
len=strlen(a); //求字符串的长度
mid=len/2-1; //求字符串的中点
 
top=0;//栈的初始化
//将mid前的字符依次入栈
for(i=0;i<=mid;i++)
s[++top]=a[i];
 
//判断字符串的长度的是奇数还是偶数，并找出需要进行字符匹配的起始下标
if(len%2==0)
next=mid+1;
else
next=mid+2;
 
//开始匹配
for(i=next;i<=len-1;i++)
{
if(a[i]!=s[top])
break;
top--;
}
 
//如果top的值为0，则说明栈内的所有的字符都被一一匹配了
if(top==0)
printf("YES");
else
printf("NO");
 
getchar();getchar();
return 0;
}

可以输入以下数据进行验证

ahaha

运行结果是

YES

栈还可以用来进行验证括号的匹配。比如输入一行只包含“()[]{}”的字符串，形如“([{}()])”或者“{()[]{}}”请判断是否可以正确匹配。显然上面两个例子都是可以正确匹配的。“([)]”是不能匹配的。有兴趣的同学可以自己动手来试一试。

堆栈最早由 Alan M. Turing（艾伦·图灵）于 1946 年提出，当时为了解决子程序的调用和返回。艾伦·图灵这个大帅哥可是个大牛人，图灵奖就是以他的名字命名的。如果你对他感兴趣不妨去读一读他的传记《艾伦图灵传：如谜的解谜者》。

【一周一算法】算法 5：解密回文——栈
http://bbs.ahalei.com/thread-4515-1-1.html
(出处: 啊哈磊_编程从这里起步)

7

算法 6：只有五行的 Floyd 最短路算法

图片 7.1 picture6.1

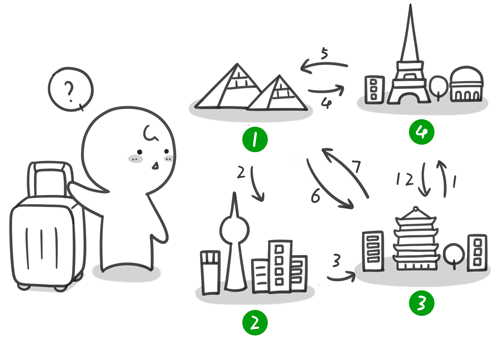
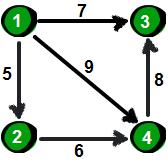
暑假，小哼准备去一些城市旅游。有些城市之间有公路，有些城市之间则没有，如下图。为了节省经费以及方便计划旅程，小哼希望在出发之前知道任意两个城市之前的最短路程。

图片 7.2 picture6.2

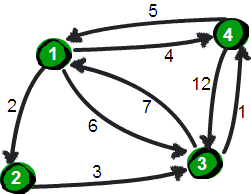
上图中有 4 个城市 8 条公路，公路上的数字表示这条公路的长短。请注意这些公路是单向的。我们现在需要求任意两个城市之间的最短路程，也就是求任意两个点之间的最短路径。这个问题这也被称为“多源最短路径”问题。

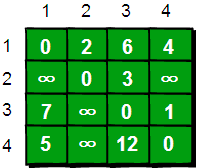
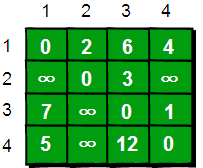
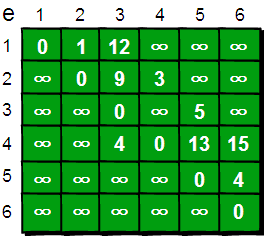
现在需要一个数据结构来存储图的信息，我们仍然可以用一个 4*4 的矩阵（二维数组 e）来存储。比如 1 号城市到 2 号城市的路程为 2，则设 e[1][2]的值为 2。2 号城市无法到达 4 号城市，则设置 e[2][4]的值为 ∞。另外此处约定一个城市自己是到自己的也是 0，例如 e[1][1]为 0，具体如下。

图片 7.3 picture6.3

现在回到问题：如何求任意两点之间最短路径呢？通过之前的学习我们知道通过深度或广度优先搜索可以求出两点之间的最短路径。所以进行 n2 遍深度或广度优先搜索，即对每两个点都进行一次深度或广度优先搜索，便可以求得任意两点之间的最短路径。可是还有没有别的方法呢？

我们来想一想，根据我们以往的经验，如果要让任意两点（例如从顶点 a 点到顶点 b）之间的路程变短，只能引入第三个点（顶点 k），并通过这个顶点 k 中转即 a->k->b，才可能缩短原来从顶点 a 点到顶点 b 的路程。那么这个中转的顶点 k 是 1~n 中的哪个点呢？甚至有时候不只通过一个点，而是经过两个点或者更多点中转会更短，即 a->k1->k2b->或者 a->k1->k2…->k->i…->b。比如上图中从 4 号城市到 3 号城市（4->3）的路程 e[4][3]原本是 12。如果只通过 1 号城市中转（4->1->3），路程将缩短为 11（e[4][1]+e[1][3]=5+6=11）。其实 1 号城市到 3 号城市也可以通过 2 号城市中转，使得 1 号到 3 号城市的路程缩短为 5（e[1][2]+e[2][3]=2+3=5）。所以如果同时经过 1 号和 2 号两个城市中转的话，从 4 号城市到 3 号城市的路程会进一步缩短为 10。通过这个的例子，我们发现每个顶点都有可能使得另外两个顶点之间的路程变短。好，下面我们将这个问题一般化。

当任意两点之间不允许经过第三个点时，这些城市之间最短路程就是初始路程，如下。

图片 7.4 picture6.4

如现在只允许经过 1 号顶点，求任意两点之间的最短路程，应该如何求呢？只需判断 e[i][1]+e[1][j]是否比 e[i][j]要小即可。e[i][j]表示的是从 i 号顶点到 j 号顶点之间的路程。e[i][1]+e[1][j]表示的是从 i 号顶点先到 1 号顶点，再从 1 号顶点到 j 号顶点的路程之和。其中 i 是 1~n 循环，j 也是 1~n 循环，代码实现如下。

 
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
if ( e[i][j] > e[i][1]+e[1][j] )
e[i][j] = e[i][1]+e[1][j];
}
}

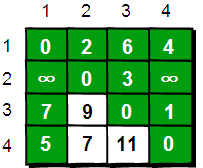
在只允许经过 1 号顶点的情况下，任意两点之间的最短路程更新为：

图片 7.5 picture6.5

通过上图我们发现：在只通过 1 号顶点中转的情况下，3 号顶点到 2 号顶点（e[3][2]）、4 号顶点到 2 号顶点（e[4][2]）以及 4 号顶点到 3 号顶点（e[4][3]）的路程都变短了。

接下来继续求在只允许经过 1 和 2 号两个顶点的情况下任意两点之间的最短路程。如何做呢？我们需要在只允许经过 1 号顶点时任意两点的最短路程的结果下，再判断如果经过 2 号顶点是否可以使得 i 号顶点到 j 号顶点之间的路程变得更短。即判断 e[i][2]+e[2][j]是否比 e[i][j]要小，代码实现为如下。

 
//经过1号顶点
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if (e[i][j] > e[i][1]+e[1][j]) e[i][j]=e[i][1]+e[1][j];
//经过2号顶点
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if (e[i][j] > e[i][2]+e[2][j]) e[i][j]=e[i][2]+e[2][j];

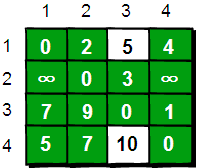
在只允许经过 1 和 2 号顶点的情况下，任意两点之间的最短路程更新为：

图片 7.6 picture6.6

通过上图得知，在相比只允许通过 1 号顶点进行中转的情况下，这里允许通过 1 和 2 号顶点进行中转，使得 e[1][3]和 e[4][3]的路程变得更短了。

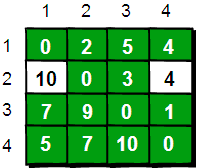
同理，继续在只允许经过 1、2 和 3 号顶点进行中转的情况下，求任意两点之间的最短路程。任意两点之间的最短路程更新为：

图片 7.7 picture6.7

最后允许通过所有顶点作为中转，任意两点之间最终的最短路程为：

图片 7.8 picture6.8

整个算法过程虽然说起来很麻烦，但是代码实现却非常简单，核心代码只有五行：

 
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(e[i][j]>e[i][k]+e[k][j])
e[i][j]=e[i][k]+e[k][j];

这段代码的基本思想就是：最开始只允许经过 1 号顶点进行中转，接下来只允许经过 1 和 2 号顶点进行中转……允许经过 1~n 号所有顶点进行中转，求任意两点之间的最短路程。用一句话概括就是：从 i 号顶点到 j 号顶点只经过前k号点的最短路程。其实这是一种“动态规划”的思想，关于这个思想我们将在《啊哈！算法 2——伟大思维闪耀时》在做详细的讨论。下面给出这个算法的完整代码：

 
#include <stdio.h>
int main()
{
int e[10][10],k,i,j,n,m,t1,t2,t3;
int inf=99999999; //用inf(infinity的缩写)存储一个我们认为的正无穷值
//读入n和m，n表示顶点个数，m表示边的条数
scanf("%d %d",&n,&m);
 
//初始化
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j) e[i][j]=0;
else e[i][j]=inf;
//读入边
for(i=1;i<=m;i++)
{
scanf("%d %d %d",&t1,&t2,&t3);
e[t1][t2]=t3;
}
 
//Floyd-Warshall算法核心语句
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(e[i][j]>e[i][k]+e[k][j] )
e[i][j]=e[i][k]+e[k][j];
 
//输出最终的结果
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
printf("%10d",e[i][j]);
}
printf("\n");
}
 
return 0;
}

有一点需要注意的是：如何表示正无穷。我们通常将正无穷定义为 99999999，因为这样即使两个正无穷相加，其和仍然不超过 int 类型的范围（C 语言 int 类型可以存储的最大正整数是 2147483647）。在实际应用中最好估计一下最短路径的上限，只需要设置比它大一点既可以。例如有 100 条边，每条边不超过 100 的话，只需将正无穷设置为 10001 即可。如果你认为正无穷和其它值相加得到一个大于正无穷的数是不被允许的话，我们只需在比较的时候加两个判断条件就可以了，请注意下面代码中带有下划线的语句。

 
//Floyd-Warshall算法核心语句
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(e[i][k]<inf && e[k][j]<inf && e[i][j]>e[i][k]+e[k][j])
e[i][j]=e[i][k]+e[k][j];

上面代码的输入数据样式为：

 
4 8
1 2 2
1 3 6
1 4 4
2 3 3
3 1 7
3 4 1
4 1 5
4 3 12

第一行两个数为 n 和 m，n 表 示顶点个数，m 表示边的条数。
接下来 m 行，每一行有三个数 t1、t2 和 t3，表示顶点 t1 到顶点 t2 的路程是 t3。
得到最终结果如下：

图片 7.9 picture6.9

通过这种方法我们可以求出任意两个点之间最短路径。它的时间复杂度是 O(N3)。令人很震撼的是它竟然只有五行代码，实现起来非常容易。正是因为它实现起来非常容易，如果时间复杂度要求不高，使用 Floyd-Warshall 来求指定两点之间的最短路或者指定一个点到其余各个顶点的最短路径也是可行的。当然也有更快的算法，请看下一节：Dijkstra 算法。

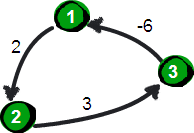
另外需要注意的是：Floyd-Warshall 算法不能解决带有“负权回路”（或者叫“负权环”）的图，因为带有“负权回路”的图没有最短路。例如下面这个图就不存在 1 号顶点到 3 号顶点的最短路径。因为 1->2->3->1->2->3->…->1->2->3 这样路径中，每绕一次 1->-2>3 这样的环，最短路就会减少 1，永远找不到最短路。其实如果一个图中带有“负权回路”那么这个图则没有最短路。

图片 7.10 picture6.10

此算法由 Robert W. Floyd（罗伯特·弗洛伊德）于 1962 年发表在“Communications of the ACM”上。同年 Stephen Warshall（史蒂芬·沃舍尔）也独立发表了这个算法。Robert W．Floyd 这个牛人是朵奇葩，他原本在芝加哥大学读的文学，但是因为当时美国经济不太景气，找工作比较困难，无奈之下到西屋电气公司当了一名计算机操作员，在 IBM650 机房值夜班，并由此开始了他的计算机生涯。此外他还和 J.W.J. Williams（威廉姆斯）于 1964 年共同发明了著名的堆排序算法 HEAPSORT。堆排序算法我们将在第七章学习。Robert W．Floyd 在 1978 年获得了图灵奖。

【一周一算法】算法 6：只有五行的 Floyd 最短路算法
http://bbs.ahalei.com/thread-4554-1-1.html
(出处: 啊哈磊_编程从这里起步)

8

算法 7：Dijkstra 最短路算法

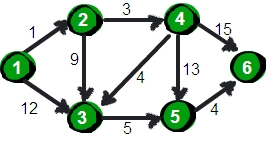
上周我们介绍了神奇的只有五行的 Floyd 最短路算法，它可以方便的求得任意两点的最短路径，这称为“多源最短路”。本周来来介绍指定一个点（源点）到其余各个顶点的最短路径，也叫做“单源最短路径”。例如求下图中的 1 号顶点到 2、3、4、5、6 号顶点的最短路径。

图片 8.1 picture7.1

与 Floyd-Warshall 算法一样这里仍然使用二维数组 e 来存储顶点之间边的关系，初始值如下。

图片 8.2 picture7.2

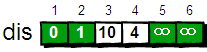
我们还需要用一个一维数组 dis 来存储 1 号顶点到其余各个顶点的初始路程，如下。

图片 8.3 picture7.3

我们将此时 dis 数组中的值称为最短路的“估计值”。

既然是求 1 号顶点到其余各个顶点的最短路程，那就先找一个离 1 号顶点最近的顶点。通过数组 dis 可知当前离 1 号顶点最近是 2 号顶点。当选择了 2 号顶点后，dis[2]的值就已经从“估计值”变为了“确定值”，即 1 号顶点到 2 号顶点的最短路程就是当前 dis[2]值。为什么呢？你想啊，目前离 1 号顶点最近的是 2 号顶点，并且这个图所有的边都是正数，那么肯定不可能通过第三个顶点中转，使得 1 号顶点到 2 号顶点的路程进一步缩短了。因为 1 号顶点到其它顶点的路程肯定没有 1 号到 2 号顶点短，对吧 O(∩_∩)O~

既然选了 2 号顶点，接下来再来看 2 号顶点有哪些出边呢。有 2->3 和 2->4 这两条边。先讨论通过 2->3 这条边能否让 1 号顶点到 3 号顶点的路程变短。也就是说现在来比较 dis[3]和 dis[2]+e[2][3]的大小。其中 dis[3]表示 1 号顶点到 3 号顶点的路程。dis[2]+e[2][3]中 dis[2]表示 1 号顶点到 2 号顶点的路程，e[2][3]表示 2->3 这条边。所以 dis[2]+e[2][3]就表示从 1 号顶点先到 2 号顶点，再通过 2->3 这条边，到达 3 号顶点的路程。

我们发现 dis[3]=12，dis[2]+e[2][3]=1+9=10，dis[3]>dis[2]+e[2][3]，因此 dis[3]要更新为 10。这个过程有个专业术语叫做“松弛”。即 1 号顶点到 3 号顶点的路程即 dis[3]，通过 2->3 这条边松弛成功。这便是 Dijkstra 算法的主要思想：通过“边”来松弛 1 号顶点到其余各个顶点的路程。

同理通过 2->4（e[2][4]），可以将 dis[4]的值从 ∞ 松弛为 4（dis[4]初始为 ∞，dis[2]+e[2][4]=1+3=4，dis[4]>dis[2]+e[2][4]，因此 dis[4]要更新为 4）。

刚才我们对 2 号顶点所有的出边进行了松弛。松弛完毕之后 dis 数组为：

图片 8.4 picture7.4

接下来，继续在剩下的 3、4、5 和 6 号顶点中，选出离 1 号顶点最近的顶点。通过上面更新过 dis 数组，当前离 1 号顶点最近是 4 号顶点。此时，dis[4]的值已经从“估计值”变为了“确定值”。下面继续对 4 号顶点的所有出边（4->3，4->5 和 4->6）用刚才的方法进行松弛。松弛完毕之后 dis 数组为：

图片 8.5 picture7.5

继续在剩下的 3、5 和 6 号顶点中，选出离 1 号顶点最近的顶点，这次选择 3 号顶点。此时，dis[3]的值已经从“估计值”变为了“确定值”。对 3 号顶点的所有出边（3->5）进行松弛。松弛完毕之后 dis 数组为：

图片 8.6 picture7.6

继续在剩下的 5 和 6 号顶点中，选出离 1 号顶点最近的顶点，这次选择 5 号顶点。此时，dis[5]的值已经从“估计值”变为了“确定值”。对5号顶点的所有出边（5->4）进行松弛。松弛完毕之后 dis 数组为：

图片 8.7 picture7.7

最后对 6 号顶点所有点出边进行松弛。因为这个例子中 6 号顶点没有出边，因此不用处理。到此，dis 数组中所有的值都已经从“估计值”变为了“确定值”。

最终 dis 数组如下，这便是 1 号顶点到其余各个顶点的最短路径。

图片 8.8 picture7.8

OK，现在来总结一下刚才的算法。算法的基本思想是：每次找到离源点（上面例子的源点就是 1 号顶点）最近的一个顶点，然后以该顶点为中心进行扩展，最终得到源点到其余所有点的最短路径。基本步骤如下：

• 将所有的顶点分为两部分：已知最短路程的顶点集合 P 和未知最短路径的顶点集合 Q。最开始，已知最短路径的顶点集合 P 中只有源点一个顶点。我们这里用一个 book[ i ]数组来记录哪些点在集合 P 中。例如对于某个顶点 i，如果 book[ i ]为 1 则表示这个顶点在集合 P 中，如果 book[ i ]为 0 则表示这个顶点在集合 Q 中。
• 设置源点 s 到自己的最短路径为 0 即 dis=0。若存在源点有能直接到达的顶点 i，则把 dis[ i ]设为 e[s][ i ]。同时把所有其它（源点不能直接到达的）顶点的最短路径为设为 ∞。
• 在集合 Q 的所有顶点中选择一个离源点 s 最近的顶点 u（即 dis[u]最小）加入到集合 P。并考察所有以点 u 为起点的边，对每一条边进行松弛操作。例如存在一条从 u 到 v 的边，那么可以通过将边 u->v 添加到尾部来拓展一条从 s 到 v 的路径，这条路径的长度是 dis[u]+e[u][v]。如果这个值比目前已知的 dis[v]的值要小，我们可以用新值来替代当前 dis[v]中的值。
• 重复第 3 步，如果集合 Q 为空，算法结束。最终 dis 数组中的值就是源点到所有顶点的最短路径。

完整的 Dijkstra 算法代码如下：

 
#include <stdio.h>
int main()
{
int e[10][10],dis[10],book[10],i,j,n,m,t1,t2,t3,u,v,min;
int inf=99999999; //用inf(infinity的缩写)存储一个我们认为的正无穷值
//读入n和m，n表示顶点个数，m表示边的条数
scanf("%d %d",&n,&m);
 
//初始化
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j) e[i][j]=0;
else e[i][j]=inf;
 
//读入边
for(i=1;i<=m;i++)
{
scanf("%d %d %d",&t1,&t2,&t3);
e[t1][t2]=t3;
}
//初始化dis数组，这里是1号顶点到其余各个顶点的初始路程
for(i=1;i<=n;i++)
dis[i]=e[1][i];
//book数组初始化
for(i=1;i<=n;i++)
book[i]=0;
book[1]=1;
 
//Dijkstra算法核心语句
for(i=1;i<=n-1;i++)
{
//找到离1号顶点最近的顶点
min=inf;
for(j=1;j<=n;j++)
{
if(book[j]==0 && dis[j]<min)
{
min=dis[j];
u=j;
}
}
book[u]=1;
for(v=1;v<=n;v++)
{
if(e[u][v]<inf)
{
if(dis[v]>dis[u]+e[u][v])
dis[v]=dis[u]+e[u][v];
}
}
}
 
//输出最终的结果
for(i=1;i<=n;i++)
printf("%d ",dis[i]);
 
getchar();
getchar();
return 0;
}

可以输入以下数据进行验证。第一行两个整数 n m。n 表示顶点个数（顶点编号为 1~n），m 表示边的条数。接下来 m 行表示，每行有 3 个数 x y z。表示顶点 x 到顶点 y 边的权值为 z。

 
6 9
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4

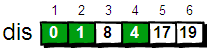
运行结果是

 
0 1 8 4 13 17

通过上面的代码我们可以看出，这个算法的时间复杂度是 O(N2)。其中每次找到离 1 号顶点最近的顶点的时间复杂度是 O(N)，这里我们可以用“堆”（以后再说）来优化，使得这一部分的时间复杂度降低到 O(logN)。另外对于边数 M 少于 N2 的稀疏图来说（我们把 M 远小于 N2 的图称为稀疏图，而 M 相对较大的图称为稠密图），我们可以用邻接表（这是个神马东西？不要着急，下周再仔细讲解）来代替邻接矩阵，使得整个时间复杂度优化到 O( (M+N)logN )。请注意！在最坏的情况下 M 就是 N2，这样的话 MlogN 要比 N2 还要大。但是大多数情况下并不会有那么多边，因此(M+N)logN 要比 N2 小很多。

【啊哈！算法】系列 7：Dijkstra 最短路算法
http://ahalei.blog.51cto.com/4767671/1387799

9

算法 8：巧妙的邻接表（数组实现）

之前我们介绍过图的邻接矩阵存储法，它的空间和时间复杂度都是 N2，现在我来介绍另外一种存储图的方法：邻接表，这样空间和时间复杂度就都是 M。对于稀疏图来说，M 要远远小于 N2。先上数据，如下。

 
4 5
1 4 9
4 3 8
1 2 5
2 4 6
1 3 7

图片 9.1 picture8.1

第一行两个整数 n m。n 表示顶点个数（顶点编号为 1~n），m 表示边的条数。接下来 m 行表示，每行有 3 个数 x y z，表示顶点 x 到顶点 y 的边的权值为 z。下图就是一种使用链表来实现邻接表的方法。

图片 9.2 picture8.2

上面这种实现方法为图中的每一个顶点（左边部分）都建立了一个单链表（右边部分）。这样我们就可以通过遍历每个顶点的链表，从而得到该顶点所有的边了。使用链表来实现邻接表对于痛恨指针的的朋友来说，这简直就是噩梦。这里我将为大家介绍另一种使用数组来实现的邻接表，这是一种在实际应用中非常容易实现的方法。这种方法为每个顶点 i（i 从 1~n）也都保存了一个类似“链表”的东西，里面保存的是从顶点 i 出发的所有的边，具体如下。

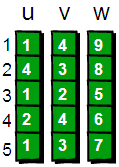
首先我们按照读入的顺序为每一条边进行编号（1~m）。比如第一条边“1 4 9”的编号就是 1，“1 3 7”这条边的编号是 5。

这里用 u、v 和 w 三个数组用来记录每条边的具体信息，即 u[i]、v[i]和 w[i]表示 第i 条边是从第 u[i]号顶点到 v[i]号顶点（u[i]àv[i]），且权值为 w[i]。

图片 9.3 picture8.3

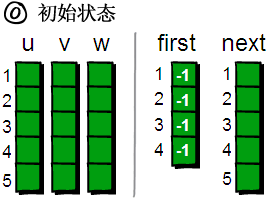
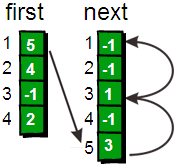
再用一个 first 数组来存储每个顶点其中一条边的编号。以便待会我们来枚举每个顶点所有的边（你可能会问：存储其中一条边的编号就可以了？不可能吧，每个顶点都需要存储其所有边的编号才行吧！甭着急，继续往下看）。比如1号顶点有一条边是 “1 4 9”（该条边的编号是 1），那么就将 first[1]的值设为 1。如果某个顶点 i 没有以该顶点为起始点的边，则将 first[i]的值设为-1。现在我们来看看具体如何操作，初始状态如下。

图片 9.4 picture8.4

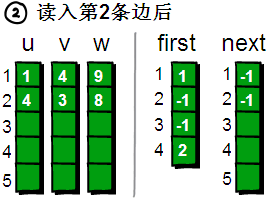
咦？上图中怎么多了一个 next 数组，有什么作用呢？不着急，待会再解释，现在先读入第一条边“1 4 9”。

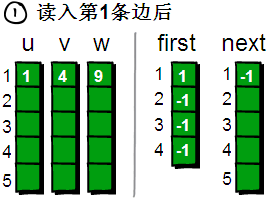
读入第 1 条边（1 4 9），将这条边的信息存储到 u[1]、v[1]和 w[1]中。同时为这条边赋予一个编号，因为这条边是最先读入的，存储在 u、v 和 w 数组下标为 1 的单元格中，因此编号就是 1。这条边的起始点是 1 号顶点，因此将 first[1]的值设为 1。

另外这条“编号为 1 的边”是以 1 号顶点（即 u[1]）为起始点的第一条边，所以要将 next[1]的值设为-1。也就是说，如果当前这条“编号为 i 的边”，是我们发现的以 u[i]为起始点的第一条边，就将 next[i]的值设为-1（貌似的这个 next 数组很神秘啊⊙_⊙）。

图片 9.5 picture8.5

读入第 2 条边（4 3 8），将这条边的信息存储到 u[2]、v[2]和 w[2]中，这条边的编号为 2。这条边的起始顶点是 4 号顶点，因此将 first[4]的值设为 2。另外这条“编号为 2 的边”是我们发现以 4 号顶点为起始点的第一条边，所以将 next[2]的值设为-1。

图片 9.6 picture8.6

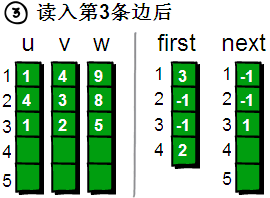
读入第 3 条边（1 2 5），将这条边的信息存储到 u[3]、v[3]和 w[3]中，这条边的编号为 3，起始顶点是 1 号顶点。我们发现 1 号顶点已经有一条“编号为 1 的边”了，如果此时将 first[1]的值设为 3，那“编号为 1 的边”岂不是就丢失了？我有办法，此时只需将 next[3]的值设为 1即可。现在你知道 next数组是用来做什么的吧。next[i]存储的是“编号为i的边”的“前一条边”的编号。

图片 9.7 picture8.7

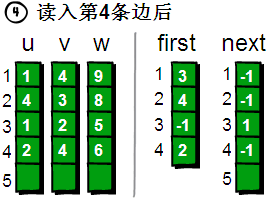
读入第 4 条边（2 4 6），将这条边的信息存储到 u[4]、v[4]和 w[4]中，这条边的编号为 4，起始顶点是 2 号顶点，因此将 first[2]的值设为 4。另外这条“编号为 4 的边”是我们发现以 2 号顶点为起始点的第一条边，所以将 next[4]的值设为-1。

图片 9.8 picture8.8

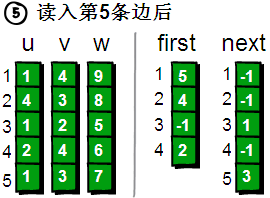
读入第 5 条边（1 3 7），将这条边的信息存储到 u[5]、v[5]和 w[5]中，这条边的编号为 5，起始顶点又是 1 号顶点。此时需要将 first[1]的值设为 5，并将 next[5]的值改为 3。

图片 9.9 picture8.9

此时，如果我们想遍历 1 号顶点的每一条边就很简单了。1 号顶点的其中一条边的编号存储在 first[1]中。其余的边则可以通过 next 数组寻找到。请看下图。

图片 9.10 picture8.10

细心的同学会发现，此时遍历边某个顶点边的时候的遍历顺序正好与读入时候的顺序相反。因为在为每个顶点插入边的时候都直接插入“链表”的首部而不是尾部。不过这并不会产生任何问题，这正是这种方法的其妙之处。

创建邻接表的代码如下。

 
int n,m,i;
//u、v和w的数组大小要根据实际情况来设置，要比m的最大值要大1
int u[6],v[6],w[6];
//first和next的数组大小要根据实际情况来设置，要比n的最大值要大1
int first[5],next[5];
scanf("%d %d",&n,&m);
//初始化first数组下标1~n的值为-1，表示1~n顶点暂时都没有边
for(i=1;i<=n;i++)
first[i]=-1;
for(i=1;i<=m;i++)
{
scanf("%d %d %d",&u[i],&v[i],&w[i]);//读入每一条边
//下面两句是关键啦
next[i]=first[u[i]];
first[u[i]]=i;
}

接下来如何遍历每一条边呢？我们之前说过其实 first 数组存储的就是每个顶点 i（i 从 1~n）的第一条边。比如 1 号顶点的第一条边是编号为 5 的边（1 3 7），2 号顶点的第一条边是编号为 4 的边（2 4 6），3 号顶点没有出向边，4 号顶点的第一条边是编号为 2 的边（2 4 6）。那么如何遍历 1 号顶点的每一条边呢？也很简单。请看下图：

遍历 1 号顶点所有边的代码如下。

 
k=first[1];// 1号顶点其中的一条边的编号（其实也是最后读入的边）
while(k!=-1) //其余的边都可以在next数组中依次找到
{
printf("%d %d %d\n",u[k],v[k],w[k]);
k=next[k];
}

遍历每个顶点的所有边的代码如下。

 
for(i=1;i<=n;i++)
{
k=first[i];
while(k!=-1)
{
printf("%d %d %d\n",u[k],v[k],w[k]);
k=next[k];
}
}

可以发现使用邻接表来存储图的时间空间复杂度是 O(M)，遍历每一条边的时间复杂度是也是 O(M)。如果一个图是稀疏图的话，M 要远小于 N2。因此稀疏图选用邻接表来存储要比邻接矩阵来存储要好很多。

【啊哈！算法】系列 8：巧妙的邻接表（数组实现）
http://ahalei.blog.51cto.com/4767671/1391988

10

算法 9：开启“树”之旅

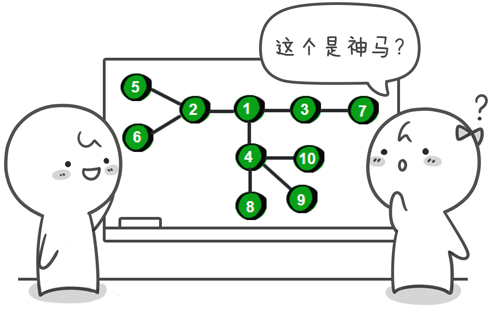
我们先来看一个例子。

图片 10.1 picture9.1

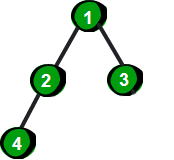
这是什么？是一个图？不对，确切的说这是一棵树。这哪里像树呢？不要着急我们来变换一下。

图片 10.2 picture9.2

是不是很像一棵倒挂的树，也就是说它是根朝上，而叶子朝下的。不像？哈哈，看完下面这幅图你就会觉得像啦。

图片 10.3 picture9.3

你可能会问：树和图有什么区别？这个称之为树的东西貌似和无向图差不多嘛。不要着急，继续往下看。树其实就是不包含回路的连通无向图。你可能还是无法理解这其中的差异，举个例子，如下。

图片 10.4 picture9.5

上面这个例子中左边的是一棵树，而右边的是一个图。因为左边的没有回路，而右边的存在 1->2->5->3->1 这样的回路。

1. 正是因为树有着“不包含回路”这个特点，所以树就被赋予了很多特性。
2. 一棵树中的任意两个结点有且仅有唯一的一条路径连通。
3. 一棵树如果有 n 个结点，那么它一定恰好有 n-1 条边。

在一棵树中加一条边将会构成一个回路。树这个特殊的数据结构在哪里会用到呢？比如足球世界杯的晋级图，家族的族谱图、公司的组织结构图、书的目录、我们用的操作系统 Windows、Liunx 或者 Mac 中的“目录（文件夹）”都是一棵树。下面就是“啊哈 C”这个软件的目录结构。

 
C:\啊哈C
├─codes
├─core
│ ├─bin
│ ├─include
│ │ ├─ddk
│ │ ├─gdb
│ │ ├─gdiplus
│ │ ├─GL
│ │ └─sys
│ ├─lib
│ │ └─gcc
│ │ └─mingw32
│ │ └─4.7.1
│ │ ├─finclude
│ │ ├─include
│ │ │ └─ssp
│ │ ├─include-fixed
│ │ └─install-tools
│ │ └─include
│ ├─libexec
│ │ └─gcc
│ │ └─mingw32
│ │ └─4.7.1
│ │ └─install-tools
│ └─mingw32
│ ├─bin
│ └─lib
│ └─ldscripts
└─skin

假如现在正处于 libexec 文件夹下，需要到 gdiplus 文件夹下。你必须先“向上”回到上层文件夹 core，再进入 include 文件夹，最后才能进入 gdiplus 文件夹。因为一棵树中的任意两个结点（这里就是文件夹）有且仅有唯一的一条路径连通。

为了之后讲解的方便，我们这里对树进行一些定义。

首先，树是指任意两个结点间有且只有一条路径的无向图。 或者说，只要是没有回路的连通无向图就是树。

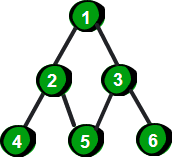
喜欢思考的同学可能会发现同一棵树可以有多种形态，比如下面这个两棵树。

图片 10.5 picture9.7

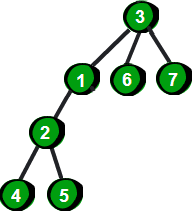
为了确定一棵树的形态，在一棵树中可以指定一个特殊的结点——根。我们在对一棵树进行讨论的时候，将树中的每个点称为结点，有的书中也称为节点。有一个根的树叫做有根树（哎，这不是废话嘛）。比如上方左边这棵树的树根是 1 号结点，右边这棵树的树根是 3 号结点。

根又叫做根结点，一棵树有且只有一个根结点。根结点有时候也称为祖先。既然有祖先，理所当然就有父亲和儿子。比如上图右边这棵树中 3 号结点是 1、6 和 7 号结点的父亲，1、6 和 7 号结点是 3 号结点的儿子。同时 1 号结点又是 2 号结点的父亲，2 号结点是 1 号结点的儿子，2 号结点与 4、5 号结点关系也显而易见了。

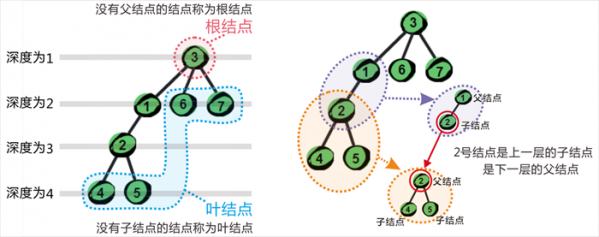
父亲结点简称为父结点，儿子结点简称为子结点。2 号结点既是父结点也是子结点，它是 1 号结点的子结点，同时也是 4 和 5 号结点的父结点。另外如果一个结点没有子结点（即没有儿子）那么这个结点称为叶结点，例如 4、5、6 和 7 号结点都是叶结点。没有父结点（即没有父亲）的结点称为根结点（祖先）。如果一个结点既不是根结点也不是叶结点则称为内部结点。最后每个结点还有深度，比如 5 号结点的深度是 4。哎，终于啰嗦完了，写的我汗都流出来了，没有理解的请看下面这幅插图吧。

图片 10.6 picture9.8

说了这么多你可能都没有感受到树究竟有什么好处。不要着急，请看下回——二叉树。

【啊哈！算法】算法 9：开启“树”之旅
http://ahalei.blog.51cto.com/4767671/1403823

11

算法 10：二叉树

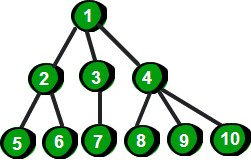
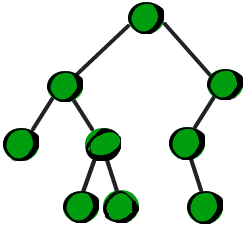
二叉树是一种特殊的树。二叉树的特点是每个结点最多有两个儿子，左边的叫做左儿子，右边的叫做右儿子，或者说每个结点最多有两棵子树。更加严格的递归定义是：二叉树要么为空，要么由根结点、左子树和右子树组成，而左子树和右子树分别是一棵二叉树。 下面这棵树就是一棵二叉树。

图片 11.1 picture10.1

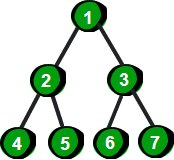
二叉树的使用范围最广，一棵多叉树也可以转化为二叉树，因此我们将着重讲解二叉树。 二叉树中还有连两种特殊的二叉树叫做满二叉树和完全二叉树。如果二叉树中每个内部结点都有两个儿子，这样的二叉树叫做满二叉树。或者说满二叉树所有的叶结点都有同样的深度。比如下面这棵二叉树，是不是感觉很“丰满”。满二叉树的严格的定义是一棵深度为 h 且有 2h-1 个结点的二叉树。

图片 11.2 picture10.2

如果一棵二叉树除了最右边位置上一个或者几个叶结点缺少外其它是丰满的，那么这样的二叉树就是完全二叉树。严格的定义是：若设二叉树的高度为 h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层从右向左连续缺若干结点，就是完全二叉树。也就是说如果一个结点有右子结点，那么它一定也有左子结点。例如下面这三棵树都是完全二叉树。其实你可以将满二叉树理解成是一种特殊的或者极其完美的完全二叉树。

图片 11.3 picture10.5

其实完全二叉树类似下面这个形状。

图片 11.4 picture10.6

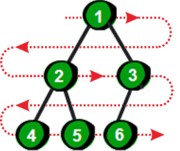
说到这里我们马上就要领略到完全二叉树的魅力了。先想一想一棵完全二叉树如何存储呢？其实完全二叉树中父亲和儿子之间有着神奇的规律，我们只需用一个一维数组就可以存储完全二叉树。首先将完全二叉树进行从上到下，从左到右编号。

图片 11.5 picture10.7

通过上图我们发现如果完全二叉树的一个父结点编号为 k，那么它左儿子的编号就是 2k，右儿子的编号就是 2k+1。如果已知儿子（左儿子或右儿子）的编号是 x，那么它父结点的编号就是 x/2，注意这里只取商的整数部分。在 C 语言中如果除号‘/’两边都是整数的话，那么商也只有整数部分（即自动向下取整），即 4/2 和 5/2 都是 2。另外如果一棵完全二叉树有 N 个结点，那么这个完全二叉树的高度为 log2 N 简写为 log N，即最多有 log N 层结点。完全二叉树的最典型应用就是——堆。那么堆又有什么作用呢？请关注下周更新：堆——神奇的优先队列。

【啊哈！算法】算法 10：二叉树
http://ahalei.blog.51cto.com/4767671/1414035

12

算法 11：堆——神奇的优先队列（上）

堆是什么？是一种特殊的完全二叉树，就像下面这棵树一样。

图片 12.1 picture11.1

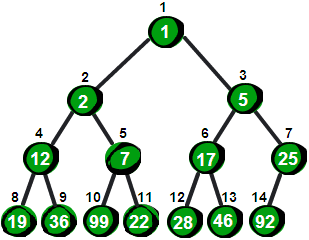
有没有发现这棵二叉树有一个特点，就是所有父结点都比子结点要小（注意：圆圈里面的数是值，圆圈上面的数是这个结点的编号，此规定仅适用于本节）。符合这样特点的完全二叉树我们称为最小堆。反之，如果所有父结点都比子结点要大，这样的完全二叉树称为最大堆。那这一特性究竟有什么用呢？

假如有 14 个数分别是 99、5、36、7、22、17、46、12、2、19、25、28、1 和 92。请找出这 14 个数中最小的数，请问怎么办呢？最简单的方法就是将这 14 个数从头到尾依次扫一遍，用一个循环就可以解决。这种方法的时间复杂度是 O(14)也就是 O(N)。

 
for(i=1;i<=14;i++)
{
if(a[ i]<min)min=a[ i];
}

现在我们需要删除其中最小的数，并增加一个新数 23，再次求这 14 个数中最小的一个数。请问该怎么办呢？只能重新扫描所有的数，才能找到新的最小的数，这个时间复杂度也是 O(N)。假如现在有 14 次这样的操作（删除最小的数后并添加一个新数）。那么整个时间复杂度就是 O(142)即 O(N2)。那有没有更好的方法呢？堆这个特殊的结构恰好能够很好地解决这个问题。

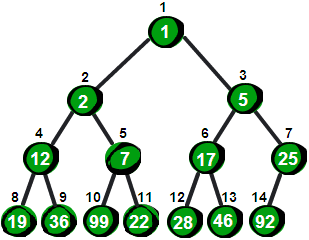
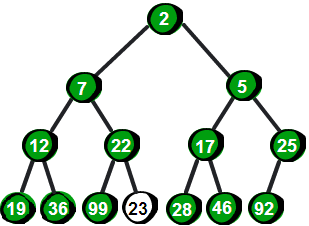
首先我们先把这个 14 个数按照最小堆的要求（就是所有父结点都比子结点要小）放入一棵完全二叉树，就像下面这棵树一样。

图片 12.2 picture11.2

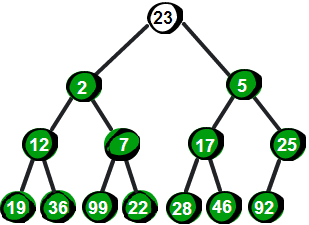
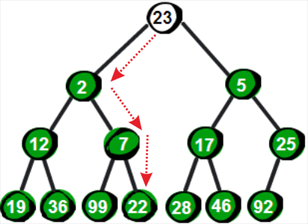
很显然最小的数就在堆顶，假设存储这个堆的数组叫做h的话，最小数就是 h[ 1]。接下来，我们将堆顶的数删除，并将新增加的数 23 放到堆顶。显然加了新数后已经不符合最小堆的特性，我们需要将新增加的数调整到合适的位置。那如何调整呢？

图片 12.3 picture11.3

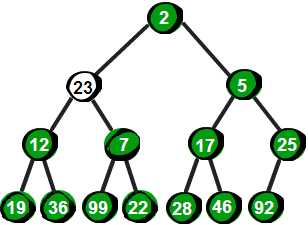
向下调整！我们需要将这个数与它的两个儿子 2 和 5 比较，并选择较小一个与它交换，交换之后如下。

图片 12.4 picture11.4

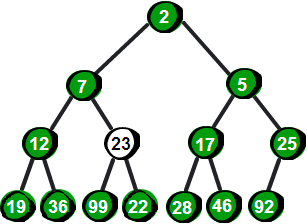
我们发现此时还是不符合最小堆的特性，因此还需要继续向下调整。于是继续将 23 与它的两个儿子 12 和7比较，并选择较小一个交换，交换之后如下。

图片 12.5 picture11.5

到此，还是不符合最小堆的特性，仍需要继续向下调整直到符合最小堆的特性为止。

图片 12.6 picture11.6

我们发现现在已经符合最小堆的特性了。综上所述，当新增加一个数被放置到堆顶时，如果此时不符合最小堆的特性，则将需要将这个数向下调整，直到找到合适的位置为止，使其重新符合最小堆的特性。

图片 12.7 picture11.7

向下调整的代码如下。

 
void siftdown(int i) //传入一个需要向下调整的结点编号i，这里传入1，即从堆的顶点开始向下调整
{
int t,flag=0;//flag用来标记是否需要继续向下调整
//当i结点有儿子的时候（其实是至少有左儿子的情况下）并且有需要继续调整的时候循环窒执行
while( i*2<=n && flag==0 )
{
//首先判断他和他左儿子的关系，并用t记录值较小的结点编号
if( h[ i] > h[ i*2] )
t=i*2;
else
t=i;
//如果他有右儿子的情况下，再对右儿子进行讨论
if(i*2+1 <= n)
{
//如果右儿子的值更小，更新较小的结点编号
if(h[ t] > h[ i*2+1])
t=i*2+1;
}
//如果发现最小的结点编号不是自己，说明子结点中有比父结点更小的
if(t!=i)
{
swap(t,i);//交换它们，注意swap函数需要自己来写
i=t;//更新i为刚才与它交换的儿子结点的编号，便于接下来继续向下调整
}
else
flag=1;//则否说明当前的父结点已经比两个子结点都要小了，不需要在进行调整了
}
}

我们刚才在对 23 进行调整的时候，竟然只进行了 3 次比较，就重新恢复了最小堆的特性。现在最小的数依然在堆顶为 2。之前那种从头到尾扫描的方法需要 14 次比较，现在只需要 3 次就够了。现在每次删除最小的数并新增一个数，并求当前最小数的时间复杂度是 O(3)，这恰好是 O(log214)即 O(log2N)简写为 O(logN)。假如现在有 1 亿个数（即 N=1 亿），进行 1 亿次删除最小数并新增一个数的操作，使用原来扫描的方法计算机需要运行大约 1 亿的平方次，而现在只需要 1 亿*log1 亿次，即 27 亿次。假设计算机每秒钟可以运行 10 亿次，那原来则需要一千万秒大约 115 天！而现在只要 2.7 秒。是不是很神奇，再次感受到算法的伟大了吧。

说到这里，如果只是想新增一个值，而不是删除最小值又该如何操作呢？即如何在原有的堆上直接插入一个新元素呢？只需要直接将新元素插入到末尾，再根据情况判断新元素是否需要上移，直到满足堆的特性为止。如果堆的大小为 N（即有 N 个元素），那么插入一个新元素所需要的时间也是 O(logN)。例如我们现在要新增一个数 3。

图片 12.8 picture11.8

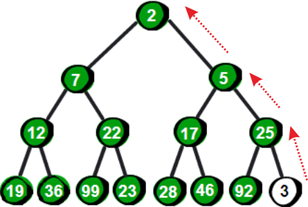
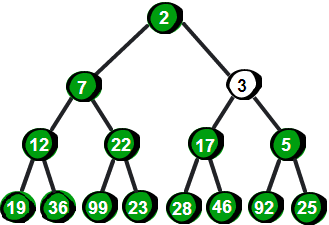
先将 3 与它的父结点 25 比较，发现比父结点小，为了维护最小堆的特性，需要与父结点的值进行交换。交换之后发现还是要比它此时的父结点 5 小，因此需要再次与父结点交换。至此又重新满足了最小堆的特性。向上调整完毕后如下。

图片 12.9 picture11.9

向上调整的代码如下。

 
void siftup(int i) //传入一个需要向上调整的结点编号i
{
int flag=0; //用来标记是否需要继续向上调整
if(i==1) return; //如果是堆顶，就返回，不需要调整了
//不在堆顶 并且 当前结点i的值比父结点小的时候继续向上调整
while(i!=1 && flag==0)
{
//判断是否比父结点的小
if(h[ i]<h[ i/2])
swap(i,i/2);//交换他和他爸爸的位置
else
flag=1;//表示已经不需要调整了，当前结点的值比父结点的值要大
i=i/2; //这句话很重要，更新编号i为它父结点的编号，从而便于下一次继续向上调整
}
}

更多信息请访问

http://wiki.jikexueyuan.com/project/easy-learn-algorithm/