本篇为PolarDB-X“全局Binlog解读”系列文章的理论篇,将对全局Binlog的理论基础和核心原理进行深入剖析,理论是对本质的描述,而全局Binlog的本质是排序,本文会围绕排序这一主线条,重点讲理论,并辅以工程案例,剥丝抽茧展开介绍,展开阅读前建议优先参考前序文章(参见[附1]和[附2])
TSO和Binlog
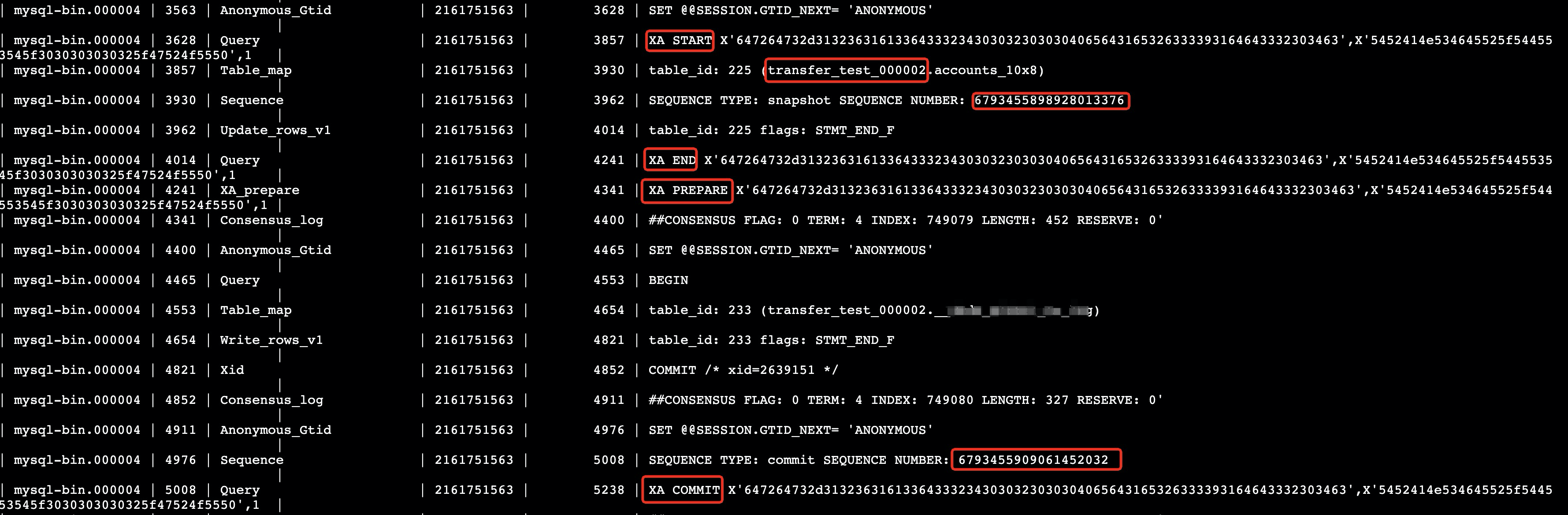
PolarDB-X提供了强一致的分布式事务策略,全局时间戳TSO(参见[附3])在其中扮演了核心角色,同样的,TSO也是全局Binlog得以实现的基础,它是全局Binlog对事务进行排序的依据,所以,在事务提交阶段,需要将TSO记录到各个DN的物理Binlog,供全局Binlog对事务进行归并排序。在PolarDB-X的工程实现中,有两种记录方式,一种是扩展出了一种新的类型为Sequence的Event(DN版本为5.7的实现方案),通过该Event,在XA Prepare阶段记录Snapshot TSO,在XA Commit阶段记录Commit TSO (全局Binlog会依据Commit TSO进行排序,后文将Commit TSO简称为CTS),如下所示:

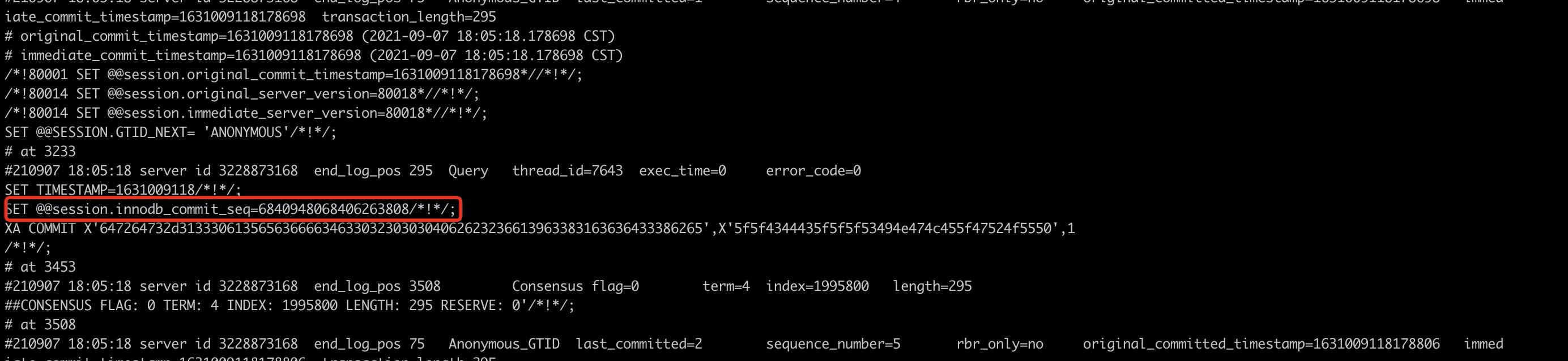
另一种是基于Binlog Event的标志位进行了扩展(DN版本为8.0的实现方案),相比于原生MySQL,增加了一个名字为innodb_commit_seq的标志位,如下所示:


事务空洞
PolarDB-X的分布式事务是基于MySQL XA来扩展实现的,属于典型的2PC事务,事务提交分为两个阶段,一阶段提交XA Prepare,二阶段提交XA Commit,多个分布式事务并发提交时,在DN的Binlog中会形成“事务空洞”,所谓“事务空洞”分析如下
- 定义
对于一个2PC事务 (Prepare+Commit),如果在其Prepare和Commit之间,穿插了其它事务的Prepare或Commit,我们称这些事务间存在空洞。
- 举例
假设有事务T1和T2,Prepare阶段简称为P,Commit阶段简称为C
有空洞:P1 P2 C1 C2、P1 P2 C2 C1、P2 P1 C1 C2、P2 P1 C2 C1
无空洞:P1 C1 P2 C2、P2 C2 P1 C1
- 体现在Binlog
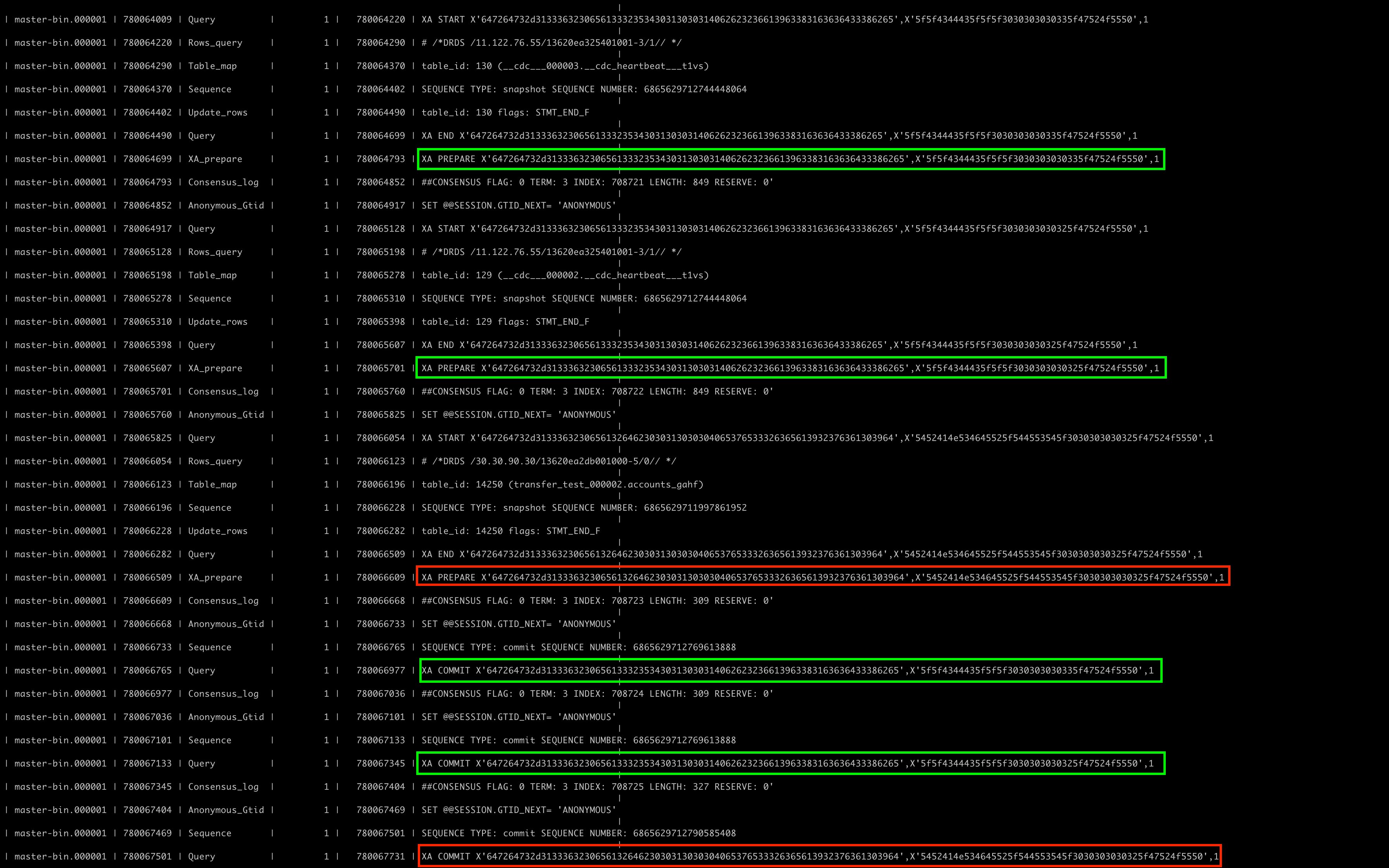
在Binlog文件中,事务空洞体现的形式为,在同一事务的XA Prepare Event和XA Commit Event之间,穿插了其它事务的Event,如下所示:
定理归纳
基于以上描述的事务空洞,可以归纳出如下一些定理:
定理一
- 定义
如果两个事务之间存在事务空洞,则这两个事务间不存在happen before约束,即这两个事务之间必不存在写冲突,调整事务的前后关系不会导致数据一致性问题。
- 证明
反证法:因为,存在写冲突的并发事务,会被排它锁转化为串行关系;所以,存在写冲突的事务,不可能同时进入Prepare阶段;因此,没有触发空洞的条件;得证。
定理二
- 定义
如果两个事务之间存在事务空洞,则这两个事务CTS(Commit Timestamp)的大小,和Commit的顺序不相关,即Commit靠前的事务的CTS不一定比Commit靠后的事务的CTS大,如P1 P2 C1 C2场景,C1的CTS可能大于C2,也可能小于C2。
- 证明
由定理一可知,存在空洞关系的事务之间必不存在写冲突,那么事务的Commit便存在随机性,又因为获取CTS和Commit并不是一个原子操作(PolarDB-X分布式事务本身的特点),那么先发起Commit的事务可能持有的是比较小的CTS,得证。
定理三
- 定义
如果两个事务之间不存在空洞,则这两个事务CTS(Commit Timestamp)的大小,和Commit的顺序正相关,即Commit靠前的事务的CTS一定小于等于Commit靠后的事务的CTS,如P1 C1 P2 C2场景,C1的CTS一定小于等于C2的CTS。
- 证明
当事务T1、T2之间没有空洞时,即满足形如 P1 C1 P2 C2 这种情况时,由两阶段事务的特性可知
a. 对于事务T1,当提交C1时,所有分片的P1一定已经完成提交
b. 对于事务T2,当提交C2时,所有分片的P2一定已经完成提交
那么,从发生顺序来看,因为C1 => P2,P2 => C2,所以C1 => C2,“=>”代表happen before关系,即:C1一定发生在C2之前,C1和C2不会出现并发,得证。
- 补充说明一
C1的CTS和P2的Snapshot Sequence并没有任何约束关系,C1 > P2 或 C1 < P2都可能发生。
- 补充说明二
为什么是小于等于?因为不存在事务空洞的两个事务之间,可能存在写冲突,也可能不存在写冲突;如果存在写冲突,那么结论则为Commit靠前的事务的CTS一定小于Commit靠后的事务的CTS;如果不存在写冲突,那么结论则为小于等于,取决于这两个事务是否被分配到了同一个CommitGroup
混合事务策略
前面所述PolarDB-X分布式事务Commit后,在物理Binlog中的体现形态,只是最常规的一种,它其实还有多种形态
单机事务
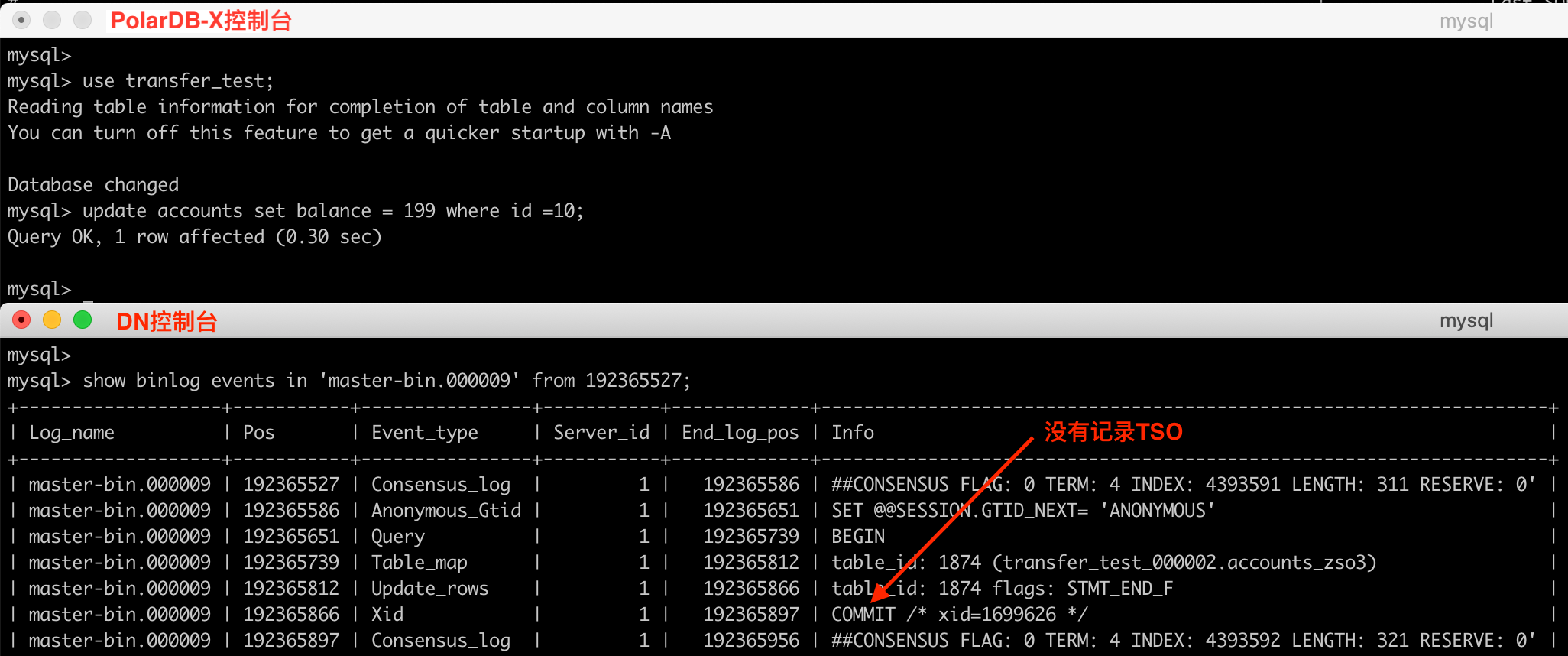
在autocommit模式下,某条sql如果只涉及单条数据的变更,PolarDB-X会将该事务优化为单机事务,此时在物理Binlog中并不会记录TSO,因为单机事务不涉及多个分片的数据变更,无需TSO进行统一协调,靠innodb的原生mvcc机制即可保证Repeatable Read,如下所示:
一阶段提交
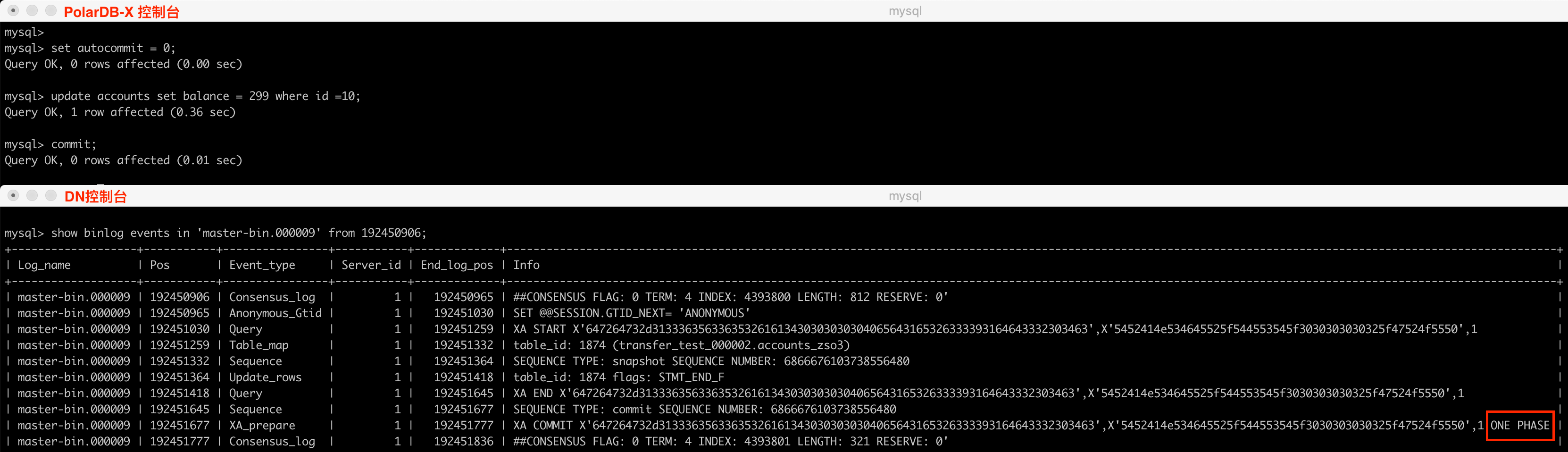
PolarDB-X在进行事务提交时,能够自动检测到当前事务操作的数据是否只涉及一个分片,如果是的话会优化为一阶段提交,节省一次RPC交互,尽最大可能提升性能(参见附[4])。反映到物理Binlog中,则呈现出如下的形态:
普通XA事务
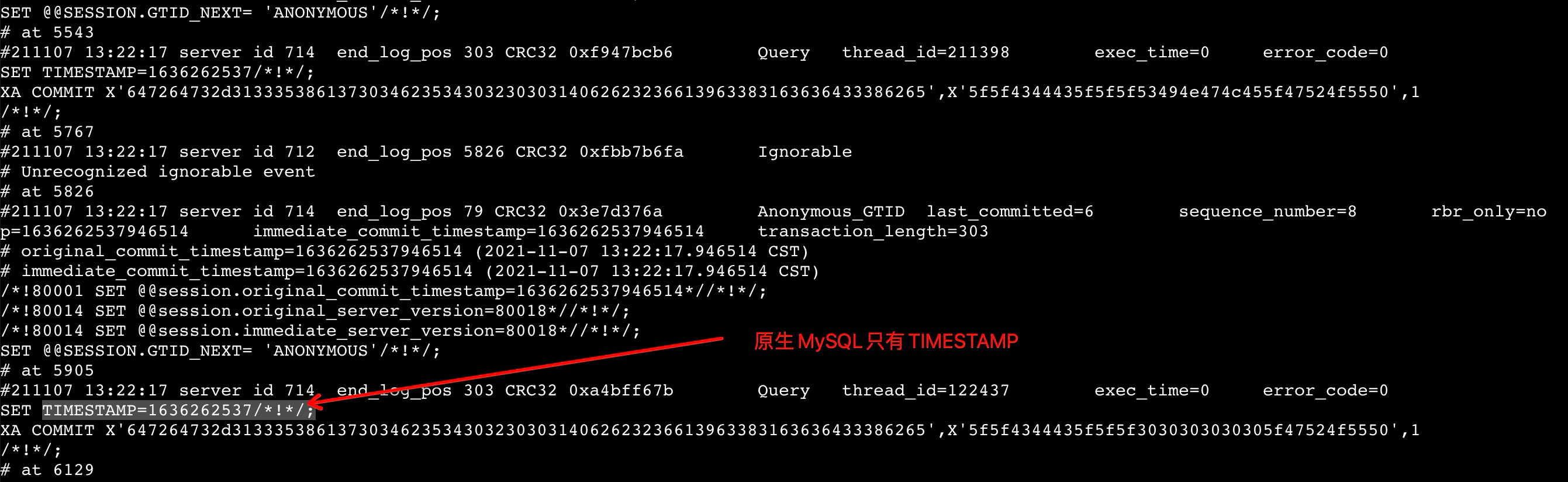
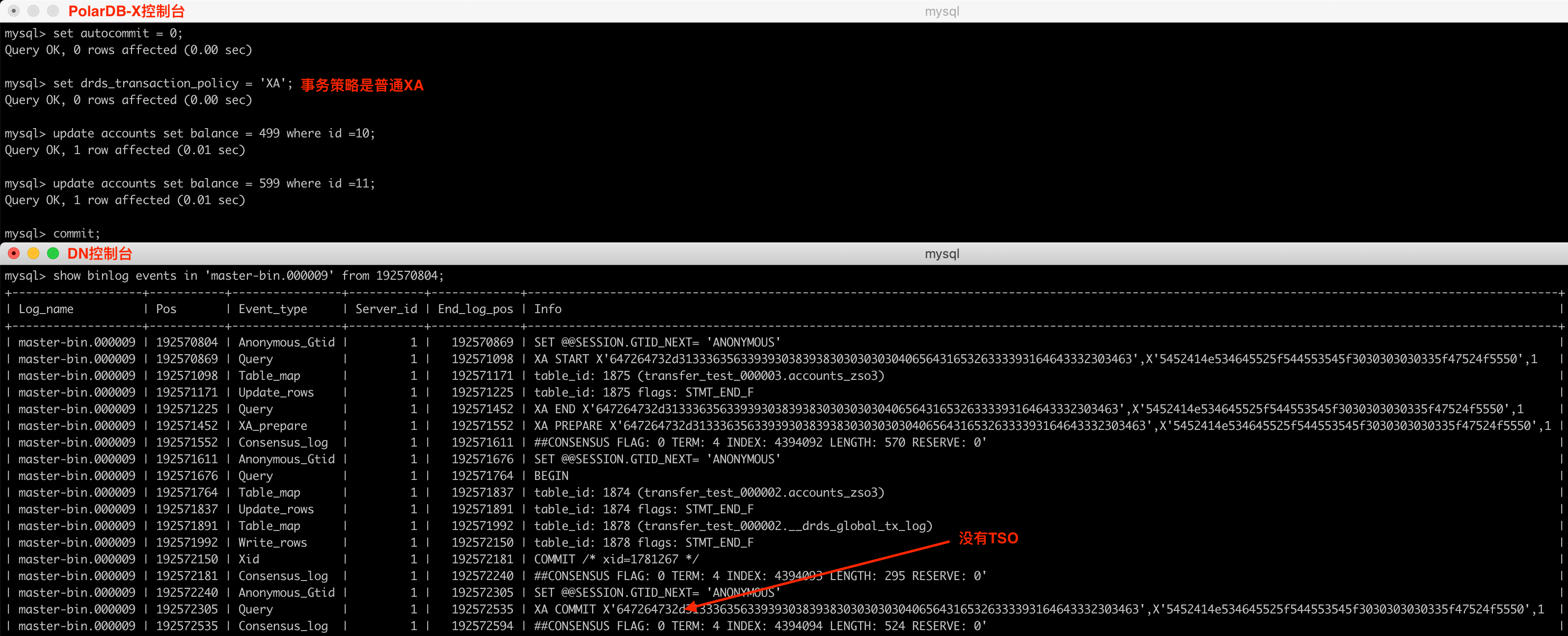
PolarDB-X的默认事务策略为TSO,但支持手动修改为普通XA策略(会话级别和全局级别),但一般不建议修改。当设置为普通XA策略时,TSO将不复存在,在物理Binlog中的存在形式如下所示:
PS:仔细观察,上图在一个事务中执行了两次update,但在物理Binlog中对应的并不是两个XA Commit,而是一个XA形态的事务和一个单机形态的事务,单机形态的事务除了记录正常的业务数据变更,还额外记录了代表Commit Point的全局事务日志(通过系统表__drds_tx_global_log,CTS会被记录到该表),这两个合并到一起提交,减少了一次RPC交互。关于Commit Point可参见附[5]
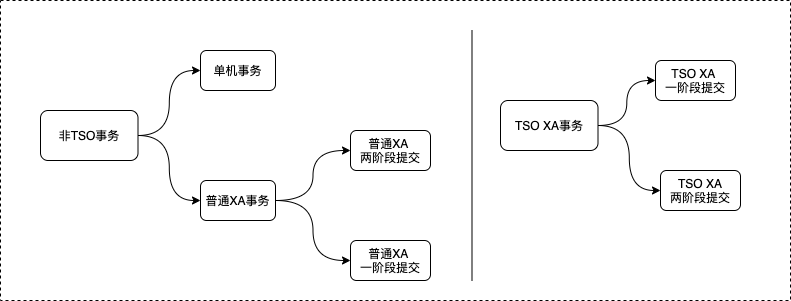
下面附图对混合事务场景做个分类,主要划分为两大类:非TSO事务和TSO事务,其中不管是普通XA事务还是TSO XA事务,都可以继续划分为一阶段提交和两阶段提交类型
虚拟TSO
全局Binlog的排序依据是TSO,但是在混合事务策略下,物理Binlog中会出现非TSO事务,那么排序操作将变成“无水之源,无本之木”,为了解决这个问题,我们在PolarDB-X TSO的基础上进行了扩展,实现了一套新的逻辑时钟——虚拟TSO。先来看一下虚拟TSO的基本格式,如下:

备注: 图中所表示的“位”是数字位,不是Bit或Byte
- 原始TSO:高19位记录物理Binlog中的原始TSO,如果是非TSO事务或TSO一阶段提交事务,则复用maxCTS
- 事务ID:后续19位记录XA事务的transactionID,如果是单机事务,则复用maxTransactionId
- 事务Sequence:后续10位记录事务的序列号,用于区分复用同一maxTransaction的多个单机事务,按序自增,非单机事务因为自身具备真实TransactionId,直接设置为0即可
- DN哈希码:后续6位用来标识局部事务所属的DN节点
虚拟TSO最终会以RowsQueryEvent的形式,记录到全局Binlog文件中,one event per transaction,示例如下:
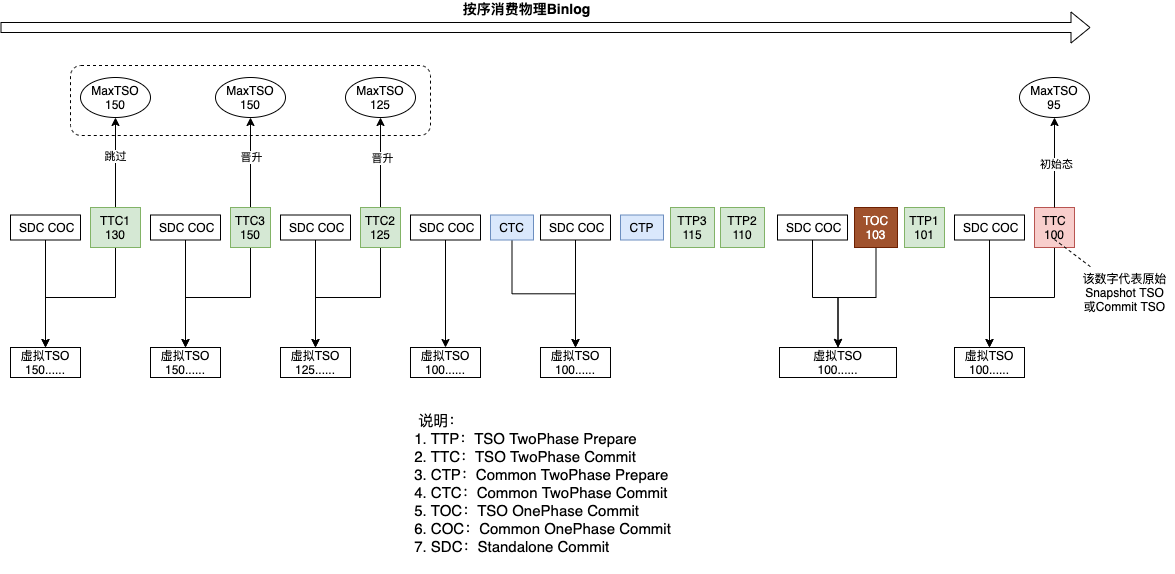
上面提到了两个复用:复用maxCTS和复用maxTransactionId,在按序消费物理Binlog时,我们会维护两个变量maxCTS和maxTransactionId,每收到一个新的CTS或TransactionId时,会和当前已知的变量值进行对比,如果新的比已知的大,则对最大值进行重置。当收到非TSO事务时,以当前已知的maxCTS为准,填充该事务虚拟TSO的高19位;当收到单机事务时,以当前已知的maxTransactionId为准,并维护一个sequence变量,填充该事务的中间29位。下图以CTS为例,进行了更加形象化的展示

接下来对上述复用maxCTS和maxTransactionId的方案进行一下正确性证明。回顾一下上文定义的事务空洞,描述的主要是两个2PC事务之间的关系,在此进行一下扩展,对于单机事务和一阶段提交事务,可以将其看作是一个特殊的2PC事务——P和C之间永远不会出现空洞的事务。当从物理Binlog依次获取数据时,每遇到一个非TSO事务或TSO一阶段提交事务(为表述方便,记为Tc)的Commit Event,存在两种情况:情况一,Tc和前序任何事务不存在空洞关系,即Tc前面的所有事务都已经收到了P和C,例如P1 C1 P2 C2 P3 P4 C4 C3 Tc,那么Tc和前序任何一个事务都可能存在数据冲突,使用maxTSO、maxTransactionId和Sequence++,一定能够保证构建出的虚拟TSO比前序所有事务的虚拟TSO都大,按照同样的规则,也一定比后序所有事务的虚拟TSO都小;情况二,Tc和前序部分事务之间存在空洞关系,即Tc前面存在只收到P还未收到C的事务,例如P1 C1 P2 C2 P3 P4 P5 C3 Tc C4 C5,由定理一可知,Tc和存在空洞关系的事务之间是不存在写冲突的,那么同情况一,依然只需要保证构建出的虚拟TSO大于前序所有已经收到了P和C的事务的最大虚拟TSO即可,如此例,Tc的虚拟TSO只需要大于Max(T1,T2,T3)即可,T4和T5的虚拟TSO大于或者小于Tc都没有任何影响,因为它们之间不存在写冲突,先后顺序无关紧要。
接下来还有几个扩展问题需要回答
- TSO一阶段提交事务,自身拥有CTS和TransactionId,为什么还要靠复用maxCTS和maxTransactionId构建虚拟TSO?
这是因为,TSO一阶段提交事务的CTS没有任何规律,比如[P1 C2 Tc]这种场景下,Tc的CTS可能大于T1的CTS,也可能小于,再比如[Tc1 Tc2]场景下,Tc1和Tc2的CTS之间的大小关系也是不确定的。这种不确定,会给排序规则带来很大的影响,所以我们采取了忽略其原始CTS的方式。
- 按照上述虚拟TSO的构建方案,对于普通XA事务来说,同一个XA事务,其在不同DN节点上构造出的虚拟TSO是不相同的,如何进行合并
普通XA事务本身也是无法保证线性一致性的,所以我们采取了一个妥协的方案,普通XA事务不进行合并,只保证最终一致
- 上述虚拟TSO的构建方案,严重依赖TSO XA事务,如果没有任何TSO事务操作怎么办?
系统内置了心跳策略,会维护一张系统表,用来强制构建TSO事务,保证全局Binlog能够持续构建
总结
- 对于单机事务和一阶段提交事务,我们将其看成一个特殊的2PC事务;通过上述构建虚拟TSO的方案,保证了混合事务场景下所有事务都有一个虚拟的CTS;基于虚拟CTS,上面的空洞理论和3个定理也是完全成立的
排序规则
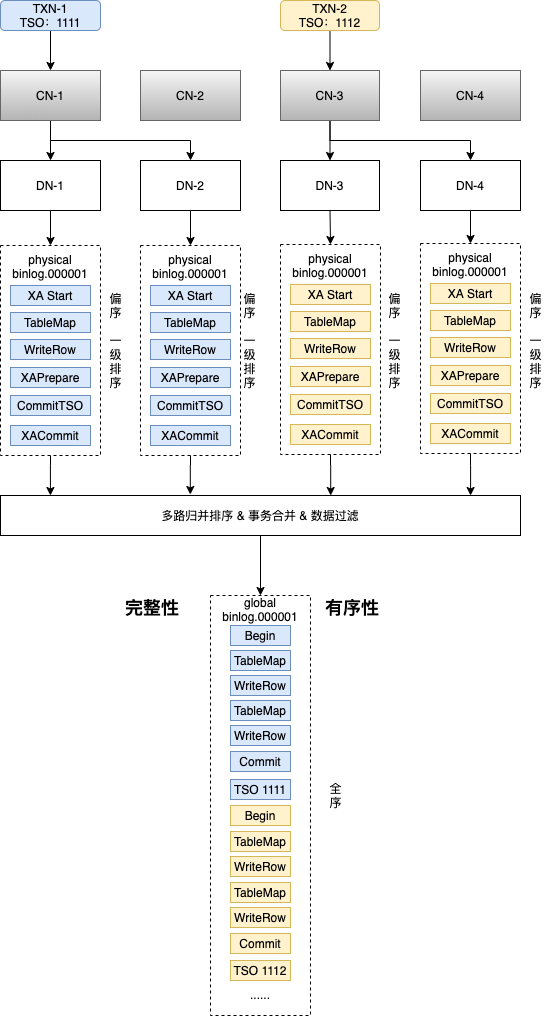
解决完排序依据的问题,下面对排序规则进行介绍,本文主要介绍一些核心流程和思想,暂不展开细讲,后续会有源码解读专栏进行详细介绍。整个排序体系划分为两个层次,一级排序和全局排序,一级排序,负责对每个DN上的事务按照CTS进行局部排序;全局排序,在一级排序的基础上,对所有DN节点的事务进行多路归并排序,构造出全局有序的事务队列。

- 一级排序
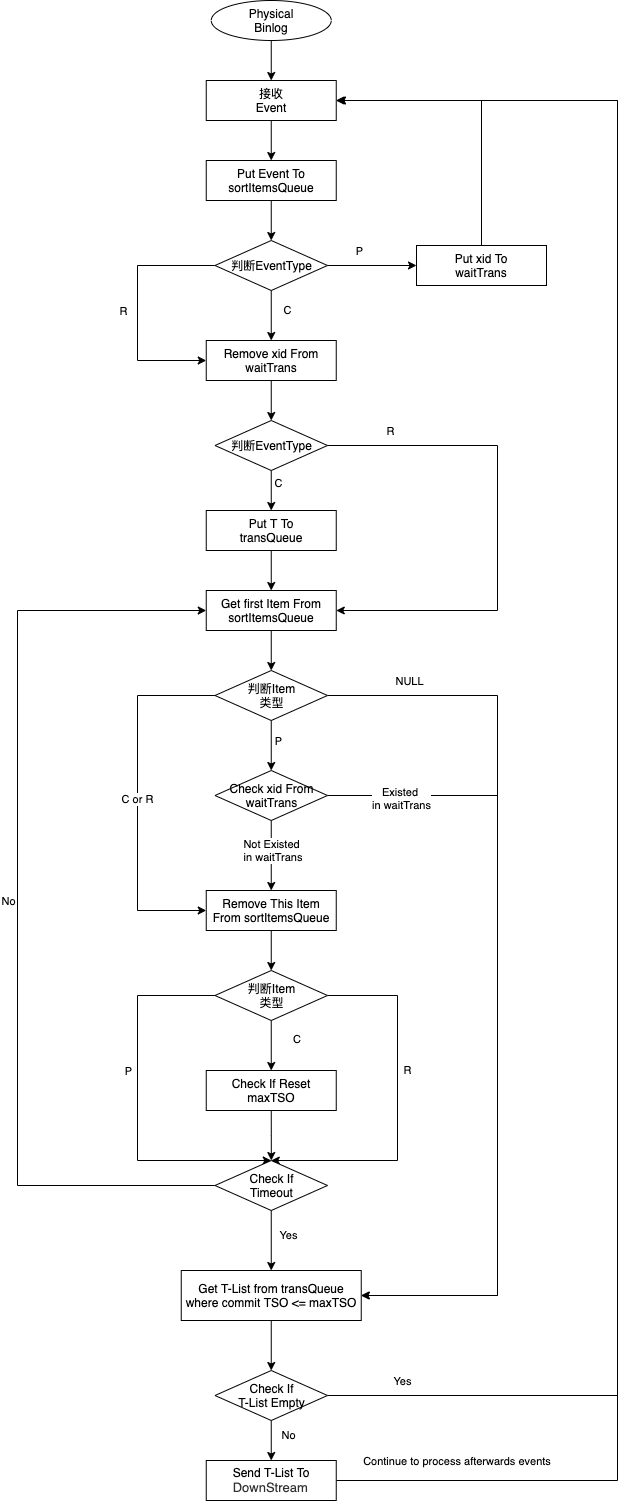
回顾一下上面的三个定理。由定理二可知,CTS在物理Binlog中并非天然有序;但由定理三可知,乱序仅限于存在空洞的事务之间;又由定理一可知,对存在乱序的事务进行排序,并不会破坏线性一致性(即不会引发数据一致性问题)。基于这三个定理,可推演出一级排序的核心流程,如下所示,想了解更多细节,可参见核心代码Sorter.java

- 全局排序
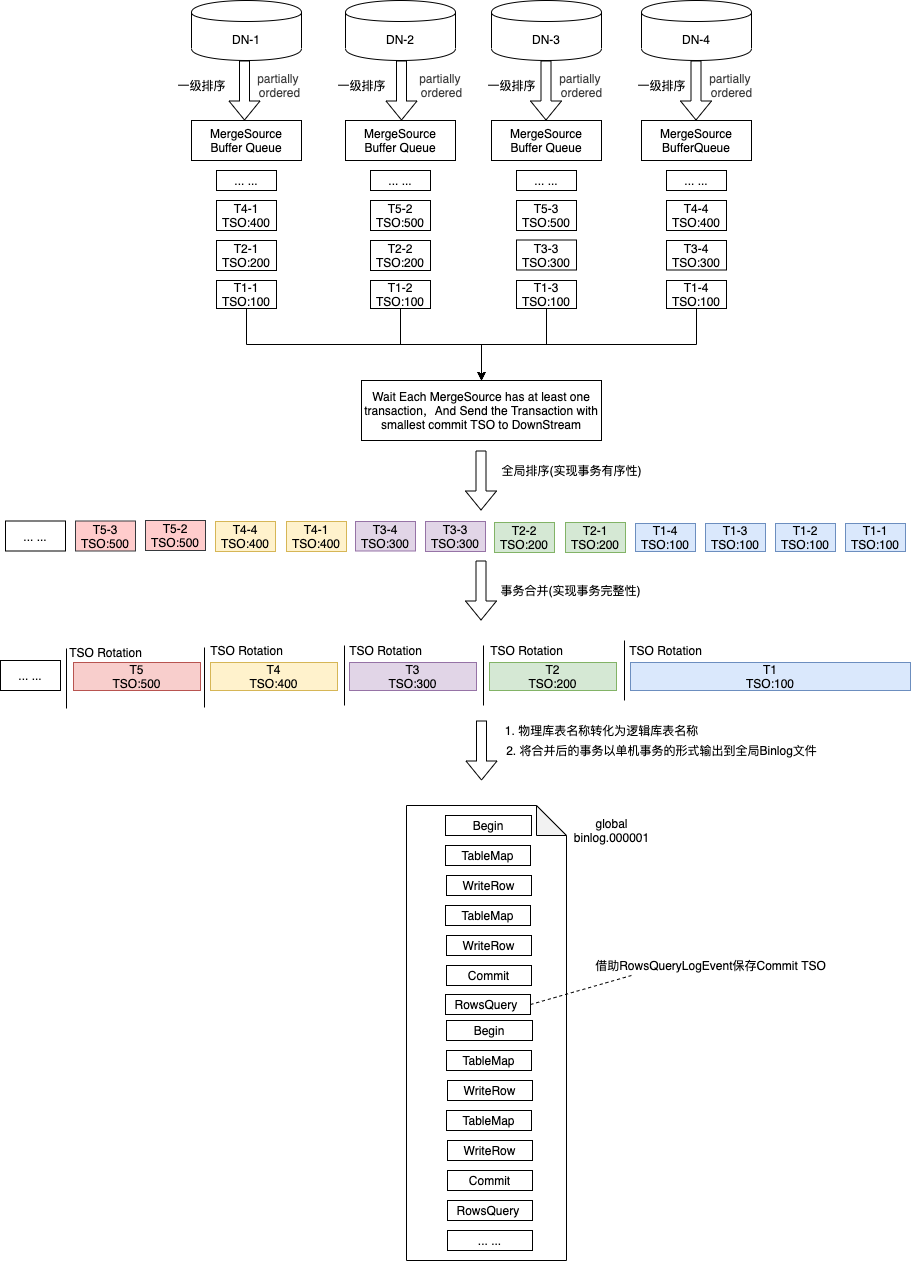
全局排序通过经典的多路归并排序算法实现,核心思路为:等待每个物理Binlog队列至少含有一个事务,然后取Commit TSO最小的事务输出到下游,循环往复,得到一个无界的全局有序事务队列。在全局有序队列的基础上完成事务合并,每当出现Commit TSO Rotation时,代表上一个事务的结束,新事务的开始,以此为基准区分不同的事务,然后进行事务的合并,将分散到各个DN的局部事务合并为一个完整的事务。在合并的过程中将类似XA Start、XA End、XA Prepare等对应XA特性的Event剔除,只保留单机特性的Event。想了解更多细节,可参见核心代码LogEventMerger.java

总结
本篇为PolarDB-X“全局Binlog解读”系列文章的理论篇,将对全局Binlog的理论基础和核心原理进行深入剖析,理论是对本质的描述,而全局Binlog的本质是排序,本文会围绕排序这一主线条,重点讲理论,并辅以工程案例,剥丝抽茧展开介绍,展开阅读前建议优先参考前序文章(参见[附1]和[附2])
TSO和Binlog
PolarDB-X提供了强一致的分布式事务策略,全局时间戳TSO(参见[附3])在其中扮演了核心角色,同样的,TSO也是全局Binlog得以实现的基础,它是全局Binlog对事务进行排序的依据,所以,在事务提交阶段,需要将TSO记录到各个DN的物理Binlog,供全局Binlog对事务进行归并排序。在PolarDB-X的工程实现中,有两种记录方式,一种是扩展出了一种新的类型为Sequence的Event(DN版本为5.7的实现方案),通过该Event,在XA Prepare阶段记录Snapshot TSO,在XA Commit阶段记录Commit TSO (全局Binlog会依据Commit TSO进行排序,后文将Commit TSO简称为CTS),如下所示:
另一种是基于Binlog Event的标志位进行了扩展(DN版本为8.0的实现方案),相比于原生MySQL,增加了一个名字为innodb_commit_seq的标志位,如下所示:
事务空洞
PolarDB-X的分布式事务是基于MySQL XA来扩展实现的,属于典型的2PC事务,事务提交分为两个阶段,一阶段提交XA Prepare,二阶段提交XA Commit,多个分布式事务并发提交时,在DN的Binlog中会形成“事务空洞”,所谓“事务空洞”分析如下
- 定义
对于一个2PC事务 (Prepare+Commit),如果在其Prepare和Commit之间,穿插了其它事务的Prepare或Commit,我们称这些事务间存在空洞。
- 举例
假设有事务T1和T2,Prepare阶段简称为P,Commit阶段简称为C
有空洞:P1 P2 C1 C2、P1 P2 C2 C1、P2 P1 C1 C2、P2 P1 C2 C1
无空洞:P1 C1 P2 C2、P2 C2 P1 C1
- 体现在Binlog
在Binlog文件中,事务空洞体现的形式为,在同一事务的XA Prepare Event和XA Commit Event之间,穿插了其它事务的Event,如下所示:
定理归纳
基于以上描述的事务空洞,可以归纳出如下一些定理:
定理一
- 定义
如果两个事务之间存在事务空洞,则这两个事务间不存在happen before约束,即这两个事务之间必不存在写冲突,调整事务的前后关系不会导致数据一致性问题。
- 证明
反证法:因为,存在写冲突的并发事务,会被排它锁转化为串行关系;所以,存在写冲突的事务,不可能同时进入Prepare阶段;因此,没有触发空洞的条件;得证。
定理二
- 定义
如果两个事务之间存在事务空洞,则这两个事务CTS(Commit Timestamp)的大小,和Commit的顺序不相关,即Commit靠前的事务的CTS不一定比Commit靠后的事务的CTS大,如P1 P2 C1 C2场景,C1的CTS可能大于C2,也可能小于C2。
- 证明
由定理一可知,存在空洞关系的事务之间必不存在写冲突,那么事务的Commit便存在随机性,又因为获取CTS和Commit并不是一个原子操作(PolarDB-X分布式事务本身的特点),那么先发起Commit的事务可能持有的是比较小的CTS,得证。
定理三
- 定义
如果两个事务之间不存在空洞,则这两个事务CTS(Commit Timestamp)的大小,和Commit的顺序正相关,即Commit靠前的事务的CTS一定小于等于Commit靠后的事务的CTS,如P1 C1 P2 C2场景,C1的CTS一定小于等于C2的CTS。
- 证明
当事务T1、T2之间没有空洞时,即满足形如 P1 C1 P2 C2 这种情况时,由两阶段事务的特性可知
a. 对于事务T1,当提交C1时,所有分片的P1一定已经完成提交
b. 对于事务T2,当提交C2时,所有分片的P2一定已经完成提交
那么,从发生顺序来看,因为C1 => P2,P2 => C2,所以C1 => C2,“=>”代表happen before关系,即:C1一定发生在C2之前,C1和C2不会出现并发,得证。
- 补充说明一
C1的CTS和P2的Snapshot Sequence并没有任何约束关系,C1 > P2 或 C1 < P2都可能发生。
- 补充说明二
为什么是小于等于?因为不存在事务空洞的两个事务之间,可能存在写冲突,也可能不存在写冲突;如果存在写冲突,那么结论则为Commit靠前的事务的CTS一定小于Commit靠后的事务的CTS;如果不存在写冲突,那么结论则为小于等于,取决于这两个事务是否被分配到了同一个CommitGroup
混合事务策略
前面所述PolarDB-X分布式事务Commit后,在物理Binlog中的体现形态,只是最常规的一种,它其实还有多种形态
单机事务
在autocommit模式下,某条sql如果只涉及单条数据的变更,PolarDB-X会将该事务优化为单机事务,此时在物理Binlog中并不会记录TSO,因为单机事务不涉及多个分片的数据变更,无需TSO进行统一协调,靠innodb的原生mvcc机制即可保证Repeatable Read,如下所示:
一阶段提交
PolarDB-X在进行事务提交时,能够自动检测到当前事务操作的数据是否只涉及一个分片,如果是的话会优化为一阶段提交,节省一次RPC交互,尽最大可能提升性能(参见附[4])。反映到物理Binlog中,则呈现出如下的形态:
普通XA事务
PolarDB-X的默认事务策略为TSO,但支持手动修改为普通XA策略(会话级别和全局级别),但一般不建议修改。当设置为普通XA策略时,TSO将不复存在,在物理Binlog中的存在形式如下所示:
PS:仔细观察,上图在一个事务中执行了两次update,但在物理Binlog中对应的并不是两个XA Commit,而是一个XA形态的事务和一个单机形态的事务,单机形态的事务除了记录正常的业务数据变更,还额外记录了代表Commit Point的全局事务日志(通过系统表__drds_tx_global_log,CTS会被记录到该表),这两个合并到一起提交,减少了一次RPC交互。关于Commit Point可参见附[5]
下面附图对混合事务场景做个分类,主要划分为两大类:非TSO事务和TSO事务,其中不管是普通XA事务还是TSO XA事务,都可以继续划分为一阶段提交和两阶段提交类型
虚拟TSO
全局Binlog的排序依据是TSO,但是在混合事务策略下,物理Binlog中会出现非TSO事务,那么排序操作将变成“无水之源,无本之木”,为了解决这个问题,我们在PolarDB-X TSO的基础上进行了扩展,实现了一套新的逻辑时钟——虚拟TSO。先来看一下虚拟TSO的基本格式,如下:
备注: 图中所表示的“位”是数字位,不是Bit或Byte
- 原始TSO:高19位记录物理Binlog中的原始TSO,如果是非TSO事务或TSO一阶段提交事务,则复用maxCTS
- 事务ID:后续19位记录XA事务的transactionID,如果是单机事务,则复用maxTransactionId
- 事务Sequence:后续10位记录事务的序列号,用于区分复用同一maxTransaction的多个单机事务,按序自增,非单机事务因为自身具备真实TransactionId,直接设置为0即可
- DN哈希码:后续6位用来标识局部事务所属的DN节点
虚拟TSO最终会以RowsQueryEvent的形式,记录到全局Binlog文件中,one event per transaction,示例如下:
上面提到了两个复用:复用maxCTS和复用maxTransactionId,在按序消费物理Binlog时,我们会维护两个变量maxCTS和maxTransactionId,每收到一个新的CTS或TransactionId时,会和当前已知的变量值进行对比,如果新的比已知的大,则对最大值进行重置。当收到非TSO事务时,以当前已知的maxCTS为准,填充该事务虚拟TSO的高19位;当收到单机事务时,以当前已知的maxTransactionId为准,并维护一个sequence变量,填充该事务的中间29位。下图以CTS为例,进行了更加形象化的展示
接下来对上述复用maxCTS和maxTransactionId的方案进行一下正确性证明。回顾一下上文定义的事务空洞,描述的主要是两个2PC事务之间的关系,在此进行一下扩展,对于单机事务和一阶段提交事务,可以将其看作是一个特殊的2PC事务——P和C之间永远不会出现空洞的事务。当从物理Binlog依次获取数据时,每遇到一个非TSO事务或TSO一阶段提交事务(为表述方便,记为Tc)的Commit Event,存在两种情况:情况一,Tc和前序任何事务不存在空洞关系,即Tc前面的所有事务都已经收到了P和C,例如P1 C1 P2 C2 P3 P4 C4 C3 Tc,那么Tc和前序任何一个事务都可能存在数据冲突,使用maxTSO、maxTransactionId和Sequence++,一定能够保证构建出的虚拟TSO比前序所有事务的虚拟TSO都大,按照同样的规则,也一定比后序所有事务的虚拟TSO都小;情况二,Tc和前序部分事务之间存在空洞关系,即Tc前面存在只收到P还未收到C的事务,例如P1 C1 P2 C2 P3 P4 P5 C3 Tc C4 C5,由定理一可知,Tc和存在空洞关系的事务之间是不存在写冲突的,那么同情况一,依然只需要保证构建出的虚拟TSO大于前序所有已经收到了P和C的事务的最大虚拟TSO即可,如此例,Tc的虚拟TSO只需要大于Max(T1,T2,T3)即可,T4和T5的虚拟TSO大于或者小于Tc都没有任何影响,因为它们之间不存在写冲突,先后顺序无关紧要。
接下来还有几个扩展问题需要回答
- TSO一阶段提交事务,自身拥有CTS和TransactionId,为什么还要靠复用maxCTS和maxTransactionId构建虚拟TSO?
这是因为,TSO一阶段提交事务的CTS没有任何规律,比如[P1 C2 Tc]这种场景下,Tc的CTS可能大于T1的CTS,也可能小于,再比如[Tc1 Tc2]场景下,Tc1和Tc2的CTS之间的大小关系也是不确定的。这种不确定,会给排序规则带来很大的影响,所以我们采取了忽略其原始CTS的方式。
- 按照上述虚拟TSO的构建方案,对于普通XA事务来说,同一个XA事务,其在不同DN节点上构造出的虚拟TSO是不相同的,如何进行合并
普通XA事务本身也是无法保证线性一致性的,所以我们采取了一个妥协的方案,普通XA事务不进行合并,只保证最终一致
- 上述虚拟TSO的构建方案,严重依赖TSO XA事务,如果没有任何TSO事务操作怎么办?
系统内置了心跳策略,会维护一张系统表,用来强制构建TSO事务,保证全局Binlog能够持续构建
总结
- 对于单机事务和一阶段提交事务,我们将其看成一个特殊的2PC事务;通过上述构建虚拟TSO的方案,保证了混合事务场景下所有事务都有一个虚拟的CTS;基于虚拟CTS,上面的空洞理论和3个定理也是完全成立的
排序规则
解决完排序依据的问题,下面对排序规则进行介绍,本文主要介绍一些核心流程和思想,暂不展开细讲,后续会有源码解读专栏进行详细介绍。整个排序体系划分为两个层次,一级排序和全局排序,一级排序,负责对每个DN上的事务按照CTS进行局部排序;全局排序,在一级排序的基础上,对所有DN节点的事务进行多路归并排序,构造出全局有序的事务队列。
- 一级排序
回顾一下上面的三个定理。由定理二可知,CTS在物理Binlog中并非天然有序;但由定理三可知,乱序仅限于存在空洞的事务之间;又由定理一可知,对存在乱序的事务进行排序,并不会破坏线性一致性(即不会引发数据一致性问题)。基于这三个定理,可推演出一级排序的核心流程,如下所示,想了解更多细节,可参见核心代码Sorter.java
- 全局排序
全局排序通过经典的多路归并排序算法实现,核心思路为:等待每个物理Binlog队列至少含有一个事务,然后取Commit TSO最小的事务输出到下游,循环往复,得到一个无界的全局有序事务队列。在全局有序队列的基础上完成事务合并,每当出现Commit TSO Rotation时,代表上一个事务的结束,新事务的开始,以此为基准区分不同的事务,然后进行事务的合并,将分散到各个DN的局部事务合并为一个完整的事务。在合并的过程中将类似XA Start、XA End、XA Prepare等对应XA特性的Event剔除,只保留单机特性的Event。想了解更多细节,可参见核心代码LogEventMerger.java
总结
本篇结合了一些具体样例,系统介绍了PolarDB-X全局Binlog的核心理论模型:以TSO为排序依据,通过一级排序解决事务空洞和事务冲突问题,通过全局排序保证线性一致性,并通过虚拟逻辑时钟解决混合事务场景下的排序问题等。理论正确性的证明一方面靠数学推导,另一方面靠工程实现来进一步验证,并且工程实现本身也需要强有力的正确性测试能力来保证工程质量,后序会有专题文章来介绍一下全局Binlog正确性测试的故事,敬请期待。本篇结合了一些具体样例,系统介绍了PolarDB-X全局Binlog的核心理论模型:以TSO为排序依据,通过一级排序解决事务空洞和事务冲突问题,通过全局排序保证线性一致性,并通过虚拟逻辑时钟解决混合事务场景下的排序问题等。理论正确性的证明一方面靠数学推导,另一方面靠工程实现来进一步验证,并且工程实现本身也需要强有力的正确性测试能力来保证工程质量,后序会有专题文章来介绍一下全局Binlog正确性测试的故事,敬请期待。