明天盘中继续大跌的话 ，可以小仓位买入部分 ，个人觉得 军工>科技>蓝筹
本文 借鉴知乎高赞的HMM推导公式 看完觉得 大受启发。
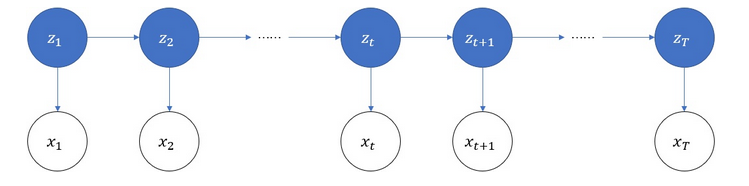
HMM模型（Hidden Markov Model）隐式马尔科夫模型
定义：是一个生成模型，描述由一个隐藏的马尔科夫链随机生成不可观测的状态序列，每个状态生成一个观测，而由此产生一个观测序列
举例说明吧：
假设有4个盒子，每个盒子里面有不同数量的红、白两种颜色的球，如下表
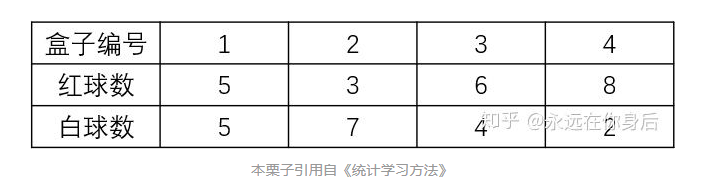
现在计划从这四个盒子中，一个一个的抽取球，共抽取T个，每次抽取后记录颜色，放回原盒子，再以不同概率选择下一盒子抽取球：
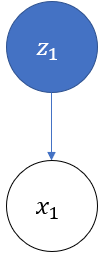
开始时，按照一个初始概率分布随机选择第一个盒子，这里将第一个盒子用 
表示：
将 的值用变量 
表示。因为有4个盒子可共选择，所以 
。然后随机从该盒子中抽取一个球，使用 
表示：
将 的值用变量 
表示。因为只有两种球可供选择，所以 
。一共有4个箱子，2种球，结合前面的箱子的详细数据，可以得到从每一个箱子取到各种颜色球的可能性，用一个表格表示：
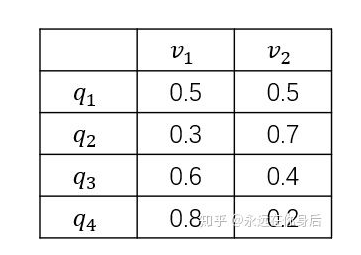
这个表格 可以用一个4*2的矩阵表示（称为观测概率矩阵，也有资料叫做发射矩阵）
其中 
表示在当前时刻给定 
的条件下， 
的概率：
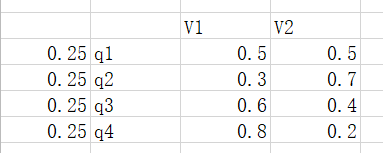
表示当前的时刻，现在是第1时刻；前面标注的初始概率分布，这个概率分布可以用一个向量（称作初始状态概率向量）来表示：
其中的 
表示 
取各个值的概率：
例如该分布是均匀分布的话，对应的向量就是
游戏规则：选择一个盒子 抽取一个球 后将其放回原盒子，按照如下规则选择下一个盒子（ 
）， 再抽取下一球：
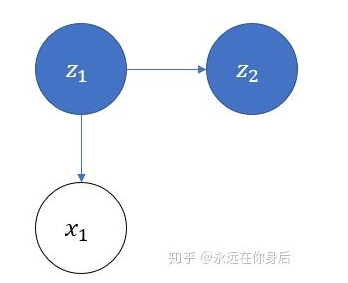
如果当前是盒子1，则选择盒子2
如果当前是盒子2或3，则分布以概率0.4和0.6选择前一个或后一个盒子
如果当前是盒子4，则各以0.5的概率停留在盒子4或者选择盒子3
同样，也可以根据以上规则做出一个表格，其中首列表示当前盒子，首行表示下一个盒子
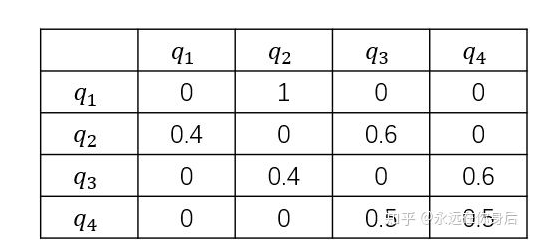
同样使用一个矩阵（称为状态转移矩阵）来表示上表
其中 
表示在当前时刻处于状态 
的条件下，到下一时刻转移到状态 
的概率
以上，生成过程的主要流程就介绍完了，简单概括就是：盒子，取球，盒子，取球……直到生成指定数量（ 
）的数据后停止。如果对这个过程还有不太理解的话，可以看看文章开头给出的关于马尔科夫链的链接
现在，整理一下参数：
一个向量（初始状态向量π），
有两个矩阵（观测状态矩阵B，状态转移矩阵(transition）A）：
其中 
表示隐变量 
的状态数量， 
表示观测变量 
可能的取值数量，在后面的讨论中，用 
表示所有的参数。
HMM的基本问题，一共有三个
（1）概率计算：给定参数
和观测序列
，计算观测序列 
的条件概率
（2）参数学习：给定观测序列 ，反推参数
（3）解码问题：给定参数 和观测序列 
，求可能性最大的
在讨论这三个问题的相关算法之前，首先要给出两个假设，在后面的推导过程中会不断的用到：
齐次马尔可夫假设：即任意时刻的状态只依赖于前一时刻的状态，与其他时刻的状态无关（当然，初始时刻的状态由参数
决定）：
2.观测独立假设：即任意时刻的观测只依赖该时刻的状态，与其他无关：
（1）概率计算
第一个问题，关于概率的计算，由于存在隐变量，所以 的边际概率需要将所有的联合概率 
加和得到：
由于给出了 个观测数据，所以相应的状态也有 个：
将（1）式中的 
展开得到：
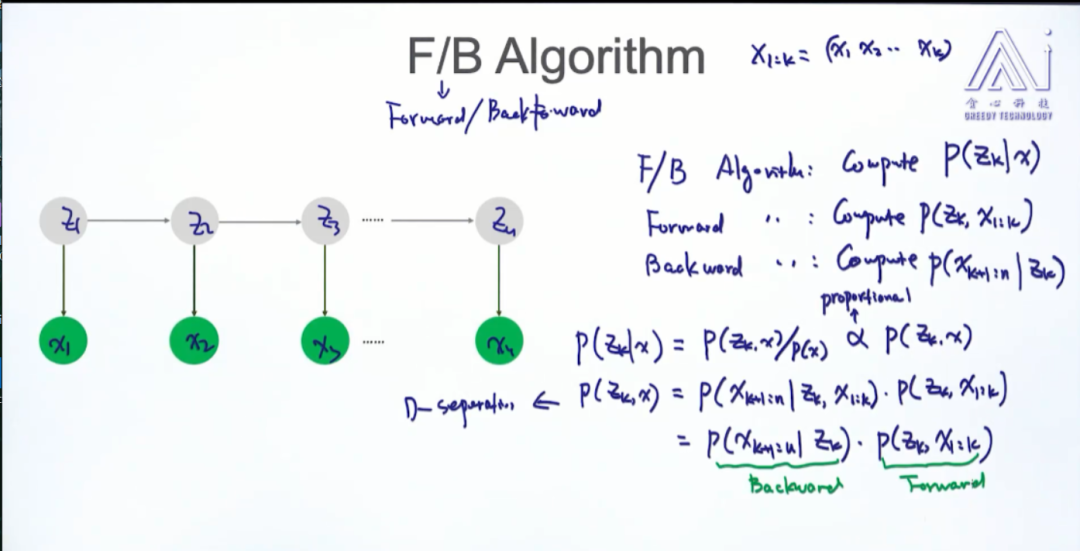
即使不考虑内部的计算，这起码也是 
阶的计算量，所以需要更有效的算法，下面介绍两种：前向算法和后向算法。
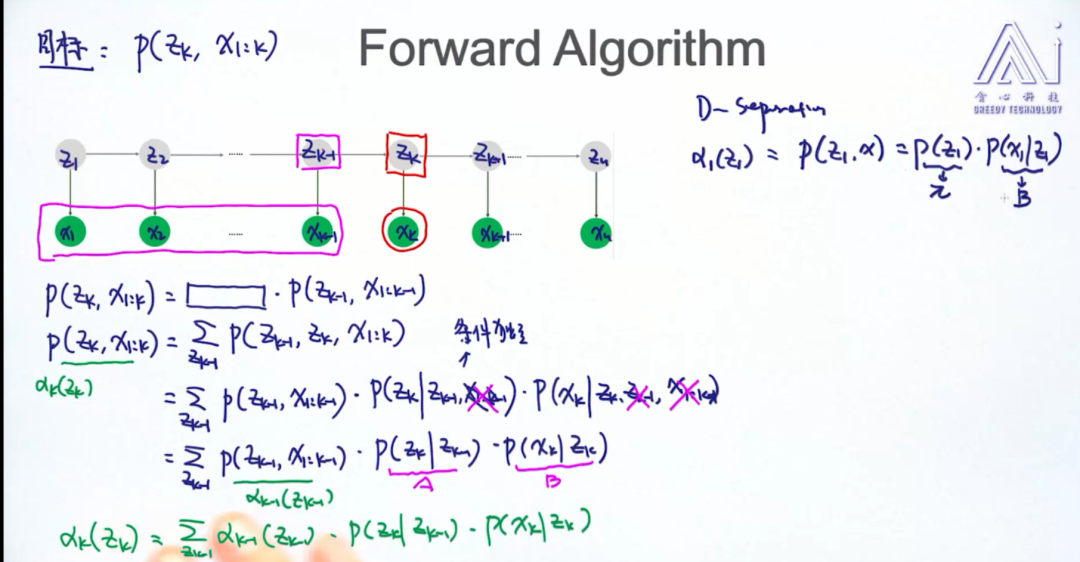
设有 个序列，如下图所示
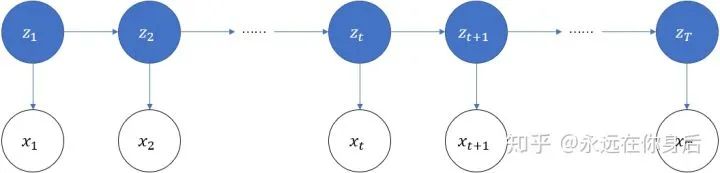
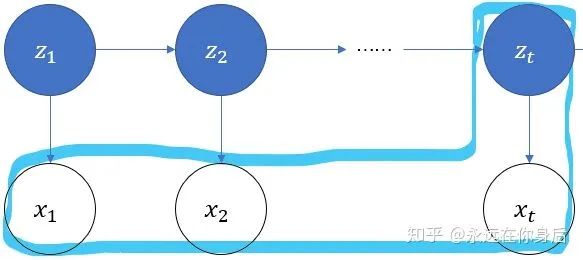
前向算法： 前向概率 
，它是 时刻的状态以及 
时刻的观测在给定参数下的联合概率：
也就是下图中标记的那一部分
根据定义，可以得到它的初值：
其中 
表示由状态 生成给定观测数据的概率，例如设 时刻观测数据 ，有
接着，根据（2）式，还可以得到：
由此公式，遍历 
的取值求和，可以得到 的边际概率
假设已知 
，推导 
，在（2）式的基础上
引入变量 ，有：
首先，来看上式中红色部分，根据观测独立假设（下文再引用该假设时称作假设2）：
然后是蓝色部分，根据齐次马尔可夫假设（下文再引用该假设时称作假设1）
将上述结果代入（3）式，得到
时间复杂度降为了 
，比之前至少 的起步价已经好太多了
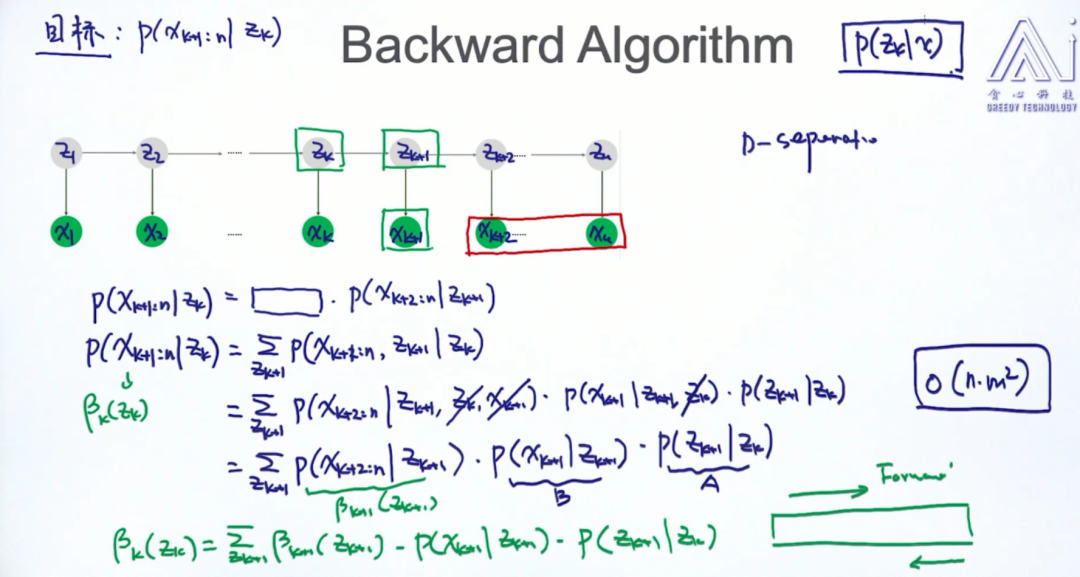
后向算法：定义后向概率：
也就是下图中的部分
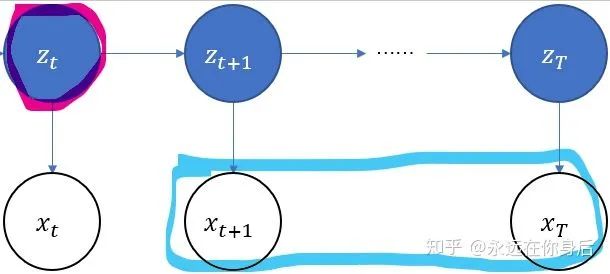
并且规定初始值
根据（4）式，还可以得到
然后来看上式和要计算的概率 之间的关系
另外说一点，如果对于前向算法还有印象的话，你会发现：上面 
也就是 
的定义。实际上，对于任意时刻 ，存在以下等式
接着，假设已知所有的 
，来推导 
观察上式，蓝色部分自然就是 。而红色部分，根据假设2， 
与 
都是无关（即互相独立），可以省去，所以这部分最终变为：
综合上述结果，最终代入到 
，得到
1：已经观测值 反推序列 inference decode
2：已知观测值 反推参数
3：已经观测值 反推可能性
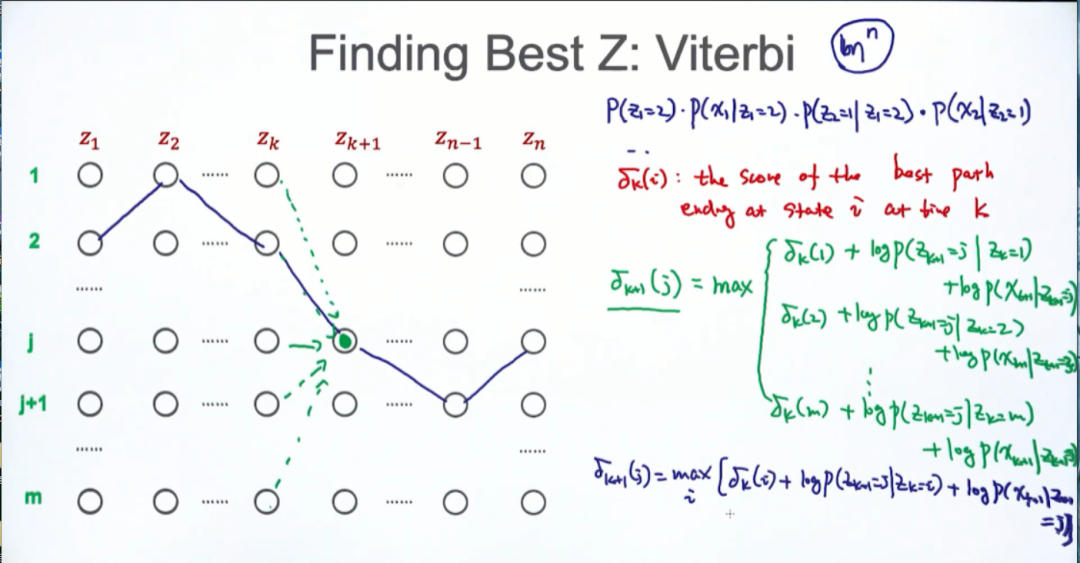
前向算法 贪心 注意目标
后向算法 贪心 注意目标
贪心 维特比算法：
