今天无操作： 继续等大跌
一：线性回归
什么是回归
一元线性回归
损失函数
最小二乘估计
回归是相对分类而言的，与我们想要预测的目标变量y的值类型有关。如果目标变量y是分类型变量，如预测用户的性别（男、女），预测月季花的颜色（红、白、黄……），预测是否患有肺癌（是、否），那我们就需要用分类算法去拟合训练数据并做出预测；如果y是连续型变量，如预测用户的收入（4千，2万，10万……），预测员工的通勤距离（500m，1km，2万里……），预测患肺癌的概率（1%，50%，99%……），我们则需要用回归模型。
聪明的你一定会发现，有时分类问题也可以转化为回归问题，例如刚刚举例的肺癌预测，我们可以用回归模型先预测出患肺癌的概率，然后再给定一个阈值，例如50%，概率值在50%以下的人划为没有肺癌，50%以上则认为患有肺癌。
都学过二元一次方程，我们将y作为因变量，x作为自变量，得到方程：
当给定参数
和
的时候，画在坐标图内是一条直线（这就是“线性”的含义）。
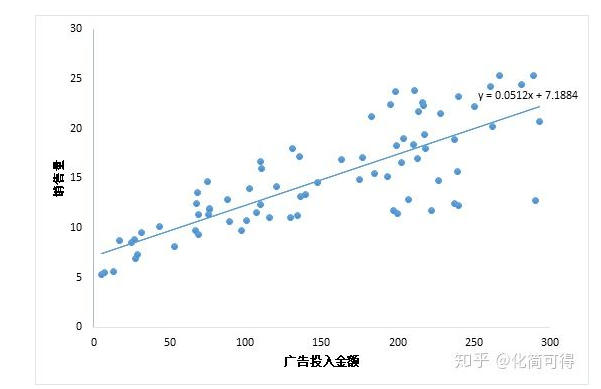
当我们只用一个x来预测y，就是一元线性回归，也就是在找一个直线来拟合数据。比如，我有一组数据画出来的散点图，横坐标代表广告投入金额，纵坐标代表销售量，线性回归就是要找一条直线，并且让这条直线尽可能地拟合图中的数据点。
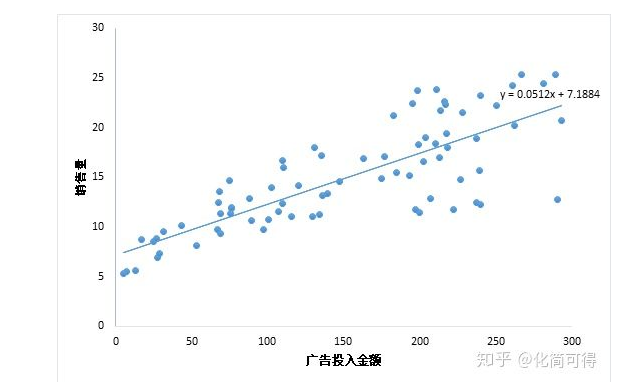
这里我们得到的拟合方程是y = 0.0512x + 7.1884，此时当我们获得一个新的广告投入金额后，我们就可以用这个方程预测出大概的销售量。
数学理论的世界是精确的，譬如你代入x=0就能得到唯一的 
，=7.1884（y上面加一个小帽子hat，表示这个不是我们真实观测到的，而是估计值）。但现实世界中的数据就像这个散点图，我们只能尽可能地在杂乱中寻找规律。用数学的模型去拟合现实的数据，这就是统计。统计不像数学那么精确，统计的世界不是非黑即白的，它有“灰色地带”，但是统计会将理论与实际间的差别表示出来，也就是“误差”。
因此，统计世界中的公式会有一个 
，用来代表误差，即：
3.损失函数
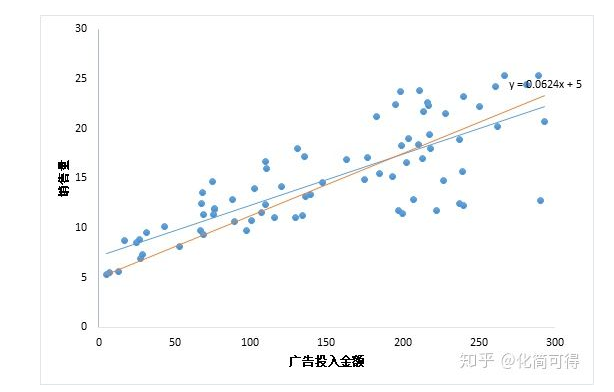
那既然是用直线拟合散点，为什么最终得到的直线是y = 0.0512x + 7.1884，而不是下图中的y = 0.0624x + 5呢？这两条线看起来都可以拟合这些数据啊？毕竟数据不是真的落在一条直线上，而是分布在直线周围，所以我们要找到一个评判标准，用于评价哪条直线才是最“合适”的。
我们先从残差说起。残差说白了就是真实值和预测值间的差值（也可以理解为差距、距离），用公式表示是：
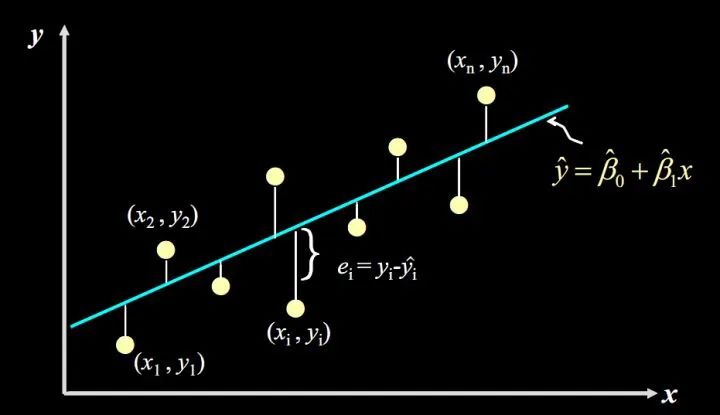
对于某个广告投入 
，我们有对应的实际销售量 
，和预测出来的销售量
（通过将代入公式计算得到），计算 
的值，再将其平方（为了消除负号），对于我们数据中的每个点如此计算一遍，再将所有的 
相加，就能量化出拟合的直线和实际之间的误差。
用公式表示就是：
这个公式是残差平方和，即SSE（Sum of Squares for Error），在机器学习中它是回归问题中常用的损失函数。
4.最小二乘估计
我们不禁会问，这个和的具体值究竟是怎么算出来的呢？
我们知道，两点确定一线，有两组x，y的值，就能算出来和。但是现在我们有很多点，且并不正好落在一条直线上，这么多点每两点都能确定一条直线，这到底要怎么确定选哪条直线呢？
当给出两条确定的线，如y = 0.0512x + 7.1884，y = 0.0624x + 5时，我们知道怎么评价这两个中哪一个更好，即用损失函数评价。那么我们试试倒推一下？
---------------------------------分割--------------------------------------
以下头疼的数据公式推导，我尽量对每个公式作解释说明。
给定一组样本观测值，（i=1,2,…n），要求回归函数尽可能拟合这组值。普通最小二乘法给出的判断标准是：残差平方和的值达到最小。
我们再来看一下残差平方和的公式：
这个公式是一个二次方程，我们知道一元二次方程差不多长下图这样
上面公式中 
和 
未知，有两个未知参数的二次方程，画出来是一个三维空间中的图像，类似下面：
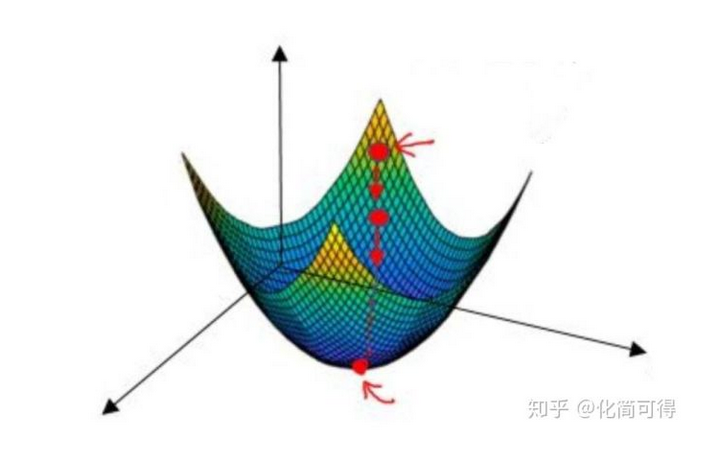
这类函数在数学中叫做凸函数，关于什么凸函数的数学定义，可以看这篇：什么是凸函数。
微积分中我们 知道导数为0时，Q取最小值，因此我们分别对和求偏导并令其为0：
，（i=1,2,…n）都是已知的，全部代入上面两个式子，就可求得和的值啦。这就是最小二乘法，“二乘”是平方的意思。
以上举的例子是一维的例子（x只有一个），如果有两个特征，就是二元线性回归，要拟合的就是二维空间中的一个平面。如果有多个特征，那就是多元线性回归：
最后再提醒一点，做线性回归，不要忘了前提假设是y和x呈线性关系，如果两者不是线性关系，就要选用其他的模型啦。
逻辑回归：
广告投入金额x和销售量y的关系，散点图如下，这种情况适用一元线性回归。
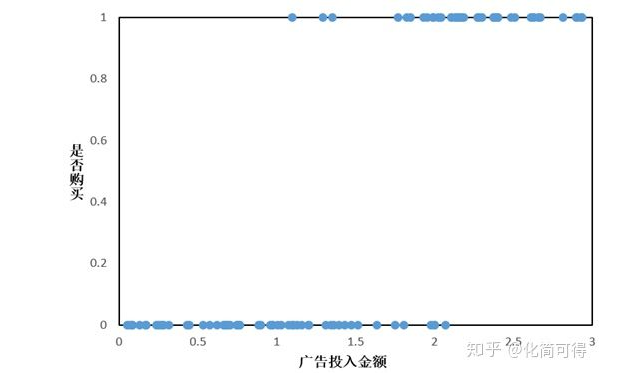
一些问题中，因变量y是分类型，只取0、1两个值，和x的关系不是上面那样。假设我们有这样一组数据：给不同的用户投放不同金额的广告，记录他们购买广告商品的行为，1代表购买，0代表未购买
假如此时依旧考虑线性回归模型，得到如下拟合曲线：
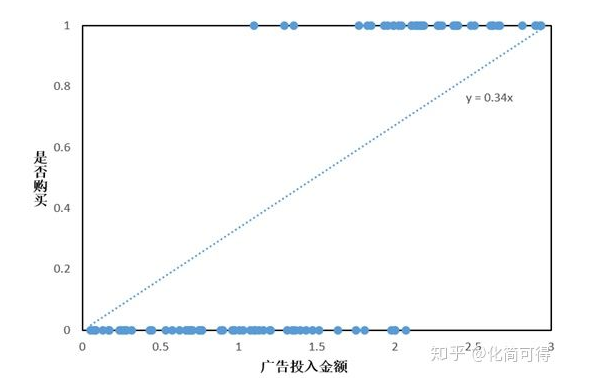
线性回归拟合的曲线，看起来和散点毫无关系，似乎没有意义。但我们可以在计算出 的结果后，加一个限制，即 
，就认为其属于1这一类，购买了商品，否则认为其不会购买，即：
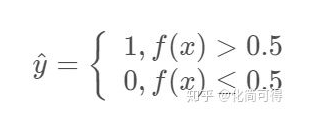
由于拟合方程为 
，那么上面的限制就等价于：
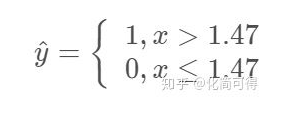
这种形式，非常像阶跃函数：
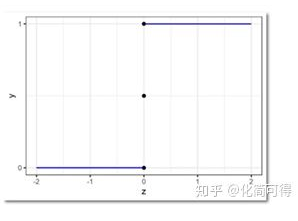
但是阶跃函数有个问题，它不是连续函数。理想的情况，是像线性回归的函数一样，X和Y之间的关系，是用一个单调可导的函数来描述的。
2.sigmond激活函数
逻辑回归算法的激活函数，叫做sigmod函数：它有一些较好的性质，如单调递增，可导，有界等
激活函数是来向神经网络中引入非线性因素的，通过激活函数，神经网络就可以拟合各种曲线。
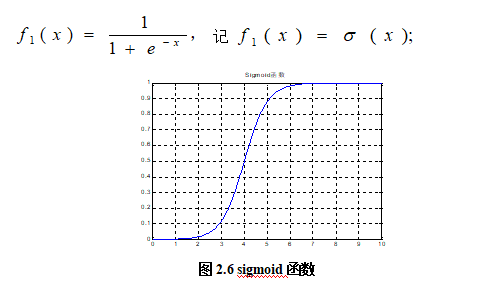
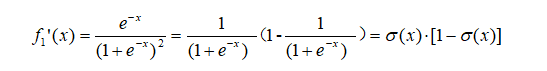
获得逻辑回归的决策函数：
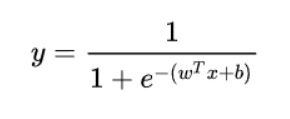
在获得决策函数之后，我们就要构造损失函数。使得损失函数最小。逻辑回归使用的是 对数损失函数 （最大似然估计）（可拓展为交叉熵损失函数 因为若用平方和损失函数 为非凸函数 不好求最优解）
常见的损失函数有
1：0-1损失函数(zero-one loss)
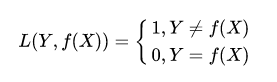
2 ：绝对值损失函数
绝对值损失函数是计算预测值与目标值的差的绝对值：
3. 平方差损失函数（SSE） 求平均就是（mse）
平方损失函数标准形式如下：
特点：
(1)经常应用与回归问题
4：log对数损失函数
log对数损失函数的标准形式如下：
特点：
(1) log对数损失函数能非常好的表征概率分布，在很多场景尤其是多分类，如果需要知道结果属于每个类别的置信度，那它非常适合。
(2)健壮性不强，相比于hinge loss对噪声更敏感。
5：交叉熵损失函数 (Cross-entropy loss function) 是可以由对数损失函数推导得来
交叉熵损失函数的标准形式如下:
注意公式中 
表示样本， 
表示实际的标签， 
表示预测的输出， 
表示样本总数量。
特点：
(1)本质上也是一种对数似然函数，可用于二分类和多分类任务中。
二分类问题中的loss函数（输入数据是softmax或者sigmoid函数的输出）：
多分类问题中的loss函数（输入数据是softmax或者sigmoid函数的输出）：
(2)当使用sigmoid作为激活函数的时候，常用交叉熵损失函数而不用均方误差损失函数，因为它可以完美解决平方损失函数权重更新过慢的问题，具有“误差大的时候，权重更新快；误差小的时候，权重更新慢”的良好性质。
所以损失函数就为：
7.梯度下降法求最优解
首先看，对于sigmoid函数 
，
推导f'(x)等于：
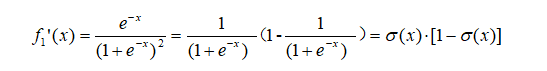
现在我们的x是已知的，未知的是β，所以后面是对β求导，记：
把它代入前面我们得到逻辑回归的损失函数：
简便起见，先撇开求和号看g(β,x,y)。这个g(β,x,y)里面也挺复杂的，我们再把里面的 
挑出来，单独先看对β向量中的某个βj求偏导是什么样。
根据上面的求导公式，有：
所以对
求偏导
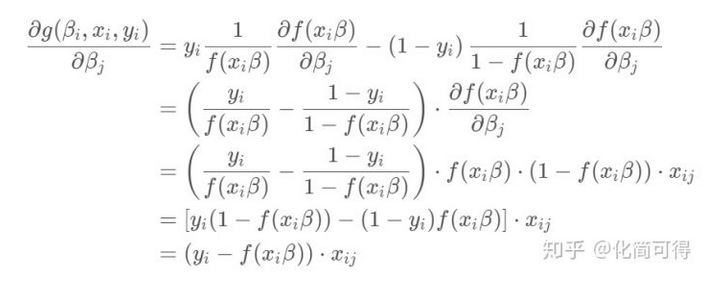
加上求和号：
有了偏导，也就有了梯度G，即偏导函数组成的向量。
梯度下降算法过程：
1. 初始化β向量的值，即 
，将其代入G得到当前位置的梯度；
2. 用步长α乘以当前梯度，得到从当前位置下降的距离；
3. 更新 
，其更新表达式为 
；
4. 重复以上步骤，直到更新到某个 
，达到停止条件，这个 就是我们求解的参数向量。
