多因子选股回测

量化分析之路 2020-03-25

2338

量化投资中经常听到的“多因子模型”是什么？

股票收益受到多重因素的影响，比如宏观、行业、流动性、公司基本面、交易情绪等等。所谓“多因子模型”，说白了就是寻找那些对股票收益率最相关的影响因素，使用这些因素（因子或指标）来刻画股票收益并进行选股。

影响股票的因子有上千种。简单举个例子

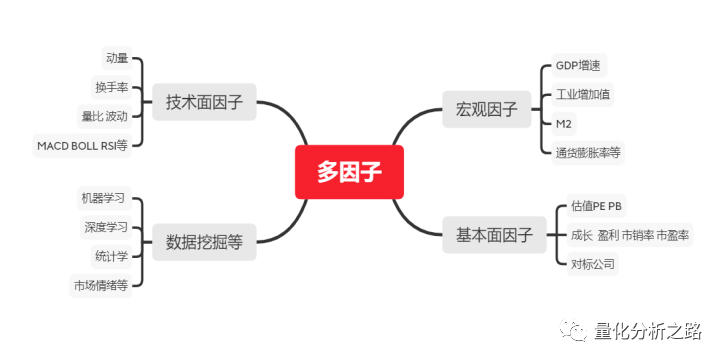
因子的选择

多因子选股模型的第一步是发掘各类与股票收益率相关的因子，因子的选择主要基于经济逻辑和市场经验

（1）市场整体：市场因子、系统性风险等;

（2）估值因子：市盈率、市净率、市销率、市现率、企业价值倍数、 PEG 等；

（3）成长因子：营业收入增长率、营业利润增长率、净利润增长率、每股收益增长率、净资产增长率、股东权益增长率、经营活动产生的现金流量金额增长率等；

（4）盈利能力因子：销售净利率、毛利率、净资产收益率、资产收益率、营业费用比例、财务费用比例、息税前利润与营业总收入比等；

（5）动量反转因子：前期涨跌幅等；

（6）交投因子：前期换手率、量比等；

（7）规模因子：流通市值、总市值、自由流通市值、流通股本、总股本等；

（8）股价波动因子：前期股价振幅、日收益率标准差等；

（9）分析师预测因子：预测净利润增长率、预测主营业务增长率、盈利预测调整等。

因子有效性的检验

一般检验方法主要采用排序的方法检验候选因子的选股有效性。例如：可以每月检验，具体而言，对于任意一个候选因子，在模型形成期的第一个月初开始计算市场中每只正常交易股票的该因子的大小，按从小到大的顺序对样本股票进行排序，并平均分为 N 个组合，一直持有到月末，在下月初再按同样的方法重新构建 N 个组合并持有到月末，一直重复到模型形成期末。

就像之前的小市值策略。

今天先来写一个比较简单地多因子选股回测。优矿API

DataAPI.MktStockFactorsOneDayGet(tradeDate=u"20150227",secID=u"",ticker=u"000001,600000",field=u"",pandas="1")

能获取到很多因子。很详细图太长我就不全截取了。今天我要用的3个因子就是

VOL 多日平均换手率。指在一定时间内市场中股票转手买卖的频率，是反映股票流通性强弱的指标之一。

MFI 资金流量指标可以简单地理解为近期某股票的资金流入流出情况

计算方法

1.典型价格（TP）=当日最高价、最低价与收盘价的算术平均值

2.货币流量（MF）=典型价格（TP）×N日内成交量

3.如果当日MF>昨日MF，则将当日的MF值视为正货币流量（PMF）

4.如果当日MF<昨日MF，则将当日的MF值视为负货币流量（NMF）

5.MFI=100-[100/(1+PMF/NMF)]

6.参数N一般设为14日。

应用法则

1.显示超买超卖是MFI指标最基本的功能。当MFI>80时为超买，在其回头向下跌破80时，为短线卖出时机。

2.当MFI<20时为超卖，当其回头向上突破20时，为短线买进时机。

3.当MFI>80，而产生背离现象时，视为卖出信号。

4.当MFI<20，而产生背离现象时，视为买进信号。

注意要点

1.经过长期测试，MFI指标的背离讯号更能忠实的反应股价的反转现象。一次完整的波段行情，至少都会维持一定相当的时间，反转点出现的次数并不会太多。

2.将MFI指标的参数设定为14天时，其背离讯号产生的时机，大致上都能和股价的顶点吻合。因此在使用MFI指标时，参数设定方面应尽量维持14日的原则。

LCAP 对数市值这个比较好理解表示股票的总市值大小

我们在买股票时对不同因子的侧重是不同的。所以需要给不同的因子不同的权重。这个简单模型的权重是

1 多日平均换手率比较高的 VOL240 权重 0.3

2 多日的MFI资金流入比较高 MFI 权重 0.3

3 市值比较小的股票 LCAP 权重0.4

所以我们对市场的3000只股票进行不同的因子排序打分。

比如某一只股票换手率得分 2800分 MFI得分 2400分市值得分 2600分

那么这只股票的最终得分为 2800*0.3 + 2400*0.3 + 2600*0.4 = 2600分

我们取出市场中得分前50的股票进行均仓买入。这只是一个简单地思路

第一部分获取股票的因子数据

def get_data(context,stocks,factors):
    '''
    获取多个股票的数据
    返回一个DataFrame
    factors为要传入的因子
    '''
    field = ['secID']
    field.extend(factors)
    data = DataAPI.MktStockFactorsOneDayGet(tradeDate=context.previous_date,secID=stocks,ticker=u"",field=field ,pandas="1")
    print(type(data))
    data.dropna(inplace = True)
    data.set_index('secID',inplace = True)
    return data

第二部分对单个因子进行排序

import numpy as np
def grade_stock_by_sorting(data,factor,ascending=True):
    '''
    处理单个因子
    '''
    data.sort_index(by= factor,ascending = ascending ,inplace = True)
    data[factor +  '_adjusted'] = np.arange(len(data))
    log.info(data)
    return data

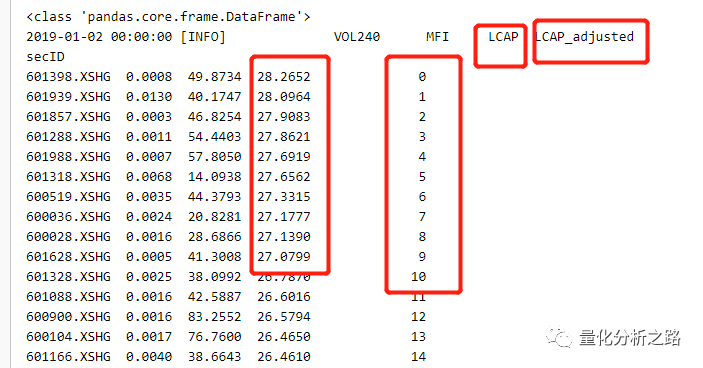
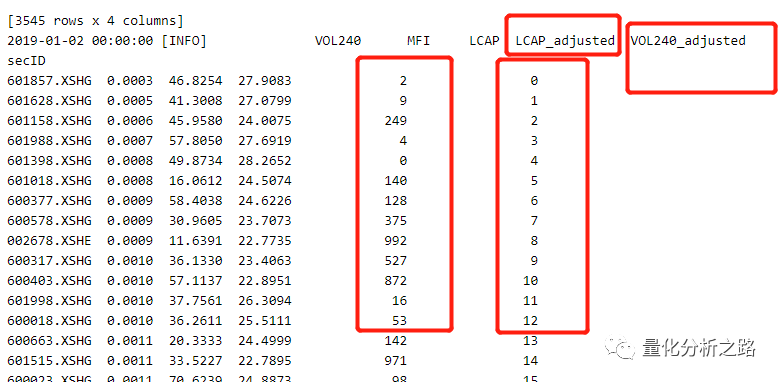
第三部得到一个最终评分的dataframe

import pandas as pd
def grade_stock_by_weight(data,factors,weight):
    '''综合三个因子之后的股票排序
    data 已经处理完成后的数据'''
    factors = list(map(lambda x: x+'_adjusted',factors))
    
    factor_weight_dictionary = dict(zip(factors,weight))
    data['final_factor_grade'] = 0
    
    for factor in factor_weight_dictionary.keys():
        data['final_factor_grade'] += factor_weight_dictionary[factor] *data[factor]
        
        #根据最终评分排序
    data.sort_index(by = 'final_factor_grade',ascending =False,inplace= True)
    log.info(data.head())
    sorted_stock = list(data.index)
    
    return sorted_stock

最后一部等权重买入股票

def buy_stock(context,buy_list,N):
    account = context.get_account('fantasy_account')
    account.close_all_positions()
    for stock in buy_list[:N]:
        account.order_pct(stock,1.0/N)

start = '2019-01-01'                       # 回测起始时间
end = '2019-06-01'                         # 回测结束时间
universe = DynamicUniverse('A')        # 证券池，支持股票、基金、期货、指数四种资产
benchmark = 'HS300'                        # 策略参考标准
freq = 'd'                                 # 策略类型，'d'表示日间策略使用日线回测，'m'表示日内策略使用分钟线回测
refresh_rate = Monthly(1)                           # 调仓频率，表示执行handle_data的时间间隔，若freq = 'd'时间间隔的单位为交易日，若freq = 'm'时间间隔为分钟
  
# 配置账户信息，支持多资产多账户
accounts = {
    'fantasy_account': AccountConfig(account_type='security', capital_base=10000000)
}
  
def initialize(context):
    context.factors = ['VOL240','MFI','LCAP']                             #因子选择
    context.ascending = [True,True,False]                                 #因子是升序还是降序 即因子影响判断
    context.weight = [0.3,0.3,0.4]                                        #因子权重
    context.N = 50                                                        #买入股票数量
    
  #每个单位时间(如果按天回测,则每天调用一次,如果按分钟,则每分钟调用一次)调用一次
def handle_data(context):    
    universe = context.get_universe(exclude_halt=True)
    
    #获取数据
    raw_data = get_data(context,universe,context.factors)
    
    #处理因子 将每个因子进行打分
    
    data = handle_factors(raw_data,grade_stock_by_sorting,context.factors,ascending=context.ascending)
    
    #计算因子评分排序后的股票代码
    sorted_stock = grade_stock_by_weight(data,context.factors,context.weight)
    
    #按照因子买入股票
    buy_stock(context,sorted_stock,context.N)

我跑了一下回测因为数据量过大只能回测半年左右的。分别是18年和19年前半年的回测结果也比较一般。

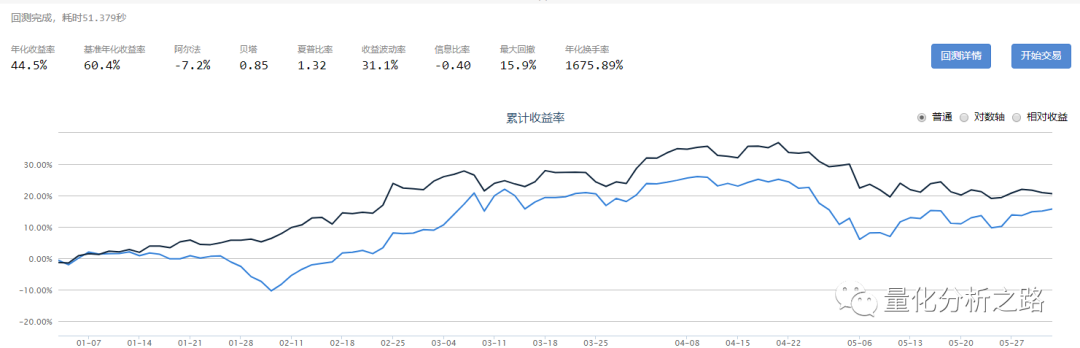
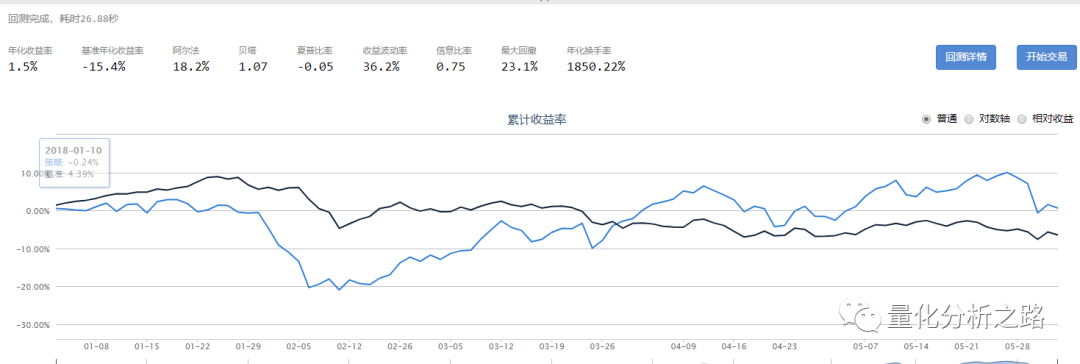
多因子分析还有很多细节比如说剔除冗余因子模型评价以及改进。

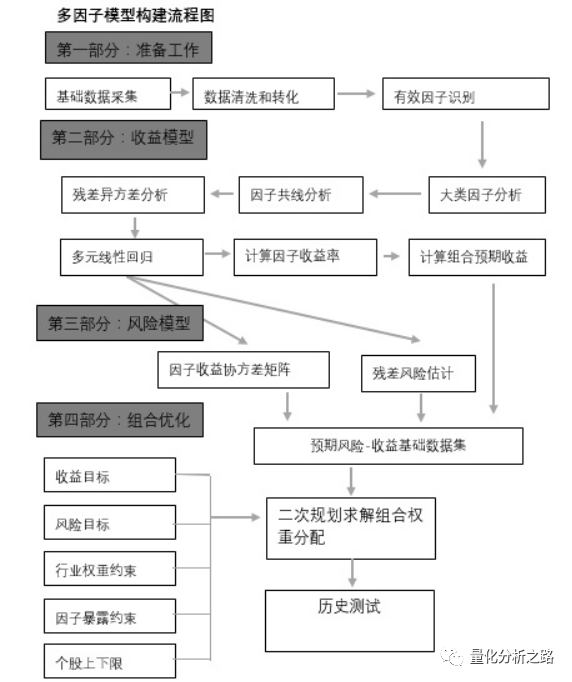
后面再分析。

数据库

文章转载自量化分析之路，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

多因子选股回测

计算方法

应用法则

注意要点

评论