当前机器学习算法中最火的无疑是深度学习,深度学习的基础是神经网络,深度学习过程也就是前向和后向传播算法不断重复迭代,直到找出预测值和实际值误差最小化时的各网络层的权重。前向算法很简单,把输入带入模型计算就可以了,后向传播需要一步步用链式法则求导,然后不断更新权重。
后向传播算法道理上不难,就是微积分中的链式求导,各种相关文章都有介绍,但是如果你没有亲自手动推导过一遍,可能都没有底气和别人说你懂深度学习。我也是抱着这种心态准备手动推导一遍,在找资料过程中发现了一篇很具体的配合图文介绍的文章,图画得也很漂亮,在此分享一下。
图片源自 https://hmkcode.github.io/ai/backpropagation-step-by-step/,我只做大概的翻译。
总览
我们先构造一个典型的3层神经网络,输入层2个神经元,隐藏层2个神经元,输出层一个神经元:
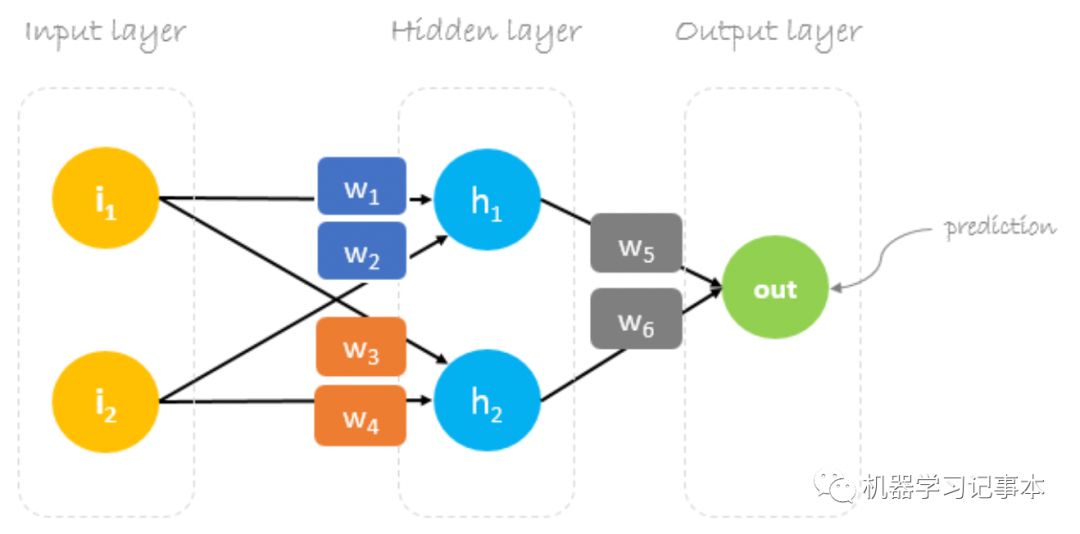
初始权重
神经网络训练的目标是找出恰当的权重去最小化预测错误,我们首先需要随机初始化权重,然后用后向传播算法不断迭代更新权重。权重初始值设置为w1 = 0.11, w2 = 0.21, w3 = 0.12, w4 = 0.08, w5 = 0.14, w6 = 0.15.
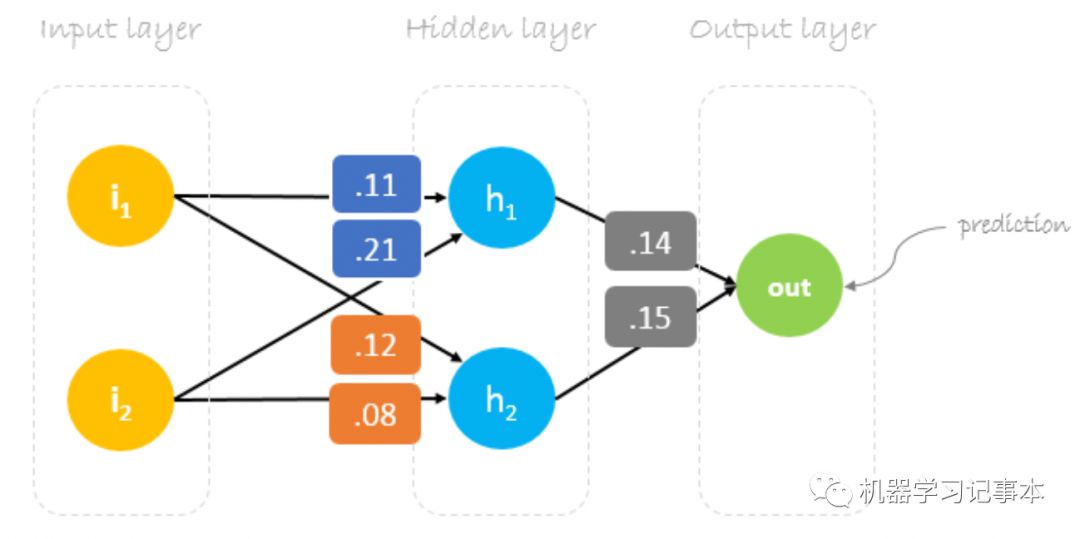
数据集
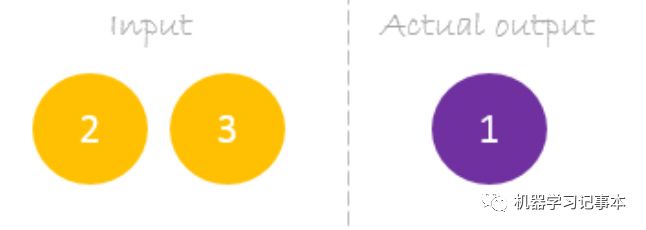
训练数据有两个输入,一个输出:

我们用inputs=[2, 3], output=[1]作为例子:
前向传播
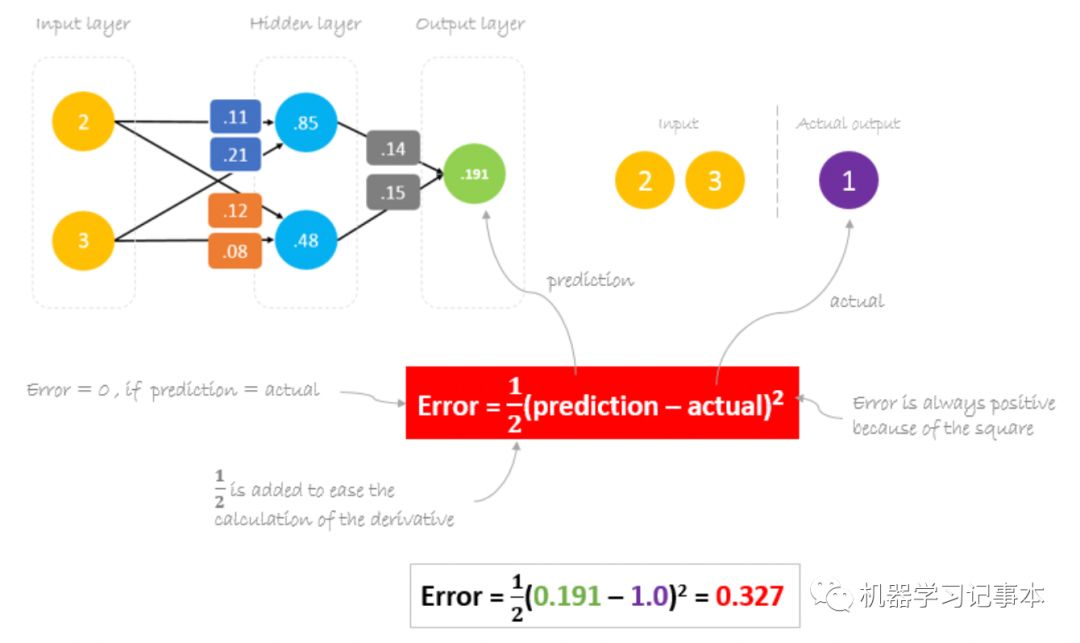
前向传播即把输入和第一层权重相乘,相加结果传入下一层隐藏层,再做权重计算最终得到预测结果。

计算和减少误差
现在通过计算预测值和实际值的差来看看网络的准确性。预测值0.191和实际值1的差距还挺大,所以需要想办法减少误差。由于实际输入输出都是确定的值,减少预测误差就需要更新各个权重让预测值更准确。
后向传播
更新权重的方法就是用著名的梯度下降算法。通过计算梯度,也就是求函数的导数,获得误差函数(损失函数)梯度下降最快的方向,更新权重让误差尽快降低。我们上面的模型中有6个权重w1,w2,w3,w4,w5,w6,需要一个一个分别计算对应方向的梯度,然后迭代更新:

其中的a为学习速度,就是梯度下降的快慢,可根据具体情况而定。
以w6为例
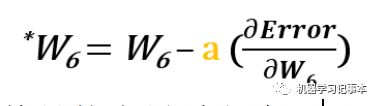
其具体求导过程为:
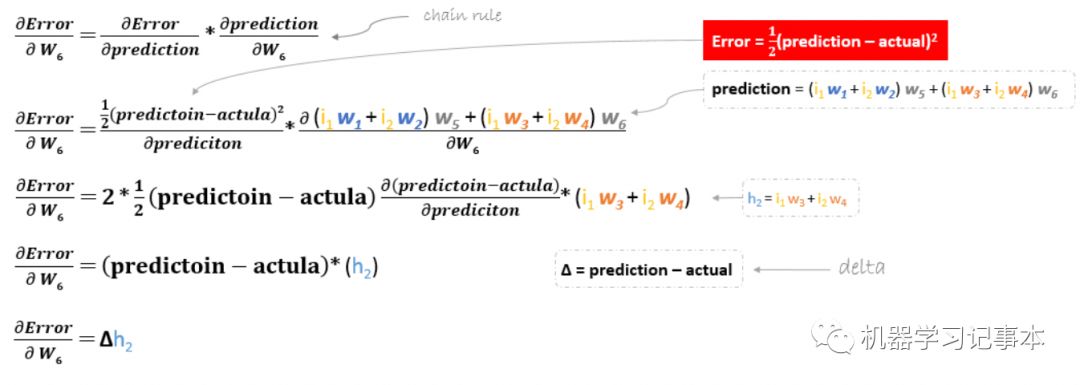
那么
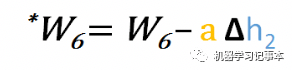
同样地,我们可得到
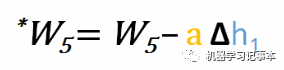
接下来,继续更新w1, w2, w3,w4。这4个权重和w6的区别在于它们不是误差函数的直接变量,需要用链式求导法则求导,以为w1例:
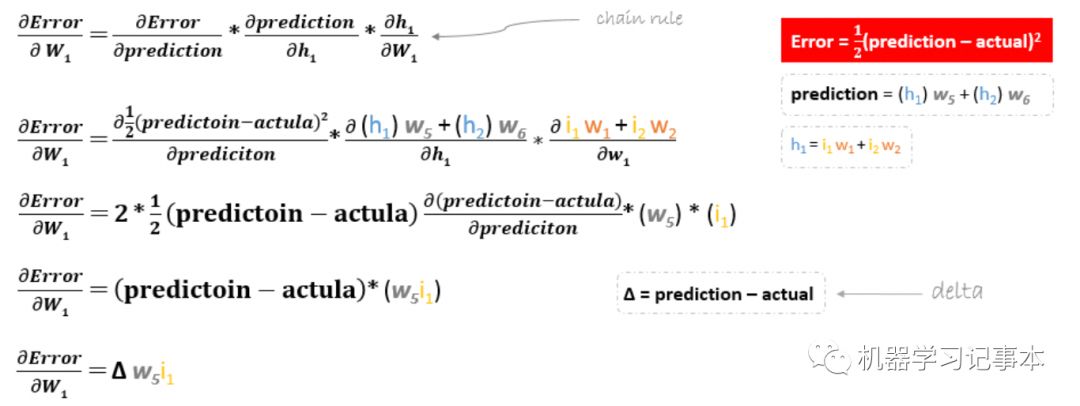
我们可以用同样的方法求得w2, w3,w4的导数。
总结起来,所有权重的更新公式如下:
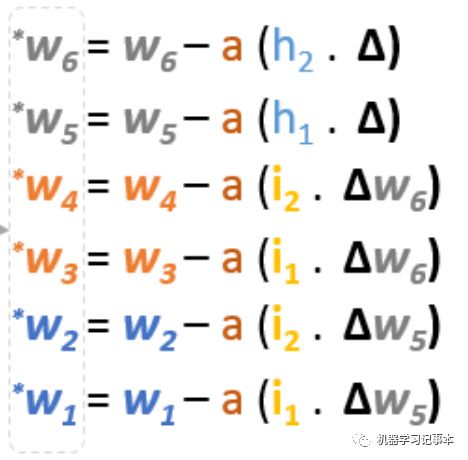
如果用矩阵来表示,则为:

权重更新具体计算
有了上面的公式,我们就可以不断迭代更新各个权重,其中的学习速度我们取0.05.

我们用新的权重作一次前向计算:

在新的权重下现在新的预测值为0.26,比初始的0.191离实际值更近了。
接下来我们用同样的权重更新公式不断更新权重,计算预测值,最终得到满意的误差对应的权重,就是我们想要的模型,当有新的输入数据来的时候,我们就可以用此模型预测了。
以上就是一个完整的神经网络前向和后向传播算法,为了方便理解,我们简化了模型和数据,以后CNN,RNN和其他深度学习的前向和后向传播算法基本思想也是一样的。如果你想进一步练练,把模型增加到4层,每层3个神经元试试看能不能类似推导出权重。






