本文介绍了梯度提升回归模型在预测区间、分位数回归等方面的应用,以及模型在不同条件下的表现。接着对模型的误差指标进行了分析,探讨了可能存在的过拟合问题。
https://scikit-learn.org/stable/auto_examples/ensemble/plot_gradient_boosting_quantile.html
步骤1:生成数据集
首先使用均匀抽样的随机输入来为一个合成回归问题生成一些数据。
import numpy as np
from sklearn.model_selection import train_test_split
def f(x):
"""The function to predict."""
return x * np.sin(x)
rng = np.random.RandomState(42)
X = np.atleast_2d(rng.uniform(0, 10.0, size=1000)).T
expected_y = f(X).ravel()
为了让问题更有趣,我们将目标 y 的观察结果生成为函数 f 计算的确定性项与遵循中心对数正态分布的随机噪声项之和。为了使问题更加有趣,我们考虑噪声的振幅取决于输入变量 x(异方差噪声)的情况。
对数正态分布是非对称的且长尾的:观察到大的离群值是可能的,但观察到小的离群值是不可能的。
sigma = 0.5 + X.ravel() / 10
noise = rng.lognormal(sigma=sigma) - np.exp(sigma**2 / 2)
y = expected_y + noise
划分数据集为训练集和验证集:
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
步骤2:拟合模型
接下来使用分位数损失和 alpha=0.05、0.5、0.95 训练梯度提升模型。对于 alpha=0.05 和 alpha=0.95 获得的模型产生一个 90% 的置信区间(95% - 5% = 90%)。
在梯度提升回归中,参数 alpha
是用于指定分位数的关键参数。当使用 quantile
损失函数时,可以通过设置 alpha
参数来指定所需的分位数。
当 alpha
设为 0.5 时,表示计算的是中位数,即目标变量在预测值两侧的概率相等。当 alpha
设为 0.25 时,表示计算的是 25% 分位数,即目标变量在预测值两侧的累积概率为 0.25。当 alpha
设为 0.75 时,表示计算的是 75% 分位数,即目标变量在预测值两侧的累积概率为 0.75。
通过调整 alpha
参数,可以实现对不同分位数的预测,从而更好地理解和解释目标变量的分布情况。因此,alpha
参数在分位数回归中具有重要的作用,可以帮助调整模型以适应不同的预测需求和数据分布情况。
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_pinball_loss, mean_squared_error
all_models = {}
common_params = dict(
learning_rate=0.05,
n_estimators=200,
max_depth=2,
min_samples_leaf=9,
min_samples_split=9,
)
for alpha in [0.05, 0.5, 0.95]:
gbr = GradientBoostingRegressor(loss="quantile", alpha=alpha, **common_params)
all_models["q %1.2f" % alpha] = gbr.fit(X_train, y_train)
考虑到中等大小的数据集(n_samples >= 10,000),HistGradientBoostingRegressor 比 GradientBoostingRegressor 要快得多,但在当前的示例中并非如此。
为了进行比较,我们还拟合了一个基线模型,该模型使用常规(均值)平方误差(MSE)进行训练。
步骤3:展示拟合结果
要绘制真实的条件均值函数 f、条件均值的预测(损失等于平方误差)、条件中位数和条件 90% 区间(从第 5 个到第 95 个条件百分位数),可以使用 Python 中的 Matplotlib 库进行绘图。
fig = plt.figure(figsize=(10, 10))
plt.plot(xx, f(xx), "g:", linewidth=3, label=r"$f(x) = x\,\sin(x)$")
plt.plot(X_test, y_test, "b.", markersize=10, label="Test observations")
plt.plot(xx, y_med, "r-", label="Predicted median")
plt.plot(xx, y_pred, "r-", label="Predicted mean")
plt.plot(xx, y_upper, "k-")
plt.plot(xx, y_lower, "k-")
plt.fill_between(
xx.ravel(), y_lower, y_upper, alpha=0.4, label="Predicted 90% interval"
)
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
plt.ylim(-10, 25)
plt.legend(loc="upper left")
plt.show()
对比预测的中位数和预测的均值,我们注意到由于噪声偏向较高的值(大的离群值),中位数平均低于均值。中位数估计也似乎更加平滑,因为它天然具有对离群值的鲁棒性。
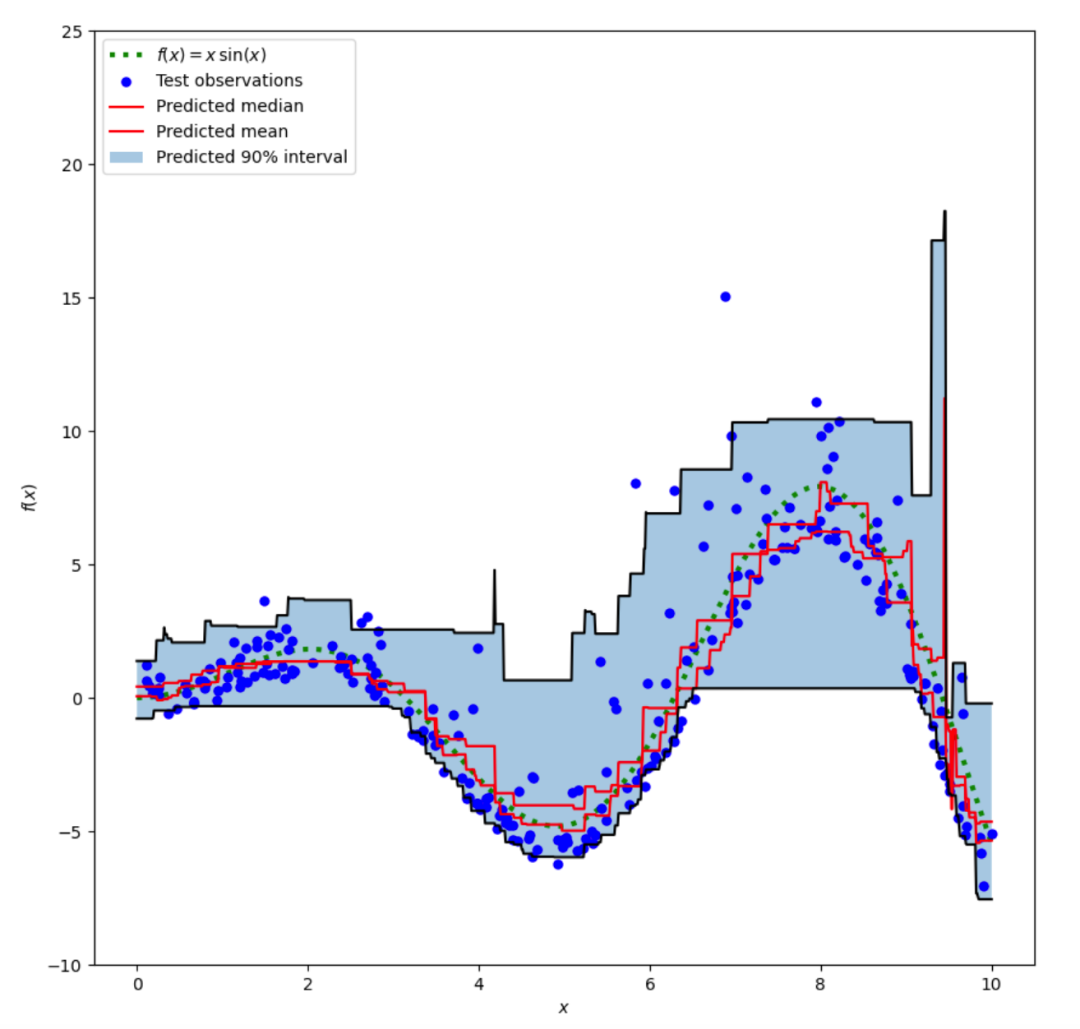
另外,请注意,梯度提升树的归纳偏差不幸地阻止了我们的 0.05 分位数完全捕获信号的正弦形状,特别是在 x=8 附近。
步骤4:分析拟合结果
在表格中,每一列显示了所有模型按照相同指标评估的结果。在一列中的最小数字应该在模型使用相同指标进行训练和测量时获得。如果训练收敛,这在训练集上应始终成立。
| Model | pbl=0.05 | pbl=0.50 | pbl=0.95 | MSE |
|---|---|---|---|---|
| mse | 0.715413 | 0.715413 | 0.715413 | 7.750348 |
| q 0.05 | 0.127128 | 1.253445 | 2.379763 | 18.933253 |
| q 0.50 | 0.305438 | 0.622811 | 0.940184 | 9.827917 |
| q 0.95 | 3.909909 | 2.145957 | 0.382005 | 28.667219 |
条件中位数估计器在测试集上的均方误差(MSE)方面与平方误差估计器相当:这可以解释为平方误差估计器对大离群值非常敏感,这可能导致显著的过拟合。