目录
1.贝叶斯定理
2.朴素贝叶斯原理
3.朴素贝叶斯作用及其优势
编辑:
校对:
版本:
zhang
zhang
python3
贝叶斯定理
在引出贝叶斯定理之前,先学习几个定义:
边缘概率(又称先验概率):某个事件发生的概率。边缘概率是这样得到的:在联合概率中,把最终结果中那些不需要的事件通过合并成它们的全概率,而消去它们(对离散随机变量用求和得全概率,对连续随机变量用积分得全概率),这称为边缘化(marginalization)。
比如A的边缘概率表示为P(A),B的边缘概率表示为P(B)。联合概率表示两个事件共同发生的概率。A与B的联合概率表示为P(A∩B)或者P(A,B)。
条件概率(又称后验概率):事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”,。
接着,考虑一个问题:P(A|B)是在B发生的情况下A发生的可能性。
首先,事件B发生之前,我们对事件A的发生有一个基本的概率判断,称为A的先验概率,用P(A)表示;
其次,事件B发生之后,我们对事件A的发生概率重新评估,称为A的后验概率,用P(A|B)表示;
类似的,事件A发生之前,我们对事件B的发生有一个基本的概率判断,称为B的先验概率,用P(B)表示;同样,事件A发生之后,我们对事件B的发生概率重新评估,称为B的后验概率,用P(B|A)表示。
贝叶斯定理便是基于下述贝叶斯公式:
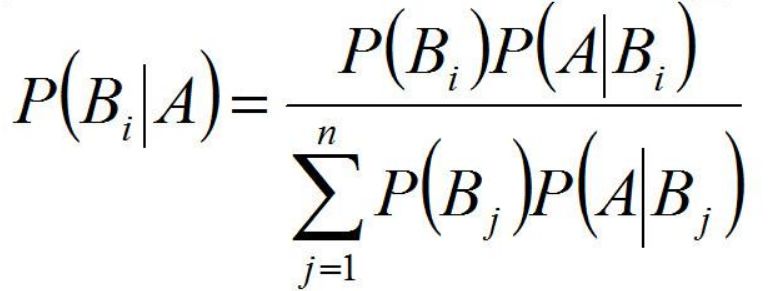
朴素贝叶斯原理
朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。
朴素贝叶斯 (naive Bayes) 是一种非常简单而又有效的分类方法. 如果因 变量的类为 c1,c2,...,cK, 朴素贝叶斯假定在给定ck的条件下自变量(x = (x1,x2,...,xn)) 都是独立的, 而且给定类别 (比如 ck) 之后假定了 它们的条件分布 p(xi|ck) 的类型, 比如正态、多项或 Bernoulli 分布等.
说白了, 朴素贝叶斯的目的就是要计算在给定数据 x 的条件下属于类 ck 的概率 (后验概率)p(ck|x), 并且求使后验概率最大的类 ck. 根据贝叶斯定理, 后验分布 (给定数据 x 的条件下属于类 ck 的概率)
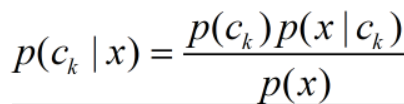
朴素贝叶斯作用及其优势
朴素贝叶斯算法是有监督的学习算法,解决的是分类问题,如客户是否流失、是否值得投资、信用等级评定等多分类问题。该算法的优点在于简单易懂、学习效率高、在某些领域的分类问题中能够与决策树、神经网络相媲美。
但由于该算法以自变量之间的独立(条件特征独立)性和连续变量的正态性假设为前提,就会导致算法精度在某种程度上受影响。
我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。

思考——学而不思则罔
那么朴素贝叶斯有什么可以改进的地方吗?先想想哦,我们下次揭晓!

理解编程语言,探索数据奥秘
每日练习|干货分享|新闻资讯|公益平台。
每天学习一点点,你将会见到全新的自己。

长按识别二维码关注






