目录
1.损失函数简介
1.1损失函数的定义
1.2经典损失函数
1.3自定义损失函数
2.交叉熵损失函数
2.1信息熵
2.2交叉熵的定义
2.3实例
编辑:
校对:
版本:
xiaoluo
xiaoluo
python3
损失函数简介
损失函数的定义
分类问题和回归问题是机器学习(有监督学习)的两个大类,当我们训练出解决问题的模型时,通常会定义一个函数来刻画对这个问题的求解精度,而这样的函数就是损失函数(Loss Function)。损失函数也被称为代价函数(Cost Function)或误差函数(Error Function)。
经典损失函数
在有监督学习中最常用的两个经典损失函数为:交叉熵(Cross Entropy)损失函数和标准均方误差(NMSE)损失函数。
自定义损失函数
在实现深度学习解决问题时,经典损失函数为我们提供了很大帮助。但是在现实生活中,对某一个问题的损失值不是一成不变的。比如,某工厂需要预测某商品的出货量以制定生产计划,若预测值大于买家购买力,则这批商品会滞销,会造成浪费生产成本的损失;若预测值小于买家的购买力,则会供不应求造成利润上的损失。不同情况下造成的损失价值是不一样的,因此在实际问题中我们需要自定义一个比较合适的损失函数。
交叉熵损失函数
信息熵
熵 (entropy) 这一词最早源于热力学。1948年,克劳德·爱尔伍德·香农将热力学中的熵引入信息论,所以也被称为香农熵 (Shannon entropy),信息熵 (information entropy)。
信息的信息量大小和它的不确定性有直接的关系,因此我们用不确定性的多少来度量信息量。一个离散的随机变量x,它的信息量依赖于概率分布p(x),我们需要寻找一个能表达信息内容的函数I(x),它是概率分布 p(x)的单调函数。怎么寻找它呢?
假设我们有两个不相关的事件 x和y,那么观察两个事件同时发生时获得的信息量应该等于观察到事件各自发生时获得的信息之和,即:I(x,y)=I(x)+I(y)。因为两个事件是独立不相关的,因此 p(x,y)=p(x)p(y)。根据这两个关系,很容易看出I(x)一定与p(x)的对数有关(因为对数的运算法则有loga(mn)=logam+logan) 因此,我们有
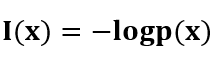
其中“-”是用来保证信息量非负。而 log函数的基选择是任意的(信息论中基选择为2;而机器学习中基常常选择为自然常数e)。I(x)也被称为随机变量x的自信息 (self-information),描述的是随机变量的某个事件发生所带来的信息量。图像如下:
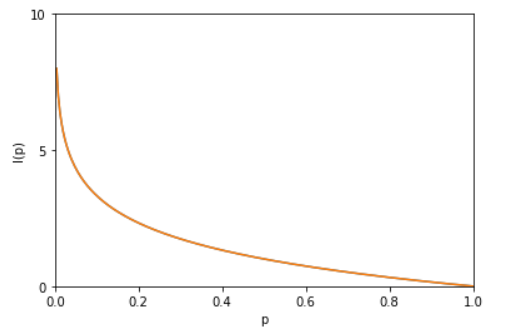
最后,我们正式引出信息熵。假设一个发送者想传送一个随机变量的值给接收者。那么在这个过程中,他们传输的平均信息量可以通过求 I(x)=−logp(x)关于概率分布的期望得到,即:
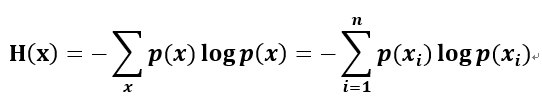
H(X)就被称为随机变量 x的信息熵,它是表示随机变量不确定的度量,是对所有可能发生的事件产生的信息量的期望。
交叉熵的定义
交叉熵的概念是由信息熵引入的,交叉熵(Cross Entropy)刻画的是实际输出(概率)与期望输出(概率)的接近程度,也就是交叉熵的值越小,两个概率分布就越接近。
假设概率分布p为期望输出,概率分布q为实际输出,H(p,q)为交叉熵,则:
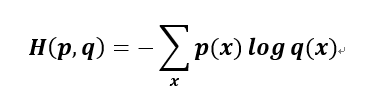
实例
我们都接触过手写数字识别,在这里举一个关于数字分类问题的简单Python实例:
>>>import numpy as np
>>>i = [0.03,0.03,0.01,0.9,0.01,0.01,0.0025,0.0025,0.0025,0.0025]
#数字3的模型预测值(概率)
>>>j = [0,0,0,1,0,0,0,0,0,0]#j=3
>>>k = [0,0,0,0,1,0,0,0,0,0]#k=4
>>>-np.log(i)
array([3.5065579 ,3.5065579 ,4.60517019,
0.10536052,4.60517019,4.60517019,
5.99146455,5.99146455,5.99146455,
5.99146455])
>>>round(np.sum(-np.multiply (np.log(i),j)),3)#保留3位小数0.105
>>>round(np.sum(-np.multiply
(np.log(i),k)),3)
4.605
我们创建了数字“3”的模型预测值(概率)向量i,j为数字3的one-hot标签,k为数字4的one-hot标签,分别与向量i进行交叉熵运算,我们可以看到当数字恰好为3时,它的交叉熵损失仅为0.105,而当真实数字为4时,它的交叉熵为4.605。
你能猜出我们的交叉熵损失给我们的价值吗? 你能看到-log(i)如何以较大的数惩罚了错误的预测结果吗?
当真实数字为4时,我们的交叉熵损失为4.605,明显模型预测不佳,它显示出了一个严重的惩罚。 由于分类器模型确信它是3时,而实际上是4,所以它受到了严厉的惩罚。
思考——学而不思则罔
你还知道有哪些损失函数?

理解编程语言,探索数据奥秘
每日练习|干货分享|新闻资讯|公益平台。
每天学习一点点,你将会见到全新的自己。

长按识别二维码关注







