点击上方蓝字获取更多新鲜资讯
安全的多方计算（MPC）允许各方对数据进行计算，同时保持数据的隐私。这为机器学习应用提供了安全MPC的巨大潜力：它有助于在不同方拥有的私有数据集上训练机器学习模型，使用另一方的私有数据评估一方的私有模型，等等。虽然有一系列研究通过安全MPC实现机器学习模型，但这种实现方式还不是主流。安全MPC的采用由于缺乏 "说机器学习研究人员和工程师的语言 "的软件框架而受到阻碍。为了促进机器学习中安全MPC的采用，我们提出了CRYPTEN：一个软件框架，它通过现代机器学习框架中常见的抽象，如张量计算、自动微分和模块化神经网络，来暴露流行的安全MPC原语。
安全的多方计算(MPC; [27])允许各方在他们的组合数据集上协作执行计算，而不向对方透露他们拥有的数据。安全MPC的这种能力有可能释放出各种机器学习应用，而这些应用目前由于数据隐私问题而不可行。例如，安全的MPC可以让医学研究机构联合训练更好的诊断模型，而不必分享他们敏感的病人数据[11]，或者让社会科学家分析性别工资差距统计，而公司不必分享敏感的工资数据[18]。这种具有严格的隐私和安全保障的机器学习应用的前景刺激了许多关于通过安全MPC的机器学习的研究[16, 24, 26]。然而，目前，考虑到其广泛的潜力，SMPC在机器学习中的应用仍然相对有限。广泛采用的主要障碍之一是SMPC技术的复杂性使其对大多数机器学习研究人员来说遥不可及，他们经常缺乏深入的加密技术知识。
为了促进SMPC技术在机器学习中的应用，我们正在开发CRYPTEN：一个软件框架，旨在使没有密码学背景的机器学习研究人员和开发人员能够使用现代SMPC技术。具体来说，CRYPTEN提供了一个全面的张量计算库，其中所有计算都是通过SMPC进行的。在这个张量库的基础上，它提供了自动分化和一个模块化的神经网络包。CRYPTEN的API与流行的机器学习框架PyTorch的API密切相关[22]，这使得它对机器学习从业者来说易于使用。CRYPTEN假设了一个诚实但好奇的威胁模型，并适用于任意数量的当事人。
本文介绍了:
CRYPTEN设计原则的概述；
CRYPTEN中实现的安全MPC协议的描述；
CRYPTEN如何用于实现现代机器学习模型的例子；
CRYPTEN的进一步发展路线图.
在CRYPTEN的开发中，我们采用了以下两个主要的设计原则。
CRYPTEN有一个通用的、机器学习优先的API设计。许多其他的安全MPC框架（见[14]的概述）采用了接近于底层MPC协议的API。这阻碍了这些框架在机器学习中的应用，例如，因为它们不支持张量操作（而只支持标量操作），也因为它们缺乏机器学习研究者所期望的功能，如自动分化。相反，CRYPTEN实现了流行的PyTorch机器学习框架[22]的张量计算API，实现了反向模式的自动分化，并提供了一个带有相应学习例程的模块化神经网络包。我们的目标是让开发者通过改变一个PyTorch的导入语句就可以将他们的代码从PyTorch切换到CRYPTEN。
CRYPTEN采用了一种命令式编程模型。这与大多数现有的MPC框架不同，它们为自己的特定领域语言实现编译器。虽然编译器方法有潜在的性能优势，但它们会减慢开发周期，使调试更加困难，并使与现有软件的整合更加复杂。相反，CRYPTEN遵循机器学习中最近的趋势，从图编译器[1]转向对计算图进行 eagar execution 的框架[22]。这使得代码跟踪和调试变得容易。然而，CRYPTEN是高性能的，因为它实现了最先进的安全MPC协议（针对任意数量的参与方的设置），因为它使用PyTorch的高度优化的张量库进行大多数计算，因为计算可以被卸载到GPU上，因为它使用专门为高性能分布式计算开发的通信库。
为了促进安全计算，CRYPTEN实现了算术秘密共享[9]和二进制秘密共享[12]，以及这两种类型的秘密共享之间的转换逻辑[10]。算术秘密共享特别适合于现代机器学习模型中常见的操作，如矩阵乘法和卷积。二进制秘密共享需要用于评估某些其他常见的函数，包括整流线性单元和 argmaxes。
算术秘密共享
在各方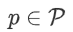
之间共享一个标量值 
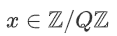，其中
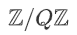表示一个有 Q 个元素的环。我们用
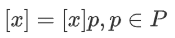来表示 x 的共享，其中 
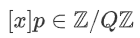表示 p 方对 x 的共享。共享的构造使其总和能够重建原始值 x，即 
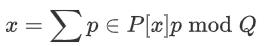。为了分享一个值 x，各方用总和为 0 的 |P| 随机数生成一个伪随机的零份额[7]。拥有值 x 的一方将 x 加入他们的份额，然后丢弃 x 。为此，我们将 
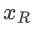与一个大的比例系数 B 相乘，然后四舍五入到最接近的整数：
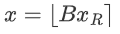，其中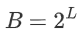 
，表示 L 位的精度。为了解码一个值，x，我们计算
。
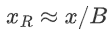二进制秘密共享
算术秘密共享的一个特例，它在二进制领域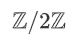 
内运行。一个值 x 的二进制秘密共享，
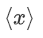，是由 x 的位的算术秘密共享形成的，设置 Q=2。每一方 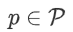持有一个份额，
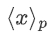，使得 
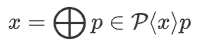得到满足。
从 [x] 到 <x> 的转换
通过让各方对他们的[x]p份额创建一个二进制秘密份额，并将产生的二进制份额相加来实现。具体来说，双方对 [x]p中的所有比特创建一个二进制秘密份额，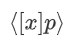
。随后，双方使用 Ripple-carry 加法器在 
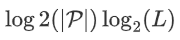通信轮中计算出 
。
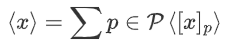从 <x> 到 [x] 的转换
通过计算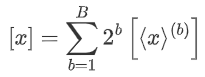 
实现的，其中 
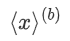表示二进制共享 
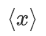的第 b 位，B 是共享秘密 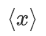的总位数。为了创建一个比特的算术共享，各方使用秘密共享，
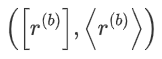的随机比特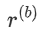 
。随机位由可信的第三方 (TTP) 提供，但我们也在研究一种通过不经意传输离线生成随机位的实现方式 [17]。双方使用 
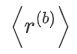来掩盖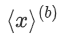
，并揭示所产生的掩盖位 
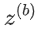。随后，他们计算 
。
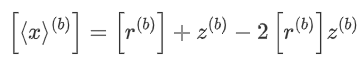算术和二进制秘密共享具有同态性，可用于实现安全计算。CRYPTEN 中的所有计算都是基于私有加法和乘法。
3.2.1 Private addition
两个算术秘密共享值的私有加法，[z]=[x]+[y]，是通过让每一方 p 将他们的[x]和[y]的份额相加实现的：每一方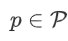 
计算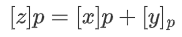 
。
3.2.2 Private multiplication
私有乘法是使用随机的 Beaver triples [4]实现的，([a],[b],[c])，c=ab。Beaver triples目前由TTP提供，但我们正在开发协议，其中各方通过加法同态加密[21]或不经意传输[17]产生Beaver triples。双方计算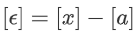
和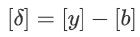 
，并解密和 δ，而不会因为屏蔽而导致信息泄露。最后，他们计算结果
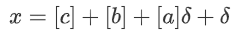，使用秘密份额与公共值的加法和乘法的 trivial 实现。
3.2.3 Linear functions
线性函数被 trivial 地实现为私有加法和乘法的组合。这使得 CRYPTEN 能够计算点积、外积、矩阵积和卷积。
3.2.4 Non-linear functions
非线性函数使用标准的近似值实现，只需要私有加法和乘法。具体来说，CRYPTEN 使用极限近似法评估指数，使用 Householder 迭代法评估对数[15]，并使用 Newton-Rhapson 迭代法评估倒数。这使得 CRYPTEN 能够实现机器学习模型中常用的函数，包括 sigmoid、softmax 和 logistic-loss 函数，以及它们的梯度。
3.2.5 Comparators
比较器使用一个函数来实现，该函数通过以下方式评估 [z < 0]。
将 [z] 转换为二进制秘密共享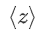 
；计算其符号位，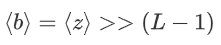 
；将所得位转换为算术共享 [b]。这个函数允许CRYPTEN实现任意的比较器。
例如，它通过计算 [z]=[x]-[y] 和评估 [z < 0] 来评估 [x < y]。
同样地，CRYPTEN可以评估。
通过 计算符号函数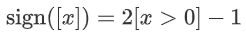 
；通过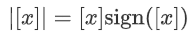 
计算绝对值函数；通过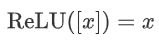 
计算整顿线性单位。CRYPTEN还支持复用；为此，它评估 
。
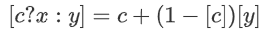图1显示了一个 PyTorch 张量在 CRYPTEN 中如何秘密共享和揭示的例子。请注意，参与多方计算的每一方都在执行相同的代码。每当各方之间需要通信时（例如，作为私有乘法的一部分），这种通信作为一个同步点。在这个例子中，用于创建算术秘密份额的输入张量是由所有各方提供的。然而，在安全MPC的实际应用中，输入张量通常由某一方提供。这可以通过在密码器构造函数中使用可选的 src 参数来实现：例如，crypten.cryptensor(x, src=0)将与其他各方秘密共享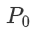 
拥有的 PyTorch 张量 x。
图 1. CRYPTEN中的秘密共享张量、揭示 (reveal) 张量和私有加法的例子
图 2 显示了如何创建和加密神经网络以及如何在 CRYPTEN 中使用自动区分。这个例子假设一些训练样本和相关的目标标签是由 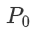提供的（注意 src 的值）。正如这个例子所说明的，CRYPTEN 的 API 与 PyTorch 的 API 密切相关。事实上，可以编写一个单一的训练循环，不需要修改代码就可以用 CRYPTEN 或 PyTorch 来训练模型。这使得改编 PyTorch 代码以使用安全的MPC 进行计算变得很容易，而且也使得调试 CRYPTEN 代码变得更容易。
图 2. 使用神经网络和加密自动微分的例子
图3展示了如何将现有的PyTorch模型导入CRYPTEN。模型是通过ONNX导入的，这使得CRYPTEN与许多其他深度学习框架兼容（TensorFlow已经被支持）。正如该例子所示，在CRYPTEN中使用ResNet-18模型进行私有推理是很直接的。图中的例子还展示了CRYPTEN的GPU支持。需要注意的是，目前，所有各方必须使用相同的设备（CPU或GPU）进行计算。另一个注意事项是，CRYPTEN只支持PyTorch所提供的操作的一个子集。由于使用了安全的MPC，CRYPTEN与PyTorch相比也有大量的计算开销。
图3. 在GPU上使用秘密共享的 ResNet-18 模型对秘密共享的图像进行私有推理
尽管 CRYPTEN 正在迅速成熟，但它仍有三个重要的发展方向。
在机器学习算法的 CRYPTEN 实现中，数值问题比 PyTorch 的对应算法要普遍得多。特别是精度为 L 比特的定点表示法（默认为 L=16）比浮点表示法更容易出现数值溢出或欠流。此外，算术秘密份额很容易出现环绕错误，即份额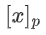 
的总和超过了环的大小，
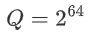。Wrap around errors 可能很难调试，因为它们可能只出现在多方环境中，在这种情况下，没有任何一方可以发现它们。我们计划在 CRYPTEN 中实现一些工具，帮助用户调试这种数字问题。
在 CRYPTEN 的一系列实际应用中，可能需要差分隐私的实现，以便为信息泄露提供严格的保证，这种泄露在私有计算的结果被公开披露时不可避免地发生。在安全的 MPC 中实现不同的私有机制很少受到关注([23]是一个明显的例外)，而且是不难的。特别是，诚实而好奇的威胁模型对于某些差分隐私的实现是不够的，而且必须确保这些实现不容易受到浮点攻击[19]。我们计划在CRYPTEN中的离散拉普拉斯机制[5]，其方式不容易受到这种攻击，也不需要主动安全。我们还计划支持主动安全，并利用这种支持来实现离散的高斯机制[3, 5]。
端到端的隐私需要在数据处理框架（如安全SQL实现[2]）和数据建模框架（如CRYPTEN）之间进行无缝整合。在 "明文 "软件中，这些框架是独立开发的，并通过 “glue code” 或平台进行组合，以促进处理和建模管道的构建。通过安全的 MPC 进行机器学习的现实世界用例需要开发一个平台，使私有数据处理和建模的整合从实施和安全的角度来看都是无缝的。
References
[1] M.Abadi,P. Barham,J.Chen,Z. Chen,A.Davis, J.Dean,M.Devin,S.Ghemawat,G.Irving.M.Isard.M.Kudlur.J.Levenberg,R.Monga.S.Moore.D.G.Murray.B.Steiner,P. Tucker,V. Vasudevan,P. Warden, M. Wicke,Y. Yu, and X.Zheng. Tensorflow: A system for large-scalemachine learning. In Usenix,2016.
[2] D.W.Archer,D.Bogdanov,L.Kamm,Y. Lindell,K. Nielsen,J.I.Pagter,N.P. Smart.and R.N.Wright. From keys to databases-real-world applications of secure multi-party computation. Computer.Journal, 61(12):1749-1771,2018.
[3] B.Balle and Y.-X. Wang.Improving the gaussian mechanism for differential privacy. In Proceedings of International Conference on Machine Learning,2018.
[4] D.Beaver. Efficient multiparty protocols using circuit randomization.In Annual International Cryptology Conference, pages 420-432. Springer, 1991.
[5] C.Canonne,G.Kamath,and T. Steinke.The discrete Gaussian for differential privacy. InarXiv2004.00010, 2020.
[6] O.Catrina and S. De Hoogh.Improved primitives for secure multiparty integercomputation. In International Conference on Security and Cryptographyfor Networks, pages 182-199.Springer,2010.
[7] R. Cramer,I.Damgard,and Y. Ishai. Share conversion,pseudorandom secret-sharing and applications to secure computation. In Lecture Notes in Computer Science, volume 3378,pages 342-362,2005.
[8] I. Damgård， M.Fitzi，E.Kiltz， J.B. Nielsen， and T. Toft.Unconditionally secure constant-rounds multi-party computation for equality, comparison, bits and exponentiation.In TCC, 2005.
[9] I. Damgård，V.Pastro， N. Smart， and S.Zakarias. Multiparty computation from somewhat homomorphic encryption. Cryptology ePrint Archive,Report 2011/535,2011.https://eprint.iacr.org/2011/535.
[10] D.Demmler,T.Schneider, and M.Zohner. ABY-a framework for efficient mixed-protocol secure two-party computation. In NDSS, 2015.
[1l] T.Dugan and X.Zou.A survey of secure multiparty computation protocols for privacy preserving genetic tests.In Proceedings of the International Symposium on Biomedical Imaging,20l6.
[12]O. Goldreich,S.Micali,and A.Wigderson. How to play any mental game or a completeness theorem for protocols with honest majority. In STOC, pages 218-229, 1987.
[13] C. Guo,A.Hannun,B.Knott,L.van der Maaten,M.Tygert,and R.Zhu. Secure multiparty computations in floating-point arithmetic.arXive-prints, page arXiv:2001.03192, Jan.2020.
[14] M.Hastings,B.Hemenway, D.Noble,and S.Zdancewic. SoK: general-purpose compilers for secure multi-party computation.In 2019IEEE Symposium on Security and Privacy(SP),2019.[15] A. S.Householder. The Numerical Treatment of a Single Nonlinear Eguation.1970.
[16] C. Juvekar, V. Vaikuntanathan,and A. Chandrakasan. Gazelle: A low latency framework for secure neural network inference. In arXiv 1801.05 507,2018.
[17] M. Keller, E. Orsini,and P. Scholl.MASCOT: Faster malicious arithmetic secure computation with oblivious transfer. In Proceedings of the ACM SIGSAC Conference on Computerand Communications Security, pages 830-842,2016.
[18] A.Lapets,N. Volgushev, A. Bestavros,F.Jansen,and M. Varia.Secure multi-party computation for analytics deployed as a lightweight web application.Technical Report BU-CS-TR 2016-008, Boston University, 2016.
[19] I. Mironov. On significance of the least significant bits for differential privacy.In Proceedings ACM Conference on Computer and Commuications Security (CCS), pages 650-661,2012.
[20] P. Mohassel and Y.Zhang. SecureML: A system for scalable privacy-preserving machine learning. In 2017 IEEE Symposium on Security and Privacy (SP), pages 19-38.IEEE,2017.
[21] P.Paillier. Public-key cryptosystems based on composite degree residuosity classes. In EUROCRYPT, pages 223-238, 1999.
[22] A.Paszke,S. Gross,S. Chintala,and G.Chanan. Pytorch: Tensors and dynamic neural networks in python with strong gpu acceleration, 2017.
[23] M. Pettai and P.Laud. Combining differential privacy and secure multiparty computation.In Proceedings of the Annual Computer Security Applications Conference, pages 421-430,2015.
[24] M.S.Riazi, C.Weinert, O.Tkachenko,E.M. Songhori,T.Schneider, and F.Koushanfar. Chameleon: A hybrid secure computation framework for machine learning applications. In Cryptology ePrint Archive, volume 2017/1164,2017.
[25] A. R. W. A. Khan, M. A. Noor. Higher-order iterative methods by using householders method for solving certain nonlinear equations. In Mathematical Science Letters, pages 107–120. Natural Sciences Publishing, May 2013.
[26] S. Wagh, D. Gupta, and N. Chandran. SecureNN: Efficient and private neural network training. In Cryptology ePrint Archive, volume 2018/442, 2018.
[27] A. C.-C. Yao. How to generate and exchange secrets. In FOCS, pages 162–167, 1986.
（上下滑动查看全部参考文献☝）
作者知乎号：六三，欢迎关注。
欢迎投稿
邮箱：kedakeyin@163.com
参与更多讨论，请添加小编微信加入交流群
