安全多方计算入门级介绍一

一、MPC problem

1.1 前提与目标

前提：

假设有  个参与方  。  持有输入  。

目标：

对于一些有  个输入和  个输出的给定函数  ，安全地计算   ，也就是说，我们想要一个这样的协议：

  学习  的正确值

除了从  和  中得到的信息外，没有任何关于输入的信息被泄露给  。

我们希望以上能够保持，甚至当（部分）参与方的行为是对抗性的。

1.2 例子

姚院士的百万富翁问题

两个百万富翁  在街上相遇，他们能否在不透露任何进一步信息的情况下比较谁更富有。我们对以上问题形式化表示：

计算安全函数  ，接受输入整数  ，如果  有  百万，结果是1，他知道  的钱少于  百万，但他不应该进一步了解任何信息。

问题：假设参与方都遵循指令，函数  很容易安全计算。你会怎么做？如果参与方可能偏离协议，你的解决方案还能用吗？

带着疑问我们往下看

1.3 通用性

MPC具有足够通用性: 一个解决方案原则上意味着任何加密协议问题的解决方案。但请注意，并非所有问题都可以通过安全计算单个函数来建模。例如，安全电子支付，它更像是几个函数的安全计算，跟踪之间的一些状态信息。

然而，这不是一个问题，我们将看到的定义是完全通用的，我们描述的协议实际上也是完全通用的，尽管为了简单起见，它们被称为计算单个函数的解决方案。

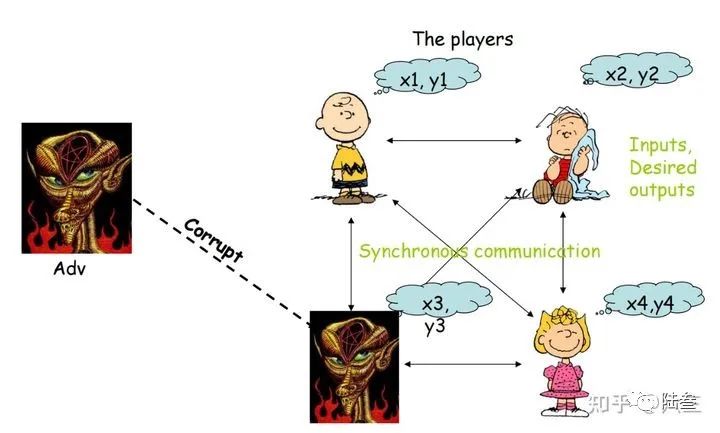
1.4 建模对抗行为

假设一个敌手  。

  可能会腐蚀一些参与方并使用它来学习他不应该知道的信息，或者破坏结果。当  被腐蚀时，  学习  的完整历史记录。

  按照属性可分类为：

• 被动或主动: 只需监控腐坏的参与方，或者对其进行完全控制。

• 静态或自适应: 所有腐蚀都发生在协议启动之前，或者在协议期间动态发生。

• 无界限或概率多项式时间。

通过对抗行为的描述，我们将得到一个更精确的 MPC 目标：希望协议工作时，就好像我们有一个值得信赖的一方  ，它从参与方那里获取输入，计算结果并将其返回给参与方一样，因此，  可以决定腐坏参与方的输入，但诚实的参与方可以获得正确的结果，协议只告诉  被腐蚀参与方的输入/输出。

1.5 腐坏的界限

如果  可以破坏参与方的任意子集，那么在大多数情况下问题无法解决，例如，如果每个参与方都被腐蚀，那么何谈安全性呢？

因此需要定义一些可以腐坏子集的界限：

敌手结构  :  的子集族，  是一个  -adversary，一组腐坏的参与方在所有时间都在  。

为了使之合理，  必须是单调的。  和  意味着  也就是说，如果  可以破坏集合  ，他可以选择破坏任何较小的集合。

Threshold-T 结构: 包含最多  大小的所有子集。

  为  ：对于任意  ，  小于  。

  为  ：对于任意  ，  小于  。

  的 Threshold-T 结构为  。

  的 Threshold-T 结构为  。

为什么使用以上通用访问结构，而不仅仅是可以腐坏的参与方数量？

门限敌手 (我们只是约束了腐坏的数量) 在一个所有节点都同样难以侵入的网络中是有意义的。但实际情况往往不是这样。

通过一般的访问结构，我们可以表达这样的意思：敌手可以突破少量的比较安全的节点和大量的不太安全的节点。

1.6 建模通信

异步网络，即敌手看到所有消息，可以无限期地延迟它们。在这种网络上，某些形式的 MP C问题更难或不可能，在任何情况下都会产生额外的复杂性。

同步网络，通信分回合进行，在每轮中，每个参与方都可以向彼此发送消息，所有消息都是在同一轮中接收的。

两个主要变体:

• 信息论场景.  没有看到诚实（未腐坏）参与方之间的通信，即可以获得不受限制的  的安全性。

• 加密场景。  可以看到所有发送的信息，但不能改变诚实玩家之间的信息交换，即只能获得（多项式时间）约束的  的安全性。

1.7 小结

腐坏可以是被动的: 只需观察计算和   。

腐坏也可以是主动的：即控制所有。

密码学场景:  能够看到所有消息；

信息论场景: 没有关于诚实对诚实的  的信息。

  可以选择静态或自适应腐坏哪些参与方，但一组腐坏的参与方必须“不太大”，即它必须在给定的敌手结构中。

信息论场景中：

被动的、自适应的、无约束的  ：在阈值  的情况下，如果且仅当  为  ,  时，任何函数都能以完美的安全性安全地计算 。“仅当” 的含义是，如果  上的条件不满足，则存在无法安全计算的函数。

被动的、自适应的、无约束的  ：在阈值  的情况下，如果且仅当  为  ,  时，任何函数都能以完美的安全性安全地计算 。

如果我们假设广播频道是免费提供的，并且我们接受非零错误概率，那么更多的可能是带有广播和主动的、自适应的、无约束的Γ对抗的场景，即在阈值  的情况下，当且仅当  为  ，  时，任何函数都能以较小的错误概率安全地计算出来。

参考文献

[CCD88, BGW88, RB89, HM99,CDDHR00]

密码学场景中：

被动，自适应，多项式时间敌手：假设存在单向陷门置换，如果腐坏的参与方数量小于  ，则可以通过计算安全性安全地计算任何函数。

主动，自适应，多项式时间：假设存在单向陷门置换，当且仅当  为  ，  时，可以使用计算安全性安全地计算任何函数。

参考文献

[Y86, GMW87,CFGN]

参考自 Ivan Damgård BRICS (Århus University) 的主题演讲，Ivan Damgård是丹麦著名的密码学家，SPDZ协议的主要开创者。这应该是20年前的一次演讲文稿，但可以从中学习一些思想。有兴趣的朋友可以读一下。

作者知乎号：六三，欢迎关注。

更多内容请点击以下链接：

安全多方计算学习路线

安全多方计算开源框架梳理

初识安全多方计算(Getting to know SMPC)

安全多方计算：理论、实践与应用

欢迎投稿

邮箱：kedakeyin@163.com

参与更多讨论，请添加小编微信加入交流群