SQ太甜了WWWWW
看到可爱的秋瞳,你充满了决心!
问题描述:
给定两个大小为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数。
进阶:你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗?
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/median-of-two-sorted-arrays
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
一、合并数组(即暴力解法)
思路及算法:
代码:
class Solution {public double findMedianSortedArrays(int[] nums1, int[] nums2) {int len = nums1.length+nums2.length;int[] list = new int[len];int m = 0, i=0, j=0;while(i<nums1.length && j<nums2.length) {if(nums1[i]<nums2[j]){list[m++] = nums1[i++];} else {list[m++] = nums2[j++];}}if(i != nums1.length){for( ; i<nums1.length; i++){list[m++] = nums1[i];}} else {for( ; j<nums2.length;j++){list[m++] = nums2[j];}}double count=0;if(len%2!=0){count = list[len/2];return count;} else {count = ((double)list[len/2]+(double)list[len/2-1])/2;return count;}}}
复杂度分析:
二、二分查找
思路及算法:
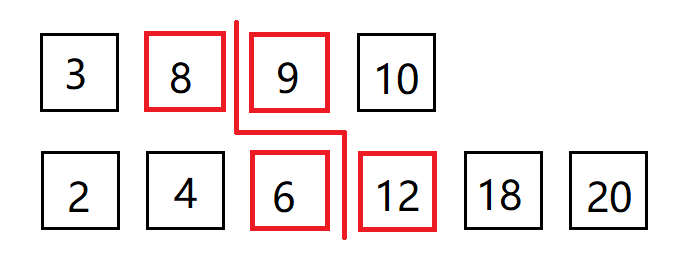
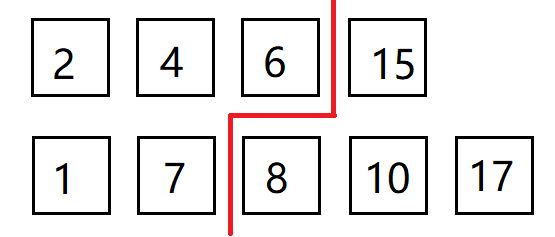
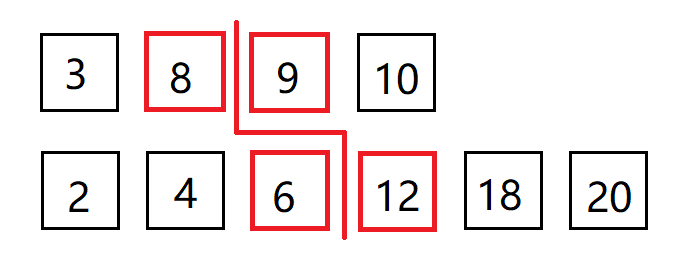

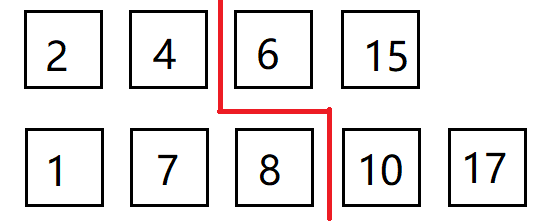
代码:
class Solution {public double findMedianSortedArrays(int[] nums1, int[] nums2) {if (nums1.length > nums2.length) {return findMedianSortedArrays(nums2, nums1);}int m = nums1.length;int n = nums2.length;int left = 0, right = m;// median1:前一部分的最大值// median2:后一部分的最小值int median1 = 0, median2 = 0;while (left <= right) {// 前一部分包含 nums1[0 .. i-1] 和 nums2[0 .. j-1]// 后一部分包含 nums1[i .. m-1] 和 nums2[j .. n-1]int i = (left + right) / 2;int j = (m + n + 1) / 2 - i;// nums_im1, nums_i, nums_jm1, nums_j 分别表示 nums1[i-1], nums1[i], nums2[j-1], nums2[j]int nums_im1 = (i == 0 ? Integer.MIN_VALUE : nums1[i - 1]);int nums_i = (i == m ? Integer.MAX_VALUE : nums1[i]);int nums_jm1 = (j == 0 ? Integer.MIN_VALUE : nums2[j - 1]);int nums_j = (j == n ? Integer.MAX_VALUE : nums2[j]);if (nums_im1 <= nums_j) {median1 = Math.max(nums_im1, nums_jm1);median2 = Math.min(nums_i, nums_j);left = i + 1;} else {right = i - 1;}}return (m + n) % 2 == 0 ? (median1 + median2) / 2.0 : median1;}}// 作者:LeetCode-Solution// 链接:https://leetcode-cn.com/problems/median-of-two-sorted-arrays/solution/xun-zhao-liang-ge-you-xu-shu-zu-de-zhong-wei-s-114/// 来源:力扣(LeetCode)// 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
(WRO,完全搞不懂

 ,我讨厌数学!!
,我讨厌数学!!
复杂度分析:

文章转载自半猫Coder,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






