BigQuant 量化教程
来源:https://bigquant.com/tutorial/
宽客学院
宽客学前
【
宽客学院】BigQuant 宽客成长攻略
欢迎您来到BigQuant。BigQuant的使命是将人工智能的能力赋予每一个投资者 (Democratize AI to empower investors)。
我们制定了一个宽客成长路径,包含如下四个阶段的教程,帮助大家一步一步的学习和深入量化,一步一步的使用并驾驭AI来开发策略,在宽客之路上走的
更快更远。
无论您是金融/量化投资从业者,还是对量化有兴趣的工程师,或者是未来希望参与量化投资的学生,本教程都将对您的成长和发展有所帮助。
下一页:您的第一个人工智能量化投资策略
目录:BigQuant学院
您的第一个人工智能量化投资策略
BigQuant平台支持可视化开发人工智能(AI)量化策略,你可以根据本文的引导,新建您的第一个AI量化策略。
1
. 在网站首页,登录账户并点击 我的策略,进入策略研究界面
2
. 进入 我的策略界面以后,新建 > 可视化策略-AI选股策略

3
. 输入策略 名称,完成策略新建
新建的策略如下:
4
. 点击 运行全部 或 运行 ,运行策略
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
上一页:BigQuant宽客成长攻略
下一页:通过策略生成器新建AI策略
目录:宽客学院
通过策略生成器新建AI策略
当您第一次进入 “我的策略” 时,即使您不会编程,您也可以根据 用户引导 一步一步的创造您的AI策略:
下面部分是这个引导的每步介绍,如果您已经熟悉,可以跳过下面部分。
1
. 新建策略 > 人工智能策略生成器
点击 新建策略,然后 人工智能策略生成器
2
. 策略生成器
策略生成器如下图:左边是配置界面,右边代码预览。我们通过可以配置 目标、数据、模型和特征等4个方面,来生成不同的策略。
在新手任务里,我们都使用默认参数。
3
. 选择因子
在 4.特征 里,点击 帮我选几个因子,让系统随机选几个常用因子。
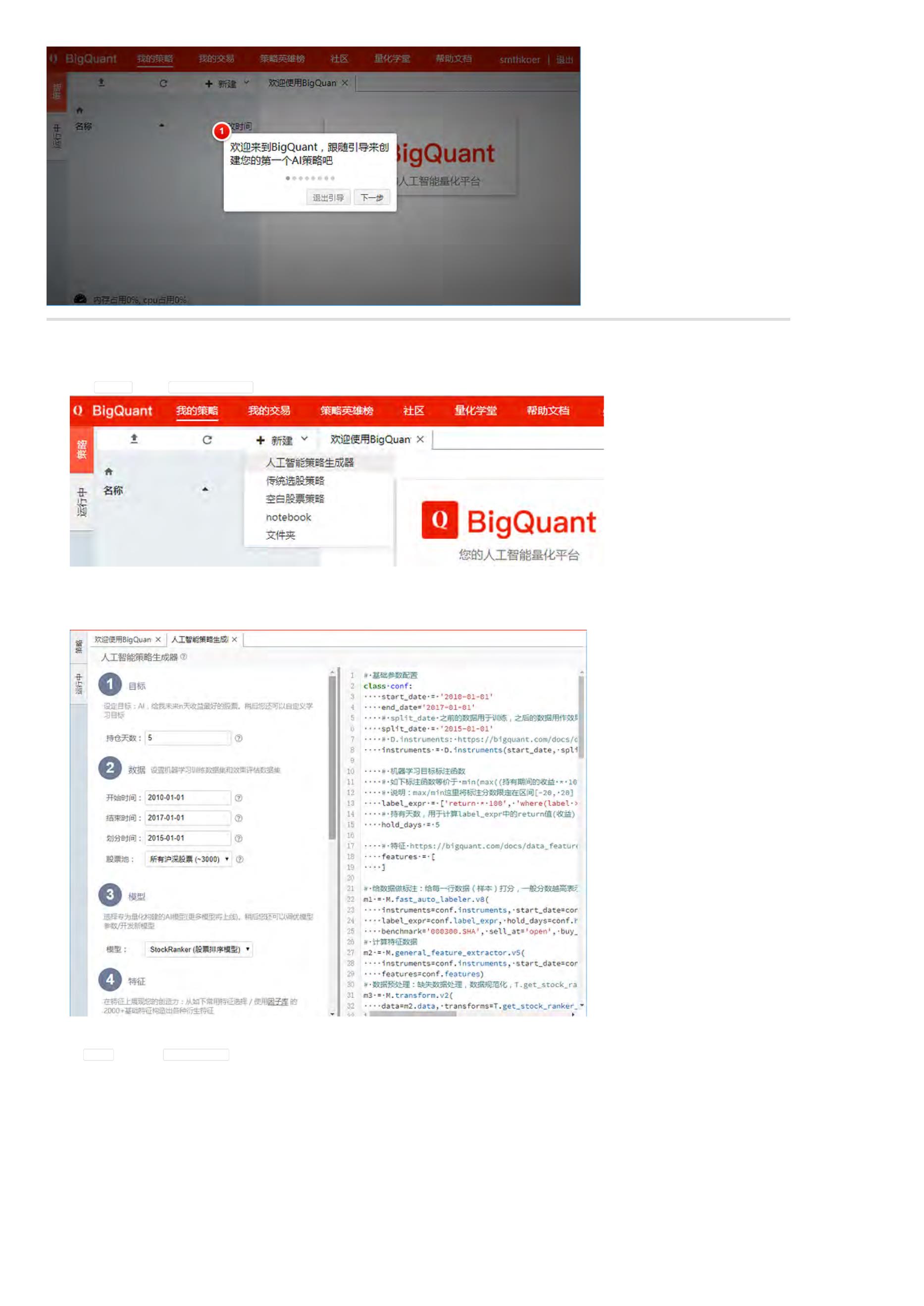
4
. 生成策略
点击 生成策略,自动生成策略代码
5
. 运行策略
点击 运行全部,运行刚才生成的策略代码。等待策略运行完成(这可能要~10分钟)。新手任务数据已经缓存,应该很快就看到结果。
6
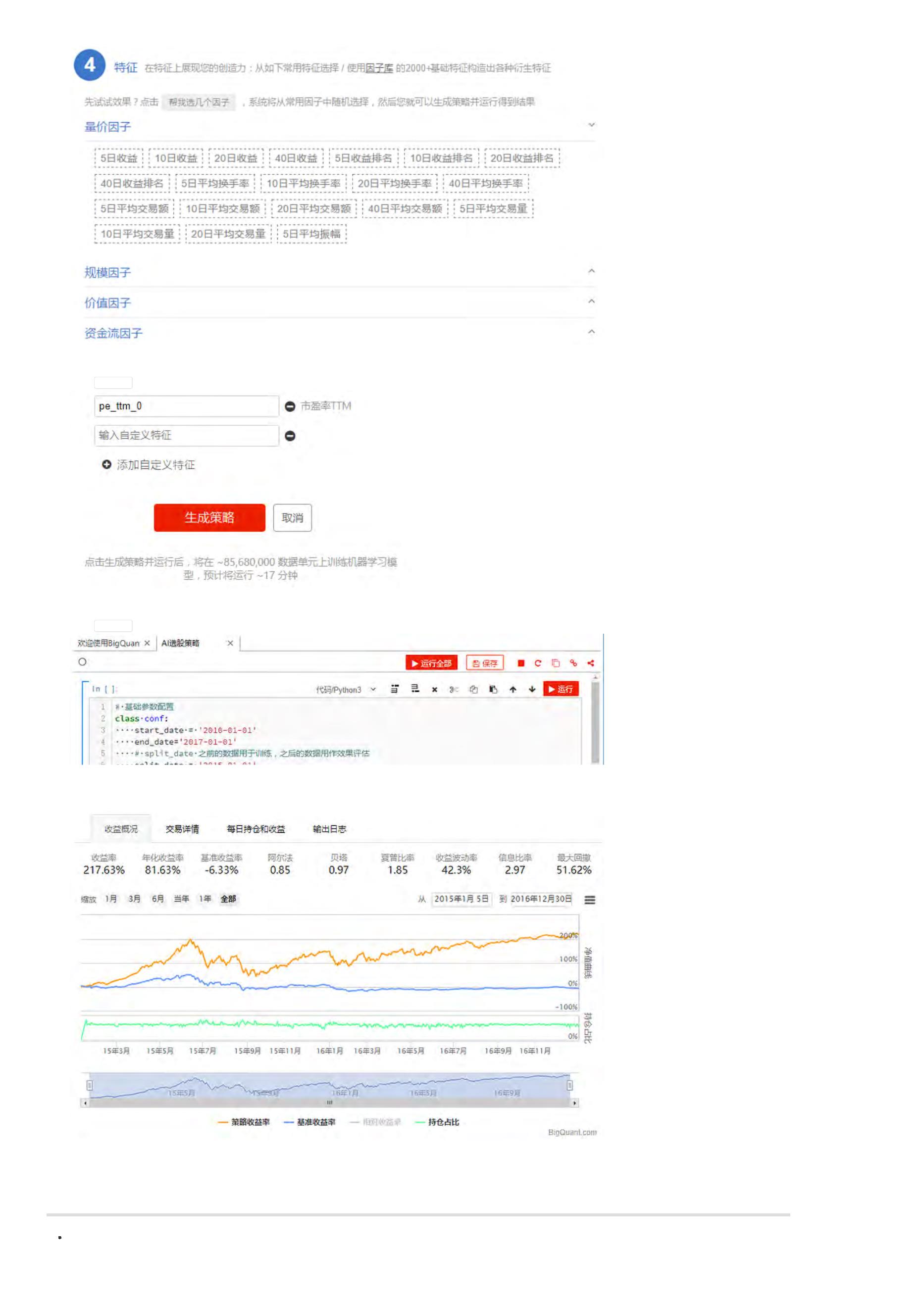
. 查看结果
策略最后的回测效果
您的一个人工智能策略 已经创建好了。是不是很简单,而且看起来收益还不错,在2015-2016的总收益达到了 217.63%。除了收益,我们还要看风险,因为
1
5年的股灾,这个策略的回撤也是很大的。这只是一个示例策略,对实际交易不具有指导价值。随着研究的深入,您将会用BigQuant开发出有实盘价值的策
略。
上一页:您的第一个人工智能量化投资策略
下一页:BigQuant人工智能量化平台 vs. 传统量化平台
目录:BigQuant学院
[
量化学堂-新手专区]BigQuant 人工智能量化平台 vs. 传统量化平台


本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
上一页:您的第一个人工智能量化投资策略
下一页:什么是人工智能?
目录:BigQuant学院
宽客小学
[
量化学堂-新手专区]什么是人工智能?
导语:谷歌围棋程序AlphaGo全面碾压专业选手,人工智能时代已经来临。
人工智能(英语:Artificial Intelligence, AI)亦称机器智能,是指由人工制造出来的系统所表现出来的智能,可以概括为:研究智能程序的科学 。这门科学
的出发点是 研究如何使程序能够像人一样思考、行为,以及如何保持理性(如图1),这里的理性可以理解为效用最大化。
图
智能程序的科学
人工智能技术(AI)已经渗透到我们日常生活的方方面面,涉及的行业更是不胜枚举,包括游戏、新闻媒体、金融,并运用到了各种领先的研究领域,例如
机器人技术、医学诊断和量子科学。人工智能的基本知识和应用领域,主要有机器学习、概率推理、机器人技术、计算机视觉和自然语言处理。图2便展示了
其中的一些基本的应用。
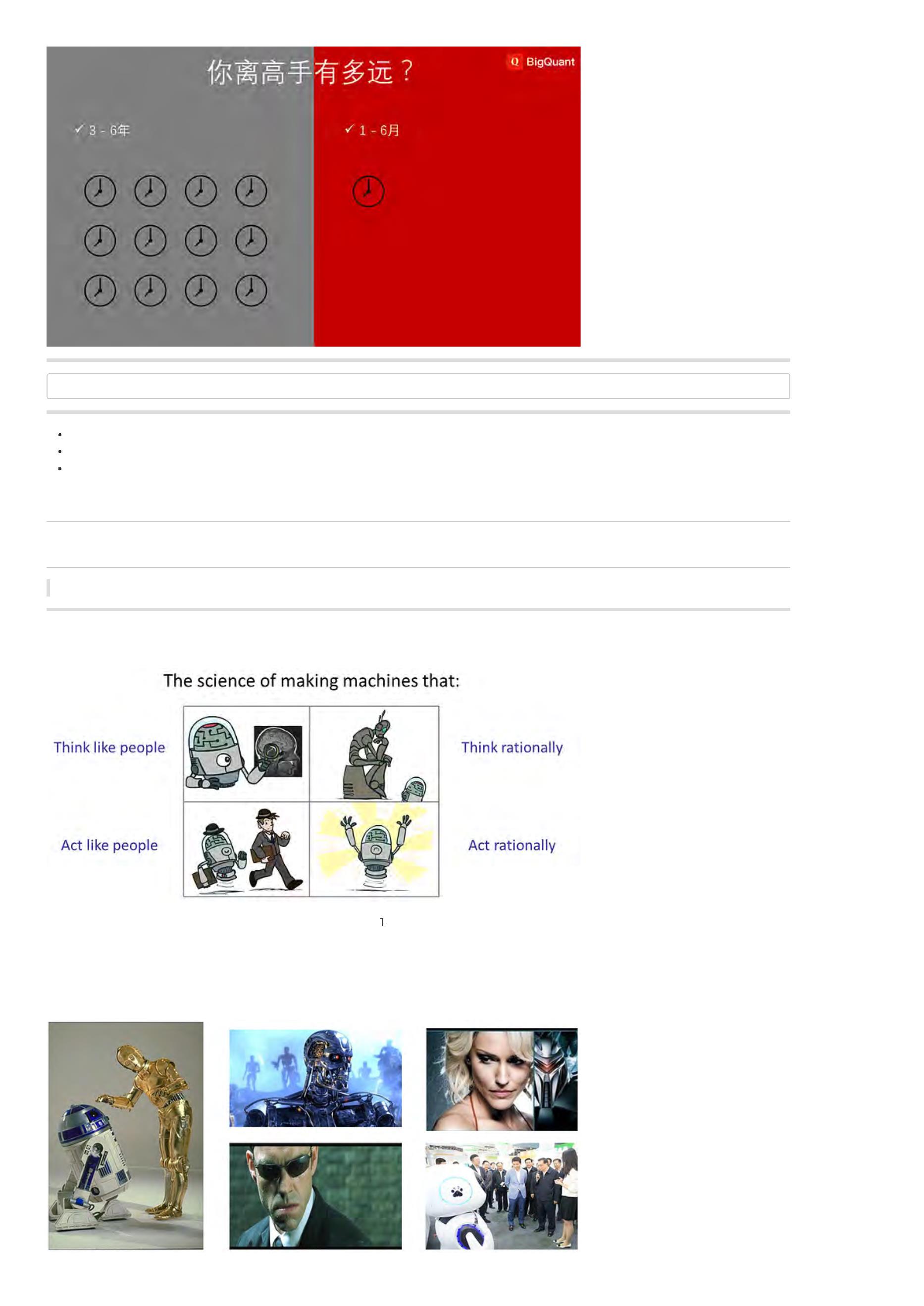
图
人工智能在日常生活中的应用
当今社会的复杂活动,包括图像识别、医学诊断、预测机器故障时间或衡量某些股票的价格,这些行为中往往涉及数千种数据集和大量变量之间的非线性关
系。例如,我们该如何通过编写一系列规则,使得程序能在任何情况下描述出一只狗的外观?如果能将做出各种复杂预测的困难工作,即数据优化和特征
(
Feature)规范,从程序员身上转嫁给程序,从交易员身上转嫁给程序,情况又会怎样?这正是现代化人工智能带给我们的承诺。
AI时代即将来临,正如90年代的互联网时代,只有拥抱变化,顺应趋势,才能跟上时代的步伐。
图
人工智能正在进入我们的生活
小结:人工智能是研究如何使程序能够像人一样思考、行为,以及如何保持理性的学科,并以非常迅猛的速度发展,已经渗透到生活的方方面面,只有
拥抱AI,才能跟上时代趋势。
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
扩展阅读
图灵奖设立50年,Raj Reddy & Jeff Dean谈人工智能的发展与未来
上一页:BigQuant人工智能量化平台 vs. 传统量化平台
下一页:什么是量化投资?
目录:BigQuant学院
[
量化学堂-新手专区]什么是量化投资?
导语:了解什么是量化投资,是成为宽客道路上的一块重要的敲门砖。本文为大家初步介绍了量化投资的相关知识,希望在阅读后能帮助新手宽客们更
快起步。
什么是量化投资?
量化投资是指通过数量化模型建立科学投资体系,以获取稳定收益。 在海外的发展已有30多年的历史,其投资业绩稳定,市场规模和份额不断扩大、得到了
越来越多投资者认可。在国内,量化投资不再是一个陌生的词汇,近几年得到了迅猛的发展。
提起量化投资,就不得不提量化投资的标杆——华尔街传奇人物詹姆斯·西蒙斯(James Simons)。视频地址:“横扫华尔街的数学家”
通过将数学理论巧妙融合到投资的实战之中,西蒙斯成为了投资界中首屈一指的“模型先生”。由其运作的大奖章基金(Medallion)在1989-2009的二十年间,平
均年收益率为35%,若算上44%的收益提成,则该基金实际的年化收益率可高达60%,比同期标普500指数年均回报率高出20多个百分点,即使相较金融大
鳄索罗斯和股神巴菲特的操盘表现,也要遥遥领先十几个百分点。最为难能可贵的是,纵然是在次贷危机全面爆发的2008年,该基金的投资回报率仍可稳稳
保持在80%左右的惊人水准。西蒙斯通过将数学模型和投资策略相结合,逐步走上神坛,开创了由他扛旗的量化时代。
价值投资和 趋势投资(技术分析)是引领过去一个世纪的投资方法,随着计算机技术的发展,已有的投资方法和计算机技术相融合,产生了量化投资。
量化投资和传统投资有啥区别?

简单来说,量化投资与传统投资方法之间的关系比较类似于中医和西医的关系。量化投资与传统投资最鲜明的区别就是模型的应用,这就类似于医学上对仪
器的应用。中医主要通过望、闻、问、切等医疗手段,很大程度上借助中医长期积累的经验进行诊断,定性的程度大一些。而西医则不同,西医主要借助于
现代仪器,首要病人去拍片子、打B超、化验等,这些都要依托于医学仪器进行检验,对于各项检查结果有详细的数据评价标准,最后判断症结所在,进而
对症下药。具体的比较见表1:
表
传统投资和量化投资的区别
量化投资的有哪些优势?
量化投资的优势在于纪律性、系统性、及时性、准确性和分散化。
纪律性:严格执行投资策略,不是投资者情绪的变化而随意更改。这样可以克服人性的弱点,如贪婪、恐惧、侥幸心理,也可以克服认知偏差。
系统性:量化投资的系统性特征包括多层次的量化模型、多角度的观察及海量数据的观察等。多层次模型包括大类资产配置模型、行业选择模型、精选
个股模型等。多角度观察主要包括对宏观周期、市场结构、估值、成长、盈利质量、市场情绪等多个角度分析。此外,海量数据的处理能力能够更好地
在广大的资本市场捕捉到更多的投资机会,拓展更大的投资机会。
及时性:及时快速地跟踪市场变化,不断发现能够提供超额收益的新的统计模型,寻找新的交易机会。
准确性:准确客观评价交易机会,克服主观情绪偏差,从而盈利。
分散化:在控制风险的条件下,量化投资可以充当分散化投资的工具。表现为两个方面:一是量化投资不断地从历史中挖掘有望在未来重复的历史规律
并且加以利用,这些历史规律都是较大概率取胜的策略;二是依靠筛选出股票组合来取胜,而不是一只或几只股票取胜,从投资组合的理念来看也是捕
捉大概率获胜的股票,而不是押宝到单个股票。
如何进行量化投资呢?
使用量化策略是进行量化投资的有效方式。
通过客观准确的交易规则构建策略,并在历史数据上进行回测,当回测结果通过评估审核后才可以称得上是一个可进行实盘交易的量化策略,许多私募在实
盘之前还有一个模拟交易阶段。
小结:量化投资是指通过数量化模型建立科学投资体系,以获取稳定收益。与传统投资方式不同的是,量化投资更加注重模型的应用,其优势在于纪律
性、系统性、及时性、准确性和分散化。使用量化策略是进行量化投资的有效方式。
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
扩展阅读
量化小课堂-Python&Pandas系列第一讲:当量化投资邂逅Python
上一页:什么是人工智能?
下一页:关于BigQuant
目录:BigQuant学院
[
量化学堂-新手专区]关于BigQuant
欢迎来到BigQuant人工智能量化平台!
BigQuant的目标是成为每一个宽客(Quant)的人工智能量化投资平台和社区。我们是首个专注量化投资的人工智能/机器学习平台。在这里,量化投资者可
以无门槛的使用最领先的人工智能技术。我们致力于用人工智能助力宽客,让投资变得更有效更简单。
We are democratizing AI technology to empower investors
BigQuant 有哪些特点?
领先的人工智能技术
首个专注量化投资的人工智能/机器学习平台,在这里,用户可以自由使用全球最受欢迎的Tensorflow、Keras、Theano、XGBoost、Sklearn等人工智能相关
模块,无门槛的使用最领先的人工智能技术开发策略

便利的云端研究平台
高性能的云计算服务器集群,提供在线的Notebook云端研究平台,采用Docker技术隔离,资源独立、安全性更高、性能更好
高质量的数据
我们拥有2005年至今完整的行情数据、上市公司财务数据及1600个以上的特色因子数据,每年投入百万用于数据购买、加工和存储上
顶尖的回测体验
支持全市场所有类型策略进行回测,回测速度超快,展示结果特别丰富,界面友好
精准的实时模拟交易
策略由实时行情驱动,运行结果和实盘结果高度吻合,除了不是真钱在跑,其他都和实盘一样,大大提高策略验证效率,让您的策略上线时成竹在胸
量化交流社区
我们为量化爱好者提供线上交流社区,便于用户交流量化策略、学习量化知识,一起成长
众包基金
如果你是学生,参加平台量化策略大赛,赢取奖金、实习和工作机会
如果你是宽客,我们会定期选拔好的策略和宽客进入我们的基金管理项目进行孵化
如果你是机构,可以通过我们的平台对接好的策略,帮你实现多策略布局
我们的团队
BigQuant核心团队主要毕业于清华、北大、中科大等,10+年微软、腾讯、小米和国内知名量化私募等工作经历,拥有丰富的互联网大数据/机器学习从业经
验和资深的量化投资经验。
常见问题
知识产权和安全保护
BigQuant 收费吗?
BigQuant量化交易平台是为量化爱好者、宽客量身打造的云平台,我们提供的服务均免费。 我们免费为您提供高质量数据、顶级回测服务、顶尖模拟交易、
量化交流社区、IPython Notebook研究平台,便于您快速实现、使用自己的量化交易策略。
策略归谁所有?
策略是每个宽客最宝贵的财富,您全权拥有在BigQuant中研究成果的知识产权。BigQuant不会也无法查看、公布您的策略、代码、数据,但您可以主动在社
区公布分享。
我的策略是否安全?
我们非常严肃对待用户的策略安全问题。我们提供业界最高的安全保护,通过https传输、加密存储、沙箱保护保障您的策略安全,除了您本人,任何人无法
获取您的策略。
联系我们
欢迎 社区内 私信 @bigquant 和我们交流
如果您有任何疑问,请发邮件到 i@bigquant.com 或者加QQ群 625326167告诉我们,谢谢。
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
上一页:什么是量化投资?
下一页:聊一聊策略生成器
目录:BigQuant学院
[
量化学堂-新手专区]聊一聊策略生成器
导语:一个好的策略是量化投资成功的关键,本文介绍了BigQuant平台的策略生成器,帮助编程基础薄弱的用户生成策略。
什么是策略生成器?
量化策略的开发一般离不开编写代码,BigQuant平台使用的策略开发语言为Python,如果会写代码,那么策略开发上手就比较快。为了满足一些编程基础薄
弱的用户能够快速上手,因此推出了策略生成器这一大“神器”。通过策略生成器,你可以通过菜单化操作来一键生成策略代码。
在BigQuant策略平台点击 新建 按钮,就可以打开 人工智能策略生成器 界面(如图1):

图
策略平台生成人工智能策略
策略生成器的界面如图2:
图
策略生成器界面
可以看出,左侧是菜单操作页面,右侧是代码生成页面。你可以在左侧页面,通过菜单化的方式构建你的策略思想,比如勾选特征 上市板(list_board_0),
一旦勾选该特征以后,我们发现,右侧的代码里,变量 features 中会增加 list_board_0 ,于是我们就可以很方便地使用菜单化的方式来形成策略代码。
点击 生成策略 以后,完整的策略代码如图3:
图
生成器默认策略
策略生成器的定位是什么?
策略生成器的目标是引导编程薄弱的用户快速上手,因此定位就是 帮助其快速上手、快速开发AI策略,使用户对BigQuant的策略平台和AI策略有一个初步简
单的认识。当用户有一定的认识之后,策略生成器扮演的角色不再那么重要。
如何使用策略生成器?
通过一个例子来介绍,如何使用策略生成器开发AI策略。
1
. 进入 我的策略
在 BigQuant 首页,点击 我的策略(如图4)
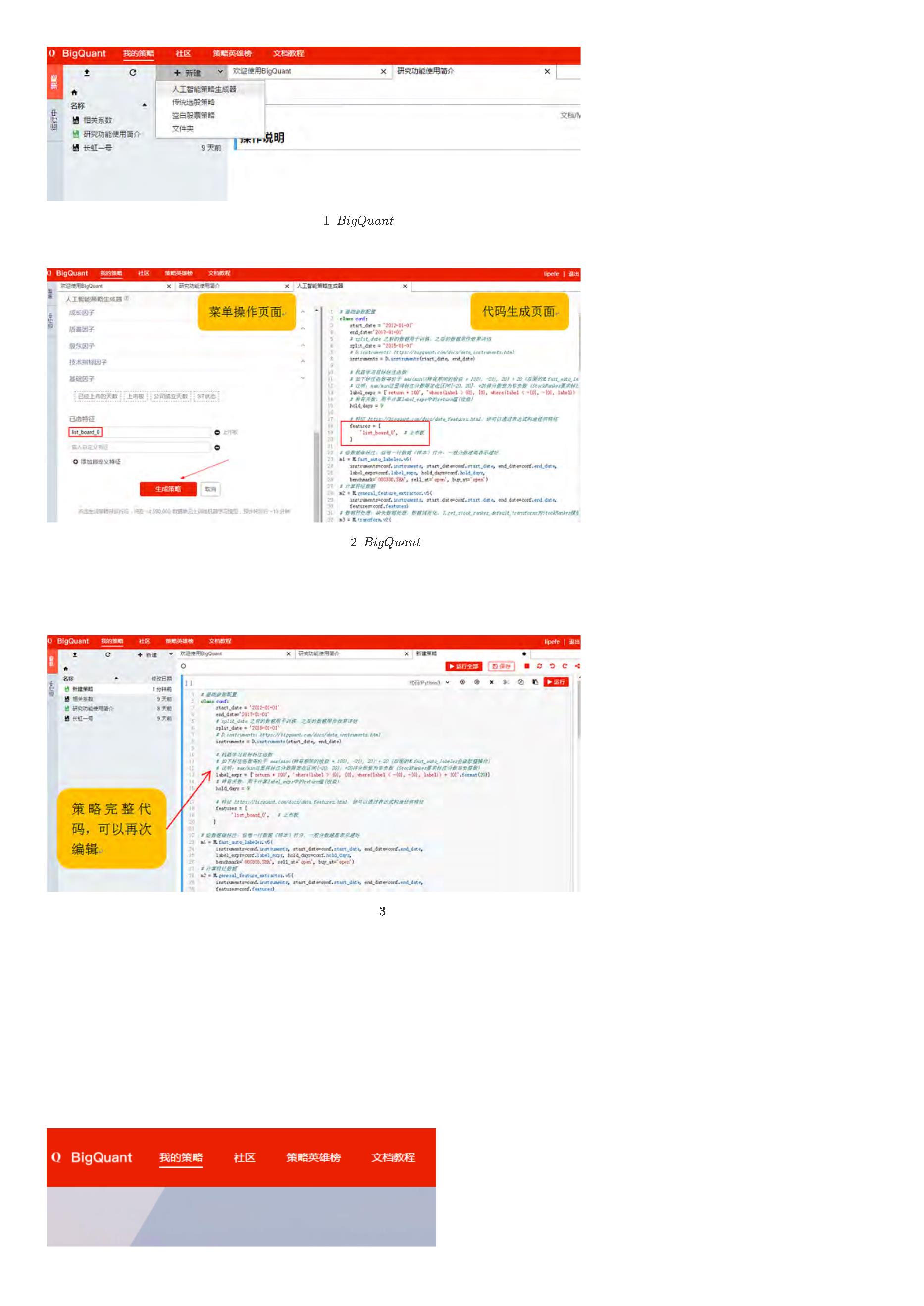
图
我的策略
2
. 新建策略 > 人工智能策略生成器
点击 新建策略,然后 人工智能策略生成器(如图5)
图
人工智能策略生成器
3
. 策略生成器
策略生成器如图6:左边是配置界面,右边代码预览。我们通过可以配置 目标、数据、模型和特征等4个方面,来生成不同的策略。
这里使用默认参数。
图
策略生成器默认参数
4
. 选择因子
在 4.特征 里,点击 帮我选几个因子,让系统随机选几个常用因子。(如图7)
图
选择因子
5
. 生成策略
点击 生成策略,自动生成策略代码。(如图8)
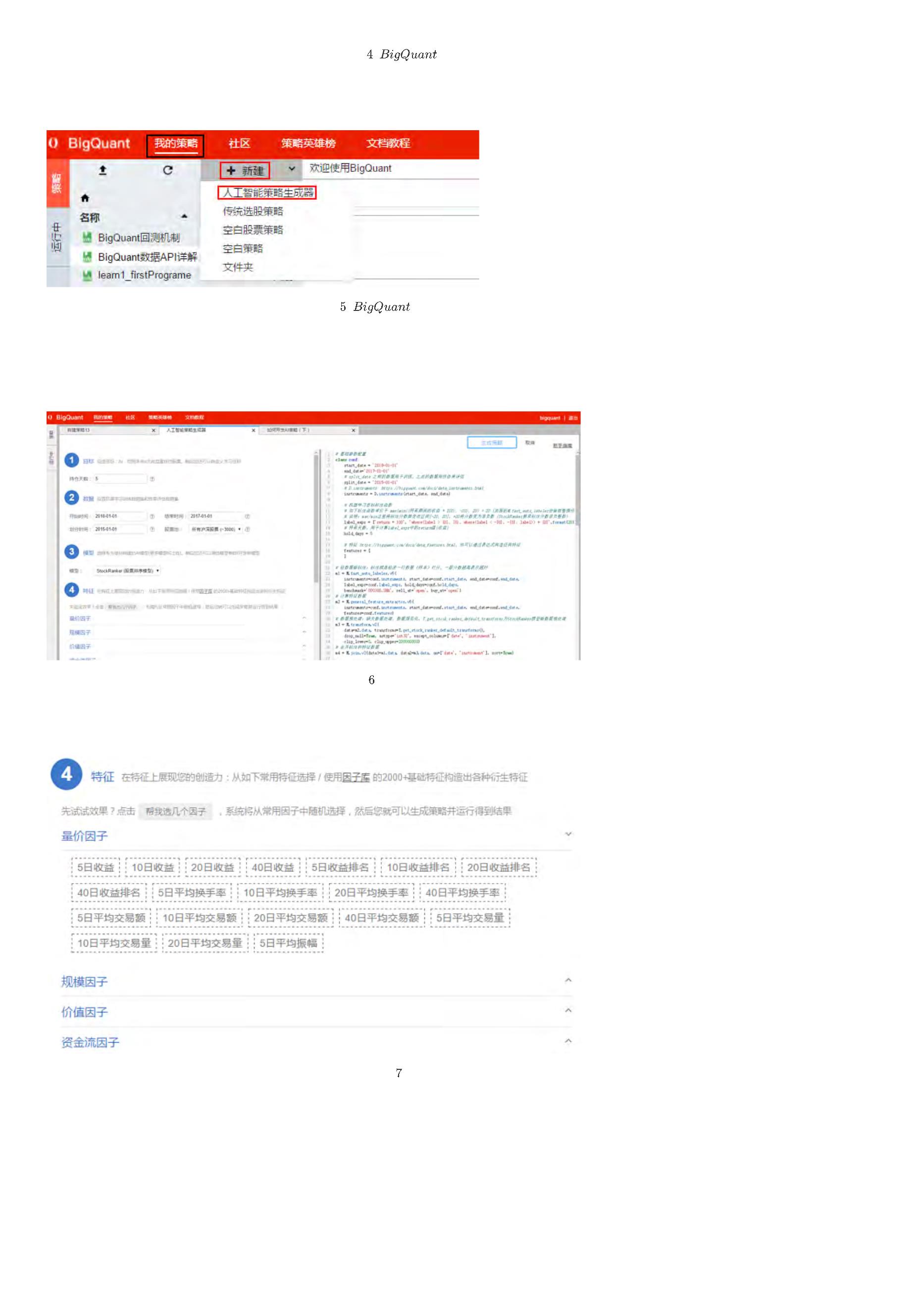
图
生成策略
6
. 运行策略
点击 运行全部,运行刚才生成的策略代码。等待策略运行完成(这可能要~10分钟)。新手任务数据已经缓存,应该很快就看到结果。(如图9)
图
运行策略
7
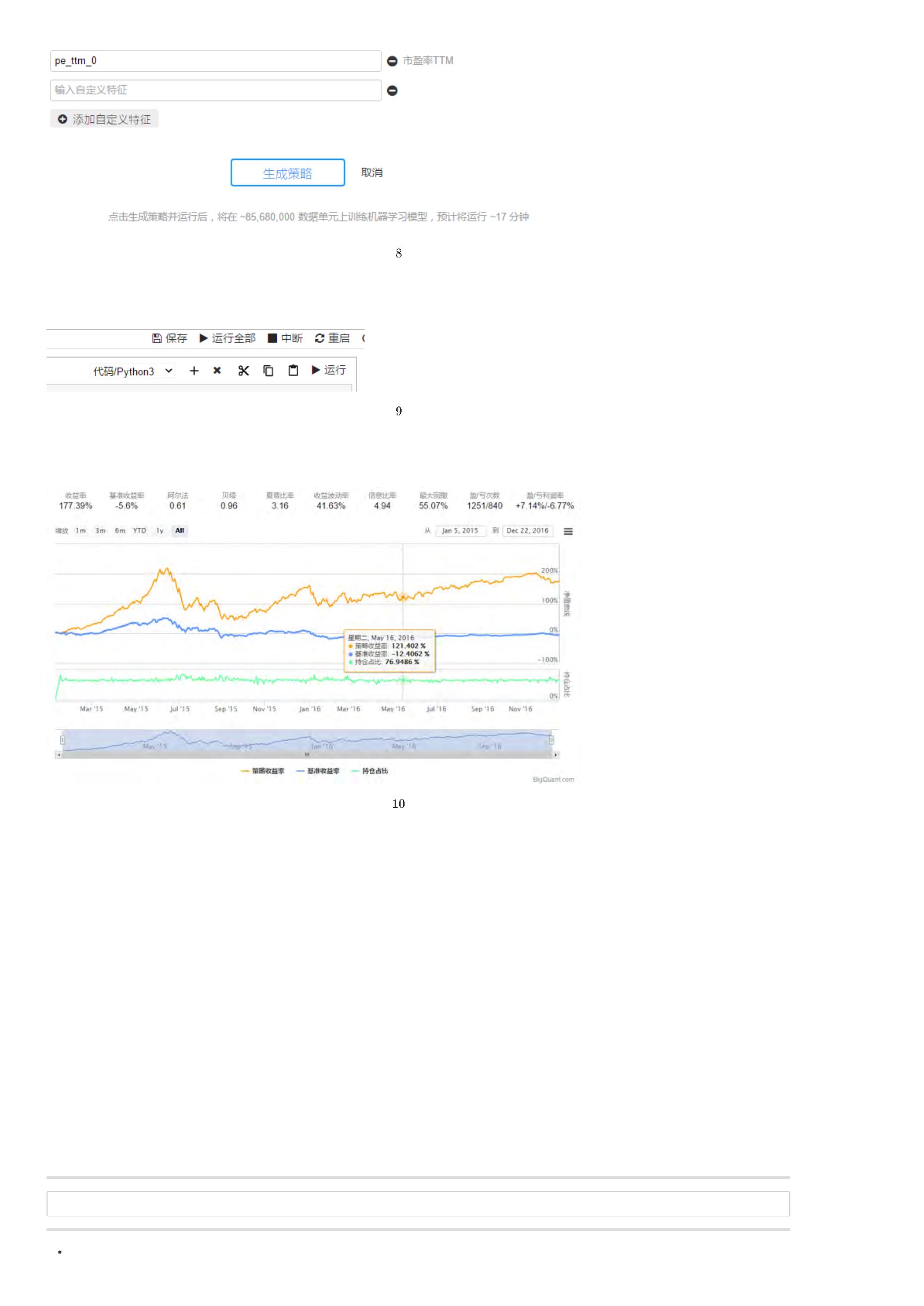
. 查看结果
效果如图10
图
结果查看
会用策略生成器,做量化还差什么?
要开发好的策略光会使用策略生成器还远远不够,还需要以下几块知识。
、了解 AI
1
因为要开发AI策略肯定要对AI、机器学习、深度学习有一定的了解,比如,必须要知道AI算法的逻辑是什么?什么是损失函数?如何避免过拟合?怎样提高算
法的预测能力?如何做特征工程?这些具体的问题直接关系到你的模型的预测性能。
2
、熟悉 平台回测
在BigQuant上开发策略需要进行回测验证,那肯定需要熟悉BigQuant的回测机制和回测函数,比如,我如何设置交易成本、如何下单、如何查询持仓和订
单,熟悉BigQuant回测才能得心应手的开发策略。
3
、会 python
很简单,策略平台采取python语言,把想法转化成代码离不开python编程基础。
、懂 量化
4
量化不仅仅包括选股,还涉及择时、仓位控制、资金管理、权重优化等知识,因此要得懂量化。
要成为策略高手,光会策略生成器还远远不够,你还得掌握上面这四大技能。路漫漫其修远兮,继续加油吧:relaxed:
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
上一页:关于BigQuant
下一页:BigQuant策略平台使用帮助
目录:BigQuant学院
[
量化学堂-新手专区]BigQuant 策略平台使用帮助
导语:BigQuant策略平台是开发试验、研究策略的重要场地,了解平台使用帮助能更快速、更高效地进行试验研究!
策略平台简介
在主页点击 我的策略就直接进入BigQuant策略平台。
图
我的策略
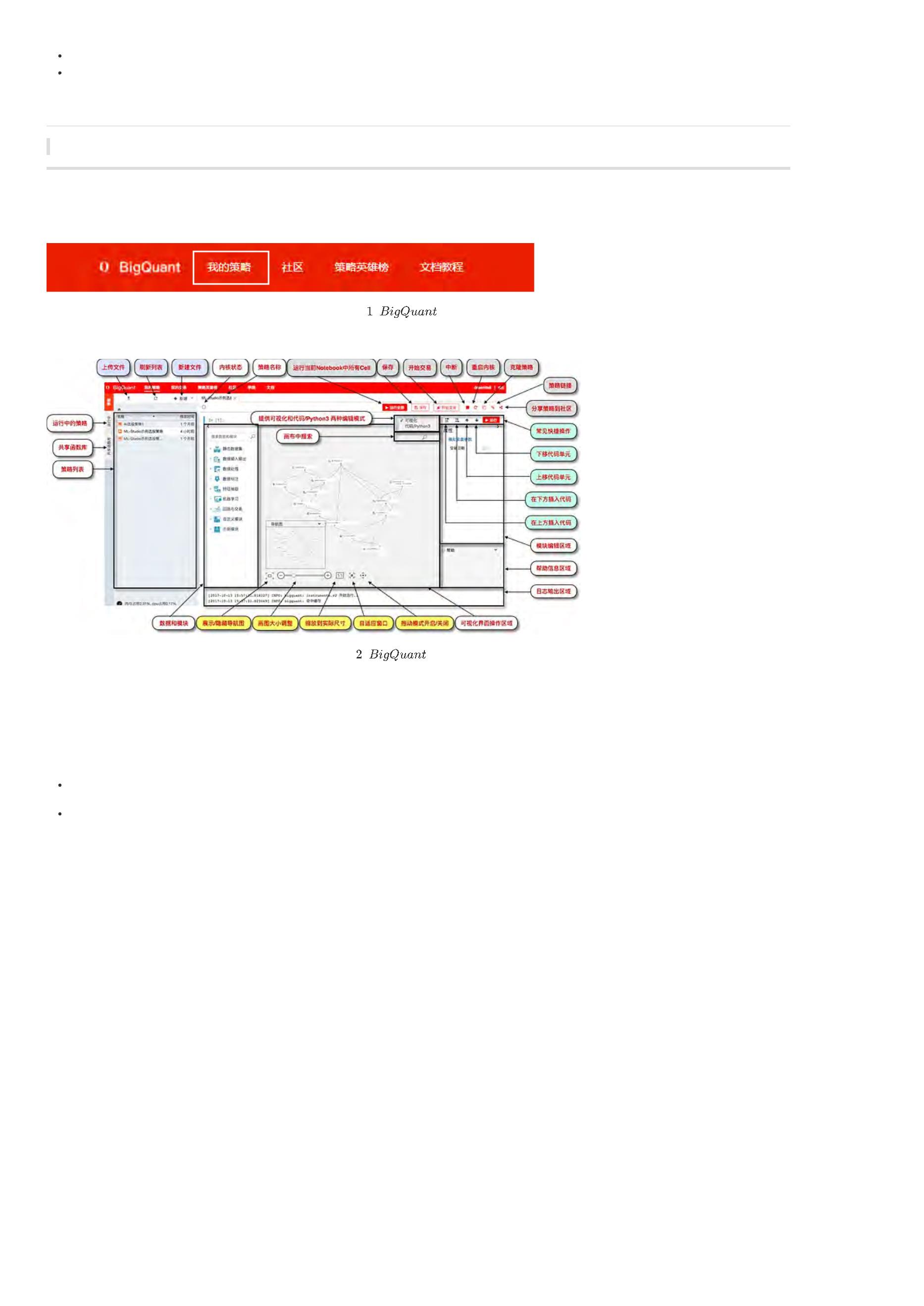
BigQuant策略平台有多强大,从图2中就可以知道。
图
策略平台简介
BigQuant 策略平台基于IPython Notebook,Notebook 是您进行量化研究、策略开发、文档编写的集成开发环境。
注意,Notebook 这个术语既可以指研究环境,也可以代表具体的 Notebook 文件。
BIgQuant策略平台采用 Docker 技术隔离,资源独立、安全性更高、性能更好。
每一个 Notebook 由多个 Cell 单元格组成,Cell 单元格可以有2种不同的运行模式。采用输入与输出混排的交互方式,让您的研究过程 所见即所得。
代码/Python3 模式:您可以在这个模式下进行数据获取、统计分析、金融建模、定价分析等量化研究工作。
文档/Markdown 模式:您可以以 Markdown 格式编写文档,进行研究或策略的相关说明。
支持哪些Python 库
在量化研究中,需要进行很多数据操作或者科学计算,这就需要借助各种类型的 第三方库。研究功能支持导入第三方库,您可以根据需要引入。BigQuant提
供了丰富的金融计算类库,包括数据获取、策略回测、金融计算等功能。除此之外,还借助 Python 的强大库体系,为您提供全方位的研究服务。
我们支持所有Python标准库,您可以通过import的方式进行引入, 图3中列出了一些常用的库:
图
策略平台支持的
库
您可以在Notebook中输入下方代码引入相关模块,比如引入 Pandas DataFrame 模块的方法:
from pandas import DataFrame
data = DataFrame()
如果您需要列表之外的 Python库,请发送邮件到 i@BigQuant.com 联系我们,为您进行扩展。
如何编写策略
策略算法具体描述了进行量化交易的信号生成条件和订单委托方法,是进行量化研究和量化交易的基础。
BigQuant提供了完整的策略框架,包括获取历史数据、订单委托、订单撮合等基础策略功能,方便您进行策略的编写。
关于BigQuant策略编写API,请查看 策略开发文档
您可以在 Notebook 中进行策略回测,对策略的历史表现进行细致的考察,相关的帮助您可以查看:
关于BigQuant回测框架的原理与机制,请查看 BigQuant回测机制。
如何编写文档(Markdown )
您可以在 Notebook 中创建文档类型的单元,该单元格支持使用 Markdown 语法进行文档写作。
您可以使用 Markdown 文档、LaTeX方程或者代码等丰富的形式自由编写文档内容。
Markdown 是一种轻量级的标记语言,由于它简单的语法、少量的标记符号,学习成本非常低,被越来越多的文档编写人员、写作爱好者所广泛使用。一单
掌握了它的语法规则,会有一劳永逸的效果。
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
上一页:聊一聊策略生成器
下一页:BigQuant AI策略详解
目录:BigQuant学院
BigQuant AI 策略详解
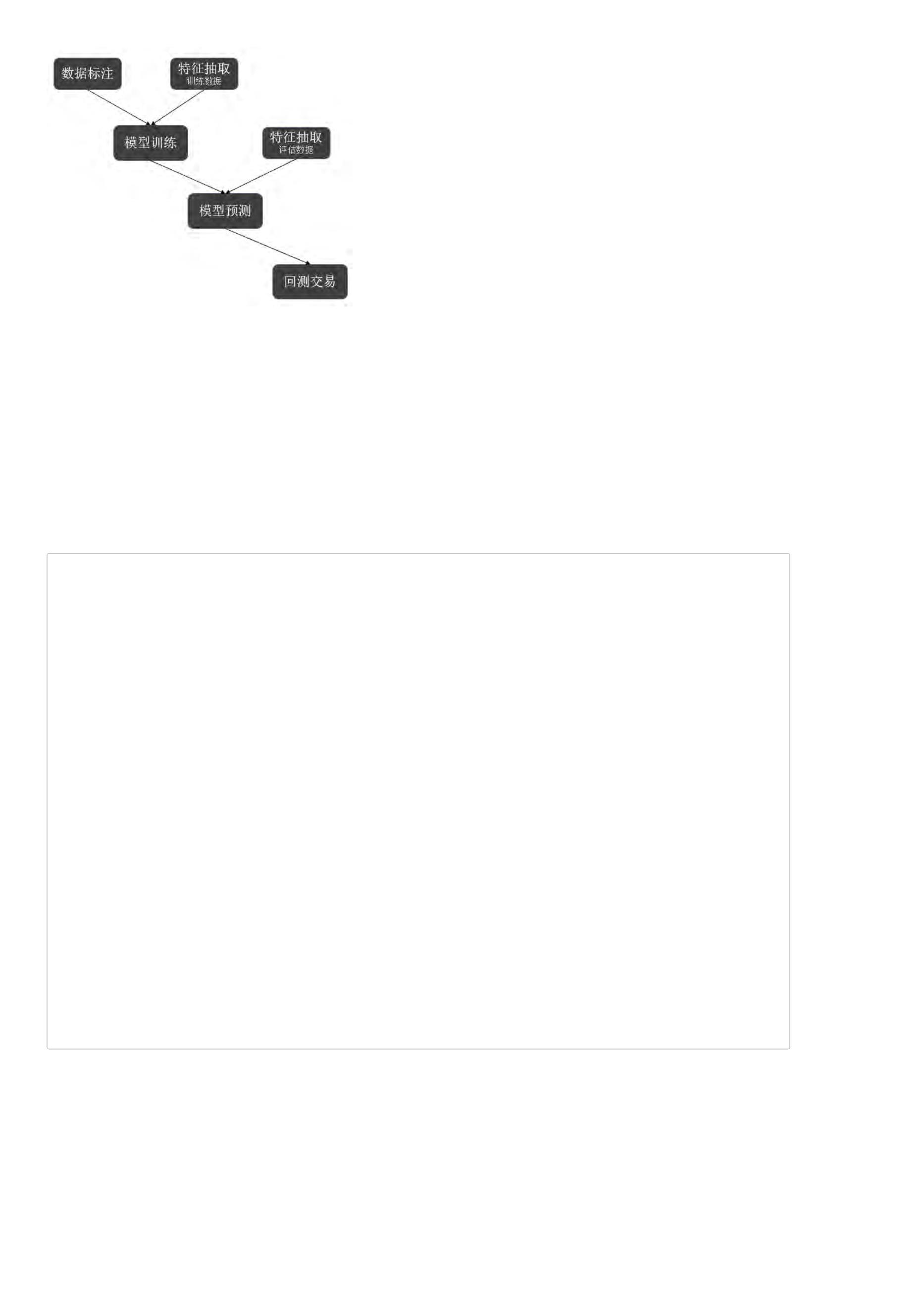
前面我们通过策略生成器,得到了一个AI策略,我们来详细解读一下生成的代码。
看看下面这个简单的AI策略抽象流程示意图,将帮助我们来理解AI策略代码。

基础配置
这些配置将在后续用到:
1
. start_date 和 end_date 确定了我们要用数据段
其中 [start_date, split_date) 区间的数据,用于模型训练
split_date, end_date] 区间的数据,用户模型回测
[
2
. instruments:股票池,D.instruments(start_date, split_date) 取A股给定时间段内所有出现过的股票。
. label_expr,用户标注的函数,更多说明见下面关于 M.advanced_auto_labeler的介绍。
. hold_days:持仓时间,用于数据标注和回测,具体见下面相关模块使用
. features:特征 (因子),具体见下面相关模块使用
3
4
5
class conf:
start_date = '2014-01-01'
end_date='2017-07-17'
split_date = '2015-01-01'
instruments = D.instruments(start_date, end_date)
hold_days = 5
features = [
'
'
'
'
'
'
'
'
'
'
'
'
'
close_5/close_0', # 5日收益
close_10/close_0', # 10日收益
close_20/close_0', # 20日收益
avg_amount_0/avg_amount_5', # 当日/5日平均交易额
avg_amount_5/avg_amount_20', # 5日/20日平均交易额
rank_avg_amount_0/rank_avg_amount_5', # 当日/5日平均交易额排名
rank_avg_amount_5/rank_avg_amount_10', # 5日/10日平均交易额排名
rank_return_0', # 当日收益
rank_return_5', # 5日收益
rank_return_10', # 10日收益
rank_return_0/rank_return_5', # 当日/5日收益排名
rank_return_5/rank_return_10', # 5日/10日收益排名
pe_ttm_0', # 市盈率TTM
]
#
数据标注标注
label_expr = [
#
'
#
'
#
'
#
'
]
计算未来一段时间(hold_days)的相对收益
shift(close, -5) / shift(open, -1) - shift(benchmark_close, -5) / shift(benchmark_open, -1)',
极值处理:用1%和99%分位的值做clip
clip(label, all_quantile(label, 0.01), all_quantile(label, 0.99))',
将分数映射到分类,这里使用20个分类,这里采取等宽离散化
all_wbins(label, 20)',
过滤掉一字涨停的情况 (设置label为NaN,在后续处理和训练中会忽略NaN的label)
where(shift(high, -1) == shift(low, -1), NaN, label)'
示例解读:
1
. shift(close, -5) / shift(open, -1) - shift(benchmark_close, -5) / shift(benchmark_open, -1):未来5天的相对收益率(股票收益率减去基准收益率),其中
shift(close,-5)为未来5天的收盘价,shift(open,-1)为明天的开盘价,基准同理。
. clip:clip用于极值处理,上面的例子就是将1%分位数和99%分位数以外的数据进行裁剪
. all_wbins:对连续性的标注数据进行离散化,上面的例子是将标注数据分为20类。详情请参考:表达式引擎
. where(shift(high, -1) == shift(low, -1), NaN, label):过滤掉一字涨停的情形
2
3
4
数据标注
之前采取的是M.fast_auto_labeler进行数据标注,但如果要使用表达式引擎构建因子、数据标注,建议使用功能更为强大的M.advanced_auto_labeler进行数
据标注。
#
给数据做标注:给每一行数据(样本)打分,一般分数越高表示越好
m1 = M.advanced_auto_labeler.v1(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.split_date,
label_expr=conf.label_expr, benchmark='000300.SHA', cast_label_int=True)
示例解读:
1
. label_expr:表示通过conf类中的标注语句进行数据标注
. benchmark:对数据进行标注的时候,偶尔会用到基准数据,因此需要制定基准
. cast_label_int:标注结果是否转换为整数;默认值是True
2
3
基础特征抽取
机器学习算法很大程度上依赖于特征工程,AI策略同样如此,特征抽取地好,对收益率的预测将更加准确。 有些因子的基础因子,直接可以抽取。
m2 = M.general_feature_extractor.v5(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.end_date,
features=conf.features)
详情请参考文档:基础特征抽取。
衍生特征抽取
很多AI策略的特征并不是简单的基础特征,而是由基础特征衍生计算出来的衍生特征。
#
计算衍生特征
m2_1 = M.derived_feature_extractor.v1(data=m2.data, features=conf.features)
详情请参考文档:衍生特征抽取。
数据转换
如果你采用的模型是StockRanker,该算法需要对输入的特征作相应转换。如果你使用的是随机森林、线性SGD模型等,这一步可以省略。
m3 = M.transform.v2(data=m2_1.data, transforms=None, drop_null=True)
当然,在之前我们的AI策略是采取的 M.fast_auto_labeler 进行数据标注,策略详解请点击展开。
点击查看代码
合并数据
通过数据标注和计算特征数据,我们获得了两个数据,只有同时包含这两部分数据的训练集才能完整地训练一个AI模型,因此需要进行数据合并。
#
合并标注和特征数据
m4 = M.join.v2(data1=m1.data, data2=m3.data, on=['date', 'instrument'], sort=True)
示例解读:
1
. 数据合并也成为数据连接,详情请参考 模块和API:数据连接。
. data1=m1.data 表示:第一个需要连接的数据,例如标注数据。
. data2=m3.data 表示:第二个需要连接的数据,例如计算完成的特征数据。
. on=[‘date’, ‘instrument’] 表示:数据合并时使用的主要列。一般使用日期和股票代码就可以对数据进行合并。
. sort=True 表示:是否对合并数据的结果按on指定的列进行排序。
2
3
4
5
模型训练
当我们将标注数据和经过数据预处理的特征数据合并以后,此时可以通过机器学习算法训练出一个AI模型。
#
StockRanker机器学习训练
m5=M.stock_ranker_train.v5(training_ds=m4.data, features=conf.features)
示例解读:
1
. 机器学习模型训练是必不可少的一步,训练时间依赖于数据量,如果是全市场股票多年数据,时间大概需要3-10分钟。详情请参考 模块和API概览:模
型训练。
. training_ds=m4.data 表示:训练模型时应以什么数据进行输入,输入的数据为上一步合并的数据。
. features=conf.features 表示:训练模型时以什么特征或因子参与模型进行训练。
. M.stock_ranker_train接口的其他参数一般采用默认值。
2
3
4
训练结果
通过上一步的训练模型,我们已经产生出了一个在训练集上表现不错的模型。我们可以这样查询训练结果:
print('模型ID:', m5.model_id)
print('模型因子得分:', m5.feature_gains)
print('模型可视化:', m5.plot_model())

示例解读:
1
. m5.model_id 表示:唯一的模型ID。
. m5.feature_gains 表示: 各个特征的得分情况,可以借此判断特征重要性程度。由于输出类型为DataSource,因此可以通过read_df方法查看——
m5.feature_gains.read_df()。
. m5.plot_model() 表示:可视化查看模型结果,这样就能打开AI算法的‘黑箱’,可以查看算法的每个细节。
2
3
模型预测
此时,我们已经产生出了一个在训练集上表现不错的模型。现在我们根据该模型来获取在测试集上的预测结果。
#
计算基础数据
n2 = M.general_feature_extractor.v5(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.end_date,
features=conf.features)
#
计算衍生特征
n2_1 = M.derived_feature_extractor.v1(data=n2.data, features=conf.features)
#
将特征数据转换机器学习算法能够接受的数据类型(只有StockRanker算法需要)
n3 = M.transform.v2(data=n2_1.data, transforms=None, drop_null=True)
#
进行预测
n4 = M.stock_ranker_predict.v5(model=m6.model, data=n3.data)
#
查看预测数据
prediction = n4.predictions.read_df()
示例解读:
1
. n1和n2和之前的特征抽取、特征转换完全一样,只是现在传入的时间是测试集的时间段。
. 机器学习算法通过模型和特征数据就可以进行预测,因此并不需要标注数据、合并数据。比如当你获得了一个回归模型后,此时传入新的自变量就可以
带入模型获得因变量。
. n3是模型预测,详情可参看 模块和API概览:模型预测
. model_id=context.options[‘model_id’] 表示:用哪个模型进行预测就传入哪个模型ID。
. data=n2.data 表示:在什么数据上进行预测就传入什么数据。一般为测试集的特征数据。
. n3.predictions.read_df() 表示:模型在测试集上的预测结果为n3.predictions,类型为DataSource,因此需要通过read_df方法查看。
2
3
4
5
6
策略回测
当我们获得测试集上的预测结果以后,我们就可以通过BigQuant回测机制进行策略回测,验证该策略是否有效。策略回测相关内容请参考 BigQuant回测机
制。
上一页:BigQuant策略平台使用帮助
下一页:适合小白的入门方式
目录:BigQuant学院
[
量化学堂-新手专区]适合小白的入门方式
导语:
BigQuant是一家人工智能量化平台,以下是BigQuant的正确打开方式:
1
.文档教程——2. 学院——3.干货贴——4.多交流,有问题随时提——5.实战
1
.文档教程
图
首页
图
文档教程
先过一遍,有一个整体的感觉,不用细究。文档教程好比一部字典,真正遇到什么需要查询的随用随查。
2
. 学院
学院主要包括:宽客学院、可视化、Python、策略开发、数学、机器学习、金融市场7块内容。目的是全方位介绍成为一名BigQuant上的宽客所具备的技
能。其中,宽客学院分为学前、小学、中学、大学四个阶段,帮助用户能够循序渐进成长起来。
图
学院
3
.干货贴
图
社区
从图4看出,社区里干货不少,这些帖子详细地介绍了策略思想、逻辑以及策略源码,最佳的方式就是点击 克隆策略将策略自动复制到个人私人研究平台
上,然后一行一行地弄明白每行代码的意义,不仅可以加深对平台的认识,而且多练习以后就可以自主开发策略,实现自己的策略想法。这种方式对新手而
言帮助最大。
4
.多交流,有问题随时提
提问
你可以直接在社区发帖提问,将你的问题描述出来,然后会有BigQuant平台工程师来回答你的问题,不仅如此,热情的宽友也会来解答你的问题。需要注意
的是:问题描述的越清楚,必要时贴上截图,问题越容易得到解答。
你也可以加入BigQuant的官方QQ群,直接在里面提问题,BigQuant的人和热心的群友会很快解答你的提问。
提需求
因为每个人可能会有各种需求,数据方面的、回测方面的、模拟交易方面的等等,BigQuant平台也是特别人性化,专门拟定了一个提需求的帖子,搬运过
5
.实战
这里的实战指根据一个机器学习算法或策略想法,不管是网上看到的还是自己构思的,将其转化成一个能够运行并输出回测曲线的一个完整策略,这是成为
BigQuant平台高手最重要的一步。
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
上一页:BigQuant AI策略详解
下一页:Python快速入门
目录:BigQuant学院
【
宽客学院】Python 快速入门
本课程帮助大家Python快速入门。
在学院页面,有一个栏目名叫Python,大家可以以次练手。
Python快速入门的学习资源如下:
上一页:适合小白的入门方式
下一页:做量化您需要知道的那些术语
目录:BigQuant学院
做量化你需要知道的那些术语!(持续更新)
本文介绍一些量化投资相关术语,帮助大家更好地了解该行业。
以下术语没有先后顺序,并将持续更新!
金融相关:
股票:股份公司发行的所有权凭证。
债券:承诺按一定利率支付利息并按约定条件偿还本金的债权债务凭证,风险较低。
固定收益:固定收益类投资指投资于银行定期存款、协议存款、国债、金融债、企业债、可转换债券、债券型基金等固定收益类资产。风险低。
利率互换:利率互换是指两笔货币相同、债务额相同(本金相同)、期限相同的资金,但交易双方分别以固定利率和浮动利率借款,为了降低资金成本和利率风险,双方做固定利率
外汇交易:外汇交易是以一种外币兑换另一种外币。报价即为汇率,通常用两种货币之间的兑换比例来表示,例如:USD/JPY、GBP/JPY。汇率是第一种货币(作为基础货币)以第二
黄金:贵金属,可用于储备和投资的特殊通货。
美元指数:综合反映美元在国际外汇市场的汇率情况的指标,用来衡量美元对一揽子货币的汇率变化程度。
基金: 从广义上说,基金是指为了某种目的而设立的具有一定数量的资金。主要包括信托投资基金、公积金、保险基金、退休基金,各种基金会的基金。
货币基金:投资于货币市场上短期有价证券的一种基金。风险较小。
封闭式基金:基金规模在发行前已确定、在发行完毕后的规定期限内固定不变并在证券市场上交易的投资基金。
开放式基金:开放式基金,是指基金规模不是固定不变的,而是可以随时根据市场供求情况发行新份额或被投资人赎回的投资基金。
期货:约定在未来某个时间以某个价格进行成交的合约。
期权:是一种衍生性金融工具,比如未来某个时间以某个价格交易的权利,这个选择权就是期权。
策略相关
Alpha:alpha一词主要来自于资本资产定价模型,模型中alpha表示来自于股票自身的收益。alpha策略表示通过股指期货对冲市场风险获取阿尔法收益的对冲策略。
Beta: 评估证券系统性风险的工具,用以度量一种证券或一个投资证券组合相对总体市场的波动性。
多因子选股: 应用最广泛的一种选股模型,基本原理是采用一系列与收益率相关的因子作为选股标准,满足这些因子的股票则被买入,不满足的则卖出。
价值投资:一种常见的投资方式。其重点是通过基本分析中的概念,例如高股息收益率、低市盈率和低股价/帐面比率,去寻找并投资股价被低估的股票。
日内策略:交易频率很高,持仓时间很短的交易,持仓不过夜。
高频交易:从那些人们无法利用的极为短暂的市场变化中寻求获利的交易,比如一分钟成交上千笔,持仓时间几秒钟。
算法交易:算法交易本质上不算一类策略,其目的更多是降低交易成本、提高执行效率、减少人力成本。常见的算法有:交易量加权平均价格算法(VWAP)和时间加权平均价格算法
程序化交易:程序化交易是指通过既定程序或特定软件,自动生成或执行交易指令的交易行为。
趋势跟踪:跟随市场价格变动的交易策略,最为常见的策略之一。

事件驱动: 包括企业分拆、企业收购、企业合并、破产重组、财务重组、资产重组以及股票回购等在内的事件可能会对股票价格有重大影响,事件驱动就是挖掘这类事件带来收益
行业轮动:利用市场趋势获利的一种主动交易策略,其本质是利用不同投资品种强势时间的错位对行业品种进行切换以达到投资收益最大化的目的。
套利:对相关性强的品种一买一卖,赚取差价。
统计套利:将套利建立对历史数据进行统计分析的基础之上,估计相关变量的概率分布,并结合基本面数据进行分析以用以指导套利交易。
协整:变量之间长期稳定的均衡关系的统计表示。
跨期套利:在同一期货品种的不同月份合约上建立数量相等、方向相反的交易头寸,最后以对冲或交割方式结束交易、获得收益的方式。
蝶式套利:套利的套利,利用不同交割月份的价差进行套期获利,由两个方向相反、共享居中交割月份合约的跨期套利组成。它是一种期权策略,风险有限,盈利有限,是由一手牛
跨产品套利:又称跨商品套利。根据套利商品之间的关系,跨品种套利可分为相关商品套利和产业链跨品种套利两种类型。
产业链套利:一般属于夸品种套利,在一个产业链条上对上游产品和下游产品进行一买一卖的操作,以期获得差价收益。
回归套利:套利的逻辑是坚信价差要回归。
对冲:一般对冲是同时进行两笔行情相关、方向相反、数量相当、盈亏相抵的交易。和跨品种套利思想一致。
市场相关
宽客:量化交易者的一个统称。
CTA基金:商品基金,该基金主要投资于商品期货,CTA是Commodity Trading Advisor的简称。
打新:就是用资金参与新股申购,如果中签的话,就买到了即将上市的股票。网下的只有机构能申购,网上的申购本人就可以申购。打新分为打新股票和打新基金。
沪深300: 全市场中具有代表性的300只股票。其指数能够反映市场走势,常用来作为各种策略的基准。
上证50:指数是根据科学客观的方法,挑选上海证券市场规模大、流动性好的最具代表性的50 只股票组成样本股,以便综合反映上海证券市场最具市场影响力的一批龙头企业的整体
创业板: 专为暂时无法在主板上市的创业型企业、中小企业和高科技产业企业等需要进行融资和发展的企业提供融资途径和成长空间的证券交易市场,是对主板市场的重要补充。在
漂亮50:原意指美国股票投资史上特定阶段出现的一个非正式术语,用来指上世纪六十和七十年代在纽约证券交易所交易的50只备受追捧的大盘股。现在更多的是指在2017年中国受
公募基金:是受政府主管部门监管的,向不特定投资者公开发行受益凭证的证券投资基金,这些基金在法律的严格监管下,有着信息披露,利润分配,运行限制等行业规范。
私募基金:一种非公开宣传的,私下向特定投资人募集资金进行的一种集合投资。
国债逆回购:个人通过国债回购市场把自己的资金借出去,获得固定的利息收益;而回购方(借款人)用自己的国债作为抵押获得这笔借款,到期后还本付息。本质上是一种短期贷

股指期货:以股价指数为标的物的标准化期货合约,交割方式为金额交割。
商品期货:标的物为实物商品的期货合约,交割方式为实物交割。
保证金:在期货市场和期权市场,交易时并不需要全部金额,只需部分金额就行,这部分金额就成为保证金。
权证:一种以约定的价格和时间(或在权证协议里列明的一系列期间内分别以相应价格)购买或者出售标的资产的期权。
杠杆比率:在期货交易中,实行的是保证金交易,交易金额和保证金的比值就称为杠杆比率。
爆仓:爆仓就是亏损大于你的账户中的保证金。
升贴水:期货市场价格和现货市场价格不一致导致升贴水存在。期货价格高于现货价格称为升水,期货价格小于现货价格称为贴水。
ETF:交易型开放式指数基金,是一种在交易所上市交易的、基金份额可变的一种开放式基金。
FOF:基金的基金(Fund Of Fund)。一种专门投资于其他投资基金的基金。FoF并不直接投资股票或债券,其投资范围仅限于其他基金。
MOM:管理人的管理人(Manager Of Manager)。是指该基金的基金经理不直接管理基金投资,而是将基金资产委托给其他的一些基金经理来进行管理。
分级基金:又叫“结构型基金”,是指在一个投资组合下,通过对基金收益或净资产的分解,形成两级(或多级)风险收益表现有一定差异化基金份额的基金品种。
量化相关
选股:选出好的股票。
择时:确定交易买卖时机。
仓位管理:在整个交易过程中,持仓比率的管理。
止盈:也称停利、止赚 ,即在目标价位挂单出货。
止损:在能够承受的风险损失的价位挂单出货。
凯利法则:用来决定每次下单手数的一种技术,属于资金管理。
风险平价理论:通过调整各类资产的权重以实现组合中各类资产的风险贡献基本均衡。
行业中性:构建投资组合,使得组合在各个行业上的暴露程度与基准指数 在各个行业上的暴露相等。
风格中性:构建投资组合,使得组合在各个风格因子上的暴露程度与基准指数在各个因子上的暴露相等。
CAPM模型:资本资产定价模型,研究的重点在于探求风险资产收益与风险的数量关系:即为了补偿某一特定程度的风险,投资者应该获得多少的报酬率。
Black-Scholes期权定价模型:由布莱克与斯科尔斯在20世纪70年代提出,为期权定价提供了理论基础。

MM理论:该理论由莫迪格利安尼(Modigliani)和默顿·米勒(Miller)提出。核心思想:公司价值与公司资本结构无关。
动量:认为股票价格走势强者越强、弱者越弱。
反转:股价朝原来趋势的相反方向移动分为向上反转和向下反转,股价由多头行情转为空头行情,或由空头行情转为多头行情。
参数调优:对策略中含有的参数进行优化。
过度拟合:模型对历史数据拟合地非常好,但是实际预测准确性很低,泛化能力不强。
未来函数:在当下的时间点运用了未来的信息。
幸存者偏差:另译为“生存者偏差”、“存活者偏差”,、“沉默的数据”等等,是指只能看到经过某种筛选而产生的结果,而没有意识到筛选的过程,因此忽略了被筛选掉的关键信息。
偷价漏价: 偷价是指以一个不切实际的价格去进行成交,往往会高估策略的收益。
夏普比率:表明投资组合每承受一单位总风险,会产生多少的超额报酬。它是市场上最常见的衡量比率:若为正值,代表基金报酬率高过波动风险;若为负值,代表基金操作风险大
最大回撤:在选定周期内任一历史时点往后推,产品净值走到最低点时的收益率回撤幅度的最大值。最大回撤用来描述买入产品后可能出现的最糟糕的情况。
年化收益:将收益折算为以年为单位的收益率。
数据挖掘:从大量的数据中通过算法搜索隐藏于其中信息的过程。
机器学习:从历史数据中发掘规律,并对未来数据进行预测的学习算法,属于人工智能一个子领域。
深度学习: 深度学习是机器学习的一个子集,包含多层感知器就是一种深度学习结构。
技术分析:以股票价格成交量为基础,计算出各种指标来指导交易的分析方法称为技术分析。
道氏理论: 它是根据价格模式的研究,推测未来价格行为的一种方法。由查尔斯·道创立。
海龟法则:一种经典的趋势跟踪策略。
指标相关
市盈率:也称“本益比”、“股价收益比率”或“市价盈利比率”,是最常用来评估股价水平是否合理的指标之一,由股价除以年度每股盈余(EPS)得出,市盈率常用来作为一个有效因子
流通市值:在某特定时间内当时可交易的流通股股数乘以当时股价得出的流通股票总价值。
每股收益:即每股盈利(EPS),又称每股税后利润、每股盈余,指税后利润与股本总数的比率。
ROE:净资产收益率。指标值越高,说明投资带来的收益越高。该指标体现了自有资本获得净收益的能力。
ROA: 总资产收益率,是用来衡量每单位资产创造多少净利润的指标。衡量的是每一美元资产所带来的利润。

市净率:每股市价与每股净资产之比,每股净资产为普通股股东权益与流通在外普通股股数之比。市净率反映普通股股东愿意为每1元净资产支付的价格。
市销率:每股市价与每股销售收入之比,每股销售收入为销售收入与流通在外普通股加权平均股数之比。市销率反映普通股股东愿意为每1元销售收入支付的价格。
布林带:根据统计学中的标准差原理设计出来的一种非常实用的技术指标。它由三条轨道线组成,其中上下两条线分别可以看成是价格的压力线和支撑线,在两条线之间是一条价格平
金叉:短期均线上穿长期均线,预示上涨。
死叉:短期均线下穿长期均线,预示下跌。
MA:以道·琼斯的“平均成本概念”为理论基础,采用统计学中“移动平均”的原理,将一段时期内的股票价格平均值连成曲线,用来显示股价的历史波动情况,进而反映股价指数未来发
RSI:相对强弱指数, 根据一定时期内上涨点数和涨跌点数之和的比率制作出的一种技术指标。
MACD:指数平滑移动平均线,是从双指数移动平均线发展而来的,由快的指数移动平均线(EMA12)减去慢的指数移动平均线(EMA26)得到快线DIF,再用2×(快线DIF-DIF的9日加
KDJ:又称随机指标,利用价格波动的真实波幅来反映价格走势的强弱和超买超卖现象,在价格尚未上升或下降之前发出买卖信号的一种技术工具。
威廉指标:表示当天的收盘价在过去一段日子的全部价格范围内所处的相对位置,是一种兼具超买超卖和强弱分界的指标。主要的作用在于辅助其他指标确认讯号。
交易相关
主力合约 :成交量最大的合约。因为它是市场上最活跃的合约,所有投机者基本上都在参与这个合约。也有说法是主力合约是持仓量最大的合约,通常来讲,持仓量最大的合约也是
连续合约:将主力合约拼接起来就成为连续合约。
合约单位:合约单位是指一张期权合约对应的标的资产(证券、股票或 ETF)数量,即买卖双方在约定的时间以约定的价格买入或卖出标的资产的数量。
夜盘交易:很多商品期货在晚上交易。
集合竞价:开盘之前的竞价属于集合竞价。按照价格优先和时间优先的原则计算出最大成交量的价格,这个价格就会是集合竞价的成交价格。
连续竞价:盘中的交易采取连续竞价。
撮合机制:指在投资者的委托指令传递到交易所后,交易所系统处理委托指令过程中的“逻辑程序”,包括不同交易时间的竞价原则、委托成交的优先顺序原则以及成交价的决定方法
股票T+1:T+1是一种股票交易制度,即当日买进的股票,要到下一个交易日才能卖出。
融券: 也称为出借证券,证券公司将自有股票或客户投资账户中的股票借给做空投资者。投资者借证券来出售,到期返还相同种类和数量的证券并支付利息,属于一种做空类型。
停牌:停牌是指股票由交易所暂停其在股票市场上进行交易。复牌之后才能在交易所挂牌交易。
涨跌停: 证券市场中为了防止交易价格的暴涨暴跌,抑制过度投机现象,对每只证券当天价格的涨跌幅度予以适当限制的一种交易制度,股票涨跌停幅度一般为10%。

熔断:熔断机制,也叫自动停盘机制,是指当股指波幅达到规定的熔断点时,交易所为控制风险采取的暂停交易措施。
乌龙指:指股票交易员、操盘手、股民等在交易的时候,不小心敲错了价格、数量、买卖方向等事件的统称。
自成交:以自己为交易对象,大量或者多次进行自买自卖。
ST股:被特别处理的股票,涨跌幅调整为5%。带ST帽子的股票风险较高。
大宗交易:又称为大宗买卖,是指达到规定的最低限额的证券单笔买卖申报,买卖双方经过协议达成一致并经交易所确定成交的证券交易。
K线:又称“蜡烛线”,起源于日本。K线记录的是某股票一天的价格变动情况,由实体、上影线、下影线等三部分组成,包含四个信息:开盘价,收盘价,全天最高价,全天最低价。
tick:参考:tick数据在技术上是什么东西?
level2:Level-2产品目前是由上海证券交易所最新推出的实时行情信息收费服务,主要提供在上海证券交易所上市交易的证券产品的实时交易数据,包括十档买卖盘,买一卖一委
前复权:在K线图上以除权后的价格为基准来测算除权前股票的市场成本价。
后复权:在K线图上以除权前的价格为基准来测算除权后股票的市场成本价。
成份指数:成份指数是通过科学客观的方法挑选出最具代表性的样本股票,建立一个反映整个证券市场的概貌和运行状况、能够作为投资评价尺度及金融衍生产品基础的基准指数。
换手率:也称“周转率”,指在一定时间内市场中股票转手买卖的频率,是反映股票流通性强弱的指标之一。
VWAP:成交量加权平均价,是将多笔交易的价格按各自的成交量加权而算出的平均价,若是计算某一证券在某交易日的VWAP,将当日成交总值除以总成交量即可。
TWAP:该算法的目标在于计算您的订单在提交之时至获得执行之间的时间加权平均价格。
其他
一价定律:即绝对购买力平价理论。是不同地区产品套利的基础。
文艺复兴科技:文艺复兴科技公司成立于1988年,创始人詹姆斯·西蒙斯。该公司旗舰产品——大奖章基金取得年化36%的回报,是最成功和著名的对冲基金之一。2005年,西蒙斯成立
长期资产管理公司:成立于1994年2月。LTCM掌门人是梅里韦瑟(Meriwehter),被誉为能"点石成金"的华尔街债务套利之父。成员有: 诺贝尔经济学奖得主默顿(Robert Merton
桥水对冲基金:成立于1975年,总部位于美国康奈迪克州,目前为世界前三对冲基金。
世坤基金:成立于2007年,创始人Igor Tulchinsky。该基金主要依靠数据挖掘进行投资。该公司在新兴市场(尤其是亚太的中国和印度)大量招募基层Quant、Data Scientist或
AQR基金:成立于1998年,由阿斯内斯与合伙人共同创办的一家量化对冲基金,主要通过算法和计算机模型来寻找市场暂时的无效性并从中获利,从名字可以看出基金的宗旨是金融应
巴林银行破产事件:英国老牌贵族银行因为一个交易员而走向破产的事件。

伊士顿股指盈利:在2015年,俄罗斯伊世顿公司通过高频程序化交易软件自动批量下单、快速下单,利用保证金杠杆比例等交易规则,以较小的资金投入反复开仓、平仓,使盈利在
上一页:Python快速入门
下一页:BigQuant数据API详解
目录:BigQuant学院
[
量化学堂-新手专区]BigQuant 数据API详解
导语:数据是开发策略的原料,知道怎么获取数据方能更为高效地开发策略!
数据为什么重要?
BigQuant是一个人工智能量化投资平台,类似于一个实验室,用户可以在实验室里发挥自己的聪明才智开发策略。计算机界有一个很有名的说法,叫
(Garbage In Garbage Out),翻译过来就是“垃圾进、垃圾出”。因此真实准确而全面的金融数据是开发优秀策略的重要前提。
BigQuant 有什么数据?
BigQuant有丰富并且高质量的金融数据,包括基础数据、历史数据、财报数据、特色因子数据等。详细可以参考 文档教程的 数据 部分
如何获取数据?
数据API是调用数据的接口,目的是快速、便捷、高效地获取数据。在BigQuant的策略平台上,通过数据API我们可以将服务器上的数据拉取到自己的策略平
台上,有了数据,相当于拿到“原料”,就可以自由发挥“厨艺”啦。
数据API举例
BigQuant数据API在设计之初就秉持对用户友好的理念,附件将详细介绍常用的数据API,欢迎大家 克隆研究 。
本文由BigQuant宽客大学推出,版权归BigQuant所有,转载请注明出处。
附件:BigQuant数据API举例
获取基础数据¶
获取指数数据——以沪深300举例
In [1]:
data = D.history_data(instruments=['000300.SHA'], start_date='2017-01-01', end_date='2017-04-07',
fields=['open', 'high', 'low', 'close', 'volume', 'amount'])
data.head() # 查看前6行数据
Out[1]:
date
instrument
open
high
low
close
volume
amount
2
017-
0
1
2
3
4
000300.SHA
3313.953369
3345.262939
3313.953369
3342.227295
8656789600
8.761277e+10
01-03
2
0
017-
1-04
000300.SHA
000300.SHA
000300.SHA
000300.SHA
3340.557617
3368.340088
3366.852295
3345.748291
3369.565918
3373.411865
3368.870605
3366.221924
3338.152588
3361.461914
3346.891357
3344.347168
3368.311768
3367.789307
3347.666504
3363.901367
9005082700
8833635700
8745911400
8370794200
9.801436e+10
9.118934e+10
9.107226e+10
8.791612e+10
2
0
017-
1-05
2
0
017-
1-06
2
0
017-
1-09
获取交易日历——获取一段日期内的交易日历
In [2]:
date = D.trading_days(start_date='2016-01-01', end_date='2016-12-01')
date[:10] # 只打印前10个
Out[2]:
date

date
6125
6126
6127
6128
6129
6130
6131
6132
6133
6134
2016-01-04
2016-01-05
2016-01-06
2016-01-07
2016-01-08
2016-01-11
2016-01-12
2016-01-13
2016-01-14
2016-01-15
获取股票代码——获取一段时间内上市股票的代码列表
In [3]:
symbols = D.instruments(start_date='2015-01-01', end_date='2016-01-01')
symbols[:10] # 只看前10个
Out[3]:
[
'000001.SZA',
'
'
'
'
'
'
'
'
'
000002.SZA',
000004.SZA',
000005.SZA',
000006.SZA',
000007.SZA',
000008.SZA',
000009.SZA',
000010.SZA',
000011.SZA']
获取历史数据——以贵州茅台举例¶
获取贵州茅台代码、证券名称、上市日期、上市板、公司名称、公司成立日期、公司省份
In [4]:
D.history_data('600519.SHA', start_date='2016-01-01', end_date='2016-01-10', fields=['name','list_date','list_board','company_name','
Out[4]:
date
instrument
name
list_date
list_board
company_name
company_found_date
1999-11-20
company_province
2016-
贵州
茅台
2001-08-
27
贵州茅台酒股份
有限公司
0
1
2
3
4
600519.SHA
主板
贵州省
01-04
2
0
016-
1-05
贵州
茅台
2001-08-
27
贵州茅台酒股份
有限公司
600519.SHA
600519.SHA
600519.SHA
600519.SHA
主板
主板
主板
主板
1999-11-20
1999-11-20
1999-11-20
1999-11-20
贵州省
贵州省
贵州省
贵州省
2
0
016-
1-06
贵州
茅台
2001-08-
27
贵州茅台酒股份
有限公司
2
0
016-
1-07
贵州
茅台
2001-08-
27
贵州茅台酒股份
有限公司
2
0
016-
1-08
贵州
茅台
2001-08-
27
贵州茅台酒股份
有限公司
获取贵州茅台交易行情数据,包括开盘价、最低价、最高价、收盘价、复权因子、成交量、换手率
In [5]:
D.history_data('600519.SHA', start_date='2016-01-01', end_date='2016-01-10', fields=['open','low','high','close','adjust_factor','vol
Out[5]:

date
instrument
open
low
high
close
adjust_factor
6.856917
volume
turn
2016-
0
1
2
3
4
600519.SHA
1494.807861
1439.884033
1494.807861
1440.089722
1734968
0.13811
01-04
2
0
016-
1-05
600519.SHA
600519.SHA
600519.SHA
600519.SHA
1439.952515
1459.014771
1433.027100
1399.976685
1422.878906
1435.152710
1371.589111
1371.383423
1467.174561
1465.048828
1433.027100
1426.238770
1459.289062
1454.900635
1386.674316
1403.130981
6.856917
6.856917
6.856917
6.856917
3190891
2376090
814868
0.2540
2
0
016-
1-06
0.18914
0.06486
0.35432
2
0
016-
1-07
2
0
016-
1-08
4451009
获取贵州茅台交易状态数据,比如是否停牌,停牌类型,停牌原因,ST状态,股价在收盘时的涨跌停状态
In [6]:
D.history_data('600519.SHA', start_date='2016-01-01', end_date='2016-01-10', fields=['suspended','suspend_type','suspend_reason','st_
Out[6]:
date
instrument
st_status
price_limit_status
suspended
False
suspend_type
suspend_reason
0
1
2
3
4
2016-01-04
2016-01-05
2016-01-06
2016-01-07
2016-01-08
600519.SHA
600519.SHA
600519.SHA
600519.SHA
600519.SHA
0
0
0
0
0
2
2
2
2
2
False
False
False
False
获取贵州茅台估值数据,总市值、流通市值、市盈率、市销率.
注:ttm是trailing twelve month的简称,表示过去12个月,pe_ttm表示过去12个月以来的市盈率.
In [7]:
D.history_data('600519.SHA', start_date='2016-01-01', end_date='2016-01-10', fields=['market_cap','market_cap_float','pe_ttm','ps_ttm
Out[7]:
date
instrument
market_cap
market_cap_float
2.638267e+11
2.673440e+11
2.665401e+11
2.540409e+11
2.570558e+11
pe_ttm
ps_ttm
0
1
2
3
4
2016-01-04
2016-01-05
2016-01-06
2016-01-07
2016-01-08
600519.SHA
600519.SHA
600519.SHA
600519.SHA
600519.SHA
2.638267e+11
2.673440e+11
2.665401e+11
2.540409e+11
2.570558e+11
16.405994
16.624722
16.574726
15.797469
15.984948
7.993675
8.100246
8.075888
7.697176
7.788523
获取财报数据——以贵州茅台举例¶
获取财报发布时间信息数据,比如发布日期、财报类型、财报对应的年份、财报对应的季度
注:财报类型如果为20131231表示13年年报,20140331表示14年一季报
In [8]:
D.financial_statements('600519.SHA', start_date='2014-01-01', end_date='2016-01-01', fields=['fs_publish_date','fs_quarter','fs_quart
Out[8]:
fs_publish_date
2014-03-25
2014-04-25
2014-08-29
fs_quarter
20131231
20140331
20140630
fs_quarter_year
2013
fs_quarter_index
0
1
2
4
1
2
2014
2014

fs_publish_date
2014-10-30
2015-04-21
2015-04-21
2015-08-28
2015-10-23
fs_quarter
20140930
20141231
20150331
20150630
20150930
fs_quarter_year
2014
fs_quarter_index
3
4
5
6
7
3
4
1
2
3
2014
2015
2015
2015
获取贵州茅台财报类型、净资产收益率 (TTM)、总资产报酬率 (TTM)、销售净利率 (TTM)、销售毛利率 (TTM)
In [9]:
D.financial_statements('600519.SHA', start_date='2014-01-01', end_date='2016-01-01', fields=['fs_quarter','fs_roe_ttm','fs_roa_ttm','
Out[9]:
fs_quarter
20131231
20140331
20140630
20140930
20141231
20150331
20150630
20150930
fs_roe_ttm
35.513500
32.930901
33.391201
30.282301
28.728600
27.715099
26.112600
26.869900
fs_roa_ttm
37.874298
37.993698
38.548801
35.400101
33.030701
32.959099
31.407101
29.377600
fs_net_profit_margin_ttm
51.629902
fs_gross_profit_margin_ttm
92.904900
0
1
2
3
4
5
6
7
51.735401
92.886803
51.448601
92.772400
51.062599
92.358200
51.527901
92.593399
51.868999
92.618500
51.374100
92.380203
51.570301
92.448601
获取特色因子数据——以贵州茅台举例¶
获取量价因子
注:$open\_\$i$中的$\$$符号表示该因子可以回溯,没有$\$$符号表示该因子不能回溯。比如$open\_\$i$中指明了$i$取值范围是[0 .. 20],$i$为0表示当天
的因子值,$i=1$表示前1天的因子值,以此类推。
In [10]:
D.features('600519.SHA', start_date='2015-01-01', end_date='2015-01-12', fields=['close_0', 'close_1','volume_0','volume_2'])
Out[10]:
date
instrument
close_0
close_1
volume_0
9451517
5502001
5479784
4052530
5398220
4991459
volume_2
5617110.0
4626936.0
9451517.0
5502001.0
5479784.0
4052530.0
0
1
2
3
4
5
2015-01-05
2015-01-06
2015-01-07
2015-01-08
2015-01-09
2015-01-12
600519.SHA
600519.SHA
600519.SHA
600519.SHA
600519.SHA
600519.SHA
1240.462891
1211.736084
1181.784180
1174.556519
1165.675049
1141.909424
1161.448608
1240.462891
1211.736084
1181.784180
1174.556519
1165.675049
获取排名因子,以收益率和平均交易额为例
注:涉及到排名的因子,将该因子在全市场所有股票进行升序排序,排名因子=从小到大排名序号/总数
In [11]:
D.features('600519.SHA', start_date='2015-01-01', end_date='2015-01-12', fields=['return_5', 'rank_return_5','avg_amount_5','rank_avg
Out[11]:
date
instrument
return_5
1.106304
1.064575
avg_amount_5
1.178067e+09
1.226070e+09
rank_return_5
0.889652
rank_avg_amount_5
0.957492
0
1
2015-01-05
2015-01-06
600519.SHA
600519.SHA
0.846220
0.955756

date
instrument
return_5
1.028629
1.045128
1.018572
0.983177
avg_amount_5
1.271168e+09
1.121106e+09
1.120563e+09
1.131073e+09
rank_return_5
0.722246
0.744854
0.421165
rank_avg_amount_5
0.955889
2
3
4
5
2015-01-07
2015-01-08
2015-01-09
2015-01-12
600519.SHA
600519.SHA
600519.SHA
600519.SHA
0.952463
0.952116
0.397002
0.951178
获取财报特色因子,以赢利因子为例
注:财报特色因子后缀为$\_0$,表明该因子不取回溯值,直接使用当期值进行实验
In [12]:
D.features('600519.SHA', start_date='2015-01-01', end_date='2015-01-12', fields=['fs_roe_ttm_0', 'rank_fs_roe_ttm_0'])
Out[12]:
date
instrument
fs_roe_ttm_0
30.282301
30.282301
30.282301
30.282301
30.282301
30.282301
rank_fs_roe_ttm_0
0.985127
0
1
2
3
4
5
2015-01-05
2015-01-06
2015-01-07
2015-01-08
2015-01-09
2015-01-12
600519.SHA
600519.SHA
600519.SHA
600519.SHA
600519.SHA
600519.SHA
0.985120
0.985153
0.986008
0.986002
0.985977
获取技术因子,以移动平均值为例
In [13]:
D.features('600519.SHA', start_date='2015-01-01', end_date='2015-01-12', fields=['ta_sma_5_0', 'ta_sma_20_0'])
Out[13]:
date
instrument
ta_sma_5_0
1163.812988
1176.381714
1187.970459
1193.997681
1194.842896
1175.132202
ta_sma_20_0
1116.284912
1124.526367
1130.642334
1136.430542
1139.612549
1142.840454
0
1
2
3
4
5
2015-01-05
2015-01-06
2015-01-07
2015-01-08
2015-01-09
2015-01-12
600519.SHA
600519.SHA
600519.SHA
600519.SHA
600519.SHA
600519.SHA
上一页:做量化您需要知道的那些术语
下一页:BigQuant模块介绍
目录:BigQuant学院
null
【
宽客学院】如何选出符合一定条件的股票
在开发股票量化策略的时候,其中非常重要的一步就是选股。因此本文的目的是希望大家阅读以后,能够更为快速、高效、便捷地在BigQuant平台上
选出符合一定条件的股票。
符合一定条件的股票可以这样理解,这类股票具有同样的特征、属性,比如属于同一个板块,或者相似的财务指标,或者是存在相似的图表形态。
那么,怎样快速地选出符合一定条件的股票呢。主要因素为下面两点:
BigQuant数据以及数据API的了解
Pandas数据分析技巧
扩展阅读
1
2

3
4
完整代码如下:
参数
In [58]:
start_date = '2016-01-01'
end_date = '2017-09-14'
instrument = D.instruments(start_date=start_date, end_date=end_date)
1
.基本信息层面¶
获取指数成分股列表
In [59]:
#
沪深300指数成分
df = D.history_data(instrument, start_date, end_date, ['in_csi300'])
instruments = list(set(df[df['in_csi300']==1]['instrument']))
print('沪深300指数成分股预览10只股票:', instruments[:10])
沪深300指数成分股预览10只股票: ['601607.SHA', '600153.SHA', '600048.SHA', '002299.SZA', '601288.SHA', '000831.SZA', '600703.SHA', '6003
获取某个行业股票列表
In [60]:
#
(举例)获取国防军工行业股票列表
df = D.history_data(instrument, start_date, end_date, ['industry_sw_level1'])
instruments = list(set(df[df['industry_sw_level1'] == 650000]['instrument']))
D.history_data(instruments, '2017-07-27', '2017-07-27', ['company_name']).head()
Out[60]:
instrument
company_name
date
441666
441690
441833
441849
442030
000519.SZA
000547.SZA
000738.SZA
000768.SZA
002013.SZA
中兵红箭股份有限公司
2017-07-27
2017-07-27
2017-07-27
2017-07-27
2017-07-27
航天工业发展股份有限公司
中国航发动力控制股份有限公司
中航飞机股份有限公司
中航工业机电系统股份有限公司
获取某个概念、板块的股票列表
In [61]:
df = D.history_data(instrument, '2017-08-23', '2017-08-23', ['concept']).dropna()
# 'concept' 是股票的概念字段
df['is_ai'] = df['concept'].map(lambda x: '人工智能' in x) # 以人工智能为例,找到相关概念股票
st = list(df[df['is_ai'] == True]['instrument'])
D.history_data(st,'2017-08-23','2017-08-23',['name', 'concept']).head()
Out[61]:
instrument
name
date
concept
0
1
2
3
4
000977.SZA
002049.SZA
002073.SZA
002184.SZA
002226.SZA
浪潮信息
紫光国芯
软控股份
海得控制
江南化工
2017-08-23
2017-08-23
2017-08-23
2017-08-23
2017-08-23
云计算;IPV6;大数据;网络安全;去IOE;人工智能;雄安新区;融资融券;融资融券标的
物联网;重组;智能IC卡;芯片国产化;国家队;高校;人工智能;融资融券;融资融券标的
机器人;工业4.0;国家队;人工智能;融资融券;融资融券标的
智能电网;浦东新区;机器人;工业4.0;军民融合;人工智能
重组;人工智能;预增;并购阶段(需定增)
获取每日创业板次新股股票列表
次新股的定义为上市90天以内
In [62]:

df = D.history_data(instrument, start_date, end_date, ['list_date', 'list_board'])
from datetime import timedelta
df[(df['list_board']=='创业板')&(df['date']<=df['list_date']+timedelta(days=20))].head(10)
Out[62]:
date
instrument
list_date
list_board
创业板
创业板
创业板
创业板
创业板
创业板
创业板
创业板
创业板
创业板
1733
1734
1735
1737
1738
1740
4580
4581
4582
4584
2016-01-04
2016-01-04
2016-01-04
2016-01-04
2016-01-04
2016-01-04
2016-01-05
2016-01-05
2016-01-05
2016-01-05
300490.SZA
300491.SZA
300492.SZA
300494.SZA
300495.SZA
300497.SZA
300490.SZA
300491.SZA
300492.SZA
300494.SZA
2015-12-31
2015-12-31
2015-12-23
2015-12-31
2015-12-22
2015-12-22
2015-12-31
2015-12-31
2015-12-23
2015-12-31
2
.财务信息层面¶
选出满足以下条件的股票
市盈率小于15倍
市净率小于1.5倍
In [63]:
#
获取市盈率、市净率、成交额数据
history_data = D.history_data(instrument, start_date=start_date, end_date= end_date, fields=[ 'pb_lf', 'pe_ttm','amount'])
result = history_data[(history_data['pb_lf'] < 1.5)
&
&
&
&
(history_data['pe_ttm'] < 15)
(history_data['amount'] > 0)
(history_data['pb_lf'] > 0)
(history_data['pe_ttm'] > 0)]
daily_buy_stock = result.groupby('date').apply(lambda df:list(df.sort_values(['pe_ttm','pb_lf']).instrument)[:30])
daily_buy_stock.head()
Out[63]:
date
2
2
2
2
2
016-01-04
016-01-05
016-01-06
016-01-07
016-01-08
[601288.SHA, 601398.SHA, 601939.SHA, 601166.SH...
[601288.SHA, 601398.SHA, 601939.SHA, 601166.SH...
[601288.SHA, 601398.SHA, 601939.SHA, 601166.SH...
[601288.SHA, 601398.SHA, 601939.SHA, 600015.SH...
[601288.SHA, 601398.SHA, 601939.SHA, 600015.SH...
dtype: object
选出满足以下条件的股票
市净率小于8
市现率大于0.4
资产周转率大于0.4
市值最小的10只股票
In [64]:
stock_num = 10
#
通过history_data接口获取历史数据
history_data = D.history_data(instrument, start_date, end_date, ['pb_lf', 'ps_ttm', 'market_cap', 'amount'])
通过feature接口获取财务数据
financial = D.features(instrument, start_date=start_date, end_date=end_date,
fields=['fs_operating_revenue_ttm_0','fs_current_assets_0','fs_non_current_assets_0'])
总资产=流动资产+非流动资产
financial['total_assets'] = financial['fs_current_assets_0'] + financial['fs_non_current_assets_0']
资产周转率=营业收入/总资产
#
#
#
financial['asset_turnover'] = financial['fs_operating_revenue_ttm_0'] / financial['total_assets']
financial_data = financial[['date','instrument','asset_turnover']]
#
两个DataFrame:历史数据、财务数据 合并
result = history_data.merge(financial_data, on=['date','instrument'], how='outer')

#
按照选股法则选出股票
daily_buy_stock = result.groupby('date').apply(lambda df:list(df[(df['ps_ttm']>0.4) & (df['pb_lf']<8) & (df['asset_turnover']>0.4)
(df['amount']>100)].sort_values('market_cap')['instrument'])[:stock_num])
&
daily_buy_stock.head()
Out[64]:
date
2
2
2
2
2
016-01-04
016-01-05
016-01-06
016-01-07
016-01-08
[600099.SHA, 300176.SZA, 600719.SHA, 300106.SZ...
[600099.SHA, 300176.SZA, 300106.SZA, 600719.SH...
[600099.SHA, 300176.SZA, 600719.SHA, 300106.SZ...
[600099.SHA, 300176.SZA, 600719.SHA, 300106.SZ...
[600099.SHA, 002109.SZA, 600719.SHA, 300106.SZ...
dtype: object
3
.技术指标层面¶
选出满足以下条件的股票
7
日均线上穿63日均线
收盘价突破ATR上轨
In [65]:
df= D.history_data(instrument, start_date, end_date, ['open', 'high', 'low', 'close'])
import talib as ta
from numpy import float as f
def seek_stocks(df):
df['ma_7'] = ta.SMA(df.close.map(f).values, 7)
df['ma_63'] = ta.SMA(df.close.map(f).values, 63)
try:
df['atr'] = ta.ATR(df.high.map(f).values, df.low.map(f).values, df.close.map(f).values, 14)
except Exception as e:
df['atr'] = np.nan
df['upperline'] = df.close.rolling(14).mean() + df['atr']
return df[(df['ma_7']>df['ma_63'])&(df['close']>=df['upperline'])].drop('instrument', axis=1)
result = df.groupby('instrument').apply(seek_stocks).reset_index()
daily_buy_stock = result.groupby('date').apply(lambda df:list(df['instrument']))
daily_buy_stock.head()
Out[65]:
date
2
2
2
2
2
016-04-07
016-04-08
016-04-11
016-04-12
016-04-13
[000009.SZA, 000018.SZA, 000040.SZA, 000049.SZ...
[000009.SZA, 000018.SZA, 000036.SZA, 000040.SZ...
[000009.SZA, 000018.SZA, 000028.SZA, 000035.SZ...
[000028.SZA, 000035.SZA, 000036.SZA, 000040.SZ...
[000009.SZA, 000014.SZA, 000016.SZA, 000028.SZ...
dtype: object
选出满足以下条件的股票
股价创60日最高点
3
日线上穿5日均线,5日均线上穿10日均线
当日成交额是昨日成交额的1.4倍
macd柱状图处于红色区域
In [67]:
df =D.history_data(instrument, start_date, end_date, ['close', 'amount','high'])
def seek_stocks(df):
df['highest_60'] = df['high'].rolling(60).max() # 计算60天最高点
df['ma3_cross_ma5'] = df['close'].rolling(3).mean() - df['close'].rolling(5).mean() > 0 # 3日均线上穿5日均线
df['ma5_cross_ma10'] = df['close'].rolling(5).mean() - df['close'].rolling(10).mean() > 0 # 5日均线上穿10日均线
df['amount_cond'] = df['amount'] / df['amount'].shift(1) - 1 >= 0.4
# 当日成交量比前一日成交量大40%
prices = df['close'].map(np.float) # 转化成float格式
#
macd:diff线 信号线:dea 柱状图:diff-dea
macd, signal, hist = ta.MACD(np.array(prices), 12, 26, 9) # 计算macd各个指标
df['is_highest'] = df['close'] == df['highest_60'] # 该列是布尔型变量,表明是否是60日最高点
df['hist_is_red'] = hist > 0
return df
# macd柱状图是否在红色区域
managed_df = df.groupby('instrument').apply(seek_stocks).reset_index()
result= managed_df[
(managed_df['hist_is_red'])&
# macd在红色区域

(managed_df['is_highest'])&
# 是60日最高点
(managed_df['ma3_cross_ma5'])& # 3日均线上穿5日均线
(managed_df['ma5_cross_ma10'])&
(managed_df['amount_cond'])]
# 5日均线上穿10日均线
# 满足成交量条件
#
整理出每日符合买入条件的列表
daily_buy_stock = result.groupby('date').apply(lambda df:list(df.instrument)).reset_index().rename(columns={0:'stocks'})
daily_buy_stock.head()
Out[67]:
date
stocks
0
1
2
3
4
2016-04-01
2016-04-05
2016-04-06
2016-04-07
2016-04-08
[000059.SZA, 000657.SZA, 000913.SZA, 300419.SZA]
[000533.SZA, 000615.SZA, 002364.SZA, 002452.SZ...
[000670.SZA, 000799.SZA, 000995.SZA, 002134.SZ...
[002455.SZA, 300187.SZA, 600168.SHA, 600311.SH...
[000953.SZA, 002139.SZA, 002537.SZA, 300134.SZ...
上一页:BigQuant模块介绍
目录:BigQuant学院
宽客中学
BigQuant 平台高效使用指南
在这里分享如何高效的使用BigQuant平台开发策略。
上一页:BigQuant模块介绍
下一页:策略回测结果解读
目录:BigQuant学院
【
宽客学院】策略回测结果解读
本文主要介绍如何对策略回测结果进行解读。
当我们完成一个策略回测时,我们会得到如下的一个图形:
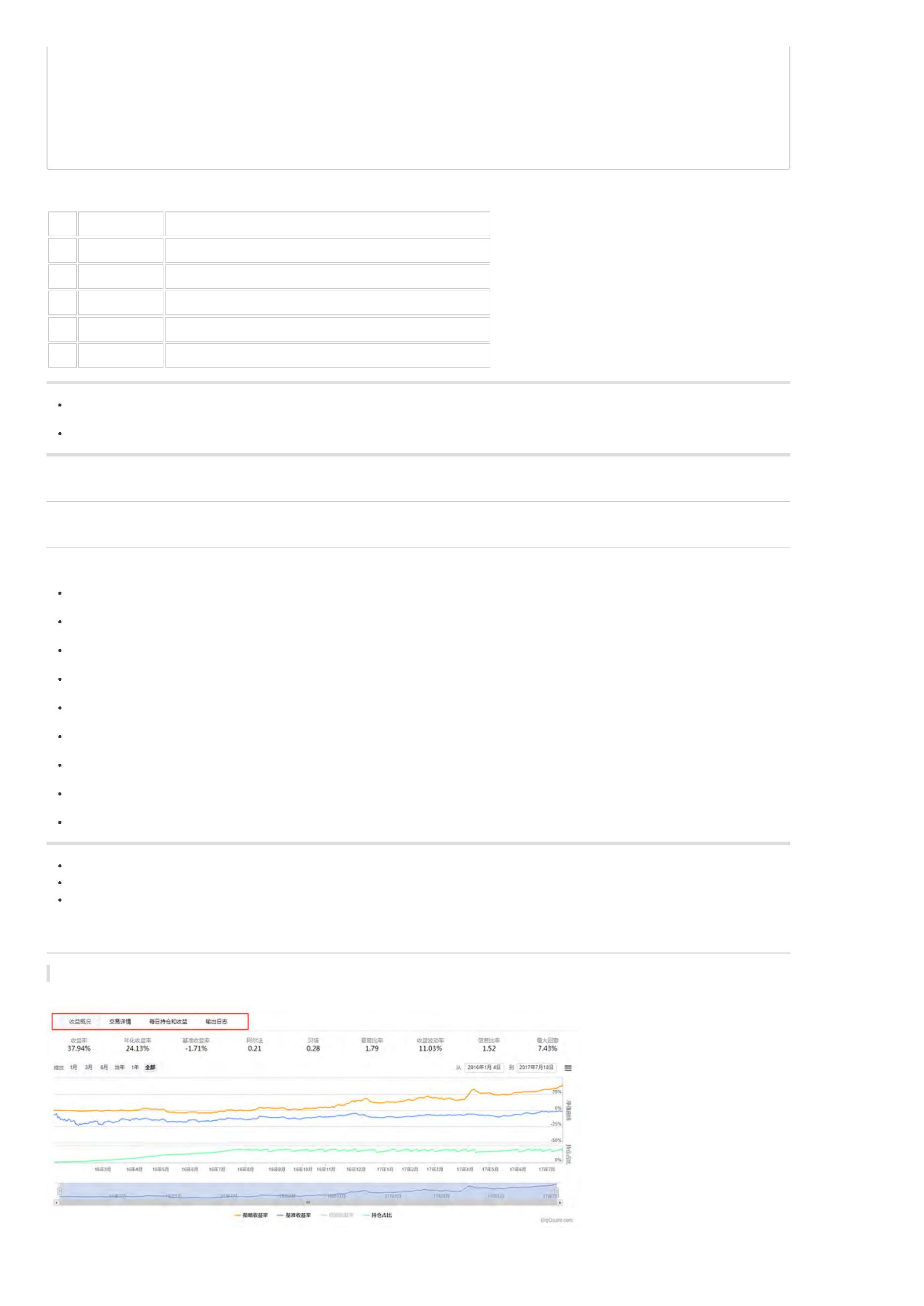
上图为策略回测结果图,红色矩形标记部分包含了策略的主要信息,包括 收益概况、交易详情、每日持仓及收益、输出日志 。接下来,我们详细介绍这几个
部分。
收益概况
收益概况以折线图的方式显示了策略在时间序列上的收益率,黄色曲线为策略收益率。同时也显示了沪深300收益率曲线作为比较基准,蓝色曲线为基准收
益率。同时,最下面的绿色曲线为持仓占比,持仓占比即仓位,10%的持仓占比表示账户里股票价值只占10%。相对收益率的曲线并没有直接绘制在图上,
点击图例 相对收益率(如下图所示),就可以将其绘制出来。
不仅如此,衡量一个策略好坏的关键指标在收益概览页面也得到展示。
收益率:策略整个回测时间段上的总收益率。比如,如果收益率为30%,表明起始时间是1万的本金,结束时间本金就变成1.3万了,一共赚了3000元。
年化收益率:该策略每一年的收益率。比如,如果回测时间段为2年,总收益率为30%,那么每年的年化收益率就在15附近(不考虑复利)。
基准收益率:策略需要有一个比较基准,比较基准为沪深300。若基准收益率为15%,表明在整个回测时间段,大盘本身就上涨了15%,如果策略收益
率小于基准收益率,说明策略表现并不好,连大盘都没有跑赢。
阿尔法:衡量策略的一个重要指标,该值越大越好。
贝塔:衡量策略的一个重要指标,该值越小越好。
夏普比率:衡量策略最重要的一个指标,该指标的计算不仅考虑收益率,还考虑了风险,因此比较具有参考价值,可以理解为经过风险调整后的收益
率。
收益波动率:收益率的标准差,是风险的一个指标。
最大回撤:策略在整个时间段上亏损最严重的时候相比净值最高值下跌的百分比。如果最大回撤为20%,表明策略在某个时间点上,相比之前的净值最
高点下降了20%。最大回撤是策略评估时非常关键的一个指标,通常与风险承受能力相关。
信息比率:信息比率也是一个常用的策略评价指标。
关于策略回测结果指标的详细信息,包括指标定义及计算公式,可以参考 策略回测结果指标详解。
交易详情
交易详情主要显示了策略在整个回测过程中每个交易日的买卖信息。包括买卖时间、股票代码、交易方向、交易数量、成交价格、交易成本。具体见下图:
每日持仓及收益
每日持仓及收益主要呈现每日持有股票代码、当日收盘价、持仓股票数量、持仓金额、收益等指标。具体见下图:
输出日志
输出日志主要为策略运行过程中的一些日志。包括涨跌停股票不能交易、停牌估计不能交易等。该日志可以便于我们检查回测结果的正确性。
上一页:BigQuant平台高效使用指南

下一页:BigQuant回测机制
目录:BigQuant学院
[
量化学堂-新手专区]BigQuant 回测机制
导语:
刚接触BigQuant平台的小伙伴可能有点困惑,不熟悉BigQuant平台的回测机制,因此不知道怎么编写策略。当使用某一回测平台时,如果不能对其回
测处理机制了解清楚,我们很可能出现偷价漏价、未来函数等问题,这些问题对策略的影响是致命的。即使不出现这样的问题,很多时候,用户可能写
的策略并没有达到预期的目的,因此了解回测机制非常重要。
事件驱动机制
在策略回测中应用最为广泛的就是 事件驱动机制。先看定义:当某个新的事件被推送到程序中时,程序立即调用和这个事件相对应的处理函数进行相关的操
作。 举个“栗子”让大家更好理解。
比如开发一个股指策略,交易程序对股指TICK数据进行监听,当没有新的行情过来时,程序保持监听状态不进行任何操作;当收到新的数据时,数据处理函
数立即更新K线和其他技术指标,并检查是否满足策略的下单条件,如果满足条件就执行下单。
BigQuant平台的回测机制就是事件驱动机制。因为用户分析的数据是股票、期货等交易数据,这类数据的一个很大特点就是本身是标准化的时间序列数据,
在各个交易软件上也是以K线的形式呈现,K线包含了交易的开盘价、最高价、最低价、收盘价。如图1所示:
图
线示意图
BigQuant平台回测机制是 把每一个K线当做一个事件,按照时间发生先后顺序,即从左往右依次运行。 在新的事件发生时,即出现了包含高开低收四个价格
的K线,回测程序会调用这个K线的数据,如果没有触发策略信号,就什么也不做,如果触发了交易信号,则产生订单。
为了避免未来函数,即在产生订单的时候不使用未来数据,只能使用当前能够获得的数据,BigQuant平台进行了如下处理:当产生订单时,只能在下一个K
线上完成订单成交,这样就能避免未来函数的问题,同时也能更加逼近现实真实情况,因为很多时候,当某根K线发出交易信号时,用户只能在下一个K线上
成交订单。不仅如此,为了控制订单以某个预期的价格成交,还可以设置成交价格,最为常见的就是设置订单价格是下一个K线的开盘价。
了解BigQuant 回测机制
先看BigQuant回测机制的概览图(图2):
图
回测机制概览图
BigQuant平台回测主体有两个使用频率很高的函数:initialize 函数和handle_data 函数,理解了这两个函数开发策略就再也不是什么难事了,结合上面K线
图来理解这两个函数(如图3)。
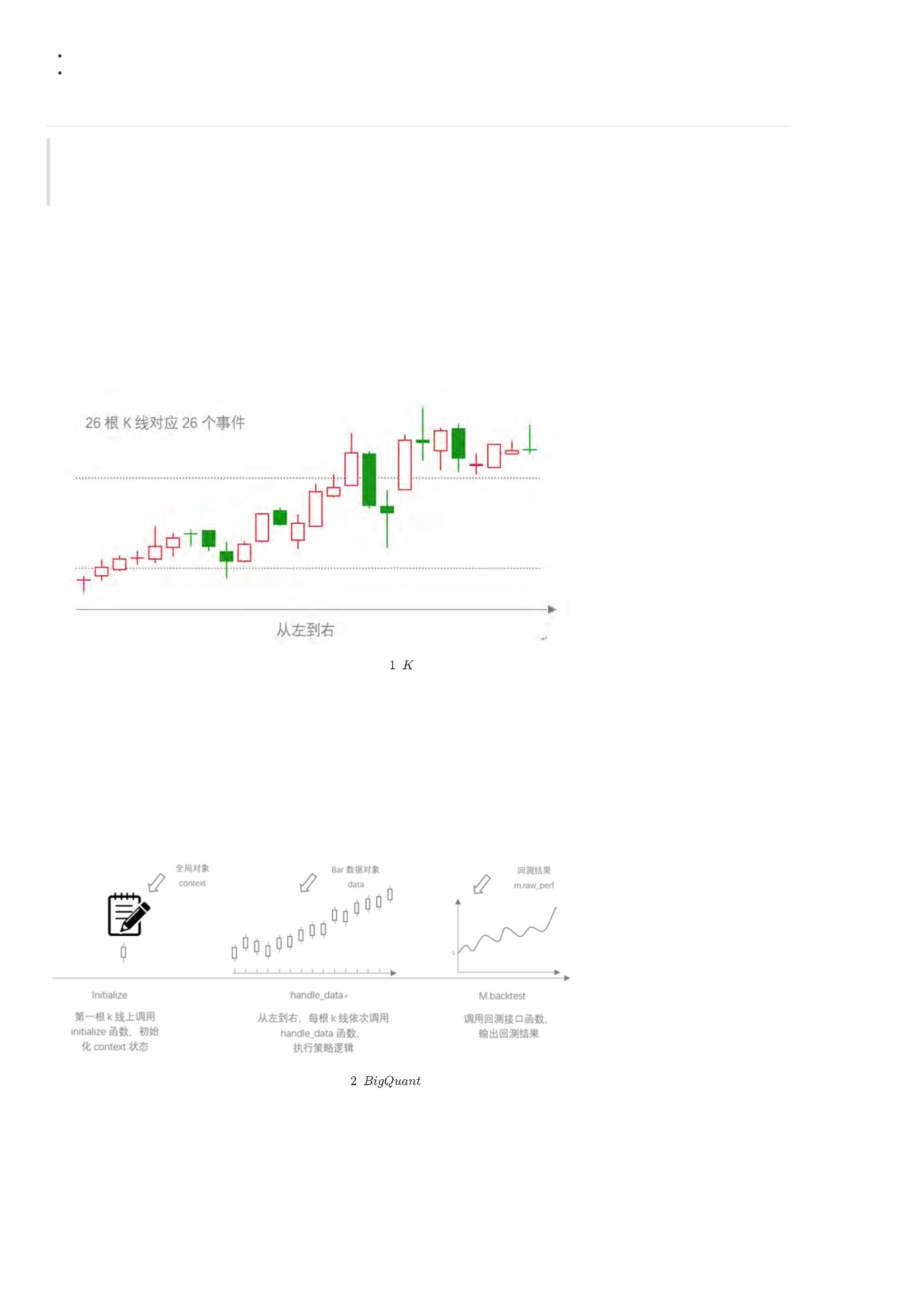
图
两个函数与 线的关系示意图
从图中可以看出,其实一共有26个事件,即26根K线,第一根K线既对应黑色箭头,又对应灰色箭头,其余都只对应灰色箭头。回测主体函数的initialize函数
只在第一个事件上调用,即第一根K线,因此很多初始设置可以放在initialize函数里面。每个K线都对应灰色箭头,表示每个事件都会调用handle_data函数,
即从第一根K线到最后一根K线都会运行handle_data一次,于是很多策略逻辑部分就可以放在handle_data里。不知道这样解释大家是否能够更容易理解?
简单策略开发
由于BigQuant提供的是提供在线的Notebook云端研究平台,因此在首页点击“编写策略”按钮就进入个人账户页面,然后点击左上角的添加按钮(“+”)新建
notebook。
策略的编写主要包含三个步骤。回测文档参考:链接
1
.确定策略参数
在回测的时候,会面临选哪只股票,回测从什么日期开始,回测在哪天结束这样的问题,因此我们需要再回测前确定这几个策略参数
instrument = ['600519.SHA']
start_date = '2014-01-01'
end_date = '2017-07-18'
2
.编写策略主体函数
def initialize(context):
context.set_commission(PerDollar(0.0015))
def handle_data(context, data):
sid = context.symbol(instrument[0])
cur_position = context.portfolio.positions[sid].amount
if cur_position == 0:
order(sid, 100)
elif cur_position > 0:
order(sid, -100)
initialize函数里我们设置了手续费。handle_data函数里我们制定了策略逻辑:当没有持仓时,产生股票数量为100的买入订单;当持仓时,产生股票数量为
1
00的卖出订单。
3
.调用回测接口
两个主体函数构建完毕之后,再调用回测接口就完成策略开发了,回测接口如下:
m=M.trade.v2(
instruments=instrument,
start_date=start_date,
end_date=end_date,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open', # 买入订单成交价格为开盘价
order_price_field_sell='open', # 卖出订单成交价格为开盘价
capital_base=200000, # 初始资金
benchmark='000300.INDX', # 基准是沪深300 指数
)
直接运行策略接口就可以让策略跑起来,回测速度非常快,直接输出回测结果,图表也是相当友好。当然了,这个简单策略没有一点实际价值,因此资金曲
线也是有的“惨”啊:joy:
不知道大家现在对BigQuant的回测机制是不是更了解一些了,快克隆下策略自己试试吧。
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
附件:一个简单的策略
In [39]:
instrument = ['600519.SHA']
start_date = '2016-01-01'
end_date = '2017-07-18'
def initialize(context):
context.set_commission(PerDollar(0.0015))
def handle_data(context, data):
sid = context.symbol(instrument[0])
cur_position = context.portfolio.positions[sid].amount
if cur_position == 0:
order(sid, 100)
elif cur_position > 0:
order(sid, -100)
In [40]:
m=M.trade.v2(
instruments=instrument,
start_date=start_date,
end_date=end_date,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open', # 买入订单成交价格为开盘价
order_price_field_sell='open', # 卖出订单成交价格为开盘价
capital_base=200000, # 初始资金
benchmark='000300.INDX', # 基准是沪深300 指数
)
[
[
2017-07-19 18:40:48.077333] INFO: bigquant: backtest.v7 start ..
2017-07-19 18:40:48.079204] INFO: bigquant: hit cache
[
2017-07-19 18:40:48.766480] INFO: bigquant: backtest.v7 end [0.689119s].
上一页:策略回测结果解读
下一页:StockRanker结果解读
目录:BigQuant学院
【
宽客学院】StockRanker 结果解读
本文对StockRanker的结果做详细介绍,希望大家对StockRanker的了解更加深入。
通过BigQuant AI策略详解,我们已经对StockRanker有了一个基本介绍。接下来我们在 模型训练和 模型预测 这两步详细介绍StockRanker模型的返回结
果,以便于能够更好地开发AI策略。
模型训练
代码部分:
#
StockRanker机器学习训练
m5=M.stock_ranker_train.v3(training_ds=m4.data, features=conf.features)
结果查看:
当我们完成模型训练以后,根据策略研究平台的自动补全功能,就可以查看模型的一些结果(属性和方法)。
模型ID
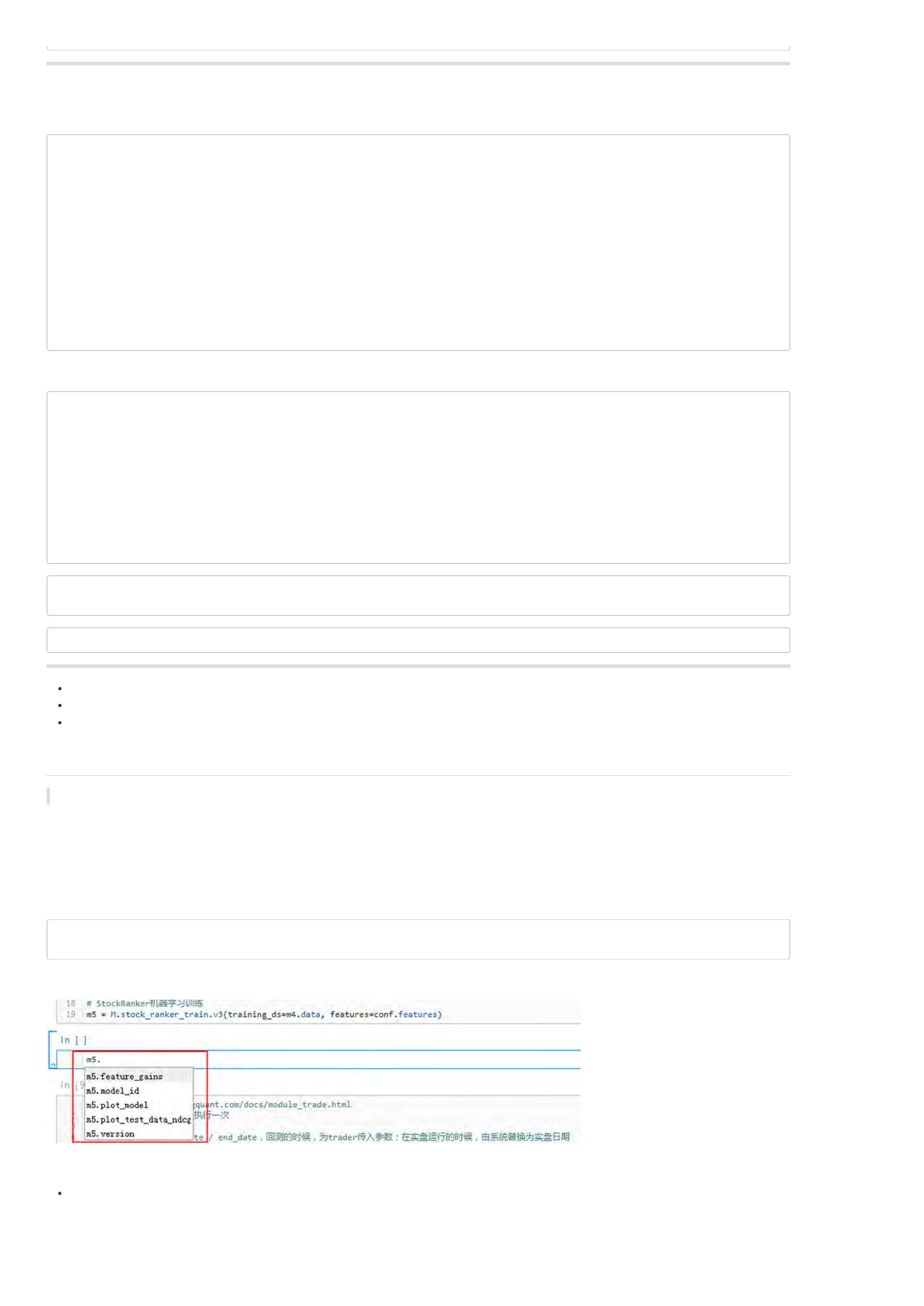
直接输入 m5.model_id接可以输出模型的ID。这个ID在平台上具有唯一性和全局性,只要记住该ID就可以在其他策略里面正常使用,策略开发就非常灵
活。
特征得分
特征得分是StockRanker模型基于各个特征对模型贡献度的一个数量型评估指标,因此我们可以通过特征得分来进行特征的选择、组合、删除等工作。
如图所示,直接输入m5.features_gains可以得到特征得分结果,不过类型为内置的DataSource,因此需要通过read_df读出来,读出来的结果为
DataFrame格式。
可视化模型
这一步,我们可以将模型的各个细节绘制出来,便于查看。详情可以参考:StockRanker模型可视化
模型预测
代码部分:
#
#
测试集为17年1月到七月的100只股票数据
特征抽取
n1 = M.general_feature_extractor.v5(
instruments=D.instruments[:100],
start_date='2017-01-01', end_date='2017-07-31',
model_id=m5.model_id)
#
特征转换
n2 = M.transform.v2(
data=n1.data, transforms=T.get_stock_ranker_default_transforms(),
drop_null=True, astype='int32', except_columns=['date', 'instrument'],
clip_lower=0, clip_upper=200000000)
#
模型在测试集上进行预测
n3 = M.stock_ranker_predict.v2(model_id=m5.model_id, data=n2.data)
结果查看:
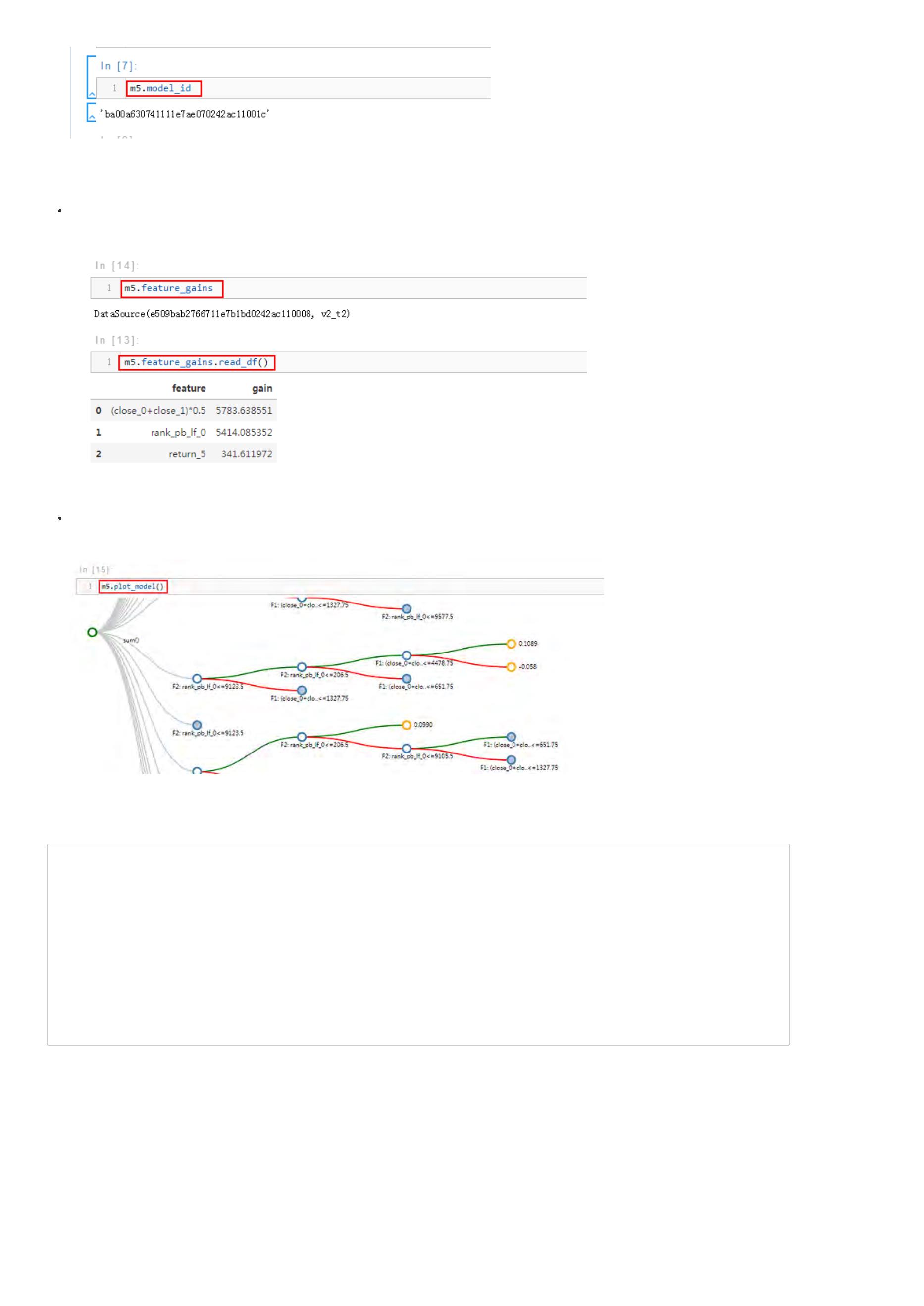
同模型训练一样,一旦我们完成模型预测以后,根据平台的代码自动补全功能,我们就可以查看模型预测结果。
股票排序结果
股票排序结果直接用来开发交易策略,输出每个交易日股票的得分情况,股票得分越高,表明该股票越值得买入。从图中可以看出,2017年1月3日,最
值得买入的股票为‘000026.SZA’。
上一页:BigQuant回测机制
下一页:无需代码构造您自己的衍生因子
目录:BigQuant学院
无需代码构造您自己的衍生因子
因子是影响机器学习效果最重要的因素之一。特别是在股票等市场,高质量的因子直接影响策略收益。
在前面的例子中,你可以能看到像 close_1/close_0 这样的因子,这是通过运算符连接,重新定义的新的衍生因子。本文主要介绍如何通过运算符构建衍生
因子。
在 BigQuant 平台上,我们提供的因子库,包括2000+基础因子;同时,我们提供的因子计算引擎,让用户无需编程,通过表达式就可以用基础因子生成新的
衍生因子。
表达式
表达式使用的语法和我们常用的数据表达式一致。求三日平均收盘价,可以按如下写:
(close_1 + close_2 + close_3) / 3
支持的运算符:
1
2
3
4
5
6
7
8
9
1
.+:加
.-:减
.*:乘
./ :除
.==:等于。逻辑运算支持,如果为True,则为1,否则为0。例如,表达式 (10 == 10) + 1,这个值是 2
.>:大于
.>=:大于等于
.>:小于
.>=:小于等于
0.and:逻辑与
1
1.or:逻辑或
1
1
1
1
1
2.iif:使用 iff(判断条件,条件为True的值,条件为False的值),例如, iif(close_1 > close_0, close_1, close_0)
3.max:最大值,支持2个或者更多参数,例如,max(high_0, high_1, high_2) / close_0
4.min:最小值,支持2个或者更多参数,例如,min(low_0, low_1, low_2) / close_0
5.ln:取自然对数
6.log:取10为底的对数
示例
1
. 过去五日均价除以今日收盘价:
(close_0 + close_1 + close_2 + close_3 + close_4) / 5 / close_0
2
. 过去三日振幅:
max(high_0, high_1, high_2) / min(low_0, low_1, low_2)
上一页:StockRanker结果解读
目录:BigQuant学院
如何按自己需求实现自定义因子计算?
在平台的因子库上看到有许多因子,但是我想计算一些自定义的因子,比如,相对大盘的收益率,这个因子怎么构造呢?谢谢!
WorldQuant 101alpha 因子构建及因子测试
本文目的是介绍如何使用bigexpr表达式对WorldQuant公开的101个alpha进行因子构建,并进行因子测试。
背景介绍
根据WorldQuant发表的论文《101 Formulaic Alphas 》 ,其中公式化地给出了101个alpha因子。与传统方法不一样的是,他们根据数据挖掘的方法构建了
1
01个alpha,据说里面80%的因子仍然还行之有效并被运用在实盘项目中。
在BigQuant策略研究平台上,可通过表达式快速进行因子构建和数据标注,再也不需要自己手动编写冗长代码。
表达式简介
因为在机器学习和深度学习中,因子是一个很重要的概念,也被称为特征,开发AI算法的关键在于特征选择。如果是简单的基础因子,比如近5日收益率:
$
close\_5/close\_0-1$,因子构建比较简单,但是如果想构建近5日每日收益率和成交量的相关性这个因子就比较棘手,需要编写大量的代码来计算该因子。
因此,我们设计了bigexpr表达式引擎。
bigexpr是BigQuant开发的表达式计算引擎,通过编写简单的表达式,就可以对数据做任何运算,而无需编写代码。
bigexpr在平台上被广泛使用,M.advanced_auto_labeler 和 M.derived_feature_extractor 都已经由bigexpr驱动,您可以用表达式就可以定义标注目标和完成
后特征抽取。
正如刚刚提到的近5日每日收益率和成交量的相关性因子可以这样定义:
其中,$correlation$表示求相关系数,$close\_0$表示当天收盘价,$shift(close\_0,1)$表示前一日收盘价,$volume\_0$表示当天成交量。因此,可以看出,
并不需要编写大量代码计算该因子,通过表达式即可快速构建。
函数说明
表达式引擎中有不少简单函数,对其中的部分函数进行解释:
可分为横截面函数和时间序列函数两大类,其中时间序列函数名多为以$ts\_$开头
大部分函数命名方式较为直观
$
$
$
$
$
$
abs(x)$ 、$log(x)$分别表示$x$的绝对值和$x$的自然对数
rank(x)$表示某股票$x$值在横截面上的升序排名序号,并将排名归一到[0,1]的闭区间
delay(x,d)$表示$x$值在$d$天前的值
delta(x,d)$表示$x$值的最新值减去$x$值在$d$天前的值
correlation(x,y,d)$、$covariance(x,y,d)$分别表示$x$和$y$在长度为$d$的时间窗口上的皮尔逊相关系数和协方差
ts\_min(x,d)$、$ts\_max(x,d)$、$ts\_argmax(x,d)$、$ts\_argmin(x,d)$、$ts\_rank(x)$、$sum(x,d)$、$stddev(x,d)$等均可以通过函数名称了解其作
用
因子说明
BigQuant平台上系统因子超过2000个,包括了基本信息因子、量价因子、估值因子、财报因子、技术指标因子等。本文简单举若干因子进行介绍。
基本信息因子
点击查看部分因子
量价因子
点击查看部分因子
估值因子
点击查看部分因子
财报因子
点击查看部分因子

数据标注
和因子构建一样,数据标注也是机器学习算法中非常重要的一部分,更详细的文档为:自定义因子。
之前没有表达式的时候,数据标注主要通过fast_auto_label实现,自从有了表达式以后,数据标注主要是通过advanced_auto_label实现。数据标注的整体思
想和内容主要体现在label_expr上,label_expr是一个列表(list)。
具体实例代码,请点击下方 点击查看代码。
点击查看代码
接下来,我们对示例代码做解释:
label_expr为一个list,列表里四个元素决定了标注的具体操作,详细文档见:表达式引擎
计算未来一段时间的相对收益作为标注的原始依据,这里可以使用bigexpr表达式,快速完成数据标注
使用clip和all_quantile函数做极值处理
将原始数据离散化,这里可以采取等宽离散化或者等频离散化,两者各有优劣
通过where函数过滤掉一字涨停的样本数据
单因子测试
这里我们以’shift(close_0,15) / close_0’因子为例,介绍如何进行单因子测试,开发基于单因子的AI策略。
(补充:由于平台升级太快,下面的单因子测试代码可能会报错,建议参考三楼 Yoga 会飞的鱼的回答)
点击查看代码
1
01 Alphas 列表
点击查看完整列表
这里展示了WorldQuant公开的101个alpha及其表达式,感兴趣的朋友可以参考 单因子测试 的代码做实验,唯一需要修改的是将具体的因子变动下,希望大
家能开发出可以稳定盈利的策略,发掘出新的alpha。
注:部分因子可能是布尔型因子,因子值要么是1,要么是-1,这样的单因子在传入StockRanker的时候可能会出错,导致模型训练失败。
相关阅读
【
宽客学院】Pandas 快速入门
本课程帮助大家Pandas快速入门
下一页:因子预处理
目录:BigQuant学院
【
宽客学院】因子预处理
在机器学习中,很多因子数据必须经过预处理才能参与模型训练。本文简单介绍使用sklearn进行因子预处理。
参考文档:使用sklearn进行数据预处理
参考文档:标准化、规范化、二值化等多种机器学习数据预处理方法
In [39]:
#
导入包
from sklearn import preprocessing
In [40]:
#
基础设置
class conf:
start_date = '2015-01-01'
end_date='2017-08-10'
split_date = '2016-01-01'

instruments = D.instruments(start_date, split_date)
features = ['fs_current_assets_0','market_cap_0','close_0']
In [41]:
#
计算特征数据
m2 = M.general_feature_extractor.v5(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.split_date,
features=conf.features)
#
数据预处理:缺失数据处理,数据规范化,T.get_stock_ranker_default_transforms为StockRanker模型做数据预处理
m3 = M.transform.v2(
data=m2.data, transforms=T.get_stock_ranker_default_transforms(),
drop_null=True, astype='int32', except_columns=['date', 'instrument'],)
[
[
[
[
[
[
2017-10-16 16:05:47.926344] INFO: bigquant: general_feature_extractor.v5 开始运行..
2017-10-16 16:05:47.936684] INFO: bigquant: 命中缓存
2017-10-16 16:05:47.938360] INFO: bigquant: general_feature_extractor.v5 运行完成[0.012008s].
2017-10-16 16:05:47.972345] INFO: bigquant: transform.v2 开始运行..
2017-10-16 16:05:47.975012] INFO: bigquant: 命中缓存
2017-10-16 16:05:47.976093] INFO: bigquant: transform.v2 运行完成[0.003792s].
In [42]:
#
# 全部数据
all_data = m2.data.read_df()
# 某一天数据
df = all_data[all_data['date']=='2015-01-05']
#
#
# 某一天数据的直方图分析,可以发现数据很粗糙,极值存在,需要做一些处理和转化
df[df.dtypes[df.dtypes == 'float32'].index.values].hist(bins=50, figsize=[15,12])
In [43]:
#
# 1. 缺失值处理
for factor in ['close_0', 'market_cap_0', 'fs_current_assets_0']:
df[factor].fillna(np.nanmean(df[factor]), inplace=True)
In [44]:
#
# 2. 极值处理
for factor in ['close_0', 'market_cap_0', 'fs_current_assets_0']:
p_95 = np.percentile(df[factor], 95)
p_5 = np.percentile(df[factor], 5)
df[factor][df[factor] > p_95] = p_95
df[factor][df[factor] < p_5] = p_5
In [45]:
#
# 3. 标准化
df = all_data[all_data['date']=='2015-01-05'].dropna()
for factor in ['close_0', 'market_cap_0', 'fs_current_assets_0']:
df[factor] = (df[factor] - df[factor].mean()) / df[factor].std()
df[['close_0', 'market_cap_0', 'fs_current_assets_0']].values
Out[45]:
array([[ 1.01638317,
2.82943988, 14.47532082],
-0.05427583, -0.21515357, -0.21295929],
0.04300562, -0.06115698, 0.07691551],
..,
-0.08408548, -0.03219347, -0.11243575],
[
[
.
[
[
[
-0.06934822,
-0.08663286,
0.05156187, -0.11314245],
0.67376161, 0.04899734]], dtype=float32)
In [46]:
#
上述标准化结果与sklearn的scale处理结果是大致一样的(因为scale函数内部实现细节有点差异)
preprocessing.scale(df[['close_0', 'market_cap_0', 'fs_current_assets_0']])
Out[46]:
array([[ 1.01660847,
2.83006714, 14.47853436],
-0.05428803, -0.21520142, -0.2130065 ],
0.04301501, -0.06117069, 0.07693265],
..,
-0.08410428, -0.03220075, -0.11246065],
[
[
.
[
[
[
-0.06936376,
-0.08665223,
0.05157316, -0.11316751],
0.67391087, 0.04900828]])
In [47]:
#
# 4. 规范化
preprocessing.normalize(df[['close_0', 'market_cap_0', 'fs_current_assets_0']])
Out[47]:
array([[ 0.06874776, 0.1913822 , 0.979105 ],
[
[
.
[
[
[
-0.1764766 , -0.69956682, -0.69243215],
0.40093092, -0.57015163, 0.71706451],
..,
-0.58374982, -0.22349793, -0.78056699],
-0.48710097, 0.36216984, -0.79471105],
-0.12720051, 0.98926461, 0.07194138]])
In [48]:
#
因子预处理函数
def preprocess(df):
# 1. 缺失值处理
for factor in ['close_0', 'market_cap_0', 'fs_current_assets_0']:
缺失值处理
df[factor].fillna(np.nanmean(df[factor]), inplace=True)
极值处理
#
#
#
p_95 = np.percentile(df[factor], 95)
p_5 = np.percentile(df[factor], 5)
df[factor][df[factor] > p_95] = p_95
df[factor][df[factor] < p_5] = p_5
#
标准化处理
df[factor] = (df[factor] - df[factor].mean()) / df[factor].std()
return df
#
按每个交易日进行因子预处理,此时因子预处理完成,我们可以用预处理后的结果加入更多的机器学习算法中
all_data.groupby('date').apply(preprocess)
Out[48]:
close_0
3.052037
3.048802
3.049037
3.031636
3.007655
2.998902
3.000345
3.004525
3.012266
3.033375
2.985070
2.996415
2.993371
3.017199
3.004288
3.022293
3.000776
3.015631
3.001202
2.976087
2.972936
2.978402
2.966676
date
fs_current_assets_0
0.556457
0.556164
0.557937
0.557385
0.560743
0.570150
0.566009
0.565694
0.562824
0.566757
0.571762
0.571735
0.571391
0.571763
0.571596
0.571354
0.570767
0.570511
0.569341
0.569285
0.533049
0.528683
0.529062
instrument
market_cap_0
3.297253
3.257948
3.270279
3.231909
3.260432
3.236919
3.222543
3.216527
3.243954
3.231477
3.156042
3.171534
3.191233
3.176629
3.205649
3.194622
3.177091
3.173037
3.138286
3.153763
3.147219
3.137114
3.147889
0
1
2
3
4
5
6
7
8
9
2015-01-05
2015-01-06
2015-01-07
2015-01-08
2015-01-09
2015-01-12
2015-01-13
2015-01-14
2015-01-15
2015-01-16
2015-01-19
2015-01-20
2015-01-21
2015-01-22
2015-01-23
2015-01-26
2015-01-27
2015-01-28
2015-01-29
2015-01-30
2015-02-02
2015-02-03
2015-02-04
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
10
11
12
13
14
15
16
17
18
19
20
21
22

close_0
date
fs_current_assets_0
0.529196
0.529368
0.528575
0.528297
0.565610
0.565225
0.560827
...
instrument
market_cap_0
3.174509
3.144080
3.154410
3.160760
3.148416
3.159806
3.134854
...
23
24
25
26
27
28
29
2.957267
2.993339
2.971802
2.980456
2.991138
2.985317
2.968544
...
2015-02-05
2015-02-06
2015-02-09
2015-02-10
2015-02-11
2015-02-12
2015-02-13
...
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
000001.SZA
...
.
..
569668
569669
569670
569671
569672
569673
569674
569675
569676
569677
569678
569679
569680
569681
569682
569683
569684
569685
569686
569687
569688
569689
569690
569691
569692
569693
569694
569695
569696
569697
-0.364151
-0.393706
-0.378904
-0.388544
-0.402664
-0.383377
-0.388683
-0.381756
-0.378545
-0.358746
-0.358682
-0.332569
-0.332485
-0.343865
-0.982238
-0.978856
-0.965441
-0.945971
-0.926357
-0.914591
-0.885378
-0.858536
-0.827869
-0.784113
-0.742582
-0.698834
-0.632080
-0.583340
-0.530886
-0.444703
2015-12-14
2015-12-15
2015-12-16
2015-12-17
2015-12-18
2015-12-21
2015-12-22
2015-12-23
2015-12-24
2015-12-25
2015-12-28
2015-12-29
2015-12-30
2015-12-31
2015-12-10
2015-12-11
2015-12-14
2015-12-15
2015-12-16
2015-12-17
2015-12-18
2015-12-21
2015-12-22
2015-12-23
2015-12-24
2015-12-25
2015-12-28
2015-12-29
2015-12-30
2015-12-31
-0.612207
-0.613224
-0.613241
-0.613026
-0.610031
-0.610888
-0.612257
-0.611544
-0.612179
-0.612344
-0.612574
-0.611711
-0.613864
-0.616675
0.590867
0.586158
0.585241
0.585689
0.585801
0.585244
0.581989
0.552980
0.553608
0.549469
0.549022
0.547223
0.547461
0.547183
0.556995
0.557870
603998.SHA
603998.SHA
603998.SHA
603998.SHA
603998.SHA
603998.SHA
603998.SHA
603998.SHA
603998.SHA
603998.SHA
603998.SHA
603998.SHA
603998.SHA
603998.SHA
603999.SHA
603999.SHA
603999.SHA
603999.SHA
603999.SHA
603999.SHA
603999.SHA
603999.SHA
603999.SHA
603999.SHA
603999.SHA
603999.SHA
603999.SHA
603999.SHA
603999.SHA
603999.SHA
-0.582843
-0.602110
-0.593836
-0.600101
-0.612462
-0.596951
-0.601776
-0.595081
-0.599207
-0.582991
-0.584567
-0.566934
-0.570732
-0.575315
-0.826569
-0.821680
-0.796086
-0.769995
-0.742622
-0.717395
-0.678198
-0.634116
-0.590174
-0.524914
-0.467260
-0.405524
-0.314254
-0.244122
-0.166064
-0.053904
569698 rows × 5 columns
【
宽客学院】机器学习模型(持续更新中)
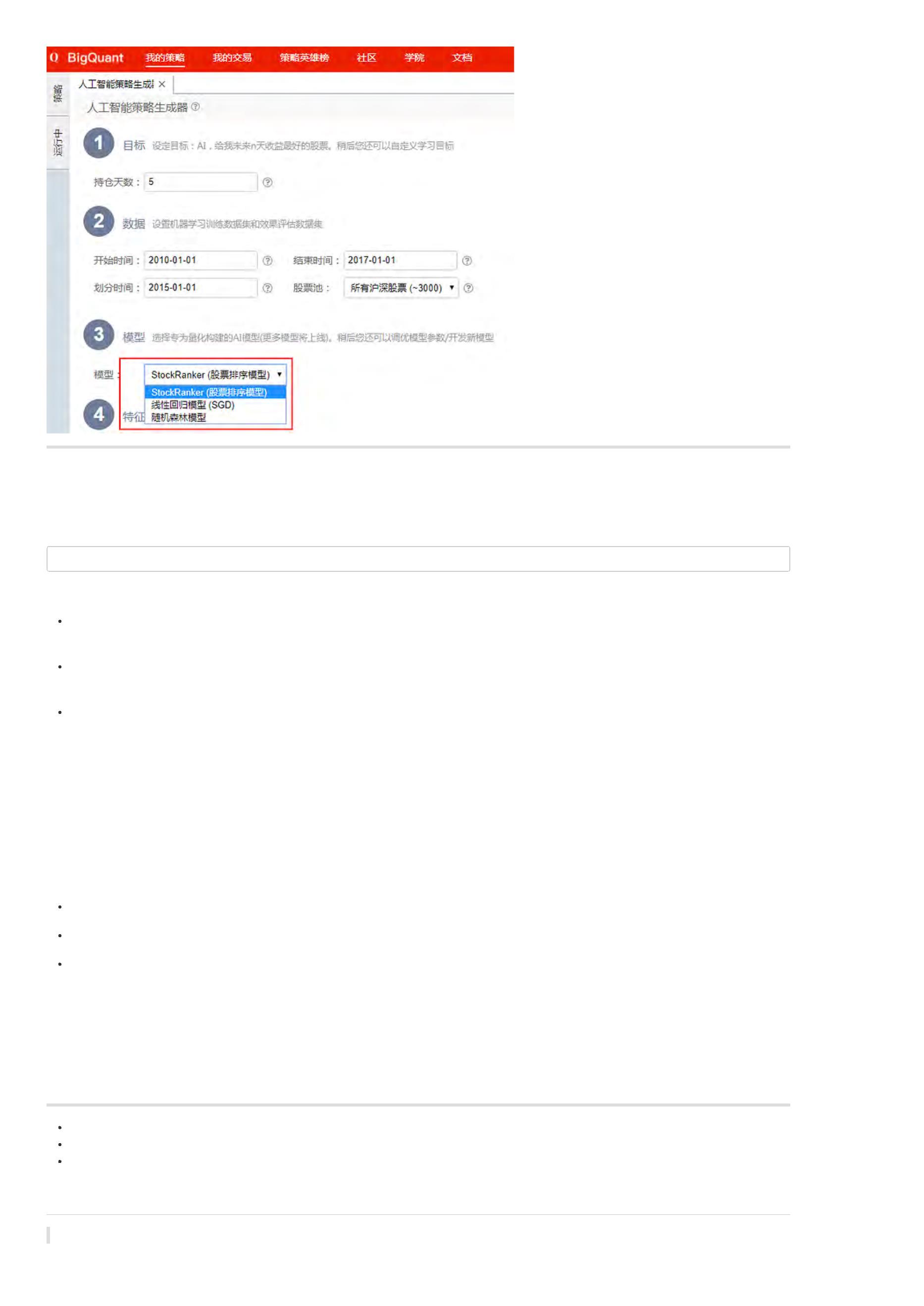
BigQuant平台会不断封装机器学习算法策略,方便用户直接使用策略生成器开发策略,降低策略开发难度。本文对BigQuant平台上策略生成器已经支
持的机器学习模型进行简单介绍。
目前,在BigQuant策略研究平台,支持的机器学习模型有:

我们依次进行介绍:
StockRanker 模型
StockRanker 是 BigQuant为量化选股而设计,核心算法主要是排序学习和梯度提升树。
StockRanker = 选股 + 排序学习 + 梯度提升树
StockRanker有如下特点:
选股:股票市场和图像识别、机器翻译等机器学习场景有很大不同。StockRanker充分考虑股票市场的特殊性,可以同时对~3000只股票的数据进行学
习,并预测出股票排序
排序学习 (Learning to Rank):排序学习是一种广泛使用的监督学习方法 (Supervised Learning),比如推荐系统的候选产品、用户排序,搜索引擎的文
档排序,机器翻译中的候选结果排序等等。StockRanker 开创性的将排序学习和选股结合,并取得显著的效果。
梯度提升树 (GBDT):有多种算法可以用来完成排序学习任务,比如VSM、逻辑回归、概率模型等等。StockRanker使用了GBDT,GBDT是一种集成学
习算法,在行业里使用广泛。
StockRanker的领先效果还得益于优秀的工程实现,我们在学习速度、学习能力和泛化性等方面,都做了大量的优化,并且提供了参数配置,让用户可以进
一步根据需要调优。
随机森林模型
随机森林模型使用多棵树进行单独预测,最后的结论由这些树预测结果的组合共同来决定,这也是“森林”名字的来源。每个基分类器可以很弱,但最后组合
的结果通常能很强,这也类似于:“三个臭皮匠顶个诸葛亮”的思想。
随机森林模型有如下特点:
很少的数据预处理。随机森林继承决策树的全部优点,只需做很少的数据准备,其他算法往往需要数据归一化。
功能强大。随机森林模型能处理连续变量,还能处理离散变量,当然也能处理多分类问题 。
鲁棒性更强。随机森林解决了决策树的过拟合问题,使模型的稳定性增加,对噪声更加鲁棒,从而使得整体预测精度得以提升。
线性回归模型(SGD)
用回归方程定量地刻画一个因变量与多个自变量间的线性依存关系,称为多元线性回归分析。多元线性回归分析是多变量分析的基础,也是理解监督类分析
方法的入口!实际上大部分学习统计分析和市场研究的人的都会用回归分析,操作比较简单。
在BigQuant上的线性回归模型的独特之处在于,在最小化损失函数——均分误差的时候,采取的是随机梯度下降法(stochastic gradient descent),因此更
高效。
上一页:因子预处理
下一页:开发传统趋势策略
目录:BigQuant学院
【
宽客学院】开发传统趋势策略
本文将告诉大家,如何开发一个传统的趋势跟踪策略。
在BigQuant策略平台上,除了开发AI策略,还可以开发传统策略,比如趋势跟踪、套利、事件驱动策略、多因子选股策略。本文以趋势跟踪策略为例,帮助
大家更好地理解BigQuant回测机制。
新建空白策略
参考新手引导 ,我的策略 > 新建 > 空白股票策略
策略命名
策略完整代码
金叉死叉策略¶
当短期均线上穿长期均线,出现金叉,买入
当短期均线下穿长期均线,出现死叉,卖出
1
. 主要参数¶
In [4]:
#
股票选择
instruments = ['600519.SHA']
#
开始时间
start_date = '2012-05-29'
结束时间
#
end_date = '2017-07-18'
2
. 策略回测主体¶
In [5]:
#
初始化账户
def initialize(context):
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5)) # 设置手续费,买入成本为万分之三,卖出为千分之1.3
context.short_period = 5 # 短期均线
context.long_period = 50 # 长期均线
def handle_data(context, data):
#
长期均线值要有意义,需要在50根k线之后
if context.trading_day_index < context.long_period:
return
k = instruments[0] # 标的为字符串格式
sid = context.symbol(k) # 将标的转化为equity格式
price = data.current(sid, 'price') # 最新价格
short_mavg = data.history(sid, 'price',context.short_period, '1d').mean() # 短期均线值
long_mavg = data.history(sid, 'price',context.long_period, '1d').mean() # 长期均线值
cash = context.portfolio.cash # 现金
cur_position = context.portfolio.positions[sid].amount # 持仓
#
#
交易逻辑
如果短期均线大于长期均线形成金叉,并且没有持仓,并且该股票可以交易
if short_mavg > long_mavg and cur_position == 0 and data.can_trade(sid):
context.order(sid, int(cash/price/100)*100) # 买入
#
如果短期均线小于长期均线形成死叉,并且有持仓,并且该股票可以交易
elif short_mavg < long_mavg and cur_position > 0 and data.can_trade(sid):
context.order_target_percent(sid, 0) # 全部卖出
3
.回测接口¶
In [6]:
m=M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open', # 以开盘价买入
order_price_field_sell='open', # 以开盘价卖出
capital_base=1000000, # 本金
)
[
[
2017-08-01 14:15:36.232518] INFO: bigquant: backtest.v7 start ..
2017-08-01 14:15:36.234645] INFO: bigquant: hit cache
[
2017-08-01 14:15:37.774814] INFO: bigquant: backtest.v7 end [1.542292s].
上一页:机器学习模型(持续更新中)
下一页:自定义买入卖出策略
目录:BigQuant学院
【
宽客学院】自定义买入卖出策略
策略思想丰富多样,尤其是在买入和卖出方面,一千个投资者可能有一千个交易想法。因此,本文告诉大家怎样进行灵活地买入和卖出,以便于大家能
够更高效地开发量化策略。
BigQuant平台提供了很多策略生成器的模板策略,其买入和卖出的思想是确定了的。由于每个人交易的想法可能千差万别,因此如果能灵活地自定义买入和
卖出岂不是更好。BigQuant的策略编写语言是Python,策略的交易主要是通过策略回测机制完成,因此一方面需要了解Python语言,另一方面,也是最重要
的是需要熟悉BigQuant回测机制。
基础策略¶
In [1]:
#
基础参数配置
class conf:
start_date = '2014-01-01'
end_date='2017-07-18'
split_date 之前的数据用于训练,之后的数据用作效果评估
split_date = '2016-01-01'
D.instruments: https://bigquant.com/docs/data_instruments.html
instruments = D.instruments(start_date, split_date)
#
#
#
#
#
机器学习目标标注函数
如下标注函数等价于 min(max((持有期间的收益 * 100), -20), 20) + 20 (后面的M.fast_auto_labeler会做取整操作)
说明:max/min这里将标注分数限定在区间[-20, 20],+20将分数变为非负数 (StockRanker要求标注分数非负整数)
label_expr = ['return * 100', 'where(label > {0}, {0}, where(label < -{0}, -{0}, label)) + {0}'.format(20)]
持有天数,用于计算label_expr中的return值(收益)
hold_days = 5
#
#
特征 https://bigquant.com/docs/data_features.html,你可以通过表达式构造任何特征
features = [
rank_market_cap_0', # 总市值排名
'
]
#
给数据做标注:给每一行数据(样本)打分,一般分数越高表示越好
m1 = M.fast_auto_labeler.v8(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.split_date,
label_expr=conf.label_expr, hold_days=conf.hold_days,
benchmark='000300.SHA', sell_at='open', buy_at='open')
#
计算特征数据
m2 = M.general_feature_extractor.v5(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.split_date,
features=conf.features)
#
数据预处理:缺失数据处理,数据规范化,T.get_stock_ranker_default_transforms为StockRanker模型做数据预处理
m3 = M.transform.v2(

data=m2.data, transforms=T.get_stock_ranker_default_transforms(),
drop_null=True, astype='int32', except_columns=['date', 'instrument'],
clip_lower=0, clip_upper=200000000)
#
合并标注和特征数据
m4 = M.join.v2(data1=m1.data, data2=m3.data, on=['date', 'instrument'], sort=True)
StockRanker机器学习训练
m5 = M.stock_ranker_train.v3(training_ds=m4.data, features=conf.features)
#
#
#
# 量化回测 https://bigquant.com/docs/module_trade.html
回测引擎:准备数据,只执行一次
def prepare(context):
#
context.start_date / end_date,回测的时候,为trader传入参数;在实盘运行的时候,由系统替换为实盘日期
n1 = M.general_feature_extractor.v5(
instruments=D.instruments(),
start_date=context.start_date, end_date=context.end_date,
model_id=context.options['model_id'])
n2 = M.transform.v2(
data=n1.data, transforms=T.get_stock_ranker_default_transforms(),
drop_null=True, astype='int32', except_columns=['date', 'instrument'],
clip_lower=0, clip_upper=200000000)
n3 = M.stock_ranker_predict.v2(model_id=context.options['model_id'], data=n2.data)
context.instruments = n3.instruments
context.options['predictions'] = n3.predictions
#
回测引擎:初始化函数,只执行一次
def initialize(context):
加载预测数据
context.ranker_prediction = context.options['predictions'].read_df()
#
#
系统已经设置了默认的交易手续费和滑点,要修改手续费可使用如下函数
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
#
#
预测数据,通过options传入进来,使用 read_df 函数,加载到内存 (DataFrame)
设置买入的股票数量,这里买入预测股票列表排名靠前的5只
stock_count = 5
每只的股票的权重,如下的权重分配会使得靠前的股票分配多一点的资金,[0.339160, 0.213986, 0.169580, ..]
context.stock_weights = T.norm([1 / math.log(i + 2) for i in range(0, stock_count)])
设置每只股票占用的最大资金比例
#
#
context.max_cash_per_instrument = 0.2
#
回测引擎:每日数据处理函数,每天执行一次
def handle_data(context, data):
#
按日期过滤得到今日的预测数据
ranker_prediction = context.ranker_prediction[
context.ranker_prediction.date == data.current_dt.strftime('%Y-%m-%d')]
#
#
#
1. 资金分配
平均持仓时间是hold_days,每日都将买入股票,每日预期使用 1/hold_days 的资金
实际操作中,会存在一定的买入误差,所以在前hold_days天,等量使用资金;之后,尽量使用剩余资金(这里设置最多用等量的1.5倍)
is_staging = context.trading_day_index < context.options['hold_days'] # 是否在建仓期间(前 hold_days 天)
cash_avg = context.portfolio.portfolio_value / context.options['hold_days']
cash_for_buy = min(context.portfolio.cash, (1 if is_staging else 1.5) * cash_avg)
cash_for_sell = cash_avg - (context.portfolio.cash - cash_for_buy)
positions = {e.symbol: p.amount * p.last_sale_price
for e, p in context.portfolio.positions.items()}
#
2. 生成卖出订单:hold_days天之后才开始卖出;对持仓的股票,按StockRanker预测的排序末位淘汰
if not is_staging and cash_for_sell > 0:
equities = {e.symbol: e for e, p in context.portfolio.positions.items()}
instruments = list(reversed(list(ranker_prediction.instrument[ranker_prediction.instrument.apply(
lambda x: x in equities and not context.has_unfinished_sell_order(equities[x]))])))
#
print('rank order for sell %s' % instruments)
for instrument in instruments:
context.order_target(context.symbol(instrument), 0)
cash_for_sell -= positions[instrument]
if cash_for_sell <= 0:
break
#
3. 生成买入订单:按StockRanker预测的排序,买入前面的stock_count只股票
buy_cash_weights = context.stock_weights
buy_instruments = list(ranker_prediction.instrument[:len(buy_cash_weights)])
max_cash_per_instrument = context.portfolio.portfolio_value * context.max_cash_per_instrument
for i, instrument in enumerate(buy_instruments):
cash = cash_for_buy * buy_cash_weights[i]
if cash > max_cash_per_instrument - positions.get(instrument, 0):
#
确保股票持仓量不会超过每次股票最大的占用资金量
cash = max_cash_per_instrument - positions.get(instrument, 0)
if cash > 0:
context.order_value(context.symbol(instrument), cash)
#
调用交易引擎

m6 = M.trade.v2(
instruments=None,
start_date=conf.split_date,
end_date=conf.end_date,
prepare=prepare,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='close',
capital_base=1000000,
benchmark='000300.SHA',
# 表示 开盘 时买入
# 表示 收盘 前卖出
# 初始资金
# 比较基准,不影响回测结果
#
通过 options 参数传递预测数据和参数给回测引擎
options={'hold_days': conf.hold_days, 'model_id': m5.model_id}
)
[
[
2017-10-26 17:16:10.856468] INFO: bigquant: fast_auto_labeler.v8 开始运行..
2017-10-26 17:16:10.909450] INFO: bigquant: 命中缓存
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
2017-10-26 17:16:10.928554] INFO: bigquant: fast_auto_labeler.v8 运行完成[0.073522s].
2017-10-26 17:16:10.994995] INFO: bigquant: general_feature_extractor.v5 开始运行..
2017-10-26 17:16:17.233126] INFO: general_feature_extractor: year 2014, featurerows=569948
2017-10-26 17:16:23.569173] INFO: general_feature_extractor: year 2015, featurerows=569698
2017-10-26 17:16:24.427619] INFO: general_feature_extractor: year 2016, featurerows=0
2017-10-26 17:16:24.445451] INFO: general_feature_extractor: total feature rows: 1139646
2017-10-26 17:16:24.448550] INFO: bigquant: general_feature_extractor.v5 运行完成[13.453584s].
2017-10-26 17:16:24.478864] INFO: bigquant: transform.v2 开始运行..
2017-10-26 17:16:24.967762] INFO: transform: transformed /y_2014, 569948/569948
2017-10-26 17:16:25.379642] INFO: transform: transformed /y_2015, 569698/569698
2017-10-26 17:16:25.411989] INFO: transform: transformed rows: 1139646/1139646
2017-10-26 17:16:25.438369] INFO: bigquant: transform.v2 运行完成[0.95954s].
2017-10-26 17:16:25.454377] INFO: bigquant: join.v2 开始运行..
2017-10-26 17:16:37.832093] INFO: join: /y_2014, rows=567861/569948, timetaken=2.826289s
2017-10-26 17:16:40.130160] INFO: join: /y_2015, rows=543963/569698, timetaken=2.22513s
2017-10-26 17:16:40.236179] INFO: join: total result rows: 1111824
2017-10-26 17:16:40.238932] INFO: bigquant: join.v2 运行完成[14.784538s].
2017-10-26 17:16:40.261549] INFO: bigquant: stock_ranker_train.v3 开始运行..
2017-10-26 17:16:41.276647] INFO: df2bin: prepare data: training ..
2017-10-26 17:16:51.326047] INFO: stock_ranker_train: 6029679c training: 1111824 rows
2017-10-26 17:18:19.825988] INFO: bigquant: stock_ranker_train.v3 运行完成[99.564195s].
2017-10-26 17:18:19.911667] INFO: bigquant: backtest.v7 开始运行..
2017-10-26 17:18:19.949332] INFO: bigquant: general_feature_extractor.v5 开始运行..
2017-10-26 17:18:21.264401] INFO: general_feature_extractor: year 2016, featurerows=641546
2017-10-26 17:19:05.947737] INFO: general_feature_extractor: year 2017, featurerows=385417
2017-10-26 17:19:05.981140] INFO: general_feature_extractor: total feature rows: 1026963
2017-10-26 17:19:05.988842] INFO: bigquant: general_feature_extractor.v5 运行完成[46.039477s].
2017-10-26 17:19:06.011547] INFO: bigquant: transform.v2 开始运行..
2017-10-26 17:19:06.975859] INFO: transform: transformed /y_2016, 641546/641546
2017-10-26 17:19:07.300161] INFO: transform: transformed /y_2017, 385417/385417
2017-10-26 17:19:07.317819] INFO: transform: transformed rows: 1026963/1026963
2017-10-26 17:19:07.332825] INFO: bigquant: transform.v2 运行完成[1.321306s].
2017-10-26 17:19:07.348135] INFO: bigquant: stock_ranker_predict.v2 开始运行..
2017-10-26 17:19:08.095533] INFO: df2bin: prepare data: prediction ..
2017-10-26 17:19:20.970389] INFO: stock_ranker_predict: prediction: 1026963 rows
2017-10-26 17:19:28.481786] INFO: bigquant: stock_ranker_predict.v2 运行完成[21.13364s].
2017-10-26 17:20:10.426804] INFO: Performance: Simulated 375 trading days out of 375.
2017-10-26 17:20:10.428657] INFO: Performance: first open: 2016-01-04 14:30:00+00:00
2017-10-26 17:20:10.429906] INFO: Performance: last close: 2017-07-18 19:00:00+00:00
注意] 有 1 笔卖出是在多天内完成的。当日卖出股票超过了当日股票交易的2.5%会出现这种情况。
[
2017-10-26 17:20:13.009438] INFO: bigquant: backtest.v7 运行完成[113.097711s].
1
.等权重买入股票¶
在基础策略中,排序靠前的股票买入资金权重会大一些,那么如果想等权重买入,应该怎样处理呢?
In [2]:
#
#
操作非常简单,如下处理:
假设买入股票为10只
weight = 1/10
context.order_target_percent(sid,1/10)
#
#
使用order_target_percent下单接口即可,更多下单接口请参看以下链接:
https://bigquant.com/docs/module_trade.html#order-method-section
File "<ipython-input-2-292e306e642e>", line 4
context.order_target_percent(sid,1/10)
^
SyntaxError: invalid character in identifier

2
.修改买入卖出时间¶
买入时间由order_price_field_buy 参数决定,如果为'open'表示以开盘价买入,买入时间就为开盘时间,'high','low','close'比较好理解
卖出时间由order_price_field_sell 参数决定,如果为'close'表示以收盘价卖出,卖出时间就为收盘时间,'high','low','open'比较好理解
In [ ]:
#
如果想实现收盘时候买入,收盘时间卖出
m6 = M.trade.v2(
instruments=None,
start_date=conf.split_date,
end_date=conf.end_date,
prepare=prepare,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='close',
order_price_field_sell='close',
capital_base=1000000,
benchmark='000300.SHA',
# 表示 收盘 时买入
# 表示 收盘 时卖出
options={'hold_days': conf.hold_days, 'model_id': m5.model_id}
)
3
.隔几天运行一次¶
由于handle_data函数是每个交易日都会运行一次,那么如果想隔几天运行一次,相当于隔几天进行一下买入卖出交易,此时应该怎样修改代码呢?
In [ ]:
#
#
# 非常简单,这里我们的目的是不用每天运行handle_data函数,而是隔几天运行一次。一个极为简单的方法就是在handle_data函数中,加入一个判断条件,
# 如果达到判断条件就返回(return),这样就实现了当天不运行handle_data函数的目的。
def handle_data(context, data):
#
#
------------------------START:加入下面if的两行代码到之前的handle_data函数的最前部分即可-------------------
相隔几天(以3举例)运行一下handle_data函数
if context.trading_day_index % 3 != 0:
return
#
------------------------END:加上这两句代码在handle_data函数就能实现隔几天运行下该函数的目的---------------------
#
按日期过滤得到今日的预测数据
ranker_prediction = context.ranker_prediction[
context.ranker_prediction.date == data.current_dt.strftime('%Y-%m-%d')]
#
#
#
1. 资金分配
平均持仓时间是hold_days,每日都将买入股票,每日预期使用 1/hold_days 的资金
实际操作中,会存在一定的买入误差,所以在前hold_days天,等量使用资金;之后,尽量使用剩余资金(这里设置最多用等量的1.5倍)
is_staging = context.trading_day_index < context.options['hold_days'] # 是否在建仓期间(前 hold_days 天)
cash_avg = context.portfolio.portfolio_value / context.options['hold_days']
cash_for_buy = min(context.portfolio.cash, (1 if is_staging else 1.5) * cash_avg)
cash_for_sell = cash_avg - (context.portfolio.cash - cash_for_buy)
positions = {e.symbol: p.amount * p.last_sale_price
for e, p in context.portfolio.positions.items()}
#
2. 生成卖出订单:hold_days天之后才开始卖出;对持仓的股票,按StockRanker预测的排序末位淘汰
if not is_staging and cash_for_sell > 0:
equities = {e.symbol: e for e, p in context.portfolio.positions.items()}
instruments = list(reversed(list(ranker_prediction.instrument[ranker_prediction.instrument.apply(
lambda x: x in equities and not context.has_unfinished_sell_order(equities[x]))])))
#
print('rank order for sell %s' % instruments)
for instrument in instruments:
context.order_target(context.symbol(instrument), 0)
cash_for_sell -= positions[instrument]
if cash_for_sell <= 0:
break
#
3. 生成买入订单:按StockRanker预测的排序,买入前面的stock_count只股票
buy_cash_weights = context.stock_weights
buy_instruments = list(ranker_prediction.instrument[:len(buy_cash_weights)])
max_cash_per_instrument = context.portfolio.portfolio_value * context.max_cash_per_instrument
for i, instrument in enumerate(buy_instruments):
cash = cash_for_buy * buy_cash_weights[i]
if cash > max_cash_per_instrument - positions.get(instrument, 0):
#
确保股票持仓量不会超过每次股票最大的占用资金量
cash = max_cash_per_instrument - positions.get(instrument, 0)
if cash > 0:
context.order_value(context.symbol(instrument), cash)
#
调用交易引擎
m6 = M.trade.v2(

instruments=None,
start_date=conf.split_date,
end_date=conf.end_date,
prepare=prepare,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='close',
capital_base=1000000,
# 表示 开盘 时买入
# 表示 收盘 前卖出
# 初始资金
benchmark='000300.SHA',
# 比较基准,不影响回测结果
#
通过 options 参数传递预测数据和参数给回测引擎
options={'hold_days': conf.hold_days, 'model_id': m5.model_id}
)
4
.持有固定天数卖出¶
在基础策略中。对持仓的股票,按StockRanker预测的排序末位淘汰,现在我们修改卖出规则,按照持有固定天数(hold_days)进行卖出,只需在
handle_data函数中进行修改即可
In [ ]:
#
回测引擎:每日数据处理函数,每天执行一次
def handle_data(context, data):
按日期过滤得到今日的预测数据
#
ranker_prediction = context.ranker_prediction[
context.ranker_prediction.date == data.current_dt.strftime('%Y-%m-%d')]
#
#
#
1. 资金分配
平均持仓时间是hold_days,每日都将买入股票,每日预期使用 1/hold_days 的资金
实际操作中,会存在一定的买入误差,所以在前hold_days天,等量使用资金;之后,尽量使用剩余资金(这里设置最多用等量的1.5倍)
is_staging = context.trading_day_index < context.options['hold_days'] # 是否在建仓期间(前 hold_days 天)
cash_avg = context.portfolio.portfolio_value / context.options['hold_days']
cash_for_buy = min(context.portfolio.cash, (1 if is_staging else 1.5) * cash_avg)
positions = {e.symbol: p.amount * p.last_sale_price
for e, p in context.portfolio.positions.items()}
#
----------------------------START:持有固定天数卖出---------------------------
today = data.current_dt
不是建仓期(在前hold_days属于建仓期)
#
if not is_staging:
equities = {e.symbol: p for e, p in context.portfolio.positions.items() if p.amount>0}
for instrument in equities:
#
print('last_sale_date: ', equities[instrument].last_sale_date)
sid = equities[instrument].sid # 交易标的
#
今天和上次交易的时间相隔hold_days就全部卖出
if today-equities[instrument].last_sale_date>=datetime.timedelta(context.options['hold_days']) and data.can_trade(context
context.order_target_percent(sid, 0)
#
#
--------------------------------END:持有固定天数卖出---------------------------
3. 生成买入订单:按StockRanker预测的排序,买入前面的stock_count只股票
buy_cash_weights = context.stock_weights
buy_instruments = list(ranker_prediction.instrument[:len(buy_cash_weights)])
max_cash_per_instrument = context.portfolio.portfolio_value * context.max_cash_per_instrument
for i, instrument in enumerate(buy_instruments):
cash = cash_for_buy * buy_cash_weights[i]
if cash > max_cash_per_instrument - positions.get(instrument, 0):
#
确保股票持仓量不会超过每次股票最大的占用资金量
cash = max_cash_per_instrument - positions.get(instrument, 0)
if cash > 0:
context.order_value(context.symbol(instrument), cash)
#
调用交易引擎
m6 = M.trade.v2(
instruments=None,
start_date=conf.split_date,
end_date=conf.end_date,
prepare=prepare,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='close',
capital_base=1000000,
benchmark='000300.SHA',
# 表示 开盘 时买入
# 表示 收盘 前卖出
# 初始资金
# 比较基准,不影响回测结果
#
通过 options 参数传递预测数据和参数给回测引擎
options={'hold_days': conf.hold_days, 'model_id': m5.model_id}
)

5
. 一次性全仓买入股票,使现金为0,然后持有固定天数,换仓¶
换仓:卖出持仓股票,买入新的股票
在基础策略中,如果hold_days = 5,那么每天都需要买入20%仓位的股票,每天也需要卖出一定股票,每天滚动进行。但是,如果我只想在第一天买入100%
资金股票, 持有五天,这五天内什么都不操作,等到5天满了以后再进行全部换仓,这样如何修改策略代码呢?方法很简单,也是修改handle_data中的代
码。
In [ ]:
#
回测引擎:每日数据处理函数,每天执行一次
def handle_data(context, data):
#
相隔几天(hold_days)进行一下换仓
if context.trading_day_index % context.options['hold_days'] != 0:
return
#
按日期过滤得到今日的预测数据
ranker_prediction = context.ranker_prediction[
context.ranker_prediction.date == data.current_dt.strftime('%Y-%m-%d')]
#
目前持仓
positions = {e.symbol: p.amount * p.last_sale_price
for e, p in context.portfolio.positions.items()}
#
权重
buy_cash_weights = context.stock_weights
今日买入股票列表
stock_to_buy = list(ranker_prediction.instrument[:len(buy_cash_weights)])
持仓上限
max_cash_per_instrument = context.portfolio.portfolio_value * context.max_cash_per_instrument
#
#
#
通过positions对象,使用列表生成式的方法获取目前持仓的股票列表
stock_hold_now = [equity.symbol for equity in context.portfolio.positions ]
继续持有的股票:调仓时,如果买入的股票已经存在于目前的持仓里,那么应继续持有
no_need_to_sell = [i for i in stock_hold_now if i in stock_to_buy]
需要卖出的股票
stock_to_sell = [i for i in stock_hold_now if i not in no_need_to_sell]
#
#
#
卖出
for stock in stock_to_sell:
#
#
#
如果该股票停牌,则没法成交。因此需要用can_trade方法检查下该股票的状态
如果返回真值,则可以正常下单,否则会出错
因为stock是字符串格式,我们用symbol方法将其转化成平台可以接受的形式:Equity格式
if data.can_trade(context.symbol(stock)):
#
#
order_target_percent是平台的一个下单接口,表明下单使得该股票的权重为0,
即卖出全部股票,可参考回测文档
context.order_target_percent(context.symbol(stock), 0)
#
如果当天没有买入的股票,就返回
if len(stock_to_buy) == 0:
return
#
买入
for i, instrument in enumerate(stock_to_buy):
cash = context.portfolio.portfolio_value * buy_cash_weights[i]
if cash > max_cash_per_instrument - positions.get(instrument, 0):
#
确保股票持仓量不会超过每次股票最大的占用资金量
cash = max_cash_per_instrument - positions.get(instrument, 0)
if cash > 0:
context.order_value(context.symbol(instrument), cash)
#
调用交易引擎
m6 = M.trade.v2(
instruments=None,
start_date=conf.split_date,
end_date=conf.end_date,
prepare=prepare,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='close',
capital_base=1000000,
benchmark='000300.SHA',
# 表示 开盘 时买入
# 表示 收盘 前卖出
# 初始资金
# 比较基准,不影响回测结果
#
通过 options 参数传递预测数据和参数给回测引擎
options={'hold_days': conf.hold_days, 'model_id': m5.model_id}
)
6
.动态择时仓位调整¶
比如,根据市场状况,每天的买入股票的仓位并不是一成不变固定的,而是会依据市场情绪、新闻事件等进行动态调整

参考链接:
7
.止盈止损处理¶
在交易中,如果需要加入更多的进场出场规则,比如止盈止损
参考链接:
上一页:开发传统趋势策略
下一页:策略止盈止损
目录:BigQuant学院
【
宽客学院】策略止盈止损
止盈止损是交易中比较常用的技巧,想要用好也比较困难。本文对其进行简单介绍,帮助大家可以在策略里面灵活添加止盈止损。
止损又叫 “割肉”, 指的是当一个投资组合亏损达到一定比例及时清仓出局, 以免形成更大的亏损的行为。 止盈是指当盈利大于一定数额, 及时获利了结。
止盈止损为什么重要呢?
1
. 侥幸的心理作祟,某些投资者尽管也知道趋势上已经到止盈止损位,但由于过于犹豫,总是想再涨一点或再跌一点就止盈止损出局,导致自己错过最佳
止盈止损的大好时机;
2
. 价格频繁的波动会让投资者犹豫不决,经常性错误的止损止盈会给投资者留下挥之不去的记忆,从而动摇投资者下次止损止盈的决心;
3
. 过于贪婪,有些投资者在趋势已经到达止盈位置了之后总抱着还会有盈利的空间而不愿意刹车止盈。
在这里提供了几个简单的止盈止损方案的模板, 在写这些代码的时候考虑了用户的体验,用户只需将相应的代码复制粘贴到自己的策略中,并设置相关参数
就能正常使用。
我们先以固定点数止盈举例,请参看下面的策略:
In [1]:
#
策略参数
instruments = ['600793.SHA','000001.SZA']
start_date = '2014-05-28'
end_date = '2017-02-08'
In [2]:
#
策略主体
def initialize(context):
context.short_period = 5
context.long_period = 50
def handle_data(context, data):
date = data.current_dt.strftime('%Y-%m-%d')
#
----------------------------止赢模块START------------------------
positions = {e.symbol: p.cost_basis for e, p in context.portfolio.positions.items()}
新建当日止赢股票列表是为了handle_data 策略逻辑部分不再对该股票进行判断
#
current_stopwin_stock = []
if len(positions) > 0:
for i in positions.keys():
stock_cost = positions[i]
stock_market_price = data.current(context.symbol(i), 'price')
#
赚3元就止赢
if stock_market_price - stock_cost >= 3:
context.order_target_percent(context.symbol(i),0)
current_stopwin_stock.append(i)
#
print('日期:',date,'股票:',i,'出现止盈状况')
---------------------------止赢模块END---------------------------
#
if context.trading_day_index < context.long_period:
return
for k in instruments:
if k in current_stopwin_stock:
continue
sid = context.symbol(k)
price = data.current(sid, 'price')
short_mavg = data.history(sid, 'price',context.short_period, '1d').mean()
long_mavg = data.history(sid, 'price',context.long_period, '1d').mean()

cash = context.portfolio.cash / len(instruments)
cur_position = context.portfolio.positions[sid].amount
if short_mavg > long_mavg and cur_position == 0 and data.can_trade(sid):
context.order(sid, int(cash/price/100)*100)
elif short_mavg < long_mavg and cur_position > 0 and
context.order_target_percent(sid, 0)
data.can_trade(sid):
In [3]:
#
策略回测接口
m=M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='open',
capital_base=float("1.0e6"),
)
[
[
[
[
2017-09-28 16:57:30.895076] INFO: bigquant: backtest.v7 开始运行..
2017-09-28 16:57:38.816442] INFO: Performance: Simulated 659 trading days out of 659.
2017-09-28 16:57:38.818078] INFO: Performance: first open: 2014-05-28 13:30:00+00:00
2017-09-28 16:57:38.818921] INFO: Performance: last close: 2017-02-08 20:00:00+00:00
[
2017-09-28 16:57:41.113077] INFO: bigquant: backtest.v7 运行完成[10.218012s].
就是这样简单,只要在handle_data部分添加止盈止损模板代码就可以,模板代码我们整理到文末。
固定点数止盈
解释:建仓以后,当盈利固定点数,达到止盈条件,止盈出场
#
------------------------------------------止赢模块START--------------------------------------------
positions = {e.symbol: p.cost_basis for e, p in context.portfolio.positions.items()}
#
新建当日止赢股票列表是为了handle_data 策略逻辑部分不再对该股票进行判断
current_stopwin_stock = []
if len(positions) > 0:
for i in positions.keys():
stock_cost = positions[i]
stock_market_price = data.current(context.symbol(i), 'price')
#
赚3元就止赢
if stock_market_price - stock_cost >= 3:
context.order_target_percent(context.symbol(i),0)
current_stopwin_stock.append(i)
#
print('日期:',date,'股票:',i,'出现止盈状况')
#
-------------------------------------------止赢模块END---------------------------------------------
固定百分比止盈
解释:建仓以后,当盈利固定百分比,达到止盈条件,止盈出场
#
------------------------------------------止赢模块START--------------------------------------------
positions = {e.symbol: p.cost_basis for e, p in context.portfolio.positions.items()}
#
新建当日止赢股票列表是为了handle_data 策略逻辑部分不再对该股票进行判断
current_stopwin_stock = []
if len(positions) > 0:
for i in positions.keys():
stock_cost = positions[i]
stock_market_price = data.current(context.symbol(i), 'price')
#
赚10%就止赢
if (stock_market_price - stock_cost ) / stock_cost>= 0.1:
context.order_target_percent(context.symbol(i),0)
current_stopwin_stock.append(i)
print('日期:',date,'股票:',i,'出现止盈状况')
#
-------------------------------------------止赢模块END---------------------------------------------
固定点数止损
解释:建仓以后,当亏损固定点数,达到止损条件,止损出场
#
------------------------------------------止损模块START--------------------------------------------
positions = {e.symbol: p.cost_basis for e, p in context.portfolio.positions.items()}
#
新建当日止损股票列表是为了handle_data 策略逻辑部分不再对该股票进行判断
current_stoploss_stock = []
if len(positions) > 0:

for i in positions.keys():
stock_cost = positions[i]
stock_market_price = data.current(context.symbol(i), 'price')
#
亏1元就止损
if stock_market_price - stock_cost <= -1:
context.order_target_percent(context.symbol(i),0)
current_stoploss_stock.append(i)
print('日期:',date,'股票:',i,'出现止损状况')
#
-------------------------------------------止损模块END---------------------------------------------
固定百分比止损
解释:建仓以后,当亏损固定百分比时,达到止损条件,止损出场
#
------------------------------------------止损模块START--------------------------------------------
positions = {e.symbol: p.cost_basis for e, p in context.portfolio.positions.items()}
#
新建当日止损股票列表是为了handle_data 策略逻辑部分不再对该股票进行判断
current_stoploss_stock = []
if len(positions) > 0:
for i in positions.keys():
stock_cost = positions[i]
stock_market_price = data.current(context.symbol(i), 'price')
#
亏5%就止损
if (stock_market_price - stock_cost) / stock_cost <= -0.05:
context.order_target_percent(context.symbol(i),0)
current_stoploss_stock.append(i)
print('日期:',date,'股票:',i,'出现止损状况')
#
-------------------------------------------止损模块END---------------------------------------------
跟踪止损
解释:建仓初期,确定一个初始止损,如果股票下跌,达到初始止损条件,出场。如果股票上涨,那么初始止损不再适用,而是采取止损位置不断抬高的跟
踪止损,能够防止利润的大幅回吐
#
------------------------------------------止损模块START--------------------------------------------
today = data.current_dt
equities = {e.symbol: p for e, p in context.portfolio.positions.items() if p.amount>0}
#
新建当日止损股票列表是为了handle_data 策略逻辑部分不再对该股票进行判断
current_stoploss_stock = []
if len(equities) > 0:
for i in equities.keys():
stock_market_price = data.current(context.symbol(i), 'price') # 最新市场价格
last_sale_date = equities[i].last_sale_date
#
上次交易日期
delta_days = today - last_sale_date
hold_days = delta_days.days # 持仓天数
#
建仓以来的最高价
highest_price_since_buy = data.history(context.symbol(i), 'high', hold_days, '1d').max()
确定止损位置
#
stoploss_line = highest_price_since_buy - highest_price_since_buy * 0.1
record('止损位置', stoploss_line)
#
如果价格下穿止损位置
if stock_market_price < stoploss_line:
context.order_target_percent(context.symbol(i), 0)
current_stoploss_stock.append(i)
print('日期:', today, '股票:', i, '出现止损状况')
#
-------------------------------------------止损模块END---------------------------------------------
上一页:自定义买入卖出策略
下一页:回测数据深入分析
目录:BigQuant学院
宽客大学
宽客学院】回测数据深入分析
【
本文介绍如何对一个回测结果进行深入分析。
1
.策略完整代码
我们先看一个AI策略,以下是完整的策略代码。
In [42]:
#
基础参数配置
class conf:
start_date = '2014-01-01'

end_date='2017-08-01'
split_date 之前的数据用于训练,之后的数据用作效果评估
split_date = '2016-01-01'
D.instruments: https://bigquant.com/docs/data_instruments.html
instruments = D.instruments(start_date, split_date)
持有天数,用于计算label_expr中的return值(收益)
#
#
#
hold_days = 120
label_expr = ['return * 100/%s'%(np.sqrt(hold_days/3)), 'where(label > {0}, {0}, where(label < -{0}, -{0}, label)) + {0}'.format(
#
特征 https://bigquant.com/docs/data_features.html,你可以通过表达式构造任何特征
features = ['rank_pb_lf_0']
#
给数据做标注:给每一行数据(样本)打分,一般分数越高表示越好
m1 = M.fast_auto_labeler.v8(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.split_date,
label_expr=conf.label_expr, hold_days=conf.hold_days,
benchmark='000300.SHA', sell_at='open', buy_at='open')
#
计算特征数据
m2 = M.general_feature_extractor.v5(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.split_date,
features=conf.features)
#
数据预处理:缺失数据处理,数据规范化,T.get_stock_ranker_default_transforms为StockRanker模型做数据预处理
m3 = M.transform.v2(
data=m2.data, transforms=T.get_stock_ranker_default_transforms(),
drop_null=True, astype='int32', except_columns=['date', 'instrument'],
clip_lower=0, clip_upper=200000000)
#
合并标注和特征数据
m4 = M.join.v2(data1=m1.data, data2=m3.data, on=['date', 'instrument'], sort=True)
StockRanker机器学习训练
m5 = M.stock_ranker_train.v3(training_ds=m4.data, features=conf.features)
#
#
#
# 量化回测 https://bigquant.com/docs/module_trade.html
回测引擎:准备数据,只执行一次
def prepare(context):
#
context.start_date / end_date,回测的时候,为trader传入参数;在实盘运行的时候,由系统替换为实盘日期
n1 = M.general_feature_extractor.v5(
instruments=D.instruments(),
start_date=context.start_date, end_date=context.end_date,
model_id=context.options['model_id'])
n2 = M.transform.v2(
data=n1.data, transforms=T.get_stock_ranker_default_transforms(),
drop_null=True, astype='int32', except_columns=['date', 'instrument'],
clip_lower=0, clip_upper=200000000)
n3 = M.stock_ranker_predict.v2(model_id=context.options['model_id'], data=n2.data)
context.instruments = n3.instruments
context.options['predictions'] = n3.predictions
#
回测引擎:初始化函数,只执行一次
def initialize(context):
加载预测数据
context.ranker_prediction = context.options['predictions'].read_df()
#
#
系统已经设置了默认的交易手续费和滑点,要修改手续费可使用如下函数
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
#
#
预测数据,通过options传入进来,使用 read_df 函数,加载到内存 (DataFrame)
设置买入的股票数量,这里买入预测股票列表排名靠前的5只
stock_count = 5
每只的股票的权重,如下的权重分配会使得靠前的股票分配多一点的资金,[0.339160, 0.213986, 0.169580, ..]
context.stock_weights = T.norm([1 / math.log(i + 2) for i in range(0, stock_count)])
设置每只股票占用的最大资金比例
#
#
context.max_cash_per_instrument = 0.2
#
回测引擎:每日数据处理函数,每天执行一次
def handle_data(context, data):
#
按日期过滤得到今日的预测数据
ranker_prediction = context.ranker_prediction[
context.ranker_prediction.date == data.current_dt.strftime('%Y-%m-%d')]
#
#
#
1. 资金分配
平均持仓时间是hold_days,每日都将买入股票,每日预期使用 1/hold_days 的资金
实际操作中,会存在一定的买入误差,所以在前hold_days天,等量使用资金;之后,尽量使用剩余资金(这里设置最多用等量的1.5倍)
is_staging = context.trading_day_index < context.options['hold_days'] # 是否在建仓期间(前 hold_days 天)
cash_avg = context.portfolio.portfolio_value / context.options['hold_days']
cash_for_buy = min(context.portfolio.cash, (1 if is_staging else 1.5) * cash_avg)
cash_for_sell = cash_avg - (context.portfolio.cash - cash_for_buy)
positions = {e.symbol: p.amount * p.last_sale_price
for e, p in context.perf_tracker.position_tracker.positions.items()}
#
2. 生成卖出订单:hold_days天之后才开始卖出;对持仓的股票,按StockRanker预测的排序末位淘汰
if not is_staging and cash_for_sell > 0:
equities = {e.symbol: e for e, p in context.perf_tracker.position_tracker.positions.items()}
instruments = list(reversed(list(ranker_prediction.instrument[ranker_prediction.instrument.apply(

lambda x: x in equities and not context.has_unfinished_sell_order(equities[x]))])))
print('rank order for sell %s' % instruments)
#
for instrument in instruments:
context.order_target(context.symbol(instrument), 0)
cash_for_sell -= positions[instrument]
if cash_for_sell <= 0:
break
#
3. 生成买入订单:按StockRanker预测的排序,买入前面的stock_count只股票
buy_cash_weights = context.stock_weights
buy_instruments = list(ranker_prediction.instrument[:len(buy_cash_weights)])
max_cash_per_instrument = context.portfolio.portfolio_value * context.max_cash_per_instrument
for i, instrument in enumerate(buy_instruments):
cash = cash_for_buy * buy_cash_weights[i]
if cash > max_cash_per_instrument - positions.get(instrument, 0):
#
确保股票持仓量不会超过每次股票最大的占用资金量
cash = max_cash_per_instrument - positions.get(instrument, 0)
if cash > 0:
context.order_value(context.symbol(instrument), cash)
#
调用交易引擎
m6 = M.trade.v2(
instruments=None,
start_date=conf.split_date,
end_date=conf.end_date,
prepare=prepare,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='close',
capital_base=1000000,
benchmark='000300.SHA',
volume_limit=0,
# 表示 开盘 时买入
# 表示 收盘 前卖出
# 初始资金
# 比较基准,不影响回测结果
#
通过 options 参数传递预测数据和参数给回测引擎
options={'hold_days': conf.hold_days, 'model_id': m5.model_id}
)
[
[
2017-08-07 10:03:14.243168] INFO: bigquant: fast_auto_labeler.v8 start ..
2017-08-07 10:03:14.245613] INFO: bigquant: hit cache
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
2017-08-07 10:03:14.249525] INFO: bigquant: fast_auto_labeler.v8 end [0.006376s].
2017-08-07 10:03:14.254888] INFO: bigquant: general_feature_extractor.v5 start ..
2017-08-07 10:03:14.256411] INFO: bigquant: hit cache
2017-08-07 10:03:14.257181] INFO: bigquant: general_feature_extractor.v5 end [0.002295s].
2017-08-07 10:03:14.265135] INFO: bigquant: transform.v2 start ..
2017-08-07 10:03:14.266623] INFO: bigquant: hit cache
2017-08-07 10:03:14.267659] INFO: bigquant: transform.v2 end [0.002515s].
2017-08-07 10:03:14.273329] INFO: bigquant: join.v2 start ..
2017-08-07 10:03:14.274966] INFO: bigquant: hit cache
2017-08-07 10:03:14.275712] INFO: bigquant: join.v2 end [0.002384s].
2017-08-07 10:03:14.282638] INFO: bigquant: stock_ranker_train.v3 start ..
2017-08-07 10:03:14.284196] INFO: bigquant: hit cache
2017-08-07 10:03:14.284958] INFO: bigquant: stock_ranker_train.v3 end [0.002331s].
2017-08-07 10:03:14.302182] INFO: bigquant: backtest.v7 start ..
2017-08-07 10:03:14.303801] INFO: bigquant: hit cache
[
2017-08-07 10:03:15.411851] INFO: bigquant: backtest.v7 end [1.109634s].
2
. 回测结果
回测结果一般指策略运行完毕之后输出的能够综合反映策略效果的综合图表,如下所示:
可以看出,回测结果包括收益概括、交易详情、每日持仓、输出日志。
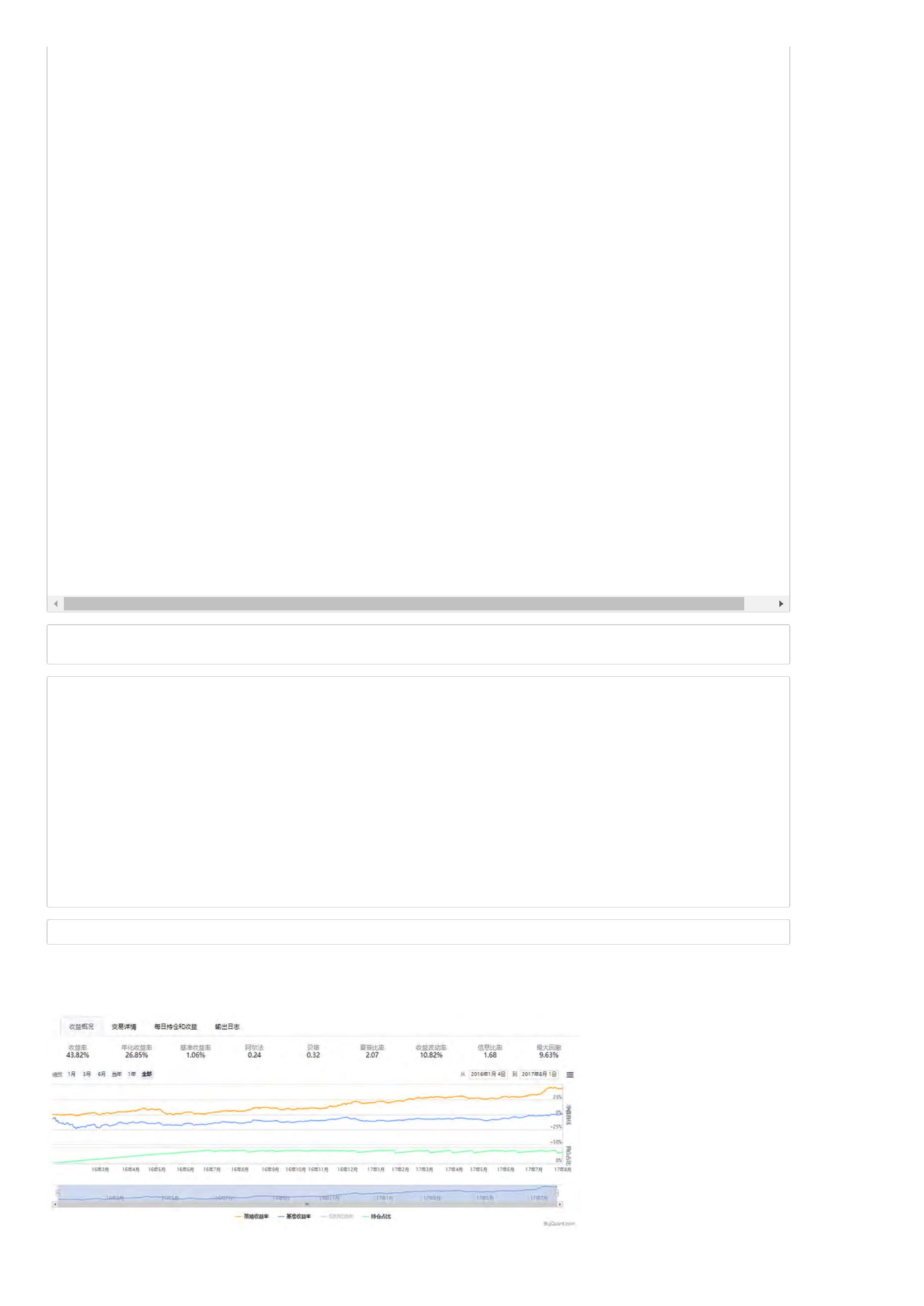
对回测结果进行深入分析需要一定的基础知识,如下:
回测结果的简单解读参考第三点即可,本文主要介绍怎样对回测数据进行深入分析以验证回测结果。
3
.读取回测详细数据
示例代码:
m6.raw_perf.read_df()
输出结果:
回测详细数据全部保存在m6.raw_perf对象中,为DataSource类型,因此需要使用read_df方法读取数据。该数据为时间序列数据,按交易日记录了详细信
息,主要包括三块数据:
策略相关,比如策略收益率、策略收益波动率、阿尔法、贝塔、夏普比率、信息比率、索提纳比率、基准收益率、基准收益波动率。
交易相关。每日账户权益、每日持仓详情、订单、交易成本、交易时间段。
起始资金、最终资金、每日盈亏、多头(空头)市值、多头(空头)风险暴露。
在策略回测结果图上,所有数据都是来自回测详细数据。
4
.回测数据深入分析技巧
检查策略杠杆是否正常
因为回测机制允许融资交易,当持仓市值超过总资金时借用资金杠杆,此时杠杆比率大于1,一方面可以通过 m6.raw_perf.read_df()[‘gross_leverage’] 查
询,一方面可以观察回测结果图。
在上图中,下方的绿色曲线表示策略的杠杆比率,可以看出杠杆比率几乎都是小于1,表明没有借用资金杠杆,同时看出,杠杆比率在前期缓慢提高,这正是
策略开始在建仓期间不断买入股票没有卖出直接相关。
抽样检查买入股票是否正确
通过回测结果查询的实际成交情况:
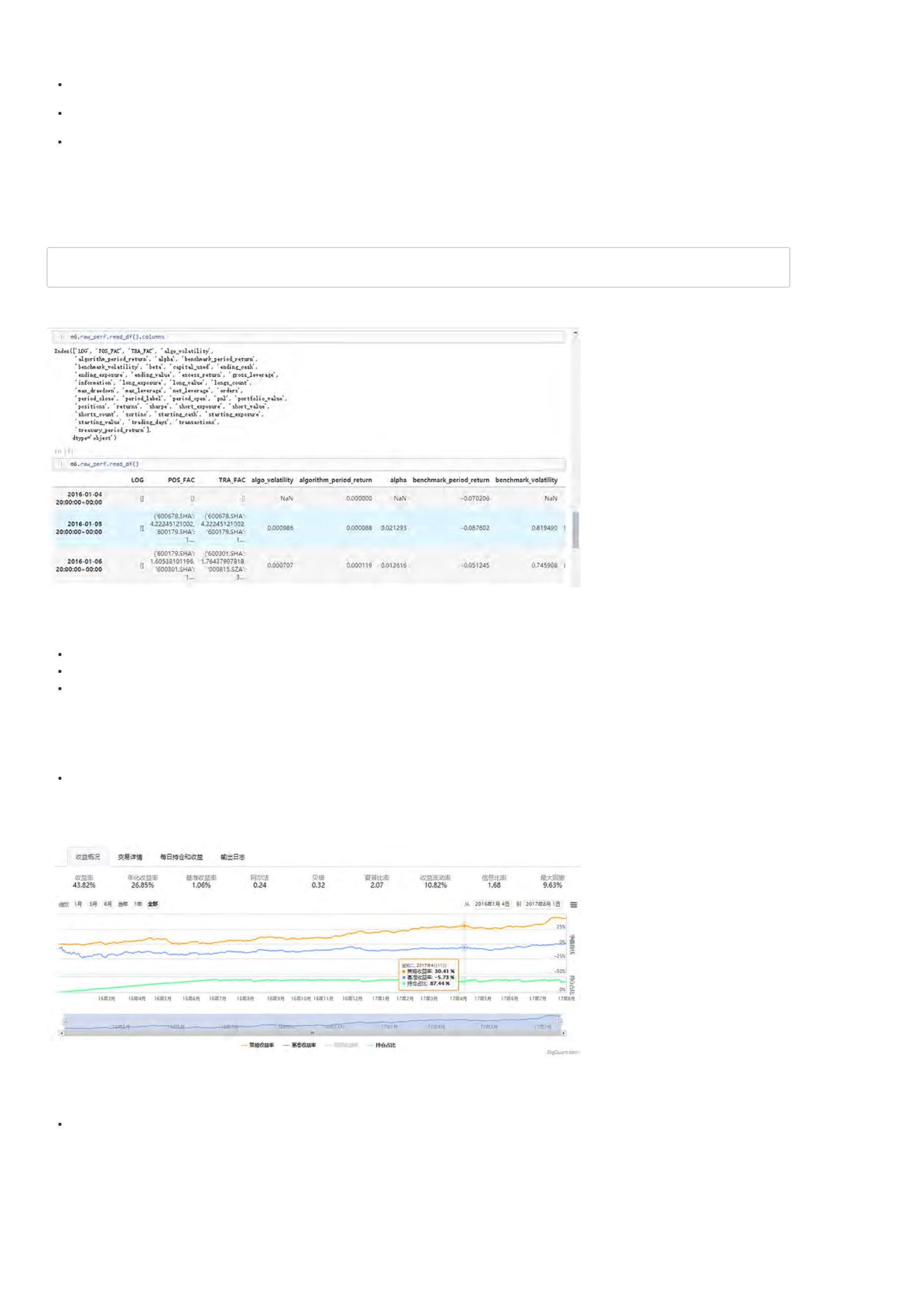
通过测试集预测结果验证买入股票:
因为是当日收盘以后,才能预测出下个交易日的股票排序,因此测试集预测结果当日的股票排序应该和下一个交易日的买入股票相对应。通过上面两图
的对比,抽样检查买入股票是正确的。
抽样检查买入价格是否是正确
通过交易详情,我们可以知道每只股票的买入价格,因此我们抽样验证股票买入价格,检查是否存在夸大策略收益的情形。我们先看2016-01-05买入的几只
股票的买入价。
通过数据API单独获取数据检验成交价格,之所以获取开盘价,是因为股票成交策略回测假设是开盘买入。
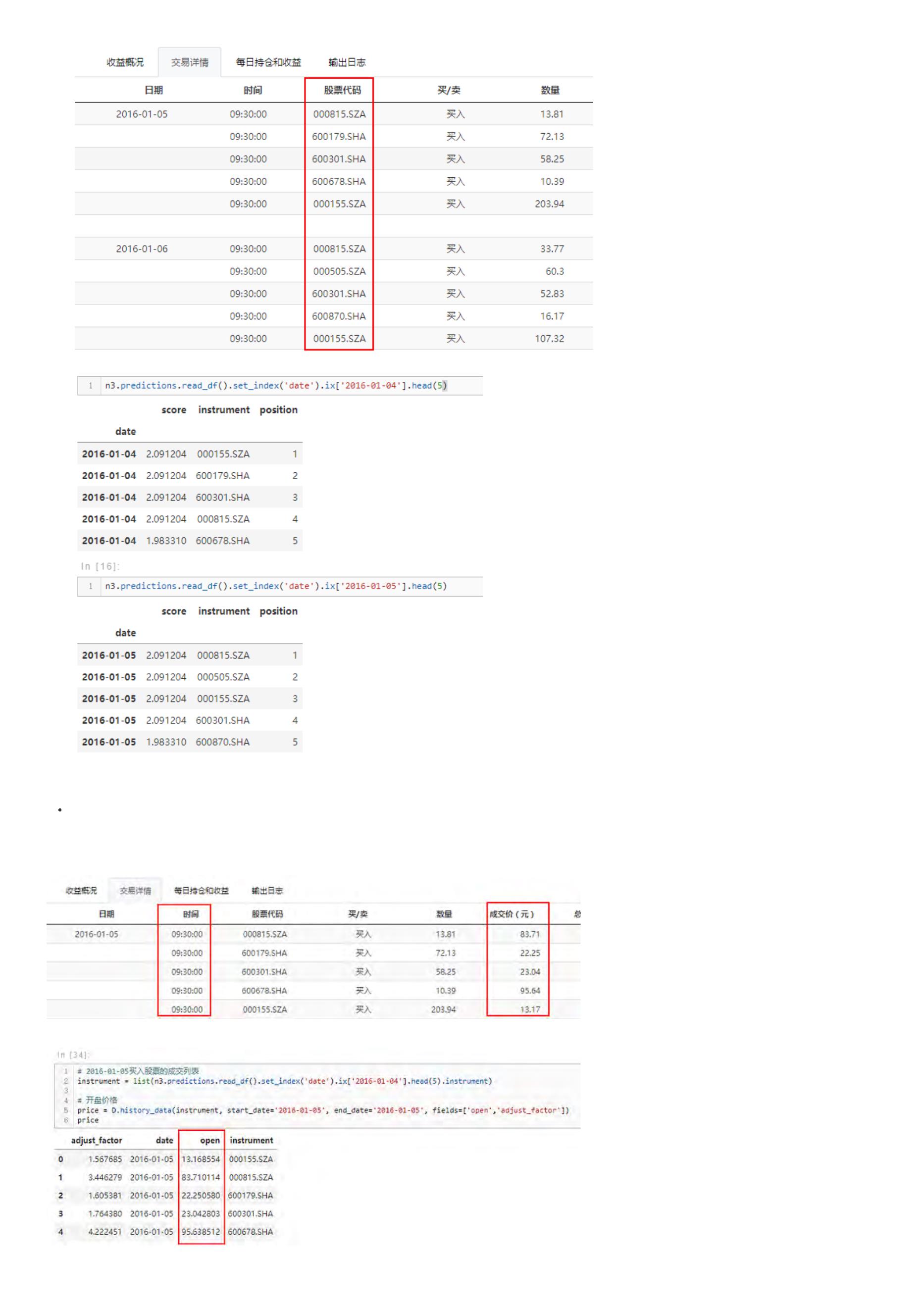
通过两图的对比,我们发现成交价格是正确的,回测过程中并没有偷价漏价的情形。
检查每只股票的成交金额是否正确
之所以检查成交金额,实际上是检查每只股票的仓位资金配置是否和策略的资金配置思想相一致。我们先看2016-01-05买入的5只股票的成交情况。
可以看出,当日买入股票的资金配置按高到低依次是:000155.SZA、600301.SHA、600179.SHA、000815.SZA、600678.SHA。
我们再看看,在测试集上当天的股票买入顺序是怎样的。
股票的买入顺序是根据股票得分(score)排序所得,得分高的股票优先买入,买入的仓位也会较大。从测试集上的股票排序顺序来看,和回测交给交易详情
是对应的,之所以600301.SHA和600179.SHA顺序略有差异这是因为测试集上股票得分相等。
检查手续费计算是否正确
手续费对策略收益率具有直接影响,如果交易频繁,持仓时间短,手续费设置不合理将会高估策略收益。因此需要对交易手续费进行检查。我们先看
2
016-01-05实际买入手续费。
在策略设置(initialize函数)中,策略手续费设置如下:
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
可以看出,买入股票交易费用为成交金额的万分之三,不足5元按5元收取。在2016-01-05买入的股票中,成交金额最大的股票为000155.SZA,成交金额为
2
685元,按照万三的手续费计算,手续费才0.8元。不足5元按五元收取,因此在手续费这块,回测试没有问题的。
抽样检查卖出股票是否正确以及卖出价格
卖出股票的股票核对以及卖出价格是否合理的检查这里不做介绍,同上述买入股票及买入价格是一样的方法。
通过代码查看回测细节
查看回测细节不仅可以通过回测结果点击可视化查询,还可以通过代码查询,查询的数据将会更加详细、深入,因为所有结果都是在m6.raw_perf.read_df()
中,所以通过该函数就可以知道全部回测细节。点击下方 “点击查看代码”通过代码运行来查看回测细节。
点击查看代码
输出结果为一个时间段上的每日持仓、每日订单、每日交易三个详细的信息,通过每日订单还能查询每个订单的具体成交结果,包括订单是否完全成交、是
否有未成交订单、是否有遇到涨跌停、停牌情形无法成交订单。输出详情点击 “点击查看图片”。
点击查看图片
上一页:策略止盈止损
下一页:使用滚动学习
目录:BigQuant学院
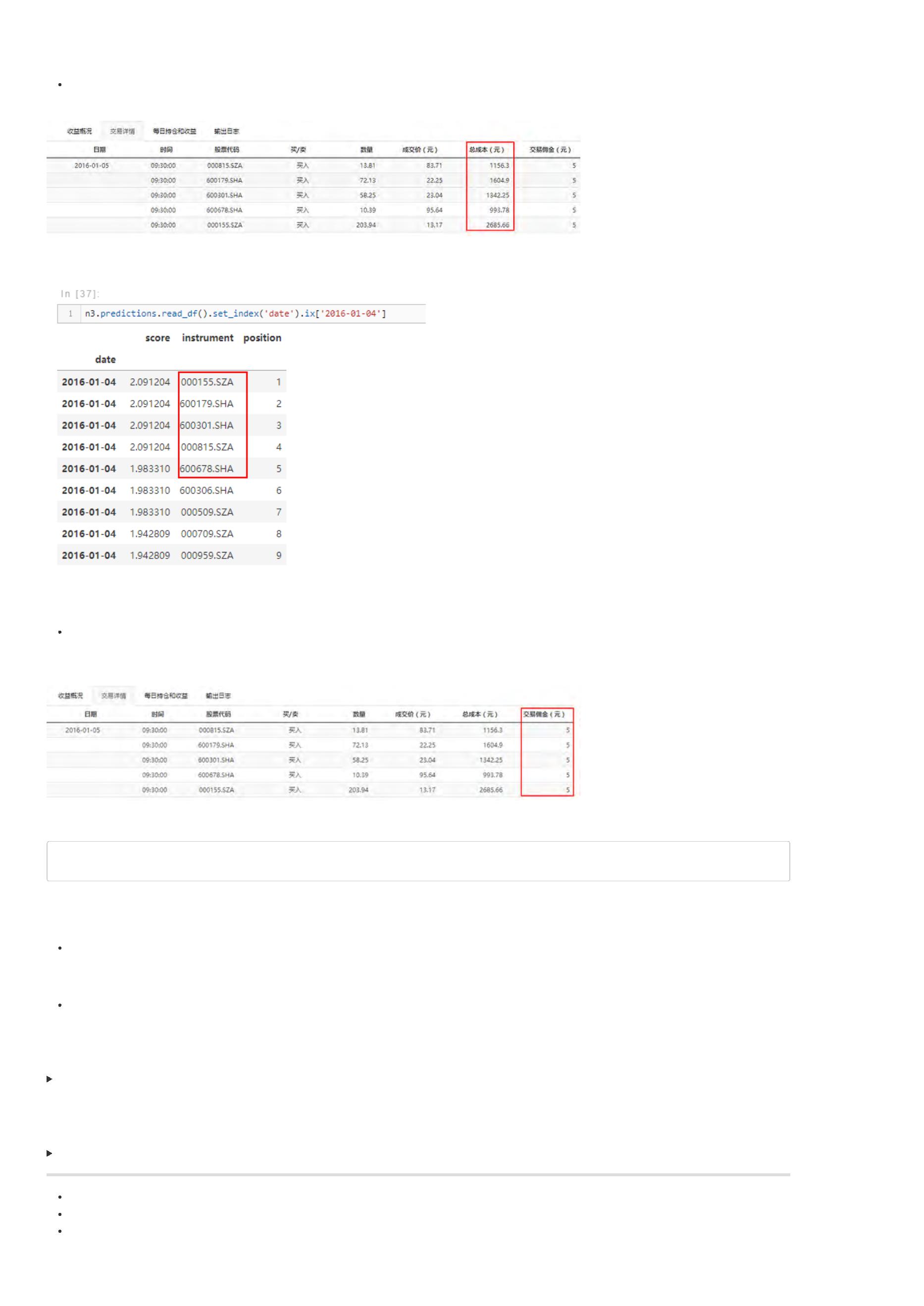
[
宽客学院]收益分析
本文主要介绍收益分析,包括风格因子收益分析和策略收益综合分析。
策略¶
In [3]:
#
基础参数配置
class conf:
start_date = '2014-01-01'
end_date='2017-08-01'
split_date 之前的数据用于训练,之后的数据用作效果评估
split_date = '2016-01-01'
D.instruments: https://bigquant.com/docs/data_instruments.html
instruments = D.instruments(start_date, split_date)
#
#
#
#
#
机器学习目标标注函数
如下标注函数等价于 min(max((持有期间的收益 * 100), -20), 20) + 20 (后面的M.fast_auto_labeler会做取整操作)
说明:max/min这里将标注分数限定在区间[-20, 20],+20将分数变为非负数 (StockRanker要求标注分数非负整数)
label_expr = ['return * 100', 'where(label > {0}, {0}, where(label < -{0}, -{0}, label)) + {0}'.format(20)]
持有天数,用于计算label_expr中的return值(收益)
hold_days = 5
#
#
特征 https://bigquant.com/docs/data_features.html,你可以通过表达式构造任何特征
features = [
rank_pb_lf_0', # 市净率排名
'
]
#
给数据做标注:给每一行数据(样本)打分,一般分数越高表示越好
m1 = M.fast_auto_labeler.v8(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.split_date,
label_expr=conf.label_expr, hold_days=conf.hold_days,
benchmark='000300.SHA', sell_at='open', buy_at='open')
#
计算特征数据
m2 = M.general_feature_extractor.v5(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.split_date,
features=conf.features)
#
数据预处理:缺失数据处理,数据规范化,T.get_stock_ranker_default_transforms为StockRanker模型做数据预处理
m3 = M.transform.v2(
data=m2.data, transforms=T.get_stock_ranker_default_transforms(),
drop_null=True, astype='int32', except_columns=['date', 'instrument'],
clip_lower=0, clip_upper=200000000)
#
合并标注和特征数据
m4 = M.join.v2(data1=m1.data, data2=m3.data, on=['date', 'instrument'], sort=True)
StockRanker机器学习训练
m5 = M.stock_ranker_train.v3(training_ds=m4.data, features=conf.features)
#
#
#
# 量化回测 https://bigquant.com/docs/module_trade.html
回测引擎:准备数据,只执行一次
def prepare(context):
#
context.start_date / end_date,回测的时候,为trader传入参数;在实盘运行的时候,由系统替换为实盘日期
n1 = M.general_feature_extractor.v5(
instruments=D.instruments(),
start_date=context.start_date, end_date=context.end_date,
model_id=context.options['model_id'])
n2 = M.transform.v2(
data=n1.data, transforms=T.get_stock_ranker_default_transforms(),
drop_null=True, astype='int32', except_columns=['date', 'instrument'],
clip_lower=0, clip_upper=200000000)
n3 = M.stock_ranker_predict.v2(model_id=context.options['model_id'], data=n2.data)
context.instruments = n3.instruments
context.options['predictions'] = n3.predictions
#
回测引擎:初始化函数,只执行一次
def initialize(context):
加载预测数据
context.ranker_prediction = context.options['predictions'].read_df()
#
#
系统已经设置了默认的交易手续费和滑点,要修改手续费可使用如下函数
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
#
#
预测数据,通过options传入进来,使用 read_df 函数,加载到内存 (DataFrame)
设置买入的股票数量,这里买入预测股票列表排名靠前的5只
stock_count = 5
每只的股票的权重,如下的权重分配会使得靠前的股票分配多一点的资金,[0.339160, 0.213986, 0.169580, ..]
context.stock_weights = T.norm([1 / math.log(i + 2) for i in range(0, stock_count)])
设置每只股票占用的最大资金比例
#
#
context.max_cash_per_instrument = 0.2
#
回测引擎:每日数据处理函数,每天执行一次

def handle_data(context, data):
按日期过滤得到今日的预测数据
#
ranker_prediction = context.ranker_prediction[
context.ranker_prediction.date == data.current_dt.strftime('%Y-%m-%d')]
#
#
#
1. 资金分配
平均持仓时间是hold_days,每日都将买入股票,每日预期使用 1/hold_days 的资金
实际操作中,会存在一定的买入误差,所以在前hold_days天,等量使用资金;之后,尽量使用剩余资金(这里设置最多用等量的1.5倍)
is_staging = context.trading_day_index < context.options['hold_days'] # 是否在建仓期间(前 hold_days 天)
cash_avg = context.portfolio.portfolio_value / context.options['hold_days']
cash_for_buy = min(context.portfolio.cash, (1 if is_staging else 1.5) * cash_avg)
cash_for_sell = cash_avg - (context.portfolio.cash - cash_for_buy)
positions = {e.symbol: p.amount * p.last_sale_price
for e, p in context.perf_tracker.position_tracker.positions.items()}
#
2. 生成卖出订单:hold_days天之后才开始卖出;对持仓的股票,按StockRanker预测的排序末位淘汰
if not is_staging and cash_for_sell > 0:
equities = {e.symbol: e for e, p in context.perf_tracker.position_tracker.positions.items()}
instruments = list(reversed(list(ranker_prediction.instrument[ranker_prediction.instrument.apply(
lambda x: x in equities and not context.has_unfinished_sell_order(equities[x]))])))
#
print('rank order for sell %s' % instruments)
for instrument in instruments:
context.order_target(context.symbol(instrument), 0)
cash_for_sell -= positions[instrument]
if cash_for_sell <= 0:
break
#
3. 生成买入订单:按StockRanker预测的排序,买入前面的stock_count只股票
buy_cash_weights = context.stock_weights
buy_instruments = list(ranker_prediction.instrument[:len(buy_cash_weights)])
max_cash_per_instrument = context.portfolio.portfolio_value * context.max_cash_per_instrument
for i, instrument in enumerate(buy_instruments):
cash = cash_for_buy * buy_cash_weights[i]
if cash > max_cash_per_instrument - positions.get(instrument, 0):
#
确保股票持仓量不会超过每次股票最大的占用资金量
cash = max_cash_per_instrument - positions.get(instrument, 0)
if cash > 0:
context.order_value(context.symbol(instrument), cash)
#
调用交易引擎
m6 = M.trade.v2(
instruments=None,
start_date=conf.split_date,
end_date=conf.end_date,
prepare=prepare,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='close',
capital_base=1000000,
benchmark='000300.SHA',
# 表示 开盘 时买入
# 表示 收盘 前卖出
# 初始资金
# 比较基准,不影响回测结果
#
通过 options 参数传递预测数据和参数给回测引擎
options={'hold_days': conf.hold_days, 'model_id': m5.model_id}
)
[
[
2017-08-22 15:10:52.809604] INFO: bigquant: fast_auto_labeler.v8 start ..
2017-08-22 15:10:52.813744] INFO: bigquant: hit cache
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
2017-08-22 15:10:52.818070] INFO: bigquant: fast_auto_labeler.v8 end [0.008488s].
2017-08-22 15:10:52.824175] INFO: bigquant: general_feature_extractor.v5 start ..
2017-08-22 15:10:52.826925] INFO: bigquant: hit cache
2017-08-22 15:10:52.827668] INFO: bigquant: general_feature_extractor.v5 end [0.003485s].
2017-08-22 15:10:52.836795] INFO: bigquant: transform.v2 start ..
2017-08-22 15:10:52.838611] INFO: bigquant: hit cache
2017-08-22 15:10:52.839817] INFO: bigquant: transform.v2 end [0.003009s].
2017-08-22 15:10:52.846279] INFO: bigquant: join.v2 start ..
2017-08-22 15:10:52.849368] INFO: bigquant: hit cache
2017-08-22 15:10:52.850178] INFO: bigquant: join.v2 end [0.003891s].
2017-08-22 15:10:52.857387] INFO: bigquant: stock_ranker_train.v3 start ..
2017-08-22 15:10:52.858994] INFO: bigquant: hit cache
2017-08-22 15:10:52.859805] INFO: bigquant: stock_ranker_train.v3 end [0.002419s].
2017-08-22 15:10:52.877060] INFO: bigquant: backtest.v7 start ..
2017-08-22 15:10:52.879577] INFO: bigquant: hit cache
[
2017-08-22 15:10:53.932540] INFO: bigquant: backtest.v7 end [1.055454s].
1
.风格因子收益分析¶
风格因子收益分析,即将组合收益归因在各个因子上,因子为:

市场因子,股票收益对基准组合(沪深300)的敏感度
财务质量因子,可以整体反映出公司的财务质量。
成长因子,通过财务指标反映出公司的成长性。
股东因子,公司户均持股比例因子。
杠杆因子,公司债务相对于其总资产的比例。
流动性因子,交易的活跃程度和流动性。
动量因子,股票价格变化的总体趋势特征。
规模因子,公司总市值。
价值因子,股票的投资价值。
波动率因子,股票价格变化幅度的度量。
In [7]:
m6.factor_profit_analyze() # 查看某个风格因子的收益,鼠标点击该因子的图例(文字)即可。
2
.策略收益综合分析¶
策略综合分析是对整个策略回测结果分析,主要包括 策略收益综合分析 和策略风险风险分析:
回测相关指标,比如年化收益、收益波动率、夏普比率、最大回撤、偏度、峰度、索提纳比率、信息比率、贝塔、阿尔法
最严重的前五次回撤,包括回撤时间段、回撤幅度、回撤天数
日收益折线图
月度收益率、年度收益率、月度收益分布图
日收益茎叶图、周收益茎叶图、年收益茎叶图
盈利最大前10股票
多头市值与空头市值
每日持仓股票数、每日杠杆、每日换手率、每日交易额
In [6]:
m6.pyfolio_full_tear_sheet()
Entire data start date: 2016-01-04
Entire data end date: 2017-08-01
Backtest Months: 18
Performance statistics
cum_returns_final
annual_return
annual_volatility
sharpe_ratio
Backtest
0.27
0.17
0.18
0.95
0.82
0.82
-0.21
1.23
1.27
-1.24
9.29
1.00
1.17
2.22
calmar_ratio
stability_of_timeseries
max_drawdown
omega_ratio
sortino_ratio
skew
kurtosis
tail_ratio
common_sense_ratio
information_ratio

Performance statistics
Backtest
0.72
alpha
beta
0.02
Worst Drawdown Periods
net drawdown in %
peak date
2016-01-06
2016-04-18
2017-04-05
2017-01-09
2016-09-05
valley date
2016-01-28
2016-05-24
2017-05-11
2017-01-16
2016-09-30
recovery date
2016-04-06
2016-08-16
2017-07-12
2017-02-20
2016-11-16
duration
66
0
1
2
3
4
20.67
8.53
5.69
5.22
3.72
87
71
31
53
[
-0.022 -0.052]
Stress Events
New Normal
mean
min
max
0.07%
-6.28%
4.84%
Top 10 long positions of all time
Equity(1881 [600179.SHA])
Equity(3257 [000505.SZA])
Equity(549 [000155.SZA])
Equity(2733 [000815.SZA])
Equity(2265 [600725.SHA])
Equity(21 15 [000968.SZA])
Equity(1401 [002306.SZA])
Equity(2807 [600319.SHA])
Equity(2781 [600581.SHA])
Equity(2994 [600301.SHA])
max
24.20%
22.55%
22.34%
21.55%
21.06%
21.00%
20.98%
20.91%
20.90%
20.85%
Top 10 short positions of all time
max
Top 10 positions of all time
Equity(1881 [600179.SHA])
Equity(3257 [000505.SZA])
Equity(549 [000155.SZA])
Equity(2733 [000815.SZA])
Equity(2265 [600725.SHA])
Equity(21 15 [000968.SZA])
Equity(1401 [002306.SZA])
Equity(2807 [600319.SHA])
Equity(2781 [600581.SHA])
Equity(2994 [600301.SHA])
max
24.20%
22.55%
22.34%
21.55%
21.06%
21.00%
20.98%
20.91%
20.90%
20.85%
All positions ever held
max
Equity(1881 [600179.SHA])
Equity(3257 [000505.SZA])
Equity(549 [000155.SZA])
Equity(2733 [000815.SZA])
Equity(2265 [600725.SHA])
Equity(21 15 [000968.SZA])
24.20%
22.55%
22.34%
21.55%
21.06%
21.00%

All positions ever held
max
Equity(1401 [002306.SZA])
Equity(2807 [600319.SHA])
Equity(2781 [600581.SHA])
Equity(2994 [600301.SHA])
Equity(1215 [000001.SZA])
Equity(1 18 [600755.SHA])
Equity(3202 [601288.SHA])
Equity(1065 [600603.SHA])
Equity(2401 [000422.SZA])
Equity(2917 [600016.SHA])
Equity(974 [600339.SHA])
Equity(1288 [601988.SHA])
Equity(215 [601898.SHA])
Equity(2176 [000898.SZA])
Equity(3291 [600269.SHA])
Equity(1604 [601328.SHA])
Equity(2856 [601818.SHA])
Equity(2860 [000709.SZA])
Equity(347 [600015.SHA])
Equity(497 [600019.SHA])
Equity(453 [601998.SHA])
Equity(3 [601398.SHA])
20.98%
20.91%
20.90%
20.85%
20.81%
20.71%
20.59%
20.50%
20.45%
20.41%
20.38%
20.35%
20.32%
20.20%
20.16%
20.15%
20.15%
20.12%
19.99%
19.95%
19.88%
19.87%
19.57%
19.19%
...
Equity(874 [300372.SZA])
Equity(3057 [600656.SHA])
.
..
Equity(2788 [000876.SZA])
Equity(2234 [002026.SZA])
Equity(1362 [000665.SZA])
Equity(21 1 [000069.SZA])
Equity(2393 [601992.SHA])
Equity(1752 [000983.SZA])
Equity(2835 [600169.SHA])
Equity(2707 [002080.SZA])
Equity(653 [000949.SZA])
Equity(1635 [601877.SHA])
Equity(1419 [000488.SZA])
Equity(352 [600185.SHA])
Equity(408 [000719.SZA])
Equity(152 [600798.SHA])
Equity(1 151 [300082.SZA])
Equity(1717 [000761.SZA])
Equity(342 [000951.SZA])
Equity(3077 [000557.SZA])
Equity(397 [600891.SHA])
Equity(1527 [002666.SZA])
3.83%
3.81%
3.78%
3.77%
3.75%
3.74%
3.73%
3.72%
3.69%
3.69%
3.68%
3.66%
3.61%
3.55%
3.52%
3.50%
3.42%
3.37%
3.36%
3.35%

All positions ever held
max
3.33%
3.27%
3.17%
3.14%
3.06%
3.00%
2.97%
2.86%
1.61%
0.72%
Equity(1856 [000612.SZA])
Equity(2384 [600096.SHA])
Equity(2221 [60061 1.SHA])
Equity(1974 [002353.SZA])
Equity(1858 [000732.SZA])
Equity(1689 [600508.SHA])
Equity(2055 [600333.SHA])
Equity(2487 [601908.SHA])
Equity(1 111 [002088.SZA])
Equity(43 [600529.SHA])
312 rows × 1 columns
【
宽客学院】策略风险分析
本文介绍如何对策略进行风险分析,希望大家能够更深刻、更全面地了解策略。
1
.一个完整的AI策略¶
In [1]:
#
基础参数配置
class conf:
start_date = '2012-01-01'
end_date='2017-08-10'
split_date 之前的数据用于训练,之后的数据用作效果评估
split_date = '2016-01-01'
D.instruments: https://bigquant.com/docs/data_instruments.html
instruments = D.instruments(start_date, split_date)
#
#
#
#
#
机器学习目标标注函数
如下标注函数等价于 min(max((持有期间的收益 * 100), -20), 20) + 20 (后面的M.fast_auto_labeler会做取整操作)
说明:max/min这里将标注分数限定在区间[-20, 20],+20将分数变为非负数 (StockRanker要求标注分数非负整数)
label_expr = ['return * 100', 'where(label > {0}, {0}, where(label < -{0}, -{0}, label)) + {0}'.format(20)]
持有天数,用于计算label_expr中的return值(收益)
hold_days = 5
#
#
特征 https://bigquant.com/docs/data_features.html,你可以通过表达式构造任何特征
features = [
rank_pb_lf_0', # 市净率排名
'
]
#
给数据做标注:给每一行数据(样本)打分,一般分数越高表示越好
m1 = M.fast_auto_labeler.v8(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.split_date,
label_expr=conf.label_expr, hold_days=conf.hold_days,
benchmark='000300.SHA', sell_at='open', buy_at='open')
#
计算特征数据
m2 = M.general_feature_extractor.v5(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.split_date,
features=conf.features)
#
数据预处理:缺失数据处理,数据规范化,T.get_stock_ranker_default_transforms为StockRanker模型做数据预处理
m3 = M.transform.v2(
data=m2.data, transforms=T.get_stock_ranker_default_transforms(),
drop_null=True, astype='int32', except_columns=['date', 'instrument'],
clip_lower=0, clip_upper=200000000)
#
合并标注和特征数据
m4 = M.join.v2(data1=m1.data, data2=m3.data, on=['date', 'instrument'], sort=True)
StockRanker机器学习训练
m5 = M.stock_ranker_train.v3(training_ds=m4.data, features=conf.features)
#
#
#
# 量化回测 https://bigquant.com/docs/module_trade.html
回测引擎:准备数据,只执行一次
def prepare(context):
#
context.start_date / end_date,回测的时候,为trader传入参数;在实盘运行的时候,由系统替换为实盘日期
n1 = M.general_feature_extractor.v5(
instruments=D.instruments(),
start_date=context.start_date, end_date=context.end_date,
model_id=context.options['model_id'])

n2 = M.transform.v2(
data=n1.data, transforms=T.get_stock_ranker_default_transforms(),
drop_null=True, astype='int32', except_columns=['date', 'instrument'],
clip_lower=0, clip_upper=200000000)
n3 = M.stock_ranker_predict.v2(model_id=context.options['model_id'], data=n2.data)
context.instruments = n3.instruments
context.options['predictions'] = n3.predictions
#
回测引擎:初始化函数,只执行一次
def initialize(context):
加载预测数据
context.ranker_prediction = context.options['predictions'].read_df()
#
#
系统已经设置了默认的交易手续费和滑点,要修改手续费可使用如下函数
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
#
#
预测数据,通过options传入进来,使用 read_df 函数,加载到内存 (DataFrame)
设置买入的股票数量,这里买入预测股票列表排名靠前的5只
stock_count = 5
每只的股票的权重,如下的权重分配会使得靠前的股票分配多一点的资金,[0.339160, 0.213986, 0.169580, ..]
context.stock_weights = T.norm([1 / math.log(i + 2) for i in range(0, stock_count)])
设置每只股票占用的最大资金比例
#
#
context.max_cash_per_instrument = 0.2
#
回测引擎:每日数据处理函数,每天执行一次
def handle_data(context, data):
#
按日期过滤得到今日的预测数据
ranker_prediction = context.ranker_prediction[
context.ranker_prediction.date == data.current_dt.strftime('%Y-%m-%d')]
#
#
#
1. 资金分配
平均持仓时间是hold_days,每日都将买入股票,每日预期使用 1/hold_days 的资金
实际操作中,会存在一定的买入误差,所以在前hold_days天,等量使用资金;之后,尽量使用剩余资金(这里设置最多用等量的1.5倍)
is_staging = context.trading_day_index < context.options['hold_days'] # 是否在建仓期间(前 hold_days 天)
cash_avg = context.portfolio.portfolio_value / context.options['hold_days']
cash_for_buy = min(context.portfolio.cash, (1 if is_staging else 1.5) * cash_avg)
cash_for_sell = cash_avg - (context.portfolio.cash - cash_for_buy)
positions = {e.symbol: p.amount * p.last_sale_price
for e, p in context.perf_tracker.position_tracker.positions.items()}
#
2. 生成卖出订单:hold_days天之后才开始卖出;对持仓的股票,按StockRanker预测的排序末位淘汰
if not is_staging and cash_for_sell > 0:
equities = {e.symbol: e for e, p in context.perf_tracker.position_tracker.positions.items()}
instruments = list(reversed(list(ranker_prediction.instrument[ranker_prediction.instrument.apply(
lambda x: x in equities and not context.has_unfinished_sell_order(equities[x]))])))
#
print('rank order for sell %s' % instruments)
for instrument in instruments:
context.order_target(context.symbol(instrument), 0)
cash_for_sell -= positions[instrument]
if cash_for_sell <= 0:
break
#
3. 生成买入订单:按StockRanker预测的排序,买入前面的stock_count只股票
buy_cash_weights = context.stock_weights
buy_instruments = list(ranker_prediction.instrument[:len(buy_cash_weights)])
max_cash_per_instrument = context.portfolio.portfolio_value * context.max_cash_per_instrument
for i, instrument in enumerate(buy_instruments):
cash = cash_for_buy * buy_cash_weights[i]
if cash > max_cash_per_instrument - positions.get(instrument, 0):
#
确保股票持仓量不会超过每次股票最大的占用资金量
cash = max_cash_per_instrument - positions.get(instrument, 0)
if cash > 0:
context.order_value(context.symbol(instrument), cash)
#
调用交易引擎
m6 = M.trade.v2(
instruments=None,
start_date=conf.split_date,
end_date=conf.end_date,
prepare=prepare,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='close',
capital_base=1000000,
benchmark='000300.SHA',
# 表示 开盘 时买入
# 表示 收盘 前卖出
# 初始资金
# 比较基准,不影响回测结果
#
通过 options 参数传递预测数据和参数给回测引擎
options={'hold_days': conf.hold_days, 'model_id': m5.model_id}
)
[
[
2017-08-11 14:17:30.090816] INFO: bigquant: fast_auto_labeler.v8 start ..
2017-08-11 14:17:30.107990] INFO: bigquant: hit cache

[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
2017-08-11 14:17:30.127272] INFO: bigquant: fast_auto_labeler.v8 end [0.036482s].
2017-08-11 14:17:30.138557] INFO: bigquant: general_feature_extractor.v5 start ..
2017-08-11 14:17:30.851399] INFO: general_feature_extractor: year 2012, featurerows=565675
2017-08-11 14:17:31.545814] INFO: general_feature_extractor: year 2013, featurerows=564168
2017-08-11 14:17:33.889522] INFO: general_feature_extractor: year 2014, featurerows=569948
2017-08-11 14:17:34.636205] INFO: general_feature_extractor: year 2015, featurerows=569698
2017-08-11 14:17:35.793971] INFO: general_feature_extractor: year 2016, featurerows=0
2017-08-11 14:17:36.097925] INFO: general_feature_extractor: total feature rows: 2269489
2017-08-11 14:17:36.099729] INFO: bigquant: general_feature_extractor.v5 end [5.961175s].
2017-08-11 14:17:36.112943] INFO: bigquant: transform.v2 start ..
2017-08-11 14:17:36.730041] INFO: transform: transformed /y_2012, 565675/565675
2017-08-11 14:17:37.310047] INFO: transform: transformed /y_2013, 564168/564168
2017-08-11 14:17:38.086013] INFO: transform: transformed /y_2014, 569948/569948
2017-08-11 14:17:38.818248] INFO: transform: transformed /y_2015, 569698/569698
2017-08-11 14:17:39.099517] INFO: transform: transformed rows: 2269489/2269489
2017-08-11 14:17:39.124434] INFO: bigquant: transform.v2 end [3.011472s].
2017-08-11 14:17:39.134693] INFO: bigquant: join.v2 start ..
2017-08-11 14:17:53.283484] INFO: join: /y_2012, rows=564579/565675, timetaken=8.980251s
2017-08-11 14:18:01.922919] INFO: join: /y_2013, rows=563133/564168, timetaken=8.591636s
2017-08-11 14:18:09.445754] INFO: join: /y_2014, rows=567861/569948, timetaken=7.447208s
2017-08-11 14:18:16.295543] INFO: join: /y_2015, rows=543963/569698, timetaken=6.798585s
2017-08-11 14:18:16.740312] INFO: join: total result rows: 2239536
2017-08-11 14:18:16.742569] INFO: bigquant: join.v2 end [37.60787s].
2017-08-11 14:18:16.755040] INFO: bigquant: stock_ranker_train.v3 start ..
2017-08-11 14:18:20.329151] INFO: df2bin: prepare data: training ..
2017-08-11 14:18:42.338539] INFO: stock_ranker_train: dcfa4754 training: 2239536 rows
2017-08-11 14:20:29.784270] INFO: bigquant: stock_ranker_train.v3 end [133.029206s].
2017-08-11 14:20:29.839649] INFO: bigquant: backtest.v7 start ..
2017-08-11 14:20:29.960562] INFO: bigquant: general_feature_extractor.v5 start ..
2017-08-11 14:20:32.257460] INFO: general_feature_extractor: year 2016, featurerows=641546
2017-08-11 14:20:34.881904] INFO: general_feature_extractor: year 2017, featurerows=437274
2017-08-11 14:20:35.048574] INFO: general_feature_extractor: total feature rows: 1078820
2017-08-11 14:20:35.061006] INFO: bigquant: general_feature_extractor.v5 end [5.100428s].
2017-08-11 14:20:35.075238] INFO: bigquant: transform.v2 start ..
2017-08-11 14:20:35.759716] INFO: transform: transformed /y_2016, 641520/641546
2017-08-11 14:20:36.200546] INFO: transform: transformed /y_2017, 437274/437274
2017-08-11 14:20:36.354123] INFO: transform: transformed rows: 1078794/1078820
2017-08-11 14:20:36.372286] INFO: bigquant: transform.v2 end [1.297074s].
2017-08-11 14:20:36.384894] INFO: bigquant: stock_ranker_predict.v2 start ..
2017-08-11 14:20:36.904712] INFO: df2bin: prepare data: prediction ..
2017-08-11 14:20:49.828869] INFO: stock_ranker_predict: prediction: 1078794 rows
2017-08-11 14:20:57.517161] INFO: bigquant: stock_ranker_predict.v2 end [21.132225s].
2017-08-11 14:21:34.437890] INFO: Performance: Simulated 392 trading days out of 392.
2017-08-11 14:21:34.439074] INFO: Performance: first open: 2016-01-04 14:30:00+00:00
2017-08-11 14:21:34.440198] INFO: Performance: last close: 2017-08-10 19:00:00+00:00
[
2017-08-11 14:21:36.411485] INFO: bigquant: backtest.v7 end [66.571817s].
2
.因子风险分析¶
因子风险分析包括:¶
风格因子分析¶
风格因子主要包括市场因子、成长因子、流动性因子、动量因子、规模因子、价值因子、波动率因子、股东因子、财务质量因子。
计算组合在各个风格因子上的风险暴露比较简单,就是组合中各个股票的因子标准化后的求和。比如小市值策略倾向于选择小市值的股票,因此组合在规模
因子上数值应该很小,本例特征为“rank_pb_lf_0” 为市净率因子排序,因此选出来的股票为价值类股票,组合在价值因子上数值应该很大,一般该类股票为
大盘股,因此在规模因子上数值应该也大。
行业因子分析¶
行业采取申万一级行业,一共28个行业。
计算组合在各个行业上的风险暴露更为简单,直接计算组合在各个行业上的持仓市值即可。
In [5]:
m6.risk_analyze()
3
.策略风险分析¶
策略风险分析是对整个策略回测以后进行风险分析,主要包括:¶
回测相关指标,比如年化收益、收益波动率、夏普比率、最大回撤、偏度、峰度、索提纳比率、信息比率、贝塔、阿尔法
最严重的前五次回撤,包括回撤时间段、回撤幅度、回撤天数

日收益折线图
月度收益率、年度收益率、月度收益分布图
日收益茎叶图、周收益茎叶图、年收益茎叶图
盈利最大前10股票
多头市值与空头市值
每日持仓股票数、每日杠杆、每日换手率、每日交易额
In [6]:
m6.pyfolio_full_tear_sheet()
Entire data start date: 2016-01-04
Entire data end date: 2017-08-10
Backtest Months: 18
Performance statistics
cum_returns_final
annual_return
annual_volatility
sharpe_ratio
calmar_ratio
stability_of_timeseries
max_drawdown
omega_ratio
sortino_ratio
skew
Backtest
0.31
0.19
0.16
1.19
1.53
0.76
-0.13
1.26
1.73
-0.42
5.10
1.21
1.44
2.13
0.78
0.02
kurtosis
tail_ratio
common_sense_ratio
information_ratio
alpha
beta
Worst Drawdown Periods
net drawdown in %
peak date
2016-01-06
2017-03-01
2016-04-13
2016-03-21
2016-08-23
valley date
2016-01-28
2017-05-24
2016-05-19
2016-03-29
2016-09-26
recovery date
2016-03-07
2017-07-21
2016-08-12
2016-04-11
2016-11-10
duration
44
0
1
2
3
4
12.56
11.69
9.43
103
88
4.84
16
4.31
58
[
-0.019 -0.039]
Stress Events
New Normal
mean
min
max
0.07%
-5.69%
4.18%
Top 10 long positions of all time
Equity(1 158 [600301.SHA])
Equity(2752 [000155.SZA])
Equity(434 [600269.SHA])
Equity(987 [000898.SZA])
max
23.42%
22.26%
21.65%
21.37%

Top 10 long positions of all time
Equity(1914 [000422.SZA])
Equity(772 [000709.SZA])
Equity(615 [601818.SHA])
Equity(2129 [300080.SZA])
Equity(764 [601288.SHA])
Equity(1618 [601998.SHA])
max
21.18%
20.98%
20.98%
20.92%
20.84%
20.75%
Top 10 short positions of all time
max
Top 10 positions of all time
Equity(1 158 [600301.SHA])
Equity(2752 [000155.SZA])
Equity(434 [600269.SHA])
Equity(987 [000898.SZA])
Equity(1914 [000422.SZA])
Equity(772 [000709.SZA])
Equity(615 [601818.SHA])
Equity(2129 [300080.SZA])
Equity(764 [601288.SHA])
Equity(1618 [601998.SHA])
max
23.42%
22.26%
21.65%
21.37%
21.18%
20.98%
20.98%
20.92%
20.84%
20.75%
All positions ever held
max
Equity(1 158 [600301.SHA])
Equity(2752 [000155.SZA])
Equity(434 [600269.SHA])
Equity(987 [000898.SZA])
Equity(1914 [000422.SZA])
Equity(772 [000709.SZA])
Equity(615 [601818.SHA])
Equity(2129 [300080.SZA])
Equity(764 [601288.SHA])
Equity(1618 [601998.SHA])
Equity(2164 [601988.SHA])
Equity(2016 [601898.SHA])
Equity(1878 [600016.SHA])
Equity(815 [601328.SHA])
Equity(2924 [600015.SHA])
Equity(2799 [600019.SHA])
Equity(1 183 [601398.SHA])
Equity(2229 [600603.SHA])
Equity(1995 [000543.SZA])
Equity(2253 [000001.SZA])
Equity(471 [600221.SHA])
Equity(1001 [600508.SHA])
Equity(2778 [600123.SHA])
Equity(591 [600219.SHA])
23.42%
22.26%
21.65%
21.37%
21.18%
20.98%
20.98%
20.92%
20.84%
20.75%
20.63%
20.61%
20.57%
20.55%
20.52%
20.41%
20.31%
20.27%
20.20%
20.19%
20.12%
20.09%
20.08%
20.03%

All positions ever held
max
Equity(1659 [000157.SZA])
Equity(1471 [600656.SHA])
Equity(1771 [600166.SHA])
Equity(1 184 [000528.SZA])
Equity(851 [000877.SZA])
Equity(2394 [000830.SZA])
Equity(2948 [600028.SHA])
Equity(2142 [000825.SZA])
Equity(2947 [600823.SHA])
Equity(261 1 [600308.SHA])
Equity(2233 [601939.SHA])
Equity(841 [601 166.SHA])
Equity(1 [60081 1.SHA])
20.00%
19.99%
19.77%
18.68%
18.68%
18.24%
17.10%
14.34%
14.34%
14.24%
14.05%
13.34%
11.76%
11.61%
11.47%
10.66%
9.60%
9.51%
9.44%
9.31%
9.00%
8.80%
8.78%
7.81%
7.23%
6.35%
4.38%
3.97%
3.92%
Equity(3235 [600805.SHA])
Equity(1721 [601 169.SHA])
Equity(1202 [002608.SZA])
Equity(896 [600755.SHA])
Equity(1585 [000488.SZA])
Equity(2386 [600971.SHA])
Equity(224 [600026.SHA])
Equity(1506 [600005.SHA])
Equity(1818 [600000.SHA])
Equity(297 [600376.SHA])
Equity(2602 [600782.SHA])
Equity(2880 [000701.SZA])
Equity(1246 [000815.SZA])
Equity(2560 [002468.SZA])
Equity(2361 [000937.SZA])
Equity(1233 [600515.SHA])
上一页:策略收益分析
下一页:选股+择时策略组合
目录:BigQuant学院
【
宽客学院】选股+择时策略组合
本文讨论交易中两个非常重要的命题:选股+择时,并将其两者结合起来开发策略。
选股就是要选一只好股票,而择时就是选一个好的买卖时机。如果投资者选了一只很差劲的股票,无论怎样择时操作,都无法获得超额的利润。但如果只选
股而不进行择时,又可能面临系统性风险爆发的困境。如何将选股和择时策略有机地结合起来?
本文列出两个策略,第一个策略为纯选股策略,没有择时,即任何时候都有股票仓位。第二个策略为选股+择时,当大盘处于死叉(短期均线下穿长期均
线)的时候就保持空仓。对比发现,有择时的策略资金曲线更为平滑。
In [4]:
#
获取股票代码
instruments = D.instruments()
确定起始时间
start_date = '2013-01-01'
确定结束时间
end_date = '2017-08-10'
获取股票市净率数据,返回DataFrame数据格式
market_cap_data = D.history_data(instruments,start_date,end_date,
#
#
#

fields=['pb_lf','amount'])
#
获取每日按市净率排序 (从低到高)的前三十只股票
daily_buy_stock = market_cap_data.groupby('date').apply(lambda df:df[(df['amount'] > 0)&((df['pb_lf'] > 0))].sort_values('pb_lf')[:30
纯选股策略¶
In [17]:
#
回测参数设置,initialize函数只运行一次
def initialize(context):
手续费设置
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
调仓规则(每月的第一天调仓)
context.schedule_function(rebalance, date_rule=date_rules.month_start(days_offset=0))
传入 整理好的调仓股票数据
#
#
#
context.daily_buy_stock = daily_buy_stock
#
handle_data函数会每天运行一次
def handle_data(context,data):
pass
#
换仓函数
def rebalance(context, data):
当前的日期
date = data.current_dt.strftime('%Y-%m-%d')
根据日期获取调仓需要买入的股票的列表
stock_to_buy = list(context.daily_buy_stock.ix[date].instrument)
通过positions对象,使用列表生成式的方法获取目前持仓的股票列表
stock_hold_now = [equity.symbol for equity in context.portfolio.positions]
继续持有的股票:调仓时,如果买入的股票已经存在于目前的持仓里,那么应继续持有
no_need_to_sell = [i for i in stock_hold_now if i in stock_to_buy]
需要卖出的股票
stock_to_sell = [i for i in stock_hold_now if i not in no_need_to_sell]
#
#
#
#
#
#
卖出
for stock in stock_to_sell:
#
#
#
如果该股票停牌,则没法成交。因此需要用can_trade方法检查下该股票的状态
如果返回真值,则可以正常下单,否则会出错
因为stock是字符串格式,我们用symbol方法将其转化成平台可以接受的形式:Equity格式
if data.can_trade(context.symbol(stock)):
#
#
order_target_percent是平台的一个下单接口,表明下单使得该股票的权重为0,
即卖出全部股票,可参考回测文档
context.order_target_percent(context.symbol(stock), 0)
#
如果当天没有买入的股票,就返回
if len(stock_to_buy) == 0:
return
#
等权重买入
weight = 1 / len(stock_to_buy)
#
买入
for stock in stock_to_buy:
if data.can_trade(context.symbol(stock)):
#
#
下单使得某只股票的持仓权重达到weight,因为
weight大于0,因此是等权重买入
context.order_target_percent(context.symbol(stock), weight)
m = M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,
#
必须传入initialize,只在第一天运行
initialize=initialize,
必须传入handle_data,每个交易日都会运行
handle_data=handle_data,
买入以开盘价成交
order_price_field_buy='open',
卖出也以开盘价成交
order_price_field_sell='open',
策略本金
capital_base=1000000,
比较基准:沪深300
#
#
#
#
#
benchmark='000300.INDX',
)
[
[
2017-08-14 12:21:13.963532] INFO: bigquant: backtest.v7 start ..
2017-08-14 12:21:13.965370] INFO: bigquant: hit cache

[
2017-08-14 12:21:15.634476] INFO: bigquant: backtest.v7 end [1.670921s].
市场状态判断¶
In [18]:
bm_price = D.history_data(['000300.SHA'], start_date='2013-01-01' , end_date='2017-08-10', fields=['close'])
bm_price['sma'] = bm_price['close'].rolling(5).mean()
bm_price['lma'] = bm_price['close'].rolling(32).mean()
bm_price['gold_cross_status'] = bm_price['sma'] > bm_price['lma']
bm_price['pos_percent'] = np.where(bm_price['gold_cross_status'],1,0)
pos_df = bm_price[['date', 'pos_percent']].set_index('date')
选股+择时策略¶
In [19]:
#
回测参数设置,initialize函数只运行一次
def initialize(context):
手续费设置
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
调仓规则(每月的第一天调仓)
context.schedule_function(rebalance, date_rule=date_rules.month_start(days_offset=0))
传入 整理好的调仓股票数据
#
#
#
context.daily_buy_stock = daily_buy_stock
context.pos = pos_df
#
handle_data函数会每天运行一次
def handle_data(context,data):
date = data.current_dt.strftime('%Y-%m-%d')
stock_hold_now = [equity.symbol for equity in context.portfolio.positions]
#
满足空仓条件
if context.pos.ix[date].pos_percent == 0:
全部卖出
#
for stock in stock_hold_now:
if data.can_trade(context.symbol(stock)):
context.order_target_percent(context.symbol(stock), 0)
#
换仓函数
def rebalance(context, data):
当前的日期
date = data.current_dt.strftime('%Y-%m-%d')
根据日期获取调仓需要买入的股票的列表
stock_to_buy = list(context.daily_buy_stock.ix[date].instrument)
通过positions对象,使用列表生成式的方法获取目前持仓的股票列表
stock_hold_now = [equity.symbol for equity in context.portfolio.positions]
继续持有的股票:调仓时,如果买入的股票已经存在于目前的持仓里,那么应继续持有
no_need_to_sell = [i for i in stock_hold_now if i in stock_to_buy]
需要卖出的股票
stock_to_sell = [i for i in stock_hold_now if i not in no_need_to_sell]
#
#
#
#
#
#
卖出
for stock in stock_to_sell:
#
#
#
如果该股票停牌,则没法成交。因此需要用can_trade方法检查下该股票的状态
如果返回真值,则可以正常下单,否则会出错
因为stock是字符串格式,我们用symbol方法将其转化成平台可以接受的形式:Equity格式
if data.can_trade(context.symbol(stock)):
#
#
order_target_percent是平台的一个下单接口,表明下单使得该股票的权重为0,
即卖出全部股票,可参考回测文档
context.order_target_percent(context.symbol(stock), 0)
#
如果当天没有买入的股票,就返回
if len(stock_to_buy) == 0:
return
#
等权重买入
weight = 1 / len(stock_to_buy)
#
买入
for stock in stock_to_buy:
if data.can_trade(context.symbol(stock)):
#
#
下单使得某只股票的持仓权重达到weight,因为
weight大于0,因此是等权重买入
context.order_target_percent(context.symbol(stock), weight)
m1 = M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,

#
必须传入initialize,只在第一天运行
initialize=initialize,
必须传入handle_data,每个交易日都会运行
handle_data=handle_data,
买入以开盘价成交
order_price_field_buy='open',
卖出也以开盘价成交
order_price_field_sell='open',
策略本金
capital_base=1000000,
比较基准:沪深300
#
#
#
#
#
benchmark='000300.INDX',
)
[
[
2017-08-14 12:24:00.642134] INFO: bigquant: backtest.v7 start ..
2017-08-14 12:24:00.644126] INFO: bigquant: hit cache
[
2017-08-14 12:24:02.475082] INFO: bigquant: backtest.v7 end [1.832932s].
结论¶
可以看出,加入择时的策略比之前的策略有较好的改善和提高,改进效果比较明显。
选股
28.53%
0.86
选股+择时
30.14%
1.40
改进效果
提高5.6%
提高62.8%
减少34.2%
减少49.2%
年化收益
夏普比率
收益波动率
最大回撤
27.91%
42.62%
18.37%
21.63%
上一页:策略风险分析
下一页:自定义标注
目录:BigQuant学院
【
宽客学院】自定义标注
本文标题为自定义标注,其实就是想告诉大家如何灵活地对数据进行标注,从而得到预测能力更强的机器学习算法。
谈标注一词之前,我们先简单了解机器学习算法中的分类和回归。
分类问题是监督学习的一个核心问题。在监督学习中,当输出变量Y取有限个离散值时,预测问题便成为分类问题。监督学习从数据中学习一个分类模型,
称为分类器(classifier)。分类器对新的输入进行输出的预测,这个过程称为分类。
当输出变量Y为有限个离散值时,成为分类问题,那如果输出变量Y是连续值时,又该怎样处理呢?可能大家马上想到这其实就是回归问题,用回归算法就可
以解决。的确如此,但很多时候,回归算法预测效果不好。此时,我们可以对连续性数值进行标注,将Y标注为多个类别,这时又可以通过分类算法来解
决。对数据进行标注在图像识别、文本分析、语音分析中经常遇到,标注的思想也广泛存在于机器学习领域。将数据标注为多个离散值成为分类标注,将数
据标注为连续性数据称为回归标注。
对股票进行标注然后结合股票的特征是否能训练出一个有预测能力的模型呢?这正是许多机器学习算法在在量化选股领域的尝试。股票标注可以直接影响到
AI策略的效果,可见其重要性,接下来我们详细介绍如何对股票进行标注。
数据标注应注意的几点:
数据标注既包括分类标注也包括回归标注。分类标注为将数据分为具有区分性的多个类别,回归标注后数据为连续性数据。分类标注比较常用。
数据标注时,应尽可能结合机器学习的算法预测目的。如果目标是想预测收益率较高的股票,在标注时应结合股票收益率;如果目标是想预测波动率较
低的股票,在标注时应结合股票波动率。
数据标注时,应尽可能将数据区别开来,但又不可分得太细。比如,通过股票收益率将股票分为五类,分别为高收益、较高收益、一般、较低收益、低
收益,因此此时就可以采取分类算法。如果分得太细,可能算法在训练集上会学到不少数据噪音,泛化能力不强。
分类标注中标注后的数据不一定是具体的类别,而是具体的数值。比如,'数值>=20’为高收益股票,"15<数值<20"为较高收益股票,"10<数值<15"为一
般股票,“5<数值<10”为较低收益股票,“数值<5”为低收益股票。
数据标注和特征工程一样重要,共同决定了机器学习算法的预测能力。数据标注确定的标注结果和特征工程确定的因子数据合并起来就形成了训练集数据,
已经可以训练出一个学习算法。当我们得到学习算法后,传入测试集的因子数据就可以得到预测结果,通过回测就可以开发AI策略。如下图所示:

在BigQuant上,数据标注有专门的模块接口,方便大家高效灵活地进行标注。本文简单枚举了一些标注数据的应用例子,希望大家理解以便开发出更好的AI
策略。
1
.根据收益率进行标注
代码示例:
#
标注语句 这句代码的意思就是根据收益率将股票标注在[0,40]之间,标注结果称为股票分数
label_expr = [
#
'
#
'
将百分比收益乘以100
return * 100',
where 将分数限定在[-20, 20]区间,+20将分数调整到 [0, 40] 区间,如果想改变标注区间,修改具体数值即可
where(label > {0}, {0}, where(label < -{0}, -{0}, label)) + {0}'.format(20)
]
#
标注函数
m = M.fast_auto_labeler.v6(
instrument表示股票池 start_date和end_date决定了股票时间段
instruments=['000001.SZA', '600519.SHA'], start_date='2017-01-01', end_date='2017-02-01',
label_expr表示标注过程 hold_days为持仓时间
label_expr=label_expr, hold_days=5,
如果涉及相对收益率,还要传入比较基准 sell_at和buy_at表示以什么价格计算持仓期间的收益率
benchmark='000300.SHA', sell_at='open', buy_at='open')
#
#
#
标注结果为:
这幅柱状图描述了整个训练集中各个label的分布情况,比如,最右边的柱状图表示标注为23分的观测有两个。
代码解读:
根据未来几天的收益率进行标注可以直接修改hold_days。
在计算持仓期间的收益率可以直接修改sell_at和buy_at参数,修改为’close’表明以收盘价计算收益率。
修改标注语句label_expr可以直接修改标注分数区间。
instrument、start_date、end_date共同决定了对什么时间段哪些股票进行标注。
如果不涉及相对收益率可以不用传入benchmark参数。
标注函数的参数:is_regression (boolean) 表明label是否用来训练回归类模型。默认是False。
标注函数的参数:filter_price_limit (boolean) 表明是否过滤一字涨跌停的数据。默认为True。
标注函数的参数:plot_charts (boolean) 表明是否绘制结果数据,默认为True。如果修改为False,就不会输出上面的label柱状分布图。
更丰富的标注表达式:
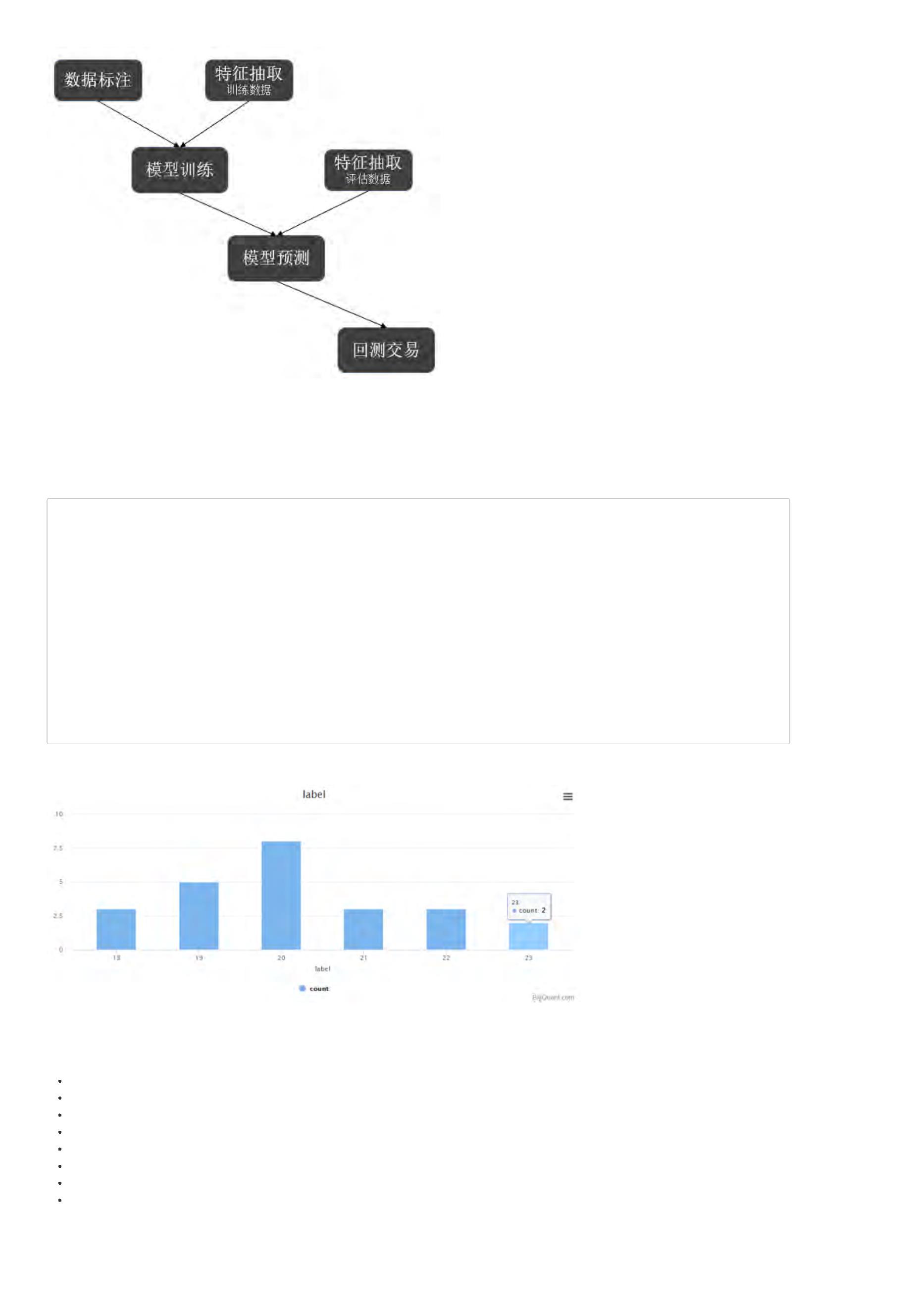
#
标注数据为:相对收益率
label_expr = ['(return-benchmark_return) * 100', 'where(label > {0}, {0}, where(label < -{0}, -{0}, label)) + {0}'.format(20)]
标注数据为:经过波动率调整后的收益率(类似于夏普比率)
label_expr = ['(return / volatility**0.5) * 20', 'where(label > {0}, {0}, where(label < -{0}, -{0}, label)) + {0}'.format(20)]
标注数据为:经过平均真实波幅调整后的收益率
label_expr = ['return / ATR * 20', 'where(label > {0}, {0}, where(label < -{0}, -{0}, label)) + {0}'.format(15)]
支持更复杂的表达式
#
#
#
label_expr = ['100 * return / exp(0.6 * log(volatility)', 'where(label > {0}, {0}, where(label < -{0}, -{0}, label)) + {0}'.format(20)]
2
.标注结果分析
代码示例:
m.data.read_df()
结果解读:
标注结果为DataSource类型,因此需要用read_df方法查看。
date和instrument为关键列,可以唯一确定一条观测。
return为持有期的收益率。一般常用其对股票进行标注。
return_f1表示持有一天的收益率。
volatility为持有期的收益率波动率,可用于衡量风险。
not_available 为布尔型变量,表明该观测当天label是否为缺失值。
benchmark_volatility 表示基准收益率波动率。
label表示标注具体的数值结果。
cannot_trading_f1表示次日是否停牌,停牌的话就不能交易。
在标注结果里,最重要的三列就是date、instrument和label。
查看标注分布和绘图:
3
.更灵活的标注
3
.1 通过内置变量自动标注
class conf:
start_date = '2011-01-01'
end_date='2017-07-04'
split_date = '2015-01-01'
instruments = D.instruments(start_date, end_date)
label_expr = ['(sell_price-buy_price)/atr*5', 'where(label > {0}, {0}, where(label < -{0}, -{0}, label)) + {0}'.format(8)]
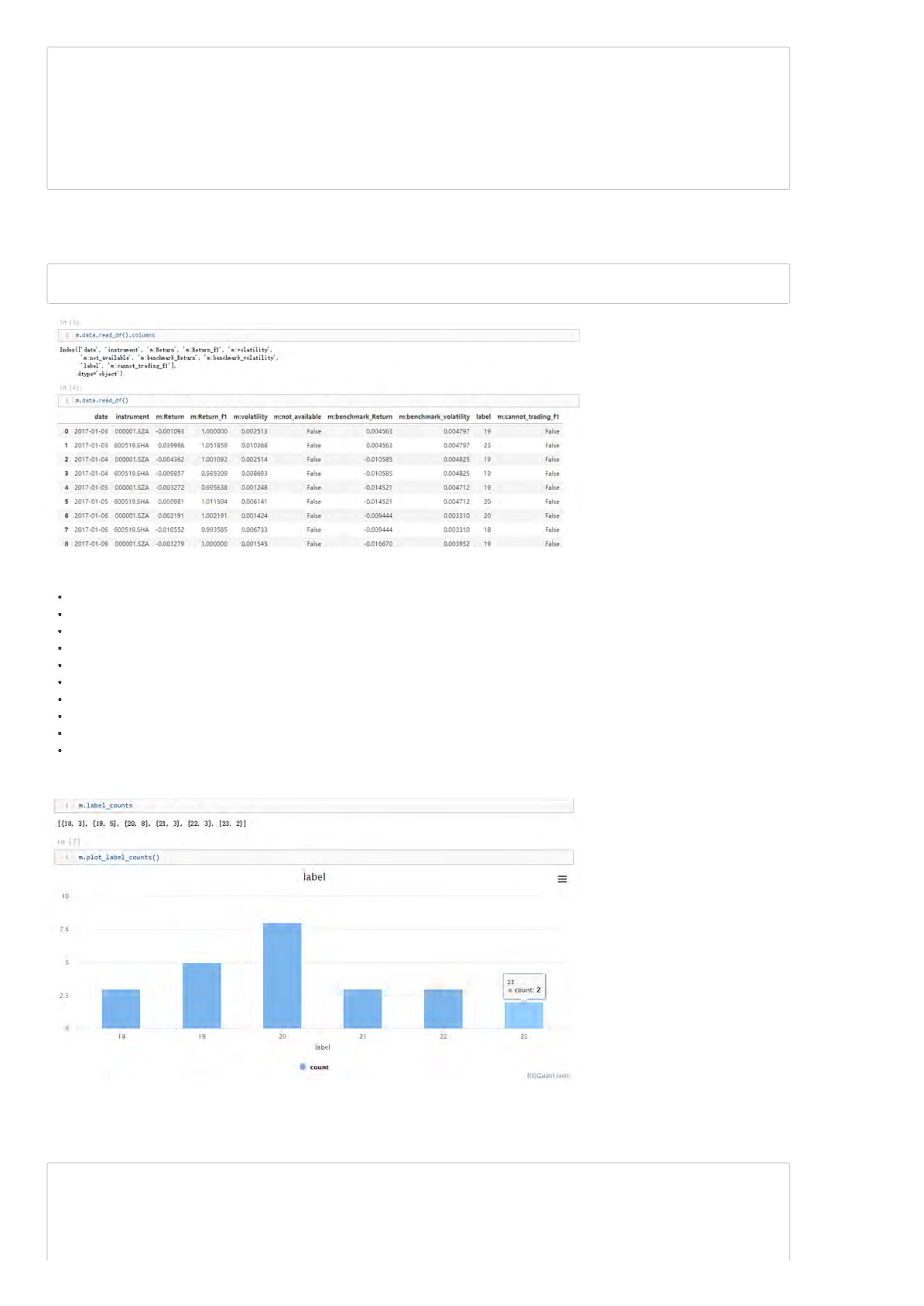
hold_days = 3
features = ['ta_sma_10_0/ta_sma_20_0']
m1 = M.fast_auto_labeler.v7(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.end_date,
label_expr=conf.label_expr, hold_days=conf.hold_days,
benchmark='000300.SHA', sell_at='open', buy_at='open')
代码解读:
buy_price指以buy_at的价格计算买入价格
sell_price指以sell_at的价格计算卖出价格
atr指50日平均真实波幅
3
.2 手动计算标注
#
基础参数配置
class conf:
start_date = '2010-01-01'
end_date='2017-07-10'
split_date = '2015-01-01'
instruments = D.instruments(start_date, end_date)
hold_days = 3
features = ['ta_sma_10_0/ta_sma_20_0']
#
手动计算标注
df = D.history_data(conf.instruments, start_date=conf.start_date,end_date=conf.end_date,fields=['close','open','high','low','amount'])
#
增加一列数据的函数
def add_column(df, series, name):
df[name] = series
return df
#
计算atr函数
def atr(high,low,close,window):
a=high-low
b=np.abs(close.shift(1)-high)
c=np.abs(close.shift(1)-low)
tr=a.where(a>b,b)
tr=tr.where(tr>c,c)
return tr.rolling(window).mean()
#
计算ATR
df = df.groupby('instrument').apply(lambda x:add_column(x,atr(x.high,x.low,x.close,50),'ATR'))
计算标注,标注这个地方可以试一试用 'close'
df = df.groupby('instrument').apply(lambda x:add_column(x,(x.open.shift(-4)-x.open.shift(-1))/x.ATR,'label'))
#
#
#
对标注数据进行一些转化,上下界限制
df['label']=df.label*5+10
df.label=df.label.where(df.label<20,20)
df.label=df.label.where(df.label>0,0)
#
删除一部分数据
df.drop(['low','high','amount','close','ATR','open'],axis=1,inplace=True)
#
#
df['label'] = df['label']*10 # 如果小数太多,这是会影响到转为整数几乎一样,导致模型训练会出错
标注要为int格式
df.label = df.label.astype('int')
label_ds = DataSource.write_df(df)
#
计算特征数据
m2 = M.general_feature_extractor.v5(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.end_date,
features=conf.features)
#
数据预处理:缺失数据处理,数据规范化,T.get_stock_ranker_default_transforms为StockRanker模型做数据预处理
m3 = M.transform.v2(
data=m2.data, transforms=T.get_stock_ranker_default_transforms(),
drop_null=True, astype='int32', except_columns=['date', 'instrument'],
clip_lower=0, clip_upper=200000000)
#
合并标注和特征数据
m4 = M.join.v2(data1=label_ds, data2=m3.data, on=['date', 'instrument'], sort=True)
训练数据集
m5_training = M.filter.v2(data=m4.data, expr='date < "%s"' % conf.split_date)
#
代码解读:
本例子对股票进行标注是纯手动计算,不是通过lebel_expr,这样更灵活。
本例单独编写了一个函数计算atr,单独计算了一个函数对数据框增加列。
标注结果保存为DataSourse类型,可直接传入M.join.v2模块。

3
.3 根据收益率排序对股票标注
#
基础参数配置
class conf:
start_date = '2011-01-01'
end_date='2017-07-04'
split_date = '2015-01-01'
instruments = D.instruments(start_date, end_date)
label_expr = ['return * 100', 'where(label > {0}, {0}, where(label < -{0}, -{0}, label)) + {0}'.format(10)]
hold_days = 3
features = ['ta_sma_10_0/ta_sma_20_0']
#
给数据做标注:给每一行数据(样本)打分,一般分数越高表示越好
m1 = M.fast_auto_labeler.v7(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.end_date,
label_expr=conf.label_expr, hold_days=conf.hold_days,
benchmark='000300.SHA', sell_at='open', buy_at='open')
#
通过收益率排序进行标注
df = m1.data.read_df()
def label(df):
#
收益率排序结果
df['label'] = df['m:Return'].rank(pct=True)/0.05+1
转化为整型
#
df['label'] = df['label'].astype(np.int32)
return df
df = df.groupby('date').apply(label)
#
标注结果存储为DataSource
label_ds = DataSource.write_df(df)
#
计算特征数据
m2 = M.general_feature_extractor.v5(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.end_date,
features=conf.features)
#
数据预处理:缺失数据处理,数据规范化,T.get_stock_ranker_default_transforms为StockRanker模型做数据预处理
m3 = M.transform.v2(
data=m2.data, transforms=T.get_stock_ranker_default_transforms(),
drop_null=True, astype='int32', except_columns=['date', 'instrument'],
clip_lower=0, clip_upper=200000000)
#
合并标注和特征数据
m4 = M.join.v2(data1=label_ds, data2=m3.data, on=['date', 'instrument'], sort=True)
训练数据集
m5_training = M.filter.v2(data=m4.data, expr='date < "%s"' % conf.split_date)
#
代码解读:
关键步骤在于label函数,对收益率数据进行排序再标注。
标注结果需要存储为DataSourse类型,以便传入M.join.v2。
可以看出,对股票数据标注的方法丰富多样,因此策略研究者的开发空间非常大,好的标注结果结合好的特征选择可以直接决定AI算法预测能力。
上一页:选股+择时策略组合
下一页:自定义数据
目录:BigQuant学院
【
宽客学院】多个策略组合
市场没有圣杯,专业投资机构长期生存下来的秘诀就是:通过相关性较低的策略构造组合获取更为平滑的资金曲线。
做过策略的朋友都知道,开发一个收益稳定、回撤较小的策略非常不容易。 很多策略单独拎出来看表现不好,但多个策略如果组合起来,组合净值曲线可能
非常漂亮。什么是策略组合呢?如果你本金3000元,目前开发出3个策略,分别为A、B、C,你每个策略配置1000元,三个策略就形成一个策略组合。通
常,组合策略的波动性比本金全部配置在一个策略上波动性更小。组合效果受策略相关性直接影响,策略相关性都是在-1到1之间,策略相关性越低,组合效
果越好。
那如何查看多个策略组合起来的效果呢?这正是本文的目的所在,帮助文档为:多策略组合分析。
目前一共有三个策略,策略A为趋势跟踪策略,策略B为多因子选股策略,策略C为AI策略。我们尝试将三个策略组合在一起,最终发现,组合后的结果策略
波动性介于三个策略的波动性之间,处于中间水平。
1
. 策略A¶
股票池:上证50
策略名称:双均线策略
策略类型:趋势跟踪策略
In [6]:

#
开始时间
start_date = '2016-10-16'
结束时间
#
end_date = '2017-07-18'
instruments = D.instruments(start_date, end_date)
df = D.history_data(instruments, start_date, end_date, fields=['in_sse50'])
instruments = list(set(df[df['in_sse50'] == 1].instrument))
#
初始化账户
def initialize(context):
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5)) # 设置手续费,买入成本为万分之三,卖出为千分之1.3
context.short_period = 5 # 短期均线
context.long_period = 50 # 长期均线
context.ins = context.instruments
context.weights = 1/len(context.instruments)
def handle_data(context, data):
#
长期均线值要有意义,需要在50根k线之后
if context.trading_day_index < context.long_period:
return
for k in context.instruments:
sid = context.symbol(k) # 将标的转化为equity格式
price = data.current(sid, 'price') # 最新价格
short_mavg = data.history(sid, 'price',context.short_period, '1d').mean() # 短期均线值
long_mavg = data.history(sid, 'price',context.long_period, '1d').mean() # 长期均线值
cash = context.portfolio.portfolio_value # 现金
cur_position = context.portfolio.positions[sid].amount # 持仓
#
#
交易逻辑
如果短期均线大于长期均线形成金叉,并且没有持仓,并且该股票可以交易
if short_mavg > long_mavg and cur_position == 0 and data.can_trade(sid):
context.order_target_percent(sid, context.weights) # 买入
#
如果短期均线小于长期均线形成死叉,并且有持仓,并且该股票可以交易
elif short_mavg < long_mavg and cur_position > 0 and data.can_trade(sid):
context.order_target_percent(sid, 0) # 全部卖出
strategy_a = M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open', # 以开盘价买入
order_price_field_sell='open', # 以开盘价卖出
capital_base=1000000, # 本金
)
[
[
[
[
2017-08-10 09:19:32.866121] INFO: bigquant: backtest.v7 start ..
2017-08-10 09:20:00.028089] INFO: Performance: Simulated 186 trading days out of 186.
2017-08-10 09:20:00.029293] INFO: Performance: first open: 2016-10-17 13:30:00+00:00
2017-08-10 09:20:00.030466] INFO: Performance: last close: 2017-07-18 19:00:00+00:00
[
2017-08-10 09:20:01.033306] INFO: bigquant: backtest.v7 end [28.167172s].
2
.策略B¶
股票池:全市场
策略名:市净率因子选股策略
策略类型:多因子选股策略
In [7]:
#
获取股票代码
instruments = D.instruments()
#
确定起始时间
start_date = '2016-10-16'
结束时间
end_date = '2017-07-18'
获取股票总市值数据,返回DataFrame数据格式
#
#
market_cap_data = D.history_data(instruments,start_date,end_date,
fields=['pb_lf','amount'])
#
获取每日按小市值排序 (从低到高)的前三十只股票
daily_buy_stock = market_cap_data.groupby('date').apply(lambda df:df[(df['amount'] > 0)].sort_values('pb_lf')[:30])

#
回测参数设置,initialize函数只运行一次
def initialize(context):
手续费设置
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
调仓规则(每月的第一天调仓)
context.schedule_function(rebalance, date_rule=date_rules.month_start(days_offset=0))
传入 整理好的调仓股票数据
#
#
#
context.daily_buy_stock = daily_buy_stock
#
handle_data函数会每天运行一次
def handle_data(context,data):
pass
#
换仓函数
def rebalance(context, data):
当前的日期
date = data.current_dt.strftime('%Y-%m-%d')
根据日期获取调仓需要买入的股票的列表
stock_to_buy = list(context.daily_buy_stock.ix[date].instrument)
通过positions对象,使用列表生成式的方法获取目前持仓的股票列表
stock_hold_now = [equity.symbol for equity in context.portfolio.positions]
继续持有的股票:调仓时,如果买入的股票已经存在于目前的持仓里,那么应继续持有
no_need_to_sell = [i for i in stock_hold_now if i in stock_to_buy]
需要卖出的股票
stock_to_sell = [i for i in stock_hold_now if i not in no_need_to_sell]
#
#
#
#
#
#
卖出
for stock in stock_to_sell:
#
#
#
如果该股票停牌,则没法成交。因此需要用can_trade方法检查下该股票的状态
如果返回真值,则可以正常下单,否则会出错
因为stock是字符串格式,我们用symbol方法将其转化成平台可以接受的形式:Equity格式
if data.can_trade(context.symbol(stock)):
#
#
order_target_percent是平台的一个下单接口,表明下单使得该股票的权重为0,
即卖出全部股票,可参考回测文档
context.order_target_percent(context.symbol(stock), 0)
#
如果当天没有买入的股票,就返回
if len(stock_to_buy) == 0:
return
#
等权重买入
weight = 1 / len(stock_to_buy)
#
买入
for stock in stock_to_buy:
if data.can_trade(context.symbol(stock)):
#
#
下单使得某只股票的持仓权重达到weight,因为
weight大于0,因此是等权重买入
context.order_target_percent(context.symbol(stock), weight)
strategy_b = M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,
#
必须传入initialize,只在第一天运行
initialize=initialize,
必须传入handle_data,每个交易日都会运行
handle_data=handle_data,
买入以开盘价成交
order_price_field_buy='open',
卖出也以开盘价成交
order_price_field_sell='open',
策略本金
capital_base=1000000,
比较基准:沪深300
#
#
#
#
#
benchmark='000300.INDX',
)
[
[
2017-08-10 09:20:03.805450] INFO: bigquant: backtest.v7 start ..
2017-08-10 09:20:03.808086] INFO: bigquant: hit cache
[
2017-08-10 09:20:04.504971] INFO: bigquant: backtest.v7 end [0.699509s].
3
.策略C¶
股票池:全市场
策略名:AI策略
策略类型:人工智能选股策略

In [8]:
#
基础参数配置
class conf:
start_date = '2012-01-01'
end_date='2017-07-18'
split_date 之前的数据用于训练,之后的数据用作效果评估
split_date = '2016-10-16'
D.instruments: https://bigquant.com/docs/data_instruments.html
instruments = D.instruments(start_date, split_date)
#
#
#
#
#
机器学习目标标注函数
如下标注函数等价于 min(max((持有期间的收益 * 100), -20), 20) + 20 (后面的M.fast_auto_labeler会做取整操作)
说明:max/min这里将标注分数限定在区间[-20, 20],+20将分数变为非负数 (StockRanker要求标注分数非负整数)
label_expr = ['return * 100', 'where(label > {0}, {0}, where(label < -{0}, -{0}, label)) + {0}'.format(20)]
持有天数,用于计算label_expr中的return值(收益)
hold_days = 5
#
#
特征 https://bigquant.com/docs/data_features.html,你可以通过表达式构造任何特征
features = [
rank_pb_lf_0',
'
]
#
给数据做标注:给每一行数据(样本)打分,一般分数越高表示越好
m1 = M.fast_auto_labeler.v8(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.split_date,
label_expr=conf.label_expr, hold_days=conf.hold_days,
benchmark='000300.SHA', sell_at='open', buy_at='open')
#
计算特征数据
m2 = M.general_feature_extractor.v5(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.split_date,
features=conf.features)
#
数据预处理:缺失数据处理,数据规范化,T.get_stock_ranker_default_transforms为StockRanker模型做数据预处理
m3 = M.transform.v2(
data=m2.data, transforms=T.get_stock_ranker_default_transforms(),
drop_null=True, astype='int32', except_columns=['date', 'instrument'],
clip_lower=0, clip_upper=200000000)
#
合并标注和特征数据
m4 = M.join.v2(data1=m1.data, data2=m3.data, on=['date', 'instrument'], sort=True)
StockRanker机器学习训练
m5 = M.stock_ranker_train.v3(training_ds=m4.data, features=conf.features)
#
#
#
# 量化回测 https://bigquant.com/docs/module_trade.html
回测引擎:准备数据,只执行一次
def prepare(context):
#
context.start_date / end_date,回测的时候,为trader传入参数;在实盘运行的时候,由系统替换为实盘日期
n1 = M.general_feature_extractor.v5(
instruments=D.instruments(),
start_date=context.start_date, end_date=context.end_date,
model_id=context.options['model_id'])
n2 = M.transform.v2(
data=n1.data, transforms=T.get_stock_ranker_default_transforms(),
drop_null=True, astype='int32', except_columns=['date', 'instrument'],
clip_lower=0, clip_upper=200000000)
n3 = M.stock_ranker_predict.v2(model_id=context.options['model_id'], data=n2.data)
context.instruments = n3.instruments
context.options['predictions'] = n3.predictions
#
回测引擎:初始化函数,只执行一次
def initialize(context):
加载预测数据
context.ranker_prediction = context.options['predictions'].read_df()
#
#
系统已经设置了默认的交易手续费和滑点,要修改手续费可使用如下函数
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
#
#
预测数据,通过options传入进来,使用 read_df 函数,加载到内存 (DataFrame)
设置买入的股票数量,这里买入预测股票列表排名靠前的5只
stock_count = 5
每只的股票的权重,如下的权重分配会使得靠前的股票分配多一点的资金,[0.339160, 0.213986, 0.169580, ..]
context.stock_weights = T.norm([1 / math.log(i + 2) for i in range(0, stock_count)])
设置每只股票占用的最大资金比例
#
#
context.max_cash_per_instrument = 0.2
#
回测引擎:每日数据处理函数,每天执行一次
def handle_data(context, data):
#
按日期过滤得到今日的预测数据
ranker_prediction = context.ranker_prediction[
context.ranker_prediction.date == data.current_dt.strftime('%Y-%m-%d')]
#
#
1. 资金分配
平均持仓时间是hold_days,每日都将买入股票,每日预期使用 1/hold_days 的资金

#
实际操作中,会存在一定的买入误差,所以在前hold_days天,等量使用资金;之后,尽量使用剩余资金(这里设置最多用等量的1.5倍)
is_staging = context.trading_day_index < context.options['hold_days'] # 是否在建仓期间(前 hold_days 天)
cash_avg = context.portfolio.portfolio_value / context.options['hold_days']
cash_for_buy = min(context.portfolio.cash, (1 if is_staging else 1.5) * cash_avg)
cash_for_sell = cash_avg - (context.portfolio.cash - cash_for_buy)
positions = {e.symbol: p.amount * p.last_sale_price
for e, p in context.perf_tracker.position_tracker.positions.items()}
#
2. 生成卖出订单:hold_days天之后才开始卖出;对持仓的股票,按StockRanker预测的排序末位淘汰
if not is_staging and cash_for_sell > 0:
equities = {e.symbol: e for e, p in context.perf_tracker.position_tracker.positions.items()}
instruments = list(reversed(list(ranker_prediction.instrument[ranker_prediction.instrument.apply(
lambda x: x in equities and not context.has_unfinished_sell_order(equities[x]))])))
#
print('rank order for sell %s' % instruments)
for instrument in instruments:
context.order_target(context.symbol(instrument), 0)
cash_for_sell -= positions[instrument]
if cash_for_sell <= 0:
break
#
3. 生成买入订单:按StockRanker预测的排序,买入前面的stock_count只股票
buy_cash_weights = context.stock_weights
buy_instruments = list(ranker_prediction.instrument[:len(buy_cash_weights)])
max_cash_per_instrument = context.portfolio.portfolio_value * context.max_cash_per_instrument
for i, instrument in enumerate(buy_instruments):
cash = cash_for_buy * buy_cash_weights[i]
if cash > max_cash_per_instrument - positions.get(instrument, 0):
#
确保股票持仓量不会超过每次股票最大的占用资金量
cash = max_cash_per_instrument - positions.get(instrument, 0)
if cash > 0:
context.order_value(context.symbol(instrument), cash)
#
调用交易引擎
strategy_c = M.trade.v2(
instruments=None,
start_date=conf.split_date,
end_date=conf.end_date,
prepare=prepare,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='close',
capital_base=1000000,
# 表示 开盘 时买入
# 表示 收盘 前卖出
# 初始资金
benchmark='000300.SHA',
# 比较基准,不影响回测结果
#
通过 options 参数传递预测数据和参数给回测引擎
options={'hold_days': conf.hold_days, 'model_id': m5.model_id}
)
[
[
2017-08-10 09:20:05.119294] INFO: bigquant: fast_auto_labeler.v8 start ..
2017-08-10 09:20:05.123075] INFO: bigquant: hit cache
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
2017-08-10 09:20:05.128997] INFO: bigquant: fast_auto_labeler.v8 end [0.009682s].
2017-08-10 09:20:05.137461] INFO: bigquant: general_feature_extractor.v5 start ..
2017-08-10 09:20:05.140071] INFO: bigquant: hit cache
2017-08-10 09:20:05.141087] INFO: bigquant: general_feature_extractor.v5 end [0.003661s].
2017-08-10 09:20:05.152243] INFO: bigquant: transform.v2 start ..
2017-08-10 09:20:05.154545] INFO: bigquant: hit cache
2017-08-10 09:20:05.156115] INFO: bigquant: transform.v2 end [0.00387s].
2017-08-10 09:20:05.164646] INFO: bigquant: join.v2 start ..
2017-08-10 09:20:05.167050] INFO: bigquant: hit cache
2017-08-10 09:20:05.168100] INFO: bigquant: join.v2 end [0.003423s].
2017-08-10 09:20:05.176580] INFO: bigquant: stock_ranker_train.v3 start ..
2017-08-10 09:20:05.179024] INFO: bigquant: hit cache
2017-08-10 09:20:05.180318] INFO: bigquant: stock_ranker_train.v3 end [0.003707s].
2017-08-10 09:20:05.202929] INFO: bigquant: backtest.v7 start ..
2017-08-10 09:20:05.205228] INFO: bigquant: hit cache
[
2017-08-10 09:20:05.850093] INFO: bigquant: backtest.v7 end [0.647145s].
4
. 模块M.multi_strategy_analysis 介绍¶
关于策略组合的相关模块 M.multi_strategy_analysis 的详细信息,可以参考:代码补全和文档帮助
5
.将A、B、C策略组合起来¶
In [9]:

m = M.multi_strategy_analysis.v1(
raw_perfs=[strategy_a.raw_perf, strategy_b.raw_perf, strategy_c.raw_perf],
weights=[1/3, 1/3, 1/3]
)
[
[
[
[
2017-08-10 09:20:06.036258] INFO: bigquant: backtest.v6 start ..
2017-08-10 09:20:07.031711] INFO: Performance: Simulated 186 trading days out of 186.
2017-08-10 09:20:07.033511] INFO: Performance: first open: 2016-10-17 13:30:00+00:00
2017-08-10 09:20:07.034646] INFO: Performance: last close: 2017-07-18 19:00:00+00:00
[
2017-08-10 09:20:07.693976] INFO: bigquant: backtest.v6 end [1.657758s].
上一页:开发新的模块
下一页:开始模拟交易
目录:BigQuant学院
【
宽客学院】开始模拟交易
本文介绍如何在BigQuant平台上进行模拟交易。
参考链接:如何使用 我的交易 进行模拟交易。
上一页:多个策略组合
目录:BigQuant学院
可视化策略
BigStudio 使用文档介绍(一)
新功能的认识是循序渐进的,本文简单介绍BigStudio,让大家对其有初步印象。
BigQuant新上线的 BigStudio 可视化策略开发功能,能够帮助大家更快速更简单地开发机器学习、深度学习试验,快速实现试验迭代。
BigStudio 提供了所见即所得的策略开发环境,集合了众多模块,包括数据输入、输出、数据变换、模型训练、预测和量化交易等。你只需要拖动数据和模
块,连连线,配置参数,就可以开发AI策略,从而将更多的创造力放在自己擅长的地方。因为提供的是可视化研究界面,因此通过BigStudio开发的AI策略被
称为可视化AI策略。
今天,我们先简单介绍BigStudio,让大家对其有一个初步印象,后面将对其进行深入细致讲解。
1
. 新建一个可视化AI策略
新建 > 可视化策略-AI选股策略
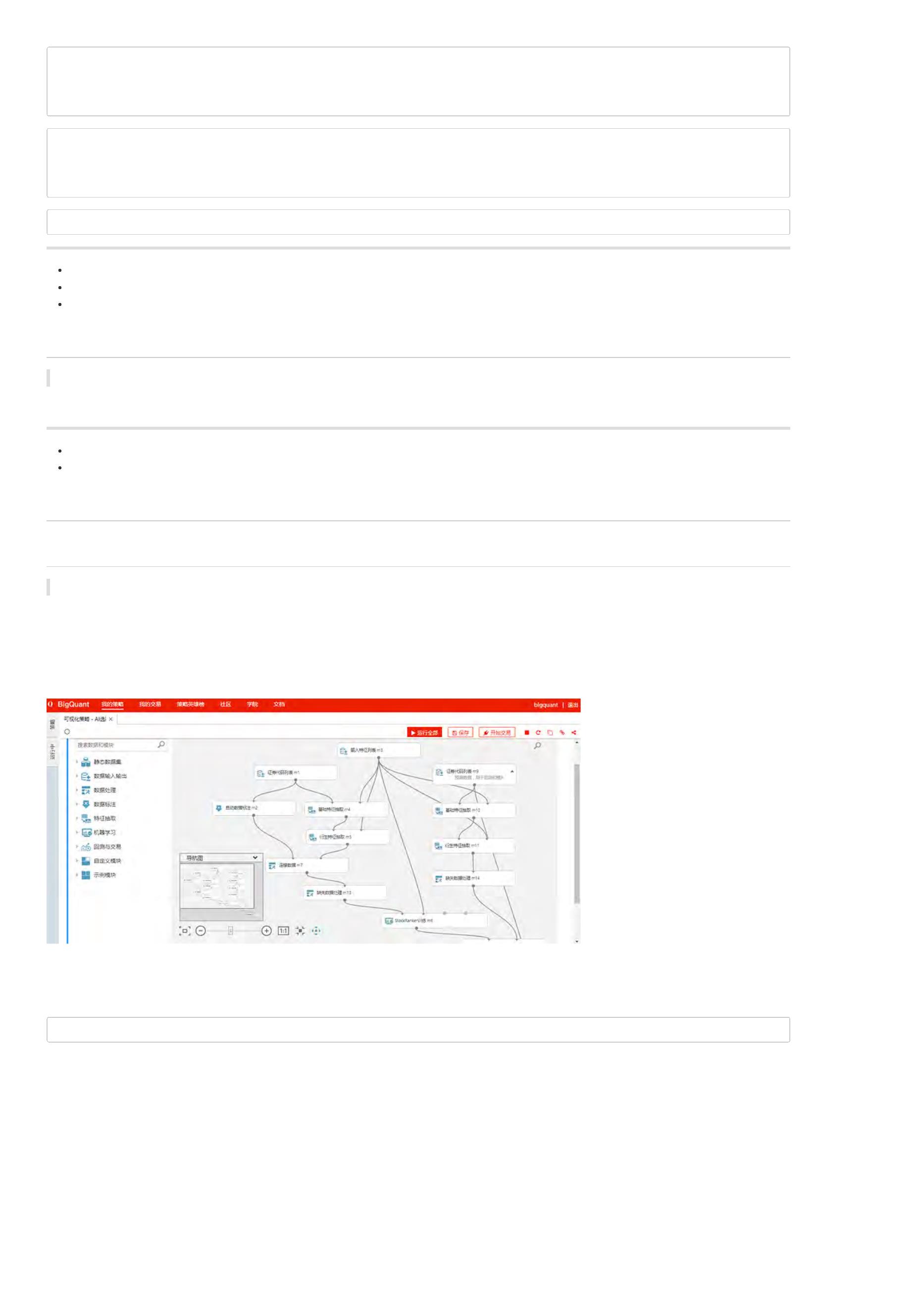
2
. 认识BigStudio 主要功能区
从左至右主要分为四个区域,依次为:策略列表区,BigStudio模块区,BigStudio画布区,模块参数和帮助区。
图中我们用绿色矩形框标记了四处位置,点击这四处位置都可以折叠其对应的区域,折叠以后再次点击可进行恢复。下图展示了折叠四处区域后的界面:
3
. 可视化界面存在于代码单元(cell )中
可视化界面的图形只是内嵌到一个代码单元(cell)中,你可以正常使用右上角的功能。
在右上角,分别有六个按钮,其功能分别是可视化/代码界面切换、在上方添加一个代码单元、在下方添加一个代码单元、上移代码单元、下移代码单元、运
行代码单元。
4
.从可视化界面切换到Python 代码界面
可视化 > 代码/Python3
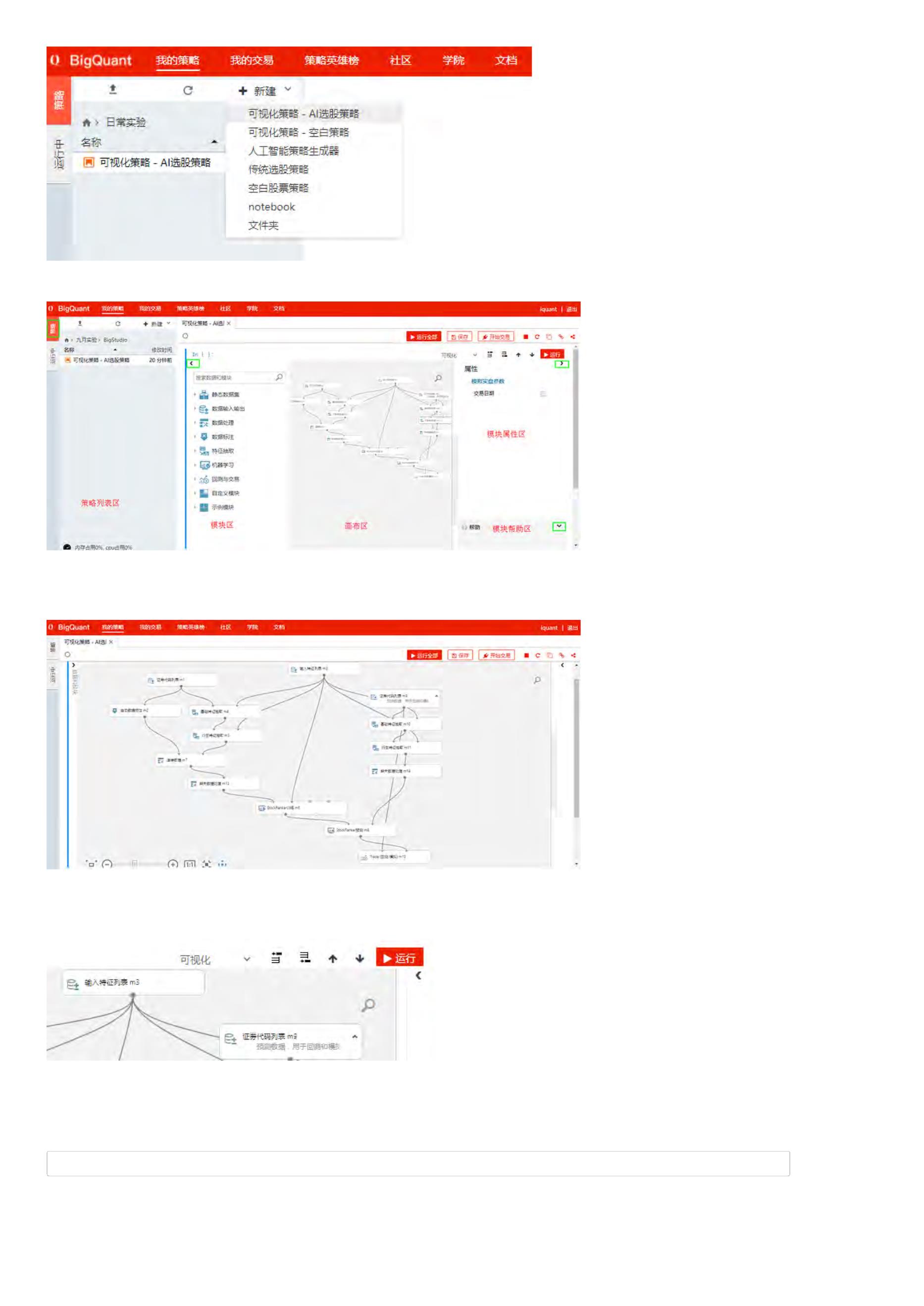
切换后,界面如下:
点击右上角的 代码/Python3 可回到之前的可视化界面。
5
. 使用搜索功能
在可视化界面中,一共有两个放大镜,如下图所示:
左侧的放大镜用来搜索 数据和模块,右侧的放大镜可在画布中搜索 模块。
BigStudio 使用文档介绍(二)
有了对BigStudio的初步直观印象后,今天我们再来认识画布、模块及简单运用。
0
.新建一个空白可视化策略
新建 > 可视化策略-空白策略
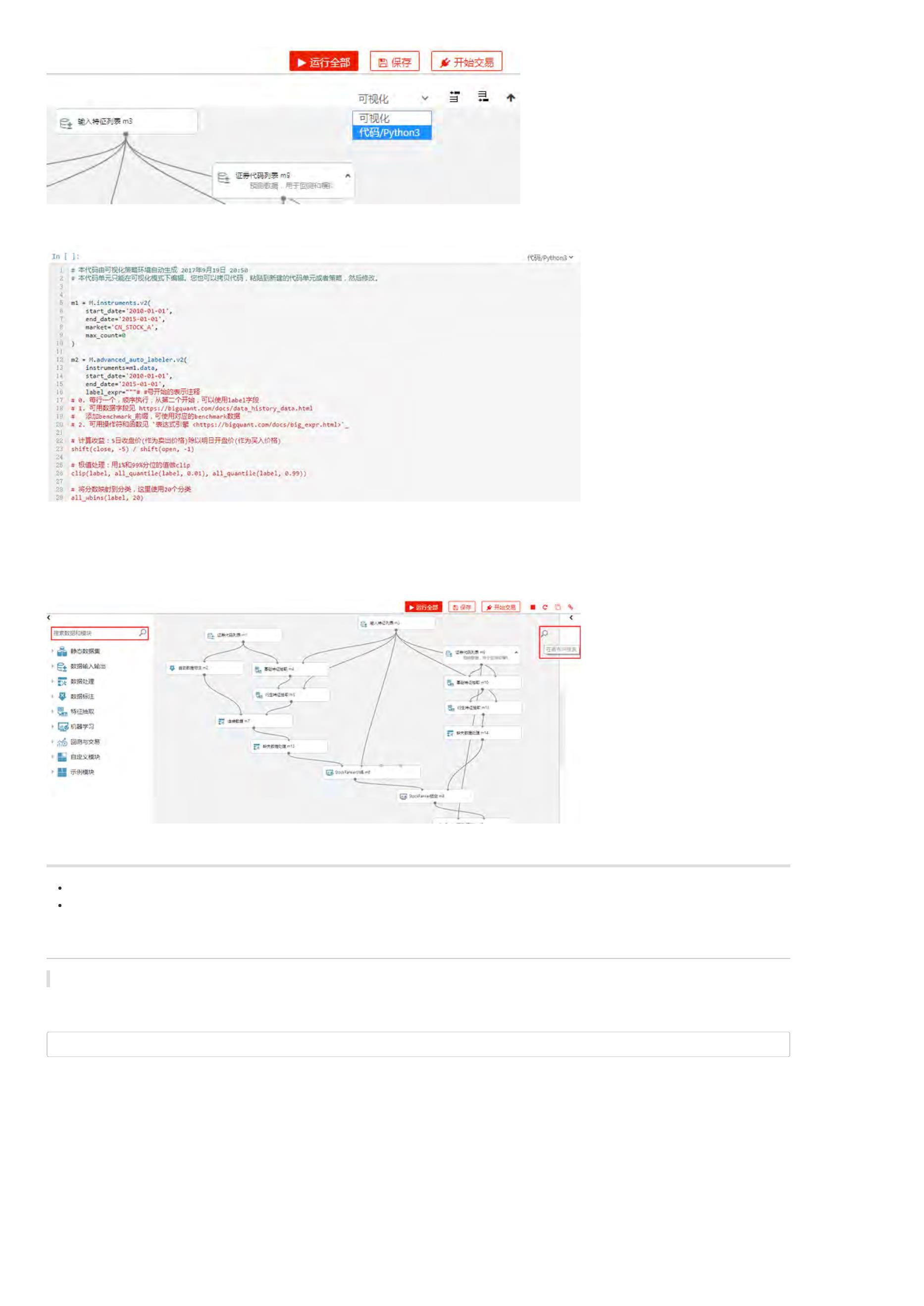
建立完成的时候,界面如下:
1
. 认识画布
上图为一个完整的机器学习AI可视化策略,右边部分为画布,画布中的模块和数据都是来自左侧。
左侧部分为模块和数据列表,可直接拖放至画布。
画布的左下方为画布的一些功能键,截图如下:
从左至右分别为:展示/隐藏导航图、画布缩小、画布放大、缩放到实际尺寸、自适应窗口、启用拖动模式,每个功能都有对应的快捷键,建议大家亲自体验
一下,印象更加深刻。
2
. 认识模块
画布中的主要构成就是模块,模块其实并不难理解,你可以将其理解为函数,就是为了实现某些功能。模块的示意图如下:
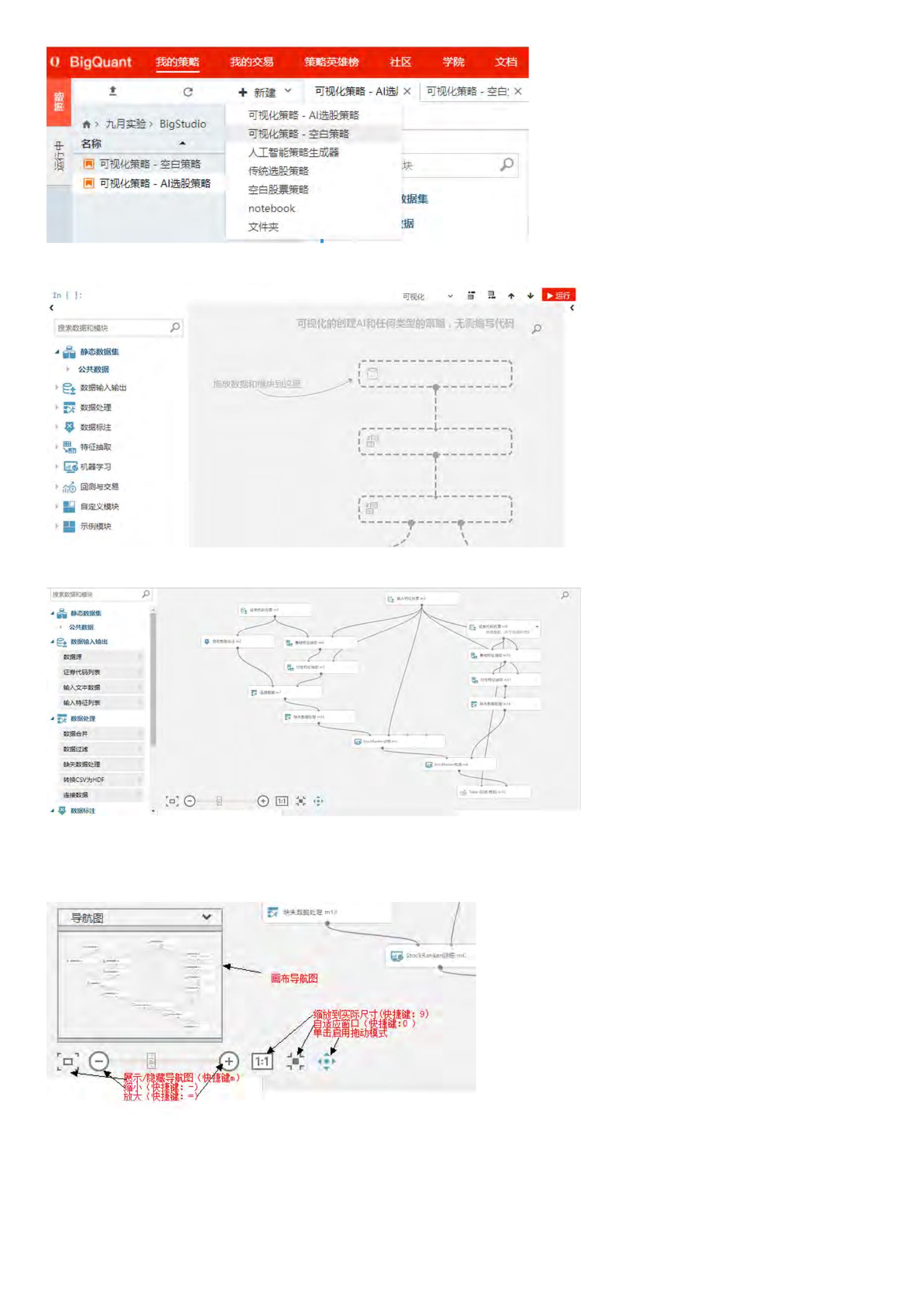
整个流程是$x$作为输入,进入函数$f$,然后得到输出结果$f(x)$,这就是我们日常理解的函数。在BigStudio中,模块的概念和函数一样,拥有输入(可以
多个输入)和输出。因此在画布中,每一个拥有输入连接线和输出连接线的矩形框都可以看成模块,仅有输出连接线的矩形框可以看成数据。
画布是实验的工作场所。实验由数据集组成,数据集将数据提供给分析模块,将这些模块连接起来即可构成预测分析模型。 具体而言,有效的实验有以下特
征:
试验至少包含一个数据集和一个模块
数据集只能连接到模块
模块可以连接到数据集或其他模块
模块的所有输入端口必须与数据流建立某种连接
必须设置每个模块的所有必需参数
点击画布左下方的最右边的按钮,可以进入拖动模式,这样我们就能自由拖动模块,按自己喜欢的风格布局画布,再次点击该按钮退出拖动模式。
3
. 模块的基本操作
模块信息
模块信息包含模块中文名称和模块英文名称,比如:
图中一共四个模块,每个模块前面的中文为模块中文名称,后面的以 $m$开头的英文为模块英文名称。这里之所以介绍模块英文名称,因为在代码界面,可
以根据模块的英文名称快速找到该模块对应的Python代码。
查看介绍
将鼠标移动至模块之上,就可以查看该模块的介绍,例如,我们将鼠标移动至 证券代码列表 m15 这个模块之上,你将会看到该模块的介绍:
选择模块
直接选择模块即可有(鼠标左击),选中后,该模块四周的边框会变为蓝色。例如,我们选中 证券代码列表 m15模块。(如果鼠标在画布中是四个箭头的标
识,那么无法选择模块,因为此时处于画布拖动模式,需要退出该模式)。
模块方法
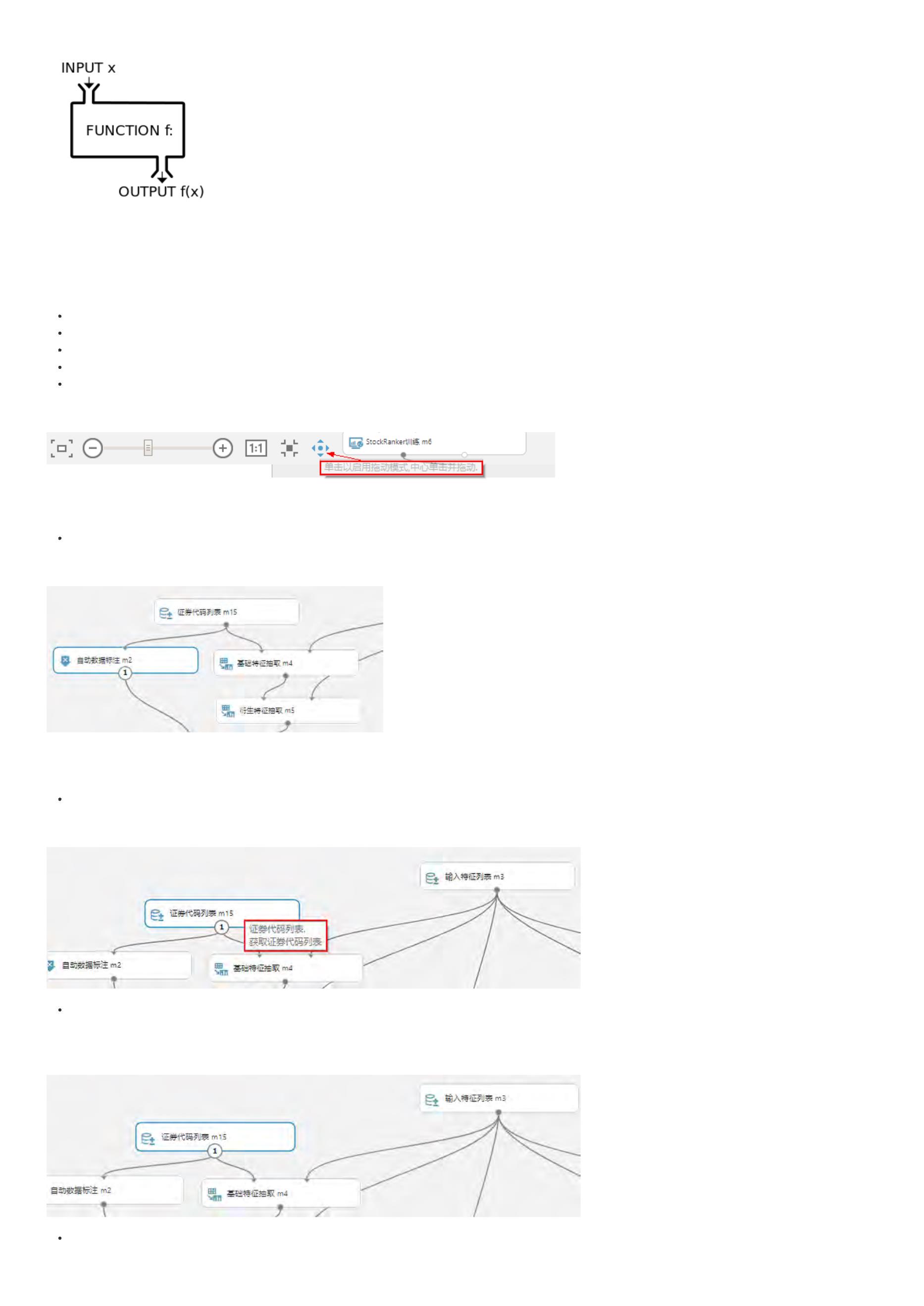
模块作为画布的基本单元,拥有多种操作方法。 当我们鼠标右击某模块,如下:
可以看出,在画布中,我们可以对该模块进行删除、复制、剪切、粘贴、直接运行、查看帮助,这些方法很好理解。
注释模块
模块以一个个矩形框的形式存在于画布中,我们可以对其进行注释。将鼠标移动到一个模块上双击就会出现文本输入框,如下:
假设我们输入文字“这是一句注释”,并确定。结果如下:
可以看出,我们对模块 证券代码列表 m1进行了注释。
. 新建模块
拖动 证券代码列表进画布
4
拖动 自动数据标注 进画布
连线和输入参数
这样,在我们的画布中,一共有两个模块。但是,此时两个模块是相互孤立没有联系的,因为 证券代码列表 m1 是 自动数据标注 m2的输入,因此我们需要
将第一个模块手动连线到第二个模块。
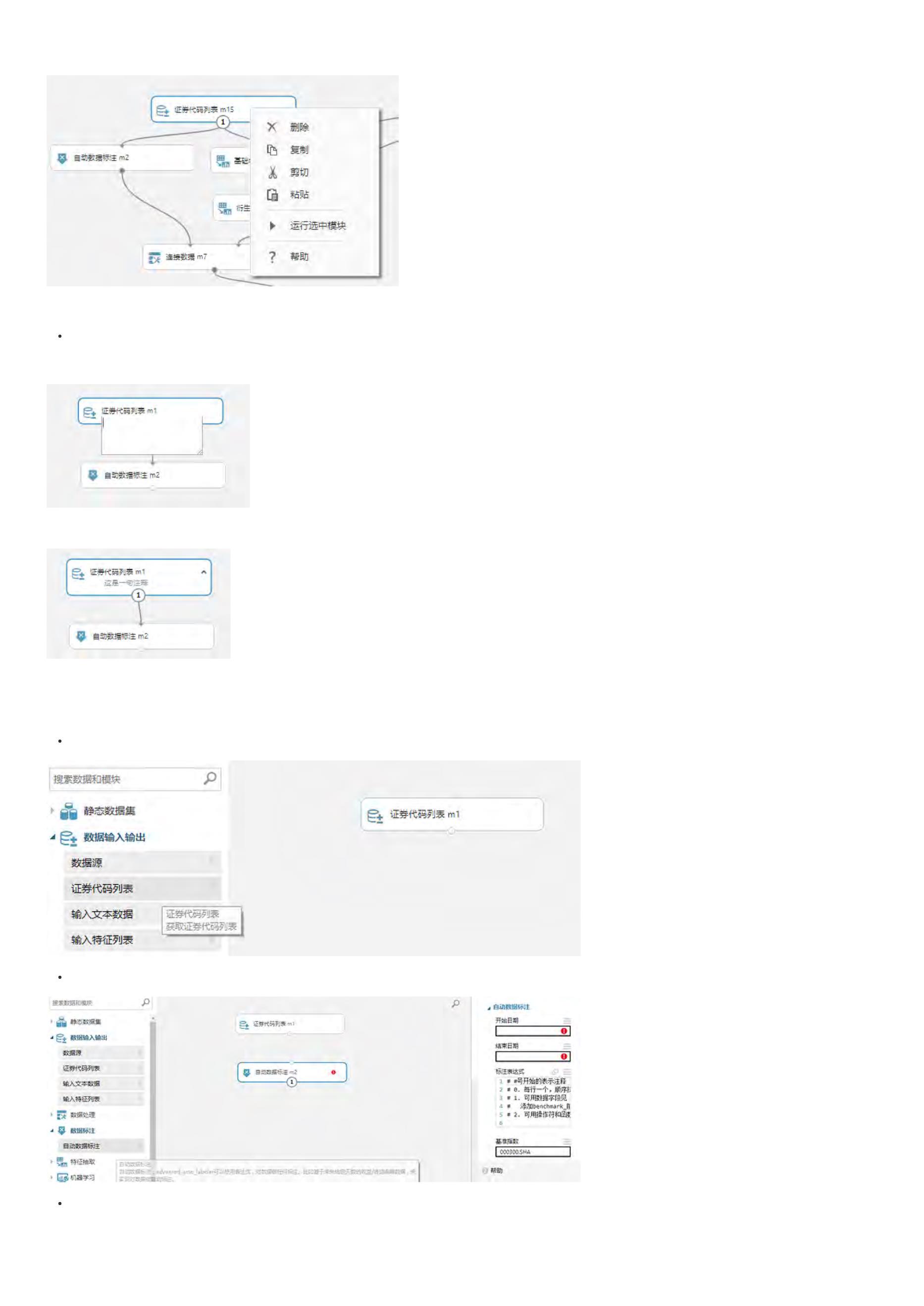
每一个模块是一个矩形框,矩形框上边界和下边界有一个空心小圆圈,这个小圆圈称为节点,模块的连接是通过连线到这样的节点完成的,其中上边界的小
圆圈连接的是输入,下边界的小圆圈连接的是输出。(注:矩形框上边界也可能是实心小圆圈,实心小圆圈表明该输入是可选输入,空心小圆圈表明该输入
是必选输入)。
细心的小伙伴可能会发现,m2模块有红色的警示,红色的警示表示参数不完备,同理,画布右侧的属性界面同样有参数不完备的红色警示,此时我们在属性
区手动输入参数(开始日期和结束日期),红色警示就会消失。
在属性界面,在弹出的代码编辑器窗口手动编辑标注表达式。
查看Python代码
点击右上方,可视化,切换到代码/Python3界面。
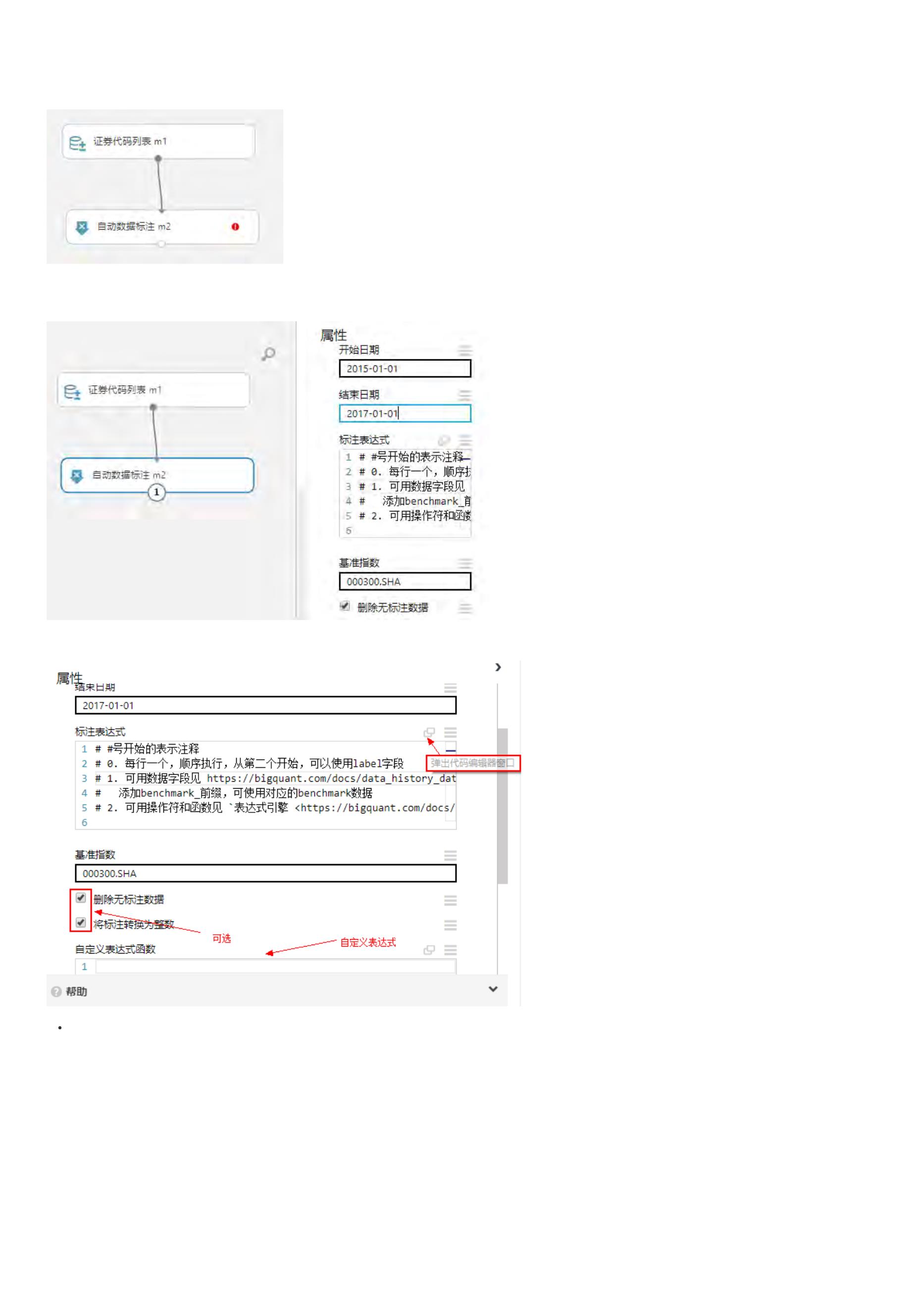
代码如下:
代码界面,我们可以浏览画布中的模块的背后的代码,但是这里这里浏览(可读模式),并不能修改。
5
. 可视化界面和代码研究界面相结合
运行可视化界面模块代码
拖选两个模块 > 右键 > 运行选中模块
拖选以后,选中的模块会变为蓝色。你也可以点击画布右上方的运行按钮来运行模块。
在可视化界面下添加代码单元(cell)
查看m2模块的输出数据
m2模块的输入是m1,那输出是什么呢?我们可以直接在代码单元运行代码进行查看,模块运行的日志也会输出,让我们对模块运行清楚把控。
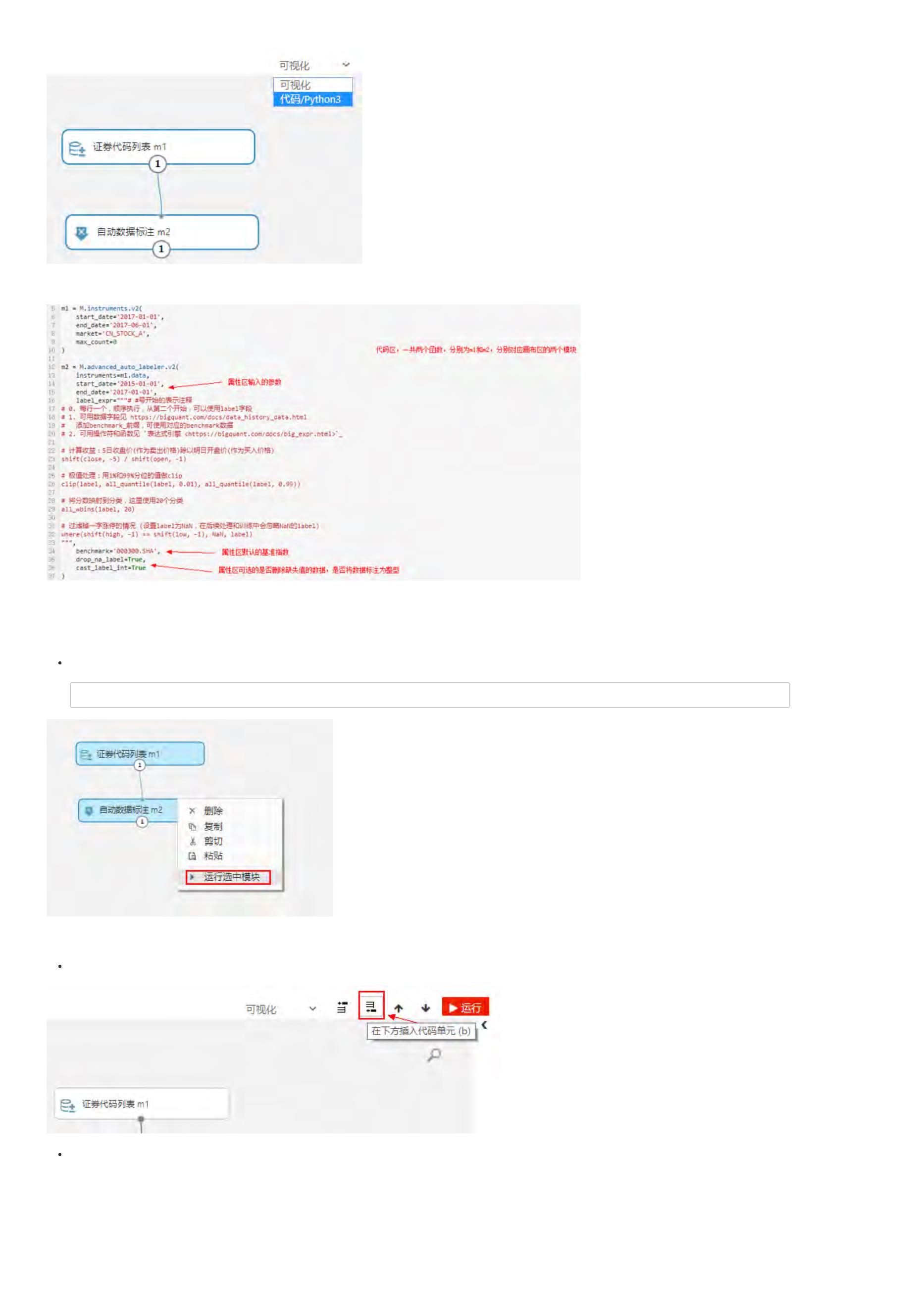
BigStudio 使用文档介绍(三)
如果你阅读了BigStudio前两篇文章,相信已经对BigStudio有一定的了解,今天我们聊聊BigStudio上默认可视化AI实验的的工作流。
什么是工作流?
简而言之就是实验在BigStudio上的工作流程。BigStudio是一个开发AI量化交易策略的平台,因此了解实验在BigStudio上的的工作流,能够帮助大家从整体
宏观上理解AI量化策略。
什么是AI量化交易策略?
人工智能(AI)技术得到了飞速发展,其在各个领域的运用也不断取得成果。机器学习被评为人工智能中最能体现人类智慧的技术,因此AI量化交易策略可
以简单理解为将机器学习应用在量化投资领域。
机器学习流程
机器学习(Machine Learning, ML)可以认为是:通过数据、算法使得机器从大量历史数据中学习规律,从而对新样本做分类或者预测。它是人工智能
(
Artificial Intelligence, AI)的核心,,其应用遍及人工智能的各个领域,主要使用归纳、综合的方法获取或总结知识。更多内容请参看:什么是机器学
习?
AI量化策略流程
AI量化策略本质上符合机器学习流程示意图,最为重要的两个模块即为训练和预测。训练是使用训练集数据拟合出一个模型,预测是使用该模型在评估集数
据,获取预测结果。想要更多地了解AI量化策略,可以点击AI量化策略的初步理解和BigQuant AI策略详解。
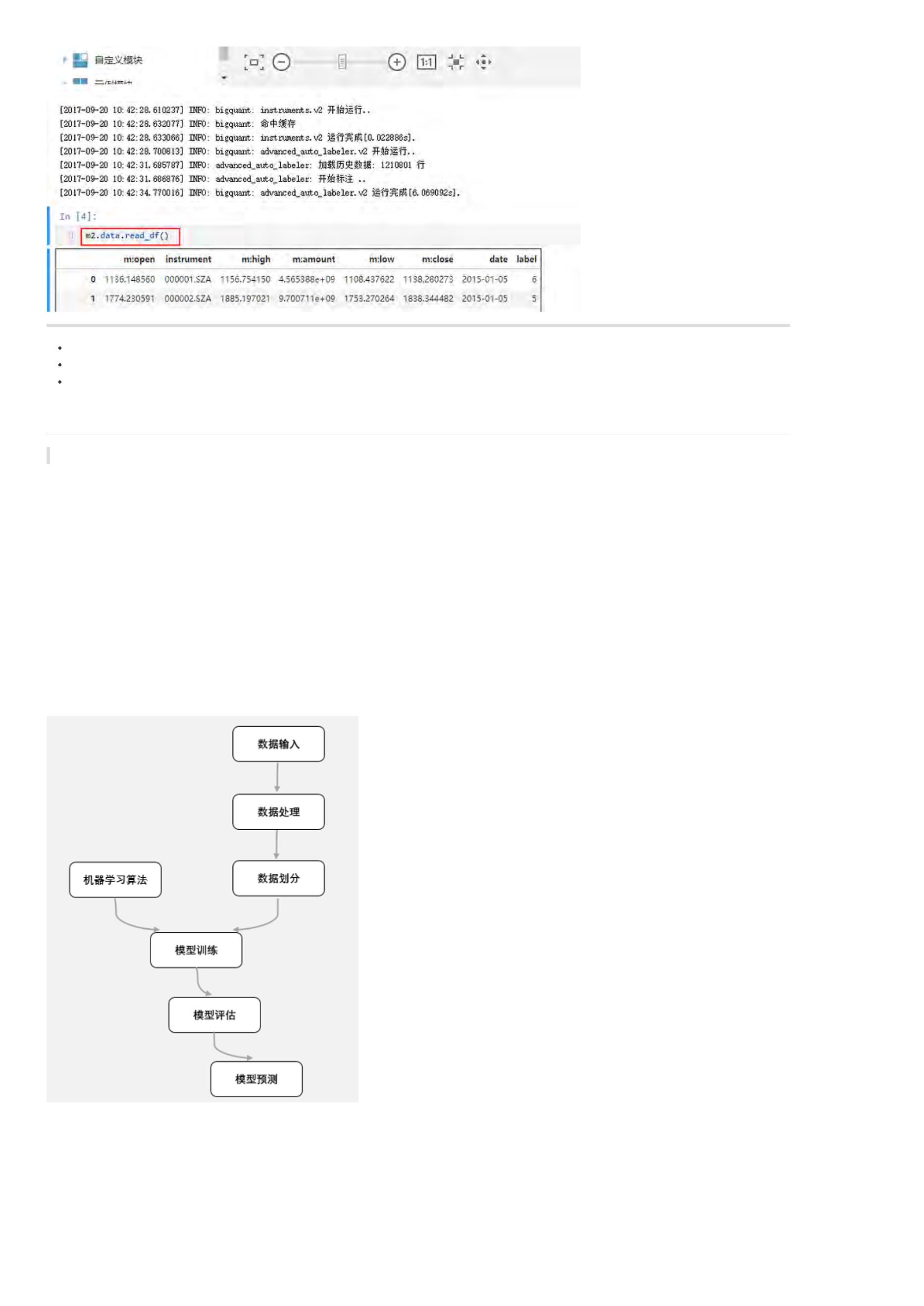
BigStudio 实验工作流
认识了机器学习流程和AI量化策略流程,能够对BigStudio实验工作流能更好地理解,BigStudio实验是AI量化策略在BigStudio上的可视化展示。如下:
在画布上,AI量化策略是由数据+模块共同组建形成的。乍一看去,实验工作流比较复杂,这里将其进行拆解和说明。
从上图可以看出,BigStudio实验主要包括数据标注、特征抽取、模型训练、模型预测、回测交易这几块,我们再结合前边介绍的AI量化策略流程,就可以很
清楚地了解BigStudio上可视化实验的工作流,这有助于帮助大家更好更快地开发AI量化策略,实现实验的快速迭代。
知道了BigStudio实验的工作流,我们在下一篇文章会详细介绍每个小模块的具体使用。
BigStudio 使用文档介绍(四)
本文详细介绍BigStudio可视化实验中各个模块,希望大家对每个模块的功能和使用更加了解。
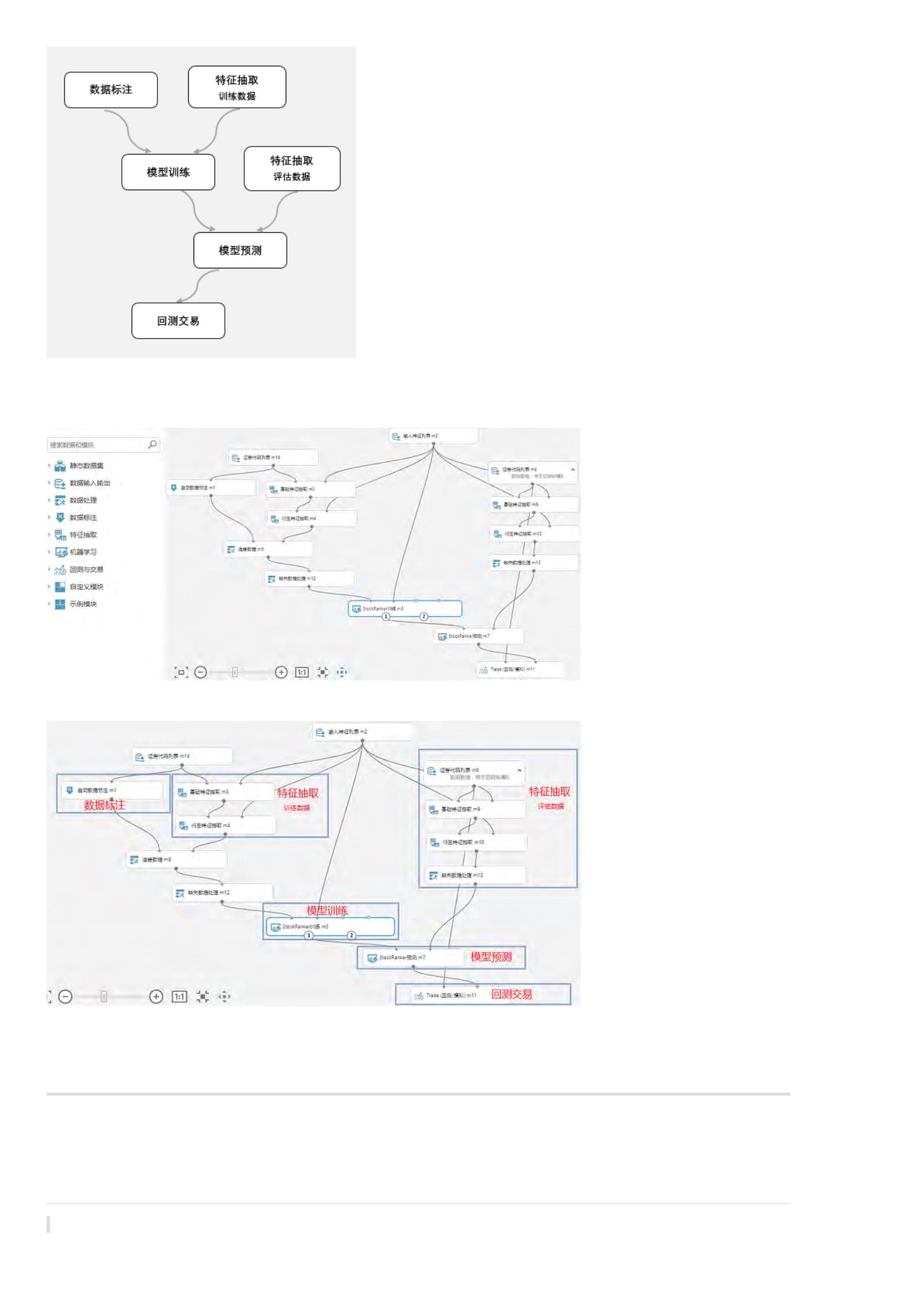
通过上一篇文章《BigStudio使用文档介绍(三)》,了解到BigStudio可视化实验工作流如下:
从这幅图可以看出,BigStudio上的可视化AI量化策略主要包括数据标注、特征抽取、模型训练、模型预测、回测交易5个部分,但却包含了多个小模块。本
文从微观层面单独介绍各个小模块。
(
由于本文篇幅较长,为增强阅读体验,部分内容需手动点击才能展开,带黑色实心三角符号的内容可直接点击展开查阅。例如 属性窗格。)
属性窗格
画布中的各个模块:
由于特征抽取部分包括训练数据的特征抽取和评估数据的特征抽取,本文只介绍训练数据的特征抽取。评估数据的特征抽取同理,只是数据不一样(数据由
start_date和end_date决定)。
证券代码列表
自动数据标注
输入特征列表
基础特征抽取
衍生特征抽取
连接数据
缺失数据处理
StockRanker训练
StockRanker预测
Trade(回测/模拟)
现在,BigStudio上的AI量化策略的模块已经介绍完毕。当我们新建一个可视化AI量化策略的时候,我们不用做太多的改动,直接使用模板,然后调一下参
数,将精力更多地放在特征抽取和数据标注上。接下来,我们会介绍如何自定义模块和使用更灵活地特征抽取和数据标注。
BigStudio 使用文档介绍(五)
在上一篇文章,我们介绍了BigStudio可视化研究的各个模块。今天我们介绍最重要的一个模块:自定义模块,之所以说最重要,是因为策略实验开发
需求多样,掌握了如何自定义模块才能在策略实验开发中更加自由灵活。
什么是模块?
模块可以将其理解为函数,目的是实现某些功能。模块的示意图如下:
整个流程是$x$作为输入,进入函数$f$,然后得到输出结果$f(x)$,这就是我们日常理解的函数。在BigStudio中,模块的概念和函数一样,拥有输入(可以
多个输入)和输出(也可以多个输出)。因此在画布中,每一个拥有输入连接线和输出连接线的矩形框都可以看成模块,仅有输出连接线的矩形框可以看成
数据。
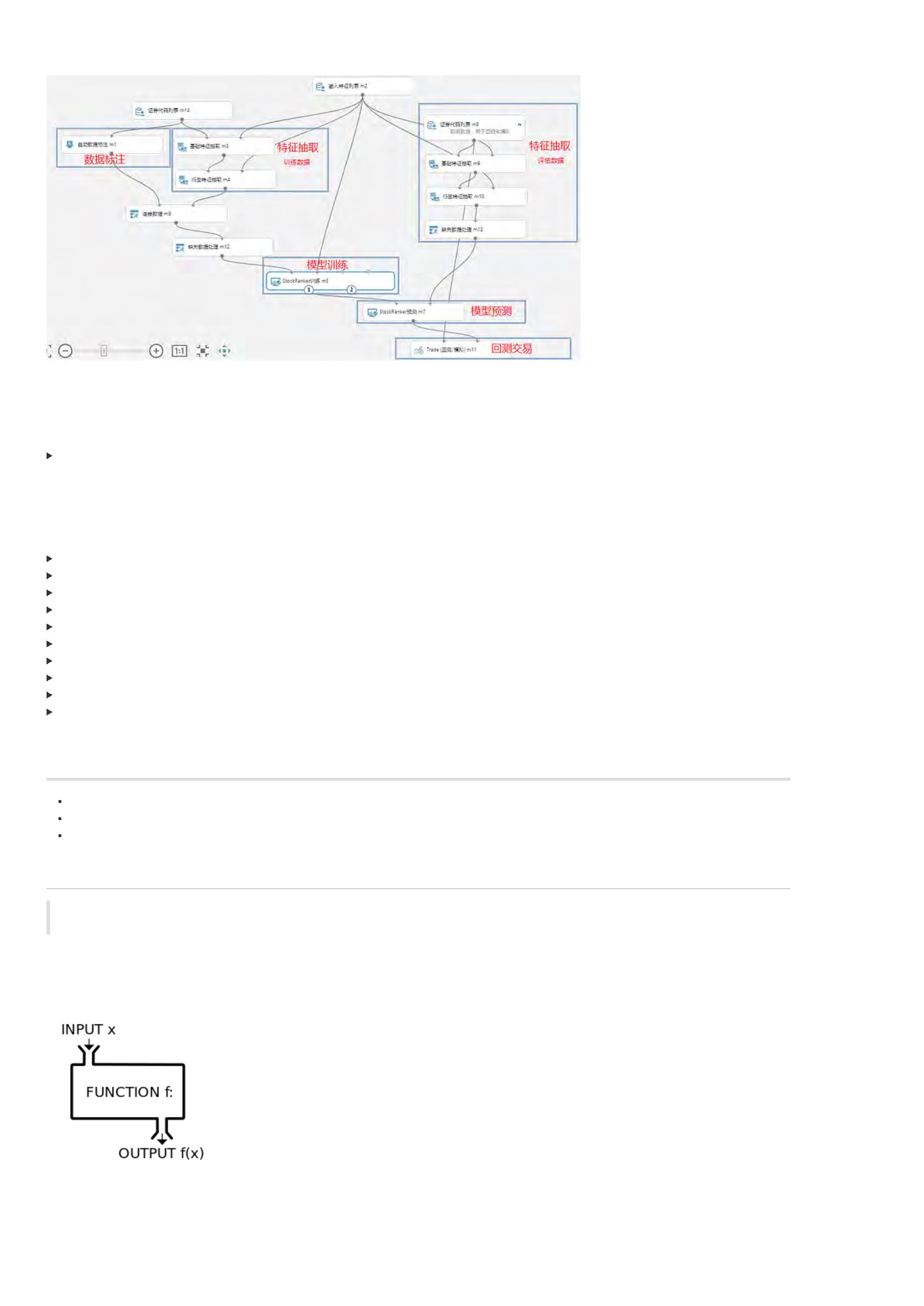
在示意图上,只有一个输入,一个输出,但BigStudio上的模块可以最多支持三个输入,三个输出。示意图如下:
如何自定义模块?
我们以这样的例子举例:假设我们希望对一段时间的股票数据进行过滤,去除st股票和上市天数小于120天的股票。我们一共构建了三个模块,第一个模块有三个输出,分别是时间、
直接拖取 自定义Python 模块到画布,连拖三次
选中第一个模块,点击右侧代码编辑器窗口,输入以下代码:
同理,选中第二个模块,点击右侧代码编辑器窗口,输入以下代码:
最后,选中第三个模块,点击右侧代码编辑器窗口,输入以下代码:
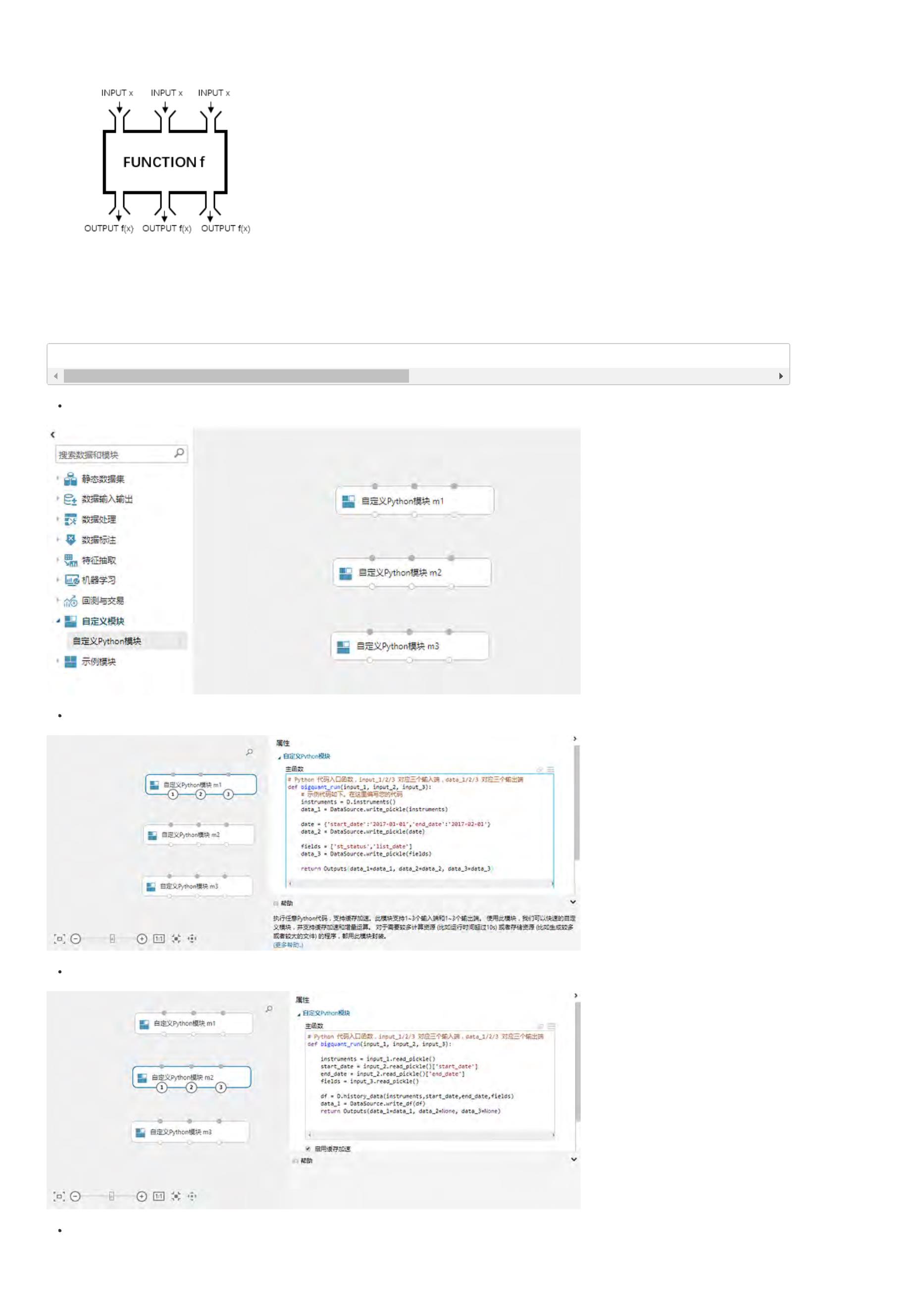
模块如下连线,并为每个模块添加注释
运行,并打印m3模块输出数据
代码编辑器窗口
什么是代码编辑器窗口?
代码编辑器窗口是BigStudio为特定模块需要输入代码进行编辑的一个窗口。
这是模块m1的右侧的代码编辑器窗口,其中点击红色箭头所指的类似于两个矩形框堆叠的按钮可以 弹出该代码编辑器窗口。
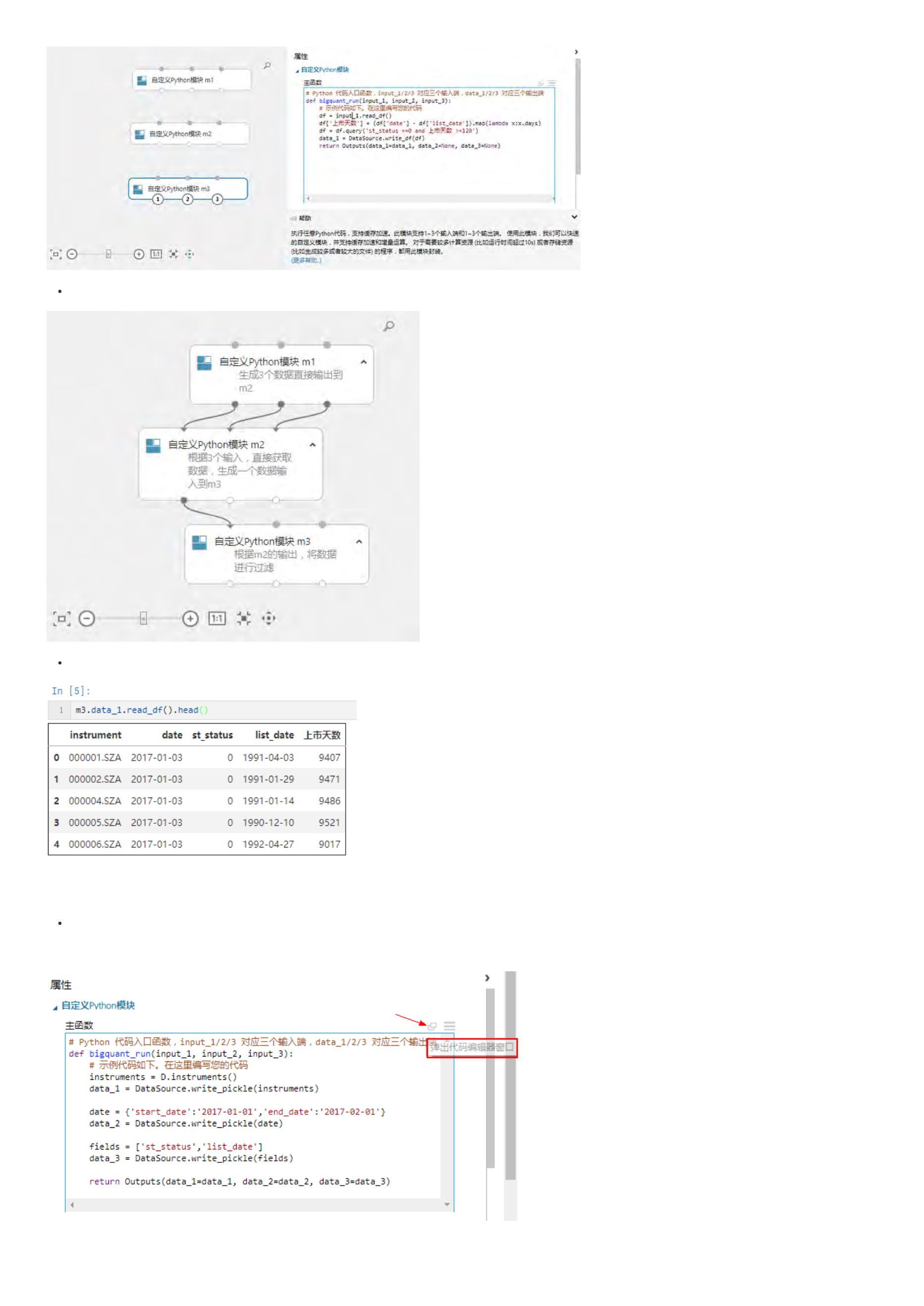
支持代码补齐功能
代码编辑器窗口和策略研究界面的单元格一样,同样具备 代码补齐功能。比如输入 “fs_” ,这样就能弹出财务相关的因子,而且能够知道各个因子的具体含
义。
今天就介绍到这里,希望大家能够自由灵活地使用自定义模块。
在AI策略中使用滚动训练
为了能更简单、更灵活同时在回测和实盘模拟中无缝支持滚动训练和模型自动更新,我们增加了滚动运行支持,并优化了相应模块。
如何在实验中增加滚动训练支持
使用模板新建一个策略:策略 > 新建 > 可视化策略 - AI选股策略
如下三步即可增加滚动训练支持:
1
. 添加滚动运行配置模块:
连接滚动运行模块 和 证券代码列表模块
设置滚动运行的参数,可以设置训练更新周期等,默认配置对应的是每365天更新一次模型,最少要有730天的数据才开始训练
清除 证券代码列表 配置的 开始时间 和 结束时间,以使用来自 滚动配置 的时间
模拟实盘中自动更新模型:将滚动运行配置的 结束日期 绑定到实盘日期
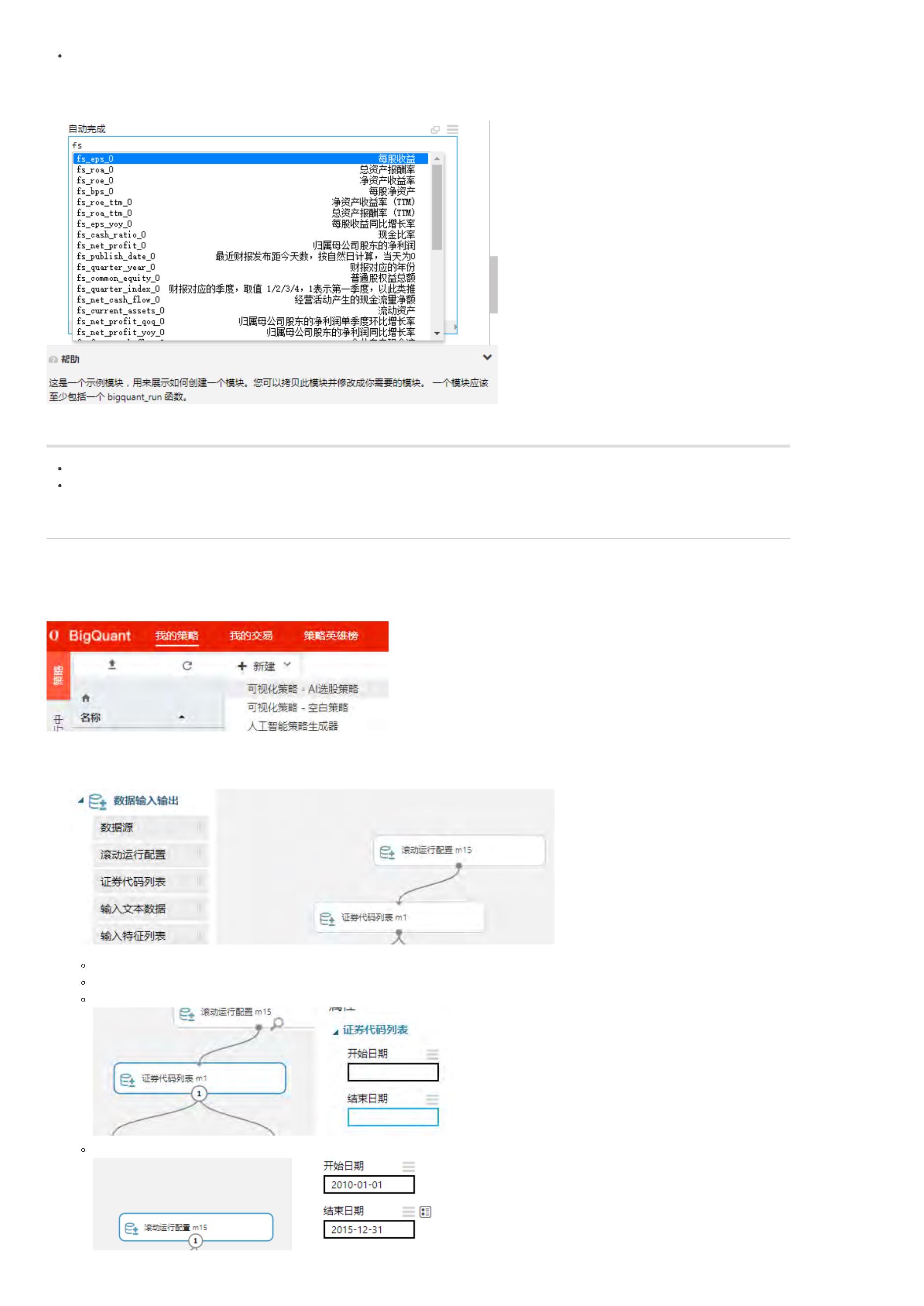
2
. 添加滚动运行到模型训练上:
如上图连接:StockRanker训练 -> 滚动运行 -> Trade(回测/模拟),注意 StockRanker训练 到 滚动运行 的连接是在 延迟运行 输出端口上
StockRanker配置:勾选 延迟运行,为了支持滚动运行和最小的代码改动,平台增加了对模块延迟运行的支持,可以将模块打包作为参数传入其他
模块,并在其中调用。这里我们将配置好的 StockRanker训练 打包到滚动运行中,由滚动决定模块的调用方式。
因为使用了滚动训练,所以我们可以使用更多的回测数据了,这里可以把开始时间设置的更早一些。预测模块已经内建了对滚动训练的支持。同时
对于较早的数据,而没有模型可用时,会自动跳过。
3
. 添加滚动预测:
如上图连接模块
勾选 StockRanker预测 延迟运行
注意:我们优化了模块时间的配置,不再需要在 自动数据标注、基础特征抽取和Trade模块里重复配置时间。可视化策略开发模板已经更新。如果您的策略
是以前生成的,您需要将 自动数据标注、基础特征抽取和Trade模块 的 开始日期 和 结束日期 参数设置为空。
滚动训练示意图
滚动运行详解
金融数据属于时间序列数据,数据之间具有自相关性,因此不能采取经典机器学习的交叉验证的方式,对训练集进行随机划分。这里,我们建议采取滚动训
练方式。滚动训练依赖于滚动运行模块,我们分别介绍不使用滚动运行和使用滚动运行,加深大家对滚动运行模块的理解。
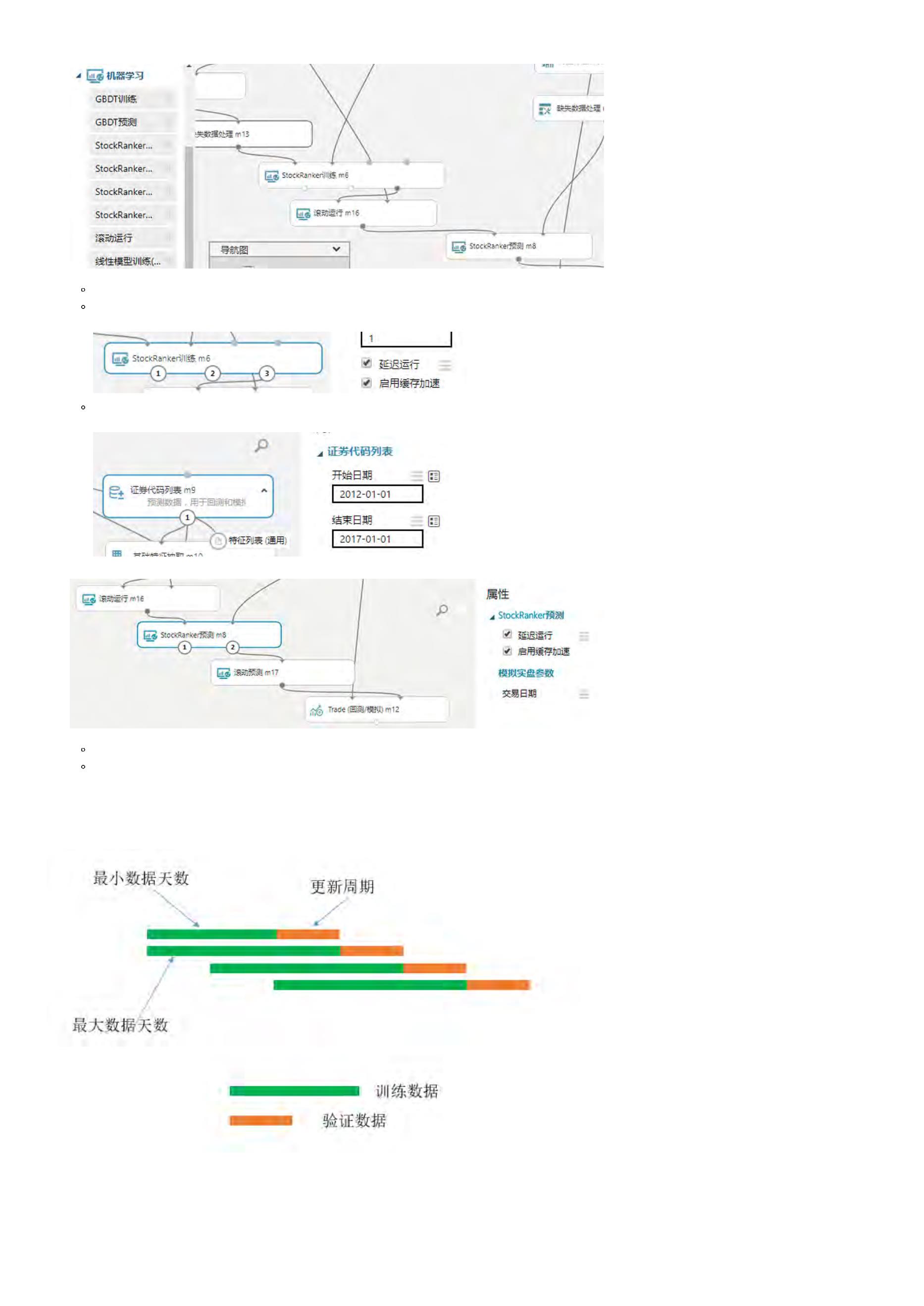
不使用滚动运行
如果我们不使用滚动运行,回测区间为2015.1.1到2017.10.01,那么模型只会在训练集上训练模型,然后对验证集数据进行预测,这样只会有一次训练
一次预测。时间较远的数据做训练来预测最近的数据可能效果不是很理想。此外,不同时期市场状况和结构也不一致,因此需要采取滚动运行。
使用滚动运行
使用滚动运行,我们就可以及时更新模型,用最近的数据来预测数据,这样从策略开发逻辑和实盘交易的角度看比较合理。
假设参数配置是这样,开始日期为2010-1-1,结束日期为2017-10-01, 其中,回测区间为2012.1.1到2017.10.1, 最小数据天数为730,最大数据天数
为1095,更新天数为365。
模块源代码
滚动运行配置:https://github.com/bigquant/bigquant-module-rolling_conf
滚动运行:https://github.com/bigquant/bigquant-module-rolling_run
滚动预测:https://github.com/bigquant/bigquant-module-rolling_run_predict
完整的示例策略
{
"Description":"实验创建于2017/8/26","Summary":"","Graph":{"EdgesInternal":[{"DestinationInputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
1
5:instruments","SourceOutputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-8:data"},{"DestinationInputPortId":"287d2cb0-f53c-4101-bdf8-
04b137c8601-29:instruments","SourceOutputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-8:data"},{"DestinationInputPortId":"287d2cb0-f53c-4101-
1
bdf8-104b137c8601-53:data1","SourceOutputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-15:data"},{"DestinationInputPortId":"287d2cb0-f53c-4101-
bdf8-104b137c8601-29:features","SourceOutputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-24:data"},{"DestinationInputPortId":"287d2cb0-f53c-
4
101-bdf8-104b137c8601-35:features","SourceOutputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-24:data"},{"DestinationInputPortId":"287d2cb0-
f53c-4101-bdf8-104b137c8601-76:features","SourceOutputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-24:data"},
"DestinationInputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-43:features","SourceOutputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
{
2
4:data"},{"DestinationInputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-70:features","SourceOutputPortId":"287d2cb0-f53c-4101-bdf8-
04b137c8601-24:data"},{"DestinationInputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-35:input_data","SourceOutputPortId":"287d2cb0-f53c-4101-
1
bdf8-104b137c8601-29:data"},{"DestinationInputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-53:data2","SourceOutputPortId":"287d2cb0-f53c-4101-
bdf8-104b137c8601-35:data"},{"DestinationInputPortId":"-107:run","SourceOutputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-43:m_lazy_run"},
{
"DestinationInputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-84:input_data","SourceOutputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-

53:data"},{"DestinationInputPortId":"-113:predict","SourceOutputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-60:m_lazy_run"},
{
"DestinationInputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-70:instruments","SourceOutputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
6
2:data"},{"DestinationInputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-81:instruments","SourceOutputPortId":"287d2cb0-f53c-4101-bdf8-
04b137c8601-62:data"},{"DestinationInputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-76:input_data","SourceOutputPortId":"287d2cb0-f53c-4101-
1
bdf8-104b137c8601-70:data"},{"DestinationInputPortId":"-86:input_data","SourceOutputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-76:data"},
"DestinationInputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-43:training_ds","SourceOutputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
4:data"},{"DestinationInputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-60:data","SourceOutputPortId":"-86:data"},
{
8
{
{
"DestinationInputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-8:rolling_conf","SourceOutputPortId":"-578:data"},
"DestinationInputPortId":"-107:input_list","SourceOutputPortId":"-578:data"},{"DestinationInputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
60:model","SourceOutputPortId":"-107:data"},{"DestinationInputPortId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
81:options_data","SourceOutputPortId":"-113:predictions"}],"ModuleNodes":[{"Id":"287d2cb0-f53c-4101-bdf8-104b137c8601-
8","ModuleId":"BigQuantSpace.instruments.instruments-v2","ModuleParameters":
[
{"Name":"start_date","Value":"","ValueType":"Literal","LinkedGlobalParameter":null},
{
{
{
{
"Name":"end_date","Value":"","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"market","Value":"CN_STOCK_A","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"instrument_list","Value":"","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"max_count","Value":"0","ValueType":"Literal","LinkedGlobalParameter":null}],"InputPortsInternal":
[
{"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"rolling_conf","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
8
8
1
#
"}],"OutputPortsInternal":[{"Name":"data","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
","OutputType":null}],"UsePreviousResults":true,"moduleIdForCode":1,"Comment":"","CommentCollapsed":true},{"Id":"287d2cb0-f53c-4101-bdf8-
04b137c8601-15","ModuleId":"BigQuantSpace.advanced_auto_labeler.advanced_auto_labeler-v2","ModuleParameters":[{"Name":"label_expr","Value":"#
号开始的表示注释\n# 0. 每行一个,顺序执行,从第二个开始,可以使用label字段\n# 1. 可用数据字段见
https://bigquant.com/docs/data_history_data.html\n# 添加benchmark_前缀,可使用对应的benchmark数据\n# 2. 可用操作符和函数见 `表达式引擎
https://bigquant.com/docs/big_expr.html>`_\n\n# 计算收益:5日收盘价(作为卖出价格)除以明日开盘价(作为买入价格)\nshift(close, -5) / shift(open, -1)\n\n#
极值处理:用1%和99%分位的值做clip\nclip(label, all_quantile(label, 0.01), all_quantile(label, 0.99))\n\n# 将分数映射到分类,这里使用20个分类
nall_wbins(label, 20)\n\n# 过滤掉一字涨停的情况 (设置label为NaN,在后续处理和训练中会忽略NaN的label)\nwhere(shift(high, -1) == shift(low, -1), NaN,
label)\n","ValueType":"Literal","LinkedGlobalParameter":null},{"Name":"start_date","Value":"","ValueType":"Literal","LinkedGlobalParameter":null},
<
\
{
{
{
{
{
"Name":"end_date","Value":"","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"benchmark","Value":"000300.SHA","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"drop_na_label","Value":"True","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"cast_label_int","Value":"True","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"user_functions","Value":"","ValueType":"Literal","LinkedGlobalParameter":null}],"InputPortsInternal":
[
{"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"instruments","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
1
1
1
5"}],"OutputPortsInternal":[{"Name":"data","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
5","OutputType":null}],"UsePreviousResults":true,"moduleIdForCode":2,"Comment":"","CommentCollapsed":true},{"Id":"287d2cb0-f53c-4101-bdf8-
04b137c8601-24","ModuleId":"BigQuantSpace.input_features.input_features-v1","ModuleParameters":[{"Name":"features","Value":"# #号开始的表示注释
\
\
[
n# 多个特征,每行一个,可以包含基础特征和衍生特征
nreturn_5\nreturn_10\nreturn_20\navg_amount_0/avg_amount_5\navg_amount_5/avg_amount_20\nrank_avg_amount_0/rank_avg_amount_5\nrank_avg_amount_
],"OutputPortsInternal":[{"Name":"data","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
2
1
4","OutputType":null}],"UsePreviousResults":true,"moduleIdForCode":3,"Comment":"","CommentCollapsed":true},{"Id":"287d2cb0-f53c-4101-bdf8-
04b137c8601-29","ModuleId":"BigQuantSpace.general_feature_extractor.general_feature_extractor-v6","ModuleParameters":
[
{"Name":"start_date","Value":"","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"end_date","Value":"","ValueType":"Literal","LinkedGlobalParameter":null}],"InputPortsInternal":
{"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"instruments","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-29"},
"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"features","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
{
[
{
2
2
1
9"}],"OutputPortsInternal":[{"Name":"data","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
9","OutputType":null}],"UsePreviousResults":true,"moduleIdForCode":4,"Comment":"","CommentCollapsed":true},{"Id":"287d2cb0-f53c-4101-bdf8-
04b137c8601-35","ModuleId":"BigQuantSpace.derived_feature_extractor.derived_feature_extractor-v2","ModuleParameters":
[
{"Name":"date_col","Value":"date","ValueType":"Literal","LinkedGlobalParameter":null},
{
{
"Name":"instrument_col","Value":"instrument","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"user_functions","Value":"","ValueType":"Literal","LinkedGlobalParameter":null}],"InputPortsInternal":
[
{"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"input_data","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-35"},
"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"features","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
{
3
3
1
5"}],"OutputPortsInternal":[{"Name":"data","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
5","OutputType":null}],"UsePreviousResults":true,"moduleIdForCode":5,"Comment":"","CommentCollapsed":true},{"Id":"287d2cb0-f53c-4101-bdf8-
04b137c8601-43","ModuleId":"BigQuantSpace.stock_ranker_train.stock_ranker_train-v5","ModuleParameters":[{"Name":"learning_algorithm","Value":"排
序","ValueType":"Literal","LinkedGlobalParameter":null},{"Name":"number_of_leaves","Value":30,"ValueType":"Literal","LinkedGlobalParameter":null},
{
{
{
{
{
{
"Name":"minimum_docs_per_leaf","Value":1000,"ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"number_of_trees","Value":20,"ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"learning_rate","Value":0.1,"ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"max_bins","Value":1023,"ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"feature_fraction","Value":1,"ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"m_lazy_run","Value":"True","ValueType":"Literal","LinkedGlobalParameter":null}],"InputPortsInternal":
[
{"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"training_ds","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-43"},
{
{
{
"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"features","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-43"},
"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"test_ds","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-43"},
"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"base_model","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
4
3"}],"OutputPortsInternal":[{"Name":"model","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-43","OutputType":null},
"Name":"feature_gains","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-43","OutputType":null},{"Name":"m_lazy_run","NodeId":"287d2cb0-f53c-
101-bdf8-104b137c8601-43","OutputType":null}],"UsePreviousResults":true,"moduleIdForCode":6,"Comment":"","CommentCollapsed":true},
"Id":"287d2cb0-f53c-4101-bdf8-104b137c8601-53","ModuleId":"BigQuantSpace.join.join-v3","ModuleParameters":
{
4
{

[
{"Name":"on","Value":"date,instrument","ValueType":"Literal","LinkedGlobalParameter":null},
{
{
"Name":"how","Value":"inner","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"sort","Value":"False","ValueType":"Literal","LinkedGlobalParameter":null}],"InputPortsInternal":
[
{"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"data1","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-53"},
"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"data2","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
{
5
5
1
3"}],"OutputPortsInternal":[{"Name":"data","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
3","OutputType":null}],"UsePreviousResults":true,"moduleIdForCode":7,"Comment":"","CommentCollapsed":true},{"Id":"287d2cb0-f53c-4101-bdf8-
04b137c8601-60","ModuleId":"BigQuantSpace.stock_ranker_predict.stock_ranker_predict-v5","ModuleParameters":
[
[
{"Name":"m_lazy_run","Value":"True","ValueType":"Literal","LinkedGlobalParameter":null}],"InputPortsInternal":
{"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"model","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-60"},
{
"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"data","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
0"}],"OutputPortsInternal":[{"Name":"predictions","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-60","OutputType":null},
"Name":"m_lazy_run","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
6
{
6
1
0
0
0","OutputType":null}],"UsePreviousResults":true,"moduleIdForCode":8,"Comment":"","CommentCollapsed":true},{"Id":"287d2cb0-f53c-4101-bdf8-
04b137c8601-62","ModuleId":"BigQuantSpace.instruments.instruments-v2","ModuleParameters":[{"Name":"start_date","Value":"2012-01-
1","ValueType":"Literal","LinkedGlobalParameter":"交易日期"},{"Name":"end_date","Value":"2017-01-
1","ValueType":"Literal","LinkedGlobalParameter":"交易日期"},
{
{
{
"Name":"market","Value":"CN_STOCK_A","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"instrument_list","Value":"","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"max_count","Value":"0","ValueType":"Literal","LinkedGlobalParameter":null}],"InputPortsInternal":
[
{"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"rolling_conf","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
6
6
2"}],"OutputPortsInternal":[{"Name":"data","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
2","OutputType":null}],"UsePreviousResults":true,"moduleIdForCode":9,"Comment":"预测数据,用于回测和模拟","CommentCollapsed":false},
{
"Id":"287d2cb0-f53c-4101-bdf8-104b137c8601-70","ModuleId":"BigQuantSpace.general_feature_extractor.general_feature_extractor-
v6","ModuleParameters":[{"Name":"start_date","Value":"","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"end_date","Value":"","ValueType":"Literal","LinkedGlobalParameter":null}],"InputPortsInternal":
{"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"instruments","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-70"},
"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"features","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
{
[
{
7
7
1
0"}],"OutputPortsInternal":[{"Name":"data","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
0","OutputType":null}],"UsePreviousResults":true,"moduleIdForCode":10,"Comment":"","CommentCollapsed":true},{"Id":"287d2cb0-f53c-4101-bdf8-
04b137c8601-76","ModuleId":"BigQuantSpace.derived_feature_extractor.derived_feature_extractor-v2","ModuleParameters":
[
{"Name":"date_col","Value":"date","ValueType":"Literal","LinkedGlobalParameter":null},
{
{
"Name":"instrument_col","Value":"instrument","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"user_functions","Value":"","ValueType":"Literal","LinkedGlobalParameter":null}],"InputPortsInternal":
[
{"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"input_data","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-76"},
"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"features","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
{
7
7
1
6"}],"OutputPortsInternal":[{"Name":"data","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
6","OutputType":null}],"UsePreviousResults":true,"moduleIdForCode":11,"Comment":"","CommentCollapsed":true},{"Id":"287d2cb0-f53c-4101-bdf8-
04b137c8601-81","ModuleId":"BigQuantSpace.trade.trade-v3","ModuleParameters":
[
{"Name":"start_date","Value":"","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"end_date","Value":"","ValueType":"Literal","LinkedGlobalParameter":null},{"Name":"handle_data","Value":"# 回测引擎:每日数据处理函数,每天
{
执行一次\ndef bigquant_run(context, data):\n # 按日期过滤得到今日的预测数据\n ranker_prediction = context.ranker_prediction[\n
context.ranker_prediction.date == data.current_dt.strftime('%Y-%m-%d')]\n\n # 1. 资金分配\n # 平均持仓时间是hold_days,每日都将买入股票,每日预期使
用 1/hold_days 的资金\n # 实际操作中,会存在一定的买入误差,所以在前hold_days天,等量使用资金;之后,尽量使用剩余资金(这里设置最多用等量的
1
.5倍)\n is_staging = context.trading_day_index < context.options['hold_days'] # 是否在建仓期间(前 hold_days 天)\n cash_avg =
context.portfolio.portfolio_value / context.options['hold_days']\n cash_for_buy = min(context.portfolio.cash, (1 if is_staging else 1.5) * cash_avg)\n
cash_for_sell = cash_avg - (context.portfolio.cash - cash_for_buy)\n positions = {e.symbol: p.amount * p.last_sale_price\n for e, p in
context.perf_tracker.position_tracker.positions.items()}\n\n # 2. 生成卖出订单:hold_days天之后才开始卖出;对持仓的股票,按StockRanker预测的排序末
位淘汰\n if not is_staging and cash_for_sell > 0:\n equities = {e.symbol: e for e, p in context.perf_tracker.position_tracker.positions.items()}\n instruments =
list(reversed(list(ranker_prediction.instrument[ranker_prediction.instrument.apply(\n lambda x: x in equities and not
context.has_unfinished_sell_order(equities[x]))])))\n # print('rank order for sell %s' % instruments)\n for instrument in instruments:\n
context.order_target(context.symbol(instrument), 0)\n cash_for_sell -= positions[instrument]\n if cash_for_sell <= 0:\n break\n\n # 3. 生成买入订单:按
StockRanker预测的排序,买入前面的stock_count只股票\n buy_cash_weights = context.stock_weights\n buy_instruments =
list(ranker_prediction.instrument[:len(buy_cash_weights)])\n max_cash_per_instrument = context.portfolio.portfolio_value *
context.max_cash_per_instrument\n for i, instrument in enumerate(buy_instruments):\n cash = cash_for_buy * buy_cash_weights[i]\n if cash >
max_cash_per_instrument - positions.get(instrument, 0):\n # 确保股票持仓量不会超过每次股票最大的占用资金量\n cash = max_cash_per_instrument -
positions.get(instrument, 0)\n if cash > 0:\n context.order_value(context.symbol(instrument), cash)\n","ValueType":"Literal","LinkedGlobalParameter":null},
{
{
"Name":"prepare","Value":"# 回测引擎:准备数据,只执行一次\ndef bigquant_run(context):\n pass\n","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"initialize","Value":"# 回测引擎:初始化函数,只执行一次\ndef bigquant_run(context):\n # 加载预测数据\n context.ranker_prediction =
context.options['data'].read_df()\n\n # 系统已经设置了默认的交易手续费和滑点,要修改手续费可使用如下函数\n
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))\n # 预测数据,通过options传入进来,使用 read_df 函数,加载到内
存 (DataFrame)\n # 设置买入的股票数量,这里买入预测股票列表排名靠前的5只\n stock_count = 5\n # 每只的股票的权重,如下的权重分配会使得靠前的股
票分配多一点的资金,[0.339160, 0.213986, 0.169580, ..]\n context.stock_weights = T.norm([1 / math.log(i + 2) for i in range(0, stock_count)])\n # 设置每只
股票占用的最大资金比例\n context.max_cash_per_instrument = 0.2\n context.options['hold_days'] =
5\n","ValueType":"Literal","LinkedGlobalParameter":null},{"Name":"before_trading_start","Value":"","ValueType":"Literal","LinkedGlobalParameter":null},
{
{
{
{
{
{
"Name":"volume_limit","Value":0.025,"ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"order_price_field_buy","Value":"open","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"order_price_field_sell","Value":"close","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"capital_base","Value":1000000,"ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"benchmark","Value":"000300.SHA","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"auto_cancel_non_tradable_orders","Value":"True","ValueType":"Literal","LinkedGlobalParameter":null},

{
{
{
"Name":"data_frequency","Value":"daily","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"plot_charts","Value":"True","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"backtest_only","Value":"False","ValueType":"Literal","LinkedGlobalParameter":null}],"InputPortsInternal":
[
{"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"instruments","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-81"},
"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"options_data","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
{
8
8
1
1"}],"OutputPortsInternal":[{"Name":"raw_perf","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
1","OutputType":null}],"UsePreviousResults":false,"moduleIdForCode":12,"Comment":"","CommentCollapsed":true},{"Id":"287d2cb0-f53c-4101-bdf8-
04b137c8601-84","ModuleId":"BigQuantSpace.dropnan.dropnan-v1","ModuleParameters":[],"InputPortsInternal":
[
{"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"input_data","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
84"}],"OutputPortsInternal":[{"Name":"data","NodeId":"287d2cb0-f53c-4101-bdf8-104b137c8601-
84","OutputType":null}],"UsePreviousResults":true,"moduleIdForCode":13,"Comment":"","CommentCollapsed":true},
{
"Id":"-86","ModuleId":"BigQuantSpace.dropnan.dropnan-v1","ModuleParameters":[],"InputPortsInternal":
[
[
{"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"input_data","NodeId":"-86"}],"OutputPortsInternal":
{"Name":"data","NodeId":"-86","OutputType":null}],"UsePreviousResults":true,"moduleIdForCode":14,"Comment":"","CommentCollapsed":true},
{
"Id":"-578","ModuleId":"BigQuantSpace.rolling_conf.rolling_conf-v1","ModuleParameters":[{"Name":"start_date","Value":"2010-01-
1","ValueType":"Literal","LinkedGlobalParameter":null},{"Name":"end_date","Value":"2015-12-31","ValueType":"Literal","LinkedGlobalParameter":"交易日
期"},{"Name":"rolling_update_days","Value":"365","ValueType":"Literal","LinkedGlobalParameter":null},
0
{
{
{
{
"Name":"rolling_update_days_for_live","Value":"","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"rolling_min_days","Value":730,"ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"rolling_max_days","Value":0,"ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"rolling_count_for_live","Value":1,"ValueType":"Literal","LinkedGlobalParameter":null}],"InputPortsInternal":[],"OutputPortsInternal":
[
{"Name":"data","NodeId":"-578","OutputType":null}],"UsePreviousResults":false,"moduleIdForCode":15,"Comment":"","CommentCollapsed":true},
{
"Id":"-107","ModuleId":"BigQuantSpace.rolling_run.rolling_run-v1","ModuleParameters":
[
[
{"Name":"param_name","Value":"rolling_input","ValueType":"Literal","LinkedGlobalParameter":null}],"InputPortsInternal":
{"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"run","NodeId":"-107"},
{
"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"input_list","NodeId":"-107"}],"OutputPortsInternal":
{"Name":"data","NodeId":"-107","OutputType":null}],"UsePreviousResults":true,"moduleIdForCode":16,"Comment":"","CommentCollapsed":true},
"Id":"-113","ModuleId":"BigQuantSpace.rolling_run_predict.rolling_run_predict-v1","ModuleParameters":
{"Name":"model_param_name","Value":"model","ValueType":"Literal","LinkedGlobalParameter":null},
"Name":"data_param_name","Value":"data","ValueType":"Literal","LinkedGlobalParameter":null}],"InputPortsInternal":
[
{
[
{
[
[
{"DataSourceId":null,"TrainedModelId":null,"TransformModuleId":null,"Name":"predict","NodeId":"-113"}],"OutputPortsInternal":
{"Name":"predictions","NodeId":"-113","OutputType":null}],"UsePreviousResults":true,"moduleIdForCode":17,"Comment":"","CommentCollapsed":true}],"SerializedCli
<
?xml version='1.0' encoding='utf-16'?><DataV1 xmlns:xsd='http://www.w3.org/2001/XMLSchema' xmlns:xsi='http://www.w3.org/2001/XMLSchema-
instance'><Meta /><NodePositions><NodePosition Node='287d2cb0-f53c-4101-bdf8-104b137c8601-8' Position='211,64,200,200'/><NodePosition
Node='287d2cb0-f53c-4101-bdf8-104b137c8601-15' Position='70,183,200,200'/><NodePosition Node='287d2cb0-f53c-4101-bdf8-104b137c8601-24'
Position='765,21,200,200'/><NodePosition Node='287d2cb0-f53c-4101-bdf8-104b137c8601-29' Position='381,188,200,200'/><NodePosition
Node='287d2cb0-f53c-4101-bdf8-104b137c8601-35' Position='385,280,200,200'/><NodePosition Node='287d2cb0-f53c-4101-bdf8-104b137c8601-43'
Position='553,545,200,200'/><NodePosition Node='287d2cb0-f53c-4101-bdf8-104b137c8601-53' Position='249,375,200,200'/><NodePosition
Node='287d2cb0-f53c-4101-bdf8-104b137c8601-60' Position='732.4429321289062,701.5533447265625,200,200'/><NodePosition Node='287d2cb0-f53c-
4101-bdf8-104b137c8601-62' Position='1074,127,200,200'/><NodePosition Node='287d2cb0-f53c-4101-bdf8-104b137c8601-70'
Position='1078,237,200,200'/><NodePosition Node='287d2cb0-f53c-4101-bdf8-104b137c8601-76' Position='1081,327,200,200'/><NodePosition
Node='287d2cb0-f53c-4101-bdf8-104b137c8601-81' Position='1058.837890625,847.34375,200,200'/><NodePosition Node='287d2cb0-f53c-4101-bdf8-
104b137c8601-84' Position='376,467,200,200'/><NodePosition Node='-86' Position='1078,418,200,200'/><NodePosition Node='-578'
Position='308,-44,200,200'/><NodePosition Node='-107' Position='613,630.8458251953125,200,200'/><NodePosition Node='-113'
Position='875.4267578125,775.1358642578125,200,200'/></NodePositions><NodeGroups />
<
/DataV1>"},"IsDraft":true,"ParentExperimentId":null,"WebService":{"IsWebServiceExperiment":false,"Inputs":[],"Outputs":[],"Parameters":[{"Name":"交易日
期","Value":"","ParameterDefinition":{"Name":"交易日期","FriendlyName":"交易日
期","DefaultValue":"","ParameterType":"String","HasDefaultValue":true,"IsOptional":true,"ParameterRules":
[
],"HasRules":false,"MarkupType":0,"CredentialDescriptor":null}}],"WebServiceGroupId":null,"SerializedClientData":"<?xml version='1.0' encoding='utf-16'?>
<
<
DataV1 xmlns:xsd='http://www.w3.org/2001/XMLSchema' xmlns:xsi='http://www.w3.org/2001/XMLSchema-instance'><Meta /><NodePositions>
/NodePositions><NodeGroups /></DataV1>"},"DisableNodesUpdate":false,"Category":"user","Tags":[],"IsPartialRun":true}
In [6]:
#
#
本代码由可视化策略环境自动生成 2017年10月20日 21:26
本代码单元只能在可视化模式下编辑。您也可以拷贝代码,粘贴到新建的代码单元或者策略,然后修改。
m3 = M.input_features.v1(
features="""# #号开始的表示注释
#
多个特征,每行一个,可以包含基础特征和衍生特征
return_5
return_10
return_20
avg_amount_0/avg_amount_5
avg_amount_5/avg_amount_20
rank_avg_amount_0/rank_avg_amount_5
rank_avg_amount_5/rank_avg_amount_10
rank_return_0
rank_return_5
rank_return_10
rank_return_0/rank_return_5
rank_return_5/rank_return_10
pe_ttm_0
"
""
)
m9 = M.instruments.v2(
start_date=T.live_run_param('trading_date', '2012-01-01'),
end_date=T.live_run_param('trading_date', '2017-01-01'),
market='CN_STOCK_A',
instrument_list='',
max_count=0
)
m10 = M.general_feature_extractor.v6(
instruments=m9.data,
features=m3.data,
start_date='',
end_date=''
)
m11 = M.derived_feature_extractor.v2(
input_data=m10.data,
features=m3.data,
date_col='date',
instrument_col='instrument'
)
m14 = M.dropnan.v1(
input_data=m11.data
)
m15 = M.rolling_conf.v1(
start_date='2010-01-01',
end_date=T.live_run_param('trading_date', '2015-12-31'),
rolling_update_days=365,
rolling_min_days=730,
rolling_max_days=0,
rolling_count_for_live=1
)
m1 = M.instruments.v2(
rolling_conf=m15.data,
start_date='',
end_date='',
market='CN_STOCK_A',
instrument_list='',
max_count=0
)
m2 = M.advanced_auto_labeler.v2(
instruments=m1.data,
label_expr="""# #号开始的表示注释
#
#
#
#
0. 每行一个,顺序执行,从第二个开始,可以使用label字段
1. 可用数据字段见 https://bigquant.com/docs/data_history_data.html
添加benchmark_前缀,可使用对应的benchmark数据
2. 可用操作符和函数见 `表达式引擎 <https://bigquant.com/docs/big_expr.html>`_
#
计算收益:5日收盘价(作为卖出价格)除以明日开盘价(作为买入价格)
shift(close, -5) / shift(open, -1)
#
极值处理:用1%和99%分位的值做clip
clip(label, all_quantile(label, 0.01), all_quantile(label, 0.99))
#
将分数映射到分类,这里使用20个分类
all_wbins(label, 20)
#
过滤掉一字涨停的情况 (设置label为NaN,在后续处理和训练中会忽略NaN的label)
where(shift(high, -1) == shift(low, -1), NaN, label)
"
"",
start_date='',
end_date='',
benchmark='000300.SHA',
drop_na_label=True,
cast_label_int=True
)
m4 = M.general_feature_extractor.v6(
instruments=m1.data,
features=m3.data,
start_date='',
end_date=''
)
m5 = M.derived_feature_extractor.v2(
input_data=m4.data,

features=m3.data,
date_col='date',
instrument_col='instrument'
)
m7 = M.join.v3(
data1=m2.data,
data2=m5.data,
on='date,instrument',
how='inner',
sort=False
)
m13 = M.dropnan.v1(
input_data=m7.data
)
m6 = M.stock_ranker_train.v5(
training_ds=m13.data,
features=m3.data,
learning_algorithm='排序',
number_of_leaves=30,
minimum_docs_per_leaf=1000,
number_of_trees=20,
learning_rate=0.1,
max_bins=1023,
feature_fraction=1,
m_lazy_run=True
)
m16 = M.rolling_run.v1(
run=m6.m_lazy_run,
input_list=m15.data,
param_name='rolling_input'
)
m8 = M.stock_ranker_predict.v5(
model=m16.data,
data=m14.data,
m_lazy_run=True
)
m17 = M.rolling_run_predict.v1(
predict=m8.m_lazy_run,
model_param_name='model',
data_param_name='data'
)
#
回测引擎:每日数据处理函数,每天执行一次
def m12_handle_data_bigquant_run(context, data):
按日期过滤得到今日的预测数据
#
ranker_prediction = context.ranker_prediction[
context.ranker_prediction.date == data.current_dt.strftime('%Y-%m-%d')]
#
#
#
1. 资金分配
平均持仓时间是hold_days,每日都将买入股票,每日预期使用 1/hold_days 的资金
实际操作中,会存在一定的买入误差,所以在前hold_days天,等量使用资金;之后,尽量使用剩余资金(这里设置最多用等量的1.5倍)
is_staging = context.trading_day_index < context.options['hold_days'] # 是否在建仓期间(前 hold_days 天)
cash_avg = context.portfolio.portfolio_value / context.options['hold_days']
cash_for_buy = min(context.portfolio.cash, (1 if is_staging else 1.5) * cash_avg)
cash_for_sell = cash_avg - (context.portfolio.cash - cash_for_buy)
positions = {e.symbol: p.amount * p.last_sale_price
for e, p in context.perf_tracker.position_tracker.positions.items()}
#
2. 生成卖出订单:hold_days天之后才开始卖出;对持仓的股票,按StockRanker预测的排序末位淘汰
if not is_staging and cash_for_sell > 0:
equities = {e.symbol: e for e, p in context.perf_tracker.position_tracker.positions.items()}
instruments = list(reversed(list(ranker_prediction.instrument[ranker_prediction.instrument.apply(
lambda x: x in equities and not context.has_unfinished_sell_order(equities[x]))])))
#
print('rank order for sell %s' % instruments)
for instrument in instruments:
context.order_target(context.symbol(instrument), 0)
cash_for_sell -= positions[instrument]
if cash_for_sell <= 0:
break
#
3. 生成买入订单:按StockRanker预测的排序,买入前面的stock_count只股票
buy_cash_weights = context.stock_weights
buy_instruments = list(ranker_prediction.instrument[:len(buy_cash_weights)])
max_cash_per_instrument = context.portfolio.portfolio_value * context.max_cash_per_instrument
for i, instrument in enumerate(buy_instruments):
cash = cash_for_buy * buy_cash_weights[i]

if cash > max_cash_per_instrument - positions.get(instrument, 0):
确保股票持仓量不会超过每次股票最大的占用资金量
cash = max_cash_per_instrument - positions.get(instrument, 0)
if cash > 0:
context.order_value(context.symbol(instrument), cash)
#
#
回测引擎:准备数据,只执行一次
def m12_prepare_bigquant_run(context):
pass
#
回测引擎:初始化函数,只执行一次
def m12_initialize_bigquant_run(context):
加载预测数据
context.ranker_prediction = context.options['data'].read_df()
#
#
系统已经设置了默认的交易手续费和滑点,要修改手续费可使用如下函数
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
#
#
预测数据,通过options传入进来,使用 read_df 函数,加载到内存 (DataFrame)
设置买入的股票数量,这里买入预测股票列表排名靠前的5只
stock_count = 5
每只的股票的权重,如下的权重分配会使得靠前的股票分配多一点的资金,[0.339160, 0.213986, 0.169580, ..]
context.stock_weights = T.norm([1 / math.log(i + 2) for i in range(0, stock_count)])
设置每只股票占用的最大资金比例
#
#
context.max_cash_per_instrument = 0.2
context.options['hold_days'] = 5
m12 = M.trade.v3(
instruments=m9.data,
options_data=m17.predictions,
start_date='',
end_date='',
handle_data=m12_handle_data_bigquant_run,
prepare=m12_prepare_bigquant_run,
initialize=m12_initialize_bigquant_run,
volume_limit=0.025,
order_price_field_buy='open',
order_price_field_sell='close',
capital_base=1000000,
benchmark='000300.SHA',
auto_cancel_non_tradable_orders=True,
data_frequency='daily',
plot_charts=True,
backtest_only=False
)
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
2017-10-20 21:23:00.948864] INFO: bigquant: input_features.v1 开始运行..
2017-10-20 21:23:00.952132] INFO: bigquant: 命中缓存
2017-10-20 21:23:00.953017] INFO: bigquant: input_features.v1 运行完成[0.004196s].
2017-10-20 21:23:00.956800] INFO: bigquant: instruments.v2 开始运行..
2017-10-20 21:23:00.958579] INFO: bigquant: 命中缓存
2017-10-20 21:23:00.959305] INFO: bigquant: instruments.v2 运行完成[0.002505s].
2017-10-20 21:23:00.965403] INFO: bigquant: general_feature_extractor.v6 开始运行..
2017-10-20 21:23:00.967222] INFO: bigquant: 命中缓存
2017-10-20 21:23:00.967922] INFO: bigquant: general_feature_extractor.v6 运行完成[0.00252s].
2017-10-20 21:23:00.972751] INFO: bigquant: derived_feature_extractor.v2 开始运行..
2017-10-20 21:23:00.974405] INFO: bigquant: 命中缓存
2017-10-20 21:23:00.975097] INFO: bigquant: derived_feature_extractor.v2 运行完成[0.002347s].
2017-10-20 21:23:00.979849] INFO: bigquant: dropnan.v1 开始运行..
2017-10-20 21:23:00.981792] INFO: bigquant: 命中缓存
2017-10-20 21:23:00.982555] INFO: bigquant: dropnan.v1 运行完成[0.002721s].
2017-10-20 21:23:00.987324] INFO: 滚动运行配置: 生成了 5 次滚动,第一次 {'end_date': '2011-12-31', 'start_date': '2010-01-01'},最后一次
2017-10-20 21:23:00.997503] INFO: bigquant: instruments.v2 开始运行..
2017-10-20 21:23:00.999232] INFO: bigquant: 命中缓存
2017-10-20 21:23:01.000081] INFO: bigquant: instruments.v2 运行完成[0.002561s].
2017-10-20 21:23:01.006614] INFO: bigquant: advanced_auto_labeler.v2 开始运行..
2017-10-20 21:23:01.008366] INFO: bigquant: 命中缓存
2017-10-20 21:23:01.009142] INFO: bigquant: advanced_auto_labeler.v2 运行完成[0.00253s].
2017-10-20 21:23:01.015016] INFO: bigquant: general_feature_extractor.v6 开始运行..
2017-10-20 21:23:01.016728] INFO: bigquant: 命中缓存
2017-10-20 21:23:01.017473] INFO: bigquant: general_feature_extractor.v6 运行完成[0.00245s].
2017-10-20 21:23:01.022882] INFO: bigquant: derived_feature_extractor.v2 开始运行..
2017-10-20 21:23:01.024728] INFO: bigquant: 命中缓存
2017-10-20 21:23:01.025480] INFO: bigquant: derived_feature_extractor.v2 运行完成[0.002594s].
2017-10-20 21:23:01.031597] INFO: bigquant: join.v3 开始运行..
2017-10-20 21:23:01.033292] INFO: bigquant: 命中缓存
2017-10-20 21:23:01.034000] INFO: bigquant: join.v3 运行完成[0.002406s].
2017-10-20 21:23:01.039198] INFO: bigquant: dropnan.v1 开始运行..
2017-10-20 21:23:01.040924] INFO: bigquant: 命中缓存
2017-10-20 21:23:01.041643] INFO: bigquant: dropnan.v1 运行完成[0.002444s].
2017-10-20 21:23:01.050254] INFO: bigquant: 延迟运行 stock_ranker_train.v5
2017-10-20 21:23:01.055494] INFO: bigquant: rolling_run.v1 开始运行..
2017-10-20 21:23:01.057264] INFO: bigquant: 命中缓存

[
[
[
[
[
[
[
[
[
[
2017-10-20 21:23:01.058057] INFO: bigquant: rolling_run.v1 运行完成[0.002558s].
2017-10-20 21:23:01.065179] INFO: bigquant: 延迟运行 stock_ranker_predict.v5
2017-10-20 21:23:01.070487] INFO: bigquant: rolling_run_predict.v1 开始运行..
2017-10-20 21:23:01.094552] INFO: bigquant: 命中缓存
2017-10-20 21:23:01.095407] INFO: bigquant: rolling_run_predict.v1 运行完成[0.024911s].
2017-10-20 21:23:01.219971] INFO: bigquant: backtest.v7 开始运行..
2017-10-20 21:24:09.449538] INFO: Performance: Simulated 1214 trading days out of 1214.
2017-10-20 21:24:09.450669] INFO: Performance: first open: 2012-01-04 14:30:00+00:00
2017-10-20 21:24:09.451652] INFO: Performance: last close: 2016-12-30 20:00:00+00:00
注意] 有 221 笔卖出是在多天内完成的。当日卖出股票超过了当日股票交易的2.5%会出现这种情况。
[
2017-10-20 21:24:14.003618] INFO: bigquant: backtest.v7 运行完成[72.783625s].
Python 编程
[
量化学堂-Python 编程]第一个Python 程序
导语:Python作为一门最热门的编程语言,目前已经成为数据分析、量化投资、机器学习的最主流语言。
Python 是什么?
Python是一种计算机程序设计语言。你可能已经听说过很多种流行的编程语言,比如非常难学的C语言,非常流行的Java语言,适合初学者的Basic语言,适
合网页编程的JavaScript语言等等。
那Python 是一种什么语言?
首先,我们普及一下编程语言的基础知识。用任何编程语言来开发程序,都是为了让计算机干活,比如下载一个MP3,编写一个文档等等,而计算机干活的
CPU只认识机器指令,所以,尽管不同的编程语言差异极大,最后都得“翻译”成CPU可以执行的机器指令。而不同的编程语言,干同一个活,编写的代码
量,差距也很大。
比如,完成同一个任务,C语言要写1000行代码,Java只需要写100行,而Python 可能只要20行。所以Python是一种相当高级的语言。
那是不是越低级的程序越难学,越高级的程序越简单?表面上来说,是的,但是,在非常高的抽象计算中,高级的Python程序设计也是非常难学的,所以,
高级程序语言不等于简单。
但是,对于初学者和完成普通任务,Python语言是非常简单易用的。连Google都在大规模使用Python,所以就不用担心学了会没用。
附件:第一个Python程序
第一个Python 程序¶
依照惯例,学习一门新语言,写的第一程序都叫"Hello World!",因为这个程序所要做的事情就是显示"Hello World!"。我们看看在Python中,它是什么样
子的:
In [2]:
print("hello world!")
hello world!
这是print语句的一个示例。print并不会真的往纸上打印文字,而是在屏幕上输出值。程序中的引号表示输出的文本的开始和结束,在输出结果中并不显示。
print语句也可以跟上多个字符串,用逗号“,”隔开,就可以连成一串输出:
In [4]:
print("hello world!", "hello everyone!")
hello world! hello everyone!
print也可以打印整数,或者计算结果:
In [5]:
print(100)
1
00
In [6]:
print(100 + 200)

3
00
因此,我们可以把计算100 + 200的结果打印得更漂亮一点:
In [7]:
print('100 + 200 =', 100 + 200)
1
00 + 200 = 300
变量¶
编程语言最强大的功能之一是操作变量的能力。变量是指向一个值的名称。
赋值语句可以建立新的变量,并给他们赋值:
In [8]:
message = 'Hello World!'
n = 666
这个例子有两个赋值。第一个将字符串'Hello World!'赋值给一个叫做message的变量;第二个将666赋值给n。
导入模块¶
是不是常常看到程序的开始处有很多的import...,他的作用就时导入模块(模块:指包含一组相关的函数的文件)。
使用import可以导入模块之后,就可以使用这个模块内包含的函数了。
In [17]:
from math import floor
floor(5.2)
Out[17]:
5
查看帮助¶
很多时候导入模块的一些函数我们并不知道是什么含义、有什么功能,因此我们可以通过以下方式查看帮助文件
In [18]:
help(floor)
Help on built-in function floor in module math:
floor(...)
floor(x)
Return the floor of x as an Integral.
This is the largest integer <= x.
从文档可以看出,该函数是对一个数值进行向下取整操作
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-Python 编程]数据类型之列表
导语:本文介绍了Python中非常重要的数据类型——列表。
Python 内嵌的数据类型主要包括以下两类:
有序:
List(列表),是有序集合,没有固定大小,可以通过对偏移量以及其他方法修改列表大小。列表的基本形式如:[1,2,3,4]
Tuple(元组),是有序集合,是不可变的,可以进行组合和复制运算后会生成一个新的元组。元组的基本形式比如:(1,3,6,10)
String(字符串),也是有序集合,字符串的基本形式比如:’hello’,这里不进行具体介绍。

无序:
Set(集合),是一个无序不重复元素的集。基本功能包括关系运算和消除重复元素。集合的基本形式如:set('abracadabra')
Dictionary(字典)是无序的键:值对 (key:value 对)集合,键必须是互不相同的(在同一个字典之内)。字典的基本形式如:{'jack': 4098, 'sape': 4139}
首先对列表进行介绍。
列表
List(列表) 是 Python 中最通用的序列。列表是一个任意类型对象位置的相关有序集合,它没有固定大小。不像字符串,其大小是可以变的,通过对偏移量
进行赋值以及其他各种列表的方法进行调用,可以修改列表大小。
索引是从0开始而非1开始!!
列表中值的分割用变量[头下标:尾下标],就可以截取相应的列表,从左到右索引默认“0”开始的,从右到左索引默认-1开始,下标可以为空表示取到头或尾。
可以对列表进行索引、切片等操作,看下面例子。
附件:列表的使用
In [1]:
#
定义列表L
L = [1,2,3,4,5,6,7,8,9]
#
使用len()函数查看列表的长度
len(L)
Out[1]:
9
列表索引
In [2]:
print(L[0]) # 表示打印列表中第一个元素
print(L[-1]) # 负数表示从后数第几个元素,-1即为列表的最后一个元素(表示从后数第一个元素那就是最后一个元素)
1
9
列表切片: (注意:切片并不会取到“尾下表”那个数)
In [3]:
L[1:5] # 表示取到第2个到第5个元素,并不会取到第6个元素
Out[3]:
[
2, 3, 4, 5]
操作可以拼接列表
In [4]:
+
L + [2,3,4]
Out[4]:
[
1, 2, 3, 4, 5, 6, 7, 8, 9, 2, 3, 4]
Python 的列表数据类型包含更多的方法¶
list.append(x) 把一个元素添加到列表的结尾。
list.extend(L) 将一个给定列表中的所有元素都添加到另一个列表中。
list.insert(i, x) 在指定位置插入一个元素。第一个参数是准备插入到其前面的那个元素的索引,例如 a.insert(0, x) 会插入到整个列表之前,而 a.insert(len(a),
x) 相当于 a.append(x).
list.remove(x) 删除列表中值为 x 的第一个元素。如果没有这样的元素,就会返回一个错误。
list.pop([i]) 从列表的指定位置删除元素,并将其返回。如果没有指定索引,a.pop() 返回最后一个元素。元素随即从链表中被删除。(方法中 i 两边的方括号表
示这个参数是可选的,而不是要求你输入一对方括号,这个经常会在 Python 库参考手册中遇到这样的标记。)
list.index(x) 返回列表中第一个值为 x 的元素的索引。如果没有匹配的元素就会返回一个错误。

list.count(x) 返回 x 在链表中出现的次数。
list.sort(cmp=None, key=None, reverse=False) 对列表中的元素进行排序(参数可以用来自定义排序方法,参考 sorted() 的更详细的解释)。
list.reverse() 就地倒排链表中的元素。
del list[i] 可以从列表中按给定的索引而不是值来删除一个子项.
del 语句。它不同于有返回值的 pop() 方法。语句 del 还可以从列表中删除切片或清空整个列表(我们以前介绍过一个方法是将空列表赋值给列表的切片)。
In [5]:
#
统计a中元素出现的次数
a = [1, 2, 3, 3, 1234.5]
print('a中 1 出现的次数:',a.count(1))
print('a中 3 出现的次数:',a.count(3))
print('a中 x 出现的次数:',a.count('x'))
a中 1 出现的次数: 1
a中 3 出现的次数: 2
a中 x 出现的次数: 0
In [6]:
#
在a的尾部添加元素
a.append(555)
a
Out[6]:
[
1, 2, 3, 3, 1234.5, 555]
In [7]:
#
将[7,8,9]于a进行拼接
a.extend([7,8,9])
a
Out[7]:
[
1, 2, 3, 3, 1234.5, 555, 7, 8, 9]
In [8]:
#
在a中第三个位置插入-1
a.insert(2, -1)
a
Out[8]:
[
1, 2, -1, 3, 3, 1234.5, 555, 7, 8, 9]
In [9]:
#
返回2在a中的位置
a.index(2)
Out[9]:
1
In [10]:
#
反向排列a
a.reverse()
a
Out[10]:
[
9, 8, 7, 555, 1234.5, 3, 3, -1, 2, 1]
In [11]:
#
逆序排列a
a.sort(reverse=True)
a

Out[11]:
[
1234.5, 555, 9, 8, 7, 3, 3, 2, 1, -1]
In [12]:
#
删除列表a中值为 3 的第一个元素
a.remove(3)
a
Out[12]:
[
1234.5, 555, 9, 8, 7, 3, 2, 1, -1]
In [13]:
#
删除a中索引为0的元素
del a[0]
a
Out[13]:
[
555, 9, 8, 7, 3, 2, 1, -1]
In [14]:
#
删除a中索引为 2:4 的元素
del a[2:4]
a
Out[14]:
[
555, 9, 3, 2, 1, -1]
del 也可以删除整个变量,此后再引用命名 a 会引发(NameError)错误(直到另一个值赋给它为止)。我们在后面的内容中可以看到 del 的其它用法。
In [15]:
del a
a
-
--------------------------------------------------------------------------
NameError Traceback (most recent call last)
ipython-input-15-ef9d13752aff> in <module>()
del a
---> 2 a
<
1
-
NameError: name 'a' is not defined
把列表当作堆栈使用¶
列表方法使得列表可以很方便的做为一个堆栈来使用,堆栈作为特定的数据结构,最先进入的元素最后一个被释放(后进先出)。用 append() 方法可以把一个
元素添加到堆栈中。用不指定索引的 pop() 方法可以把一个元素从堆栈顶释放出来。例如:
In [ ]:
stack = [3, 4, 5]
stack.append(6)
stack.append(7)
stack
In [ ]:
#
后进先出
stack.pop()
In [ ]:
stack
In [ ]:
print(stack.pop())
print(stack.pop())
print(stack)

把列表当作队列使用¶
你也可以把列表当做队列使用,队列作为特定的数据结构,最先进入的元素最先释放(先进先出)。不过,列表这样用效率不高。相对来说从列表末尾添加和
弹出很快;在头部插入和弹出很慢(因为为了一个元素,要移动整个列表中的所有元素)。
要实现队列,使用 collections.deque,它为在首尾两端快速插入和删除而设计。例如:
In [ ]:
from collections import deque
queue = deque(["Eric", "John", "Michael"])
queue.append("Terry")
queue.append("Graham")
queue
In [ ]:
print(queue.popleft())
print(queue.popleft())
print(queue)
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-Python 编程]数据类型之字典
导语:本文介绍了Python中非常重要的数据类型——字典
附件:字典的使用
字典(dictionary )¶
字典在某些语言中可能称为 联合内存 (associative memories) 或 联合数组 (associative arrays)。序列是以连续的整数为索引,与此不同的是,字典以"关键
字"为索引,关键字可以是任意不可变类型,通常用字符串或数值。如果元组中只包含字符串和数字,它可以作为关键字,如果它直接或间接地包含了可变对
象,就不能当做关键字。不能用列表做关键字,因为列表可以用索引、切割或者 append() 和 extend() 等方法改变。
字典是无序的键:值对 (key:value 对)集合,键必须是互不相同的(在同一个字典之内)。使用大括号创建一个空的字典:{}。初始化列表时,在大括号内放置
一组逗号分隔的键:值对,这也是字典输出的方式。
字典的主要操作是依据键来存储和取值。也可以用 del 来删除键:值对(key:value),从一个不存在的键中取值会导致错误。
In [1]:
#
房价的一个例子
house_price = {'beijing': 60980, 'shenzhen': 49390, 'haikou':24000}
house_price['chengdu'] = 12000
print('存储房价信息的字典:', house_price)
print( '海口的房价为:', house_price['haikou'])
存储房价信息的字典: {'beijing': 60980, 'chengdu': 12000, 'shenzhen': 49390, 'haikou': 24000}
海口的房价为: 24000
In [2]:
del house_price['haikou']
house_price['shanghai'] = 50000
print(house_price)
print(house_price.keys())
print('chengdu' in house_price)
print('hefei' in house_price)
{
'beijing': 60980, 'chengdu': 12000, 'shenzhen': 49390, 'shanghai': 50000}
dict_keys(['beijing', 'chengdu', 'shenzhen', 'shanghai'])
True
False
常见字典操作方法¶
D.clear()删除字典内所有元素
D.copy()返回一个字典的复制
D.fromkeys(seq,val)创建一个新字典,以序列seq中元素做字典的键,val为字典所有键对应的初始值
D.get(key, default=None)返回指定键的值,如果值不在字典中返回default值

D.has_key(key)如果键在字典dict里返回true,否则返回false
D.items()以列表返回可遍历的(键, 值) 元组数组
D.keys()以列表返回一个字典所有的键
D.setdefault(key, default=None)和get()类似, 但如果键不存在于字典中,将会添加键并将值设为default
D.update(dict2)把字典dict2的键/值对更新到dict里
D.values()以列表返回字典中的所有值
D.pop(key)删除一个键并返回它的值,类似于列表的pop,只不过删除的是一个键不是一个可选的位置
del D[key]删除键
D[key] = 42新增或修改键
字典用法注意事项:¶
1
. 序列运算无效,字典元素间是没有顺序的概念
. 对新索引赋值会添加项
. 键不一定总是字符串
In [3]:
2
3
print('北京房价', house_price.get('beijing', 0)) #返回指定键的值,如果值不在字典中返回default值
print('重庆房价', house_price.get('chongqing', 0))
北京房价 60980
重庆房价 0
多种构造字典方式¶
dict() 构造函数可以直接从 key-value 对中创建字典
In [4]:
#
另外一种构造字典的方式
dict([('beijing', 60980), ('shenzhen', 49390), ('haikou', 24000)])
Out[4]:
{
'beijing': 60980, 'haikou': 24000, 'shenzhen': 49390}
In [5]:
dict.fromkeys(['a','b'],0) #创建一个新字典,以序列seq中元素做字典的键,val为字典所有键对应的初始值
Out[5]:
{
'a': 0, 'b': 0}
In [6]:
dict(zip(['beijing','shenzhen','haikou'],[60980,49390,24000]))
Out[6]:
{
'beijing': 60980, 'haikou': 24000, 'shenzhen': 49390}
In [7]:
{
k:v for (k,v) in zip(['beijing','shenzhen','haikou'],[60980,49390,24000])}
Out[7]:
{
'beijing': 60980, 'haikou': 24000, 'shenzhen': 49390}
In [8]:
#
{
通过字典推导式构造字典
x: x**2 for x in (2, 4, 6)}
Out[8]:

{
2: 4, 4: 16, 6: 36}
In [9]:
{
c:c*4 for c in 'bigQuant'}#默认是集合
Out[9]:
{
'Q': 'QQQQ',
'
'
'
'
'
'
'
a': 'aaaa',
b': 'bbbb',
g': 'gggg',
i': 'iiii',
n': 'nnnn',
t': 'tttt',
u': 'uuuu'}
In [10]:
dict(a=1,b=2,c=3)
Out[10]:
{
'a': 1, 'b': 2, 'c': 3}
In [11]:
{
c.lower():c*4+'!' for c in 'bigQuant'}
Out[11]:
{
'a': 'aaaa!',
'
'
'
'
'
'
'
b': 'bbbb!',
g': 'gggg!',
i': 'iiii!',
n': 'nnnn!',
q': 'QQQQ!',
t': 'tttt!',
u': 'uuuu!'}
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-Python 编程]数据类型之元组、集合
导语:本文介绍了非常重要的数据类型——元组、集合
元组(Tuple)是任意对象的有序集合
元组与字符串和列表类似,是一个位置有序的对象的集合(也就是其内容维持从左到右的顺序)。与列表相同,可以嵌入到任何类别的对象中。
通过偏移存取 通过偏移而不是键来访问,例如可以使用索引,切片
属于不可变序列类型 不能在原处修改(因为他们是不可变的),但可以进行组合和复制,运算后会生成一个新的元组。
附件:元组、集合的使用
创建空元组¶
In [1]:
tup1 = ()
元组中只包含一个元素时,需要在元素后面添加逗号
In [2]:
tup1 = (50,)
tup1
Out[2]:
(50,)

元组与字符串类似,下标索引从0开始,可以进行截取,组合等。元组可以使用下标索引来访问元组中的值,如下实例:
In [3]:
tup1 = ('physics', 'chemistry', 1997, 2000)
tup2 = (1, 2, 3, 4, 5, 6, 7 )
print("tup1[0]: ", tup1[0])
print("tup2[1:5]: ", tup2[1:5])
tup1[0]: physics
tup2[1:5]: (2, 3, 4, 5)
修改元组¶
元组与列表不同,元组中的元素值是不允许修改的,但我们可以对元组进行连接组合,如下实例:
In [4]:
tup1 = (12, 34.56)
tup2 = ('abc', 'xyz')
#
以下修改元组元素操作是非法的,会出现TypeError错误。
tup1[0] = 100;
-
--------------------------------------------------------------------------
TypeError Traceback (most recent call last)
ipython-input-4-e008270ca851> in <module>()
<
3
4
# 以下修改元组元素操作是非法的,会出现TypeError错误。
-
---> 5 tup1[0] = 100;
TypeError: 'tuple' object does not support item assignment
In [ ]:
#
创建一个新的元组
tup3 = tup1 + tup2
print(tup3)
删除元组¶
元组中的元素值是不允许删除的,但我们可以使用del语句来删除整个元组,实例中元组被删除后,输出变量会有异常信息,如下实例:
In [ ]:
tup = ('physics', 'chemistry', 1997, 2000)
print(tup)
In [ ]:
del tup
print(tup)
任意无符号的对象,以逗号隔开,默认为元组,如下实例:
In [ ]:
print('abc', -4.24e93, 18+6.6j, 'xyz')
x, y = 1, 2
print("Value of x , y : ", x,y)
Python 的元组数据类型包含更多的方法。¶
tup.index(x, [start, [stop]])) 返回元组中start到stop索引中第一个值为 x 的元素在整个列表中的索引。如果没有匹配的元素就会返回一个错误。
tup.count(x) 返回 x 在元组中出现的次数。
cmp(tuple1, tuple2) 比较元组中两个元素。
len(tuple) 计算元组元素个数。
max(tuple) 返回元组中元素最大值。
min(tuple) 返回元组中元素最小值。
tuple(seq) 将列表转换为元组。

元组不提供字符串、列表和字典中的方法。如果相对元组排序,通常先得将它转换为列表并使其成为一个可变对象,才能获得使用排序方法,或使用sorted
内置方法。
In [ ]:
T = ('c','a','d','e')
tmp = list(T)
tmp.sort()
print(tmp)
print(tuple(tmp))
In [ ]:
T = ('c','a','d','e')
sorted(T) # 按字母顺序排序
列表解析也可用于元组的转换
In [ ]:
T = (1,2,3,4,5)
L = [x+20 for x in T]
L
In [ ]:
T = (1,2,3,2,3,5,2)
print(T.index(2))
print(T.index(5,2,7))
print(T.count(2))
集合¶
Python 还包含一种数据类型 set (集合)。集合是一个无序不重复元素的集。基本功能包括关系运算和消除重复元素。比如支持 union(联合),
intersection(交),difference(差)和 sysmmetric difference(对称差集)等数学关系运算。
大括号或 set() 函数可以用来创建集合。注:创建空集合,你必须使用 set() 而不是 {},后者用于创建空字典
所有集合方法
S.issubset(t) 如果 s 是 t 的子集,则返回True,否则返回False
S.issuperset(t) 如果 s 是 t 的超集,则返回True,否则返回False
S.unoin(t) 返回一个新集合,该集合是s和t的并集,也可用s1|s2,但不能用s1+s2
S.intersection(t) 返回一个新集合,该集合是s和t的交集,,也可用s1&s2
S.difference(t) 返回一个新集合,该集合是s的成员,但不是t的成员,,也可用s1-s2
S.symmetric_difference(t) 对称差分是集合的异或,返回一个新集合,该集合是s或t的成员,但不是s和t共有的成员,也可用s1^s2
S.copy() 返回一个新集合,该集合是s的复制
仅适合可变集合
S.update(t) 用t中的元素修改s,即s现在包括s或t的成员
S.intersection_update s中的成员是共同属于s和t的元素
S.difference_update s中的成员是属于s但不包含在t中的元素
S.symmetric_difference_update s中的成员更新为那些包含在s或t中,但不是s和t共有的元素
S.add(obj) 在集合s中添加对象obj
S.remove(obj) 从集合s中删除对象obj,如果obj不是集合s中的元素将有错误
S.discard(obj) 如果obj是集合s中的元素,从集合s中删除对象obj
S.pop() 删除集合s中的任意一个对象,并返回它
S.clear() 删除集合s中的所有元素
In [ ]:
basket = ['apple', 'orange', 'apple', 'pear', 'orange', 'banana']
fruit = set(basket)
print(fruit)
print('orange' in fruit)
print('crabgrass' in fruit)
In [ ]:
a = set('abracadabra')
b = set('alacazam')
print('a:\t',a)
# 唯一值
# 在a不在b里面
print('a - b:\t',a - b)
print('a | b:\t',a | b)
print('a & b:\t',a & b)
print('a ^ b:\t',a ^ b)
print('a>b,a<b:\t',a>b,a<b)
# 在a或b里
# a、b里面都有
# 在a或b里但是不同时在两个里面
集合推导式语法
In [ ]:
a = {x for x in 'abracadabra' if x not in 'abc'}#'abc'默认是集合
a
In [ ]:
basket = ['apple', 'orange', 'apple', 'pear', 'orange', 'banana']
fruit = set(basket)
print(fruit)
列表和字典不能嵌入到集合中,但是元组是可以嵌入的
In [ ]:
S = set()
S.add([1,2,3])
In [ ]:
S.add((1,2,3))
S
In [ ]:
type(S)
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-Python 编程]条件与循环:if、while 、for
导语:本文介绍Python编程中非常重要的条件与循环的相关知识点。
附件:Python编程之条件与循环
条件if¶
条件语句格式:
if 判断条件:
执行语句……
else:
执行语句……
当if有多个条件时可使用括号来区分判断的先后顺序,括号中的判断优先执行,此外 and 和 or 的优先级低于>(大于)、<(小于)等判断符号,即大于和小
于在没有括号的情况下会比与或要优先判断。
由于 python 并不支持 switch 语句,所以多个条件判断,只能用 elif 来实现,如果判断需要多个条件需同时判断时,可以使用 or (或),表示两个条件有一
个成立时判断条件成功;使用 and (与)时,表示只有两个条件同时成立的情况下,判断条件才成功。
if 判断条件1:
执行语句1……
elif 判断条件2:
执行语句2……
elif 判断条件3:
执行语句3……

else:
执行语句4……
In [1]:
#
实现成绩统计,分数在0-100之间,0-59 为不合格,60-80为合格,80-90为良,90-100为优
num = int(input("input a score between 0 ~ 100: "))
if num < 0 or num > 100:
print("输入的数字不在范围之内")
elif 0 <= num < 60:
print("不合格")
elif 60 <= num < 80:
print("合格")
elif 80 <= num < 90:
print("良")
elif 90 <= num < 100:
print("优")
else:
print("excelent")
合格
循环¶
稍后会介绍更加奇特的迭代工具,如生成器、filter和reduce。现在先从最基础的学起。
Python提供了for循环和while循环(在Python中没有do...while循环),for循环一般比while计数器循环运行得更快
break 语句,在语句块执行过程中终止循环,并且跳出整个循环
continue 语句,在语句块执行过程中终止当前循环,跳出该次循环,执行下一次循环。
pass 语句,是空语句,是为了保持程序结构的完整性。不做任何事情,一般用做占位语句。
循环else块,只有当循环正常离开时才会执行(也就是没有碰到break语句)
while ¶
计算1到1000之间的所有数之和:
In [2]:
#
计算1到1000之间的所有数之和:
sum_while = 0
i = 1
while i <= 1000:
sum_while += i
i += 1
print("the sum between 1 and 1000 is : {}".format(sum_while))
the sum between 1 and 1000 is : 500500
for¶
下面将用for来实现上面求和的功能
In [3]:
sum_for = 0
for i in range(0, 1001):
sum_for += i
print("the sum between 1 and 1000 is : {}".format(sum_for))
the sum between 1 and 1000 is : 500500
In [4]:
#
对字符串遍历
for s in 'hello world':
print(s)
h
e
l
l
o
w

o
r
l
d
In [5]:
#
对列表中进行遍历
seq = ['hello', 'world', 'hello', 'every']
for s in seq:
print(s)
hello
world
hello
every
break 的用法¶
In [6]:
#
break
for letter in 'Python':
if letter == 'h':
break
print('Current Letter :', letter)
Current Letter : P
Current Letter : y
Current Letter : t
continue 的用法¶
In [7]:
for letter in 'Python':
if letter == 'h':
continue
print('Current Letter :', letter)
Current Letter : P
Current Letter : y
Current Letter : t
Current Letter : o
Current Letter : n
pass 的用法¶
In [8]:
for letter in 'Python':
if letter == 'h':
pass
print('这是 pass 块')
print('当前字母 :', letter)
当前字母 : P
当前字母 : y
当前字母 : t
这是 pass 块
当前字母 : h
当前字母 : o
当前字母 : n
In [9]:
#
一个例子
def calc(numbers):
amount = 0
for num in numbers:
amount += num
return amount
numbers = [100, 200, 3, 4]
calc(numbers)
Out[9]:
3
07
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-Python 编程]函数调用与定义
导语:本文介绍Python编程中非常重要的函数调用与定义的相关知识点。
1
、调用函数¶
Python内置了很多有用的函数,我们可以直接调用。
要调用一个函数,需要知道函数的名称和参数,比如求绝对值的函数abs,只有一个参数。
也可以在交互式命令行通过help(abs)查看abs函数的帮助信息。
In [1]:
help(abs)
Help on built-in function abs in module builtins:
abs(x, /)
Return the absolute value of the argument.
In [2]:
abs(-10)
Out[2]:
1
0
2
、定义函数¶
在Python中,定义一个函数要使用def语句,依次写出函数名、括号、括号中的参数和冒号:,然后,在缩进块中编写函数体,函数的返回值用return语句返
回。
下面我们定义一个求两数之和的函数:
In [3]:
def add_two(a, b):
return a + b
add_two(10, 22)
Out[3]:
3
2
请注意,函数体内部的语句在执行时,一旦执行到return时,函数就执行完毕,并将结果返回。因此,函数内部通过条件判断和循环可以实现非常复杂的逻
辑。
如果没有return语句,函数执行完毕后也会返回结果,只是结果为None。
return None可以简写为return。
3
、函数的参数¶
定义函数的时候,我们把参数的名字和位置确定下来,函数的接口定义就完成了。对于函数的调用者来说,只需要知道如何传递正确的参数,以及函数将返
回什么样的值就够了,函数内部的复杂逻辑被封装起来,调用者无需了解。
Python的函数定义非常简单,但灵活度却非常大。除了正常定义的必选参数外,还可以使用默认参数、可变参数和关键字参数,使得函数定义出来的接口,
不但能处理复杂的参数,还可以简化调用者的代码。
3
.1 默认参数¶
In [4]:
#
求x的平方
def power(x):
return x * x
power(5)

Out[4]:
2
5
In [5]:
#
求x的n次幂,设置n的默认值为2。
def power(x, n=2):
return x ** n
power(5, 3)
Out[5]:
1
25
设置默认参数时,有几点要注意:
1
. 必选参数在前,默认参数在后,否则Python的解释器会报错(思考一下为什么默认参数不能放在必选参数前面);
2
. 如何设置默认参数。
当函数有多个参数时,把变化大的参数放前面,变化小的参数放后面。变化小的参数就可以作为默认参数。
使用默认参数有什么好处?最大的好处是能降低调用函数的难度。
3
.2 可变参数¶
在Python函数中,还可以定义可变参数。顾名思义,可变参数就是传入的参数个数是可变的,可以是1个、2个到任意个,还可以是0个。
我们以数学题为例子,给定一组数字$a,b,c……$,请计算$a+b+c....$
要定义出这个函数,我们必须确定输入的参数。由于参数个数不确定,我们首先想到可以把a,b,c……作为一个 list 或 tuple 传进来,这样,函数可以定义
如下:
In [6]:
def calc(numbers):
amount = 0
for num in numbers:
amount += num
return amount
numbers = [100, 200, 3, 4]
calc(numbers)
Out[6]:
3
07
如果利用可变参数,我们把函数的参数改为可变参数:
In [7]:
def calc(*numbers):
amount = 0
for num in numbers:
amount += num
return amount
calc(1,2,3,4,5,7)
Out[7]:
2
2
3
.3 关键字参数¶
可变参数允许你传入 0 个或任意个参数,这些可变参数在函数调用时自动组装为一个 tuple。而关键字参数允许你传入 0 个或任意个含参数名的参数,这些
关键字参数在函数内部自动组装为一个 dict。
In [8]:
def get_kwargs(**kwargs):
print(kwargs)
get_kwargs(a=10, b="hello", c=['a', 1, 'bcd'])
{
'a': 10, 'b': 'hello', 'c': ['a', 1, 'bcd']}
3
.4 混合参数¶

在Python中定义函数,可以用必选参数、默认参数、可变参数和关键字参数,这4种参数都可以一起使用,或者只用其中某些,但是请注意,参数定义的顺
序必须是:必选参数、默认参数、可变参数和关键字参数。
In [9]:
def func(a, b, c=0, *args, **kw):
print('a =', a, 'b =', b, 'c =', c, 'args =', args, 'kw =', kw)
func(10, 20, 30, 'd', 'e', 'f', x=99, y ='hello')
a = 10 b = 20 c = 30 args = ('d', 'e', 'f') kw = {'y': 'hello', 'x': 99}
4
、匿名函数 lambda ¶
python 使用 lambda 来创建匿名函数。
lambda只是一个表达式,函数体比def简单很多。
lambda的主体是一个表达式,而不是一个代码块。仅仅能在lambda表达式中封装有限的逻辑进去。
lambda函数拥有自己的名字空间,且不能访问自有参数列表之外或全局名字空间里的参数。
虽然lambda函数看起来只能写一行,却不等同于C或C++的内联函数,后者的目的是调用小函数时不占用栈内存从而增加运行效率。
In [10]:
#
定义lambda函数
f = lambda x: x*x
f(i) for i in range(10)]
[
Out[10]:
[
0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-Python 编程]Numpy 库
导语:本文介绍数值分析的一大利器——Numpy
附件:Numpy介绍
Numpy是高性能科学计算和数据分析的基础包,是Python在科学计算领域使用最广的一个包。
1
、ndarray 数组基础¶
Pyhton 中用列表保存一组值,可将列表当成是数组使用。此外,Python 有 array 模快,但他不支持多维数组,无论是列表还是 array 模块都没有科学运算函
数,不适合做矩阵等科学计算。因此,Numpy没有使用 Python 本身的数组机制,而是提供了 ndarray 数组对象,该对象能方便的存取数组,而且拥有丰富
的数组计算函数,比如向量的加法、减法、乘法等。
使用 ndarray 数组,首先需要导入 Numpy 函数库,也可以直接导入该函数库:
In [1]:
from numpy import *
使用别名导入
In [2]:
import numpy as np
1
.1 创建数组¶
创建数组是进行数组计算的先决条件,可以通过array()函数定义数组实例对象,其参数为Python 的序列对象(比如列表。)如果想定义多维数组,则传递多
层嵌套的序列。例如下面这条语句定义了一个二维数组,其大小为(2,3),即有2行,3列。
In [3]:
a = np.array([[1,2,4.0],[3,6,9]])
a
Out[3]:

array([[ 1., 2., 4.],
3., 6., 9.]])
[
接着我们看下数组的一些属性:
In [4]:
#
查看行数
a.ndim
Out[4]:
2
In [5]:
#
查看数组的维数,返回(n,m), 其中 n 为行数,m 为列数。
a.shape
Out[5]:
(2, 3)
In [6]:
#
查看元素的类型,比如 numpy.int32、numpy.float64
a.dtype
Out[6]:
dtype('float64')
1
.2 特殊数组¶
Numpy的特殊数组主要有以下几种:
zeros数组:全零数组,元素全为0;
ones数组:全1数组,元素全为1;
empty数组:空数组,元素全近似为0;
下面是全零、全1、空数组的创建方法:
In [7]:
np.zeros((2,3))
Out[7]:
array([[ 0., 0., 0.],
[
0., 0., 0.]])
In [8]:
np.ones((3,5))
Out[8]:
array([[ 1., 1., 1., 1., 1.],
[
[
1., 1., 1., 1., 1.],
1., 1., 1., 1., 1.]])
In [9]:
np.empty((3,3))
Out[9]:
array([[ 6.90771382e-310,
6.90771382e-310,
6.90776702e-310,
6.90776702e-310,
6.90771382e-310],
6.90776702e-310],
6.90776702e-310]])
[
[
6.90771382e-310,
6.90776702e-310,
1
.3 序列数组¶
arange函数:他与 Python 的 range 函数相似,但他属于Numpy 库,其参数依次为:开始值、结束值、步长。
In [10]:

np.arange(1,20,5)
Out[10]:
array([ 1, 6, 11, 16])
我们还可以使用 linspace 函数创建等差序列数组,其参数依次为:开始值、结束值、元素数量。
In [11]:
np.linspace(0,2,9)
Out[11]:
array([ 0. , 0.25, 0.5 , 0.75, 1. , 1.25, 1.5 , 1.75, 2. ])
1
.4 数组索引¶
Numpy 数组的每个元素、每行元素、每列元素都可以用索引访问,不过注意:索引是从 0 开始的。 其操作与列表基本相同。
In [12]:
a = np.array([[1,2,4.0],[3,6,9]])
a
Out[12]:
array([[ 1., 2., 4.],
[
3., 6., 9.]])
In [13]:
#
取 a 的第一行元素
a[0]
Out[13]:
array([ 1., 2., 4.])
In [14]:
#
取 a 的第二列元素
a[:,1]
Out[14]:
array([ 2., 6.])
In [15]:
#
取 a 的第一行的第三个元素
a[0,2]
Out[15]:
4
.0
1
.5 数组运算¶
In [16]:
a = np.array([1,2,3])
b = np.array([4.,5,6])
In [17]:
#
加法运算
a + b
Out[17]:
array([ 5., 7., 9.])
In [18]:

#
减法运算
a - b
Out[18]:
array([-3., -3., -3.])
In [19]:
#
乘法运算
a * b
Out[19]:
array([ 4., 10., 18.])
In [20]:
#
乘方运算:a的2次方
a ** 2
Out[20]:
array([1, 4, 9])
In [21]:
#
除法运算
a/b
Out[21]:
array([ 0.25, 0.4 , 0.5 ])
In [22]:
#
数组点乘
np.dot(a,b)
Out[22]:
3
2.0
In [23]:
#
判断大小,返回 bool 值
a >= 2
Out[23]:
array([False, True, True], dtype=bool)
In [24]:
#
a中最大的元素
a.max()
Out[24]:
3
In [25]:
#
a中最小的元素
a.min()
Out[25]:
1
In [26]:
#
a的和
a.sum()

Out[26]:
6
1
.6 数组拷贝¶
数组的拷贝分为浅拷贝和深拷贝两种,浅拷贝通过数组变量的复制完成,深拷贝使用数组对象的copy方法完成。
浅拷贝只拷贝数组的引用,如果对拷贝对象修改。原数组也将修改。
下面的代码演示了浅拷贝的方法:
In [27]:
a = np.ones((2,3))
a
Out[27]:
array([[ 1., 1., 1.],
[
1., 1., 1.]])
In [28]:
#
b 为 a 的浅拷贝
b = a
b
Out[28]:
array([[ 1., 1., 1.],
[
1., 1., 1.]])
In [29]:
#
对 b 进行修改,a 也会被修改
b[1,2] = 9
a
Out[29]:
array([[ 1., 1., 1.],
[
1., 1., 9.]])
深拷贝会复制一份和原数组一样的数组,但他们在内存中是分开存放的,所以改变拷贝数组,原数组不会改变。
下面的代码演示了 b 使用 copy 方法从原数组 a 复制一份拷贝的情况。
In [30]:
a = np.ones((2,3))
a
Out[30]:
array([[ 1., 1., 1.],
[
1., 1., 1.]])
In [31]:
b = a.copy()
b[1,2] = 9
b
Out[31]:
array([[ 1., 1., 1.],
[
1., 1., 9.]])
In [32]:
a
Out[32]:

array([[ 1., 1., 1.],
[
1., 1., 1.]])
2
、矩阵¶
2
.1 创建矩阵¶
Numpy的矩阵对象与数组对象相似,主要不同之处在于,矩阵对象的计算遵循矩阵数学运算规律。矩阵使用 matrix 函数创建,以(2,2)大小的矩阵为例(2
行2列),定义方法如下:
In [33]:
A = np.matrix([[1.0,2.0],[3.0,4.0]])
A
Out[33]:
matrix([[ 1., 2.],
[
3., 4.]])
In [34]:
#
查看A的类型
type(A)
Out[34]:
numpy.matrixlib.defmatrix.matrix
2
.2 矩阵运算¶
矩阵的常用数学运算有转置、乘法、求逆等。下面的代码演示了矩阵的基本运算。
In [35]:
#
转置
A.T
Out[35]:
matrix([[ 1., 3.],
[
2., 4.]])
In [36]:
B = np.matrix([[3.0],[5.0]])
B
Out[36]:
matrix([[ 3.],
[
5.]])
In [37]:
#
矩阵乘法
A * B
Out[37]:
matrix([[ 13.],
29.]])
[
In [38]:
#
逆矩阵
A.I
Out[38]:
matrix([[-2. , 1. ],
1.5, -0.5]])
[
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。

[
量化学堂-Python 编程]Pandas 查看和选择数据
导语:本节主要讲解Pandas库中 DataFrame 的数据查看与选择
Pandas 是基于 Numpy 构建的,让以 Numpy 为中心的应用变得更加简单。平台获取的数据主要是以 Pandas 中DataFrame 的形式。除此之外,Pandas 还
包括 一维数组Series 以及三维的Panel。
下面将进行详细介绍:
Series :一维数组,与Numpy中的一维array类似。二者与Python基本的数据结构List也很相近,其区别是:List中的元素可以是不同的数据类型,而Array和
Series中则只允许存储相同的数据类型,这样可以更有效的使用内存,提高运算效率。
DataFrame :二维的表格型数据结构。很多功能与R中的data.frame类似。可以将DataFrame理解为Series的容器。以下的内容主要以DataFrame为主。
In [1]:
#
首先导入库
import pandas as pd
1
、Series ¶
由一组数据(各种Numpy数据类型),以及一组与之相关的标签数据(即索引)组成。仅由一组数据即可产生最简单的Series,可以通过传递一个list对象来
创建一个Series,Pandas会默认创建整型索引。
创建一个Series:
In [2]:
s = pd.Series([1,3,5,np.nan,6,8])
s
Out[2]:
0
1
2
3
4
5
1.0
3.0
5.0
NaN
6.0
8.0
dtype: float64
获取 Series 的索引:
In [3]:
s.index
Out[3]:
RangeIndex(start=0, stop=6, step=1)
2
、DataFrame ¶
DataFrame是一个表格型的数据结构,它含有一组有序的列,每一列的数据结构都是相同的,而不同的列之间则可以是不同的数据结构(数值、字符、布尔
值等)。或者以数据库进行类比,DataFrame中的每一行是一个记录,名称为Index的一个元素,而每一列则为一个字段,是这个记录的一个属性。
DataFrame既有行索引也有列索引,可以被看做由Series组成的字典(共用同一个索引)。
2
.1 创建一个DataFrame ,包括一个numpy array , 时间索引和列名字:¶
In [4]:
dates = pd.date_range('20130101',periods=6)
dates
Out[4]:
DatetimeIndex(['2013-01-01', '2013-01-02', '2013-01-03', '2013-01-04',
'
2013-01-05', '2013-01-06'],
dtype='datetime64[ns]', freq='D')
In [5]:
df = pd.DataFrame(np.random.randn(6,4),index=dates,columns=list('ABCD'))
df

Out[5]:
A
B
C
D
2
2
2
2
2
2
013-01-01
-1.971026
1.248603
0.572176
0.343039
0.835942
-1.240034
-1.149504
0.158524
-0.093579
-0.820224
-0.209759
1.753316
-0.886253
0.047291
0.892276
0.220198
-0.740630
0.209350
-1.423737
0.834145
0.376732
-0.026627
0.234057
0.027492
013-01-02
013-01-03
013-01-04
013-01-05
013-01-06
2
.2 查看数据¶
我们以平台获取的数据为例进行讲解:
In [6]:
#
获取沪深300的数据
df = D.history_data(instruments=['000300.SHA'], start_date='2017-01-01', end_date='2017-01-20',
fields=['open', 'high', 'low', 'close', 'volume', 'amount'])
df
Out[6]:
date
instrument
open
high
low
close
volume
amount
2
017-
0
1
2
3
4
5
6
7
8
9
000300.SHA
3313.953369
3345.262939
3313.953369
3342.227295
8656789600
8.761277e+10
01-03
2
0
017-
1-04
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
3340.557617
3368.340088
3366.852295
3345.748291
3361.639404
3355.800781
3332.685791
3317.962402
3314.150635
3305.600098
3323.338867
3330.952148
3326.977295
3369.565918
3373.411865
3368.870605
3366.221924
3370.505127
3366.631592
3343.127930
3338.174072
3322.781982
3327.376709
3350.961914
3346.495850
3358.412109
3338.152588
3361.461914
3346.891357
3344.347168
3354.087891
3334.297852
3315.962891
3309.374023
3264.207031
3292.204346
3320.406250
3324.683594
3326.374023
3368.311768
3367.789307
3347.666504
3363.901367
3358.271484
3334.495361
3317.624023
3319.912109
3319.445557
3326.356201
3339.365234
3329.289062
3354.889160
9005082700
8833635700
8745911400
8370794200
8381916000
9107143800
8123913500
8418058900
15777913500
6945332800
7062322700
6615980800
6530046200
9.801436e+10
9.118934e+10
9.107226e+10
8.791612e+10
8.253397e+10
8.675045e+10
7.503189e+10
8.455610e+10
1.532625e+11
7.475451e+10
7.568068e+10
6.386971e+10
7.083133e+10
2
0
017-
1-05
2
0
017-
1-06
2
0
017-
1-09
2
0
017-
1-10
2
0
017-
1-11
2
0
017-
1-12
2
0
017-
1-13
2
0
017-
1-16
2
0
017-
1-17
10
2
0
017-
1-18
11
2
0
017-
1-19
1
2
3
2
0
017-
1-20
1
查看前几条数据:
In [7]:
df.head() # 默认是查询5条
Out[7]:
date
instrument
open
high
low
close
volume
amount

date
instrument
open
high
low
close
volume
amount
2
017-
0
1
2
3
4
000300.SHA
3313.953369
3345.262939
3313.953369
3342.227295
8656789600
8.761277e+10
01-03
2
0
017-
1-04
000300.SHA
000300.SHA
000300.SHA
000300.SHA
3340.557617
3368.340088
3366.852295
3345.748291
3369.565918
3373.411865
3368.870605
3366.221924
3338.152588
3361.461914
3346.891357
3344.347168
3368.311768
3367.789307
3347.666504
3363.901367
9005082700
8833635700
8745911400
8370794200
9.801436e+10
9.118934e+10
9.107226e+10
8.791612e+10
2
0
017-
1-05
2
0
017-
1-06
2
0
017-
1-09
查看后几条数据:
In [8]:
df.tail()
Out[8]:
date
instrument
open
high
low
close
volume
amount
2
0
017-
1-16
9
000300.SHA
3314.150635
3322.781982
3264.207031
3319.445557
15777913500
1.532625e+11
2
0
017-
1-17
1
0
000300.SHA
000300.SHA
000300.SHA
000300.SHA
3305.600098
3323.338867
3330.952148
3326.977295
3327.376709
3350.961914
3346.495850
3358.412109
3292.204346
3320.406250
3324.683594
3326.374023
3326.356201
3339.365234
3329.289062
3354.889160
6945332800
7062322700
6615980800
6530046200
7.475451e+10
7.568068e+10
6.386971e+10
7.083133e+10
2
0
017-
1-18
11
2
0
017-
1-19
1
2
3
2
0
017-
1-20
1
查看 DataFrame 的索引
In [9]:
df.index
Out[9]:
RangeIndex(start=0, stop=14, step=1)
查看 DataFrame 的列名
In [10]:
df.columns
Out[10]:
Index(['date', 'instrument', 'open', 'high', 'low', 'close', 'volume',
amount'],
dtype='object')
'
查看 DataFrame 的值
In [11]:
df.values
Out[11]:
array([[Timestamp('2017-01-03 00:00:00'), '000300.SHA', 3313.953369140625,
3
8
345.262939453125, 3313.953369140625, 3342.227294921875,
656789600, 87612768256.0],
[
[
Timestamp('2017-01-04 00:00:00'), '000300.SHA', 3340.5576171875,
3
9
369.56591796875, 3338.152587890625, 3368.311767578125, 9005082700,
8014355456.0],
Timestamp('2017-01-05 00:00:00'), '000300.SHA', 3368.340087890625,
3
373.411865234375, 3361.4619140625, 3367.789306640625, 8833635700,

9
1189338112.0],
[
[
[
[
[
[
[
[
[
[
[
Timestamp('2017-01-06 00:00:00'), '000300.SHA', 3366.852294921875,
3
9
368.87060546875, 3346.891357421875, 3347.66650390625, 8745911400,
1072258048.0],
Timestamp('2017-01-09 00:00:00'), '000300.SHA', 3345.748291015625,
3
8
366.221923828125, 3344.34716796875, 3363.9013671875, 8370794200,
7916118016.0],
Timestamp('2017-01-10 00:00:00'), '000300.SHA', 3361.639404296875,
3
8
370.505126953125, 3354.087890625, 3358.271484375, 8381916000,
2533965824.0],
Timestamp('2017-01-11 00:00:00'), '000300.SHA', 3355.80078125,
3
8
366.631591796875, 3334.2978515625, 3334.495361328125, 9107143800,
6750453760.0],
Timestamp('2017-01-12 00:00:00'), '000300.SHA', 3332.685791015625,
3
7
343.1279296875, 3315.962890625, 3317.6240234375, 8123913500,
5031887872.0],
Timestamp('2017-01-13 00:00:00'), '000300.SHA', 3317.96240234375,
3
8
338.174072265625, 3309.3740234375, 3319.912109375, 8418058900,
4556103680.0],
Timestamp('2017-01-16 00:00:00'), '000300.SHA', 3314.150634765625,
3
1
322.781982421875, 3264.20703125, 3319.445556640625, 15777913500,
53262522368.0],
Timestamp('2017-01-17 00:00:00'), '000300.SHA', 3305.60009765625,
3
6
327.376708984375, 3292.204345703125, 3326.356201171875,
945332800, 74754506752.0],
Timestamp('2017-01-18 00:00:00'), '000300.SHA', 3323.3388671875,
3
7
350.9619140625, 3320.40625, 3339.365234375, 7062322700,
5680677888.0],
Timestamp('2017-01-19 00:00:00'), '000300.SHA', 3330.9521484375,
3
6
346.495849609375, 3324.68359375, 3329.2890625, 6615980800,
3869710336.0],
Timestamp('2017-01-20 00:00:00'), '000300.SHA', 3326.977294921875,
3
7
358.412109375, 3326.3740234375, 3354.88916015625, 6530046200,
0831325184.0]], dtype=object)
使用 describe() 函数对于数据的快速统计汇总:
In [12]:
df.describe()
Out[12]:
open
high
low
close
volume
amount
count
mean
std
14.000000
14.000000
14.000000
14.000000
1.400000e+01
8.612489e+09
2.248143e+09
6.530046e+09
7.327720e+09
8.399987e+09
8.811705e+09
1.577791e+10
1.400000e+01
8.736257e+10
2.110282e+10
6.386971e+10
7.519409e+10
8.565328e+10
9.028322e+10
1.532625e+11
3336.040283
20.855013
3353.414062
16.710600
3324.742920
25.615406
3342.110596
18.314083
min
3305.600098
3319.306519
3331.818970
3353.287659
3368.340088
3322.781982
3343.661682
3354.687012
3368.310852
3373.411865
3264.207031
3314.455750
3325.528809
3342.798523
3361.461914
3317.624023
3327.089417
3340.796265
3357.425903
3368.311768
25%
50%
75%
max
对数据的转置:
In [13]:
df.T
Out[13]:
0
1
2
3
4
5
6
2
0
017-01-03
0:00:00
2017-01-04
2017-01-05
2017-01-06
00:00:00
2017-01-09
00:00:00
2017-01-10
00:00:00
2017-01-11
00:00:00
201
00:0
date
00:00:00
000300.SHA
3340.56
00:00:00
000300.SHA
3368.34
instrument
open
000300.SHA
3313.95
000300.SHA
3366.85
000300.SHA
3345.75
3366.22
3344.35
3363.9
000300.SHA
3361.64
000300.SHA
3355.8
000
333
334
331
331
high
3345.26
3369.57
3373.41
3368.87
3370.51
3366.63
3334.3
low
3313.95
3338.15
3361.46
3346.89
3354.09
close
3342.23
3368.31
3367.79
3347.67
3358.27
3334.5

0
1
2
3
4
5
6
volume
amount
8656789600
8.76128e+10
9005082700
9.80144e+10
8833635700
9.11893e+10
8745911400
9.10723e+10
8370794200
8.79161e+10
8381916000
8.2534e+10
9107143800
8.67505e+10
812
7.50
按列对 DataFrame 进行排序
In [14]:
df.sort(columns='open')
Out[14]:
date
instrument
open
high
low
close
volume
amount
2
017-
1
0
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
3305.600098
3327.376709
3292.204346
3326.356201
6945332800
7.475451e+10
01-17
2
0
017-
1-03
0
3313.953369
3314.150635
3317.962402
3323.338867
3326.977295
3330.952148
3332.685791
3340.557617
3345.748291
3355.800781
3361.639404
3366.852295
3368.340088
3345.262939
3322.781982
3338.174072
3350.961914
3358.412109
3346.495850
3343.127930
3369.565918
3366.221924
3366.631592
3370.505127
3368.870605
3373.411865
3313.953369
3264.207031
3309.374023
3320.406250
3326.374023
3324.683594
3315.962891
3338.152588
3344.347168
3334.297852
3354.087891
3346.891357
3361.461914
3342.227295
3319.445557
3319.912109
3339.365234
3354.889160
3329.289062
3317.624023
3368.311768
3363.901367
3334.495361
3358.271484
3347.666504
3367.789307
8656789600
15777913500
8418058900
7062322700
6530046200
6615980800
8123913500
9005082700
8370794200
9107143800
8381916000
8745911400
8833635700
8.761277e+10
1.532625e+11
8.455610e+10
7.568068e+10
7.083133e+10
6.386971e+10
7.503189e+10
9.801436e+10
8.791612e+10
8.675045e+10
8.253397e+10
9.107226e+10
9.118934e+10
2
0
017-
1-16
9
8
2
0
017-
1-13
2
0
017-
1-18
11
2
0
017-
1-20
1
3
2
2
0
017-
1-19
1
2
0
017-
1-12
7
2
0
017-
1-04
1
2
0
017-
1-09
4
2
0
017-
1-11
6
2
0
017-
1-10
5
3
2
0
017-
1-06
2
0
017-
1-05
2
In [15]:
df.sort_values(by='open')
Out[15]:
date
instrument
open
high
low
close
volume
amount
2
017-
1
0
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
3305.600098
3327.376709
3292.204346
3326.356201
6945332800
7.475451e+10
01-17
2
0
017-
1-03
0
3313.953369
3314.150635
3317.962402
3323.338867
3326.977295
3345.262939
3322.781982
3338.174072
3350.961914
3358.412109
3313.953369
3264.207031
3309.374023
3320.406250
3326.374023
3342.227295
3319.445557
3319.912109
3339.365234
3354.889160
8656789600
15777913500
8418058900
7062322700
6530046200
8.761277e+10
1.532625e+11
8.455610e+10
7.568068e+10
7.083133e+10
2
0
017-
1-16
9
8
2
0
017-
1-13
2
0
017-
1-18
11
2
0
017-
1-20
13

date
instrument
open
high
low
close
volume
amount
2
017-
12
000300.SHA
3330.952148
3346.495850
3324.683594
3329.289062
6615980800
6.386971e+10
01-19
2
0
017-
1-12
7
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
3332.685791
3340.557617
3345.748291
3355.800781
3361.639404
3366.852295
3368.340088
3343.127930
3369.565918
3366.221924
3366.631592
3370.505127
3368.870605
3373.411865
3315.962891
3338.152588
3344.347168
3334.297852
3354.087891
3346.891357
3361.461914
3317.624023
3368.311768
3363.901367
3334.495361
3358.271484
3347.666504
3367.789307
8123913500
9005082700
8370794200
9107143800
8381916000
8745911400
8833635700
7.503189e+10
9.801436e+10
8.791612e+10
8.675045e+10
8.253397e+10
9.107226e+10
9.118934e+10
2
0
017-
1-04
1
4
6
5
3
2
2
0
017-
1-09
2
0
017-
1-11
2
0
017-
1-10
2
0
017-
1-06
2
0
017-
1-05
2
.3 选择数据¶
2
.3.1 通过下标选取数据:¶
df['open'],df.open
以上两个语句是等效的,都是返回 df 名称为 open 列的数据,返回的为一个 Series。
df[0:3], df['2016-07-05':'2016-07-08']
下标索引选取的是 DataFrame 的记录,与 List 相同 DataFrame 的下标也是从0开始,区间索引的话,为一个左闭右开的区间,即[0:3]选取的为0-2三条记
录。
与此等价,还可以用起始的索引名称和结束索引名称选取数据,如:df['a':'b']。有一点需要注意的是使用起始索引名称和结束索引名称时,也会包含结束索引
的数据。具体看 下方示例:
以上两种方式返回的都是DataFrame。
选择一列数据:
In [16]:
df['open'] # 返回Series
Out[16]:
0
1
2
3
4
5
6
7
8
9
1
1
1
1
3313.953369
3340.557617
3368.340088
3366.852295
3345.748291
3361.639404
3355.800781
3332.685791
3317.962402
3314.150635
3305.600098
3323.338867
3330.952148
3326.977295
0
1
2
3
Name: open, dtype: float32
In [17]:
df[['open']] # 返回DataFrame
Out[17]:
open
0
1
2
3313.953369
3340.557617
3368.340088

open
3
4
5
6
7
8
9
3366.852295
3345.748291
3361.639404
3355.800781
3332.685791
3317.962402
3314.150635
3305.600098
3323.338867
3330.952148
3326.977295
10
11
1
2
3
1
选择多列
In [18]:
df[['open', 'high']]
Out[18]:
open
high
0
1
2
3
4
5
6
7
8
9
3313.953369
3340.557617
3368.340088
3366.852295
3345.748291
3361.639404
3355.800781
3332.685791
3317.962402
3314.150635
3305.600098
3323.338867
3330.952148
3326.977295
3345.262939
3369.565918
3373.411865
3368.870605
3366.221924
3370.505127
3366.631592
3343.127930
3338.174072
3322.781982
3327.376709
3350.961914
3346.495850
3358.412109
10
11
1
2
3
1
选择多行
In [19]:
df[0:3]
Out[19]:
date
instrument
open
high
low
close
volume
amount
2
0
017-
1-03
0
1
2
000300.SHA
000300.SHA
000300.SHA
3313.953369
3340.557617
3368.340088
3345.262939
3313.953369
3342.227295
8656789600
8.761277e+10
2
0
017-
1-04
3369.565918
3373.411865
3338.152588
3361.461914
3368.311768
3367.789307
9005082700
8833635700
9.801436e+10
9.118934e+10
2
0
017-
1-05
2
.3.2 使用标签选取数据:¶
df.loc[行标签,列标签]

df.loc['a':'b'] #选取 ab 两行数据
df.loc[:,'open'] #选取 open 列的数据
df.loc 的第一个参数是行标签,第二个参数为列标签(可选参数,默认为所有列标签),两个参数既可以是列表也可以是单个字符,如果两个参数都为列表
则返回的是 DataFrame,否则,则为 Series。
PS:loc为location的缩写。
In [20]:
df.loc[3,'open']
Out[20]:
3
366.8523
In [21]:
df.loc[1:3]
Out[21]:
date
instrument
open
high
low
close
volume
amount
2
017-
1
000300.SHA
3340.557617
3369.565918
3338.152588
3368.311768
9005082700
9.801436e+10
01-04
2
0
017-
1-05
2
3
000300.SHA
000300.SHA
3368.340088
3366.852295
3373.411865
3368.870605
3361.461914
3346.891357
3367.789307
3347.666504
8833635700
8745911400
9.118934e+10
9.107226e+10
2
0
017-
1-06
In [22]:
df.loc[:, 'open']
Out[22]:
0
1
2
3
4
5
6
7
8
9
1
1
1
1
3313.953369
3340.557617
3368.340088
3366.852295
3345.748291
3361.639404
3355.800781
3332.685791
3317.962402
3314.150635
3305.600098
3323.338867
3330.952148
3326.977295
0
1
2
3
Name: open, dtype: float32
2
.3.3. 使用位置选取数据:¶
df.iloc[行位置,列位置]
df.iloc[1,1] #选取第二行,第二列的值,返回的为单个值
df.iloc[[0,2],:] #选取第一行及第三行的数据
df.iloc[0:2,:] #选取第一行到第三行(不包含)的数据
df.iloc[:,1] #选取所有记录的第二列的值,返回的为一个Series
df.iloc[1,:] #选取第一行数据,返回的为一个Series
PS:iloc 则为 integer & location 的缩写
In [23]:
df
Out[23]:
date
instrument
open
high
low
close
volume
amount

date
instrument
open
high
low
close
volume
amount
2
017-
0
1
2
3
4
5
6
7
8
9
000300.SHA
3313.953369
3345.262939
3313.953369
3342.227295
8656789600
8.761277e+10
01-03
2
0
017-
1-04
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
3340.557617
3368.340088
3366.852295
3345.748291
3361.639404
3355.800781
3332.685791
3317.962402
3314.150635
3305.600098
3323.338867
3330.952148
3326.977295
3369.565918
3373.411865
3368.870605
3366.221924
3370.505127
3366.631592
3343.127930
3338.174072
3322.781982
3327.376709
3350.961914
3346.495850
3358.412109
3338.152588
3361.461914
3346.891357
3344.347168
3354.087891
3334.297852
3315.962891
3309.374023
3264.207031
3292.204346
3320.406250
3324.683594
3326.374023
3368.311768
3367.789307
3347.666504
3363.901367
3358.271484
3334.495361
3317.624023
3319.912109
3319.445557
3326.356201
3339.365234
3329.289062
3354.889160
9005082700
8833635700
8745911400
8370794200
8381916000
9107143800
8123913500
8418058900
15777913500
6945332800
7062322700
6615980800
6530046200
9.801436e+10
9.118934e+10
9.107226e+10
8.791612e+10
8.253397e+10
8.675045e+10
7.503189e+10
8.455610e+10
1.532625e+11
7.475451e+10
7.568068e+10
6.386971e+10
7.083133e+10
2
0
017-
1-05
2
0
017-
1-06
2
0
017-
1-09
2
0
017-
1-10
2
0
017-
1-11
2
0
017-
1-12
2
0
017-
1-13
2
0
017-
1-16
2
0
017-
1-17
10
2
0
017-
1-18
11
2
0
017-
1-19
1
2
3
2
0
017-
1-20
1
In [24]:
df.iloc[1,1] # 选取第二行,第二列的值,返回的为单个值
Out[24]:
'
000300.SHA'
In [25]:
df.iloc[[0,2],:] # 选取第一行及第三行的数据
Out[25]:
date
instrument
open
high
low
close
volume
amount
2
017-
0
2
000300.SHA
3313.953369
3345.262939
3313.953369
3342.227295
8656789600
8.761277e+10
01-03
2
0
017-
1-05
000300.SHA
3368.340088
3373.411865
3361.461914
3367.789307
8833635700
9.118934e+10
In [26]:
df.iloc[0:2,:] # 选取第一行到第三行(不包含)的数据
Out[26]:
date
instrument
open
high
low
close
volume
amount
2
017-
0
1
000300.SHA
3313.953369
3345.262939
3313.953369
3342.227295
8656789600
8.761277e+10
01-03
2
0
017-
1-04
000300.SHA
3340.557617
3369.565918
3338.152588
3368.311768
9005082700
9.801436e+10
In [27]:
df.iloc[:,1] # 选取所有记录的第一列的值,返回的为一个Series

Out[27]:
0
1
2
3
4
5
6
7
8
9
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
1
1
1
1
0
1
2
3
Name: instrument, dtype: object
In [28]:
df.iloc[1,:] # 选取第一行数据,返回的为一个Series
Out[28]:
date
2017-01-04 00:00:00
000300.SHA
3340.56
instrument
open
high
3369.57
low
3338.15
close
volume
amount
3368.31
9005082700
9.80144e+10
Name: 1, dtype: object
2
.3.4. 更广义的切片方式是使用.ix,它自动根据给到的索引类型判断是使用位置还是标签进行切片¶
df.ix[1,1]
df.ix['a':'b']
In [29]:
df
Out[29]:
date
instrument
open
high
low
close
volume
amount
2
017-
0
1
2
3
4
5
6
7
8
9
000300.SHA
3313.953369
3345.262939
3313.953369
3342.227295
8656789600
8.761277e+10
01-03
2
0
017-
1-04
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
3340.557617
3368.340088
3366.852295
3345.748291
3361.639404
3355.800781
3332.685791
3317.962402
3314.150635
3305.600098
3369.565918
3373.411865
3368.870605
3366.221924
3370.505127
3366.631592
3343.127930
3338.174072
3322.781982
3327.376709
3338.152588
3361.461914
3346.891357
3344.347168
3354.087891
3334.297852
3315.962891
3309.374023
3264.207031
3292.204346
3368.311768
3367.789307
3347.666504
3363.901367
3358.271484
3334.495361
3317.624023
3319.912109
3319.445557
3326.356201
9005082700
8833635700
8745911400
8370794200
8381916000
9107143800
8123913500
8418058900
15777913500
6945332800
9.801436e+10
9.118934e+10
9.107226e+10
8.791612e+10
8.253397e+10
8.675045e+10
7.503189e+10
8.455610e+10
1.532625e+11
7.475451e+10
2
0
017-
1-05
2
0
017-
1-06
2
0
017-
1-09
2
0
017-
1-10
2
0
017-
1-11
2
0
017-
1-12
2
0
017-
1-13
2
0
017-
1-16
2
0
017-
1-17
10

date
instrument
open
high
low
close
volume
amount
2
017-
11
000300.SHA
3323.338867
3350.961914
3320.406250
3339.365234
7062322700
7.568068e+10
01-18
2
0
017-
1-19
1
2
3
000300.SHA
000300.SHA
3330.952148
3326.977295
3346.495850
3358.412109
3324.683594
3326.374023
3329.289062
3354.889160
6615980800
6530046200
6.386971e+10
7.083133e+10
2
0
017-
1-20
1
In [30]:
df.ix[1,1]
Out[30]:
'
000300.SHA'
In [31]:
df.ix[1,'open']
Out[31]:
3
340.5576
2
.3.5 通过逻辑指针进行数据切片:¶
df[逻辑条件]
df[df.one >= 2] #单个逻辑条件
df[(df.one >=1 ) & (df.one < 3) ] #多个逻辑条件组合
In [32]:
df
Out[32]:
date
instrument
open
high
low
close
volume
amount
2
017-
0
1
2
3
4
5
6
7
8
9
000300.SHA
3313.953369
3345.262939
3313.953369
3342.227295
8656789600
8.761277e+10
01-03
2
0
017-
1-04
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
3340.557617
3368.340088
3366.852295
3345.748291
3361.639404
3355.800781
3332.685791
3317.962402
3314.150635
3305.600098
3323.338867
3330.952148
3369.565918
3373.411865
3368.870605
3366.221924
3370.505127
3366.631592
3343.127930
3338.174072
3322.781982
3327.376709
3350.961914
3346.495850
3338.152588
3361.461914
3346.891357
3344.347168
3354.087891
3334.297852
3315.962891
3309.374023
3264.207031
3292.204346
3320.406250
3324.683594
3368.311768
3367.789307
3347.666504
3363.901367
3358.271484
3334.495361
3317.624023
3319.912109
3319.445557
3326.356201
3339.365234
3329.289062
9005082700
8833635700
8745911400
8370794200
8381916000
9107143800
8123913500
8418058900
15777913500
6945332800
7062322700
6615980800
9.801436e+10
9.118934e+10
9.107226e+10
8.791612e+10
8.253397e+10
8.675045e+10
7.503189e+10
8.455610e+10
1.532625e+11
7.475451e+10
7.568068e+10
6.386971e+10
2
0
017-
1-05
2
0
017-
1-06
2
0
017-
1-09
2
0
017-
1-10
2
0
017-
1-11
2
0
017-
1-12
2
0
017-
1-13
2
0
017-
1-16
2
0
017-
1-17
10
2
0
017-
1-18
11
2
0
017-
1-19
12

date
instrument
open
high
low
close
volume
amount
2
017-
13
000300.SHA
3326.977295
3358.412109
3326.374023
3354.889160
6530046200
7.083133e+10
01-20
In [33]:
df[df.open > 3340]
Out[33]:
date
instrument
open
high
low
close
volume
amount
2
017-
1
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
3340.557617
3369.565918
3338.152588
3368.311768
9005082700
9.801436e+10
01-04
2
0
017-
1-05
2
3368.340088
3366.852295
3345.748291
3361.639404
3355.800781
3373.411865
3368.870605
3366.221924
3370.505127
3366.631592
3361.461914
3346.891357
3344.347168
3354.087891
3334.297852
3367.789307
3347.666504
3363.901367
3358.271484
3334.495361
8833635700
8745911400
8370794200
8381916000
9107143800
9.118934e+10
9.107226e+10
8.791612e+10
8.253397e+10
8.675045e+10
2
0
017-
1-06
3
2
0
017-
1-09
4
2
0
017-
1-10
5
6
2
0
017-
1-11
In [34]:
df[(df.open > 3310) & (df.close < 3350)]
Out[34]:
date
instrument
open
high
low
close
volume
amount
2
017-
0
3
6
7
8
9
000300.SHA
3313.953369
3345.262939
3313.953369
3342.227295
8656789600
8.761277e+10
01-03
2
0
017-
1-06
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
3366.852295
3355.800781
3332.685791
3317.962402
3314.150635
3323.338867
3330.952148
3368.870605
3366.631592
3343.127930
3338.174072
3322.781982
3350.961914
3346.495850
3346.891357
3334.297852
3315.962891
3309.374023
3264.207031
3320.406250
3324.683594
3347.666504
3334.495361
3317.624023
3319.912109
3319.445557
3339.365234
3329.289062
8745911400
9107143800
8123913500
8418058900
15777913500
7062322700
6615980800
9.107226e+10
8.675045e+10
7.503189e+10
8.455610e+10
1.532625e+11
7.568068e+10
6.386971e+10
2
0
017-
1-11
2
0
017-
1-12
2
0
017-
1-13
2
0
017-
1-16
2
0
017-
1-18
11
2
0
017-
1-19
12
In [35]:
df[df>3360]
Out[35]:
date
instrument
open
NaN
high
NaN
low
close
NaN
volume
amount
2017-
1-03
0
1
2
3
000300.SHA
NaN
8656789600
8.761277e+10
0
2
0
017-
1-04
000300.SHA
000300.SHA
000300.SHA
NaN
3369.565918
3373.411865
3368.870605
NaN
3368.311768
3367.789307
NaN
9005082700
8833635700
8745911400
9.801436e+10
9.118934e+10
9.107226e+10
2
0
017-
1-05
3368.340088
3366.852295
3361.461914
NaN
2
0
017-
1-06

date
instrument
open
NaN
high
low
close
volume
amount
2017-
4
5
6
7
8
9
000300.SHA
3366.221924
NaN
NaN
NaN
NaN
NaN
NaN
NaN
NaN
NaN
NaN
3363.901367
8370794200
8.791612e+10
01-09
2
0
017-
1-10
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
3361.639404
NaN
3370.505127
3366.631592
NaN
NaN
NaN
NaN
NaN
NaN
NaN
NaN
NaN
NaN
8381916000
9107143800
8123913500
8418058900
15777913500
6945332800
7062322700
6615980800
6530046200
8.253397e+10
8.675045e+10
7.503189e+10
8.455610e+10
1.532625e+11
7.475451e+10
7.568068e+10
6.386971e+10
7.083133e+10
2
0
017-
1-11
2
0
017-
1-12
NaN
2
0
017-
1-13
NaN
NaN
2
0
017-
1-16
NaN
NaN
2
0
017-
1-17
10
NaN
NaN
2
0
017-
1-18
11
NaN
NaN
2
0
017-
1-19
1
2
3
NaN
NaN
2
0
017-
1-20
1
NaN
NaN
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-Python 编程]Pandas 库之数据处理与规整
导语:本文继续讲解Pandas库在数据分析和处理上的一些应用。
In [1]:
#
首先导入库
import pandas as pd
import numpy as np
In [2]:
df = D.history_data(instruments=['000300.SHA'], start_date='2016-01-01',
end_date='2016-02-01',fields=['open', 'high', 'low', 'close', 'volume', 'amount'])
df.head()
Out[2]:
high
low
volume
open
close
amount
instrument
date
2
016-
0
1
2
3
4
3726.244629
3468.948486
11537067400
3725.856201
3469.066162
1.459682e+11
1.960171e+11
1.609472e+11
4.713080e+10
2.034989e+11
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
01-04
2
0
016-
1-05
3518.217041
3543.739502
3481.149902
3418.850830
3377.279785
3468.466553
3284.737305
3237.930664
16211698400
14596614400
4410264100
18595945100
3382.177002
3482.406494
3481.149902
3371.871094
3478.779785
3539.808105
3294.383789
3361.563232
2
0
016-
1-06
2
0
016-
1-07
2
0
016-
1-08
1
、缺失数据处理¶
1
. 1去掉包含缺失值的行:¶
In [3]:
df_drop = df.dropna()
df_drop.head()

Out[3]:
high
low
volume
open
close
amount
instrument
date
2
016-
0
1
2
3
4
3726.244629
3468.948486
11537067400
3725.856201
3469.066162
1.459682e+11
000300.SHA
01-04
2
0
016-
1-05
3518.217041
3543.739502
3481.149902
3418.850830
3377.279785
3468.466553
3284.737305
3237.930664
16211698400
14596614400
4410264100
18595945100
3382.177002
3482.406494
3481.149902
3371.871094
3478.779785
3539.808105
3294.383789
3361.563232
1.960171e+11
1.609472e+11
4.713080e+10
2.034989e+11
000300.SHA
000300.SHA
000300.SHA
000300.SHA
2
0
016-
1-06
2
0
016-
1-07
2
0
016-
1-08
1
.2 对缺失值进行填充:¶
In [4]:
df_fillna = df.fillna(value=0)
df_fillna.head()
Out[4]:
high
low
volume
open
close
amount
instrument
date
2
016-
0
1
2
3
4
3726.244629
3468.948486
11537067400
3725.856201
3469.066162
1.459682e+11
000300.SHA
01-04
2
0
016-
1-05
3518.217041
3543.739502
3481.149902
3418.850830
3377.279785
3468.466553
3284.737305
3237.930664
16211698400
14596614400
4410264100
18595945100
3382.177002
3482.406494
3481.149902
3371.871094
3478.779785
3539.808105
3294.383789
3361.563232
1.960171e+11
1.609472e+11
4.713080e+10
2.034989e+11
000300.SHA
000300.SHA
000300.SHA
000300.SHA
2
0
016-
1-06
2
0
016-
1-07
2
0
016-
1-08
1
.3 判断数据是否为nan,并进行布尔填充:¶
In [5]:
df_isnull = pd.isnull(df)
df_isnull.head()
Out[5]:
high
low
volume
False
False
False
False
False
open
close
False
False
False
False
False
amount
False
False
False
False
False
instrument
date
0
1
2
3
4
False
False
False
False
False
False
False
False
False
False
False
False
False
False
False
False
False
False
False
False
False
False
False
False
False
2
、函数的应用和映射¶
In [6]:
df.mean()#列计算平均值
Out[6]:
high
low
3.238047e+03
3.116849e+03
1.207993e+10
3.191507e+03
3.165315e+03
1.300057e+11
volume
open
close
amount
dtype: float32

In [7]:
df.mean(1)#行计算平均值
Out[7]:
0
1
2
3
4
5
6
7
8
9
2.625088e+10
3.537146e+10
2.925730e+10
8.590179e+09
3.701580e+10
3.365465e+10
2.581192e+10
2.382546e+10
2.637089e+10
2.405715e+10
1.992852e+10
2.594551e+10
2.606307e+10
2.216253e+10
1.764680e+10
1.565532e+10
2.332401e+10
2.337010e+10
1.759769e+10
2.013213e+10
1.526850e+10
1
1
1
1
1
1
1
1
1
1
2
0
1
2
3
4
5
6
7
8
9
0
dtype: float32
In [8]:
df.mean(axis = 1,skipna = False) # skipna参数默认是 True 表示排除缺失值
Out[8]:
0
2.625088e+10
3.537146e+10
2.925730e+10
8.590179e+09
3.701580e+10
3.365465e+10
2.581192e+10
2.382546e+10
2.637089e+10
2.405715e+10
1.992852e+10
2.594551e+10
2.606307e+10
2.216253e+10
1.764680e+10
1.565532e+10
2.332401e+10
2.337010e+10
1.759769e+10
2.013213e+10
1.526850e+10
1
2
3
4
5
6
7
8
9
1
1
1
1
1
1
1
1
1
1
2
0
1
2
3
4
5
6
7
8
9
0
dtype: float32
In [9]:
sorted_row_df = df.sort_index()#行名字排序
sorted_row_df.head()
Out[9]:
high
low
volume
open
close
amount
instrument
date
2
016-
0
1
2
3
3726.244629
3468.948486
11537067400
3725.856201
3469.066162
1.459682e+11
000300.SHA
01-04
2
0
016-
1-05
3518.217041
3543.739502
3481.149902
3377.279785
3468.466553
3284.737305
16211698400
14596614400
4410264100
3382.177002
3482.406494
3481.149902
3478.779785
3539.808105
3294.383789
1.960171e+11
1.609472e+11
4.713080e+10
000300.SHA
000300.SHA
000300.SHA
2
0
016-
1-06
2
0
016-
1-07

high
low
volume
open
close
amount
instrument
date
2
016-
4
3418.850830
3237.930664
18595945100
3371.871094
3361.563232
2.034989e+11
000300.SHA
01-08
In [10]:
sorted_col_df = df.sort_index(axis=1) # 列名字排序
sorted_col_df.head()
Out[10]:
amount
close
date
high
instrument
low
open
volume
2
016-
0
1.459682e+11
3469.066162
3726.244629
3518.217041
3543.739502
3481.149902
3418.850830
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
3468.948486
3377.279785
3468.466553
3284.737305
3237.930664
3725.856201
11537067400
01-04
2
0
016-
1-05
1
1.960171e+11
1.609472e+11
4.713080e+10
2.034989e+11
3478.779785
3539.808105
3294.383789
3361.563232
3382.177002
3482.406494
3481.149902
3371.871094
16211698400
14596614400
4410264100
18595945100
2
0
016-
1-06
2
3
2
0
016-
1-07
2
0
016-
1-08
4
In [11]:
#
数据默认是按升序排序的,也可以降序排序
df.sort_index(axis=1,ascending = False)
Out[11]:
volume
open
low
instrument
high
date
close
amount
2
0
016-
1-04
0
1
2
3
4
5
6
7
8
9
11537067400
3725.856201
3468.948486
3377.279785
3468.466553
3284.737305
3237.930664
3192.449951
3174.549805
3155.878662
3072.038818
3101.052246
3066.727051
3119.216309
3154.425781
3081.345459
3053.958008
3105.100342
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
3726.244629
3469.066162
1.459682e+11
2
0
016-
1-05
16211698400
14596614400
4410264100
18595945100
17463838700
12822579600
12066649400
13453767100
12460177900
10112838600
12765389300
13065050400
11118973300
8995108700
8154006100
3382.177002
3482.406494
3481.149902
3371.871094
3303.124512
3214.823486
3240.483887
3076.644531
3200.887939
3068.234863
3132.704590
3204.218262
3136.384033
3114.895020
3129.027832
3518.217041
3543.739502
3481.149902
3418.850830
3342.480713
3242.253174
3257.295410
3226.657715
3216.797607
3165.616455
3227.907959
3225.949707
3202.538086
3132.170898
3149.332275
3478.779785
3539.808105
3294.383789
3361.563232
3192.449951
3215.709961
3155.878662
3221.571289
3118.729980
3130.729004
3223.125000
3174.378174
3081.345459
3113.462646
3128.885986
1.960171e+11
1.609472e+11
4.713080e+10
2.034989e+11
1.844640e+11
1.420489e+11
1.308861e+11
1.447716e+11
1.318827e+11
1.094583e+11
1.429077e+11
1.433133e+11
1.218562e+11
9.688567e+10
8.577789e+10
2
0
016-
1-06
2
0
016-
1-07
2
0
016-
1-08
2
0
016-
1-11
2
0
016-
1-12
2
0
016-
1-13
2
0
016-
1-14
2
0
016-
1-15
2
0
016-
1-18
10
2
0
016-
1-19
11
2
0
016-
1-20
12
13
14
15
2
0
016-
1-21
2
0
016-
1-22
2
0
016-
1-25

volume
open
low
instrument
high
date
close
amount
2
016-
16
17
18
19
20
12693392100
3099.595703
2934.646973
000300.SHA
3106.530273
2940.508545
1.272507e+11
01-26
2
0
016-
1-27
13222936600
9922275600
11330425900
8679534200
2953.182617
2909.333984
2855.598389
2939.040039
2839.289795
2841.844238
2854.371094
2869.561279
000300.SHA
000300.SHA
000300.SHA
000300.SHA
2963.543701
2941.886719
2965.309326
2944.517090
2930.351807
2853.756104
2946.090088
2901.047607
1.269977e+11
9.566387e+10
1.094624e+11
8.293145e+10
2
0
016-
1-28
2
0
016-
1-29
2
0
016-
2-01
常用的方法如上所介绍们,还要其他许多,可自行学习,下面罗列了一些,可供参考:
count 非na值的数量
describe 针对Series或个DataFrame列计算汇总统计
min 、max 计算最小值和最大值
argmin 、argmax 计算能够获取到最大值和最小值得索引位置(整数)
idxmin 、idxmax 计算能够获取到最大值和最小值得索引值
quantile 计算样本的分位数(0到1)
sum 值的总和
mean 值得平均数
median 值得算术中位数(50%分位数)
mad 根据平均值计算平均绝对离差
var 样本值的方差
std 样本值的标准差
skew 样本值得偏度(三阶矩)
kurt 样本值得峰度(四阶矩)
cumsum 样本值得累计和
cummin ,cummax 样本值得累计最大值和累计最小值
cumprod 样本值得累计积
diff 计算一阶差分(对时间序列很有用)
pct_change 计算百分数变化
3
、数据规整¶
Pandas提供了大量的方法能够轻松的对Series,DataFrame和Panel对象进行各种符合各种逻辑关系的合并操作
concat 可以沿一条轴将多个对象堆叠到一起
append 将一行连接到一个DataFrame上
duplicated 移除重复数据
3
.1 数据堆叠 concat ¶
In [12]:
df1 = D.history_data(instruments=['000300.SHA'], start_date='2017-01-01', end_date='2017-01-05',
fields=['open', 'high', 'low', 'close'])
df1
Out[12]:
high
low
open
close
instrument
date
0
1
3345.262939
3369.565918
3313.953369
3338.152588
3313.953369
3340.557617
3342.227295
3368.311768
000300.SHA
000300.SHA
2017-01-03
2017-01-04

high
low
open
close
instrument
date
2
3373.411865
3361.461914
3368.340088
3367.789307
000300.SHA
2017-01-05
In [13]:
df2 = D.history_data(instruments=['000300.SHA'], start_date='2017-01-06', end_date='2017-01-10',
fields=['open', 'high', 'low', 'close'])
df2
Out[13]:
high
low
open
close
instrument
date
0
1
2
3368.870605
3366.221924
3370.505127
3346.891357
3344.347168
3354.087891
3366.852295
3345.748291
3361.639404
3347.666504
3363.901367
3358.271484
000300.SHA
000300.SHA
000300.SHA
2017-01-06
2017-01-09
2017-01-10
纵向拼接(默认):
In [14]:
pd.concat([df1, df2], axis=0)
Out[14]:
high
low
open
close
instrument
date
0
1
2
0
1
2
3345.262939
3369.565918
3373.411865
3368.870605
3366.221924
3370.505127
3313.953369
3338.152588
3361.461914
3346.891357
3344.347168
3354.087891
3313.953369
3340.557617
3368.340088
3366.852295
3345.748291
3361.639404
3342.227295
3368.311768
3367.789307
3347.666504
3363.901367
3358.271484
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
000300.SHA
2017-01-03
2017-01-04
2017-01-05
2017-01-06
2017-01-09
2017-01-10
横向拼接,index对不上的会用 NaN 填充:
In [15]:
pd.concat([df1, df2], axis=1)
Out[15]:
high
low
open
close
instrument
date
high
low
2
0
017-
1-03
0
1
2
3345.262939
3313.953369
3313.953369
3342.227295
000300.SHA
3368.870605
3346.891357
336
334
336
2
0
017-
1-04
3369.565918
3373.411865
3338.152588
3361.461914
3340.557617
3368.340088
3368.311768
3367.789307
000300.SHA
000300.SHA
3366.221924
3370.505127
3344.347168
3354.087891
2
0
017-
1-05
3
.2 数据连接 append ¶
In [16]:
df1
Out[16]:
high
low
open
close
instrument
date
0
1
2
3345.262939
3369.565918
3373.411865
3313.953369
3338.152588
3361.461914
3313.953369
3340.557617
3368.340088
3342.227295
3368.311768
3367.789307
000300.SHA
000300.SHA
000300.SHA
2017-01-03
2017-01-04
2017-01-05
In [17]:

s = df1.iloc[0]
s
Out[17]:
high
3345.26
3313.95
low
open
3313.95
close
instrument
3342.23
000300.SHA
date
2017-01-03 00:00:00
Name: 0, dtype: object
In [18]:
df1.append(s, ignore_index=False) # ignore_index=False 表示索引不变
Out[18]:
high
low
open
close
instrument
date
0
1
2
0
3345.262939
3369.565918
3373.411865
3345.262939
3313.953369
3338.152588
3361.461914
3313.953369
3313.953369
3340.557617
3368.340088
3313.953369
3342.227295
3368.311768
3367.789307
3342.227295
000300.SHA
000300.SHA
000300.SHA
000300.SHA
2017-01-03
2017-01-04
2017-01-05
2017-01-03
In [19]:
df1.append(s, ignore_index=True) # ignore_index=True 表示索引重置
Out[19]:
high
low
open
close
instrument
date
0
1
2
3
3345.262939
3369.565918
3373.411865
3345.262939
3313.953369
3338.152588
3361.461914
3313.953369
3313.953369
3340.557617
3368.340088
3313.953369
3342.227295
3368.311768
3367.789307
3342.227295
000300.SHA
000300.SHA
000300.SHA
000300.SHA
2017-01-03
2017-01-04
2017-01-05
2017-01-03
3
.3 移除重复数据duplicated ¶
In [20]:
z = df1.append(s, ignore_index=False)
z
Out[20]:
high
low
open
close
instrument
date
0
1
2
0
3345.262939
3369.565918
3373.411865
3345.262939
3313.953369
3338.152588
3361.461914
3313.953369
3313.953369
3340.557617
3368.340088
3313.953369
3342.227295
3368.311768
3367.789307
3342.227295
000300.SHA
000300.SHA
000300.SHA
000300.SHA
2017-01-03
2017-01-04
2017-01-05
2017-01-03
查看重复数据:
In [21]:
z.duplicated()
Out[21]:
0
1
2
0
False
False
False
True
dtype: bool
移除重复数据:

In [22]:
z.drop_duplicates()
Out[22]:
high
low
open
close
instrument
date
0
1
2
3345.262939
3369.565918
3373.411865
3313.953369
3338.152588
3361.461914
3313.953369
3340.557617
3368.340088
3342.227295
3368.311768
3367.789307
000300.SHA
000300.SHA
000300.SHA
2017-01-03
2017-01-04
2017-01-05
4
、分组¶
In [23]:
z.groupby('open').sum()
Out[23]:
high
low
close
open
3313.953369
3340.557617
3368.340088
6690.525879
6627.906738
3338.152588
3361.461914
6684.454590
3368.311768
3367.789307
3369.565918
3373.411865
In [24]:
z.groupby(['open','close']).sum()
Out[24]:
high
low
open
close
3313.953369
3340.557617
3368.340088
3342.227295
3368.311768
3367.789307
6690.525879
3369.565918
3373.411865
6627.906738
3338.152588
3361.461914
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
策略与应用
[
量化学堂-策略开发]金叉死叉策略
金叉死叉策略其实就是双均线策略。策略思想是:当短期均线上穿长期均线时,形成金叉,此时买入股票。当短期均线下穿长期均线时,形成死叉,此时卖
出股票。研究表明,双均线系统虽然简单,但只要严格执行,也能长期盈利。
首先,我们选择要交易的股票,用instruments表示,然后确定回测的开始时间和结束时间。记住,如果是单只股票,那么instruments就是含有一个元素的列
表,如果是多只股票,instruments就是含有多个元素的列表。
#
选择投资标的
instruments = ['600519.SHA']
设置回测开始时间
start_date = '2012-05-28'
设置回测结束时间
#
#
end_date = '2017-07-18'
然后,编写策略初始化部分。
#
initialize函数只会运行一次,在第一个日期运行,因此可以把策略一些参数放在该函数定义
def initialize(context):
设置手续费,买入时万3,卖出是千分之1.3,不足5元以五元计
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
短均线参数
context.short_period = 5
#
#

#
长均线参数
context.long_period = 50
接着,编写策略主体部分。
#
#
handle_data函数会每个日期运行一次,可以把行情数据理解成K线,然后handle_data函数会在每个K
线上依次运行
def handle_data(context, data):
#
当运行的K线数量还达不到长均线时直接返回
if context.trading_day_index < context.long_period:
return
#
投资标的
k = instruments[0]
sid = context.symbol(k)
#
最新价格
price = data.current(sid, 'price')
短周期均线值
short_mavg = data.history(sid, 'price',context.short_period, '1d').mean()
长周期均线值
long_mavg = data.history(sid, 'price',context.long_period, '1d').mean()
账户现金
cash = context.portfolio.cash
账户持仓
cur_position = context.portfolio.positions[sid].amount
#
#
#
#
#
#
策略逻辑部分
空仓状态下,短周期均线上穿长周期均线,买入股票
if short_mavg > long_mavg and cur_position == 0 and data.can_trade(sid):
context.order(sid, int(cash/price/100)*100)
#
持仓状态下,短周期均线下穿长周期均线,卖出股票
elif short_mavg < long_mavg and cur_position > 0 and
context.order_target_percent(sid, 0)
data.can_trade(sid):
最后,编写策略回测接口。
m=M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,
initialize=initialize,
handle_data=handle_data,
#
股票买入的时候,假设以次日开盘价成交
order_price_field_buy='open',
股票卖出的时候,假设以次日开盘价成交
#
order_price_field_sell='open',
capital_base=100000,
)
如果执行代码,策略就跑起来了,测试结果很快就显示在你的眼前了,是不是很神奇。点击 克隆策略按钮就可以把完整策略复制到你的个人账户里啦。宽客
们快去试试吧
金叉死叉策略¶
当短期均线上穿长期均线,出现金叉,买入
当短期均线下穿长期均线,出现死叉,卖出
1
. 主要参数¶
In [1]:
instruments = ['600519.SHA']
start_date = '2012-05-28'
end_date = '2017-07-18'
2
. 策略回测主体¶
In [2]:
def initialize(context):
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5)) # 设置手续费
context.short_period = 5 # 短期均线
context.long_period = 50 # 长期均线
def handle_data(context, data):
if context.trading_day_index < context.long_period: # 长期均线值要有意义,需要在50根k线之后
return
k = instruments[0] # 标的为字符串格式
sid = context.symbol(k) # 将标的转化为equity格式
price = data.current(sid, 'price') # 最新价格
short_mavg = data.history(sid, 'price',context.short_period, '1d').mean() # 短期均线值
long_mavg = data.history(sid, 'price',context.long_period, '1d').mean() # 长期均线值
cash = context.portfolio.cash # 现金
cur_position = context.portfolio.positions[sid].amount # 持仓
#
交易逻辑
if short_mavg > long_mavg and cur_position == 0 and data.can_trade(sid):
context.order(sid, int(cash/price/100)*100) # 买入
elif short_mavg < long_mavg and cur_position > 0 and data.can_trade(sid):
context.order_target_percent(sid, 0) # 全部卖出
3
.回测接口¶
In [3]:
m=M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='open',
capital_base=1000000,
)
[
[
[
[
2017-07-19 09:26:18.508739] INFO: bigquant: backtest.v7 start ..
2017-07-19 09:26:26.084446] INFO: Performance: Simulated 1202 trading days out of 1202.
2017-07-19 09:26:26.085803] INFO: Performance: first open: 2012-05-28 13:30:00+00:00
2017-07-19 09:26:26.087307] INFO: Performance: last close: 2017-05-05 19:00:00+00:00
[
2017-07-19 09:26:29.467536] INFO: bigquant: backtest.v7 end [10.958797s].
[
量化学堂-策略开发]海龟策略
几乎所有的宽客(Quant)都听说过海龟交易策略,该策略以海龟交易法则为核心。海龟交易法则,起源于八十年代的美国,是一套简单有效的交易法则。这个
法则以及使用这个法则的人的故事被写成了一本书——《海龟交易法则》,这是一本入门量化投资的经典书籍。
海龟交易的具体规则是:
1
. 当今天的收盘价大于过去20个交易日中的最高价时,以收盘价买入;
2
. 买入后,当收盘价小于过去10个交易日中的最低价时,以收盘价卖出。
这篇文章我们只介绍如何快速编写海龟交易策略(代码如下),暂不涉及复杂的头寸管理和风险控制。
#
策略参数设置
instruments = ['600519.SHA'] # 选择的投资标的
start_date = '2014-07-17'
end_date = '2017-07-18'
#
回测开始日期
#
回测结束日期
#
策略主体函数
def initialize(context):
context.set_commission(PerDollar(0.0015)) # 手续费设置
def handle_data(context, data):
if context.trading_day_index < 20: # 在20个交易日以后才开始真正运行
return
sid = context.symbol(instruments[0])
price = data.current(sid, 'price') # 当前价格
high_point = data.history(sid, 'price', 20, '1d').max() # 20日高点
low_point = data.history(sid, 'price', 10, '1d').min() # 10日低点
#
持仓
cur_position = context.portfolio.positions[sid].amount

#
#
交易逻辑
最新价大于等于20日高点,并且处于空仓状态,并且该股票当日可以交易
if price >= high_point and cur_position == 0 and data.can_trade(sid):
context.order_target_percent(sid, 1)
#
最新价小于等于10日低点,并且持有股票,并且该股票当日可以交易
elif price <= low_point and cur_position > 0 and data.can_trade(sid):
context.order_target_percent(sid, 0)
#
策略回测接口
m=M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open', # 买入股票订单成交价为收盘价
order_price_field_sell='open', # 卖出股票订单成交价为收盘价
capital_base=float("1.0e6"), # 初始资金为100万
benchmark='000300.INDX',) # 比较基准为沪深300指数
好了,海龟交易策略就是这么简单,但它确实可以长期盈利,是不是很神奇?点击 克隆策略按钮就可把完整策略复制到自己的账户了,赶紧试试吧
海龟策略¶
当今天的收盘价,大于过去20个交易日中的最高价时,以收盘价买入
买入后,当收盘价小于过去10个交易日中的最低价时,以收盘价卖出
1
. 策略参数¶
In [11]:
instruments = ['600519.SHA'] # 选择的投资标的
start_date = '2014-07-17' # 回测开始日期
end_date = '2017-07-18' # 回测结束日期
2
. 策略主体函数¶
In [12]:
def initialize(context):
context.set_commission(PerDollar(0.0015)) # 手续费设置
def handle_data(context, data):
if context.trading_day_index < 20: # 在20个交易日以后才开始真正运行
return
sid = context.symbol(instruments[0])
price = data.current(sid, 'price') # 当前价格
high_point = data.history(sid, 'price', 20, '1d').max() # 20日高点
low_point = data.history(sid, 'price', 10, '1d').min() # 10日低点
#
持仓
cur_position = context.portfolio.positions[sid].amount
#
#
交易逻辑
最新价大于20日高点,并且处于空仓状态,并且该股票当日可以交易
if price >= high_point and cur_position == 0 and data.can_trade(sid):
context.order_target_percent(sid, 1)
#
最新价小鱼等于10日低点,并且持有股票,并且该股票当日可以交易
elif price <= low_point and cur_position > 0 and data.can_trade(sid):
context.order_target_percent(sid, 0)
3
. 回测接口¶
In [13]:
m=M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',# 买入股票订单成交价为收盘价
order_price_field_sell='open',# 卖出股票订单成交价为收盘价
capital_base=float("1.0e6"),# 初始资金为100万
benchmark='000300.INDX',# 比较基准为沪深300指数
)
[
[
2017-07-19 09:51:54.660710] INFO: bigquant: backtest.v7 start ..
2017-07-19 09:51:54.662489] INFO: bigquant: hit cache
[
2017-07-19 09:51:55.760507] INFO: bigquant: backtest.v7 end [1.099776s].
In [14]:
result = m.raw_perf.read_df() # 回测结果
algo_daily_returns = (result.algorithm_period_return+1).pct_change().dropna() # 策略每日收益率
benchmark_daily_returns = (result.benchmark_period_return+1).pct_change().dropna() # 基准每日收益率
print('策略收益率与基准收益率的相关系数:',algo_daily_returns.corr(benchmark_daily_returns))
策略收益率与基准收益率的相关系数: 0.289028819681
In [15]:
algo_daily_returns.corr(benchmark_daily_returns)
Out[15]:
0
.2890288196805586
[
量化学堂-策略开发]浅谈小市值策略
前几篇的教程都是关于择时的策略,今天打算写一篇选股的策略——基于市值的选股策略。
了解Alpha策略和Fama_French三因子模型的人都知道,市值因子是一个长期有效的超额收益来源,对股票收益率有一定的解释作用,小市值的股票更容易
带来超额收益。这也比较好理解,因为小市值类股票往往表现活跃,容易引发炒作风潮。此外,还有IPO管制的原因(大量排队企业选择借壳),也有市场
风险偏好提升的原因(市场恶性循环越来越偏爱小市值)。
现在,开始正式介绍策略部分吧。为方便小伙伴们理解,我们会介绍更详细和具体。
策略逻辑:市值可以带来超额收益
策略内容:每月月初买入市值最小的30只股票,持有至下个月月初再调仓
资金管理:等权重买入
风险控制:无单只股票仓位上限控制、无止盈止损
第一步:获取数据,并整理买入股票列表
BigQuant平台具有丰富的金融数据,包括行情数据和财报数据,并且具有便捷、简单的API调用接口。获取数据的代码如下:
def prepare(context):
#
#
引进prepare数据准备函数是为了保持回测和模拟能够通用
获取股票代码
instruments = D.instruments()
start_date = context.start_date
#
确定结束时间
end_date = context.end_date
获取股票总市值数据,返回DataFrame数据格式
#
market_cap_data = D.history_data(instruments,context.start_date,context.end_date,
fields=['market_cap','amount'])
#
获取每日按小市值排序 (从低到高)的前三十只股票
daily_buy_stock = market_cap_data.groupby('date').apply(lambda df:df[(df['amount'] > 0)].sort_values('market_cap')[:30])
context.daily_buy_stock = daily_buy_stock
在上面的代码中,history_data是我们平台获取数据的一个重要API。fields参数为列表形式,传入的列表即为我们想要获取的数据。
第二步:回测主体
我们平台策略回测有丰富的文档介绍,请参考:
#
回测参数设置,initialize函数只运行一次
def initialize(context):
手续费设置
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
调仓规则(每月的第一天调仓)
context.schedule_function(rebalance, date_rule=date_rules.month_start(days_offset=0))
#
#
#
handle_data函数会每天运行一次
def handle_data(context,data):
pass
#
换仓函数
def rebalance(context, data):
当前的日期
date = data.current_dt.strftime('%Y-%m-%d')
根据日期获取调仓需要买入的股票的列表
stock_to_buy = list(context.daily_buy_stock.ix[date].instrument)
通过positions对象,使用列表生成式的方法获取目前持仓的股票列表
stock_hold_now = [equity.symbol for equity in context.portfolio.positions]
继续持有的股票:调仓时,如果买入的股票已经存在于目前的持仓里,那么应继续持有
no_need_to_sell = [i for i in stock_hold_now if i in stock_to_buy]
需要卖出的股票
stock_to_sell = [i for i in stock_hold_now if i not in no_need_to_sell]
#
#
#
#
#
#
卖出
for stock in stock_to_sell:
#
#
#
如果该股票停牌,则没法成交。因此需要用can_trade方法检查下该股票的状态
如果返回真值,则可以正常下单,否则会出错
因为stock是字符串格式,我们用symbol方法将其转化成平台可以接受的形式:Equity格式
if data.can_trade(context.symbol(stock)):
#
#
order_target_percent是平台的一个下单接口,表明下单使得该股票的权重为0,
即卖出全部股票,可参考回测文档
context.order_target_percent(context.symbol(stock), 0)
#
如果当天没有买入的股票,就返回
if len(stock_to_buy) == 0:
return
#
等权重买入
weight = 1 / len(stock_to_buy)
#
买入
for stock in stock_to_buy:
if data.can_trade(context.symbol(stock)):
#
#
下单使得某只股票的持仓权重达到weight,因为
weight大于0,因此是等权重买入
context.order_target_percent(context.symbol(stock), weight)
第三步:回测接口
m=M.trade.v2(
instruments=D.instruments(),
start_date= '2013-01-01',
end_date='2017-10-27',
#
必须传入initialize,只在第一天运行
prepare=prepare,
initialize=initialize,
#
必须传入handle_data,每个交易日都会运行
handle_data=handle_data,
买入以开盘价成交
order_price_field_buy='open',
卖出也以开盘价成交
order_price_field_sell='open',
策略本金
capital_base=1000000,
比较基准:沪深300
benchmark='000300.INDX',
#
#
#
#
)
好嘞,策略就完全写好了。我们运行完曲线如下:

回测结果比较真实,小市值策略在过去几年确实是这样的表现。2017年以来,中小盘风格转换明显,创业板、中小板走势比较弱,因此该策略也面临较大回
撤。
纸上得来终觉浅,绝知此事须躬行。还是请小伙伴自己动手去实现吧:slight_smile: 点击 克隆策略就可以把策略克隆到自己的账户了。
定义相关函数¶
In [5]:
def prepare(context):
#
#
引进prepare数据准备函数是为了保持回测和模拟能够通用
获取股票代码
instruments = D.instruments()
start_date = context.start_date
#
确定结束时间
end_date = context.end_date
获取股票总市值数据,返回DataFrame数据格式
#
market_cap_data = D.history_data(instruments,context.start_date,context.end_date,
fields=['market_cap','amount'])
#
获取每日按小市值排序 (从低到高)的前三十只股票
daily_buy_stock = market_cap_data.groupby('date').apply(lambda df:df[(df['amount'] > 0)].sort_values('market_cap')[:30])
context.daily_buy_stock = daily_buy_stock
#
回测参数设置,initialize函数只运行一次
def initialize(context):
手续费设置
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
调仓规则(每月的第一天调仓)
#
#
context.schedule_function(rebalance, date_rule=date_rules.month_start(days_offset=0))
#
handle_data函数会每天运行一次
def handle_data(context,data):
pass
#
换仓函数
def rebalance(context, data):
当前的日期
date = data.current_dt.strftime('%Y-%m-%d')
根据日期获取调仓需要买入的股票的列表
stock_to_buy = list(context.daily_buy_stock.ix[date].instrument)
通过positions对象,使用列表生成式的方法获取目前持仓的股票列表
stock_hold_now = [equity.symbol for equity in context.portfolio.positions]
继续持有的股票:调仓时,如果买入的股票已经存在于目前的持仓里,那么应继续持有
no_need_to_sell = [i for i in stock_hold_now if i in stock_to_buy]
需要卖出的股票
stock_to_sell = [i for i in stock_hold_now if i not in no_need_to_sell]
#
#
#
#
#
#
卖出
for stock in stock_to_sell:
#
#
#
如果该股票停牌,则没法成交。因此需要用can_trade方法检查下该股票的状态
如果返回真值,则可以正常下单,否则会出错
因为stock是字符串格式,我们用symbol方法将其转化成平台可以接受的形式:Equity格式
if data.can_trade(context.symbol(stock)):
#
#
order_target_percent是平台的一个下单接口,表明下单使得该股票的权重为0,
即卖出全部股票,可参考回测文档
context.order_target_percent(context.symbol(stock), 0)
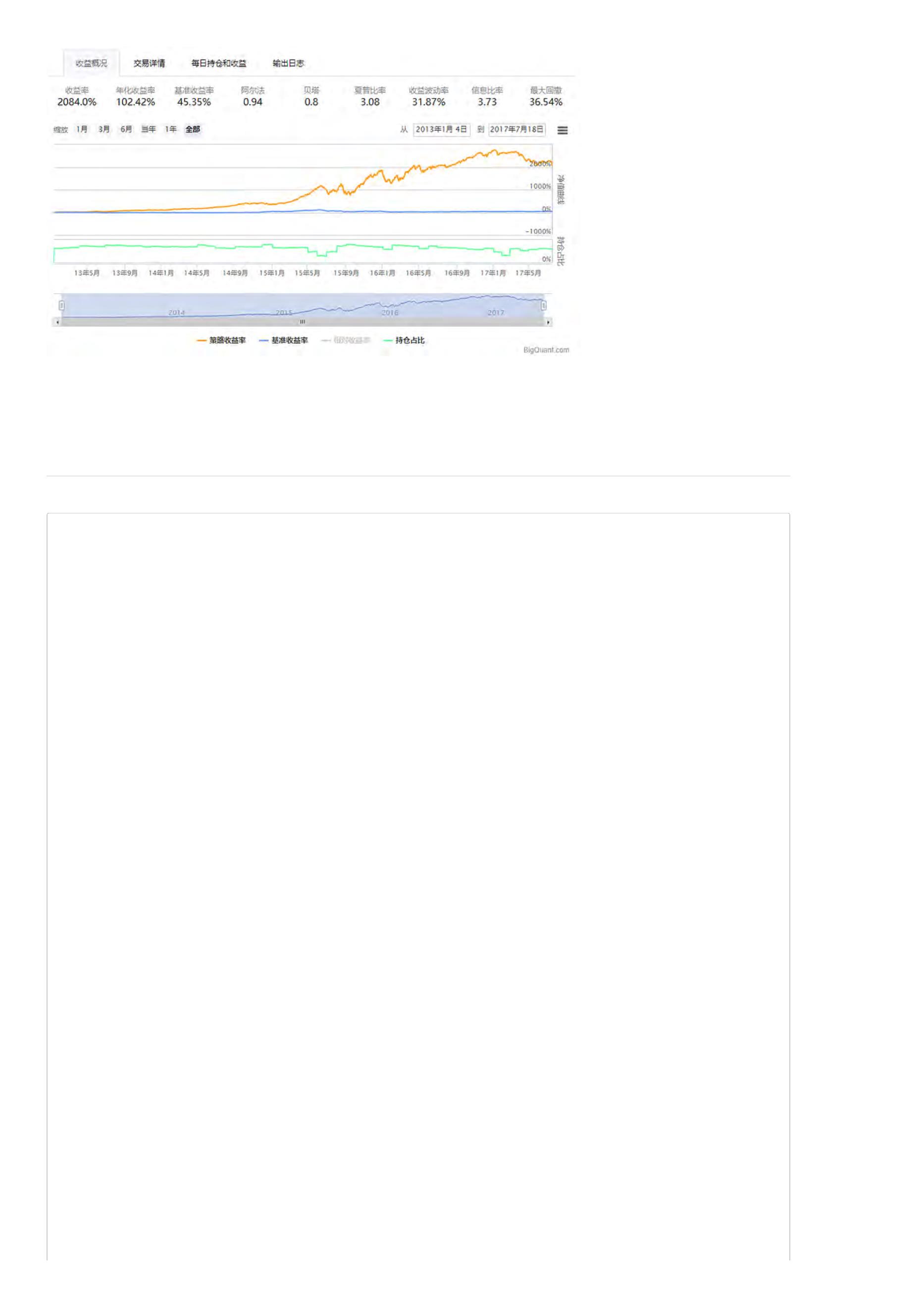
#
如果当天没有买入的股票,就返回
if len(stock_to_buy) == 0:
return
#
等权重买入
weight = 1 / len(stock_to_buy)
#
买入
for stock in stock_to_buy:
if data.can_trade(context.symbol(stock)):
#
#
下单使得某只股票的持仓权重达到weight,因为
weight大于0,因此是等权重买入
context.order_target_percent(context.symbol(stock), weight)
交易函数调用¶
In [6]:
m=M.trade.v2(
instruments=D.instruments(),
start_date= '2013-01-01',
end_date='2017-10-27',
#
必须传入initialize,只在第一天运行
prepare=prepare,
initialize=initialize,
#
必须传入handle_data,每个交易日都会运行
handle_data=handle_data,
买入以开盘价成交
order_price_field_buy='open',
卖出也以开盘价成交
order_price_field_sell='open',
策略本金
capital_base=1000000,
比较基准:沪深300
benchmark='000300.INDX',
#
#
#
#
)
[
[
[
[
2017-10-27 21:29:52.553618] INFO: bigquant: backtest.v7 开始运行..
2017-10-27 21:31:23.992974] INFO: Performance: Simulated 1170 trading days out of 1170.
2017-10-27 21:31:23.994829] INFO: Performance: first open: 2013-01-04 14:30:00+00:00
2017-10-27 21:31:23.996232] INFO: Performance: last close: 2017-10-27 19:00:00+00:00
[
2017-10-27 21:31:29.360513] INFO: bigquant: backtest.v7 运行完成[96.806889s].
[
量化学堂-策略开发]多头排列回踩买入策略
什么是均线
金融市场上每个人都有一套自己的分析方法,无论你是一个技术派、基本面派、消息派还是量化投资派,对于“均线”这个名词一定不会陌生。虽说这个概念
诞生于市场技术分析领域,但由于它的通俗易用,均线一直受到投资者和市场分析人士的青睐。
均线的全称是移动平均线(MA)。移动平均线是个什么概念?即通过等权或指数加权的方式,计算一段时期内的平均价格,是将某一段时间的收盘价之和除
以该周期。 比如,日线MA5的意思就是说,5天内的收盘价除以5。
从这张图你应该可以看出,移动平均线,由于是一个均值的画线,因此它平滑了市场数据中的棱角和起伏波动,并且展示出已经走出来的基本价格趋势。
挺好理解吧?正因为均线是一个简洁易懂的概念,因此成为目前市场上运用最广泛的技术指标。不同周期的均线如何组合排列?如何交叉背离?与其他指标
有怎么样的关系?这些问题背后的逻辑,都成为了均线应用最基本的理念支撑,这些不同的理念也创造了不同的均线策略。
今天给大家讲一讲,由均线衍生的策略:多头排列回踩点。
正如标题所言,这个策略有两个非常醒目的特点,好懂、好用。好懂,是指这个策略本身并没有什么复杂的概念,理解起来非常容易;好用,是指这个策略
的应用效果非常不错。本文就从这两个角度入手,手把手教大家如何玩赚这个策略!
什么是多头排列回踩点?
想明白这7个字组合在一起的含义,咱们先把它拆分一下。什么是多头排列?什么是回踩点?
多头排列首先是一个均线排列形态,能够预判趋势目前是多头占上风的。而这个预判背后所支撑的逻辑,源于均线的排列方式。人们在长期使用均线这个指
标的过程中,通过总结经验和数据,认为均线的排列可以粗分为两种情况:多头排列和空头排列。多头排列就是市场趋势是强势上升势,均线在5—10—20
—
40—120K线下支撑排列向上为多头排列。我们先看一个简单的三均线多头排列形态。
从图可以看出,多头排列形态的判定标准是:短期均线依次在长期均线之上,因此股价有较好的支撑。说的再简单一些,如果把均线理解为买入成本的平均
值,均线排列依次短期线、中期线、长期线由上而下依次排列,这说明我们过去买进的成本很低,做短线的、中线的、长线的都有赚头,市场一片向上均线
多头排列趋势为强势上升势,操作思维为多头思维。
回踩点又是什么含义呢?很简单,就是价格前期冲高后出现了小幅回调下行。值得注意的是,在这个策略中,回踩是有条件的,即回踩幅度并没有破坏均线
多头排列的格局。在这种情况下,由于每一条不同周期的均线都是支撑,所以回撤往往成为一个较理想的进场点位。假如某只股票,前期多头排列,但是回
踩之后,整体均线形态受到巨大破坏,那么这只股票就不符合我们的筛选条件了。
回踩点能够具体的量化,如果在多头排列的状态下当根K线击穿了10日均线,那么可以视作这根K线是一个回踩点,发出买入信号。咱们来看看2017年2月以
来贵州茅台(600519)的K线图上出现的几个多头趋势回踩点,现在看来,这几个回踩点都是绝好的回调买入机会。
多头排列回踩买入策略蕴含了投资过程中最重要的两个核心思想,一是选股,从3000只股票中选出目前走势符合多头排列的股票,因为这样的股票后市更有
上涨空间,如果某只股票有一波趋势,那么这种简单的选股法则并不会遗漏这只股票,就拿贵州茅台举例,这只“白马股”一路走牛,通过市盈率、市值等因
子很可能选不到这只股票,但是多头排列选股并不会错失这只股票。二是择时,当股票选出来以后,我们要择时买入,而回踩点正是一个绝好的时机进场。
交易系统
验证策略有效性需要通过在历史数据上进行客观准确的回测,我们先构建该策略完整交易系统:
1
. 股票池为所有沪深A股
. 均线周期选择为[5,10,20,40,120],短期均线值依次大于长期均线值
. 回踩点的定义为当根K线击穿10日均线,未击穿更长周期均线,并扔满足多头排列
. 买入股票数上限为100只,等权重买入,当持有股票数100只时,有股票卖出才买入股票
. 买入时机:多头策略回踩点的第二天开盘买入
. 卖出时机:当5日均线下穿40日均线,第二天开盘卖出
2
3
4
5
6
回测结果
以下为回测结果。回测时间为2010年年初到2017年4月,总收益68.75%,年化收益率为7.72%,是银行理财收益的2-3倍了,策略Sharpe值达到了3.32,已经
算比较不错的策略了,最大回撤主要发生在15年股灾期间,因此该策略最大的风险为股灾,当市场出现崩盘的时候,该策略会失效,因此使用该策略实盘一
定注意股灾,如果判断股灾来临,立马止损清仓,待市场企稳后再启动该策略,当然这样的话,因为减少了股灾期间的损失,年化收益肯定比7.72%要高出
一部分了。
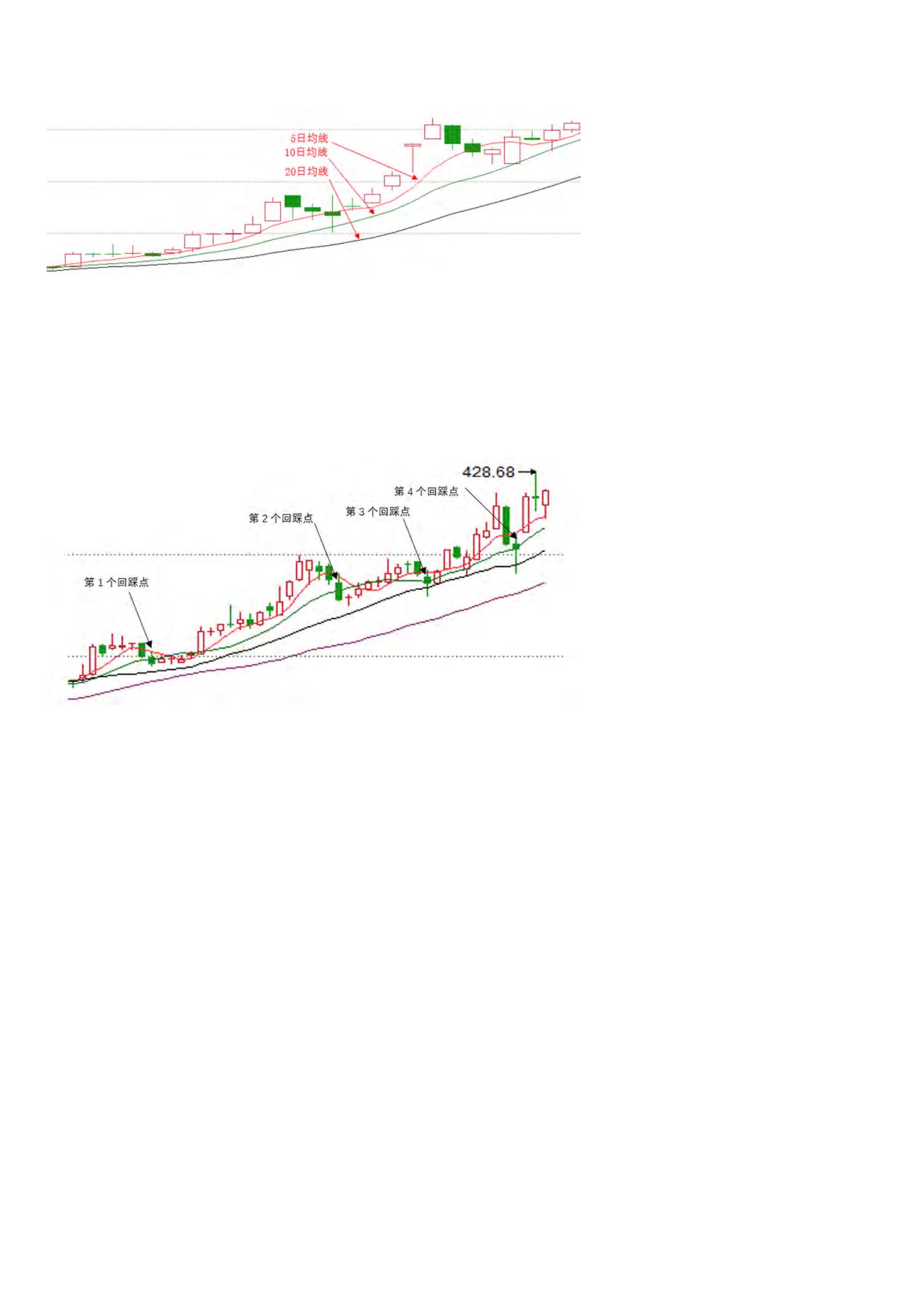
完整的策略如下,大家可以 克隆到自己的账户进行研究。
In [13]:
start_date = '2010-01-01' # 开始日期
end_date = '2017-07-18' # 结束日期
#
获取股票列表
instruments = D.instruments(start_date, end_date)
In [14]:
#
加载原始数据
stock_raw_data = D.history_data(instruments, start_date, end_date, ['close','low'])
计算多个周期均线的函数
#
def ma_calculate(df):
ma_list = [5,10,20,40,120]
for ma_len in ma_list:
df['ma_'+str(ma_len)] = pd.rolling_mean(df['close'], ma_len)
return df
#
包含多个周期均线值的股票数据
stock_ma_data = stock_raw_data.groupby('instrument').apply(ma_calculate)
#
函数:求满足开仓条件的股票列表
def open_pos_con(df):
return list(df[(df['ma_5']>df['ma_10'])&(df['ma_10']>df['ma_20'])&(df['ma_20']>df['ma_40'])&(df['ma_40']>df['ma_120'])&(df['low']
#
函数:求满足平仓条件的股票列表
def close_pos_con(df):
return list(df[df['ma_5']<df['ma_40']].instrument)
#
每日买入股票的数据框
daily_stock_to_buy= stock_ma_data.groupby('date').apply(open_pos_con)
每日卖出股票的数据框
daily_stock_to_sell= stock_ma_data.groupby('date').apply(close_pos_con)
#
In [ ]:
In [15]:
#
策略比较参考标准,以沪深300为例
benchmark = '000300.INDX'
#
起始资金
capital_base = 1000000
#
#
策略主体函数
初始化虚拟账户状态,只在第一个交易日运行
def initialize(context):
设置手续费,买入时万3,卖出是千分之1.3,不足5元以5元计
#
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
context.num_stock = 100 # 最多同时持有100只股票
context.daily_stock_to_buy = daily_stock_to_buy # 符合买入条件的股票列表
context.daily_stock_to_sell = daily_stock_to_sell # 符合卖出条件的股票列表
#
策略交易逻辑,每个交易日运行一次
def handle_data(context, data):
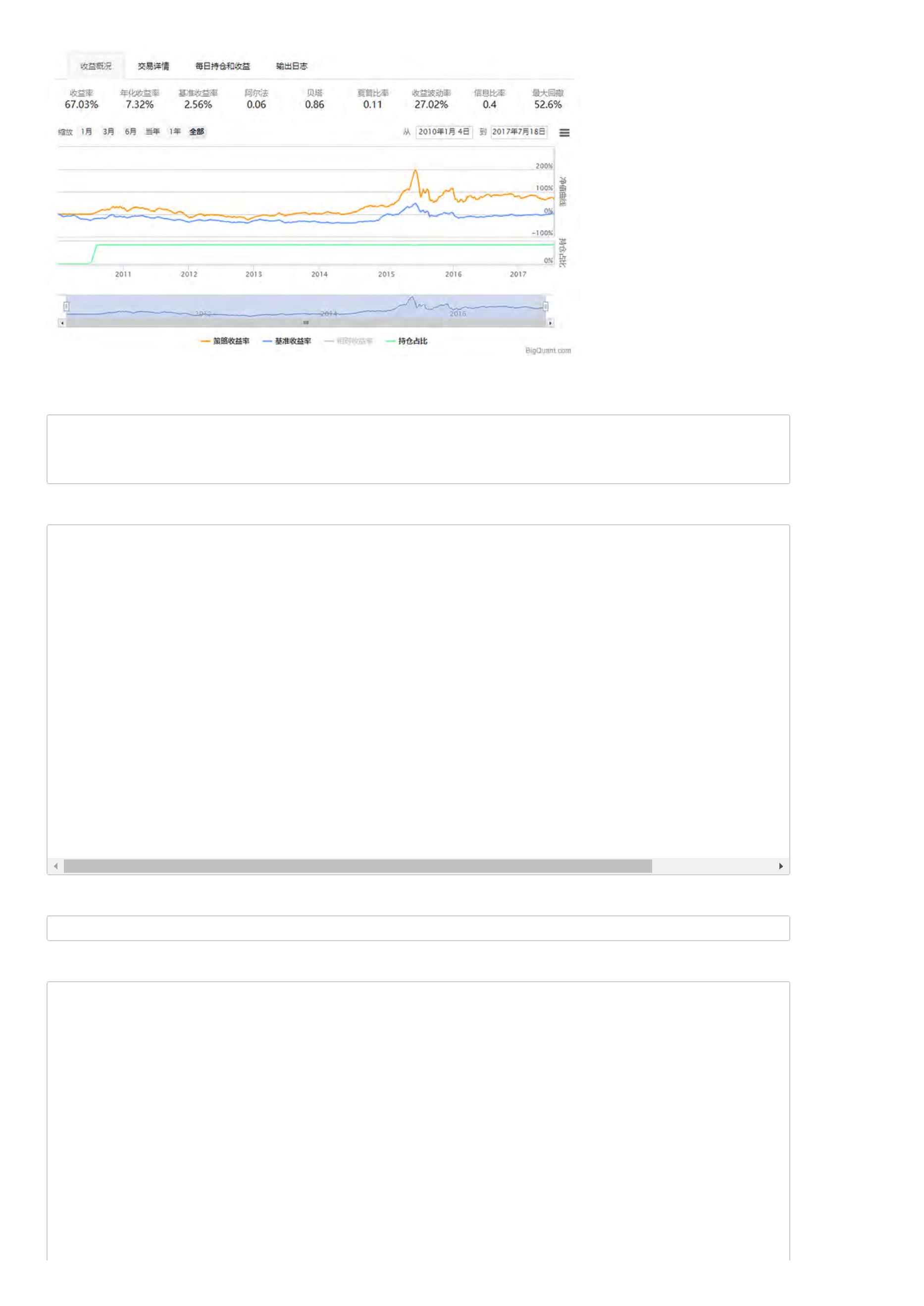
date = data.current_dt.strftime('%Y-%m-%d') # 日期
buy_stock = context.daily_stock_to_buy[date] # 当日符合买入条件的股票
sell_stock = context.daily_stock_to_sell[date] # 当日符合卖出条件的股票
weight = 1/context.num_stock
# 等权重配置
stock_hold_num = len(context.portfolio.positions) # 目前持有的股票数量
remain_num = context.num_stock - stock_hold_num # 还可以买入的股票数量,需要把卖出的股票加回来
#
初始化当日买入订单的数量为0
order_count = 0
买入股票
for i in buy_stock:
#
#
如果发送买入订单的股票数量已经超过了还可以买入的股票数量,那么应退出for循环
if order_count >= remain_num:
break
#
对于没有买入的股票且可以交易的股票,应买入
if context.portfolio.positions[i].amount == 0 and data.can_trade(context.symbol(i)):
order_target_percent(context.symbol(i), weight)
order_count += 1 # 统计一下当天股票买入数量
#
卖出股票
for j in sell_stock:
if context.portfolio.positions[j].amount > 0 and data.can_trade(context.symbol(j)):
order_target_percent(context.symbol(j), 0)
#
#
启动回测
策略回测接口: https://bigquant.com/docs/strategy_backtest.html
m = M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,
initialize=initialize,
handle_data=handle_data,
#
买入订单以开盘价成交
order_price_field_buy='open',
卖出订单以开盘价成交
#
order_price_field_sell='open',
capital_base=capital_base,
benchmark=benchmark,
)
[
[
[
[
2017-07-19 10:10:58.828482] INFO: bigquant: backtest.v7 start ..
2017-07-19 10:12:17.223008] INFO: Performance: Simulated 1831 trading days out of 1831.
2017-07-19 10:12:17.224045] INFO: Performance: first open: 2010-01-04 14:30:00+00:00
2017-07-19 10:12:17.224851] INFO: Performance: last close: 2017-07-18 19:00:00+00:00
[
2017-07-19 10:12:23.880429] INFO: bigquant: backtest.v7 end [85.051927s].
[
量化学堂-策略开发]借助talib 使用技术分析指标来炒股
什么是技术分析
所谓股票的技术分析,是相对于基本面分析而言的。基本分析法着重于对一般经济情况以及各个公司的经营管理状况、行业动态等因素进行分析,以此来研
究股票的价值,衡量股价的高低。而技术分析则是透过图表或技术指标的记录,研究市场过去及现在的行为反应,以推测未来价格的变动趋势。其依据的技
术指标的主要内容是由股价、成交量或涨跌指数等数据计算而得的,技术分析只关心证券市场本身的变化,而不考虑会对其产生某种影响的经济方面、政治
方面的等各种外部的因素。
什么是talib
talib的简称是Technical Analysis Library,主要功能是计算股价的技术分析指标。先简单看看talib都给我们提供了那些计算技术指标的函数,按技术指标的类
型示例如下:
函数名:CDL2CROWS
名称:Two Crows 两只乌鸦
简介:三日K线模式,第一天长阳,第二天高开收阴,第三天再次高开继续收阴,收盘比前一日收盘价低,预示股价下跌。
例子:integer = CDL2CROWS(open, high, low, close)
函数名:CDL3STARSINSOUTH
名称:Three Stars In The South 南方三星
简介:三日K线模式,与大敌当前相反,三日K线皆阴,第一日有长下影线,第二日与第一日类似,K线整体小于第一日,第三日无下影线实体信号,成交价
格都在第一日振幅之内,预示下跌趋势反转,股价上升。
例子:integer = CDL3STARSINSOUTH(open, high, low, close)
函数名 : MA
名称:Moving average 移动平均值
简介:移动平均值是在一定范围内的价格平均值
例子:ma = MA(close, timeperiod=30, matype=0)

函数名:ADX
名称:Average Directional Movement Index 平均趋向指数
简介:ADX指数是反映趋向变动的程度,而不是方向的本身。
例子:adx = ADX(high, low, close, timeperiod=14)
函数名:ATR
名称:Average True Range 平均真实波幅
简介:主要用来衡量价格的波动。因此,这一技术指标并不能直接反映价格走向及其趋势稳定性,而只是表明价格波动的程度。
例子:atr = ATR(high, low, close, timeperiod=14)
函数名:OBV
名称:On Balance Volume 能量潮
简介:通过统计成交量变动的趋势推测股价趋势
计算公式:以某日为基期,逐日累计每日上市股票总成交量,若隔日指数或股票上涨,则基期OBV加上本日成交量为本日OBV。隔日指数或股票下跌,则基
期OBV减去本日成交量为本日OBV
例子:obv = OBV(close, volume)
由于篇幅有限,技术分析指标不能在此充分介绍,可以参考talib官方文档
如何使用:MA实例
已知MA这个函数的调用方式为:ma = MA(close, timeperiod=30, matype=0)
close表示收盘价序列,timeperiod指定义好均线的计算长度即几日均线,不输入的话,默认为30日, matype可以默认不用输入,然后就可以得到均线
的值
因此简单来讲,只取获取收盘价,就可以轻松计算移动平均值
下面以平安银行(000001.SZA)为例进行说明:
#
获取数据
df = D.history_data(['000001.SZA'],'2015-12-01','2016-02-20',
fields=['date','close']).set_index('date')
#
通过rolling_mean函数计算移动平均值(方法1)
df['MA10_rolling'] = pd.rolling_mean(df['close'],10)
将价格数据转化成float类型
close = [float(x) for x in df['close']]
通过talib计算移动平均值(方法2)
df['MA10_talib'] = talib.MA(np.array(close), timeperiod=10)
检查两种方法计算结果是否一致
#
#
#
df.tail(12)
计算结果如下所示:
我们就这样跟方便的计算出了移动平均线的值,接下来我们计算下稍微复杂一点的EMA和MACD
#
调用talib计算6日指数移动平均线的值
df['EMA12'] = talib.EMA(np.array(close), timeperiod=6)
df['EMA26'] = talib.EMA(np.array(close), timeperiod=12)
#
调用talib计算MACD指标
df['MACD'],df['MACDsignal'],df['MACDhist'] = talib.MACD(np.array(close),
fastperiod=6, slowperiod=12, signalperiod=9)
df.tail(12)
close
timeperiod
EMA
fastperiod
EMA
slowperiod
EMA
signalperiod DEA

可以看到,talib模块可以很方便地帮助我们计算技术分析指标。
4
.策略实战:MACD策略
当macd下穿signal时,卖出股票
当macd上穿signal时,买入股票
完整的策略我贴在下面,小伙伴们赶紧 克隆下面的策略练手吧
技术分析指标策略: 基于MACD指标¶
1
. 策略参数¶
In [13]:
import talib
instruments = ['000651.SZA'] #以格力电器为例
start_date = '2010-09-16'# 起始时间
end_date = '2017-07-18' # 结束时间
2
. 策略主体¶
In [14]:
def initialize(context):
context.set_commission(PerDollar(0.0015)) # 手续费设置
# 需要设置计算MACD的相关参数参数
context.short = 12
context.long = 26
context.smoothperiod = 9
context.observation = 100
def handle_data(context, data):
if context.trading_day_index < 100: # 在100个交易日以后才开始真正运行
return
sid = context.symbol(instruments[0])
#
获取价格数据
prices = data.history(sid, 'price', context.observation, '1d')
用Talib计算MACD取值,得到三个时间序列数组,分别为macd, signal 和 hist
#
macd, signal, hist = talib.MACD(np.array(prices), context.short,
context.long, context.smoothperiod)
#
计算现在portfolio中股票的仓位
cur_position = context.portfolio.positions[sid].amount
#
#
策略逻辑
卖出逻辑 macd下穿signal
if macd[-1] - signal[-1] < 0 and macd[-2] - signal[-2] > 0:
#
进行清仓
if cur_position > 0 and data.can_trade(sid):
context.order_target_value(sid, 0)
#
买入逻辑 macd上穿signal
if macd[-1] - signal[-1] > 0 and macd[-2] - signal[-2] < 0:
#
买入股票
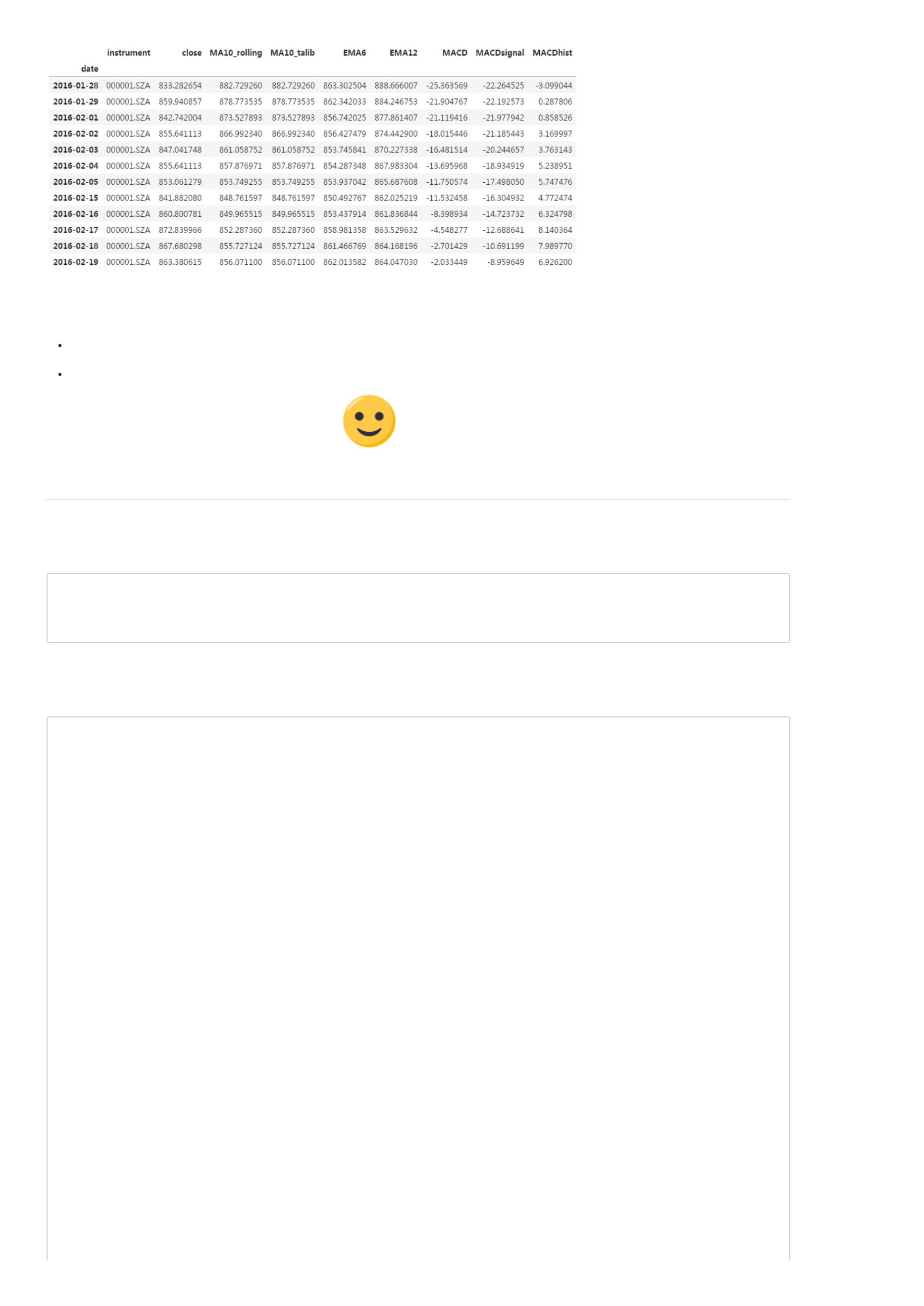
if cur_position == 0 and data.can_trade(sid):
context.order_target_percent(sid, 1)
3
. 回测接口¶
In [15]:
m=M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='open',
capital_base=float("1.0e6"),
benchmark='000300.INDX',
)
[
[
2017-07-19 10:35:47.762957] INFO: bigquant: backtest.v7 start ..
2017-07-19 10:35:47.765690] INFO: bigquant: hit cache
[
2017-07-19 10:35:49.985184] INFO: bigquant: backtest.v7 end [2.222251s].
[
量化学堂-策略开发]大师系列之价值投资法
国外证券市场比较悠久,曾出现过本杰明·格雷厄姆、彼得·林奇、詹姆斯·奥肖内西、查尔斯·布兰德斯等多位投资大师,这些投资大师有一个共同点,他们在
证券市场上保持了常年的稳定持续盈利,他们的投资法则及选股标准在一些著作中有详细的描述。值得欣慰的是,申万宏源证券研究所发布了<申万宏源-申
万大师系列价值投资篇>系列第一季共20篇研究报告。学习这些报告主要有两个目的:
一是我们自身想去认真的学习经典,复制这些策略本身就是自我学习过程,我们深信向这些被市场证明长期优秀,被后世尊为经典的投资大师学习,必然值
得,必有所得;
二是复制和验证大师策略的过程, 会自然的驱使我们更多的从投资逻辑和投资思维上思考收益之源,而不再是不停的数据挖掘和数理分析。大师系列的尝
试,于我们是一个求道,而非求术的旅程。
本贴主要是帮助用户怎样开发大师系列的策略,让大家更了解我们的平台,同时帮助大家在我们的平台上开发更丰富的策略。因此我们介绍一种简单的价值
投资法来选取股票,规则如下:
策略逻辑:当股票处于价值洼地时,具备投资价值
策略内容:每月月初买入市盈率小于15倍、市净率小于1.5倍的30只股票,持有至下个月月初再调仓
资金管理:等权重买入
风险控制:无单只股票仓位上限控制、无止盈止损
第一步:获取数据
BigQuant平台具有丰富的金融数据,包括行情数据和财报数据,并且具有便捷、简单的API调用接口。获取数据的代码如下:
start_date = '2013-02-01'
end_date = '2017-07-18'
instruments = D.instruments()
#
获取市盈率、市净率、成交额数据
history_data = D.history_data(instruments, start_date=start_date,
end_date= end_date, fields=[ 'pb_lf', 'pe_ttm','amount'])
在上面的代码中,history_data是我们平台获取数据的一个重要API。fields参数为列表形式,传入的列表即为我们想要获取的数据。
第二步:整理买入股票列表
#
该函数的目的是通过history_data这个大的原始数据,获取每日满足价值投资股票列表
def seek_symbol(df):
selected = df[(df['pb_lf'] < 1.5)
&
&
&
&
(df['pe_ttm'] < 15)
(df['amount'] > 0)
(df['pb_lf'] > 0)
(df['pe_ttm'] > 0 ) ]
#
按pe_ttm和pb_lf 升序排列
selected = selected.sort_values(['pe_ttm','pb_lf'])
return list(selected.instrument)[:30] # 记得转化成list
daily_buy_stock = history_data.groupby('date').apply(seek_symbol)

第三步:回测主体
我们平台策略回测有丰富的文档介绍,请参考:
def initialize(context):
#
设置交易费用,买入是万三,卖出是千分之1.3,如果不足5元按5元算
context.set_commission(PerOrder(buy_cost=0.0003,
sell_cost=0.0013, min_cost=5))
#
设置换仓规则,即每个月月初换仓,持有至下个月,再换仓
context.schedule_function(rebalance,
date_rule=date_rules.month_start(days_offset=0))
#
上面schedule_function函数的这句代码,其实可以写到一行,分两行是为了便于展示
def handle_data(context,data):
pass
#
换仓
def rebalance(context, data):
日期
date = data.current_dt.strftime('%Y-%m-%d')
#
#
买入股票列表
stock_to_buy = daily_buy_stock[date]
目前持仓列表
stock_hold_now = [equity.symbol for equity
in context.portfolio.positions]
#
#
继续持有股票列表
no_need_to_sell = [i for i in stock_hold_now
if i in stock_to_buy]
#
卖出股票列表
stock_to_sell = [i for i in stock_hold_now if
i not in no_need_to_sell]
#
执行卖出
for stock in stock_to_sell:
if data.can_trade(context.symbol(stock)):
context.order_target_percent(context.symbol(stock), 0)
if len(stock_to_buy) == 0:
return
#
等权重
weight = 1 / len(stock_to_buy)
执行买入
#
for cp in stock_to_buy:
if data.can_trade(context.symbol(cp)):
context.order_target_percent(context.symbol(cp), weight)
第四步:回测接口
#
使用第四版的回测接口,需要传入多个策略参数
m=M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,
#
必须传入initialize,只在第一天运行
initialize=initialize,
必须传入handle_data,每个交易日都会运行
handle_data=handle_data,
买入以开盘价成交
order_price_field_buy='open',
卖出也以开盘价成交
order_price_field_sell='open',
策略本金
capital_base=1000000,
比较基准:沪深300
benchmark='000300.INDX',
#
#
#
#
#
)
好嘞,策略就完全写好了。我们运行完曲线如下:

整体来看,该策略算得上是正收益系统策略。
是不是发现我们平台很方便开发策略?之前朋友问我,为什么Python运行速度不是最快但会成为量化的主流语言。其实对于量化研究人员来说,虽然速度是
一方面考虑,但更多的是为了验证策略思想,Python语言的优势就是在此,有一个思想就可以很快的将思想验证,然而C++虽然速度快,但要验证一个简单
的思想却要编写大量的代码。好比为什么飞机速度快,但市里面上班开汽车就足够了(不考虑其他因素),因为汽车足够灵活。所以,还在犹豫选择什么语
言从事量化投资的小伙伴们,Python就是你比较好的选择。本文到此就要结束了,策略的完整代码分享在文末,小伙伴们赶紧 克隆策略吧。
1
.获取数据¶
In [21]:
start_date = '2013-02-01' # 开始日期
end_date = '2017-07-18' # 结束日期
instruments = D.instruments()
#
获取市盈率、市净率、成交额数据
history_data = D.history_data(instruments, start_date=start_date,
end_date= end_date, fields=[ 'pb_lf', 'pe_ttm','amount'])
2
.整理换仓时买入股票列表¶
In [22]:
#
该函数的目的是通过history_data这个大的原始数据,获取每日满足价值投资股票列表
def seek_symbol(df):
selected = df[(df['pb_lf'] < 1.5)
&
&
&
&
(df['pe_ttm'] < 15)
(df['amount'] > 0)
(df['pb_lf'] > 0)
(df['pe_ttm'] > 0 ) ]
#
按pe_ttm和pb_lf 升序排列
selected = selected.sort_values(['pe_ttm','pb_lf'])
return list(selected.instrument)[:30] # 记得转化成list
daily_buy_stock = history_data.groupby('date').apply(seek_symbol)
3
. 回测主体¶
In [23]:
def initialize(context):
设置交易费用,买入是万三,卖出是千分之1.3,如果不足5元按5元算
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
设置换仓规则,即每个月月初换仓,持有至下个月,再换仓
context.schedule_function(rebalance, date_rule=date_rules.month_start(days_offset=0))
上面schedule_function函数的这句代码,其实可以写到一行,分两行是为了便于展示
#
#
#
def handle_data(context,data):
pass
#
换仓
def rebalance(context, data):
日期
date = data.current_dt.strftime('%Y-%m-%d')
#
#
买入股票列表
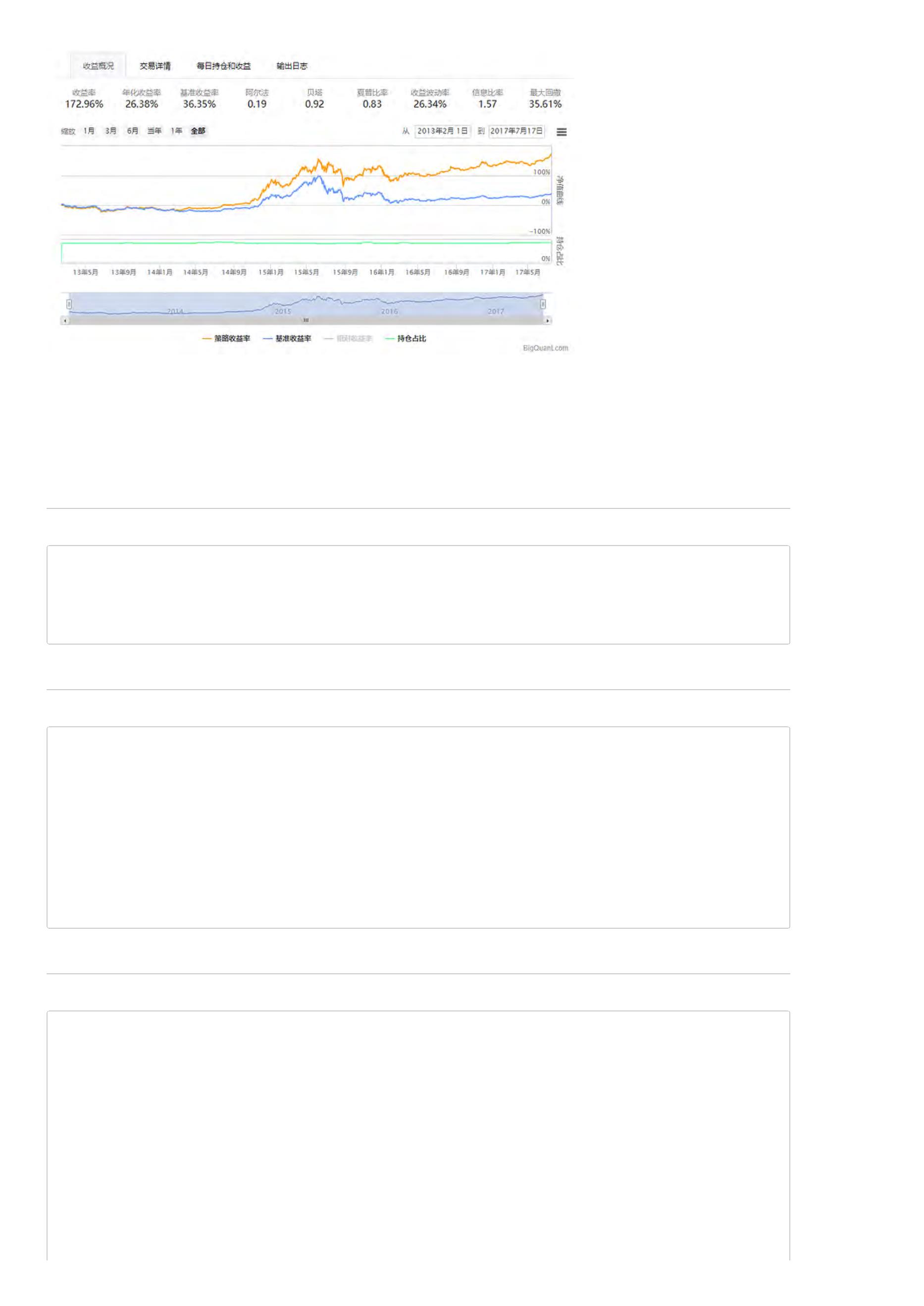
stock_to_buy = daily_buy_stock.ix[date]
目前持仓列表
stock_hold_now = [equity.symbol for equity
in context.portfolio.positions]
#
#
继续持有股票列表
no_need_to_sell = [i for i in stock_hold_now
if i in stock_to_buy]
#
卖出股票列表
stock_to_sell = [i for i in stock_hold_now if
i not in no_need_to_sell]
#
执行卖出
for stock in stock_to_sell:
if data.can_trade(context.symbol(stock)):
context.order_target_percent(context.symbol(stock), 0)
if len(stock_to_buy) == 0:
return
#
等权重
weight = 1 / len(stock_to_buy)
执行买入
#
for cp in stock_to_buy:
if data.can_trade(context.symbol(cp)):
context.order_target_percent(context.symbol(cp), weight)
4
.回测接口¶
In [24]:
#
使用该回测接口,需要传入多个策略参数
m=M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,
#
必须传入initialize,只在第一天运行
initialize=initialize,
必须传入handle_data,每个交易日都会运行
handle_data=handle_data,
买入以开盘价成交
order_price_field_buy='open',
卖出也以开盘价成交
order_price_field_sell='open',
策略本金
capital_base=1000000,
比较基准:沪深300
#
#
#
#
#
benchmark='000300.INDX',
)
[
[
[
[
2017-07-19 10:40:19.311175] INFO: bigquant: backtest.v7 start ..
2017-07-19 10:40:56.409711] INFO: Performance: Simulated 1082 trading days out of 1082.
2017-07-19 10:40:56.410899] INFO: Performance: first open: 2013-02-01 14:30:00+00:00
2017-07-19 10:40:56.411845] INFO: Performance: last close: 2017-07-18 19:00:00+00:00
[
2017-07-19 10:41:00.164708] INFO: bigquant: backtest.v7 end [40.853501s].
[
量化学堂-策略开发]事件驱动策略(基于业绩快报)
事件驱动(Event Driven)属于量化投资之中的一个重要类别,涵盖投资机会广泛。广义上说,市场上任何发生的有可能与股票市场相关的新闻、事件、公
告均有可能成为事件驱动的投资机会。 目前我国业界事件驱动策略中包括的常用重大事件有:业绩预告、业绩快报、分红送转、大股东增减持、高管增减
持、定向增发、限售股解禁、股权激励、重组并购、ST摘和评级上调等,如下图所示。

可以看出,目前市场经过验证有效的事件已经不少,涵盖了影响股票价格的多个方面。事件驱动策略由于其策略逻辑的独特性,因此与其他常规股票策略相
关性很低,再加上事件众多,资金容量大这一特点,使得事件驱动策略成为国外对冲基金非常大类的投资策略。
BigQuant回测引擎能够快速验证事件的有效性,从而开发事件驱动策略。为方便小伙伴顺利开发事件驱动策略,本文以业绩快报中净利润大幅增长为事件,
验证该事件是否可以带来超额收益,未来我们会发布更多的基于其他事件的策略,敬请耐心等待。
在回测之前,我们先看策略的完整介绍:
策略逻辑:认为业绩快报中净利润大幅增长为利好消息,会导致价格在一定期限内上涨
事件定义:当业绩快报中公布净利润同比增增长超过30%
股票持有不超过50只,仅当持有数量小于50只时,才买入股票
持有时间:40个交易日
我们的策略流程是:每日更新数据,查看当日发布财务报表并且(归属母公司)净利润季度同比增长率超过30%的公司,如果出现这样的事件,就买入该股
票。因此这里的分析和"选股系列"以及"大师系列"的策略依然相似,大家可以结合来看。
策略回测结果为:
从测试结果来看,该事件驱动策略为长期正收益系统。因为财报公布事件会有一个期限规定(年度报告是每年结束后4个月内,半年度是上半年结束后2个月
内,季度报告是季度结束后1个月内),所以某些时间段不会有公司公布财务报表,当然那段时间就不会出现业绩快报净利润大幅增长的事件,因此仓位很多
时候并不是100%。
8
想要查看完整策略,点击 克隆策略一键搞定。
事件驱动策略:基于业绩快报¶
In [6]:
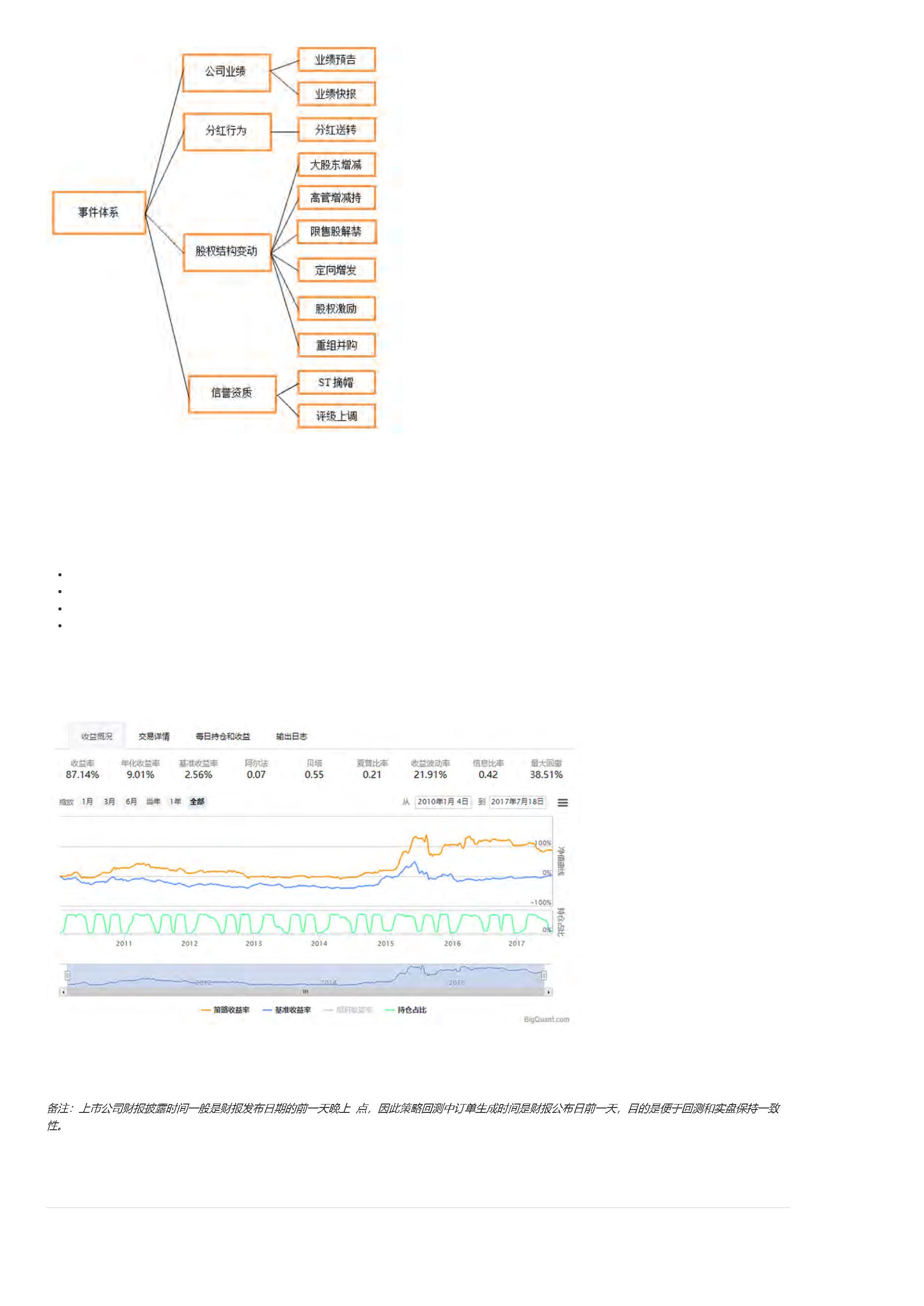
instruments = D.instruments()
start_date = '2010-01-01'
end_date = '2017-07-18'
#
获取数据
data = D.financial_statements(instruments, start_date, end_date,
fields=['instrument','fs_publish_date','fs_quarter_year',
'
fs_quarter_index','fs_net_profit_yoy'])
选择净利润同比增长率大于30%的股票
selected = data[data['fs_net_profit_yoy'] > 30]
#
In [7]:
#
获取交易日历
date = D.trading_days(start_date=start_date,end_date=end_date)
将日期型格式转化为字符型格式
date = date['date'].apply(lambda x : x.strftime('%Y-%m-%d'))
为尽量接近实盘,事件日期应为财报公布日的前一天
#
#
publish_date = date.shift(-1)
shift = dict(zip(date, publish_date))
In [8]:
#
建立事件表
event = {}
for dt in date:
if type(shift[dt]) is str:
event[dt] = list(selected[selected['fs_publish_date'] == shift[dt]].sort_values(
fs_net_profit_yoy',ascending=False ).instrument)
'
else:
event[dt] = []
策略回测主体¶
In [9]:
def initialize(context):
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
context.daily_buy_stock = event
context.hold_periods = 40 # 持有40天,固定持仓期
context.stock_max_num = 50 # 最大持仓数量为50只
context.hold_days = {}
def handle_data(context,data):
date = data.current_dt.strftime('%Y-%m-%d') # 日期
#
目前仓位里面的股票列表
equities = {e.symbol: e for e, p in context.perf_tracker.position_tracker.positions.items()}
for k in equities.keys():
#
如果持仓时间大于40天
if context.trading_day_index - context.hold_days[k] >= context.hold_periods \
and data.can_trade(context.symbol(k)):
#
卖完
context.order_target_percent(context.symbol(k),0)
#
还允许建仓的股票数目
stock_can_buy_num = context.stock_max_num - len(equities)
获取当日买入股票的代码
stock_to_buy = context.daily_buy_stock[date][:stock_can_buy_num]
#
#
等权重买入
weight = 1 / context.stock_max_num
#
买入
for stock in stock_to_buy:
if data.can_trade(context.symbol(stock)):
context.order_target_percent(context.symbol(stock), weight)
#
记录建仓时间的日期索引
context.hold_days[stock] = context.trading_day_index
回测接口¶
In [10]:
m=M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='open',
capital_base=1000000,
benchmark='000300.INDX',
)
[
[
[
[
2017-07-19 10:44:36.208018] INFO: bigquant: backtest.v7 start ..
2017-07-19 10:45:30.161025] INFO: Performance: Simulated 1831 trading days out of 1831.
2017-07-19 10:45:30.162282] INFO: Performance: first open: 2010-01-04 14:30:00+00:00
2017-07-19 10:45:30.163409] INFO: Performance: last close: 2017-07-18 19:00:00+00:00
[
2017-07-19 10:45:36.257471] INFO: bigquant: backtest.v7 end [60.049397s].
参考文献:
1
2
3
4
.“事件驱动策略在国内能不能行得通?” 知乎回答
.“全面解析对冲基金事件驱动策略” 上海交大 陈欣
.事件驱动策略系列研报 广发证券
.事件驱动策略系列研报 长江证券
[
量化学堂-策略开发]使用cvxopt 包实现马科维茨投资组合优化:以一个股票策略为例
介绍¶
在这篇文章中,你将了解Markowitz投资组合优化的基本思想,以及如何在Python中实现。然后,我们将展示如何创建一个简单的策略回测,以Markowitz最
佳方式重新平衡其投资组合,对各个资产的权重进行调整。
文章开始,我们将使用随机数据而不是实际的股票数据,这将有助于你了解如何通过建模和模拟来提高你对Markowitz均值方差模型的理解。
cvxopt是一个求解最优化问题的Python包,在数值计算、运筹学、规划问题中有广泛的运用。目前已经在BigQuant策略研究平台上,你可以直接使用。
我们先从导入模块开始
模拟¶
In [29]:
import numpy as np
import matplotlib.pyplot as plt
import cvxopt as opt
from cvxopt import blas, solvers
import pandas as pd
np.random.seed(123)
#
关掉进度展示,进度展示是运行过程进度的一个打印输出,可以通过其查看代码运行进度
solvers.options['show_progress'] = False
假设我们有4个资产,每个资产的收益率序列长度为1000,即1000个交易日.我们可以使用numpy.random.randn从正态分布中抽样。
In [30]:
#
# N资产数量
n_assets = 4
#
# 收益率长度
n_obs = 1000
return_vec = np.random.randn(n_assets, n_obs)
In [31]:
plt.plot(return_vec.T, alpha=.4);
plt.xlabel('time')
plt.ylabel('returns')
Out[31]:
<
matplotlib.text.Text at 0x7f95efd8b780>
这些收益率序列可用于创建广泛的投资组合,这些投资组合都有不同的收益和风险(标准差)。 我们可以生成大量的随机权重向量并绘制这些投资组合。
一个权重向量对应一个投资组合。

In [32]:
#
产生随机权重的函数
def rand_weights(n):
'
'' Produces n random weights that sum to 1 '''
k = np.random.rand(n)
return k / sum(k)
print(rand_weights(n_assets))
print(rand_weights(n_assets))
[
[
0.54066805 0.2360283
0.11660484 0.1066988 ]
0.27638339 0.03006307 0.47850085 0.21505269]
接下来,让我们评估这些随机投资组合将表现如何。 为了实现这一目标,我们计算收益率和波动率(这里我们使用标准差)。 这里,我们设置了一个过滤
器,只允许绘制标准偏差<2的投资组合,以便更好地展示说明。
In [33]:
#
返回组合收益率和波动性
def random_portfolio(returns):
p = np.asmatrix(np.mean(returns, axis=1))
w = np.asmatrix(rand_weights(returns.shape[0]))
C = np.asmatrix(np.cov(returns))
mu = w * p.T
sigma = np.sqrt(w * C * w.T)
#
过滤器
if sigma > 2:
return random_portfolio(returns)
return mu, sigma
在代码中计算投资组合收益率的公式为:
其中$R$是预期收益率,$p^T$是每个时间序列收益率所形成的列向量的转置,w是投资组合的权重向量。$p$是N×1列向量,所以$p^T$变成1×N行向量,其
可以与N×1权重(列)向量w相乘以给出一个标量(数值)。
我们计算投资组合波动性的公式为:
其中$C$是为N×N矩阵的协方差矩阵。 在协方差矩阵中,对角线的值代表每个资产的波动性(方差),而其他位置的值代表了资产之间的协方差。
让我们产生500个随机投资组合,并输出每个组合的收益率和波动率
In [34]:
n_portfolios = 500
means, stds = np.column_stack([
random_portfolio(return_vec)
for _ in range(n_portfolios)
]
)
In [35]:
plt.plot(stds, means, 'o', markersize=5)
plt.xlabel('std') # 标准差-波动性
plt.ylabel('mean') # 平均值-收益率
plt.title('Mean and standard deviation of returns of randomly generated portfolios') # 每个投资组合的收益率和波动性的散点图
Out[35]:
<
matplotlib.text.Text at 0x7f95effcd0b8>
这幅图是金融工程学里面可以说是最重要的一副图,横轴是波动率,纵轴是收益率。这个散点图中的每一个散点表示了一个投资组合(权重向量不一样),
由于其形状类似子弹,所以又被称为子弹图。因为我们追求的组合有两个标准:相同的收益下,波动性最小;相同的波动性下,收益最高,因此越靠近左上
角的资产组合其实是越优的,从下文可以看出,那是有效前沿。于是本文最重要的问题出来了,在给定多个资产历史数据的条件下,我们如何确定组合权
重?这不得不引出马科维茨优化和有效前沿。
马科维茨优化和有效前沿¶
如何获取一个既定收益下风险(波动性)最低的投资组合?于是就转化成这样一个最优化问题:
优化问题描述:
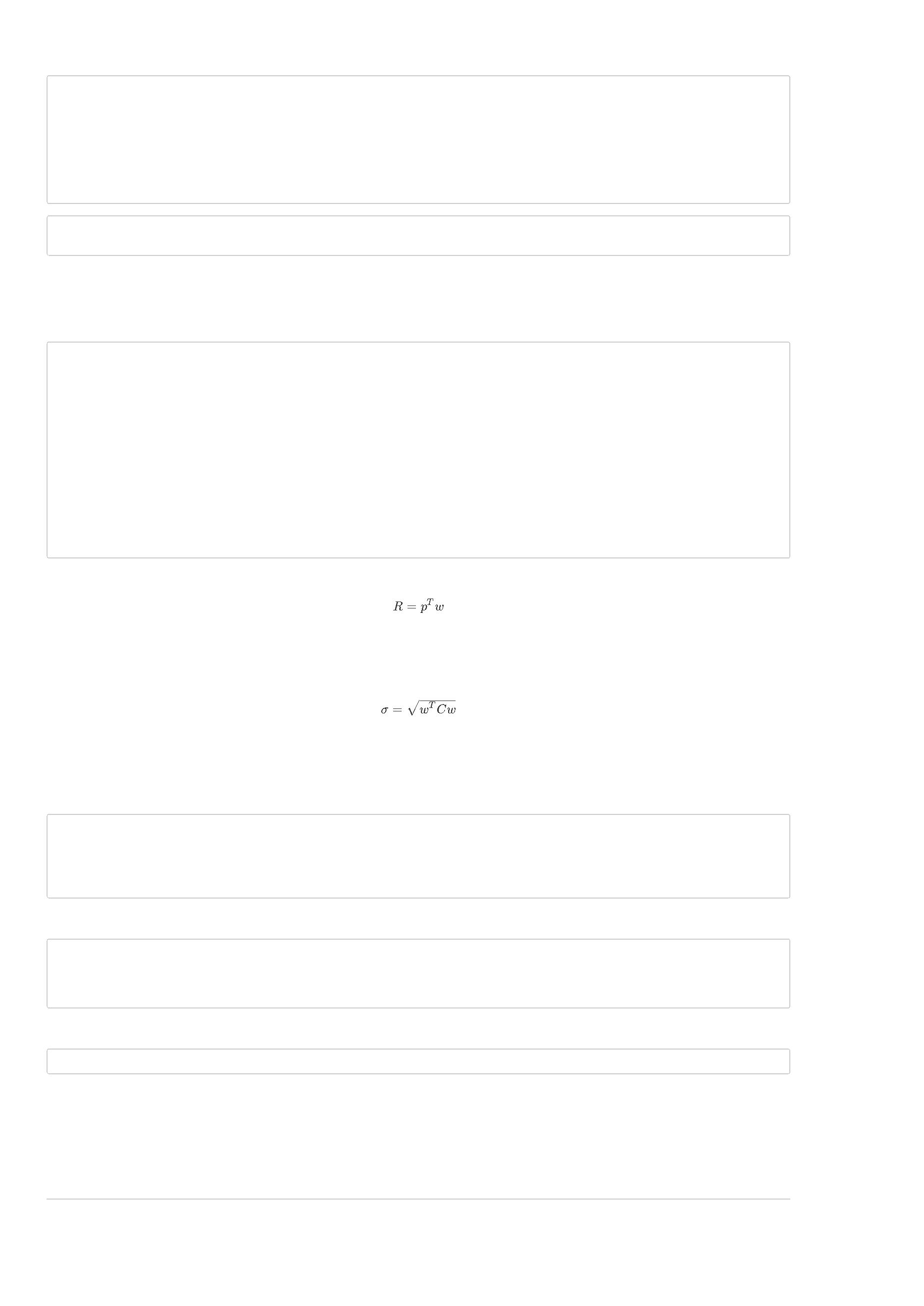
目标函数(求风险最小值):
约束条件(既定收益且权重之和为1):
输出结果(返回一个权重向量): $w$
In [36]:
def optimal_portfolio(returns):
n = len(returns)
returns = np.asmatrix(returns)
N = 100
mus = [10**(5.0 * t/N - 1.0) for t in range(N)]
#
转化为cvxopt matrices
S = opt.matrix(np.cov(returns))
pbar = opt.matrix(np.mean(returns, axis=1))
#
约束条件
G = -opt.matrix(np.eye(n))
h = opt.matrix(0.0, (n ,1))
A = opt.matrix(1.0, (1, n))
b = opt.matrix(1.0)
# opt默认是求最大值,因此要求最小化问题,还得乘以一个负号
#
使用凸优化计算有效前沿
portfolios = [solvers.qp(mu*S, -pbar, G, h, A, b)['x']
for mu in mus]
#
# 计算有效前沿的收益率和风险
returns = [blas.dot(pbar, x) for x in portfolios]
risks = [np.sqrt(blas.dot(x, S*x)) for x in portfolios]
m1 = np.polyfit(returns, risks, 2)
x1 = np.sqrt(m1[2] / m1[0])
#
计算最优组合
wt = solvers.qp(opt.matrix(x1 * S), -pbar, G, h, A, b)['x']
return np.asarray(wt), returns, risks
weights, returns, risks = optimal_portfolio(return_vec)
plt.plot(stds, means, 'o')
plt.ylabel('mean')
plt.xlabel('std')
plt.plot(risks, returns, 'y-o')
Out[36]:
[
<matplotlib.lines.Line2D at 0x7f95efffc2e8>]
上图,靠近左上角的黄色线条描绘了有效前沿,我们在确定组合的时候,当然是选这些黄色的点所代表的组合了。从有效前沿可以看出投资的一个定理:风
险与收益基本成正比。
通过上面函数,我们可以立马知道最优组合为:
In [37]:
print('最优组合' ,weights)
最优组合 [[ 2.77880107e-09]
[
[
[
3.20322848e-06]
1.54301198e-06]
9.99995251e-01]]
在真实股票市场的回测¶
上面的例子特别有趣但不是很适用。 接下来,我们将演示如何在BigQuant中创建一个策略。
本实验的目的是验证在一个买入固定5只股票的多头组合,利用马科维茨组合优化确定的投资组合是否比等权重的投资组合表现更好。
首先,使用BigQuant的D.history_data方法加载一些历史数据。
In [38]:

#
获取数据
start_date = '2012-02-01'
end_date = '2017-07-18'
instruments = ['000069.SZA', '002337.SZA','000333.SZA','000338.SZA','000100.SZA']
data = D.history_data(instruments,start_date,end_date,
fields=['close'])
#
整理数据
data = pd.pivot_table(data,values='close',index=['date'],columns=['instrument'])
T.plot(data)
In [39]:
def initialize(context):
context.days = 0
context.ins = instruments
def handle_data(context, data):
context.days += 1
if context.days < 100:
return
#
每60天调仓一次
if context.days % 30 != 0:
return
#
获取数据的时间窗口并计算收益率
prices = data.history(context.symbols(context.ins[0],context.ins[1],context.ins[2],context.ins[3],context.ins[4]), 'price',100, '
returns = prices.pct_change().dropna()
try:
#
马科维茨组合优化
weights, _, _ = optimal_portfolio(returns.T)
print(weights)
#
#
对持仓进行权重调整
for stock, weight in zip(prices.columns, weights):
if data.can_trade(stock):
order_target_percent(stock, weight[0])
except ValueError as e:
pass
使用马科维茨组合优化的投资组合的回测表现:
In [40]:
m=M.trade.v2(
instruments=instruments,
start_date='2014-01-01', # 在5只股票同时上市,并且满足100个交易日后,所以开始日期我们选择14年
end_date=end_date,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='open',
capital_base=100000,
benchmark='000300.INDX',
)
[
[
[
[
2017-07-19 10:51:48.113126] INFO: bigquant: backtest.v7 start ..
2017-07-19 10:51:53.991858] INFO: Performance: Simulated 864 trading days out of 864.
2017-07-19 10:51:53.992992] INFO: Performance: first open: 2014-01-02 14:30:00+00:00
2017-07-19 10:51:53.993795] INFO: Performance: last close: 2017-07-18 19:00:00+00:00
[
2017-07-19 10:51:56.328786] INFO: bigquant: backtest.v7 end [8.21565s].
In [41]:
def handle_data_1(context, data):
context.days += 1
weight = 1/len(context.ins)
if context.days == 1:
for stock in context.ins:
stock = context.symbol(stock)
if data.can_trade(stock):
order_target_percent(stock, weight)
直接等权重配置的投资组合的表现:

从两个对比实验,等权重组合的收益只有使用优化技术的组合的收益的三分之一。可以看出马科维茨投资组合优化理论可以帮助我们获得更好的表现。
In [42]:
m=M.trade.v2(
instruments=instruments,
start_date='2014-01-01',
end_date=end_date,
initialize=initialize,
handle_data=handle_data_1,
order_price_field_buy='open',
order_price_field_sell='open',
capital_base=100000,
benchmark='000300.INDX',
)
[
[
[
[
2017-07-19 10:51:56.363401] INFO: bigquant: backtest.v7 start ..
2017-07-19 10:51:59.402136] INFO: Performance: Simulated 864 trading days out of 864.
2017-07-19 10:51:59.403301] INFO: Performance: first open: 2014-01-02 14:30:00+00:00
2017-07-19 10:51:59.404255] INFO: Performance: last close: 2017-07-18 19:00:00+00:00
[
2017-07-19 10:52:01.914092] INFO: bigquant: backtest.v7 end [5.550661s].
[
量化学堂-策略开发]策略回测结果指标详解
$
Total \ Returns$ $ $ 策略总收益
策略最终股票和现金总价值
策略开始股票和现金总价值
$
Total \ Annualized \ Returns$ $ $ 策略年化收益
策略总收益
策略执行天数
$
Benchmark \ Returns $ $ $ 基准总收益
基准最终价值
基准开始价值
$
Benchmark \ Annualized \ Returns$ $ $ 基准年化收益
基准总收益
策略执行天数
$
Alpha$ $ 阿尔法$
投资中面临着系统性风险(即$Beta$)和非系统性风险(即$Alpha$ ),$Alpha$ 是投资者获得与市场波动无关的回报。比如投资者获得了15%的回报,其
基准获得了10%的回报,那么$Alpha$ 或者价值增值的部分就是5%。
策略年化收益率
基准年化收益率
无风险利率(默认
)
策略
值
$
Alpha$值 解释
$
\alpha>0$ 策略相对于市场,获得了超额收益
$
\alpha=0$ 策略相对于市场,获得了适当收益
$
\alpha<0$ 策略相对于市场,获得了较少收益
$
Beta$ $贝塔$

表示投资的系统性风险,反映了策略对大盘变化的敏感性。例如一个策略的$Beta$为1.5,则大盘涨1%的时候,策略可能涨1.5%,反之亦然;如果一个策略
的$Beta$为-1.5,说明大盘涨1%的时候,策略可能跌1.5%,反之亦然。
策略每日收益
基准每日收益
策略每日收益与基准每日收益的协方差
基准每日收益的方差
$
$
$
$
$
$
$
Beta$值 解释
\beta<0$ 投资组合和基准的走向通常反方向,如空头头寸类
\beta=0$ 投资组合和基准的走向没有相关性,如固定收益类
0<\beta<1$ 投资组合和基准的走向相同,但是比基准的移动幅度更小
\beta=1$ 投资组合和基准的走向相同,并且和基准的移动幅度贴近
\beta>1$ 投资组合和基准的走向相同,但是比基准的移动幅度更大
Sharpe$ $ 夏普比率$
表示每承受一单位总风险,会产生多少的超额报酬,可以同时对策略的收益与风险进行综合考虑。
策略年化收益率
无风险利率(默认
策略年化波动率
)
$
Information \ Ratio$ $信息比率$
衡量单位超额风险带来的超额收益。信息比率越大,说明该策略单位跟踪误差所获得的超额收益越高,因此,信息比率较大的策略的表现要优于信息比率较
低的基准。合理的投资目标应该是在承担适度风险下,尽可能追求高信息比率。
策略年化收益率
基准年化收益率
策略与基准每日收益差值的年化标准差
$
Daily \ \ Volatility \ \ 策略日收益率标准差$
策略每日收益率
策略每日收益率的平均值
策略执行天数
$
Volatility \ \ 波动率之间转化$
波动率按不同的时间框架划分为:年度波动率(年化)、月度波动率(月化)
注:一般策略波动率指的是年度波动率
策略日收益率标准差
策略日收益率标准差
$
Algorithm \ Volatility$ $策略波动率$
策略每日收益率的标准差的年化值,即年度波动率。用来测量策略的风险性,波动越大代表策略风险越高。
策略每日收益率

策略每日收益率的平均值
策略执行天数
$
Benchmark \ Volatility$ $基准波动率$
基准每日收益率的标准差的年化值。用来测量基准的风险性,波动越大代表基准风险越高。
基准每日收益率
基准每日收益率的平均值
基准执行天数
$
Max \ Drawdown$ $最大回撤$
描述策略可能出现的最糟糕的情况,最极端可能的亏损情况。
策略某日股票和现金的总价值,
[
量化学堂-策略开发]基于协整的配对交易
配对交易¶
相信很多同学都了解过 Pairs Trading,即配对交易策略。其基本原理就是找出两只走势相关的股票。这两只股票的价格差距从长期来看在一个固定的水平内
波动,如果价差暂时性的超过或低于这个水平,就买多价格偏低的股票,卖空价格偏高的股票。等到价差恢复正常水平时,进行平仓操作,赚取这一过程中
价差变化所产生的利润。
使用这个策略的关键就是“必须找到一对价格走势高度相关的股票”,而高度相关在这里意味着在长期来看有一个稳定的价差,这就要用到协整关系的检验。
在量化课堂介绍协整关系的文章里,我们知道如果用 $X_t$ 和 $Y_t$ 代表两支股票价格的时间序列,并且发现它们存在协整关系,那么便存在实数 $a$ 和
$
b$,并且线性组合 $Z_t=aX_t−bY_t$ 是一个(弱)平稳的序列。如果 $Z_t$ 的值较往常相比变得偏高,那么根据弱平稳性质,$Z_t$ 将回归均值,这时,应
该买入 $b$ 份 $Y$ 并卖出 $a$ 份 $X$,并在 $Z_t$ 回归时赚取差价。反之,如果 $Z_t$ 走势偏低,那么应该买入 $a$ 份 $X$ 卖出 $b$ 份 $Y$,等待
Z_t$ 上涨。所以,要使用配对交易,必须找到一对协整相关的股票。
$
协整关系的检验¶
我们想使用协整的特性进行配对交易,那么要怎么样发现协整关系呢?
在 Python 的 Statsmodels 包中,有直接用于协整关系检验的函数 coint,该函数包含于 statsmodels.tsa.stattools 中。 首先,我们构造一个读取股票价格,
判断协整关系的函数。该函数返回的两个值分别为协整性检验的 p 值矩阵以及所有传入的参数中协整性较强的股票对。我们不需要在意 $p$ 值具体是什么,
可以这么理解它: $p$ 值越低,协整关系就越强;$p$ 值低于 0.05 时,协整关系便非常强。
In [14]:
import numpy as np
import pandas as pd
import statsmodels.api as sm
import seaborn as sns
In [15]:
#
输入是一DataFrame,每一列是一支股票在每一日的价格
def find_cointegrated_pairs(dataframe):
得到DataFrame长度
n = dataframe.shape[1]
初始化p值矩阵
pvalue_matrix = np.ones((n, n))
抽取列的名称
keys = dataframe.keys()
初始化强协整组
pairs = []
对于每一个i
for i in range(n):
对于大于i的j
for j in range(i+1, n):
#
#
#
#
#
#
#
获取相应的两只股票的价格Series
stock1 = dataframe[keys[i]]
stock2 = dataframe[keys[j]]
#
分析它们的协整关系
result = sm.tsa.stattools.coint(stock1, stock2)

#
取出并记录p值
pvalue = result[1]
pvalue_matrix[i, j] = pvalue
#
如果p值小于0.05
if pvalue < 0.05:
#
记录股票对和相应的p值
pairs.append((keys[i], keys[j], pvalue))
#
返回结果
return pvalue_matrix, pairs
其次,我们挑选10只银行股,认为它们是业务较为相似,在基本面上具有较强联系的股票,使用上面构建的函数对它们进行协整关系的检验。在得到结果
后,用热力图画出各个股票对之间的 $p$ 值,较为直观地看出他们之间的关系。
我们的测试区间为2015年1月1日至2017年7月18日。热力图画出的是 1 减去 $p$ 值,因此颜色越红的地方表示 $p$ 值越低。
In [16]:
instruments = ["002142.SZA", "600000.SHA", "600015.SHA", "600016.SHA", "600036.SHA", "601009.SHA",
"
601166.SHA", "601169.SHA", "601328.SHA", "601398.SHA", "601988.SHA", "601998.SHA"]
#
确定起始时间
start_date = '2015-01-01'
确定结束时间
end_date = '2017-07-18'
获取股票总市值数据,返回DataFrame数据格式
#
#
prices_temp = D.history_data(instruments,start_date,end_date,
fields=['close'] )
prices_df=pd.pivot_table(prices_temp, values='close', index=['date'], columns=['instrument'])
pvalues, pairs = find_cointegrated_pairs(prices_df)
#
画协整检验热度图,输出pvalue < 0.05的股票对
sns.heatmap(1-pvalues, xticklabels=instruments, yticklabels=instruments, cmap='RdYlGn_r', mask = (pvalues == 1))
print(pairs)
[
('601328.SHA', '601988.SHA', 0.0050265192277696939), ('601328.SHA', '601998.SHA', 0.0069352163995946518)]
In [17]:
df = pd.DataFrame(pairs, index=range(0,len(pairs)), columns=list(['Name1','Name2','pvalue']))
#pvalue越小表示相关性越大,按pvalue升序排名就是获取相关性从大到小的股票对
df.sort_values(by='pvalue')
Out[17]:
Name1
Name2
pvalue
0
1
601328.SHA
601328.SHA
601988.SHA
601998.SHA
0.005027
0.006935
可以看出,上述10只股票中有3对具有较为显著的协整性关系的股票对(红色表示协整关系显著)。我们选择使用其中 $p$ 值最低(0.004)的交通银行
(601328.SHA)和中信银行(601998.SHA)这一对股票来进行研究。首先调取交通银行和中信银行的历史股价,画出两只股票的价格走势。
In [18]:
T.plot(prices_df[['601328.SHA','601998.SHA']], chart_type='line', title='Price')
接下来,我们用这两支股票的价格来进行一次OLS线性回归,以此算出它们是以什么线性组合的系数构成平稳序列的。
In [19]:
#
ols
x = prices_df['601328.SHA']
y = prices_df['601998.SHA']
X = sm.add_constant(x)
result = (sm.OLS(y,X)).fit()
print(result.summary())
OLS Regression Results
=============================================================================
=
Dep. Variable:
Model:
601998.SHA
R-squared:
0.682
0.682
OLS
Least Squares
Wed, 19 Jul 2017
10:57:47
619
Adj. R-squared:
F-statistic:
Prob (F-statistic):
Log-Likelihood:
AIC:
Method:
1323.
Date:
1.20e-155
-566.43
1137.
Time:
No. Observations:
Df Residuals:
Df Model:
617
BIC:
1146.
1
Covariance Type:
nonrobust
=
=============================================================================

coef
std err
t
P>|t|
[0.025
0.975]
-
-----------------------------------------------------------------------------
const
0.3818
0.8602
0.226
0.024
1.687
0.092
0.000
-0.063
0.814
0.826
0.907
6
=
01328.SHA
36.378
=============================================================================
Omnibus:
0.497
0.780
0.003
3.115
Durbin-Watson:
Jarque-Bera (JB):
Prob(JB):
0.070
0.340
0.844
90.0
Prob(Omnibus):
Skew:
Kurtosis:
Cond. No.
=
=============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
系数是 0.8753,画出数据和拟合线。
In [20]:
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label="data")
ax.plot(x, result.fittedvalues, 'r', label="OLS")
ax.legend(loc='best')
Out[20]:
<
matplotlib.legend.Legend at 0x7efd449cb7b8>
设中信银行的股价为 $Y$,交通银行为 $X$,回归拟合的结果是
也就是说 $Y−0.8753⋅X$ 是平稳序列。
依照这个比例,我们画出它们价差的平稳序列。可以看出,虽然价差上下波动,但都会回归中间的均值。
In [21]:
#
T.plot(pd.DataFrame({'Stationary Series':0.8753*x-y, 'Mean':[np.mean(0.8753*x-y)]}), chart_type='line')
df = pd.DataFrame({'Stationary Series':y-0.8753*x, 'Mean':np.mean(y-0.8753*x)})
T.plot(df, chart_type='line', title='Stationary Series')
买卖时机的判断¶
这里,我们先介绍一下, $z-score$ 是对时间序列偏离其均值程度的衡量,表示时间序列偏离了其均值多少倍的标准差。首先,我们定义一个函数来计算 $z-
score$:
一个序列在时间 $t$ 的 $z-score$,是它在时间 $t$ 的值,减去序列的均值,再除以序列的标准差后得到的值。
In [22]:
def zscore(series):
return (series - series.mean()) / np.std(series)
In [23]:
zscore_calcu = zscore(y-0.8753*x)
T.plot(pd.DataFrame({'zscore':zscore_calcu, 'Mean':np.mean(y-0.8753*x), 'upper':1, 'lower':-1}) ,chart_type='line', title='zscore')
策略完整交易系统设计¶
1
2
3
4
.交易标的:中信银行(601998.SHA)和交通银行(601328.SHA)
.交易信号: 当zscore大于1时,全仓买入交通银行,全仓卖出中信银行→做空价差 当zscore小于-1时,全仓卖出中信银行,全仓买入交通银行→做多价差
.风险控制:暂时没有风险控制
.资金管理:暂时没有择时,任何时间保持满仓
策略回测部分¶
In [24]:
instrument = {'y':'601998.SHA','x':'601328.SHA'} # 协整股票对
start_date = '2015-01-01' # 起始日期
end_date = '2017-07-18' # 结束日期
In [25]:

#
初始化账户和传入需要的变量
def initialize(context):
context.set_commission(PerDollar(0.0015)) # 手续费设置
context.zscore = zscore_calcu # 交易信号需要根据zscore_calcu的具体数值给出
context.ins = instrument # 传入协整股票对
#
策略主题函数
def handle_data(context, data):
date = data.current_dt.strftime('%Y-%m-%d') # 运行到当根k线的日期
zscore = context.zscore.ix[date] # 当日的zscore
stock_1 = context.ins['y'] # 股票y
stock_2 = context.ins['x'] # 股票x
symbol_1 = context.symbol(stock_1) # 转换成回测引擎所需要的symbol格式
symbol_2 = context.symbol(stock_2)
#
持仓
cur_position_1 = context.portfolio.positions[symbol_1].amount
cur_position_2 = context.portfolio.positions[symbol_2].amount
#
#
交易逻辑
如果zesore大于上轨(>1),则价差会向下回归均值,因此需要买入股票x,卖出股票y
if zscore > 1 and cur_position_2 == 0 and data.can_trade(symbol_1) and data.can_trade(symbol_2):
context.order_target_percent(symbol_1, 0)
context.order_target_percent(symbol_2, 1)
print(date, '全仓买入:交通银行')
#
如果zesore小于下轨(<-1),则价差会向上回归均值,因此需要买入股票y,卖出股票x
elif zscore < -1 and cur_position_1 == 0 and data.can_trade(symbol_1) and data.can_trade(symbol_2):
context.order_target_percent(symbol_1, 1)
print(date, '全仓买入:中信银行')
context.order_target_percent(symbol_2, 0)
In [26]:
#
回测启动接口
m=M.trade.v2(
instruments=list(instrument.values()),# 保证instrument是有字符串的股票代码组合成的列表(list)
start_date=start_date,
end_date=end_date,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='open',
capital_base=10000,
benchmark='000300.INDX',
)
[
2
2
2
2
2
2
2
2
[
[
[
2017-07-19 10:57:48.483480] INFO: bigquant: backtest.v7 start ..
015-01-05 全仓买入:交通银行
015-06-04 全仓买入:中信银行
015-07-08 全仓买入:交通银行
015-08-31 全仓买入:中信银行
015-11-18 全仓买入:交通银行
016-06-20 全仓买入:中信银行
016-11-23 全仓买入:交通银行
017-04-26 全仓买入:中信银行
2017-07-19 10:57:50.791302] INFO: Performance: Simulated 619 trading days out of 619.
2017-07-19 10:57:50.792254] INFO: Performance: first open: 2015-01-05 14:30:00+00:00
2017-07-19 10:57:50.793197] INFO: Performance: last close: 2017-07-18 19:00:00+00:00
[
2017-07-19 10:57:52.645455] INFO: bigquant: backtest.v7 end [4.161958s].
参考资料
基本面量化(Quantamental )——财务指标量化策略
公司的基本面因素一直具备滞后性,令基本面的量化出现巨大困难。而从上市公司的基本面因素来看,一般只有每个季度的公布期才会有财务指标的更
新,而这种财务指标的滞后性对股票表现是否有影响呢?如何去规避基本面滞后产生的风险呢?下面我们将重点介绍量化交易在公司基本面分析上的应
用,即平时常说的 基本面量化(Quantamental)。

哪些财务指标较真实反映上市公司经营优劣?
首先我们简单介绍下可能运用在量化策略上的基本面指标,相信大部分投资者都对上市公司的基本面有一定的了解,上市公司的基本面情况总是同公司业绩
相关,而衡量业绩的主要基本面指标有每股收益、净资产收益率、主营业务收入等等。
而上市公司财务指标又常常存在相关的性质,比如每股收益和主营业务收入和产品毛利率相关,所以当我们把一堆财务指标放在一起统计可能就会产生相关
性问题,从而降低了模型对市场走势的解释程度。因此,如何选出合适的独立性指标就成为我们进行财务指标量化模型设计的基础。
那么怎样的财务指标会较真实的反映上市公司的经营优劣呢?
具有延续性的财务指标,比如近三年净利润增速,这一个指标把3年的净利润增速平均起来,这种增长性具备一定的长期特征;
与现金流相关的指标,由于涉及真实的资金往来,现金流能够比较真实反映上市公司的经营状况。
选择用作财务量化模型的指标
1
、每股现金流量/每股业绩
每股现金流量比每股盈余更能显示从事资本性支出及支付股利的能力。每股现金流量通常比每股盈余要高,这是因为公司正常经营活动所产生的净现金流量
还会包括一些从利润中扣除出去但又不影响现金流出的费用调整项目,如折旧费等。但每股现金流量也有可能低于每股盈余。一家公司的每股现金流量越
高,说明这家公司的每股普通股在一个会计年度内所赚得的现金流量越多;反之,则表示每股普通股所赚得的现金流量越少。
而每股现金流量常常与上市公司的业绩、总股本相关,所以用每股现金流量/每股业绩来衡量上市公司的现金流动情况,比单纯用每股盈余更为合理。
2
、净资产收益率
净资产收益率又称股东权益收益率,是净利润与平均股东权益的百分比,是公司税后利润除以净资产得到的百分比率,该指标反映股东权益的收益水平,用
以衡量公司运用自有资本的效率。指标值越高,说明投资带来的收益越高。
净资产收益率通过净资金去计量每年上市公司收益的百分比,净资产收益率比每股净利润,资产收益率等更合理的衡量归于于股东的上市公司权益的增值速
度。
3
、销售毛利率
销售毛利率,表示每一元销售收入扣除销售成本后,有多少钱可以用于各项期间费用和形成盈利。 销售毛利率是企业销售净利率的最初基础,没有足够大的
毛利率便不能盈利。
在分析企业主营业务的盈利空间和变化趋势时,销售毛利率是一个重要指标。该指标的优点在于可以对企业某一主要产品或主要业务的盈利状况进行分析,
这对于判断企业核心竞争力的变化趋势及其企业成长性极有帮助。
基本面量化的具体实现:
确定三个财务因子为销售毛利率、净资产收益率、每股现金流量/每股业绩
通过features数据接口获取全市场3000多家上市公司的财务数据
单独筛选每个财务因子前500的上市公司
最终确定三个因子都能排在前500的股票篮子
买入该股票篮子,等权重买入
一个月换仓一次,买入新确定的股票篮子
从策略结果来看,年化收益14%,应该超过了大部分公募基金,虽然回撤很大,但细心地伙伴可以看出是发生在15年股灾期间和16年熔断期间,如果配合择
时模型,想必效果会更好。尤其是值得注意的是,该策略在17年还取得了稳定正收益。本例子只作为如何使用财务数据进行基本面量化的样例策略,便于大
家能够快速上手开发策略。
还在犹豫什么呢?赶紧点击 克隆策略,把策略收入自己的账户开始研究吧!
In [56]:
#
#
该函数可以参考:https://bigquant.com/docs/module_cached.html?highlight=cache
缓存的目的是第一次运行后,以后运行可以直接使用第一次缓存的结果
def mycache():
#
确定起始时间
start_date = '2013-01-01'
#
确定结束时间
end_date = '2017-05-07'
获取股票代码
#
instruments = D.instruments(start_date, end_date)
fields = ['fs_gross_profit_margin_0', 'fs_roe_0', 'fs_free_cash_flow_0', 'fs_net_profit_0']
raw_data = D.features(instruments, start_date, end_date, fields)
raw_data['cash_flow/profit'] = raw_data['fs_free_cash_flow_0'] / raw_data['fs_net_profit_0']
def seek_stock(df):
ahead_f1 = set(df.sort_values('fs_roe_0',ascending=False)['instrument'][:500])
ahead_f2 = set(df.sort_values('fs_gross_profit_margin_0',ascending=False)['instrument'][:500])
ahead_f3 = set(df.sort_values('cash_flow/profit',ascending=False)['instrument'][:500])
return list(ahead_f1 & ahead_f2 & ahead_f3)
daily_buy_stock = pd.DataFrame(raw_data.groupby('date').apply(seek_stock))

ds = DataSource.write_df(daily_buy_stock)
return Outputs(daily_buy_stock=ds)
mycache = M.cached.v2(run=mycache)
[
[
2017-07-06 21:29:05.582128] INFO: bigquant: cached.v2 start ..
2017-07-06 21:29:38.101232] INFO: bigquant: cached.v2 end [32.519196s].
In [ ]:
In [62]:
#
回测参数设置,initialize函数只运行一次
def initialize(context):
#
手续费设置
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
调仓规则(每月的第一天调仓)
context.schedule_function(rebalance, date_rule=date_rules.month_start(days_offset=0))
传入 整理好的调仓股票数据
#
#
context.daily_buy_stock = mycache.daily_buy_stock.read_df()
#
handle_data函数会每天运行一次
def handle_data(context,data):
pass
#
换仓函数
def rebalance(context, data):
当前的日期
date = data.current_dt.strftime('%Y-%m-%d')
根据日期获取调仓需要买入的股票的列表
stock_to_buy = list(context.daily_buy_stock.ix[date][0])
通过positions对象,使用列表生成式的方法获取目前持仓的股票列表
stock_hold_now = [equity.symbol for equity in context.portfolio.positions]
继续持有的股票:调仓时,如果买入的股票已经存在于目前的持仓里,那么应继续持有
no_need_to_sell = [i for i in stock_hold_now if i in stock_to_buy]
需要卖出的股票
stock_to_sell = [i for i in stock_hold_now if i not in no_need_to_sell]
#
#
#
#
#
#
卖出
for stock in stock_to_sell:
#
#
#
如果该股票停牌,则没法成交。因此需要用can_trade方法检查下该股票的状态
如果返回真值,则可以正常下单,否则会出错
因为stock是字符串格式,我们用symbol方法将其转化成平台可以接受的形式:Equity格式
if data.can_trade(context.symbol(stock)):
#
#
order_target_percent是平台的一个下单接口,表明下单使得该股票的权重为0,
即卖出全部股票,可参考回测文档
context.order_target_percent(context.symbol(stock), 0)
#
如果当天没有买入的股票,就返回
if len(stock_to_buy) == 0:
return
#
等权重买入
weight = 1 / len(stock_to_buy)
#
买入
for stock in stock_to_buy:
if data.can_trade(context.symbol(stock)):
#
#
下单使得某只股票的持仓权重达到weight,因为
weight大于0,因此是等权重买入
context.order_target_percent(context.symbol(stock), weight)
In [63]:
#
策略运行调用函数
m=M.trade.v1(
instruments=instruments,
start_date=start_date,
end_date=end_date,
#
必须传入initialize,只在第一天运行
initialize=initialize,
必须传入handle_data,每个交易日都会运行
handle_data=handle_data,
买入以开盘价成交
order_price_field_buy='open',
卖出也以开盘价成交
order_price_field_sell='open',
策略本金
#
#
#
#

capital_base=1000000,
# 比较基准:沪深300
benchmark='000300.INDX',
m_deps='quantamental'
)
[
[
[
[
2017-07-06 21:40:53.161536] INFO: bigquant: backtest.v6 start ..
2017-07-06 21:41:29.771812] INFO: Performance: Simulated 1052 trading days out of 1052.
2017-07-06 21:41:29.774763] INFO: Performance: first open: 2013-01-04 14:30:00+00:00
2017-07-06 21:41:29.776196] INFO: Performance: last close: 2017-05-05 19:00:00+00:00
[
2017-07-06 21:41:34.168819] INFO: bigquant: backtest.v6 end [41.007239s].
数学课堂
[
量化学堂-数学知识]数据集中趋势的度量:平均值
导语:本文我们将讨论如何使用平均值来描述一组数据。
算术平均值¶
算术平均值非常频繁地用于描述一组数据,即“平均值”。 它被定义为观测的总和除以观测个数:
这里 $X_1, X_2, \ldots , X_N$ 是我们的观测值.
In [1]:
#
两个常用的统计包
import scipy.stats as stats
import numpy as np
#
我们拿两个数据集来举例
x1 = [1, 2, 2, 3, 4, 5, 5, 7]
x2 = x1 + [100]
print('x1的平均值:', sum(x1), '/', len(x1), '=', np.mean(x1))
print('x2的平均值:', sum(x2), '/', len(x2), '=', np.mean(x2))
x1的平均值: 29 / 8 = 3.625
x2的平均值: 129 / 9 = 14.3333333333
我们还可以定义一个加权算术平均值,加权算术平均值计算定义为:
这里 $\sum_{i=1}^n w_i = 1$. 在通常的算术平均值计算中,对所有的$i$ 都有$w_i = 1/n$.
中位数¶
顾名思义,一组数据的中位数是当以递增或递减顺序排列时出现在数据中间位置的数字。 当我们有奇数n个数据点时,中位数就是位置(n + 1)/ 2的值。 当
我们有偶数的数据点时,数据分成两半,中间位置没有任何数据点; 所以我们将中位数定义为位置n / 2和(n + 2)/ 2中的两个数值的平均值。
数据中位数不容易受极端数值的影响。 它告诉我们处于中间位置的数据。
In [2]:
print('x1的中位数:', np.median(x1))
print('x2的中位数:', np.median(x2))
x1的中位数: 3.5
x2的中位数: 4.0
众数¶
众数是数据集中出现次数最多的数据点。 它可以应用于非数值数据,与平均值和中位数不同。
In [3]:
#
Scipy具有内置的求众数功能,但它只返回一个值,即使两个值出现相同的次数,也是只返回一个值。

print('One mode of x1:', stats.mode(x1)[0][0])
#
因此我们自定义一个求众数的函数
def mode(l):
#
统计列表中每个元素出现的次数
counts = {}
for e in l:
if e in counts:
counts[e] += 1
else:
counts[e] = 1
#
返回出现次数最多的元素
maxcount = 0
modes = {}
for (key, value) in counts.items():
if value > maxcount:
maxcount = value
modes = {key}
elif value == maxcount:
modes.add(key)
if maxcount > 1 or len(l) == 1:
return list(modes)
return 'No mode'
print('All of the modes of x1:', mode(x1))
One mode of x1: 2
All of the modes of x1: [2, 5]
可以看出,我们自定义的mode函数更加合理.
对于可能呈现不同数值的数据,比如收益率数据,也许收益率数据没有哪个数据点会出现超过一次。在这种情形下,我们可以使用bin值,正如我们构建直方
图一样,这个时候我们统计哪个bin里数据点出现次数最多
In [4]:
#
获取收益率数据并计算出mode
start = '2014-01-01'
end = '2015-01-01'
pricing = D.history_data('000002.SZA', fields=['close'], start_date=start, end_date=end)['close']
returns = pricing.pct_change()[1:]
print('收益率众数:', mode(returns))
#
由于所有的收益率都是不同的,所以我们使用频率分布来变相计算mode
hist, bins = np.histogram(returns, 20) # 将数据分成20个bin
maxfreq = max(hist)
#
找出哪个bin里面出现的数据点次数最大,这个bin就当做计算出来的mode
print('Mode of bins:', [(bins[i], bins[i+1]) for i, j in enumerate(hist) if j == maxfreq])
收益率众数: [0.0]
Mode of bins: [(-0.0030533790588378878, 0.0055080294609069907)]
确实如此,在收益率数据中,很多数据点都不一样,因此计算众数的方式就显得有失偏颇。我们此时转化了思路,不是计算众数,而是将数据分成很多个组
(
bin),然后找出数据点最多的组(bin)来代替收益率数据的众数(mode)
几何平均值¶
虽然算术平均值使用加法,但几何平均值使用乘法:
该式子等价于:
几何平均值总是小于或等于算术平均值(当使用非负观测值时),当所有观测值都相同时,两者相等。
In [ ]:
#
使用Scipy包中的gmean函数来计算几何平均值
print('x1几何平均值:', stats.gmean(x1))
print('x2几何平均值:', stats.gmean(x2))
如果在计算几何平均值的时候遇到负数的观测值,怎么办呢?在资产收益率这个例子中其实很好解决,因为收益率最低为-1,因此我们可以+1将其转化为正
数。 因此我们可以这样来计算几何收益率:

In [ ]:
#
在每个元素上增加1来计算几何平均值
ratios = returns + np.ones(len(returns))
R_G = stats.gmean(ratios) - 1
print('收益率的几何平均值:', R_G)
几何平均收益率是将各个单个期间的收益率乘积,然后开n次方,因此几何平均收益率使用了复利的思想,从而克服了算术平均收益率有时会出现的上偏倾
向。我们来看下面的例子:
In [ ]:
T = len(returns)
init_price = pricing[0]
final_price = pricing[T]
print('最初价格:', init_price)
print('最终价格:', final_price)
print('通过几何平均收益率计算的最终价格:', init_price*(1 + R_G)**T)
从上例可以看出,几何收益率的优势在于体现了复利的思想,我们知道初始资金和几何收益率,很容易计算出最终资金
调和平均值¶
调和平均值(harmonic mean)又称倒数平均数,是总体各统计变量倒数的算术平均数的倒数。调和平均值是平均值的一种。
调和平均值恒小于等于算术平均值,当所有观测值相等的时候,两者相等。
应用:调和平均值可以用在相同距离但速度不同时,平均速度的计算;如一段路程,前半段时速60公里,后半段时速30公里〔两段距离相等〕,则其平均速
度为两者的调和平均值时速40公里。在现实中很多例子,需要使用调和平均值。
In [ ]:
#
我们可以使用现成的函数来计算调和平均值
print('x1的调和平均值:', stats.hmean(x1))
print('x2的调和平均值:', stats.hmean(x2))
点估计的欺骗性¶
平均值的计算隐藏了大量的信息,因为它们将整个数据分布整合成一个数字。 因此,常常使用“点估计”或使用一个数字的指标,往往具有欺骗性。 你应该小
心地确保你不会通过平均值来丢失数据分布的关键信息,在使用平均值的时候也应该保持警惕。
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-数学知识]数据离散状况的测量:离散度
导语:本文我们将讨论如何使用离散度来描述一组数据。
离散度能够更好地测量一个数据分布。 这在金融方面尤其重要,因为风险的主要测量方法之一是看历史上收益率的数据分布特征。 如果收益率紧挨着平均
值,那么我们就不用特别担心风险。 如果收益率很多数据点远离平均值,那风险就不小。具有低离散度的数据围绕平均值聚集,而高离散度的数据表明有许
多非常大且非常小的数据点。
让我们生成一个随机整数先来看看。
In [1]:
import numpy as np
np.random.seed(121)
In [2]:
#
生成20个小于100的随机整数
X = np.random.randint(100, size=20)
#
Sort them
X = np.sort(X)
print('X: %s' %(X))
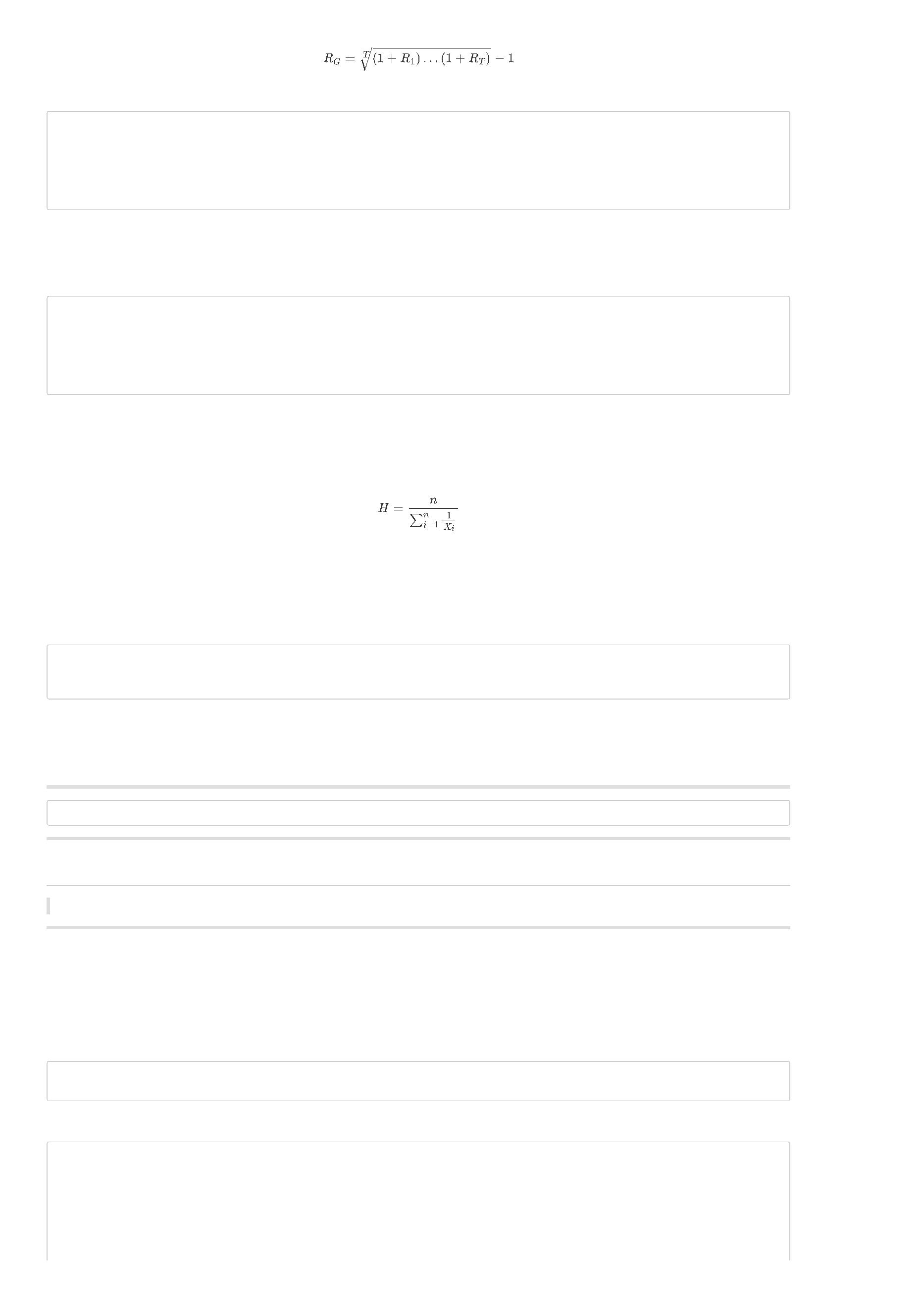
mu = np.mean(X)
print('X的平均值:', mu)
X: [ 3 8 34 39 46 52 52 52 54 57 60 65 66 75 83 85 88 94 95 96]
X的平均值: 60.2
Range(范围)¶
Range(范围)是数据集中最大值和最小值之间的差异。 毫不奇怪,它对异常值非常敏感。 我们使用numpy的ptp的函数来计算Range。
In [3]:
print('Range of X: %s' %(np.ptp(X)))
Range of X: 93
MAD(平均绝对偏差)¶
平均绝对偏差是数据点距离算术平均值的偏差。 我们使用偏差的绝对值,这使得比平均值大5的数据点和比平均值小5的数据点对MAD均贡献5,否则偏差总
和为0。
这里$n$是数据点的个数,$\mu$是其平均值。
In [4]:
abs_dispersion = [np.abs(mu - x) for x in X]
MAD = np.sum(abs_dispersion)/len(abs_dispersion)
print('X的平均绝对偏差:', MAD)
X的平均绝对偏差: 20.52
方差和标准差¶
关于数据离散程度的度量最常用的指标就是方差和标准差,在金融市场更是如此,诺贝尔经济学奖得主马科维茨创造性地将投资的风险定义为收益率的方
差,因此为现代金融工程的大厦做了坚实奠基。量化投资更是更是如此,对于风险的度量大多时候是通过方差、标准差来完成。
方差 $\sigma^2$的定义如下:
标准差的定义为方差的平方根:$\sigma$。 标准差的运用更为广泛,因为它和观测值在同一个数据维度,可以进行加减运算。
In [5]:
print('X的方差:', np.var(X))
print('X的标准差:', np.std(X))
X的方差: 670.16
X的标准差: 25.8874486962
解释标准差的一种方式是切比雪夫不等式。 它告诉我们,对于任意的值$k$($k> 1$),平均值的$k$个标准差(即,在k倍标准偏差的距离内)的样本比例至
少为$1-1 / k2$。我们来检查一下这个定理是否正确。
In [6]:
k = 1.25 # 随便举的一个k值
dist = k*np.std(X)
l = [x for x in X if abs(x - mu) <= dist]
print('k值', k, '在k倍标准差距离内的样本为:', l)
print('验证', float(len(l))/len(X), '>', 1 - 1/k**2)
k值 1.25 在k倍标准差距离内的样本为: [34, 39, 46, 52, 52, 52, 54, 57, 60, 65, 66, 75, 83, 85, 88]
验证 0.75 > 0.36
半方差和半标准差¶
虽然方差和标准差告诉我们收益率是如何波动,但它们并不区分向上的偏差和向下的偏差。 通常情况下,在金融市场投资中,我们更加担心向下的偏差。 因
此半方差更多是在金融市场上的应用。
半方差是目标导向,认为只有负的收益才是投资真正的风险。半方差的定义与方差类似,唯一的区别在于半方差仅试用低于均值的收益率样本。
半方差的定义如下:

这里$n_{less}$表示小于均值的数据样本的数量。半标准差就是半方差的平方根。
In [7]:
#
没有现成的计算半方差的函数,因此我们手动计算:
lows = [e for e in X if e <= mu]
semivar = np.sum( (lows - mu) ** 2 ) / len(lows)
print('X的半方差:', semivar)
print('X的半标准差:', np.sqrt(semivar))
X的半方差: 689.512727273
X的半标准差: 26.2585743572
另外一个相关的是目标半方差,是仅关注低于某一目标的样本,定义如下:
In [8]:
B = 19 # 目标为19
lows_B = [e for e in X if e <= B]
semivar_B = sum(map(lambda x: (x - B)**2,lows_B))/len(lows_B)
print('X的目标半方差:', semivar_B)
print('X的目标半标准差:', np.sqrt(semivar_B))
X的目标半方差: 188.5
X的目标半标准差: 13.7295302177
注:
所有这些计算将给出样本统计,即数据的标准差。 这是否反映了目前真正的标准差呢?其实还需要做出更多的努力来确定这一点,比如绘制出数据样本直方
图、概率密度图,这样更能全面了解数据分布状况。 这在金融方面尤其是,因为所有金融数据都是时间序列数据,平均值和方差可能随时间而变化。因此,
金融数据方差、标准差有许多不同的技巧和微妙之处。
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-数学知识]相关关系
导语:相关性经常用来度量两个变量的相关关系,本文将对相关系数做详细讨论。
诺贝尔经济学奖得主马科维茨曾说过“资产配置多元化是投资的唯一免费午餐”。投资中有句谚语,不要把鸡蛋放在一个篮子,实际上讲的就是选择相关性不
高的资产进行配置。资产之间的相关性用什么指标衡量呢?著名统计学家卡尔·皮尔逊设计了统计指标——相关系数,相关系数就是用以反映变量之间相关关
系密切程度的统计指标。
两个变量$X$、$Y$的相关系数可以用$\rho_{XY}$表示。$\rho_{XY}$的计算公式为:
(
其中,$\sigma_X$表示$X$的方差,$\sigma_Y$表示$Y$的方差,$cov(X,Y)$表示变量$X$与变量$Y$的协方差,$\mu_X$表示$X$的均值,$\mu_Y$表示
$
Y$的均值。
相关系数$\rho_{XY}$取值在-1到1之间,$\rho_{XY}$ = 0时,称$X$,$Y$不相关;$ | \rho_{XY} |$ = 1时,称X,Y完全相关,此时,$X$,$Y$之间具有线性函
数关系; $ | \rho_{XY} |$< 1时,$X$的变动引起$Y$的部分变动,$ | \rho_{XY} |$的绝对值越大,$X$的变动引起$Y$的变动就越大,$ | \rho_{XY} |$ > 0.8
时称为高度相关,当 $ | \rho_{XY} |$ < 0.3时称为低度相关,其它时候为中度相关。$\rho_{XY}$>0时,称其为正相关,$\rho_{XY}$<0时,称其为反相关。
理论知识介绍完了,我们就在BigQuant研究平台试试计算相关系数和绘图。完整的代码 克隆一下就可以到自己的账户进行研究。
附件:相关关系的应用
使用Python 计算变量之间的相关系数和绘图¶
In [1]:

#
导入包
import numpy as np
import statsmodels.tsa.stattools as sts
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import statsmodels.api as sm
1
、随机变量¶
In [2]:
X = np.random.randn(1000)
Y = np.random.randn(1000)
plt.scatter(X,Y)
plt.show()
print("correlation of X and Y is ")
np.corrcoef(X,Y)[0,1] # 可以看出,随机变量几乎不相关
correlation of X and Y is
Out[2]:
0
.010505052938688659
2
、使用生成的相关序列,并加入正态分布的噪音¶
In [3]:
X = np.random.randn(1000)
Y = X + np.random.normal(0,0.1,1000)
plt.scatter(X,Y)
plt.show()
print("correlation of X and Y is ")
np.corrcoef(X,Y)[0,1]
correlation of X and Y is
Out[3]:
0
.99509473689553696
3
、转向更为实际的对象¶
我们探索两只股票相关关系,因为在金融市场上,对价格的分析较少,而对收益率的关注较多,因此相关性也是从收益率的角度来看
In [6]:
#
计算两只股票的日收益率
Stock1 = D.history_data(["601186.SHA"],start_date='2016-12-01',end_date='2017-05-01',fields = ['close'])['close'].pct_change()[1:]
Stock2 = D.history_data(["601390.SHA"],start_date='2016-12-01',end_date='2017-05-01',fields = ['close'])['close'].pct_change()[1:]
In [17]:
plt.scatter(Stock1,Stock2)
plt.xlabel("601186.SHA daily return")
plt.ylabel("601390.SHA daily return")
plt.show()
print("the corrlation for two stocks is: ")
Stock2.corr(Stock1)
the corrlation for two stocks is:
Out[17]:
0
.8846017046026351
4
、计算滚动相关系数¶
相关关系的计算离不开一个时间窗口,通过时间窗口我们也能看出相关性随时间的一个变动情况
In [8]:
Stock1 = D.history_data(["601186.SHA"],start_date='2010-01-01',end_date='2017-05-01',fields = ['close'])['close'].pct_change()[1:]
Stock2 = D.history_data(["601390.SHA"],start_date='2010-01-01',end_date='2017-05-01',fields = ['close'])['close'].pct_change()[1:]

In [11]:
#
借助Pandas包计算滚动相关系数
rolling_corr = pd.rolling_corr(Stock1,Stock2,60)
rolling_corr.index = D.trading_days(start_date='2010-01-01',end_date='2017-05-01').date[1:]
In [18]:
plt.plot(rolling_corr)
plt.xlabel('Day')
plt.ylabel('60-day Rolling Correlation')
plt.show()
但是对于成百上千的股票,怎样才能找到高度相关的股票对?
In [19]:
#
我们以10只股票举例
instruments = D.instruments()[:10]
Stock_matrix = D.history_data(instruments,start_date='2016-01-01',end_date='2016-09-01',fields=['close'])
#
#
不用收盘价数据,而是用收益率数据
通过pivot_table函数将Stock_matrix整理成一个以股票日收益率为列的df
Stock_matrix = pd.pivot_table(Stock_matrix,values='close',index=['date'],columns=['instrument']).apply(lambda x:x.pct_change())
Stock_matrix.head()
Out[19]:
instrument
date
000001.SZA
000002.SZA
000004.SZA
000005.SZA
000006.SZA
000007.SZA
000008.SZA
000009
2016-01-04
2016-01-05
2016-01-06
2016-01-07
2016-01-08
NaN
NaN
0.0
0.0
0.0
0.0
NaN
NaN
NaN
NaN
0.0
0.0
0.0
0.0
NaN
NaN
0.006178
0.011404
-0.051171
0.016453
-0.063665
0.012926
-0.100051
0.006239
-0.015487
0.031461
-0.099129
0.003628
-0.032755
0.025897
-0.100000
0.009709
0.018850
0.013876
-0.088504
-0.002002
-0.0470
0.0363
-0.1002
0.0097
In [20]:
#
相关系数矩阵
Stock_matrix.corr()
Out[20]:
instrument
instrument
000001.SZA
000002.SZA
000004.SZA
000005.SZA
000006.SZA
000007.SZA
000008.SZA
00000
0
00001.SZA
00002.SZA
00004.SZA
00005.SZA
00006.SZA
00007.SZA
00008.SZA
00009.SZA
00010.SZA
00011.SZA
1.000000
0.018993
0.595322
0.600269
0.622749
0.027863
0.531736
0.657898
0.591505
0.458707
0.018993
1.000000
0.000170
0.050937
0.138133
0.169131
0.026653
0.018328
0.054138
0.072238
0.595322
0.000170
1.000000
0.597882
0.659429
-0.000203
0.528496
0.621535
0.642140
0.544813
0.600269
0.050937
0.597882
1.000000
0.665327
0.060434
0.590306
0.681779
0.665582
0.568800
0.622749
0.138133
0.659429
0.665327
1.000000
0.055961
0.507439
0.681861
0.670731
0.777092
0.027863
0.169131
-0.000203
0.060434
0.055961
1.000000
0.054658
0.043501
0.032836
0.002523
0.531736
0.026653
0.528496
0.590306
0.507439
0.054658
1.000000
0.554532
0.562442
0.421347
0.6578
0.0183
0.6215
0.6817
0.6818
0.0435
0.5545
1.0000
0.6727
0.5233
0
0
0
0
0
0
0
0
0
5
、通过相关关系热力图可视化股票相关性¶
In [15]:
#
绘制相关系数热力图
mask = np.zeros_like(Stock_matrix.corr(), dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
cmap = sns.diverging_palette(220, 10, as_cmap=True)

sns.heatmap(Stock_matrix.corr(), mask=mask, cmap=cmap)
plt.show()
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-数学知识]线性回归
导语: 线性回归模型的最大特点就是简单高效,本文将对线性回归做详细介绍。
线性回归是衡量两个变量之间线性关系的一种建模技术。 如果我们有一个变量$X$和一个依赖变量$X$的变量$Y$,则线性回归可以确定哪个线性模型
Y=α+βX$能够最好地解释数据。 例如,我们考虑浦发银行和沪深300的价格指数, 我们想知道浦发银行如何随着沪深300的变化而变化,因此我们将对这
$
两个标的的日收益率进行回归。
Python的statsmodels库具有内置的线性回归功能。 它将给出最能够拟合数据的一条的直线,并且能够帮助你决定该线性关系是否显著。 线性回归的输出还
包括一些有关模型的数值统计信息,如$R方$和$F值$,可以帮助您量化模型的实际的解释能力。
附件:线性回归的使用
In [1]:
#
导入库
import numpy as np
from statsmodels import regression
import statsmodels.api as sm
import matplotlib.pyplot as plt
import math
In [2]:
#
编辑线性回归函数
def linreg(X,Y):
运行线性回归
#
X = sm.add_constant(X)
model = regression.linear_model.OLS(Y, X).fit()
a = model.params[0]
b = model.params[1]
X = X[:, 1]
#
返回信息并绘图
X2 = np.linspace(X.min(), X.max(), 100)
Y_hat = X2 * b + a
plt.scatter(X, Y, alpha=0.3) # 显示原始数据
plt.plot(X2, Y_hat, 'r', alpha=0.9); # 添加拟合直线
plt.xlabel('X Value')
plt.ylabel('Y Value')
return model.summary()
In [3]:
start_date = '2016-01-01'
end_date = '2017-04-11'
#
获取浦发银行的价格数据
asset = D.history_data('600000.SHA',start_date,end_date,fields=['close']).set_index('date')['close']
benchmark = D.history_data('000300.SHA',start_date,end_date,fields=['close']).set_index('date')['close']
#
通过价格数据计算收益率数据并删除第一个元素,因为其为缺失值
r_a = asset.pct_change()[1:]
r_b = benchmark.pct_change()[1:]
linreg(r_b.values, r_a.values)
Out[3]:
OLS Regression Results
Dep. Variable:
y
R-squared:
Adj. R-squared:
F-statistic:
0.196
Model:
Method:
Date:
OLS
0.194
Least Squares
Tue, 09 May 2017
18:56:57
74.53
Prob (F-statistic):
Log-Likelihood:
3.37e-16
967.26
Time:
No. Observations:
Df Residuals:
307
AIC:
BIC:
-1931.
-1923.
305
Df Model:
1
Covariance T ype:
nonrobust
coef
std err
0.001
0.049
t
P>|t|
0.931
0.000
[0.025
0.975]
const
x1
5.152e-05
0.4253
0.087
8.633
-0.001
0.328
0.001
0.522
Omnibus:
91.263
Durbin-W atson:
Jarque-Bera (JB):
Prob(JB):
1.880
4735.483
0.00
Prob(Omnibus):
Skew:
0.000
-0.037
22.240
Kurtosis:
Cond. No.
83.0
上述图表中的每个点表示每一个交易日,x坐标是沪深300的收益率,y坐标是浦发银行的收益率。 我们可以看到,拟合度最好的线条告诉我们,沪深300收
益每增加1个百分点,浦发银行会增加0.42%。 这由参数$β$表示,估计值为0.4253。 当然,对于收益下降,我们也会看到浦发银行的损失大约不到一半,
所以我们看到,浦发银行比沪深300还要稳定
了解参数与估计值¶
非常重要的是,通过线性回归估计的$α$和$β$参数只是估计值。 除非你知道数据产生的的真实过程,否则你永远不会知道的真实参数。 你今天得到的估计
值和明天得到的估计值很可能不一样,即使使用相同的分析方法,真实参数可能也不断在变化。 因此,在进行实际分析时关注参数估计的标准误差是非常重
要的。 关于标准误差的更多资料我们将在后文中介绍。 了解估计值的稳定性的一种方法是使用 滚动数据窗口来估计它们。
例子¶
现在我们看看如果我们对两个随机变量进行回归会发生什么。
In [4]:
X = np.random.rand(100)
Y = np.random.rand(100)
linreg(X, Y)
Out[4]:
OLS Regression Results
Dep. Variable:
Model:
y
R-squared:
Adj. R-squared:
F-statistic:
0.059
0.049
6.090
0.0153
-18.045
40.09
45.30
OLS
Method:
Least Squares
Date:
Tue, 09 May 2017
Prob (F-statistic):
Log-Likelihood:
AIC:
Time:
18:59:02
No. Observations:
Df Residuals:
Df Model:
100
98
BIC:
1
Covariance T ype:
nonrobust
coef
std err
t
P>|t|
[0.025
0.277
0.048
0.975]
const
x1
0.3917
0.2450
0.058
0.099
6.765
2.468
0.000
0.015
0.507
0.442
Omnibus:
26.817
0.000
0.015
1.849
Durbin-W atson:
Jarque-Bera (JB):
Prob(JB):
1.605
Prob(Omnibus):
Skew:
5.519
0.0633
4.31
Kurtosis:
Cond. No.
上面显示了一个具有 正态分布 的云点。需要注意的是,即使有100个随机样本,拟合的直线依然具有可见的斜率。 这就是为什么使用统计数据而不是可视化
来验证结果的重要性。
现在,我们在X变量的基础上加 随机噪声来构造变量Y

In [21]:
Y = X + 0.2*np.random.randn(100)
linreg(X,Y)
Out[21]:
OLS Regression Results
Dep. Variable:
y
R-squared:
Adj. R-squared:
F-statistic:
0.684
Model:
Method:
OLS
0.681
Least Squares
212.4
Date:
Thu, 13 Apr 2017
Prob (F-statistic):
Log-Likelihood:
AIC:
2.85e-26
25.939
-47.88
-42.67
Time:
16:26:06
No. Observations:
Df Residuals:
Df Model:
100
98
BIC:
1
Covariance T ype:
nonrobust
coef
std err
t
P>|t|
0.454
0.000
[0.025
-0.050
0.849
0.975]
const
x1
0.0303
0.9827
0.040
0.067
0.751
14.573
0.110
1.116
Omnibus:
4.565
0.102
0.327
3.768
Durbin-W atson:
Jarque-Bera (JB):
Prob(JB):
2.210
4.238
0.120
4.64
Prob(Omnibus):
Skew:
Kurtosis:
Cond. No.
在上述情况下,拟合度最高的直线确实对因变量Y进行了很好的建模(因为具有较高的 R方值)。
基于模型进行预测时,不仅输出预测值,而且还输出 置信区间通常是非常有用的。我们可以使用python的 seaborn 库来进行可视化,不仅绘制拟合直线,还
会突出显示拟合直线的95%(默认)置信区间:
In [6]:
import seaborn
start_date = '2016-01-01'
end_date = '2017-05-08'
asset = D.history_data('600000.SHA',start_date,end_date,fields=['close']).set_index('date')['close']
benchmark = D.history_data('000300.SHA',start_date,end_date,fields=['close']).set_index('date')['close']
#
删除第一个元素(0th),因为其为缺失值
r_a = asset.pct_change()[1:]
r_b = benchmark.pct_change()[1:]
seaborn.regplot(r_b.values, r_a.values)
Out[6]:
<
matplotlib.axes._subplots.AxesSubplot at 0x7fac4a4556d8>
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-数学知识]多元线性回归
导语:多元线性回归的应用比较普遍,本文将对其做相关介绍。
金融理论从资本资产定价模型(CAPM)发展到套利定价理论(APT),在数理统计方面就是从应用一元线性回归发展到应用多元线性回归。在实际运用中,多元
线性回归比较普遍。
一元线性回归研究的是一个因变量和一个自变量的线性关系的模型,多元线性回归研究的是一个因变量和多个自变量的线性关系的模型。 多元线性回归模型
表示为:

其中,$i=1,2,...,n,n表示样本容量$,$K$表示自变量的个数。
与一元线性回归分析相同,其基本思想是根据 最小二乘($OLS$)原理,求解$\beta_0、\beta_1、\beta_2、...、\beta_K$使得全部观测值$Y_i$与回归值
$
\hat{Y_i}$的残差平方和达到最小值,该方法旨在最小化预测和观测之间的平方误差 ,$\sum_{i=0}^n\hat{u_i}^2$,平方项使得正的残差和负的残差同样被认为
是糟糕,并且将其放大。残差平方和表示如下:
本文将介绍多元线性回归模型的相关理论和实际运用,感兴趣的小朋友可以 克隆到自己的策略研究平台进行研究。
附件:多元线性回归的使用
In [3]:
import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels import regression
import matplotlib.pyplot as plt
In [1]:
Y = np.array([1, 3.5, 4, 8, 12])
Y_hat = np.array([1, 3, 5, 7, 9])
print('Error ' + str(Y_hat - Y))
#
计算残差平方
SE = (Y_hat - Y) ** 2
残差平方
print('Squared Error' + str(SE))
残差平方和
#
#
print('Sum Squared Error ' + str(np.sum(SE)))
Error [ 0. -0.5 1. -1. -3. ]
Squared Error[ 0.
0.25 1.
1.
9. ]
Sum Squared Error 11.25
一旦我们使用多元线性回归来确定回归的系数,我们将能够使用$X$的新观察值来预测$Y$的值。
每个系数$\beta_j$告诉我们,如果在保持所有其他因变量不变的情况下将$X_j$改变1个百分比,$Y_i$将会改变多少。这使我们可以分离不同自变量变化导
致因变量变化所产生的边际贡献。
In [4]:
#
我们首先人为构建一个我们知道精确关系的Y,X1和X2
X1 = np.arange(100)
#
X2 = X1^2 + X1
X2 = np.array([i ** 2 for i in range(100)]) + X1
Y = X1 + X2
plt.plot(X1, label='X1')
plt.plot(X2, label='X2')
plt.plot(Y, label='Y')
plt.legend();
In [5]:
#
使用 column_stack连接X1和X2这两个变量, 然后将单位向量作为截距项
X = sm.add_constant( np.column_stack( (X1, X2) ) )
#
运行回归模型
results = regression.linear_model.OLS(Y, X).fit()
print('Beta_0:', results.params[0])
print('Beta_1:', results.params[1])
print('Beta_2:', results.params[2])
Beta_0: 1.36424205266e-12
Beta_1: 1.0
Beta_2: 1.0

可以看出,$X_1$的系数为1,这是因为如果在保持$X_2$不变的情况下将$X_1$增加1%,则$Y$也增加1%。 可以看出,多元线性回归能够分析不同变量的
边际贡献。
如果我们使用一元线性回归来分析两个变量的关系,我们很可能会得到一个比较高的贝塔值,这样的分析是有失偏颇的,因此需要加入另外一个变量。请看
下面这个例子
In [6]:
#
获得贵州茅台、中国平安、沪深300的数据
start_date = '2014-01-01'
end_date = '2015-01-01'
asset1 = D.history_data('600519.SHA',start_date,end_date,fields=['close']).set_index('date')['close']
asset2 = D.history_data('000001.SZA',start_date,end_date,fields=['close']).set_index('date')['close']
benchmark = D.history_data('000300.SHA',start_date,end_date,fields=['close']).set_index('date')['close']
#
First, run a linear regression on the two assets
slr = regression.linear_model.OLS(asset1, sm.add_constant(asset2)).fit()
print('SLR beta of asset2:', slr.params[1])
SLR beta of asset2: 0.664051496894
In [8]:
#
将asset2和benchmark两个变量都看成自变量,然后进行多元回归
mlr = regression.linear_model.OLS(asset1, sm.add_constant(np.column_stack((asset2, benchmark)))).fit()
prediction = mlr.params[0] + mlr.params[1]*asset2 + mlr.params[2]*benchmark
prediction.name = 'Prediction'
print('MLR beta of asset2:', mlr.params[1], '\nMLR beta of 000300:', mlr.params[2])
MLR beta of asset2: -0.0133063437023
MLR beta of 000300: 0.237182936686
可以看出,之前只是一元线性回归的时候获取了一个较高的$\beta$(贝塔值)
得到分析结果以后,下一步是看看我们是否可以相信结果。一个简单有效的方法就是将变量值和预测者绘制在图表进行观察
In [82]:
asset1.name = 'asset1'
asset2.name = 'asset2'
benchmark.name = 'benchmark'
asset1.plot()
asset2.plot()
benchmark.plot()
prediction.plot(color='y')
plt.xlabel('return')
plt.legend(bbox_to_anchor=(1,1), loc=2);
In [9]:
#
只看观测值和预测值,可以看出预测的走势还是比较接近的
asset1.plot()
prediction.plot(color='y')
plt.xlabel('Price')
plt.legend();
我们可以从回归返回的结果中得到详细统计信息
In [84]:
mlr.summary()
Out[84]:
OLS Regression Results
Dep. Variable:
Model:
asset1
R-squared:
Adj. R-squared:
F-statistic:
0.461
OLS
0.456
Method:
Least Squares
Fri, 14 Apr 2017
11:02:09
103.4
Date:
Prob (F-statistic):
Log-Likelihood:
AIC:
3.53e-33
-1421.9
2850.
Time:
No. Observations:
245
Df Residuals:
Df Model:
242
BIC:
2860.
2
Covariance T ype:
nonrobust
coef
std err
39.897
0.189
0.064
t
P>|t|
[0.025
276.494
-0.385
0.111
0.975]
const
x1
355.0840
-0.0133
0.2372
8.900
-0.070
3.706
0.000
0.944
0.000
433.674
0.359
x2
0.363
Omnibus:
42.022
Durbin-W atson:
Jarque-Bera (JB):
Prob(JB):
0.039
Prob(Omnibus):
Skew:
0.000
-1.087
4.006
58.618
1.87e-13
1.94e+04
Kurtosis:
Cond. No.
下面是一个关于如何 选择模型的一个例子¶
当你决定应该包括哪些自变量的最佳模型时,有几种不同的方法来确定。如果你使用太多的自变量,你可能会增加模型 过拟合的风险,但如果你使用的太
少,你可能会 欠拟合。决定最佳模型的一个常用方法是 逐步回归。前向逐步回归从空模型开始,并测试每个变量,选择可以形成最佳模型的变量,通常用
AIC或BIC判定(该值越低越好)。然后,依次添加一个其余变量,在回归中测试每个随后的变量组合,并在每个步骤中计算AIC或BIC值。在回归结束时,
选择 具有AIC最低的模型,并将其确定为最终模型。但这确实也有局限性。它不能测试所有变量中的的每一个全部可能的组合,因此如果在逐步回归提前删
除了某个特定的变量,那么最终模型可能不是理论最佳模型。因此,逐步回归应结合你对模型变量的初始判断。
In [10]:
X1 = np.arange(100)
X2 = [i**2 for i in range(100)] - X1
X3 = [np.log(i) for i in range(1, 101)] + X2
X4 = 5 * X1
Y = 2 * X1 + 0.5 * X2 + 10 * X3 + X4
plt.plot(X1, label='X1')
plt.plot(X2, label='X2')
plt.plot(X3, label='X3')
plt.plot(X4, label='X4')
plt.plot(Y, label='Y')
plt.legend();
In [11]:
results = regression.linear_model.OLS(Y, sm.add_constant(np.column_stack((X1,X2,X3,X4)))).fit()
print("Beta_0: ", results.params[0])
print("Beta_1: ", results.params[1])
print("Beta_2: ", results.params[2])
print("Beta_3: ", results.params[3])
print("Beta_4: ", results.params[4])
Beta_0: -6.36646291241e-12
Beta_1: 0.269230769231
Beta_2: 0.499999999994
Beta_3: 10.0
Beta_4: 1.34615384615
In [12]:
data = pd.DataFrame(np.column_stack((X1,X2,X3,X4)), columns = ['X1','X2','X3','X4'])
response = pd.Series(Y, name='Y')
In [13]:
#
逐步回归
def forward_aic(response, data):
#
#
This function will work with pandas dataframes and series
Initialize some variables
explanatory = list(data.columns)
selected = pd.Series(np.ones(data.shape[0]), name="Intercept")
current_score, best_new_score = np.inf, np.inf
#
Loop while we haven't found a better model
while current_score == best_new_score and len(explanatory) != 0:

scores_with_elements = []
count = 0
#
For each explanatory variable
for element in explanatory:
Make a set of explanatory variables including our current best and the new one
tmp = pd.concat([selected, data[element]], axis=1)
Test the set
#
#
result = regression.linear_model.OLS(Y, tmp).fit()
score = result.aic
scores_with_elements.append((score, element, count))
count += 1
#
Sort the scoring list
scores_with_elements.sort(reverse = True)
# Get the best new variable
best_new_score, best_element, index = scores_with_elements.pop()
if current_score > best_new_score:
#
If it's better than the best add it to the set
explanatory.pop(index)
selected = pd.concat([selected, data[best_element]],axis=1)
current_score = best_new_score
#
Return the final model
model = regression.linear_model.OLS(Y, selected).fit()
return model
In [14]:
result = forward_aic(Y, data)
result.summary()
Out[14]:
OLS Regression Results
Dep. Variable:
Model:
y
R-squared:
Adj. R-squared:
F-statistic:
1.000
OLS
1.000
Method:
Least Squares
3.092e+26
0.00
Date:
Tue, 09 May 2017
Prob (F-statistic):
Log-Likelihood:
AIC:
Time:
19:42:06
1700.7
-3393.
-3383.
No. Observations:
Df Residuals:
Df Model:
100
96
BIC:
3
Covariance T ype:
nonrobust
coef
-1.455e-11
std err
t
P>|t|
0.998
0.000
0.000
0.000
0.000
[0.025
-1.39e-08
10.000
0.269
0.975]
1.39e-08
10.000
0.269
Intercept
X3
7.01e-09
4.24e-09
1.3e-11
-0.002
10.0000
0.2692
0.5000
1.3462
2.36e+09
2.08e+10
1.18e+08
2.08e+10
X1
X2
4.24e-09
6.48e-11
0.500
0.500
X4
1.346
1.346
Omnibus:
14.070
0.001
-0.647
2.152
Durbin-W atson:
Jarque-Bera (JB):
Prob(JB):
0.001
Prob(Omnibus):
Skew:
9.981
0.00680
6.22e+17
Kurtosis:
Cond. No.
在模型的构建中,可以很明显地看到变量$X_4$与变量$X_1$密切相关,只是将其乘以一个标量而已。 然而,逐步回归的方法并没有捕捉到这个信息,而是
简单地调整了$X_1$项的系数。 但是我们自己的判断会说,我们建模时应该剔除变量$X_4$,因此这显示出逐步回归的局限性。
还有其他方法来诊断模型,比如给予更复杂模型的不同程度的 惩罚。 我们以后再做深入介绍。
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。

[
量化学堂-数学知识]初识协整
导语: 本文介绍了协整的初步内容。
1
、 协整
1
.1 直观理解
协整是什么这个问题回答起来不是那么直观,因此我们先看下图,了解一下具有协整性的两只股票其价格走势有什么规律。
图
两只协整股票的走势
从图1中可以看出,两只股票具有同涨同跌的规律,长期以来两只股票的价差比较平稳,这种性质就是平稳性。如果两个股票具有强协整性,那么无论它们中
途怎么走的,它们前进的方向总是一样的。
1
.2 平稳性
提到协整,就不得不提平稳性。简单地说,平稳性(stationarity)是一个序列在时间推移中保持稳定不变的性质,它是我们在进行数据的分析预测时非常喜
欢的一个性质。如果一组时间序列数据是平稳的,那就意味着它的均值和方差保持不变,这样我们可以方便地在序列上使用一些统计技术。我们先看一个例
子,了解平稳和非平稳序列直观上长什么样。
图
平稳序列和非平稳序列
图2中,靠上的序列是一个平稳的序列,我们能看到它始终是围绕着一个长期均值在波动,靠下的序列是一个非平稳序列,我们能看到它的长期均值是变动
的。
1
.3 问题的提出
由于许多经济问题是非平稳的,这就给经典的回归分析方法带来了很大限制。在金融市场上也是如此,很多时间序列数据也是非平稳的,通常采用差分方法
消除序列中含有的非平稳趋势,使得序列平稳化后建立模型,比如使用ARIMA模型。
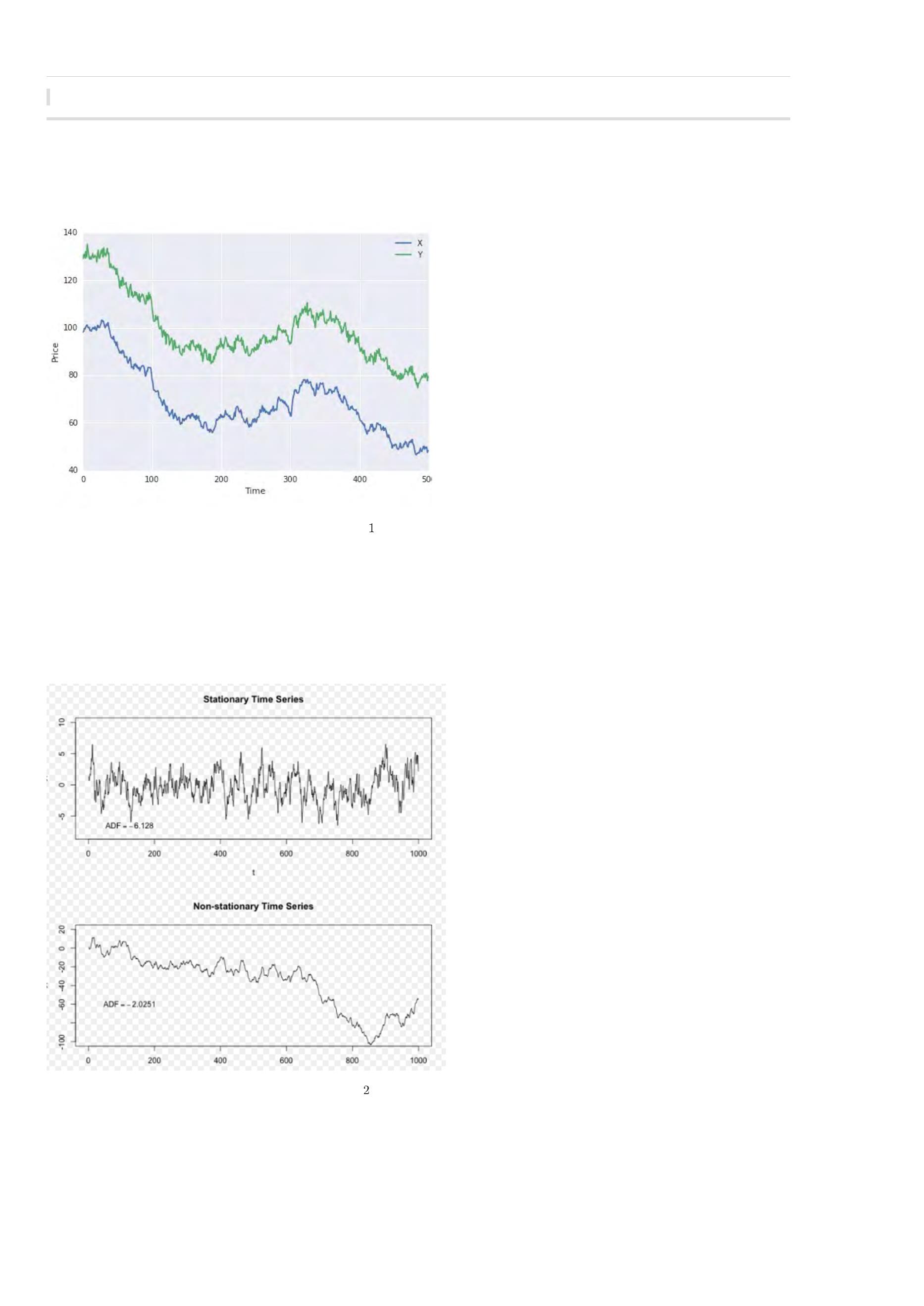
1
987年Engle和Granger提出的协整理论及其方法,为非平稳序列的建模提供了另一种途径。虽然一些经济变量的本身是非平稳序列,但是,它们的线性组合
却有可能是平稳序列。这种平稳的线性组合被称为协整方程,且可解释为变量之间的长期稳定的均衡关系。协整(co-integration)可被看作这种均衡关系性质
的统计表示。 如果两个变量是协整的,在短期内,因为季节影响或随机干扰,这些变量有可能偏离均值,但因为具有长期稳定的均衡关系,它们终将回归均
值。
1
.4 协整应用在量化投资中
基于协整的配对交易是一种基于数学分析交易策略,其盈利模式是通过两只证券的差价(spread)来获取,两者的股价走势虽然在中途会有所偏离,但是最终
都会趋于一致。具有这种关系的两个股票,在统计上称作协整性(cointegration),即它们之间的差价会围绕某一个均值来回摆动,这是配对交易策略可以
盈利的基础。当两只股票的价差过大,根据平稳性我们预期价差会收敛,因此买入低价的股票,卖空高价的股票,等待价格回归的时候进行反向操作从而获
利。
需要特别注意的是协整性和相关性虽然比较像,但实际是不同的两个东西。两个变量之间可以相关性强,协整性却很弱,比如说两条直线,y=x和y=2x,它
们之间的相关性是1,但是协整性却比较差;方波信号和白噪声信号,它们之间相关性很弱,但是却有强协整性。
图
相关性很弱,但是具有强协整性
2
、平稳性和检验方法
严格地说,平稳性可以分为严平稳(strictly stationary)和弱平稳(或叫协方差平稳,covariance stationary等)两种。严平稳是指一个序列始终具有不变的
分布函数,而弱平稳则是指具序列有不变的常量的描述性统计量。严平稳和弱平稳性质互不包含;但如果一个严平稳序列的方差是有限的,那么它是弱平稳
的。我们一般所说的平稳都是指弱平稳。在时间序列分析中,我们通常通过单位根检验(unit root test)来判断一个过程是否是弱平稳的。
一个常见的单位根检验方法是Dickey-Fuller test,大致思路如下:假设被检测的时间序列$Y_t$满足自回归模型$Y_t = \alpha Y_t−1+\epsilon_t$,其中
$
\alpha$为回归系数,$\epsilon_t$为噪声的随机变量。若经过检验,发现$\alpha<1$,则可以肯定序列是平稳的。
3
、举个应用的例子
附件:初始调整的例子:
我们人为地构造两组数据,由此直观地看一下协整关系。
In [17]:
import numpy as np
import pandas as pd
import seaborn
import statsmodels
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import coint
构造数据¶
首先,我们构造两组数据,每组数据长度为100。第一组数据为100加一个向下趋势项再加一个标准正态分布。第二组数据在第一组数据的基础上加30,再加
一个额外的标准正态分布。有:
其中$\gamma_t$为趋势项,$\epsilon_t$和$\mu_t$为无相关性的正态随机变量。
代码如下:
In [18]:
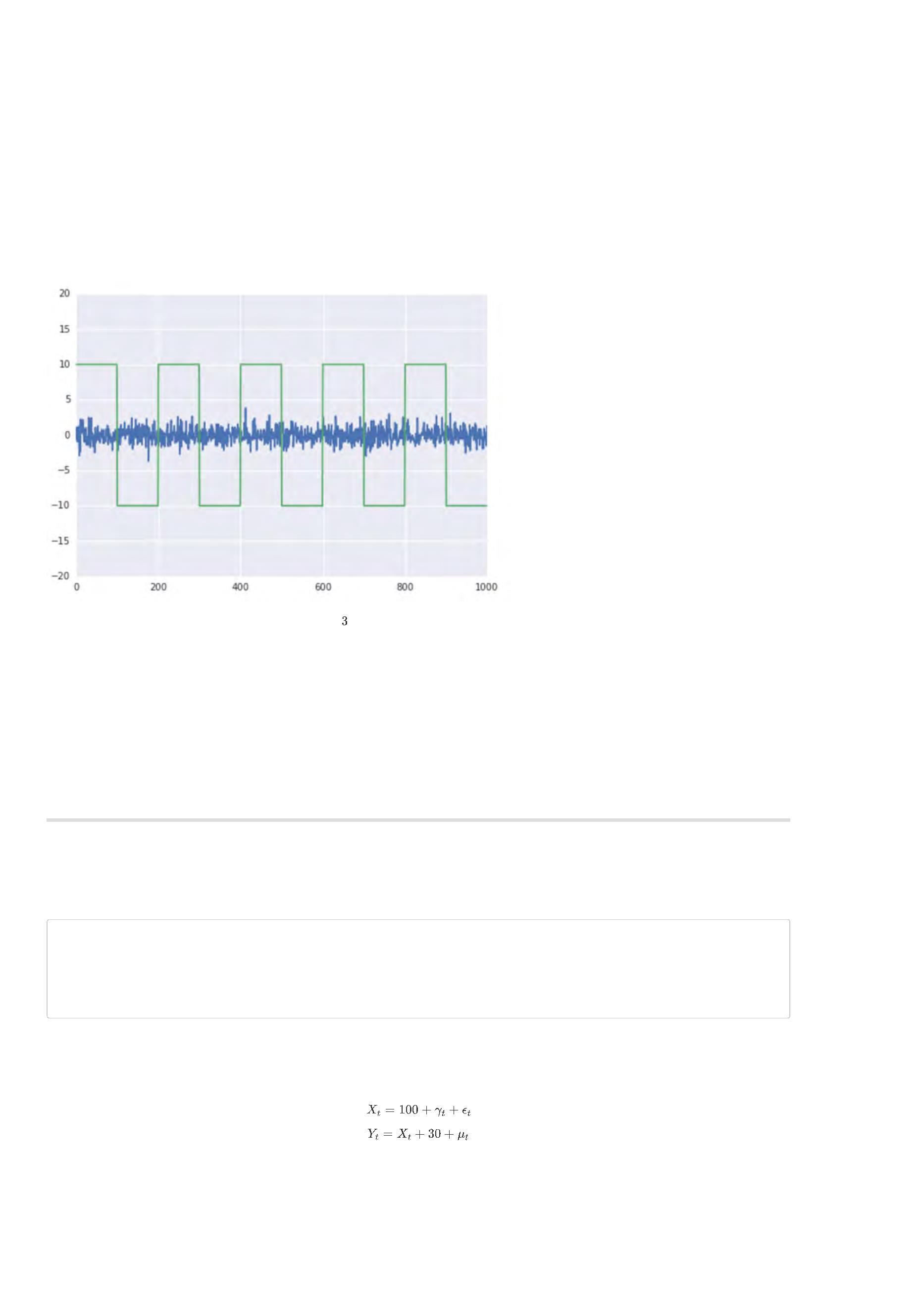
np.random.seed(100)
x = np.random.normal(0, 1, 500)
y = np.random.normal(0, 1, 500)
X = pd.Series(np.cumsum(x)) + 100
Y = X + y + 30
for i in range(500):
X[i] = X[i] - i/10
Y[i] = Y[i] - i/10
T.plot(pd.DataFrame({'X':X, 'Y':Y}), chart_type='line', title='Price')
显然,这两组数据都是非平稳的,因为均值随着时间的变化而变化。但这两组数据是具有协整关系的,因为他们的差序列$Y_t−X_t$是平稳的:
In [21]:
T.plot(pd.DataFrame({'Y-X':Y-X,'Mean':np.mean(Y-X)}),chart_type='line', title='Price')
上图中,可以看出蓝线$Y_t−X_t$一直围绕均值波动。而均值不随时间变化(其实方差也不随时间变化)。
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-数学知识]深入理解协整
导语:在上一篇文章《初始协整》我们已经对协整有一个直观的认识,本文将进行深入理解协整。
In [69]:
import numpy as np
import pandas as pd
import statsmodels
import statsmodels.api as sm
from statsmodels.tsa.stattools import coint, adfuller
import matplotlib.pyplot as plt
平稳性数据¶
时间序列分析中通常假设是数据具有平稳性。 当数据生成过程的参数不随时间变化时,数据是平稳的。 例如,我们考虑两个序列(Series)A和B,序列A是
从不变参数的过程生成的,系列B由随时间变化的参数生成。
In [70]:
#
该函数是产生服从正态分布的随机变量
def generate_datapoint(params):
mu = params[0]
sigma = params[1]
return np.random.normal(mu, sigma)
序列A
In [71]:
#
设置参数和数据量的个数
params = (0, 1)
T = 100
A = pd.Series(index=range(T))
A.name = 'A'
for t in range(T):
A[t] = generate_datapoint(params)
plt.plot(A)
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend(['Series A']);
序列B
In [72]:
T = 100
B = pd.Series(index=range(T))
B.name = 'B'

for t in range(T):
#
#
参数随时间变化
特别地,正态分布的均值随时间变化
params = (t * 0.1, 1)
B[t] = generate_datapoint(params)
plt.plot(B)
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend(['Series B']);
非平稳数据的危险性¶
许多统计实验深深地依赖于他们的假设,他们要求被测数据是平稳的。 另外,如果您在非平稳数据集上使用某些统计信息,您将获得没有意义的结果。 我们
来看一个例子:
In [73]:
m = np.mean(B)
plt.plot(B)
plt.hlines(m, 0, len(B), linestyles='dashed', colors='r')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend(['Series B', 'Mean']);
计算的平均值将显示所有数据点的平均值,但对于未来状态的任何预测都不会有用。 与任何特定时间相比,平均值是无意义的,因为它是不同时期的不同状
态的集合。 这只是一个简单而清楚的例子,说明为什么非平稳性实际上可能会出现更多的微妙问题。
平稳性检验¶
我们使用统计方法检验数据平稳性(借助statsmodels中的adfuller单位根检验函数)
In [74]:
def check_for_stationarity(X, cutoff=0.01):
#
#
原假设H0:单位根存在(非平稳)
我们通过重要的p值,以确认自己这个序列是平稳的
pvalue = adfuller(X)[1]
if pvalue < cutoff:
print('p-value = ' + str(pvalue) + ' The series ' + X.name +' is likely stationary.')
return True
else:
print('p-value = ' + str(pvalue) + ' The series ' + X.name +' is likely non-stationary.')
return False
In [75]:
check_for_stationarity(A);
check_for_stationarity(B);
p-value = 4.49381475504e-20 The series A is likely stationary.
p-value = 0.927553344971 The series B is likely non-stationary.
果然,序列A稳定,序列B不稳定。 我们接着尝试一个更微妙的例子。
In [76]:
#
设置数据量
T = 100
C = pd.Series(index=range(T))
C.name = 'C'
for t in range(T):
#
正态分布的均值也随时间改变
params = (np.sin(t), 1)
C[t] = generate_datapoint(params)
plt.plot(C)
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend(['Series C']);
平均值的周期运动将很难分离出随机噪声。 实际上,在噪声数据和样本量有限的情况下,很难确定一个序列是否是平稳的,以及漂移到底是是随机噪声还是
趋势。 你可以多次通过下面这个函数来检验序列C的平稳性,不同的实验得到的检验结果也不一样,有时候平稳有时候非平稳。
In [77]:

check_for_stationarity(C);
p-value = 2.47864416964e-07 The series C is likely stationary.
单个序列平稳性检验¶
In [78]:
symbol_list = ['000002.SZA'] # 以万科A数据举例
prices = D.history_data(symbol_list, fields=['close']
,
start_date='2014-01-01', end_date='2014-10-01')[['date','close']].set_index('date')
prices = prices['close']
prices.name = symbol_list[0]
In [79]:
check_for_stationarity(prices);
p-value = 0.836173033163 The series 000002.SZA is likely non-stationary.
检验得出万科A的股价数据并不符合平稳性特征,我们看下走势图
In [81]:
plt.plot(prices.index, prices.values)
plt.ylabel('Price')
plt.legend([prices.name]);
现在我们来看看这个序列的一阶差分,然后检查其平稳性。
In [82]:
X1 = prices.diff()[1:]
X1.name = prices.name + ' Additive Returns'
check_for_stationarity(X1)
plt.plot(X1.index, X1.values)
plt.ylabel('Additive Returns')
plt.legend([X1.name]);
p-value = 2.83752930846e-25 The series 000002.SZA Additive Returns is likely stationary.
通过价格这个序列,我们来检查每日收益率这个序列的平稳性。
In [83]:
X1 = prices.pct_change()[1:]
X1.name = prices.name + ' Daily Returns'
check_for_stationarity(X1)
plt.plot(X1.index, X1.values,)
plt.ylabel('Daily Returns')
plt.legend([X1.name]);
p-value = 1.05773457588e-25 The series 000002.SZA Daily Returns is likely stationary.
两只股票价格协整性检验¶
获取中信银行和交通银行的股票数据
In [84]:
symbol_list = ['601998.SHA', '601328.SHA']
prices = D.history_data(symbol_list, fields=['close']
,
start_date='2012-01-01', end_date='2017-01-01')
prices_df=pd.pivot_table(prices, values='close', index=['date'], columns=['instrument'])
X1 = prices_df[symbol_list[0]]
X2 = prices_df[symbol_list[1]]
绘制两只股票股价实际走势图
In [85]:
plt.plot(X1.index, X1.values)
plt.plot(X1.index, X2.values)
plt.xlabel('Time')

plt.ylabel('Series Value')
plt.legend([X1.name, X2.name]);
通过线性回归挖掘两只股票股价之间的关系
In [86]:
X1 = sm.add_constant(X1)
results = sm.OLS(X2, X1).fit()
#
Get rid of the constant column
X1 = X1[symbol_list[0]]
results.params
Out[86]:
const
01998.SHA
dtype: float64
1.221847
0.941158
6
可以发现两股票之间价格关系为: $601328.SHA = 0.94 * 601998.SHA + 1.22$
通过回归系数挖掘其长期稳定的关系
In [87]:
b = results.params[symbol_list[0]]
Z = X2 - b * X1
Z.name = 'Z'
plt.plot(Z.index, Z.values)
plt.xlabel('Time')
plt.ylabel('Series Value')
plt.legend([Z.name]);
check_for_stationarity(Z);
p-value = 0.00240769676666 The series Z is likely stationary.
可以看到,在我们看过的时间框架内,结果Z应该是平稳的。 这使得我们接受两个资产在同一时间框架内协整的假设。
此外,幸运地是对两个序列协整性的检验已经有现成的函数,通过stattools包的coint函数可直接检验协整性。
In [88]:
from statsmodels.tsa.stattools import coint
coint(X1, X2)
Out[88]:
(-3.9175752861575646,
0
.0093791668399287216,
array([-3.90549156, -3.34117182, -3.0479483 ]))
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-数学知识]峰度和偏度
导语:本文介绍了峰度和偏度以及如何运用这两个统计指标进行数据的正态性检验。
峰度和偏度这两个统计指标,在统计学上是非常重要的指标。在金融市场上,我们并不需要对其有深入了解,本文只是科普一些相关知识,重点是让大家明
白峰度、偏度是什么以及通过这两个指标如何做到数据的 正态性检验
之所以金融市场上正态性检验如此重要,这是因为很多模型假设就是数据服从正态分布,因此我们在使用模型前应该对数据进行正态性检验,否则前面假设
都没有满足,模型预测结果有何意义?
In [1]:
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats

有时候,平均值和方差不足以描述数据分布。 当我们计算方差时,我们对平均值的偏差进行了平方。 在偏差很大的情况下,我们不知道他们是否可能是积极
的或消极的。 这里涉及到了分布的偏斜度和对称性。如果一个分布中,均值的一侧的部分是另一侧的镜子,则分布是对称的。 例如,正态分布是对称的。
平均值$\mu$和标准差$\sigma$的正态分布定义为:
我们可以绘制它来确认它是对称的:
In [2]:
xs = np.linspace(-6,6, 300)
normal = stats.norm.pdf(xs)
plt.plot(xs, normal);
偏度¶
偏度是描述数据分布形态的一个常用统计量,其描述的是某总体取值分布的对称性。这个统计量同样需要与正态分布相比较,偏度为0表示其数据分布形态与
正态分布的偏斜程度相同;偏度大于0表示其数据分布形态与正态分布相比为正偏或右偏,即有一条长尾巴拖在右边,数据右端有较多的极端值;偏度小于0
表示其数据分布形态与正态分布相比为负偏或左偏,即有一条长尾拖在左边,数据左端有较多的极端值。偏度的绝对值数值越大表示其分布形态的偏斜程度
越大。
例如,分布可以具有许多小的正数和数个大的负值,这种情况是偏度为负,但仍然具有0的平均值,反之亦然(正偏度)。 对称分布的偏度0。正偏度分布
中,平均值>中值>众数 。 负偏度刚好相反,平均值<中位数<众数。 在一个完全对称的分布中,即偏度为0,此时平均值=中位数=众数。
偏度的计算公式为:
这里$n$所有观测值的个数, $\mu$是平均值, $\sigma$ 是标准差.
偏度的正负符号描述了数据分布的偏斜方向。
我们可以绘制一个正偏度和负偏度的分布,看看他们的样子。
对于单峰分布,负偏度通常表示尾部在左侧较大(长尾巴拖在左边),而正偏度表示尾部在右侧较大(长尾巴拖在右边)。
In [3]:
#
产生数据
xs2 = np.linspace(stats.lognorm.ppf(0.01, .7, loc=-.1), stats.lognorm.ppf(0.99, .7, loc=-.1), 150)
#
偏度>0
lognormal = stats.lognorm.pdf(xs2, .7)
plt.plot(xs2, lognormal, label='Skew > 0')
#
偏度<0
plt.plot(xs2, lognormal[::-1], label='Skew < 0')
plt.legend();
虽然在绘制离散数据集时,偏度不太明显,但我们仍然可以计算它。 例如,下面是2012-2014年沪深300收益率的偏度,平均值和中位数。
In [4]:
start = '2012-01-01'
end = '2015-01-01'
pricing = D.history_data('000300.SHA', start_date=start, end_date=end, fields='close')['close']
returns = pricing.pct_change()[1:]
print('Skew:', stats.skew(returns))
print('Mean:', np.mean(returns))
print('Median:', np.median(returns))
plt.hist(returns, 30);
Skew: 0.2597515285015106
Mean: 0.0006775385700166225
Median: 5.55515e-05
沪深300日收益率数据从图形上可以看出(但不是很明显),尾巴是拖在了右侧,因此有点右偏,这和计算的偏度值Skew=0.26为正刚好一致
峰度¶
峰度是描述总体中所有取值分布形态陡缓程度的统计量。这个统计量需要与正态分布相比较,峰度为3表示该总体数据分布与正态分布的陡缓程度相同;峰度
大于3表示该总体数据分布与正态分布相比较为陡峭,为尖顶峰;峰度小于3表示该总体数据分布与正态分布相比较为平坦,为平顶峰。峰度的绝对值数值越
大表示其分布形态的陡缓程度与正态分布的差异程度越大。

峰度的具体计算公式为:
在Scipy中,使用峰度与正态分布峰度的差值来定义分布形态的陡缓程度——超额峰度,用$K_E$表示:
如果数据量很大,那么
In [5]:
plt.plot(xs,stats.laplace.pdf(xs), label='Leptokurtic')
print('尖峰的超额峰度:', (stats.laplace.stats(moments='k')))
plt.plot(xs, normal, label='Mesokurtic (normal)')
print('正态分布超额峰度:', (stats.norm.stats(moments='k')))
plt.plot(xs,stats.cosine.pdf(xs), label='Platykurtic')
print('平峰超额峰度:', (stats.cosine.stats(moments='k')))
plt.legend();
尖峰的超额峰度: 3.0
正态分布超额峰度: 0.0
平峰超额峰度: -0.5937628755982794
接着沪深300的例子,我们可以使用Scipy包来计算沪深300日收益率的超额峰度
In [6]:
print("沪深300的超额峰度: ", stats.kurtosis(returns))
沪深300的超额峰度: 2.1539229504687754
使用Jarque-Bera 的正态检验¶
Jarque-Bera检验是一个通用的统计检验,可以比较样本数据是否具有与正态分布一样的偏度和峰度。 Jarque Bera检验的零假设是数据服从正态分布。 默认
时p值为0.05。
接着上面沪深300的例子我们来检验沪深300收益率数据是否服从正态分布。
In [7]:
from statsmodels.stats.stattools import jarque_bera
_
, pvalue, _, _ = jarque_bera(returns)
if pvalue > 0.05:
print('沪深300收益率数据服从正态分布.')
else:
print('沪深300收益率数据并不服从正态分布.')
沪深300收益率数据并不服从正态分布.
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-数学知识]数据异常值处理
导论:异常值问题在数据分析中经常遇到,本文介绍了多种处理数据异常值的方法。
在金融数据分析中,常常会遇到一些值过大或者过小的情况,当用这些值来构造其他特征的时候,可能使得其他的特征也是异常点,这将严重影响对金融数
据的分析,或者是影响模型的训练。下面将带大家学习一些关于异常点处理的常用方法。
1
、固定比例法
这种方法非常容易理解,我们把上下2%的值重新设置,若大于99%分位数的数值,则将其设置为99%分位数值,若低于1%分位数的数值,则将其重新设置
为1%分位数值
2
、均值标准差法

这种想法的思路来自于正态分布,假设$X∼N(μ,σ^2)$,那么:
通常把三倍标准差之外的值都视为异常值,不过要注意的是样本均值和样本标准差都不是稳健统计量,其计算本身受极值的影响就非常大,所以可能会出现
一种情况,那就是我们从数据分布图上能非常明显的看到异常点,但按照上面的计算方法,这个异常点可能仍在均值三倍标准差的范围内。因此按照这种方
法剔除掉异常值后,需要重新观察数据的分布情况,看是否仍然存在显著异常点,若存在则继续重复上述步骤寻找异常点。
3
、MAD法
MAD 法是针对均值标准差方法的改进,把均值和标准差替换成稳健统计量,样本均值用样本中位数代替,样本标准差用样本MAD(Median Absolute
Deviation)代替:
一般将偏离中位数三倍以上的数据作为异常值,和均值标准差法相比,其中位数和$MAD$不受异常值的影响。
4
、BOXPLOT法
我们知道箱线图上也会注明异常值,假设Q1和Q3分别为数据从小到大排列的25%和75%分位数,记 $ IQR=Q1-Q3 $ ,把
区间里的数据标识为异常点。分位数也是稳健统计量,因此Boxplot 方法对极值不敏感,但如果样本数据正偏严重,且右尾分布明显偏厚时,Boxplot 方法会
把过多的数据划分为异常数据,因此Hubert& Vandervieren (2007)对原有Boxplot 方法进行了偏度调整。首先样本偏度定义采用了Brys(2004)提出的
MedCouple方法
然后给出了经偏度调整boxplot方法上下限:
附件:处理数据异常值的方法
异常数据的影响和识别¶
我们以2017年4月21日的A股所有股票的净资产收益率数据为例,这是一个横截面数据
In [268]:
fields = ['fs_roe_0']
start_date = '2017-04-21'
end_date = '2017-04-21'
instruments = D.instruments(start_date, end_date)
roe = D.features(instruments, start_date, end_date, fields=fields)['fs_roe_0']
1
、描述性统计¶
In [269]:
print('均值:',roe.mean())
print('标准差:',roe.std())
roe.describe()
均值: 6.321435932147683
标准差: 21.523493941199046
Out[269]:
count
mean
std
2782.000000
6.321436
21.523494
-190.077896
1.913875
min
2
5%

5
7
0%
5%
5.625300
10.413725
949.800476
max
Name: fs_roe_0, dtype: float64
可以看出,接近2800家公司的净资产收益率的平均值为6.32,标准差为21.52,最大值为949.8,最小值为-190.08
2
、绘制 直方图¶
In [270]:
roe.hist(bins=100)
Out[270]:
<
matplotlib.axes._subplots.AxesSubplot at 0x7f969c64fa58>
四种关于异常值处理的方法¶
1
、固定比例法¶
In [271]:
roe = D.features(instruments, start_date, end_date, fields=fields)['fs_roe_0']
roe[roe >= roe.quantile(0.99)] = roe.quantile(0.99)
roe[roe <= roe.quantile(0.01)] = roe.quantile(0.01)
print('均值:',roe.mean())
print('标准差:',roe.std())
roe.hist(bins=100)
均值: 6.2873811630663585
标准差: 8.225571051255967
Out[271]:
<
matplotlib.axes._subplots.AxesSubplot at 0x7f96a0a9d7f0>
2
、均值标准差方法¶
通常把三倍标准差之外的值都视为异常值,然后将这些异常值重新赋值
In [272]:
roe = D.features(instruments, start_date, end_date, fields=fields)['fs_roe_0']
roe[roe >= roe.mean() + 3*roe.std()] = roe.mean() + 3*roe.std()
roe[roe <= roe.mean() - 3*roe.std()] = roe.mean() - 3*roe.std()
print('均值:',roe.mean())
print('标准差:',roe.std())
roe.hist(bins=100)
均值: 6.380022262323887
标准差: 8.907421676828216
Out[272]:
<
matplotlib.axes._subplots.AxesSubplot at 0x7f969b5e7a90>
3
、MAD方法¶
In [273]:
roe = D.features(instruments, start_date, end_date, fields=fields)['fs_roe_0']
roe = roe.dropna()
median = np.median(list(roe))
MAD = np.mean(abs(roe) - median)
roe = roe[abs(roe-median)/MAD <=6] # 剔除偏离中位数6倍以上的数据
print('均值:',roe.mean())
print('标准差:',roe.std())
roe.hist(bins=100)
均值: 6.379718635607307
标准差: 5.917957128386792
Out[273]:

<
matplotlib.axes._subplots.AxesSubplot at 0x7f969b467f60>
4
、boxplot 法¶
In [274]:
from statsmodels.stats.stattools import medcouple
roe = D.features(instruments, start_date, end_date, fields=fields)['fs_roe_0']
roe = roe.dropna()
def boxplot(data):
#
mc可以使用statsmodels包中的medcouple函数直接进行计算
mc = medcouple(data)
data.sort()
q1 = data[int(0.25 * len(data))]
q3 = data[int(0.75 * len(data))]
iqr = q3-q1
if mc >= 0:
l = q1-1.5 * np.exp(-3.5 * mc) * iqr
u = q3 + 1.5 * np.exp(4 * mc) * iqr
else:
l = q1 - 1.5 * np.exp(-4 * mc) * iqr
u = q3 + 1.5 * np.exp(3.5 * mc) * iqr
data = pd.Series(data)
data[data < l] = l
data[data > u] = u
return data
print('均值',boxplot(list(roe)).mean())
print('标准差',boxplot(list(roe)).std())
boxplot(list(roe)).hist(bins=100)
均值 6.734053462301644
标准差 7.026413849518903
Out[274]:
<
matplotlib.axes._subplots.AxesSubplot at 0x7f969c152630>
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
机器学习
[
量化学堂-机器学习]什么是机器学习
导语:本文介绍了机器学习的相关内容。
先从一个故事讲起
机器学习这个词是让人疑惑的,首先它是英文名称Machine Learning(简称ML)的直译,在计算界Machine一般指计算机。这个名字使用了拟人的手法,说明
了这门技术是让机器“学习”的技术。但是计算机是死的,怎么可能像人类一样“学习”呢?
传统上如果我们想让计算机工作,我们给它一串指令,然后它遵照这个指令一步步执行下去。有因有果,非常明确。但这样的方式在机器学习中行不通。机
器学习根本不接受你输入的指令,相反,它接受你输入的数据! 也就是说,机器学习是一种让计算机利用数据而不是指令来进行各种工作的方法。这听起来非
常不可思议,但结果上却是非常可行的。“统计”思想将在你学习“机器学习”相关理念时无时无刻不伴随,相关而不是因果的概念将是支撑机器学习能够工作的
核心概念。你会颠覆对你以前所有程序中建立的因果无处不在的根本理念。
下面我通过一个故事来简单地阐明什么是机器学习。这个故事比较适合用在知乎上作为一个概念的阐明。在这里,这个故事没有展开,但相关内容与核心是
存在的。如果你想简单的了解一下什么是机器学习,那么看完这个故事就足够了。如果你想了解机器学习的更多知识以及与它关联紧密的当代技术,那么请
你继续往下看,后面有更多的丰富的内容。
这个例子来源于我真实的生活经验,我在思考这个问题的时候突然发现它的过程可以被扩充化为一个完整的机器学习的过程,因此我决定使用这个例子作为
所有介绍的开始。这个故事称为“等人问题”。
我相信大家都有跟别人相约,然后等人的经历。现实中不是每个人都那么守时的,于是当你碰到一些爱迟到的人,你的时间不可避免的要浪费。我就碰到过
这样的一个例子。
对我的一个朋友小Y而言,他就不是那么守时,最常见的表现是他经常迟到。当有一次我跟他约好3点钟在某个麦当劳见面时,在我出门的那一刻我突然想到
一个问题:我现在出发合适么?我会不会又到了地点后,花上30分钟去等他?我决定采取一个策略解决这个问题。
要想解决这个问题,有好几种方法。第一种方法是采用知识:我搜寻能够解决这个问题的知识。但很遗憾,没有人会把如何等人这个问题作为知识传授,因
此我不可能找到已有的知识能够解决这个问题。第二种方法是问他人:我去询问他人获得解决这个问题的能力。但是同样的,这个问题没有人能够解答,因

为可能没人碰上跟我一样的情况。第三种方法是准则法:我问自己的内心,我有否设立过什么准则去面对这个问题?例如,无论别人如何,我都会守时到
达。但我不是个死板的人,我没有设立过这样的规则。
事实上,我相信有种方法比以上三种都合适。我把过往跟小Y相约的经历在脑海中重现一下,看看跟他相约的次数中,迟到占了多大的比例。而我利用这来
预测他这次迟到的可能性。如果这个值超出了我心里的某个界限,那我选择等一会再出发。假设我跟小Y约过5次,他迟到的次数是1次,那么他按时到的比
例为80%,我心中的阈值为70%,我认为这次小Y应该不会迟到,因此我按时出门。如果小Y在5次迟到的次数中占了4次,也就是他按时到达的比例为20%,
由于这个值低于我的阈值,因此我选择推迟出门的时间。这个方法从它的利用层面来看,又称为经验法。在经验法的思考过程中,我事实上利用了以往所有
相约的数据。因此也可以称之为依据数据做的判断。
依据数据所做的判断跟机器学习的思想根本上是一致的。
刚才的思考过程我只考虑“频次”这种属性。在真实的机器学习中,这可能都不算是一个应用。一般的机器学习模型至少考虑两个量:一个是因变量,也就是
我们希望预测的结果,在这个例子里就是小Y迟到与否的判断。另一个是自变量,也就是用来预测小Y是否迟到的量。假设我把时间作为自变量,譬如我发现
小Y所有迟到的日子基本都是星期五,而在非星期五情况下他基本不迟到。于是我可以建立一个模型,来模拟小Y迟到与否跟日子是否是星期五的概率。如图
1:
图
决策树模型
这样的图就是一个最简单的机器学习模型,称之为决策树。
当我们考虑的自变量只有一个时,情况较为简单。如果把我们的自变量再增加一个。例如小Y迟到的部分情况时是在他开车过来的时候(你可以理解为他开车
水平较臭,或者路较堵)。于是我可以关联考虑这些信息。建立一个更复杂的模型,这个模型包含两个自变量与一个因变量。
再更复杂一点,小Y的迟到跟天气也有一定的原因,例如下雨的时候,这时候我需要考虑三个自变量。
如果我希望能够预测小Y迟到的具体时间,我可以把他每次迟到的时间跟雨量的大小以及前面考虑的自变量统一建立一个模型。于是我的模型可以预测值,
例如他大概会迟到几分钟。这样可以帮助我更好的规划我出门的时间。在这样的情况下,决策树就无法很好地支撑了,因为决策树只能预测离散值,但许多
其他机器学习模型,比如线性回归可以预测连续值。
如果我把这些建立模型的过程交给电脑。比如把所有的自变量和因变量输入,然后让计算机帮我生成一个模型,同时让计算机根据我当前的情况,给出我是
否需要迟出门,需要迟几分钟的建议。那么计算机执行这些辅助决策的过程就是机器学习的过程。
机器学习方法是计算机利用已有的数据(经验),得出了某种模型(迟到的规律),并利用此模型预测未来(是否迟到)的一种方法。
通过上面的分析,可以看出机器学习与人类思考的经验过程是类似的,不过它能考虑更多的情况,执行更加复杂的计算。事实上,机器学习的一个主要目的
就是把人类思考归纳经验的过程转化为计算机通过对数据的处理计算得出模型的过程。经过计算机得出的模型能够以近似于人的方式解决很多灵活复杂的问
题。
机器学习的定义
从广义上来说,机器学习是一种能够赋予机器学习的能力以此让它完成直接编程无法完成的功能的方法。但从实践的意义上来说,机器学习是一种通过利用
数据,训练出模型,然后使用模型预测的一种方法。
让我们具体看一个例子。(见图2)
图
房价的例子
拿国民话题的房子来说。现在我手里有一栋房子需要售卖,我应该给它标上多大的价格?房子的面积是100平方米,价格是100万,120万,还是140万?
很显然,我希望获得房价与面积的某种规律。那么我该如何获得这个规律?用报纸上的房价平均数据么?还是参考别人面积相似的?无论哪种,似乎都并不
是太靠谱。
我现在希望获得一个合理的,并且能够最大程度的反映面积与房价关系的规律。于是我调查了周边与我房型类似的一些房子,获得一组数据。这组数据中包
含了大大小小房子的面积与价格,如果我能从这组数据中找出面积与价格的规律,那么我就可以得出房子的价格。
对规律的寻找很简单,拟合出一条直线,让它“穿过”所有的点,并且与各个点的距离尽可能的小。
通过这条直线,我获得了一个能够最佳反映房价与面积规律的规律。这条直线同时也是一个下式所表明的函数:
房价 = 面积 * a + b
上述中的a、b都是直线的参数。获得这些参数以后,我就可以计算出房子的价格。
假设a = 0.75,b = 50,则房价 = 100 * 0.75 + 50 = 125万。这个结果与我前面所列的100万,120万,140万都不一样。由于这条直线综合考虑了大部分的情
况,因此从“统计”意义上来说,这是一个最合理的预测。
在求解过程中透露出了两个信息:
1
.房价模型是根据拟合的函数类型决定的。如果是直线,那么拟合出的就是直线方程。如果是其他类型的线,例如抛物线,那么拟合出的就是抛物线方程。
机器学习有众多算法,一些强力算法可以拟合出复杂的非线性模型,用来反映一些不是直线所能表达的情况。
2
.如果我的数据越多,我的模型就越能够考虑到越多的情况,由此对于新情况的预测效果可能就越好。这是机器学习界“数据为王”思想的一个体现。一般来说
(不是绝对),数据越多,最后机器学习生成的模型预测的效果越好。
通过我拟合直线的过程,我们可以对机器学习过程做一个完整的回顾。首先,我们需要在计算机中存储历史的数据。接着,我们将这些 数据通过机器学习算
法进行处理,这个过程在机器学习中叫做“训练”,处理的结果可以被我们用来对新的数据进行预测,这个结果一般称之为“模型”。对新数据 的预测过程在机
器学习中叫做“预测”。“训练”与“预测”是机器学习的两个过程,“模型”则是过程的中间输出结果,“训练”产生“模型”,“模型”指导 “预测”。
让我们把机器学习的过程与人类对历史经验归纳的过程做个比对。(见图3)
图
机器学习与人类思考的类比
人类在成长、生活过程中积累了很多的历史与经验。人类定期地对这些经验进行“归纳”,获得了生活的“规律”。当人类遇到未知的问题或者需要对未来进
行“推测”的时候,人类使用这些“规律”,对未知问题与未来进行“推测”,从而指导自己的生活和工作。
机器学习中的“训练”与“预测”过程可以对应到人类的“归纳”和“推测”过程。通过这样的对应,我们可以发现,机器学习的思想并不复杂,仅仅是对人类在生活
中学习成长的一个模拟。由于机器学习不是基于编程形成的结果,因此它的处理过程不是因果的逻辑,而是通过归纳思想得出的相关性结论。
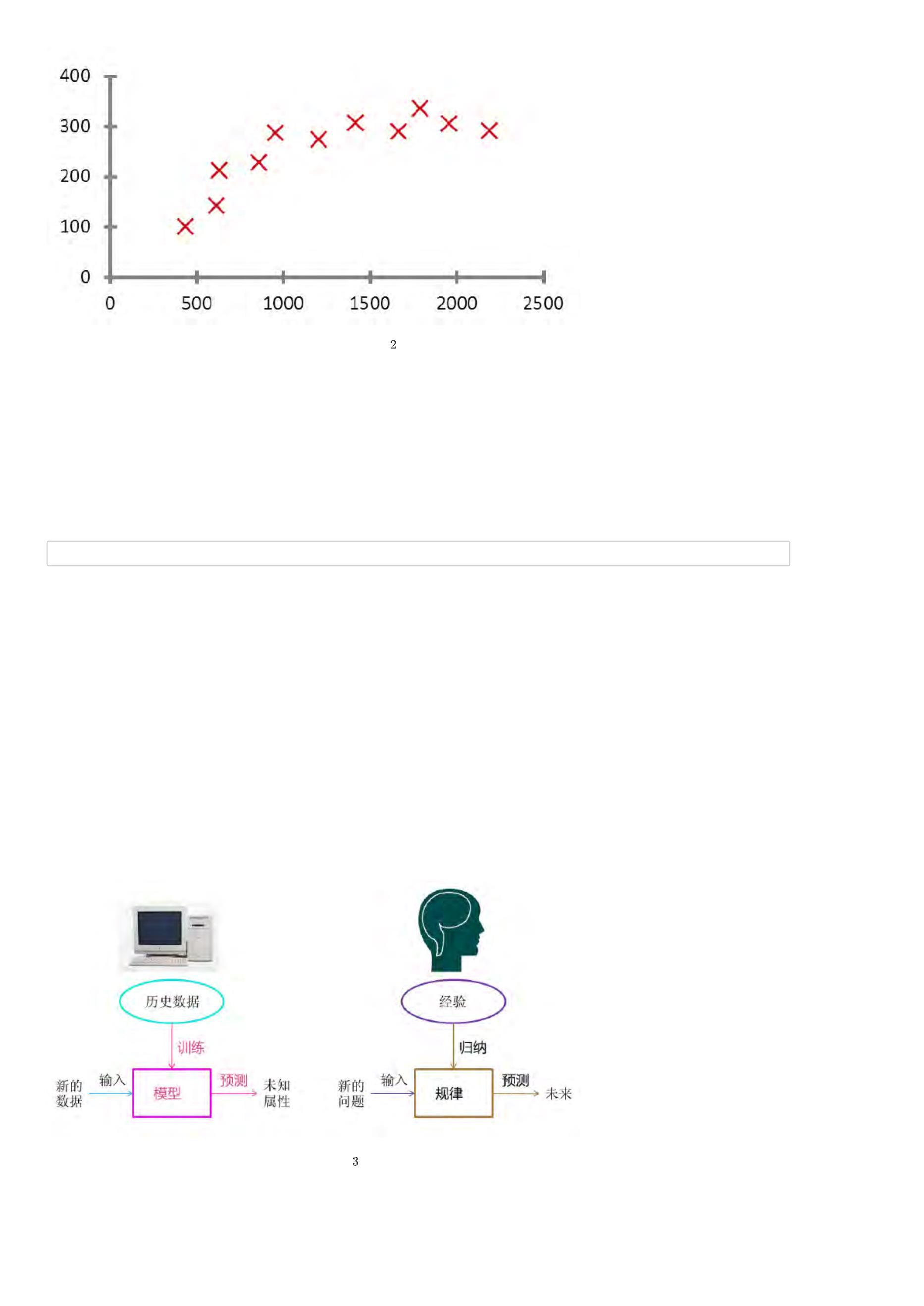
这也可以联想到人类为什么要学习历史,历史实际上是人类过往经验的总结。有句话说得很好,“历史往往不一样,但历史总是惊人的相似”。通过学习历
史,我们从历史中归纳出人生与国家的规律,从而指导我们的下一步工作,这是具有莫大价值的。当代一些人忽视了历史的本来价值,而是把其作为一种宣
扬功绩的手段,这其实是对历史真实价值的一种误用。
机器学习的范围
上文虽然说明了机器学习是什么,但是并没有给出机器学习的范围。
其实,机器学习跟模式识别,统计学习,数据挖掘,计算机视觉,语音识别,自然语言处理等领域有着很深的联系。
从范围上来说,机器学习跟模式识别,统计学习,数据挖掘是类似的,同时,机器学习与其他领域的处理技术的结合,形成了计算机视觉、语音识别、自然
语言处理等交叉学科。因此,一般说数据挖掘时,可以等同于说机器学习。同时,我们平常所说的机器学习应用,应该是通用的,不仅仅局限在结构化数
据,还有图像,音频等应用。
在这节对机器学习这些相关领域的介绍有助于我们理清机器学习的应用场景与研究范围,更好的理解后面的算法与应用层次。
下图是机器学习所牵扯的一些相关范围的学科与研究领域。(见图4)
图
机器学习与相关学科
模式识别
模式识别=机器学习。两者的主要区别在于前者是从工业界发展起来的概念,后者则主要源自计算机学科。在著名的《Pattern Recognition And Machine
Learning》这本书中,Christopher M. Bishop在开头是这样说的“模式识别源自工业界,而机器学习来自于计算机学科。不过,它们中的活动可以被视为同一
个领域的两个方面,同时在过去的10年间,它们都有了长足的发展”。
数据挖掘
数据挖掘=机器学习+数据库。这几年数据挖掘的概念实在是太耳熟能详。几乎等同于炒作。但凡说数据挖掘都会吹嘘数据挖掘如何如何,例如从数据中挖出
金子,以及将废弃的数据转化为价值等等。但是,我尽管可能会挖出金子,但我也可能挖的是“石头”啊。这个说法的意思是,数据挖掘仅仅是一种思考方
式,告诉我们应该尝试从数据中挖掘出知识,但不是每个数据都能挖掘出金子的,所以不要神话它。一个系统绝对不会因为上了一个数据挖掘模块就变得无
所不能(这是IBM最喜欢吹嘘的),恰恰相反,一个拥有数据挖掘思维的人员才是关键,而且他还必须对数据有深刻的认识,这样才可能从数据中导出模式指引
业务的改善。大部分数据挖掘中的算法是机器学习的算法在数据库中的优化。
统计学习
统计学习近似等于机器学习。统计学习是个与机器学习高度重叠的学科。因为机器学习中的大多数方法来自统计学,甚至可以认为,统计学的发展促进机器
学习的繁荣昌盛。例如著名的支持向量机算法,就是源自统计学科。但是在某种程度上两者是有分别的,这个分别在于:统计学习者重点关注的是统计模型
的发展与优化,偏数学,而机器学习者更关注的是能够解决问题,偏实践,因此机器学习研究者会重点研究学习算法在计算机上执行的效率与准确性的提
升。
计算机视觉
计算机视觉=图像处理+机器学习。图像处理技术用于将图像处理为适合进入机器学习模型中的输入,机器学习则负责从图像中识别出相关的模式。计算机视
觉相关的应用非常的多,例如百度识图、手写字符识别、车牌识别等等应用。这个领域是应用前景非常火热的,同时也是研究的热门方向。随着机器学习的
新领域深度学习的发展,大大促进了计算机图像识别的效果,因此未来计算机视觉界的发展前景不可估量。
语音识别
语音识别=语音处理+机器学习。语音识别就是音频处理技术与机器学习的结合。语音识别技术一般不会单独使用,一般会结合自然语言处理的相关技术。目
前的相关应用有苹果的语音助手siri等。
自然语言处理
自然语言处理=文本处理+机器学习。自然语言处理技术主要是让机器理解人类的语言的一门领域。在自然语言处理技术中,大量使用了编译原理相关的技
术,例如词法分析,语法分析等等,除此之外,在理解这个层面,则使用了语义理解,机器学习等技术。作为唯一由人类自身创造的符号,自然语言处理一
直是机器学习界不断研究的方向。按照百度机器学习专家余凯的说法“听与看,说白了就是阿猫和阿狗都会的,而只有语言才是人类独有的”。如何利用机器
学习技术进行自然语言的的深度理解,一直是工业和学术界关注的焦点。
可以看出机器学习在众多领域的外延和应用。机器学习技术的发展促使了很多智能领域的进步,改善着我们的生活。
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-机器学习]机器学习有哪些常用算法
导语:通过文章《什么是机器学习》我们大概知晓了机器学习,那么机器学习里面究竟有多少经典的算法呢?本文简要介绍一下机器学习中的常用算
法。这部分介绍的重点是这些方法内涵的思想,数学与实践细节不会在这讨论。
1
、回归算法
在大部分机器学习课程中,回归算法都是介绍的第一个算法。原因有两个:一.回归算法比较简单,介绍它可以让人平滑地从统计学迁移到机器学习中。二.回
归算法是后面若干强大算法的基石,如果不理解回归算法,无法学习那些强大的算法。回归算法有两个重要的子类:即 线性回归 和 逻辑回归 。
线性回归就是我们前面说过的房价求解问题。如何拟合出一条直线最佳匹配我所有的数据?一般使用“最小二乘法”来求解。“最小二乘法”的思想是这样的,假
设我们拟合出的直线代表数据的真实值,而观测到的数据代表拥有误差的值。为了尽可能减小误差的影响,需要求解一条直线使所有误差的平方和最小。最
小二乘法将最优问题转化为求函数极值问题。函数极值在数学上我们一般会采用求导数为0的方法。但这种做法并不适合计算机,可能求解不出来,也可能计
算量太大。
计算机科学界专门有一个学科叫“数值计算”,专门用来提升计算机进行各类计算时的准确性和效率问题。例如,著名的“梯度下降”以及“牛顿法”就是数值计算
中的经典算法,也非常适合来处理求解函数极值的问题。梯度下降法是解决回归模型中最简单且有效的方法之一。从严格意义上来说,由于后文中的神经网
络和推荐算法中都有线性回归的因子,因此梯度下降法在后面的算法实现中也有应用。
逻辑回归是一种与线性回归非常类似的算法,但是,从本质上讲,线型回归处理的问题类型与逻辑回归不一致。线性回归处理的是数值问题,也就是最后预
测出的结果是数字,例如房价。而逻辑回归属于分类算法,也就是说,逻辑回归预测结果是离散的分类,例如判断这封邮件是否是垃圾邮件,以及用户是否
会点击此广告等等。
实现方面的话,逻辑回归只是对对线性回归的计算结果加上了一个Sigmoid函数,将数值结果转化为了0到1之间的概率(Sigmoid函数的图像一般来说并不直
观,你只需要理解对数值越大,函数越逼近1,数值越小,函数越逼近0),接着我们根据这个概率可以做预测,例如概率大于0.5,则这封邮件就是垃圾邮
件,或者肿瘤是否是恶性的等等。从直观上来说,逻辑回归是画出了一条分类线,见图1。
图
逻辑回归的直观解释
假设我们有一组肿瘤患者的数据,这些患者的肿瘤中有些是良性的(图中的蓝色点),有些是恶性的(图中的红色点)。这里肿瘤的红蓝色可以被称作数据的“标
签”。同时每个数据包括两个“特征”:患者的年龄与肿瘤的大小。我们将这两个特征与标签映射到这个二维空间上,形成了我上图的数据。
当我有一个绿色的点时,我该判断这个肿瘤是恶性的还是良性的呢?根据红蓝点我们训练出了一个逻辑回归模型,也就是图中的分类线。这时,根据绿点出
现在分类线的右侧,因此我们判断它的标签应该是红色,也就是说属于恶性肿瘤。
逻辑回归算法划出的分类线基本都是线性的(也有划出非线性分类线的逻辑回归,不过那样的模型在处理数据量较大的时候效率会很低),这意味着当两类之
间的界线不是线性时,逻辑回归的表达能力就不足。下面的两个算法是机器学习界最强大且重要的算法,都可以拟合出非线性的分类线。
2
、神经网络
神经网络(也称之为人工神经网络,ANN)算法是80年代机器学习界非常流行的算法,不过在90年代中途衰落。现在,携着“深度学习”之势,神经网络重装归
来,重新成为最强大的机器学习算法之一。
神经网络的诞生起源于对大脑工作机理的研究。早期生物界学者们使用神经网络来模拟大脑。机器学习的学者们使用神经网络进行机器学习的实验,发现在
视觉与语音的识别上效果都相当好。在BP算法(加速神经网络训练过程的数值算法)诞生以后,神经网络的发展进入了一个热潮。BP算法的发明人之一是前面
介绍的机器学习大牛Geoffrey Hinton(图1中的中间者)。
具体说来,神经网络的学习机理是什么?简单来说,就是 分解与整合。在著名的Hubel-Wiesel试验中,学者们研究猫的视觉分析机理是这样的。(如图2)

图
试验与大脑视觉机理
比方说,一个正方形,分解为四个折线进入视觉处理的下一层中。四个神经元分别处理一个折线。每个折线再继续被分解为两条直线,每条直线再被分解为
黑白两个面。于是,一个复杂的图像变成了大量的细节进入神经元,神经元处理以后再进行整合,最后得出了看到的是正方形的结论。这就是大脑视觉识别
的机理,也是神经网络工作的机理。
让我们看一个简单的神经网络的逻辑架构。在这个网络中,分成输入层,隐藏层,和输出层。输入层负责接收信号,隐藏层负责对数据的分解与处理,最后
的结果被整合到输出层。每层中的一个圆代表一个处理单元,可以认为是模拟了一个神经元,若干个处理单元组成了一个层,若干个层再组成了一个网络,
也就是”神经网络”(图3)。
图
神经网络的逻辑架构
在神经网络中,每个处理单元事实上就是一个逻辑回归模型,逻辑回归模型接收上层的输入,把模型的预测结果作为输出传输到下一个层次。通过这样的过
程,神经网络可以完成非常复杂的非线性分类。
下图会演示神经网络在图像识别领域的一个著名应用,这个程序叫做LeNet,是一个基于多个隐层构建的神经网络。通过LeNet可以识别多种手写数字,并且
达到很高的识别精度与拥有较好的鲁棒性。(见图4)
图
的效果展示
右下方的方形中显示的是输入计算机的图像,方形上方的红色字样“answer”后面显示的是计算机的输出。左边的三条竖直的图像列显示的是神经网络中三个
隐藏层的输出,可以看出,随着层次的不断深入,越深的层次处理的细节越低,例如层3基本处理的都已经是线的细节了。LeNet的发明人就是前文介绍过的
机器学习的大牛Yann LeCun(图1右者)。
进入90年代,神经网络的发展进入了一个瓶颈期。其主要原因是尽管有BP算法的加速,神经网络的训练过程仍然很困难。因此90年代后期支持向量机(SVM)
算法取代了神经网络的地位。
3
、SVM(支持向量机)
支持向量机算法是诞生于统计学习界,同时在机器学习界大放光彩的经典算法。
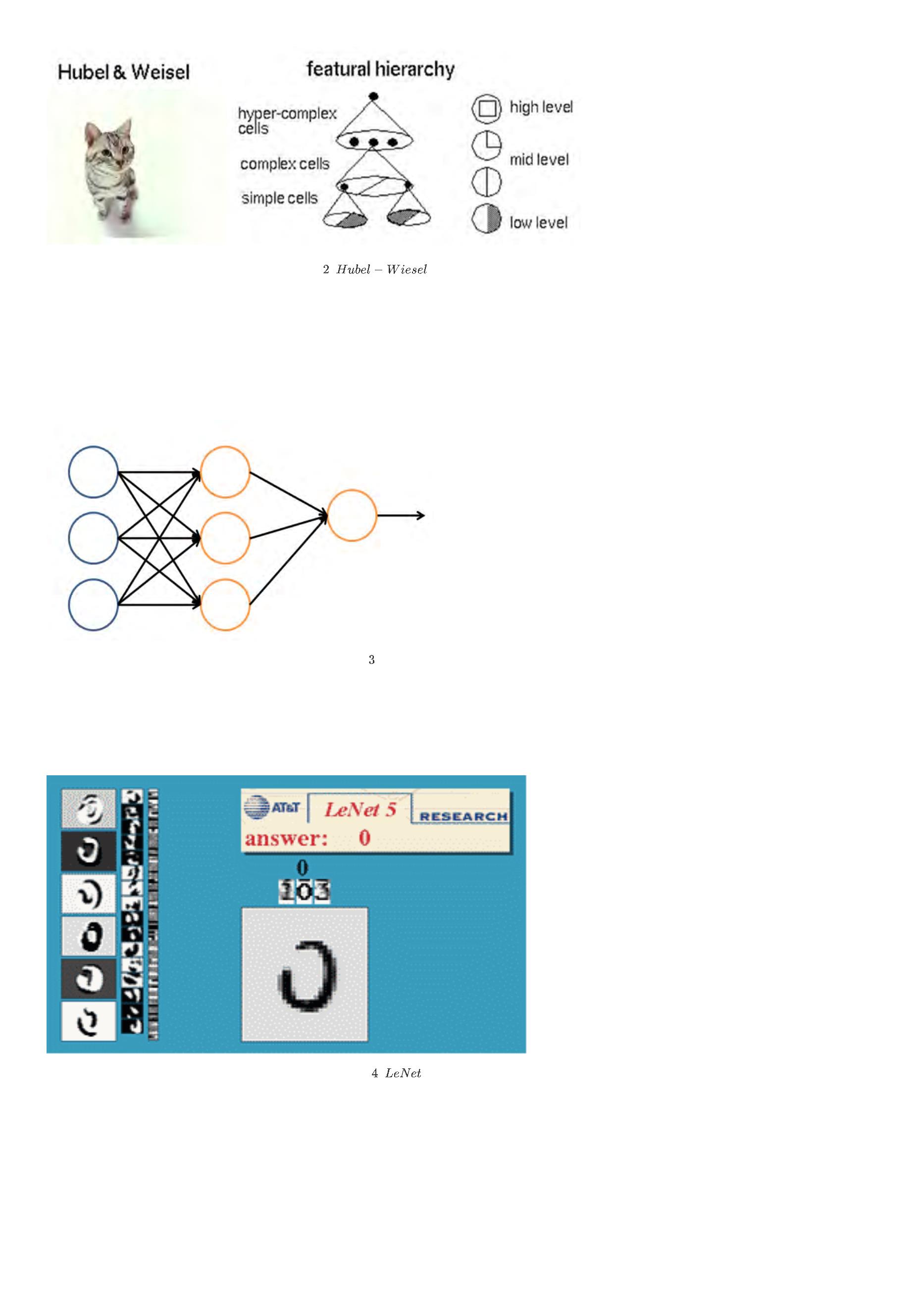
支持向量机算法从某种意义上来说是逻辑回归算法的强化:通过给予逻辑回归算法更严格的优化条件,支持向量机算法可以获得比逻辑回归更好的分类界
线。但是如果没有某类函数技术,则支持向量机算法最多算是一种更好的线性分类技术。
但是,通过跟高斯“核”的结合,支持向量机可以表达出非常复杂的分类界线,从而达成很好的的分类效果。“核”事实上就是一种特殊的函数,最典型的特征就
是可以将低维的空间映射到高维的空间。
例如图5所示:
图
支持向量机图例
我们如何在二维平面划分出一个圆形的分类界线?在二维平面可能会很困难,但是通过“核”可以将二维空间映射到三维空间,然后使用一个线性平面就可以
达成类似效果。也就是说,二维平面划分出的非线性分类界线可以等价于三维平面的线性分类界线。于是,我们可以通过在三维空间中进行简单的线性划分
就可以达到在二维平面中的非线性划分效果。(见图6)
图
三维空间的切割
支持向量机是一种数学成分很浓的机器学习算法(相对的,神经网络则有生物科学成分)。在算法的核心步骤中,有一步证明,即将数据从低维映射到高维
不会带来最后计算复杂性的提升。于是,通过支持向量机算法,既可以保持计算效率,又可以获得非常好的分类效果。因此支持向量机在90年代后期一直占
据着机器学习中最核心的地位,基本取代了神经网络算法。直到现在神经网络借着深度学习重新兴起,两者之间才又发生了微妙的平衡转变。
4
、聚类算法
前面的算法中的一个显著特征就是我的训练数据中包含了标签,训练出的模型可以对其他未知数据预测标签。在下面的算法中,训练数据都是不含标签的,
而算法的目的则是通过训练,推测出这些数据的标签。这类算法有一个统称,即无监督算法(前面有标签的数据的算法则是有监督算法)。无监督算法中最典
型的代表就是聚类算法。
让我们还是拿一个二维的数据来说,某一个数据包含两个特征。我希望通过聚类算法,给他们中不同的种类打上标签,我该怎么做呢?简单来说,聚类算法
就是计算种群中的距离,根据距离的远近将数据划分为多个族群。
聚类算法中最典型的代表就是K-Means算法。
5
、降维算法
降维算法也是一种无监督学习算法,其主要特征是 将数据从高维降低到低维层次。在这里,维度其实表示的是数据的特征量的大小,例如,房价包含房子的
长、宽、面积与房间数量四个特征,也就是维度为4维的数据。可以看出来,长与宽事实上与面积表示的信息重叠了,例如面积=长 × 宽。通过降维算法我们
就可以去除冗余信息,将特征减少为面积与房间数量两个特征,即从4维的数据压缩到2维。于是我们将数据从高维降低到低维,不仅利于表示,同时在计算
上也能带来加速。
刚才说的降维过程中减少的维度属于肉眼可视的层次,同时压缩也不会带来信息的损失(因为信息冗余了)。如果肉眼不可视,或者没有冗余的特征,降维算
法也能工作,不过这样会带来一些信息的损失。但是,降维算法可以从数学上证明,从高维压缩到的低维中最大程度地保留了数据的信息。因此,使用降维
算法仍然有很多的好处。
降维算法的主要作用是压缩数据与提升机器学习其他算法的效率。通过降维算法,可以将具有几千个特征的数据压缩至若干个特征。另外,降维算法的另一
个好处是数据的可视化,例如将5维的数据压缩至2维,然后可以用二维平面来可视。降维算法的主要代表是PCA算法(即主成分分析算法)。
6
、推荐算法
推荐算法是目前业界非常火的一种算法,在电商界,如亚马逊,天猫,京东等得到了广泛的运用。推荐算法的主要特征就是可以自动向用户推荐他们最感兴
趣的东西,从而增加购买率,提升效益。推荐算法有两个主要的类别:
一类是基于物品内容的推荐,是将与用户购买的内容近似的物品推荐给用户,这样的前提是每个物品都得有若干个标签,因此才可以找出与用户购买物品类
似的物品,这样推荐的好处是关联程度较大,但是由于每个物品都需要贴标签,因此工作量较大。
另一类是基于用户相似度的推荐,则是将与目标用户兴趣相同的其他用户购买的东西推荐给目标用户,例如小A历史上买了物品B和C,经过算法分析,发现
另一个与小A近似的用户小D购买了物品E,于是将物品E推荐给小A。
两类推荐都有各自的优缺点,在一般的电商应用中,一般是两类混合使用。推荐算法中最有名的算法就是协同过滤算法。
7
、其他
除了以上算法之外,机器学习界还有其他的如高斯判别,朴素贝叶斯,决策树等等算法。但是上面列的六个算法是使用最多,影响最广,种类最全的典型。
机器学习界的一个特色就是算法众多,发展百花齐放。
下面做一个总结,按照训练的数据有无标签,可以将上面算法分为监督学习算法和无监督学习算法,但推荐算法较为特殊,既不属于监督学习,也不属于非
监督学习,是单独的一类。
监督学习算法:线性回归,逻辑回归,神经网络,SVM
无监督学习算法:聚类算法,降维算法
特殊算法:推荐算法
除了这些算法以外,有一些算法的名字在机器学习领域中也经常出现。但他们本身并不算是一个机器学习算法,而是为了解决某个子问题而诞生的。你可以
理解他们为以上算法的子算法,用于大幅度提高训练过程。其中的代表有:梯度下降法,主要运用在线型回归,逻辑回归,神经网络,推荐算法中;牛顿
法,主要运用在线型回归中;BP算法,主要运用在神经网络中;SMO算法,主要运用在SVM中。
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-机器学习]量化投资中的特征工程
导语:近年来,国内量化投资迎来了发展的黄金期,但涉及机器学习的量化投资还比较少。机器学习领域的大神Andrew Ng(吴恩达)老师曾经说过机器
学习很大程度上就是特征工程,因此本文主要介绍下特征工程在量化投资领域的应用。
1
.特征工程是什么?
有这么一句话在业界广泛流传: 数据和特征决定了机器学习的上限。那特征工程到底是什么呢?顾名思义,其本质是一项工程活动,目的是最大限度地从原
始数据中提取特征以供算法和模型使用。简单理解为:特征工程是使用专业背景知识和技巧处理数据,使得特征能在机器学习算法上发挥更好的作用的过
程。
特征工程在量化投资领域有非常适宜的土壤,首先金融市场拥有海量数据,数据比较规整;其次,金融市场量化研究员开发优异策略离不开专业背景知识、行
业经验和数据处理技巧;最后,金融市场的投资收益、风险可以直接检验机器学习算法性能。
特征工程之所以重要是因为它直接决定了机器学习算法的性能,对于量化交易员策略开发也是如此,特征工程的相关工作将直接决定策略的盈利能力。
2
.开发策略就是特征工程
特征工程是一项工程活动,和量化交易有什么关系呢?量化交易员开发策略的过程本质就是特征工程。我们以一个量化领域比较经典的双均线模型(也称金
叉死叉模型)来解释,该模型的策略核心是当短期均线上穿长期均线时,形成金叉,买入股票,当短期均线下穿长期均线时,形成死叉,卖出股票。在金融
市场上,双均线模型可以实现长期盈利,那么量化交易员开发双均线模型的择时策略为什么就是特征工程呢。我们不局限在双均线模型的交易规则这一个层
面,而是上升到K线数据的另一个特征层面,对于每一根均线而言,我们可以计算一个短期移动平均值与长期均线移动平均值之差这个特征,定义如下:
因此本质上双均线模型就是基于$feature$这个特征进行交易。这个特征的构建先是通过每日收盘价计算短期和长期移动平均值,然后再做减法获得,如果你
是涉足金融市场刚第一天的人,你很可能不会联想到这个特征,但是如果你是长期待在金融市场上的人那么你拥有了投资交易经验和金融背景知识,因此你
很可能会开发出基于该特征的策略——双均线模型,你无须关心其他数据,只需知道每个$K$线上的$feature$特征值即可。因此,量化交易员开发策略就是
特征工程。
量化交易员发现股票收益和股票的某些因子之间存在线性关系,因此在开发策略时,更多的是关注具有超额收益的这些因子,选择符合因子条件的股票本质
上也是特征工程。
3
.特征工程的重要性
数据工程项目往往严格遵循着RIRO(rubbish in, rubbish out) 的原则,所以我们经常说数据预处理是数据工程师或者数据科学家80%的工作,它保证了数据原
材料的质量。 如何从成百上千个特征中发现其中哪些对结果最具影响,进而利用它们构建可靠的机器学习算法是特征选择工作的中心内容。
也有人曾这样描述特征工程:特征工程就是研究我们应该输入什么数据。我们可以把量化交易员开发策略获取收益的过程看成以下映射:

其中$x$为输入的数据,$f$为策略,$f(x)$为输出的策略收益。
金融市场上每天产生海量的数据,比如交易数据、行业数据、企业财务数据、宏观经济数据等,这些原始数据可以形成天量的特征,如何从这些特征中发现
能够产生策略超额收益的好的特征对于量化交易员至关重要。
如果市场符合有效市场假说,那么量化交易员只需关心交易数据中的价格和成交量就可以,但是大多数的市场都不是有效市场。因此,量化交易员必须设计
好选择什么作为输入。如果做不好特征工程,输入的数据有问题,那么输出的策略收益也不会高。因此在开发策略过程中,特征工程非常重要。
4
.如何做好特征工程
要做好特征工程主要是解决以下几个特征工程子问题。(如图1)
图
特征工程子问题
4
.1 特征提取
在数据挖掘领域,特征提取是将原始特征转换为一组具有明显物理意义(Gabor、几何特征[角点、不变量]、纹理[LBP HOG])或者统计意义或核的特征。比
如通过变换特征取值来减少原始数据中某个特征的取值个数等。对于表格数据,可以在设计的特征矩阵上使用主要成分分析(Principal Component
Analysis,PCA)来进行特征提取从而创建新的特征。对于图像数据,可能还包括了线或边缘检测。常用的特征提取的方法有:主成分分析(PCA)和线性判
别分析(LDA)。
金融领域也是如此。特征提取的对象是原始数据(raw data),它的目的是从原始数据中提取特征,比如我们获取股票的行情数据,行情数据里包含开盘
价、最高价、最低价、收盘价、复权因子,我们不能直接使用这些股票价格作为特征,因为公司可能会有分红、派息等行为,因此股票价格不能反映真实的
股价,所以要对其进行复权处理,进行处理以后,得到复权后的价格数据可以提取成新的特征了。
4
.2 特征选择
当数据预处理完成后,我们需要选择有意义的特征输入机器学习的算法和模型进行训练。通常来说,从两个方面考虑来选择特征:
特征是否发散:如果一个特征不发散,例如方差接近于0,也就是说样本在这个特征上基本上没有差异,这个特征对于样本的区分并没有什么用。比如
我们选取股票ST状态(ST:0,非ST:1)这个特征,这个特征较长时间会保持不变,因此该特征不发散,这样的特征我们尽量不选取。
特征与目标的相关性:这点比较显见,与目标相关性高的特征,应当优选选择。在有效市场或强有效市场中,类似于成交价格、成交量这类行情特征能
够很充分地反映股票的大部分信息,因此这类特征应该优先选择。另外,量化交易员开发策略时,特征的选择与策略的模式也高度相关,比如,希望开
发一个策略能够挖掘“长期低量盘整,价格突然持续拉高”的股票,如果这样的选股模式在金融市场上是可以盈利的,那么在选择特征的时候,应该选择
长期平均成交量与短期成交量之比、长期移动平均值与短期移动平均值之比这类特征。这两个特征能够将具有“长期低量盘整,价格突然持续拉高”模式
的股票选择出来。
4
.3 特征构造
有时,原始数据集的特征具有必要的信息,但其形式不适合数据挖掘算法,在这种情况下, 由原特征构造的新特征可能比原特征更有用。
我们举一个例子,考虑一个包含人工制品信息的历史数据集,该数据集包含每个人工制品的体积和质量,以及其他信息。假设这些人工制品使用少量材料
(
木材、陶土、铜、黄金)制造,并且我们希望根据制造材料对它们分类。在此情况下,由质量和体积特征构造的密度特征(即密度=质量/体积)可以直接
地产生准确的分类。尽管有些人试图通过考察已有特征的简单的数学组合来自动地进行特征构造,但是最常见的方法还是使用专家意见构造特征。
在金融领域也是如此,比如我们想区分股票价格的波动性,我们可以构造一个收盘价标准差的一个特征,这个特征能够反映顾及近期的波动情况;此外,我
们也可以构造一个平均振幅的一个特征,该特征是每日最高价减每日最低价的差值的平均值,从数值的角度反映股票价格的近期波情况。
如果你是专业的量化交易员,那么面临众多的特征,你可以根据你的行业经验和投资心得在浩瀚的特征海洋里构造新的特征来开发策略。
小结:特征工程已经是很古老很常见的话题,引用几句大师的一些原话吧。
“Coming up with features is difficult, time-consuming, requires expert knowledge. "Applied machine learning" is basically feature engineering.”—
Andrew Ng
直译:构思特征很困难,很花时间,需要专家经验。机器学习的应用很大程度就是特征工程
“some machine learning projects succeed and some fail. What makes the difference? Easily the
most important factor is the features used.” —Pedro Domingos
直译:机器学习项目有些成功了,有些失败了,主要因为特征使用不一样
“Actually the success of all machine learning algorithms depend on how you present the data.” — Mohammad Pezeshki
直译:事实上所有机器学习算法上面的成功都在于你怎么样去展示这些数据
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。

参考资料
Discover Feature Engineering, How to Engineer Features and How to Get Good at It
数据挖掘导论(完整版).Introduction.To.Data.Mining.(美)Pang-Ning_Tan.范明译.人民邮电.2011
[
量化学堂-机器学习]AI量化策略的初步理解
导语:人工智能(AI)技术得到了飞速发展,其在各个领域的运用也不断取得成果。机器学习被评为人工智能中最能体现人类智慧的技术,因此开发AI
量化策略可以理解为将机器学习应用在量化投资领域。
理解机器学习算法——以StockRanker 为例
机器学习算法太多,本文讨论只针对适用于金融数据预测的常用有监督型机器学习(Supervised Machine Learning)算法:StockRanker。假设我们要去预
测某个连续变量$ Y$未来的取值,并找到了影响变量$ Y$取值的$K$ 个变量,这些变量也称为特征变量(Feature Variable)。机器学习 即是要找到一个拟合
函数$f(X_1,X_2,\ldots,X_K|\Theta)$去描述 $Y$和特征变量之间的关系,$\Theta$为这个函数的参数。
要找到这样的函数,必须要足够量的观测数据,假设有 N 个样本数据$ { y_1,y_2,\ldots,y_n }$和 $x_{1i},x_{2i},\ldots,x_{Ki}$(其中$i=1,2,\ldots,n$)。然后定
义一个函数$L$来衡量真实观测数据和模型估计数据偏差,函数 L 也称作损失函数(Loss Function)。基于历史观测数据,我们可以求解下列的最化问题来
得到参数$\Theta$ 的估计值 。
求解(1.1)过程称作模型训练(Model Traing)。基于特征变量的最新观测值和训练出来的模型参数就可以预测$y$的数值。 接下来,我们以一个具体的AI
量化策略看一下用机器学习方法开发策略的具体流程。
开发AI量化策略的流程
使用机器学习开发策略的流程如图1所示:
图
使用机器学习开发策略的流程
为便于理解,以StockRanker为例介绍。StockRanker是一种监督式股票排序学习算法,假设我们要预测个股未来$n$天的收益率,然后将其进行排序, 使用
该算法在新的一天数据上进行预测,可以向我们推荐应该买入哪些股票。我们结合上图介绍下使用StockRanker算法来开发量化策略的流程。
首先,确定目标。因为是监督学习,因此需要对收益率数据进行标注。
接着,数据划分。将所有数据划分为训练数据和测试数据,训练数据用来训练模型,测试数据用来检验模型的表现。
然后,特征构造。特征构造是至关重要的一步,特征构造的好将会直接影响模型效果和策略表现。在这一步,你在金融行业的专业知识和投资经验将发
挥很大的作用。
然后,训练和预测。在特征构造完毕后,就可以训练好StockRanker算法并进行预测。
最后,策略回测。根据StockRanker预测结果进行策略回测,获取策略表现。
关于AI策略的预测能力
量化交易人员对机器学习的态度很复杂,一方面自己实际投资中发现选股因子和股票收益之间关系并非完全线性,需要能力更强的分析预测工具,另一方面
又担心机器学习工具过于复杂,导致数据挖掘,样本内过拟合的结果外推性不强,经济含义也不好解释。我们这里想说明的是,ML(Machine learning)虽然
没法完全避免过拟合的可能性,但配合使用一些方法是可以降ML低过拟合的概率,提升样本外预测能力的。
假设输入变量$ X$ 和输出变量 $Y$ 的真实关系可以表示为 $Y=f(X)+\epsilon$,$\epsilon$为误差项,满足
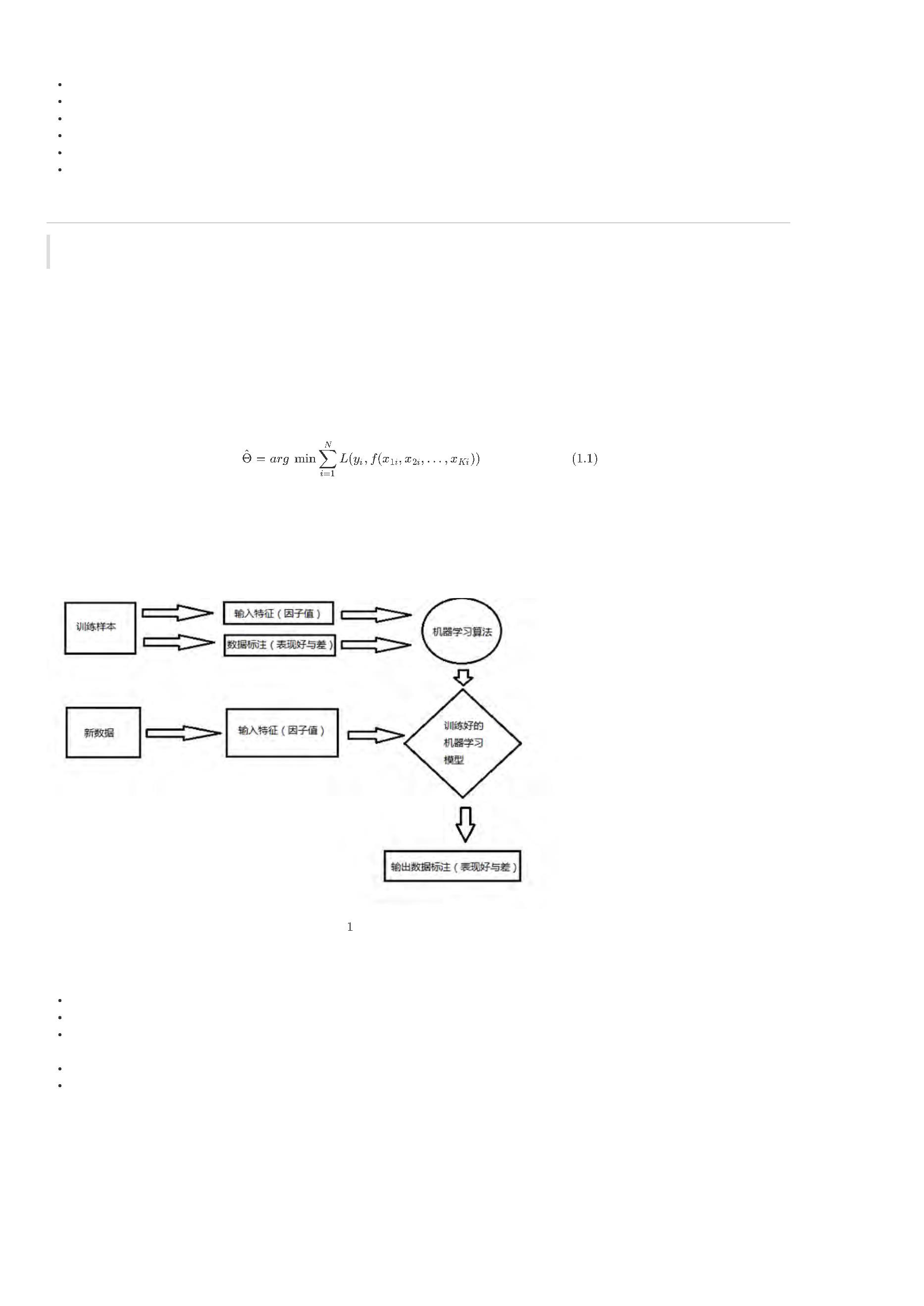
$
E(\epsilon)=0$,$Var(\epsilon)={\sigma_\epsilon}^2$ 。投资者者通过 ML 方法找到了 $f(X)$ 的一个拟合函数 $\hat{f(x)}$ 。对于一个新的数据点 $X=x_0$ ,
它的预测偏差定义为:
ML模型的预测偏差取决于(1.2)的这三项,第一项取值与 ML 模型选择无关,第二项 $Bias$ 和第三项$Variance$ 的理解可以参考图2,两者都受 ML 模型复
杂度的影响;
图
模型的预测偏差
一般来讲,模型复杂度越高,$Bias$ 越小,但 $Variance$ 越大;模型复杂度越低,$Bias$越大,$Variance$越小。从图3可以看出,当模型复杂度较高的时
候,虽然偏差很小,但是模型方差很大,因此模型的泛化能力不高。
图
模型复杂度和预测误差的关系
因此要想提高 ML模型的预测能力,模型并不是越复杂越好,而是要在 $Bias$ 和 $Variance$ 间做权衡,降低总体预测误差,也就是所谓的 $Bias -Variance
\ trade-off$。
\
对待机器学习,我们应该摆脱固有的“黑箱“和”过拟合“概念,一些 ML 算法的逻辑非常直白,而且 ML 在求解优化问题估计模型参数时,通常会带正则化约束
条件,通过交叉验证的方式来选择参数,避免过拟合。 众多的实践研究说明, ML 方法的预测能力大部分情况下都强于线性模型。
小结:AI量化策略由于其结构简单、参数少、欠拟合概率较低,同时还具有非常强的样本外预测能力。因此策略在收益和稳健性上都要比传统的线性模
型高,更重要的是它可以帮助我们省去Barra结构风险模型中”因子筛选“、”因子加权“和”组合优化“的过程,提升策略开发效率。
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-机器学习]StockRanker 模型可视化
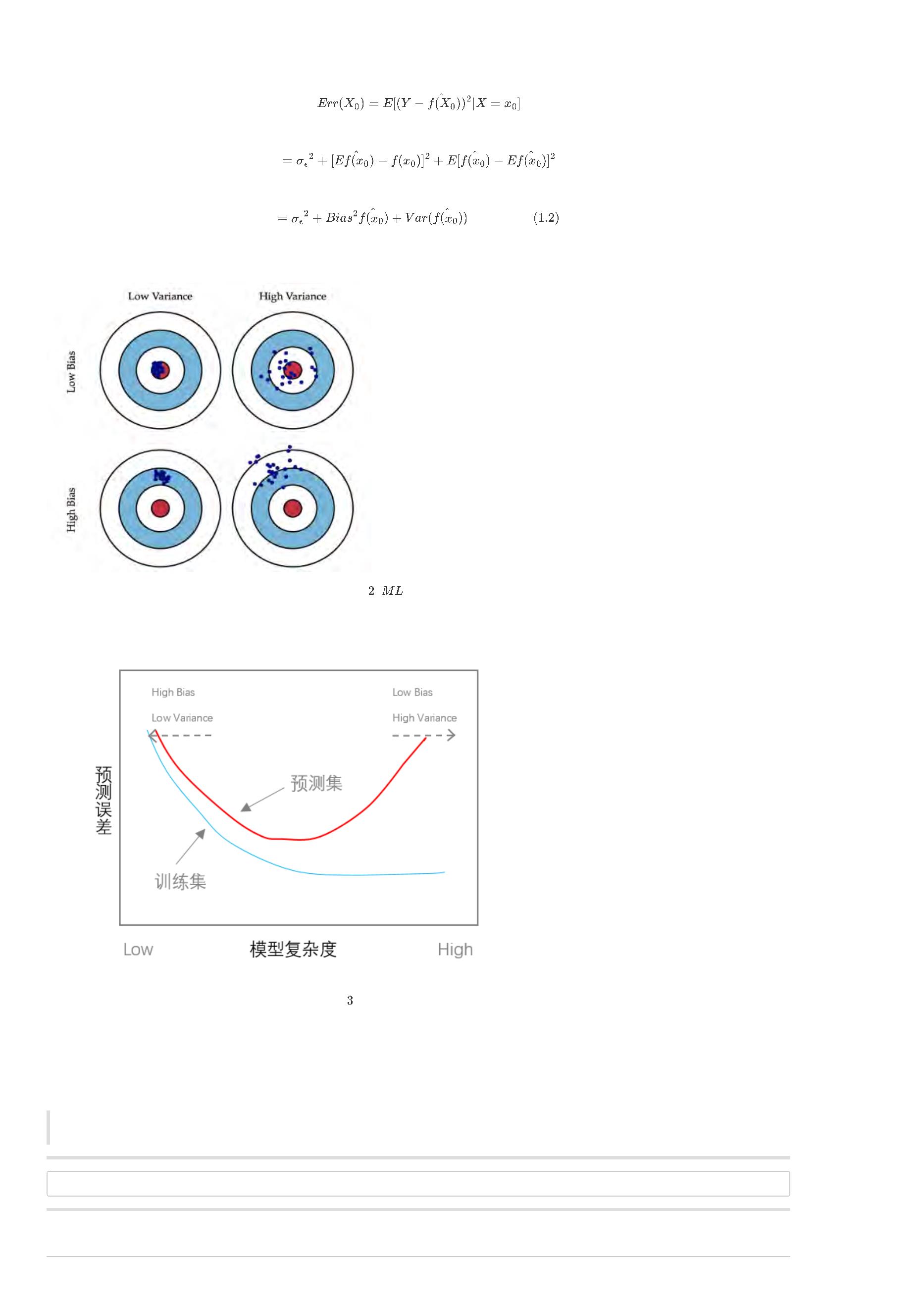
导语:本文介绍了如何用BigQuant的策略生成器进行StockRanker模型可视化。
在策略生成器中,可以直接菜单化操作的方式新建一个StockRanker实验,通过plot_model我们可以看到StockRanker模型是什么样子的,这样就能够完全透
明的将模型可视化的展示出来,包括结构和参数等信息。
#
m6 = M.stock_ranker_train.v2
m6.plot_model()
一般情况下AI机器在大量数据上训练出来的模型会远比人做出来的复杂,这也是AI有更好的效果的原因之一。
如图1这个模型有20棵决策树组成,每棵决策树最多有30个叶节点。给定一个样本,每个决策树会对样本打分(分数为样本根据判定条件到达的叶节点的
值);最后的分数是所有决策树打分的总和。决策树的结构、判定条件和叶节点的分数等等都是由机器学习算法在大量数据上学习出来的。
图
决策树
附件:StockRanker训练模型
In [10]:
#
基础参数配置
class conf:
start_date = '2010-01-01'
end_date='2017-07-19'
split_date 之前的数据用于训练,之后的数据用作效果评估
split_date = '2015-01-01'
D.instruments: https://bigquant.com/docs/data_instruments.html
instruments = D.instruments(start_date, end_date)
#
#
#
#
#
机器学习目标标注函数
如下标注函数等价于 min(max((持有期间的收益 * 100), -20), 20) + 20 (后面的M.fast_auto_labeler会做取整操作)
说明:max/min这里将标注分数限定在区间[-20, 20],+20将分数变为非负数 (StockRanker要求标注分数非负整数)
label_expr = ['return * 100', 'where(label > {0}, {0}, where(label < -{0}, -{0}, label)) + {0}'.format(20)]
持有天数,用于计算label_expr中的return值(收益)
hold_days = 5
#
#
特征 https://bigquant.com/docs/data_features.html,你可以通过表达式构造任何特征
features = [
'
'
'
'
'
'
'
'
'
'
'
'
'
close_5/close_0', # 5日收益
close_10/close_0', # 10日收益
close_20/close_0', # 20日收益
avg_amount_0/avg_amount_5', # 当日/5日平均交易额
avg_amount_5/avg_amount_20', # 5日/20日平均交易额
rank_avg_amount_0/rank_avg_amount_5', # 当日/5日平均交易额排名
rank_avg_amount_5/rank_avg_amount_10', # 5日/10日平均交易额排名
rank_return_0', # 当日收益
rank_return_5', # 5日收益
rank_return_10', # 10日收益
rank_return_0/rank_return_5', # 当日/5日收益排名
rank_return_5/rank_return_10', # 5日/10日收益排名
pe_ttm_0', # 市盈率TTM
]
#
给数据做标注:给每一行数据(样本)打分,一般分数越高表示越好
m1 = M.fast_auto_labeler.v8(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.end_date,
label_expr=conf.label_expr, hold_days=conf.hold_days,
benchmark='000300.SHA', sell_at='open', buy_at='open')
#
计算特征数据
m2 = M.general_feature_extractor.v5(
instruments=conf.instruments, start_date=conf.start_date, end_date=conf.end_date,
features=conf.features)
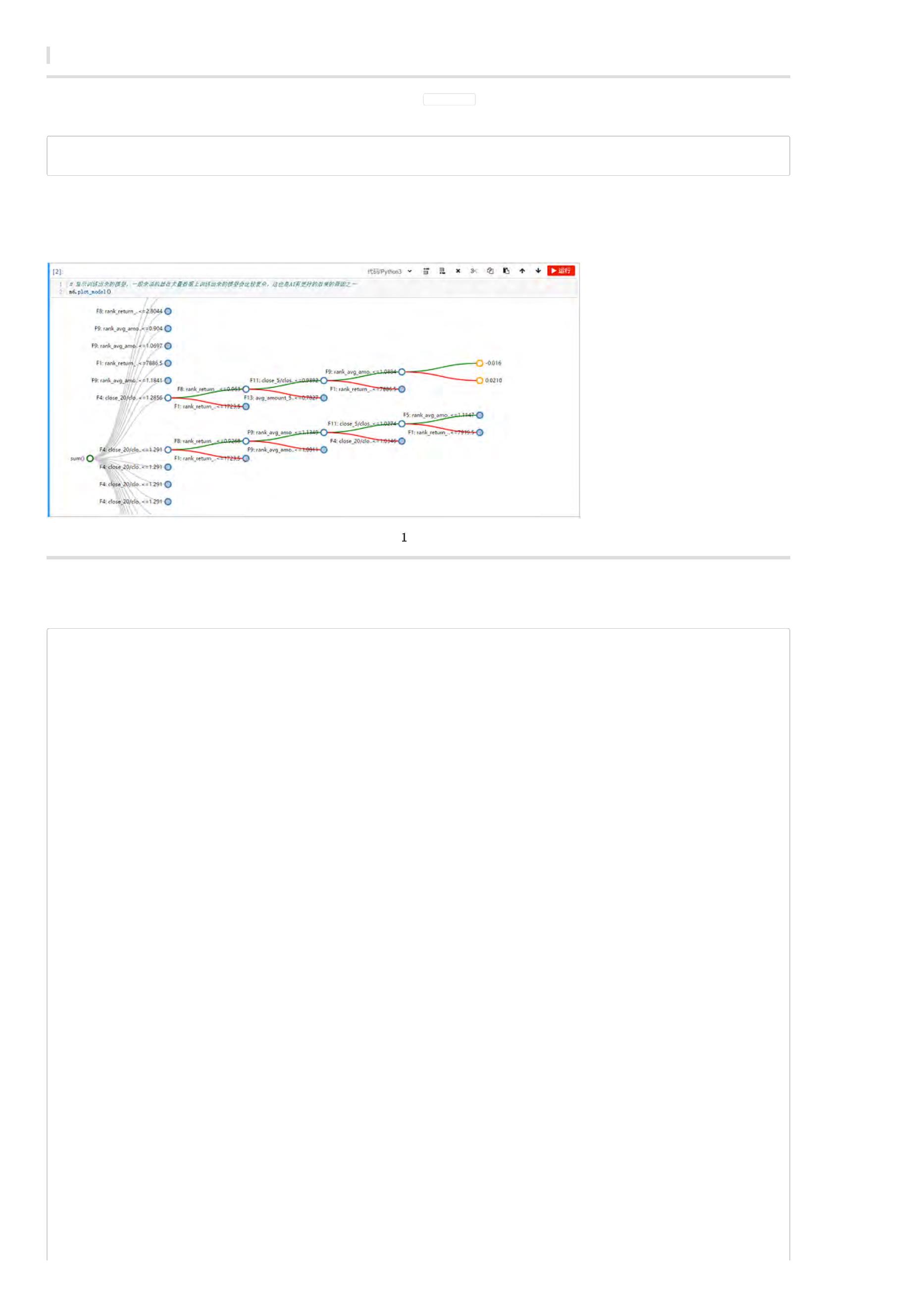
#
数据预处理:缺失数据处理,数据规范化,T.get_stock_ranker_default_transforms为StockRanker模型做数据预处理
m3 = M.transform.v2(
data=m2.data, transforms=T.get_stock_ranker_default_transforms(),
drop_null=True, astype='int32', except_columns=['date', 'instrument'],
clip_lower=0, clip_upper=200000000)
#
合并标注和特征数据
m4 = M.join.v2(data1=m1.data, data2=m3.data, on=['date', 'instrument'], sort=True)
#
训练数据集
m5_training = M.filter.v2(data=m4.data, expr='date < "%s"' % conf.split_date)
评估数据集
m5_evaluation = M.filter.v2(data=m4.data, expr='"%s" <= date' % conf.split_date)
StockRanker机器学习训练
m6 = M.stock_ranker_train.v3(training_ds=m5_training.data, features=conf.features)
#
#
[
[
2017-07-20 11:39:13.630497] INFO: bigquant: fast_auto_labeler.v8 start ..
2017-07-20 11:39:13.633376] INFO: bigquant: hit cache
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
[
2017-07-20 11:39:13.637674] INFO: bigquant: fast_auto_labeler.v8 end [0.007199s].
2017-07-20 11:39:13.643768] INFO: bigquant: general_feature_extractor.v5 start ..
2017-07-20 11:39:13.645508] INFO: bigquant: hit cache
2017-07-20 11:39:13.646379] INFO: bigquant: general_feature_extractor.v5 end [0.002588s].
2017-07-20 11:39:13.656035] INFO: bigquant: transform.v2 start ..
2017-07-20 11:39:13.658065] INFO: bigquant: hit cache
2017-07-20 11:39:13.658829] INFO: bigquant: transform.v2 end [0.002798s].
2017-07-20 11:39:13.664468] INFO: bigquant: join.v2 start ..
2017-07-20 11:39:13.666044] INFO: bigquant: hit cache
2017-07-20 11:39:13.667241] INFO: bigquant: join.v2 end [0.002768s].
2017-07-20 11:39:13.671594] INFO: bigquant: filter.v2 start ..
2017-07-20 11:39:13.672965] INFO: bigquant: hit cache
2017-07-20 11:39:13.673641] INFO: bigquant: filter.v2 end [0.002046s].
2017-07-20 11:39:13.678026] INFO: bigquant: filter.v2 start ..
2017-07-20 11:39:13.679482] INFO: bigquant: hit cache
2017-07-20 11:39:13.680164] INFO: bigquant: filter.v2 end [0.002137s].
2017-07-20 11:39:13.687280] INFO: bigquant: stock_ranker_train.v3 start ..
2017-07-20 11:39:13.688784] INFO: bigquant: hit cache
2017-07-20 11:39:13.689642] INFO: bigquant: stock_ranker_train.v3 end [0.002335s].
可视化查看模型¶
In [11]:
#
每一个节点都可以点击展开
m6.plot_model()
对评估集做预测¶
In [12]:
m7 = M.stock_ranker_predict.v2(model_id=m6.model_id, data=m5_evaluation.data)
[
[
[
2017-07-20 11:39:13.721570] INFO: bigquant: stock_ranker_predict.v2 start ..
2017-07-20 11:39:13.744314] INFO: bigquant: hit cache
2017-07-20 11:39:13.745629] INFO: bigquant: stock_ranker_predict.v2 end [0.024104s].
执行回测¶
In [13]:
#
回测引擎:初始化函数,只执行一次
def initialize(context):
#
系统已经设置了默认的交易手续费和滑点,要修改手续费可使用如下函数
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
预测数据,通过options传入进来,使用 read_df 函数,加载到内存 (DataFrame)
context.ranker_prediction = context.options['ranker_prediction'].read_df()
设置买入的股票数量,这里买入预测股票列表排名靠前的5只
stock_count = 5
每只的股票的权重,如下的权重分配会使得靠前的股票分配多一点的资金,[0.339160, 0.213986, 0.169580, ..]
context.stock_weights = T.norm([1 / math.log(i + 2) for i in range(0, stock_count)])
设置每只股票占用的最大资金比例
#
#
#
#
context.max_cash_per_instrument = 0.2
#
回测引擎:每日数据处理函数,每天执行一次
def handle_data(context, data):
按日期过滤得到今日的预测数据
ranker_prediction = context.ranker_prediction[context.ranker_prediction.date == data.current_dt.strftime('%Y-%m-%d')]
#
#
1. 资金分配
#
#
平均持仓时间是hold_days,每日都将买入股票,每日预期使用 1/hold_days 的资金
实际操作中,会存在一定的买入误差,所以在前hold_days天,等量使用资金;之后,尽量使用剩余资金(这里设置最多用等量的1.5倍)
is_staging = context.trading_day_index < context.options['hold_days'] # 是否在建仓期间(前 hold_days 天)
cash_avg = context.portfolio.portfolio_value / context.options['hold_days']
cash_for_buy = min(context.portfolio.cash, (1 if is_staging else 1.5) * cash_avg)
cash_for_sell = cash_avg - (context.portfolio.cash - cash_for_buy)
positions = {e.symbol: p.amount * p.last_sale_price
for e, p in context.perf_tracker.position_tracker.positions.items()}
#
2. 生成卖出订单:hold_days天之后才开始卖出;对持仓的股票,按StockRanker预测的排序末位淘汰
if not is_staging and cash_for_sell > 0:
equities = {e.symbol: e for e, p in context.perf_tracker.position_tracker.positions.items()}
instruments = list(reversed(list(ranker_prediction.instrument[ranker_prediction.instrument.apply(
lambda x: x in equities and not context.has_unfinished_sell_order(equities[x]))])))
#
print('rank order for sell %s' % instruments)
for instrument in instruments:
context.order_target(context.symbol(instrument), 0)
cash_for_sell -= positions[instrument]
if cash_for_sell <= 0:
break
#
3. 生成买入订单:按StockRanker预测的排序,买入前面的stock_count只股票
buy_cash_weights = context.stock_weights
buy_instruments = list(ranker_prediction.instrument[:len(buy_cash_weights)])
max_cash_per_instrument = context.portfolio.portfolio_value * context.max_cash_per_instrument
for i, instrument in enumerate(buy_instruments):
cash = cash_for_buy * buy_cash_weights[i]
if cash > max_cash_per_instrument - positions.get(instrument, 0):
#
确保股票持仓量不会超过每次股票最大的占用资金量
cash = max_cash_per_instrument - positions.get(instrument, 0)
if cash > 0:
context.order_value(context.symbol(instrument), cash)
#
调用回测引擎
m8 = M.trade.v2(
instruments=m7.instruments,
start_date=m7.start_date,
end_date=m7.end_date,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='close',
capital_base=1000000,
# 表示 开盘 时买入
# 表示 收盘 前卖出
# 初始资金
benchmark='000300.SHA',
# 比较基准,不影响回测结果
#
通过 options 参数传递预测数据和参数给回测引擎
options={'ranker_prediction': m7.predictions, 'hold_days': conf.hold_days}
)
[
[
2017-07-20 11:39:13.917933] INFO: bigquant: backtest.v7 start ..
2017-07-20 11:39:13.920362] INFO: bigquant: hit cache
[
2017-07-20 11:39:15.714039] INFO: bigquant: backtest.v7 end [1.796057s].
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-机器学习]基于LSTM的股票价格预测模型
导语:本文介绍了LSTM的相关内容和在股票价格预测上的应用。
LSTM(Long Short Term Memory)是一种 特殊的RNN类型,同其他的RNNs相比可以更加方便地学习长期依赖关系,因此有很多人试图将其应用于 时间序列
的预测问题 上。
汇丰银行全球资产管理开发副总裁Jakob Aungiers在他的个人网站上比较详细地介绍了LSTM在Time Series Prediction上的运用(http://www.jakob-
Time-Series-Prediction“的流程。
Keras是实现LSTM最方便的python库(Bigquant平台已经装好了,不用自己安装了)
from keras.layers.core import Dense, Activation, Dropout
from keras.layers.recurrent import LSTM
from keras.models import Sequential
from keras import optimizers
#
#加载转换数据
例如希望根据前seq_len天的收盘价预测第二天的收盘价,那么可以将data转换为(len(data)-seq_len)(seq_len+1)
input+output (len(data)-seq_len)(seq_len+1)*1的数组
LSTM
input
3

def load_data(instrument,start_date,end_date,field,seq_len,prediction_len,train_proportion,normalise=True):
data=D.history_data(instrument,start_date,end_date,fields)
…
…
seq_len=seq_len+1
result=[]
for index in range(len(data)-seq_len):
result.append(data[index:index+seq_len])
…
#
…
规范化之后
x_train = train[:, :-1]
y_train = train[:, -1]
x_train = np.reshape(x_train, (x_train.shape[0], x_train.shape[1], 1))
#
测试数据同样处理
#
#构建LSTM神经网络
model = Sequential()
model.add(LSTM(input_dim=layers[0],output_dim=layers[1],return_sequences=True))
model.add(Dropout(0.2))
model.add(LSTM(layers[1],return_sequences=False))
model.add(Dropout(0.2))
model.add(Dense(input_dim=layers[1],output_dim=layers[2]))
model.add(Activation("linear"))
rms=optimizers.RMSprop(lr=conf.lr, rho=0.9, epsilon=1e-06)
model.compile(loss="mse", optimizer=rms)
此神经网络共三层,第一层为LSTM层,输入数据维度是1,输出数据维度为seq_len;第二层也为LSTM层,输入和输出维度均为seq_len层;第三层为
Dense层,输入数据维度是seq_len,输出数据维度为1,最终将input与output对应起来。
compile:编译用来配置模型的学习过程,可选参数有loss,optimizer等。模型在使用前必须编译,否则在调用fit或evaluate时会抛出异常
loss为损失函数,可用mse,mae,binary_crossentropy等;
optimizers为优化器,即优化参数的算法,可供选择为SGD(随机梯度下降法),RMSprop(处理递归神经网络时的一个良好选择),Adagrad等(具体参
见http://keras-cn.readthedocs.io/en/latest/ ,网页提供Keras相关函数的详细介绍)。
model.fit(X_train,y_train,batch_size=conf.batch,nb_epoch=conf.epochs,validation_split=conf.validation_split
fit为训练函数,batch_size:整数,训练时一个batch的样本会被计算一次梯度下降,使目标函数优化一步;nb_epoch:迭代次数;validation_split:0~1之
间的浮点数,用来指定训练集的一定比例数据作为验证集
predicted = model.predict(data)
predicted = np.reshape(predicted, (predicted.size,))
模型在test_data集上的预测,根据前seq_len长度预测下一时间的close。
另外,在此基础上,若希望预测prediction_len长度的close,则可在第一个predict_close的基础上,以此predict_close和前seq_len-1个true_close为input,预
测下一个close,以此类推,可预测一定长度甚至全部长度的时间序列(predict_sequences_multiple,predict_sequence_full)
#
#回测(以predict_sequences_multiple为例)
思路是这样:看prediction_len长度内的涨跌,若prediction_len最后一天收盘价大于第一天的收盘价,则下买单;反之,不做单或者平仓
#
#效果
效果不是特别好,可能和我没有优化参数有很大关系,希望能抛砖引玉,完整策略代码如下,欢迎指正和讨论:slight_smile:
补充:如果运行出错,请检查M.trade模块是否是最新版本。
附件:基于LSTM的股票价格预测模型实例
In [19]:
class conf:
instrument = '000300.SHA' #股票代码
#
设置用于训练和回测的开始/结束日期
start_date = '2005-01-01'
end_date='2017-07-19'
field='close'
seq_len=100 #每个input的长度
prediction_len=20 #预测数据长度
train_proportion=0.8 #训练数据占总数据量的比值,其余为测试数据
normalise=True #数据标准化
epochs = 1 #LSTM神经网络迭代次数
batch=100 #整数,指定进行梯度下降时每个batch包含的样本数,训练时一个batch的样本会被计算一次梯度下降,使目标函数优化一步
validation_split=0.1 # 0~1之间的浮点数,用来指定训练集的一定比例数据作为验证集。
lr=0.001 #学习效率
#
2. LSTM策略主体
import time
import numpy as np
import matplotlib.pyplot as plt
from numpy import newaxis
from keras.layers.core import Dense, Activation, Dropout
from keras.layers.recurrent import LSTM
from keras.models import Sequential
from keras import optimizers
def load_data(instrument,start_date,end_date,field,seq_len,prediction_len,train_proportion,normalise=True):
#
加载数据,数据变化,提取数据模块
fields=[field,'amount']
data=D.history_data(instrument,start_date,end_date,fields)
data=data[data.amount>0]
datetime=list(data['date'])
data=list(data[field])
seq_len=seq_len+1
result=[]
for index in range(len(data)-seq_len):
result.append(data[index:index+seq_len])
if normalise:
norm_result=normalise_windows(result)
else:
norm_result=result
result=np.array(result)
norm_result=np.array(norm_result)
row=round(train_proportion*norm_result.shape[0])
data_test=result[int(row):,:]
datetime=datetime[int(row):]
test_datetime=[]
for index in range(len(datetime)):
if index % prediction_len==0 and index+seq_len<len(datetime)-prediction_len:
test_datetime.append(datetime[index+seq_len])
train=norm_result[:int(row),:]
np.random.shuffle(train)
x_train = train[:, :-1]
y_train = train[:, -1]
#随机打乱训练样本
x_test = norm_result[int(row):, :-1]
y_test = norm_result[int(row):, -1]
x_train = np.reshape(x_train, (x_train.shape[0], x_train.shape[1], 1))
x_test = np.reshape(x_test, (x_test.shape[0], x_test.shape[1], 1))
return [x_train, y_train, x_test, y_test, data_test, test_datetime]
def normalise_windows(window_data):
#
数据规范化
normalised_data = []
for window in window_data:
normalised_window = [((float(p) / float(window[0])) - 1) for p in window]
normalised_data.append(normalised_window)
return normalised_data
def denormalise_windows(normdata,data,seq_len):
#
数据反规范化
denormalised_data = []
wholelen=0
for i, rowdata in enumerate(normdata):
denormalise=list()
if isinstance(rowdata,float)|isinstance(rowdata,np.float32):
denormalise = [(rowdata+1)*float(data[wholelen][0])]
denormalised_data.append(denormalise)
wholelen=wholelen+1
else:
for j in range(len(rowdata)):
denormalise.append((float(rowdata[j])+1)*float(data[wholelen][0]))
wholelen=wholelen+1
denormalised_data.append(denormalise)
return denormalised_data
def build_model(layers):
#
#
LSTM神经网络层
详细介绍请参考http://keras-cn.readthedocs.io/en/latest/
model = Sequential()
model.add(LSTM(input_dim=layers[0],output_dim=layers[1],return_sequences=True))
model.add(Dropout(0.2))
model.add(LSTM(

layers[1],
return_sequences=False))
model.add(Dropout(0.2))
model.add(Dense(
input_dim=layers[1],
output_dim=layers[2]))
model.add(Activation("linear"))
rms=optimizers.RMSprop(lr=conf.lr, rho=0.9, epsilon=1e-06)
model.compile(loss="mse", optimizer=rms)
start = time.time()
print("> Compilation Time : ", time.time() - start)
return model
def predict_point_by_point(model, data):
#
每次只预测1步长
predicted = model.predict(data)
predicted = np.reshape(predicted, (predicted.size,))
return predicted
def predict_sequence_full(model, data, seq_len):
#
根据训练模型和第一段用来预测的时间序列长度逐步预测整个时间序列
curr_frame = data[0]
predicted = []
for i in range(len(data)):
predicted.append(model.predict(curr_frame[newaxis,:,:])[0,0])
curr_frame = curr_frame[1:]
curr_frame = np.insert(curr_frame, [seq_len-1], predicted[-1], axis=0)
return predicted
def predict_sequences_multiple(model, data, seq_len, prediction_len):
#
根据训练模型和每段用来预测的时间序列长度逐步预测prediction_len长度的序列
prediction_seqs = []
for i in range(int(len(data)/prediction_len)):
curr_frame = data[i*prediction_len]
predicted = []
for j in range(prediction_len):
predicted.append(model.predict(curr_frame[newaxis,:,:])[0,0])
curr_frame = curr_frame[1:]
curr_frame = np.insert(curr_frame, [seq_len-1], predicted[-1], axis=0)
prediction_seqs.append(predicted)
return prediction_seqs
def plot_results(predicted_data, true_data):
#
做图函数,用于predict_point_by_point和predict_sequence_full
fig = plt.figure(facecolor='white')
ax = fig.add_subplot(111)
ax.plot(true_data, label='True Data')
plt.plot(predicted_data)
plt.legend()
figure=plt.gcf()
figure.set_size_inches(20,10)
plt.show()
def plot_results_multiple(predicted_data, true_data, prediction_len):
#
做图函数,用于predict_sequences_multiple
fig = plt.figure(facecolor='white')
ax = fig.add_subplot(111)
ax.plot(true_data, label='True Data')
for i, data in enumerate(predicted_data):
padding = [None for p in range(i * prediction_len)]
plt.plot(padding + data)
plt.legend()
figure=plt.gcf()
figure.set_size_inches(20,10)
plt.show()
#
主程序
global_start_time = time.time()
print('> Loading data... ')
X_train,y_train,X_test,y_test,data_test,test_datetime=load_data(conf.instrument,conf.start_date,conf.end_date,conf.field,conf.seq_len
print('> Data Loaded. Compiling...')
model = build_model([1, conf.seq_len, 1])
model.fit(
X_train,
y_train,

batch_size=conf.batch,
nb_epoch=conf.epochs,
validation_split=conf.validation_split)
predictions = predict_sequences_multiple(model, X_test, conf.seq_len, conf.prediction_len)
#
#
predictions = predict_sequence_full(model, X_test, conf.seq_len)
predictions = predict_point_by_point(model, X_test)
if conf.normalise==True:
predictions=denormalise_windows(predictions,data_test,conf.seq_len)
y_test=denormalise_windows(y_test,data_test,conf.seq_len)
print('Training duration (s) : ', time.time() - global_start_time)
plot_results_multiple(predictions, y_test, conf.prediction_len)
#
plot_results(predictions, y_test)
>
>
>
Loading data...
Data Loaded. Compiling...
Compilation Time : 9.5367431640625e-07
Train on 2121 samples, validate on 236 samples
Epoch 1/1
2
121/2121 [==============================] - 15s - loss: 0.0139 - val_loss: 0.0039
Training duration (s) : 37.46438002586365
In [20]:
len(predictions)
Out[20]:
2
9
In [21]:
#
#
#
#
1. 策略基本参数
3.回测
目前回测结构主要针对predict_sequences_multiple的预测结果,并且股票最好没有停牌
回测其他结果可自行修改handle_data
def initialize(context):
系统已经设置了默认的交易手续费和滑点,要修改手续费可使用如下函数
context.set_commission(PerOrder(buy_cost=0.0003, sell_cost=0.0013, min_cost=5))
传入预测数据和真实数据
#
#
context.predictions=predictions
context.true_data=y_test
context.date_time=test_datetime
#
设置持仓比
context.percent = 0.7
设置持仓天数
context.hold_days=conf.prediction_len
传入起止时间
#
#
context.start_date=context.date_time[0].strftime('%Y-%m-%d')
context.end_date=context.date_time[-1].strftime('%Y-%m-%d')
#
结束时间预计至少比开始时间多gap点才进场
context.gap=0
context.dt = 0
#
回测引擎:每日数据处理函数,每天执行一次
def handle_data(context, data):
current_dt = data.current_dt.strftime('%Y-%m-%d')
can_do=pd.Timestamp(current_dt) in context.date_time
if can_do:
context.dt = current_dt
sid = context.symbol(conf.instrument)
cur_position = context.portfolio.positions[sid].amount
# 持仓
row=context.date_time.index(pd.Timestamp(context.dt))
prediction=context.predictions[row]
#
满足开仓条件
if prediction[-1]-prediction[0]>=context.gap and cur_position == 0 and data.can_trade(sid):
context.order_target_percent(sid, 1)
elif prediction[-1]-prediction[0]<context.gap and cur_position > 0 and data.can_trade(sid):
context.order_target(sid, 0)
#
调用回测引擎
m8 = M.trade.v2(

instruments=conf.instrument,
start_date=test_datetime[0].strftime('%Y-%m-%d'),
end_date=test_datetime[len(test_datetime)-1].strftime('%Y-%m-%d'),
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='close',
capital_base=10000,
# 表示 开盘 时买入
# 表示 收盘 前卖出
benchmark='000300.SHA',
#
通过 options 参数传递预测数据和参数给回测引擎
options={'predictions': predictions}
)
[
[
[
[
2017-07-20 12:20:09.734573] INFO: bigquant: backtest.v7 start ..
2017-07-20 12:20:12.030542] INFO: Performance: Simulated 561 trading days out of 561.
2017-07-20 12:20:12.031667] INFO: Performance: first open: 2015-02-17 14:30:00+00:00
2017-07-20 12:20:12.032472] INFO: Performance: last close: 2017-06-09 19:00:00+00:00
[
2017-07-20 12:20:14.872765] INFO: bigquant: backtest.v7 end [5.138171s].
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
参考资料:
LSTM策略主体参考http://www.jakob-aungiers.com/articles/a/LSTM-Neural-Network-for-Time-Series-Prediction,在一些地方做了一些更改,使之能在
bigquant平台上使用以及能够自己调整更多参数
对keras有兴趣者可参考http://keras-cn.readthedocs.io/en/latest/,这里有对keras每个函数的详细介绍
使用sklearn 进行数据预处理
1
. 数据标准化¶
数据标准化(Standardization or Mean Removal and Variance Scaling)
进行标准化缩放的数据均值为0,具有单位方差。
scale函数提供一种便捷的标准化转换操作,如下:
In [42]:
from sklearn import preprocessing #导入数据预处理包
X=[[1.,-1.,2.],
[
[
2.,0.,0.],
0.,1.,-1.]]
X_scaled = preprocessing.scale(X)
X_scaled
Out[42]:
array([[ 0.
, -1.22474487, 1.33630621],
[
[
1.22474487, 0.
, -0.26726124],
-1.22474487, 1.22474487, -1.06904497]])
In [43]:
X_scaled.mean(axis=0)
Out[43]:
array([ 0., 0., 0.])
In [44]:
X_scaled.std(axis=0)
Out[44]:
array([ 1., 1., 1.])
同样我们也可以通过preprocessing模块提供的Scaler(StandardScaler 0.15以后版本)工具类来实现这个功能:
In [45]:

scaler = preprocessing.StandardScaler().fit(X)
print(scaler)
print(scaler.mean_)
print(scaler.std_)
StandardScaler(copy=True, with_mean=True, with_std=True)
[
[
1.
0.
0.33333333]
0.81649658 0.81649658 1.24721913]
/
opt/conda/lib/python3.5/site-packages/sklearn/utils/deprecation.py:70: DeprecationWarning: Function std_ is deprecated; Attribute ``
warnings.warn(msg, category=DeprecationWarning)
In [46]:
scaler.transform(X)
Out[46]:
array([[ 0.
, -1.22474487, 1.33630621],
[
[
1.22474487, 0. , -0.26726124],
-1.22474487, 1.22474487, -1.06904497]])
2
. 特征缩放¶
2
.1 MinMaxScaler( 最小最大值标准化)¶
将数据缩放至给定的最小值与最大值之间,通常是0与1之间
公式:X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0)) ;
In [47]:
#
例子:将数据缩放至[0, 1]间。训练过程: fit_transform()
X_train = np.array([[1., -1., 2.], [2., 0., 0.], [0., 1., -1.]])
min_max_scaler = preprocessing.MinMaxScaler()
X_train_minmax = min_max_scaler.fit_transform(X_train)
X_train_minmax
Out[47]:
array([[ 0.5
, 0.
, 0.5
, 1.
, 1.
, 0.33333333],
, 0. ]])
],
[
[
1.
0.
In [48]:
#
将上述得到的scale参数应用至测试数据
X_test = np.array([[ -3., -1., 4.]])
X_test_minmax = min_max_scaler.transform(X_test) #out: array([[-1.5 , 0. , 1.66666667]])
#
可以用以下方法查看scaler的属性
print(min_max_scaler.scale_)
print(min_max_scaler.min_)
#out: array([ 0.5 , 0.5, 0.33...])
#out: array([ 0., 0.5, 0.33...])
[
[
0.5
0.
0.5
0.5
0.33333333]
0.33333333]
2
.2 MaxAbsScaler (绝对值最大标准化)¶
它通过除以最大值将训练集缩放至[-1,1]。这意味着数据已经以0为中心或者是含有非常非常多0的稀疏数据。
In [49]:
X_train = np.array([[ 1., -1., 2.],
[
2., 0., 0.],
0., 1., -1.]])
[
max_abs_scaler = preprocessing.MaxAbsScaler()
X_train_maxabs = max_abs_scaler.fit_transform(X_train)
X_train_maxabs
Out[49]:
array([[ 0.5, -1. , 1. ],
[
[
1. , 0. , 0. ],
0. , 1. , -0.5]])
In [50]:
X_test = np.array([[ -3., -1., 4.]])
X_test_maxabs = max_abs_scaler.transform(X_test)
X_test_maxabs
Out[50]:
array([[-1.5, -1. , 2. ]])
In [51]:
max_abs_scaler.scale_
Out[51]:
array([ 2., 1., 2.])
3
. 数据规范化(Normalization )¶
把数据集中的每个样本所有数值缩放到(-1,1)之间。
In [52]:
X = [[ 1., -1., 2.],
[
[
2., 0., 0.],
0., 1., -1.]]
X_normalized = preprocessing.normalize(X, norm='l2')
X_normalized
Out[52]:
array([[ 0.40824829, -0.40824829, 0.81649658],
[
[
1.
0.
, 0.
, 0.
],
, 0.70710678, -0.70710678]])
In [53]:
normalizer = preprocessing.Normalizer().fit(X) # fit does nothing
normalizer
Out[53]:
Normalizer(copy=True, norm='l2')
In [54]:
normalizer.transform(X)
Out[54]:
array([[ 0.40824829, -0.40824829, 0.81649658],
[
[
1.
0.
, 0.
, 0.
],
, 0.70710678, -0.70710678]])
In [55]:
normalizer.transform([[-1., 1., 0.]])
Out[55]:
array([[-0.70710678, 0.70710678, 0.
]])
4
. 二进制化(Binarization )¶
将数值型数据转化为布尔型的二值数据,可以设置一个阈值(threshold)
In [56]:
X = [[ 1., -1., 2.],
[
[
2., 0., 0.],
0., 1., -1.]]
binarizer = preprocessing.Binarizer().fit(X) # fit does nothing
binarizer

Out[56]:
Binarizer(copy=True, threshold=0.0)
In [57]:
binarizer.transform(X)
Out[57]:
array([[ 1., 0., 1.],
[
[
1., 0., 0.],
0., 1., 0.]])
In [58]:
binarizer = preprocessing.Binarizer(threshold=1.1)
binarizer.transform(X)
Out[58]:
array([[ 0., 0., 1.],
[
[
1., 0., 0.],
0., 0., 0.]])
5
. 标签预处理(Label preprocessing )¶
4
.1 标签二值化(Label binarization )¶
LabelBinarizer通常用于通过一个多类标签(label)列表,创建一个label指示器矩阵
In [59]:
lb = preprocessing.LabelBinarizer()
lb.fit([1, 2, 6, 4, 2])
Out[59]:
LabelBinarizer(neg_label=0, pos_label=1, sparse_output=False)
In [60]:
lb.classes_
Out[60]:
array([1, 2, 4, 6])
In [61]:
lb.transform([1, 6])
Out[61]:
array([[1, 0, 0, 0],
[
0, 0, 0, 1]])
4
.2 标签编码(Label encoding )¶
In [62]:
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
le.fit([1, 2, 2, 6])
Out[62]:
LabelEncoder()
In [63]:
le.classes_
Out[63]:

array([1, 2, 6])
In [64]:
le.transform([1, 1, 2, 6])
Out[64]:
array([0, 0, 1, 2])
In [65]:
le.inverse_transform([0, 0, 1, 2])
Out[65]:
array([1, 1, 2, 6])
金融,经济与市场
[
量化学堂-金融市场]Beta对冲
导语:本文介绍了因子模型、对冲以及Beta因子的相关内容,并针对如何进行市场风险对冲给出了具体的案例。
因子模型
因子模型是通过其他若干项资产回报的线性组合来解释一项资产回报的一种方式,因子模型的一般形式是:
这看起来很熟悉,因为它正是多元线性回归模型。
什么是beta?
一项资产的$beta$是该资产收益率与其他资产收益率通过上述模型回归拟合的$\beta$。比如,我们用回归模型$Y_{gzmt} = \alpha + \beta
X_{benchmark}$来描述贵州茅台收益率相对于沪深300回归的$\beta$值,如果我们使用模型$Y_{gzmt} = \alpha + \beta_1 X_{benchmark}+\beta_2
X_{wly}$,那么就会出现两个$beta$,一个是贵州茅台对沪深300的风险暴露,一个是贵州茅台对五粮液的风险暴露。
通常而言,$beta$更多地 指该资产相对于基准指数的风险暴露,即只相对于市场基准的一元线性回归所得到的回归系数。
什么是对冲?
如果我们确定我们的投资组合的回报与市场的关系如下面公式所示:
于是,我们可以建立沪深300空头头寸来对冲市场风险,对冲的市值为$-\beta V$,如果我们持有多头组合的市值是$V$。因为我们多头组合的收益为
$
\alpha+\beta X_{hs300}$,沪深300对冲空头的收益为$-\beta X_{hs300}$,于是我们最终的收益为$\alpha + \beta X_{hs300} - \beta X_{hs300} = \alpha$,于是
我们的收益来源只有$\alpha$,而与市场系统风险没有关系。
风险暴露
一般而言,beta描述的是持有资产所承担的系统风险敞口这一概念。 如果一项资产相对沪深300基准指数具有较高的$\beta$暴露水平,那么在市场上涨时,
它的表现将会很好,当市场下跌时,它表现很差。 高$\beta$对应于高系统风险(高市场风险),意味着你的投资更具有波动性。
在BigQuant,我们重视尽可能没有系统风险暴露的市场中性策略。 这意味着策略中的所有回报都在模型的$\alpha$部分,而与市场无关。 因为这意味着该策
略与市场系统风险无关,不管是牛市还是熊市,它都具有稳定的业绩表现。 市场中性策略对于拥有大量现金池的机构(银行、保险、公募基金等)最具吸引
力。
风险管理
减少因子风险暴露的过程称为风险管理。 对冲是在实践中进行风险管理的最佳方式之一。
本文通过具体案例来了解如何做到市场风险对冲的,我们使用贵州茅台和基准沪深300来构建我们的投资组合,将沪深300的权重设为-$\beta$(由于持有基
准空头头寸)。
附件:市场风险对冲的具体案例
In [22]:
#
导入相应的模块
import numpy as np
from statsmodels import regression
import statsmodels.api as sm

import matplotlib.pyplot as plt
import math
In [23]:
#
获取一段时间的股票数据
start_date = '2014-01-01'
end_date = '2015-01-01'
asset = D.history_data('600519.SHA',start_date,end_date,fields=['close']).set_index('date')['close']
benchmark = D.history_data('000300.SHA',start_date,end_date,fields=['close']).set_index('date')['close']
asset.name = '600519.SHA'
benchmark.name = '000300.SHA'
#
计算收益率
r_a = asset.pct_change()[1:]
r_b = benchmark.pct_change()[1:]
#
绘制
r_a.plot(figsize=[9,6])
r_b.plot()
plt.ylabel("Daily Return")
plt.legend();
现在我们可以通过回归求出 alpha($\alpha$) 和beta($\beta$)
In [24]:
X = r_b.values
Y = r_a.values
x = sm.add_constant(X)
def linreg(x,y):
#
增加一个常数项
x = sm.add_constant(x)
model = regression.linear_model.OLS(y,x).fit()
#
再把常数项去掉
x = x[:, 1]
return model.params[0], model.params[1]
alpha, beta = linreg(X,Y)
print('alpha: ' + str(alpha))
print('beta: ' + str(beta))
alpha: 0.00116253939056
beta: 0.672934653004
In [25]:
X2 = np.linspace(X.min(), X.max(), 100)
Y_hat = X2 * beta + alpha
plt.scatter(X, Y, alpha=0.3) # 画出原始数据散点
plt.xlabel("000300.SHA Daily Return")
plt.ylabel("600519.SHA Daily Return")
#
增加一条红色的回归直线
plt.plot(X2, Y_hat, 'r', alpha=0.9);
风险暴露¶
一般而言,beta描述的是持有资产所承担的 系统风险敞口这一概念,用$\beta$表示。 如果一项资产相对沪深300基准指数具有较高的$\beta$暴露水平,那
么在市场上涨时,它的表现将会很好,当市场下跌时,它表现很差。 高$\beta$对应于高系统风险(高市场风险),意味着你的投资更具有波动性。
在BigQuant,我们重视尽可能没有系统风险暴露的 市场中性策略。 这意味着策略中的所有回报都在模型的$\alpha$部分,而与市场无关。 因为这意味着该
策略与市场系统风险无关,不管是牛市还是熊市,它都具有稳定的业绩表现。 市场中性策略对于拥有大量现金池的机构(银行、保险、公募基金等)最具吸
引力。
风险管理¶
减少因子风险暴露的过程称为 风险管理。对冲是在实践中进行风险管理的最佳方式之一。
通过案例来了解如何做到市场风险对冲的
现在我们已经知道要对冲多少市值,让我们看看它如何影响我们的收益。 我们使用贵州茅台和基准沪深300来构建我们的投资组合,将沪深300的权重设
为-$\beta$(由于持有基准空头头寸)
In [26]:

#
构建一个市场中性组合
portfolio = -1*beta*r_b + r_a
portfolio.name = "600519.SHA + Hedge"
#
绘制各自的收益曲线
portfolio.plot(alpha=0.9,figsize=[9,6])
r_b.plot(alpha=0.5);
r_a.plot(alpha=0.5);
plt.ylabel("Daily Return")
plt.legend();
看来组合(贵州茅台+沪深300)的收益和贵州茅台走势相当接近。 我们可以通过计算两者的平均回报率和风险(收益率的标准差)来量化其表现的差异
In [27]:
print("means: ", portfolio.mean(), r_a.mean())
print("volatilities: ", portfolio.std(), r_a.std())
means: 0.0011625392362475395 0.002370904665440321
volatilities: 0.01785176992416382 0.019634943455457687
可以看出,我们以收益率为代价降低了波动,在降低风险的同时,收益也相应降低了。 接下来,我们来检查一下$\alpha$是否与以前一样,而$\beta$已被消
除
In [28]:
P = portfolio.values
alpha, beta = linreg(X,P)
print('alpha: ' + str(alpha))
print('beta: ' + str(beta)) # alpha 和以前仍然一样 beta 已经被消除,beta几乎为0
alpha: 0.00116253937709
beta: -1.24623534062e-09
请注意,我们使用历史数据构建了 市场中性策略。 我们可以通过在不同的时间框架内验证资产和对冲投资组合的$\alpha$和$\beta$值来检查其是否仍然有
效
In [29]:
#
得到过去一年得到的alpha 和beta值
start_date = '2014-01-01'
end_date = '2015-01-01'
asset = D.history_data('600519.SHA',start_date,end_date,fields=['close']).set_index('date')['close']
benchmark = D.history_data('000300.SHA',start_date,end_date,fields=['close']).set_index('date')['close']
r_a = asset.pct_change()[1:]
r_b = benchmark.pct_change()[1:]
X = r_b.values
Y = r_a.values
historical_alpha, historical_beta = linreg(X,Y)
print('Asset Historical Estimate:')
print('alpha: ' + str(historical_alpha))
print('beta: ' + str(historical_beta))
#
获取下一年的数据:
start_date = '2015-01-01'
end_date = '2015-06-01'
asset = D.history_data('600519.SHA',start_date,end_date,fields=['close']).set_index('date')['close']
benchmark = D.history_data('000300.SHA',start_date,end_date,fields=['close']).set_index('date')['close']
asset.name = '600519.SHA'
benchmark.name = '000300.SHA'
#
重复前面的过程来计算alpha 和beta值
r_a = asset.pct_change()[1:]
r_b = benchmark.pct_change()[1:]
X = r_b.values
Y = r_a.values
alpha, beta = linreg(X,Y)
print('Asset Out of Sample Estimate:')
print('alpha: ' + str(alpha))
print('beta: ' + str(beta))
#
构建对冲投资组合来计算alpha、beta
portfolio = -1*historical_beta*r_b + r_a
P = portfolio.values
alpha, beta = linreg(X,P)
print('Portfolio Out of Sample:')
print ('alpha: ' + str(alpha))
print ('beta: ' + str(beta))
#
绘制图形
portfolio.name = "600519.SHA + Hedge"
portfolio.plot(alpha=0.9,figsize=[9,6])
r_a.plot(alpha=0.5);
r_b.plot(alpha=0.5)
plt.ylabel("Daily Return")
plt.legend();
Asset Historical Estimate:
alpha: 0.00116253939056
beta: 0.672934653004
Asset Out of Sample Estimate:
alpha: 0.00020366206079
beta: 0.866552969103
Portfolio Out of Sample:
alpha: 0.000203662008879
beta: 0.193618313006
从上图可以看出,对冲后的收益降低了,但波动性也降低了。历史估计出的贝塔值在样本外的一年中是有效的,将资产的贝塔值0.673通过对冲降低到了
0
.193,也就是说降低了2/3,这样的对冲效果是比较明显的,而且也反映出历史的贝塔值是有效的,当然,要做到更好的效果,可以采取滚动估计贝塔的方
法。
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-金融市场]跌了这么多,创业板可以买了吗?
导语:股神巴菲特坦然其投资理念非常简单——价值投资,专买具有安全边际处于价值“洼地”的股票。在股票市场上,一般以市盈率指标来衡量股票的
价值,市盈率相对较低的话,股票更具有投资价值。 本文介绍了市盈率以及相关的金融市场信息。
什么是市盈率¶
市盈率是衡量股价高低和企业盈利能力的一个重要指标。由于市盈率把股价和企业盈利能力结合起来,其水平高低更真实地反映了股票价格的高低。例如,
股价同为50元的两只股票,其每股收益分别为5元和1元,则其市盈率分别是10倍和50倍,也就是说具当前的实际价格水平相差5倍。若企业盈利能力不变,
这说明投资者以同样50元价格购买的两种股票,要分别在10年和50年以后才能从企业盈利中收回投资。因此市盈率倍数可以简单地理解为要收回投资,最少
需要多少年,很明显市盈率越低,越具有吸引力。
我们先看看创业板指数:¶
3
99006.SZA代表创业板指数,不清楚的小伙伴可以参看文档。T.plot是我们平台封装的一个绘图函数,有些小伙伴可能要问了,为什么Python绘图功能如此
强大还要自己封装绘图函数呢?那是因为T.plot是绘制交互式图表,功能更强大,去试试大家就知道了(Pandas DataFrame数据图表可视化),而且一旦使
用之后,就不会再用普通的绘图函数啦。
In [1]:
start_date = '2013-01-01'
end_date = '2017-07-18'
index = D.history_data('399006.SZA', start_date, end_date, fields=['close']).set_index('date')
T.plot(index[['close']], chart_type='line', title='创业板指数')
从上图我们看出,创业板指数在13年以来一路走牛,曾在2015年6月到达了3900点的高度,然后经历了数次大级别调整。创业板是市场中的热点板块,比较
容易受到投资者的青睐,各种题材、热点都是经常出现在创业板中,那么现在的创业板是否具有投资价值呢?要回答这个问题,就必须计算创业板的平均市
盈率。
股票列表¶
我们先把股票代码列表拿出来,参看文档:
In [2]:
stock = D.instruments(start_date=start_date, end_date=end_date)
然后,获取创业板股票(股票代码以3开始)的总市值和市盈率数据,参看数据获取API详解。然后根据总市值和市盈率我们再计算净利润数据,最后将其放
在一张大表:
In [3]:
df = pd.DataFrame()
for i in stock:
if i[0] == '3':
data = D.history_data(i, start_date, end_date, fields =['pe_ttm','market_cap','list_board'])
data['net_profit'] = data['market_cap'] / data['pe_ttm'] # 净利润
data = data.set_index('date')[['instrument', 'market_cap', 'net_profit']]
df = df.append(data)

平均市盈率计算¶
现在,我们有了创业板中每只股票的总市值和市盈率数据,据此来计算创业板平均市盈率:
groupby 方法¶
这里,尤其要介绍的是groupby方法,它是一种数据处理的聚合分组运算方法,可以参看10分钟学会Pandas。Pandas提供了一个灵活高效的groupby功能,
它使你能以一种自然的方式对数据集进行切片、切块、摘要等操作。根据一个或多个键(可以是函数、数组或DataFrame列名)拆分Pandas对象。计算分组
摘要统计,如计数、平均值、标准差,或用户自定义函数。
In [4]:
output = df.reset_index().groupby('date')['market_cap','net_profit'].sum()
output['average_pe'] = output['market_cap'] / output['net_profit']
T.plot(output[['average_pe']], chart_type='line', title='平均市盈率')
可以看出,在15年牛市顶部的时候,创业板平均市盈率曾经达到了150倍,即这是一笔需要150年才会收回本金的投资,想想这是多么疯狂啊,因为欧美等发
达国家股市的市盈率一般保持在15~20倍左右,而亚洲一些发展中国家的股市正常情况下的市盈率在30倍左右。现在我们创业板市盈率在50倍左右,你会觉
得它处于价值“洼地”吗?
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-金融市场]因子风险暴露
导语:本文介绍了如何计算因子风险暴露的内容。
通常,此分析是基于历史数据,而对历史风险暴露的估计可能会影响未来的风险暴露。 因此,计算因子风险暴露是不够的。 你必须对风险暴露保持信心,并
明白对风险暴露的建模是否合理。
运用多因子模型计算因子风险暴露
我们可以运用多因子模型分析一个组合中风险和收益的来源,多因子模型对收益的分解如下:
通过对历史收益率进行建模,我们可以分析出收益中有多少是来自因子收益率,有多少来自资产特质波动($\epsilon$)。 我们也可以研究投资组合所面临
的风险来源,即投资组合的因子暴露。
在风险分析中,我们经常对主动回报(相对于基准的回报)和主动风险(主动回报的标准差,也称为跟踪误差或跟踪风险)进行建模。
例如,我们可计算到一个因子对主动风险的边际贡献——FMCAR。 对于因子$j$,表示为:
$
b_j$表示组合对因子$j$的风险暴露,$b_i$表示组合对因子$i$的风险暴露,$K$表示一共$K$个因子。$FMCAR_j$这项指标这告诉我们,假设其他条件不变,
暴露在因子$j$下我们增加了多少风险。
附件:运用Fama-French三因子模型演示因子风险暴露
In [1]:
#
导入要用到的模块
import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
from statsmodels import regression
import matplotlib.pyplot as plt
import pandas as pd
获取总市值、总市值排序、市净率、市净率排序、日收益率¶
In [ ]:
start_date = '2016-01-01'
end_date = '2017-05-10'
raw_data = D.features(D.instruments(),start_date,end_date,fields=
[
'market_cap_0','rank_market_cap_0','pb_lf_0','rank_pb_lf_0','daily_return_0'])
#
每日股票数量
stock_count = raw_data[['date','instrument']].groupby('date').count()
result=raw_data.merge(stock_count.reset_index('date'), on=['date'], how='outer')
result = result.rename(columns={'instrument_x':'instrument','instrument_y':'stock_count'})

我们将市值最小的600只股票记为smallest组,将市值最大的600只股票记为biggest组
我们将市净率最小的600股票记为lowpb组,将市净率最大的600只股票记为highpb组
In [ ]:
def is_smallest(x):
if x.rank_market_cap_0 < 600/x.stock_count:
return True
else:
return False
result['smallest'] = result.apply(is_smallest,axis=1)
def is_biggest(x):
if x.rank_market_cap_0 > 1-600/x.stock_count:
return True
else:
return False
result['biggest'] = result.apply(is_biggest,axis=1)
def is_lowpb(x):
if x.rank_pb_lf_0 < 600/x.stock_count:
return True
else:
return False
result['lowpb'] = result.apply(is_lowpb,axis=1)
def is_highpb(x):
if x.rank_pb_lf_0 > 1-600/x.stock_count:
return True
else:
return False
result['highpb'] = result.apply(is_highpb,axis=1)
result = result.set_index('date')
计算每日因子收益率¶
In [ ]:
#
因子收益的定义,以市值因子举例,市值因子收益率=biggest组的平均收益率-smallest组的平均收益率
R_biggest = result[result.biggest]['daily_return_0'].groupby(level=0).mean()
R_smallest = result[result.smallest]['daily_return_0'].groupby(level=0).mean()
R_highpb = result[result.highpb]['daily_return_0'].groupby(level=0).mean()
R_lowpb = result[result.lowpb]['daily_return_0'].groupby(level=0).mean()
#
市值因子和市净率因子收益率
SMB = R_smallest - R_biggest
HML = R_lowpb - R_highpb
因子累计收益率并绘图¶
In [ ]:
SMB_CUM = np.cumprod(SMB+1)
HML_CUM = np.cumprod(HML+1)
plt.plot(SMB_CUM.index, SMB_CUM.values,)
plt.plot(HML_CUM.index, HML_CUM.values)
plt.ylabel('Cumulative Return')
plt.legend(['SMB Portfolio Returns', 'HML Portfolio Returns']);
计算风险暴露程度¶
下面我们运用多因素模型和线性回归工具来计算某只股票的回报率相对于这些因子的风险暴露程度。我们以某个资产组合的主动收益作为被解释变量,对因
子做回归,一个因子对主动收益贡献越大,那么这个资产组合的主动收益对于该因子的暴露程度也越高。
In [ ]:
#
我们以5只股票的组合(portfolio)举例
instruments = D.instruments()[:5]
Stock_matrix = D.history_data(instruments,start_date,end_date,fields=['close'])
Stock_matrix = pd.pivot_table(Stock_matrix,values='close',index=['date'],columns=['instrument'])
portfolio = Stock_matrix.pct_change()[1:]
#
组合的每日收益率(等权重组合)
R = np.mean(portfolio, axis=1)
基准收益率
bench = D.history_data('000300.SHA',start_date, end_date, fields=['close']).set_index('date')['close'].pct_change()[1:]
主动收益率
active = R - bench
建立一个常数项,为下文回归做准备
#
#
#
constant = pd.TimeSeries(np.ones(len(active.index)), index=active.index)
df = pd.DataFrame({'R': active,
'
'
'
F1': SMB,
F2': HML,
Constant': constant})
#
删除含有缺失值的行
df = df.dropna()
线性回归并获取回归系数¶
In [ ]:
b1, b2 = regression.linear_model.OLS(df['R'], df[['F1', 'F2']]).fit().params
#
因子对于主动收益的敏感性(即因子暴露)
print('Sensitivities of active returns to factors:\nSMB: %f\nHML: %f' % (b1, b2))
边际贡献¶
利用前文中的公式,计算因子对主动收益风险平方的边际贡献(factors' marginal contributions to active risk squared,FMCAR )
In [ ]:
#
计算因子风险贡献
F1 = df['F1']
F2 = df['F2']
cov = np.cov(F1, F2)
ar_squared = (active.std())**2
fmcar1 = (b1*(b2*cov[0,1] + b1*cov[0,0]))/ar_squared
fmcar2 = (b2*(b1*cov[0,1] + b2*cov[1,1]))/ar_squared
print('SMB Risk Contribution:', fmcar1)
print('HML Risk Contribution:', fmcar2)
余下的风险可以归结于一些特有的风险因素,即我们没有加入模型的因子或者资产组合本身独有的某种风险。 通常我们会关注一下对这些因子的风险暴露随
时间如何变化。让我们rolling一下~
In [ ]:
#
计算滚动的beta
model = pd.stats.ols.MovingOLS(y = df['R'], x=df[['F1', 'F2']],
window_type='rolling',
window=100)
rolling_parameter_estimates = model.beta
rolling_parameter_estimates.plot()
plt.title('Computed Betas');
plt.legend(['F1 Beta', 'F2 Beta', 'Intercept']);
现在我们来看看FMCAR是如何随时间变化的
In [ ]:
#
#
计算方差协方差
去除有缺省值的日期,从有实际有效值的日期开始
covariances = pd.rolling_cov(df[['F1', 'F2']], window=100)[99:]
计算主动风险
active_risk_squared = pd.rolling_std(active, window = 100)[99:]**2
计算beta
betas = rolling_parameter_estimates[['F1', 'F2']]
#
#
#
新建一个空的dataframe
FMCAR = pd.DataFrame(index=betas.index, columns=betas.columns)
#
每个因子循环
for factor in betas.columns:
每一天循环
for t in betas.index:
#
#
求beta与协方差之积的和,见公式
s = np.sum(betas.loc[t] * covariances[t][factor])
#
获取beta
b = betas.loc[t][factor]
获取主动风险
AR = active_risk_squared.loc[t]
估计当天的FMCAR
#
#
FMCAR[factor][t] = b * s / AR
因子对于主动收益风险的边际贡献¶
In [ ]:
plt.plot(FMCAR['F1'].index, FMCAR['F1'].values)
plt.plot(FMCAR['F2'].index, FMCAR['F2'].values)
plt.ylabel('Marginal Contribution to Active Risk Squared')
plt.legend(['F1 FMCAR', 'F2 FMCAR'])
存在的问题¶
了解历史数据中组合对各个因子的暴露程度是很有趣的,但只有将它用在对未来预测上时,它才有用武之地。但我们不是总能够放心地认为未来的情况与现
在相同,由于随时间会变化,对风险暴露程度取平均值也很容易出现问题。我们可以给均值加上一个置信区间,但只有当其分布是正态分布或者表现很稳健
才行。我们来看看Jarque-Bera测验的结果。
In [ ]:
from statsmodels.stats.stattools import jarque_bera
_
_
, pvalue1, _, _ = jarque_bera(FMCAR['F1'].dropna().values)
, pvalue2, _, _ = jarque_bera(FMCAR['F2'].dropna().values)
print('p-value F1_FMCAR is normally distributed', pvalue1)
print('p-value F2_FMCAR is normally distributed', pvalue2)
p_value显示我们可以显著的拒绝其为正态分布,可见对于未来这些因素会导致多少风险暴露是很难估计的,所以在使用这些统计模型去估计风险暴露并以此
为依据来对冲是需要万分小心的。
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
[
量化学堂-金融市场]Barra 风险结构管理模型
导语:本文挑选了著名的风险结构模型进行介绍,具体的细节并没有深入展开,旨在抛砖引玉,了解Barra对于风险结构模型的思维方式和理念。
多因子模型
相似的资产会有相似的回报,这是多因子模型的基本假设。由于某些特定的原因(因子),资产会表现的十分类似,例如价量变化、行业、规模或者利率变
化。多因子模型就是为了发掘这些因子,并且确定收益率随因子变化的敏感程度。通常来说,多因子模型包括了宏观因子模型、基本面因子模型和统计因子
模型。这几种模型在分析不同的大类资产风险收益的时候也有不同的效果。
实现原理
单个资产的多因子模型可以表示成:
其中,
$
x_{ik}$是第$k$个因子的风险暴露,比如我们常说的市值、PE这些值
$
f_k$是第$k$个因子的收益率,是通过多元回归得到的系数
$
u_i$是第$i$个资产的非因子收益率
在历史上的某个时间截面,每个资产相当于一个样本,那么所有的资产就可以通过多元线性回归得到得到$f_k$。
图
种资产对
个不同因子的风险暴露矩阵
图
个因子的因子收益率协方差矩阵

图
非因子收益率方差对角矩阵
这个几个矩阵到底有什么用呢?重要的结论如下:
Risk = XFX^T + \Delta$
$
上面式子是通过矩阵运算,得到资产组合的总风险。
多因子模型的价值
1
. 提供了一种全面分析风险的框架
. 大大降低了运算量。假设有1000种资产的组合,传统基于收益的方法需要计算1000x1000的协方差矩阵,而假设这里只有50种因子,矩阵的规模减少到
了50x50
. 每个周期都更新数据,更好地适应变化的市场环境
. 因子具有经济意义,可以更好地解释收益,收益可以跟踪
2
3
4
5
. 缺点是一般只用于预测大部分风险,但是无法预测收益
站在历史的角度
预测股票未来波动率的方法有很多,其中比较流行的一种就是分析历史数据,然后推测未来可能具有类似的表现。这种方法最大的问题在于,历史数据的长
短,并且和测试的历史市场环境紧密相关。也就是说,随着时间的变化,股票的特性可能发生变化,比如公司的并购重组、战略转型等行为,都会造成股价
的波动,过去的数据并不能预测未来。而经典的CAPM模型里面,就是通过这些历史数据来计算Beta值的。
1
950年之前,系统性、或者市场相关的收益这种概念,还未出现,直到1950年初HarryMarkowitz首先将风险定量地用标准差来表示。随着后来有学者不断完
善和补充这一理论,认为市场的风险是由不可被分散的系统性风险和可以被投资组合分散的残余风险:(如图4)
图
系统性风险和残余风险的关系
随着对市场认识的不断加深,一种叫做资本资产定价模型(CAPM)的理论也被提出,用来描述收益和市场风险的关系:(如图5)
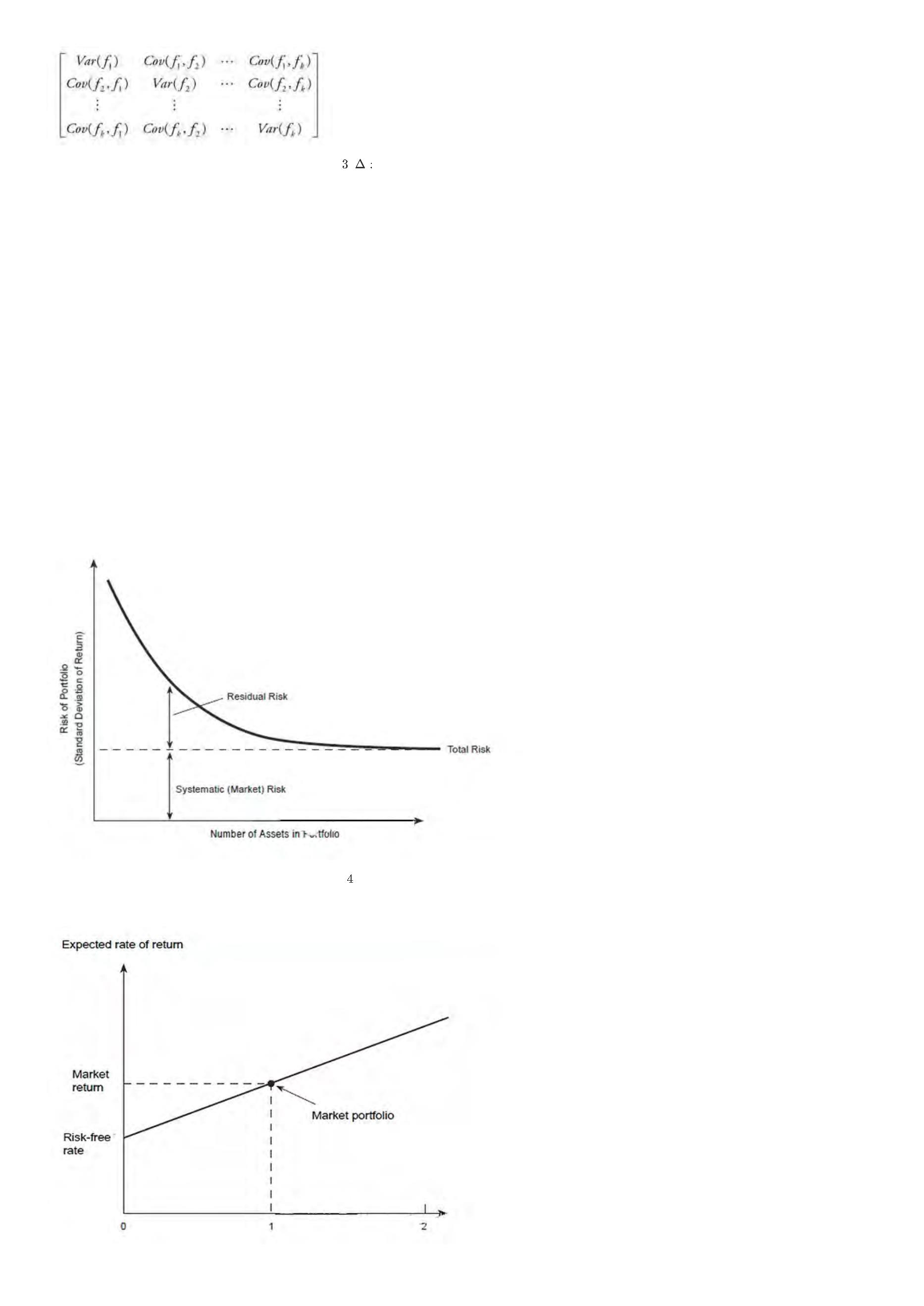
图
收益和市场风险的关系
这个理论认为证券的预期收益正比于系统性风险系数,即Beta。形象地说,Beta就是描述证券组合对市场波动的敏感程度,比如Beta= 2时,市场上涨
0%,那么该证券就上涨20%。
1
模型演变
CAPM描述的是一种市场的平衡状态,前提假设是市场是有效的,但不要求残余收益是不相关的。威廉夏普基于对这种理论进行了延伸,提出了单因子风险
模型,其实就是CAPM公式的一个变形,但是假设了残余收益是不相关的。
后来,学者们逐渐发现,相似的资产总是表现出一些共同的特点,后来就总结出了套利定价模型(APT),认为资产的预期收益等于一些未知的系统性因子
的线性组合。APT模型的提出是为了用来预测收益的,后来逐渐就演变成了多因子模型。
Barra 怎么做
如前文所述,基于历史数据的定价模型存在诸多不合理之处,用这样的方法计算出来的Beta也称为“历史Beta”,而Barra基于风险模型,提出了“预测Beta”的
方法。Barra所使用的风险因子主要来自于基本面,包括行业、规模、波动性等。由于这些风险因子是每月重新计算的,因此这种“预测Beta”可以很好地反应
公司的近期风险结构。
Barra的模型将风险按照图6的方式进行划分:
图
模型的风险划分
其中,共同风险包括了风险指数,代表资产的一些共同特点,如成长/价值、小盘/大盘;也包括了不同行业的区分。特有风险是将每种资产的风险和市场风险
的相对值,进行标准化处理之后得到。
Barra 风险模型建立过程
1
.数据获取
获取数据和处理数据是第一步,在权益风险模型中,以市场数据和基本面的数据为主,其中市场数据一般是可以每日获取的,而基本面数据一般是一个季度
甚至半年以上。在这里,尤其要注意到一些数据的跳跃,如资产规模的突变,缺失的价格数据等;此外,还要尤其注意公司的特殊事件,如资产重组,这些
都会导致数据的不连续。
2
.统计量(因子)筛选和测试
这是核心!因子来源很广泛,传统的方法里面主要包括了市场量价指标和基本面指标,以及它们的组合。因子的检验是很严格的,不仅需要在逻辑上有意
义,同时还要经过严格的统计测试。这些因子必须是要能够预测风险,并且在时间上体现出一定的时效性,换句话说,它一定是可以给模型带来一定的预测
效果的。
3
.标准化
各种因子指标的大小范围差距很大,需要标准化。方法有很多,可以通过排序,然后分布在(0,1)之间,也可以用高斯标准化的方法,因情况而定。
4
.风险指数建立
数据处理全部完毕之后,每个风险因子都要在不同行业之间回归并做统计显著性测试,检验其对收益的解释性,通过测试的因子就可以成为一个风险指数。
风险指数建立的过程是一个迭代的过程,首先入选的是解释性最好的因子,此后的因子都要保证能够带来更多的解释效果,才可以入选。
5
.行业分配
不同行业的收益、风险都会表现出很大的区别,因此在模型中有必要进行这样的划分。
6
.因子收益估计
在每个时间截面上,可以通过横截面回归的方法确定因子收益,也就是回归系数。接着,在对于历史数据,对因子收益的时间序列求协方差矩阵。这里有一
个很重要的问题,就是因子收益之间的相关性是在随时变化的,比如高波动性的月份可能比较集中。对此,主要有两种解决方案:
1
是通过指数加权,约近的月份获得越大的权重,而距离现在越远的月份获得越小的权重,这可以通过一个指数衰减的公式确定。
是通过市场指数的波动率来估计这个协方差矩阵,这里需要将因子的协方差矩阵乘上一个由市场收益率方差确定的系数。
2
7
.特有风险
这个风险矩阵常规来说就是通过历史方差确定,但是这里假设了收益方差是稳定的。Barra提出了一种新的方法,可以捕获特有风险的市场平均水平,以及特
有风险和资产基本面的相关关系。建立这样一种模型包括了计算特有风险的市场平均水平和资产特有风险和基本面特征的相对值。
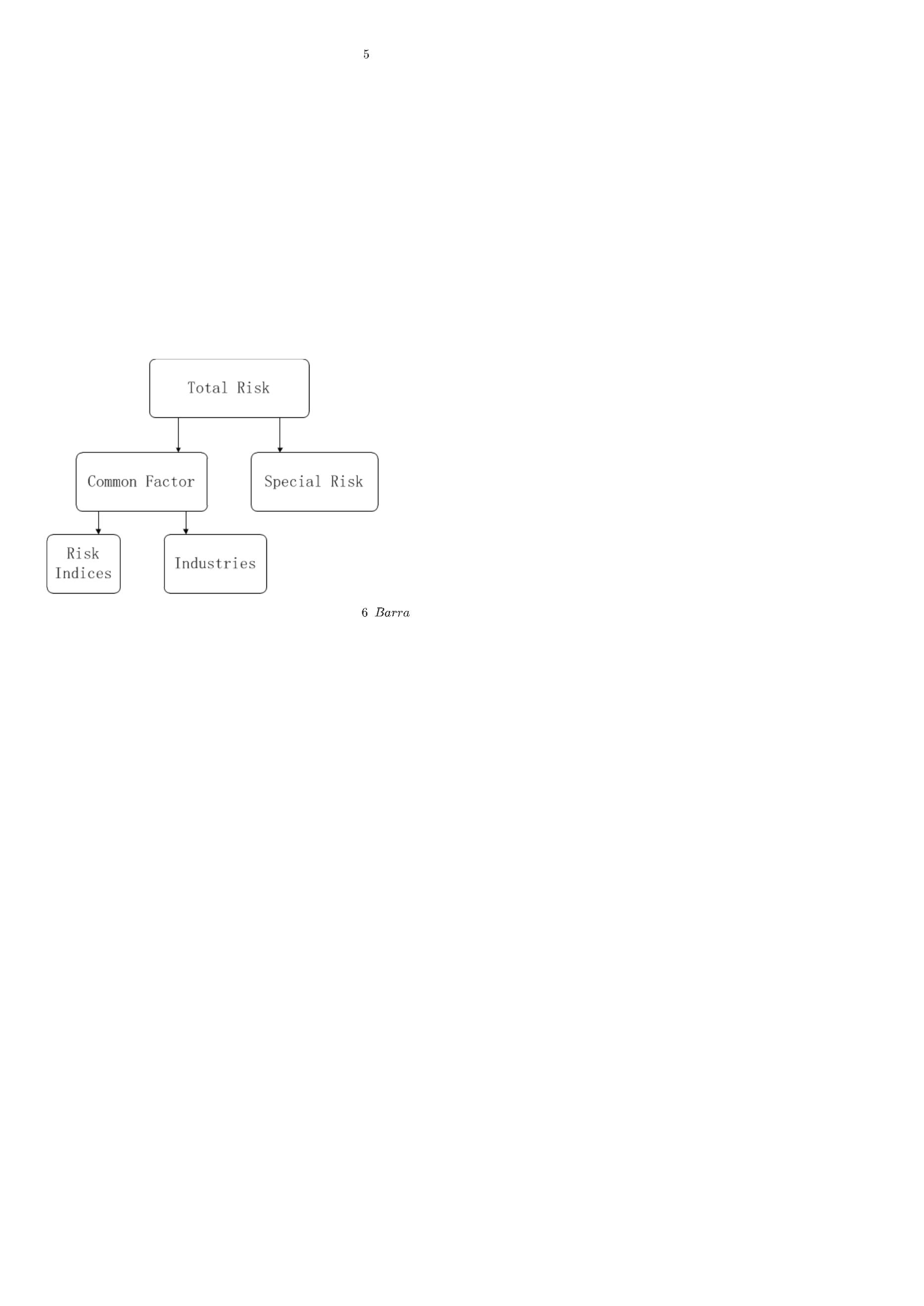
8
.更新模型
以上的计算过程在每个时间截面都需要更新和重新计算,一般选择一个月为周期。
总流程图:
图
风险结构管理模型总流程图
本文由BigQuant宽客学院推出,版权归BigQuant所有,转载请注明出处。
参考书籍:Barra Risk Model Handbook
风险平价组合(risk parity) 理论与实践
本文介绍了风险平价组合的理论与实践;后续文章将对risk parity组合进行更深入探讨以及引入预期收益后的资产配置实战策略。
前言
资产配置是个很广泛的话题,在投资中是一个非常重要的话题
从使用场景分类上来看,资产配置可以是宏观的资产配置,比如货币类、债券类、权益类之间的配置;当然也可以是某一大类资产下的配置,比如在沪
深300成分股不同标的之间的权重配置
但不管怎么说,从方法层面上看,对于不同场景下的使用都是一致的,只不过需要注意不同场景使用下的一些特殊处理
本篇作为资产配置研究系列,理论结合实践,深入浅出,可直接使用
后续会根据时间安排,逐步介绍资产配置领域的相关理论与实践
摘要
介绍了风险平价理论知识
介绍了怎样做到风险平价
风险平价实践的Python代码
简介
资产配置在投资中是非常重要的过程,经典的资产配置方式就是马格维茨的均值-方差模型。目标是在给定预期收益率下最小化方差(风险),或给定风险
水平下最大化收益,通过拉格朗日乘子法,可以计算出一个有效前沿,我们可以根据有效前沿来配置资产。但在实践过程中,我们常常发现计算的结果
是某几个资产的权重特别大,收益和风险都集中在了这些资产上
也有许多对均值方差进行优化的方法,比如加入风险厌恶系数考虑效用函数的最大化,或者加入个性化条件,要求每一大类的配置比例都不得超过35%
等,还有从统计的角度出发,找一些更好的估计协方差阵的方法
基于均值方差模型的不足,PanAgora基金的首席投资官Edward Qian博士提出了著名的风险平价(Risk Parity)策略,这一思想被Bridgewater基金运用于
实际投资中,本贴将详细介绍风险平价配置方法的理论与实践
理论介绍¶
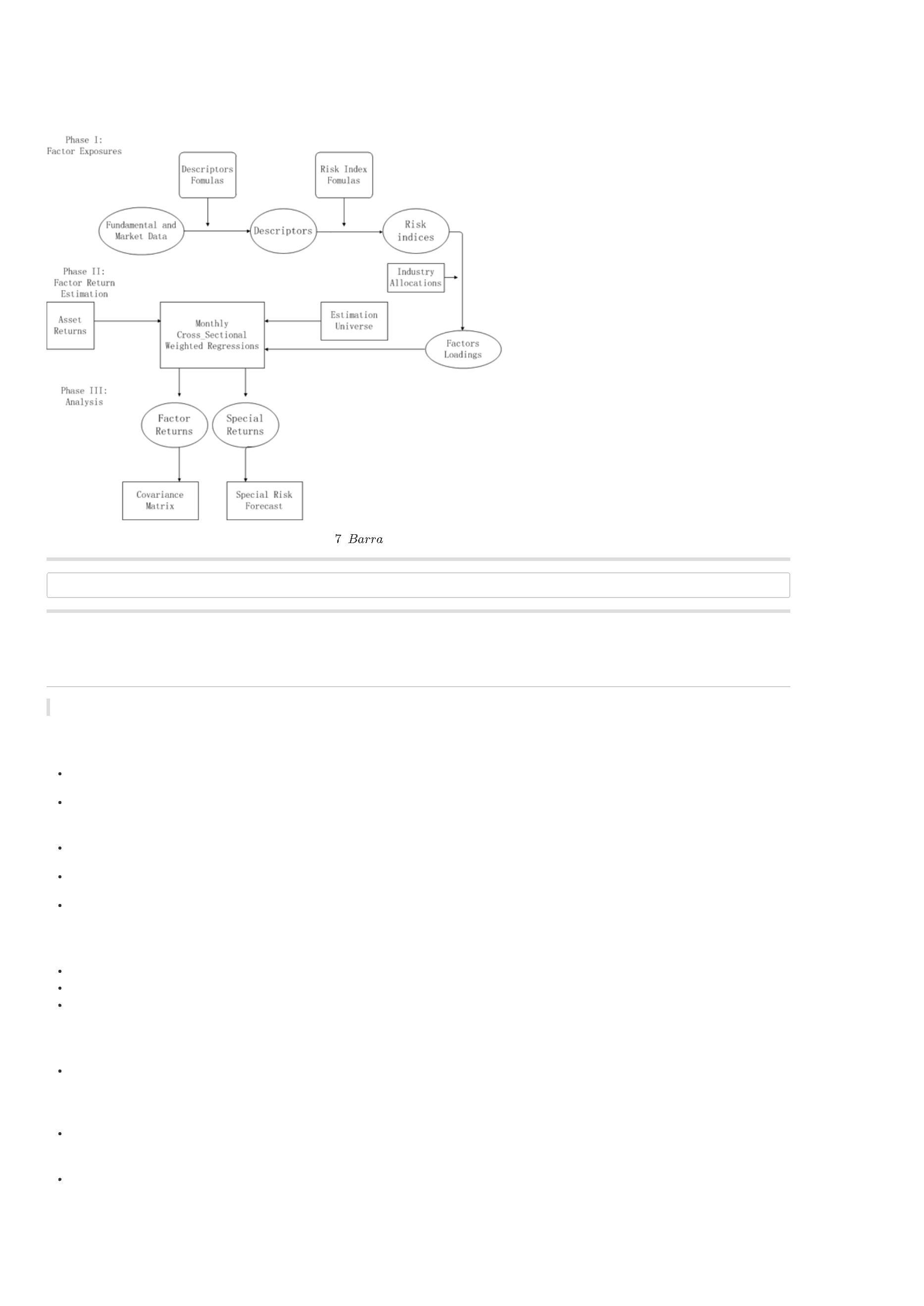
风险平价投资组合是一种资产配置,其重点是配置风险,而不是配置资产。例如,典型的债券40%、股票60%投资组合中,股票风险很大。风险平价(等同
风险)是这样一种投资组合:单个资产(在这种情况下为债券和股票)对整体投资组合总风险具有相同的风险贡献。该理论在过去几十年中得到普及和发
展,基于风险的资产配置理念已被用于许多策略,如管理期货策略和着名的桥水全天候基金。有研究表明,这种资产配置策略比基于资产的配置策略提供更
好的风险调整回报。
我将讨论风险平价的一个非常基本的例子,以及如何构建简单的风险平价(相等风险)投资组合,并将其扩展到风险预算组合(目标风险分配)的具体实
现。
首先将资产j的边际风险贡献($MRC_j$)定义为:
其中:
$
$
$
w_j$表示第j个资产的权重
V$表示资产的协方差矩阵
\sigma_p = \sqrt{w*V*w^T}$ 表示组合风险
然后,资产j对总投资组合的风险贡献($RC_j$)为:
风险平价投资组合是所有资产中每个资产的$RC$相等的投资组合。
计算风险平价组合的权重,本质上属于一个二次优化问题。
让投资组合资产$RC$的平方误差的总和为(优化问题的目标函数):
优化问题的约束条件为:
代码实现¶
假设组合有四项资产
资产收益率为$R$
资产协方差为$V$
In [1]:
#
协方差矩阵和收益率向量
from scipy.optimize import minimize
V = np.matrix('123 37.5 70 30; 37.5 122 72 13.5; 70 72 321 -32; 30 13.5 -32 52')/100 # covariance
R = np.matrix('14; 12; 15; 7')/100 # return
In [2]:
#
风险预算优化
def calculate_portfolio_var(w,V):
计算组合风险的函数
#
w = np.matrix(w)
return (w*V*w.T)[0,0]
def calculate_risk_contribution(w,V):
#
计算单个资产对总体风险贡献度的函数
w = np.matrix(w)
sigma = np.sqrt(calculate_portfolio_var(w,V))
#
边际风险贡献
MRC = V*w.T
风险贡献
#
RC = np.multiply(MRC,w.T)/sigma
return RC
def risk_budget_objective(x,pars):
#
计算组合风险
V = pars[0]# 协方差矩阵
x_t = pars[1] # 组合中资产预期风险贡献度的目标向量
sig_p = np.sqrt(calculate_portfolio_var(x,V)) # portfolio sigma

risk_target = np.asmatrix(np.multiply(sig_p,x_t))
asset_RC = calculate_risk_contribution(x,V)
J = sum(np.square(asset_RC-risk_target.T))[0,0] # sum of squared error
return J
def total_weight_constraint(x):
return np.sum(x)-1.0
def long_only_constraint(x):
return x
In [3]:
#
根据资产预期目标风险贡献度来计算各资产的权重
def calcu_w(x):
w0 = [0.2, 0.2, 0.2, 0.6]
x_t = [0.25, 0.25, 0.25, 0.25] # 目标是让四个资产风险贡献度相等,即都为25%
x_t = x
cons = ({'type': 'eq', 'fun': total_weight_constraint},
'type': 'ineq', 'fun': long_only_constraint})
#
{
res= minimize(risk_budget_objective, w0, args=[V,x_t], method='SLSQP',constraints=cons, options={'disp': True})
w_rb = np.asmatrix(res.x)
return w_rb
In [4]:
#
将各资产风险贡献度绘制成柱状图
def plot_rc(w):
rc = calculate_risk_contribution(w, V)
rc = rc.tolist()
rc = [i[0] for i in rc]
rc = pd.DataFrame(rc,columns=['rick contribution'],index=[1,2,3,4])
T.plot(rc, chart_type='column', title = 'Contribution to risk')
In [5]:
#
假设四个资产的风险贡献度相等
w_rb = calcu_w([0.25, 0.25, 0.25, 0.25])
print('各资产权重:', w_rb)
plot_rc(w_rb)
Optimization terminated successfully.
(Exit mode 0)
Current function value: 3.925640895972104e-09
Iterations: 6
Function evaluations: 38
Gradient evaluations: 6
各资产权重: [[ 0.19537778 0.21532757 0.16250521 0.42678944]]
In [6]:
#
假设风险贡献度依次为0.3,0.3,0.1,0.3
w = calcu_w([0.3, 0.3 ,0.1,0.3])
print('各资产权重:', w)
plot_rc(w)
Optimization terminated successfully.
(Exit mode 0)
Current function value: 2.8381885095817227e-07
Iterations: 8
Function evaluations: 51
Gradient evaluations: 8
各资产权重: [[ 0.2277006
0.25093779 0.08862556 0.43273605]]







