降维，从字面上来讲，即降低数据的维度
从狭义上讲，更为准确的是定义是：采取某种映射关系f，将原高维空间重的数据x映射到低维空间中y，本质上就是学习这个映射关系 f
本文主要是介绍机器学习中降维相关知识。先介绍为什么要降维，然后通过PCA和LDA举例介绍如何降维
为什么要降维
1. 维数灾难
维数灾难(curse of dimensionality) 又叫维度诅咒，指到了高维空间后，机器学习工作中将会面临众多难以克服的问题。
典型的有如下问题：
1.1 稀疏的样本
机器学习整个学科都是基于一个基本假设：独立同分布
即采样得到的部分样本是一定程度上能够表征整体的，而通过采样得到合适样本的前提是：样本尽可能的稠密并且均匀
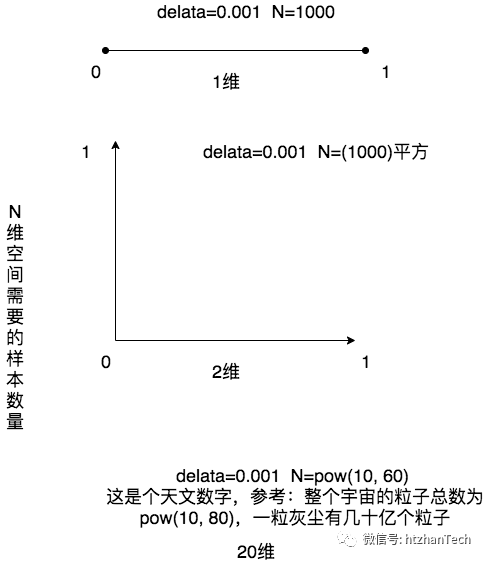
通过上面的分析，我们发现，数据量和维度是成指数级别增长的，例如CTR场景，数据维度都是很高的。
所以，高维必然是会导致更为稀疏的样本
1.2 巨大数据量带来的问题
如果不降维，为了满足假设，只能增加数据量，但是数据量的上升同样会带来问题
(1) 距离的计算问题：例如KNN，每次确认类别都会和周边K个数据进行距离计算，数据一多，为了避免欠拟合，就需要增加K，距离的计算将会耗时耗力
(2) 算法的迭代：以最常用的梯度下降距离，大数据量使用SGD，mini-batch，因为使用的数据点少，使用的信息有限，所以梯度下降的路线会曲折跳跃，迟迟无法收敛
2. 降维的意义
通过上面的分析，可以发现，数据降维是十分的必要的
降维能带来如下好处：
降低空间和时间复杂度，减少不必要开销
去除数据中夹杂的噪音和冗余
实现数据的可视化
如何降低数据维度
1. 特征选择
特征选择是目前工业界采用较多的降低数据维度的方式，简单高效。常见的方式包括：缺失值比率，低方差滤波，高相关滤波，随机森林等。
特征选择和狭义上的降维差别在于：
特征选择仅仅保留原数据的部分特征信息，会丢失数据量
降维则是希望降低维度的同时，尽可能保留原数据的所有信息
2. 降维
狭义上的降维，即找到某种映射关系，将高维数据映射到低维空间。
较常见的有如下两个：主成分分析(PCA)
，线性判别分析(LDA)
。
2.1 Principal component analysis (PCA：主成分分析)
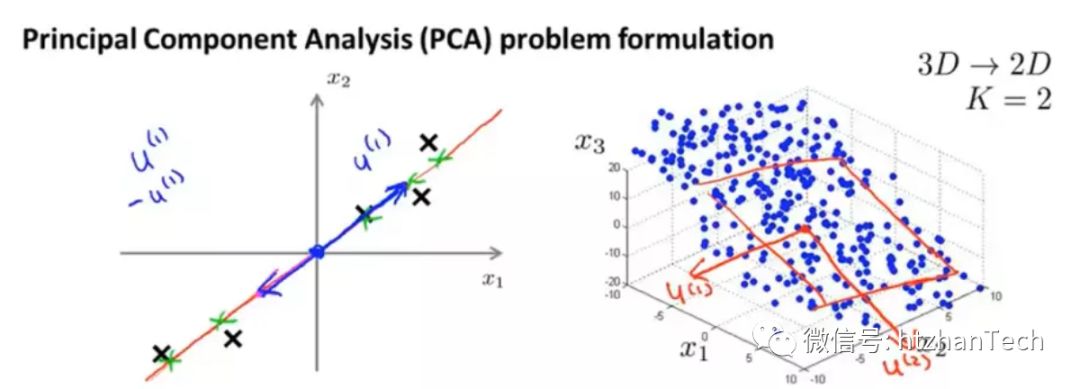
直观的理解下，我们如果想将数据进行降维，我们如何做到降维后数据的信息尽可能的少丢失？
高方差
低关联
这样的话，在新的数据空间中，我们的数据才能尽可能的区分开来。如果降维后样本都几乎重合到一起了，那么数据呈现出低方差，高关联的特点，降维后的数据将无法得到很好的区分。
公式推导前，简单复习几个数学概念
方差
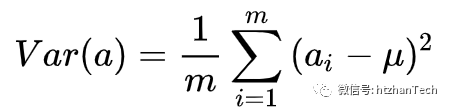,将均值归化到0后，表达式变为
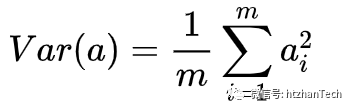
协方差
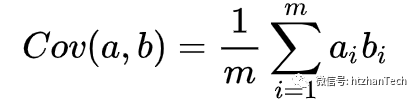
协方差矩阵
假设数据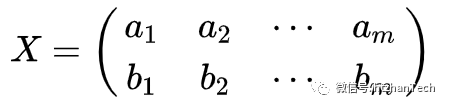
，那么它的协方差矩阵为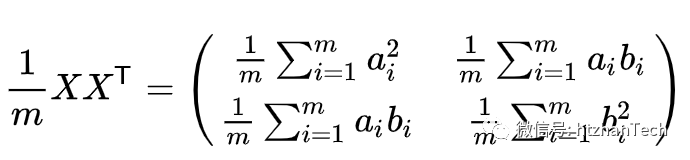
基的变换
4.1 投影
A向量在B向量上的投影，即|A|cos(a)，即A.B/|B|，当B为单位向量的时候，投影即为A.B
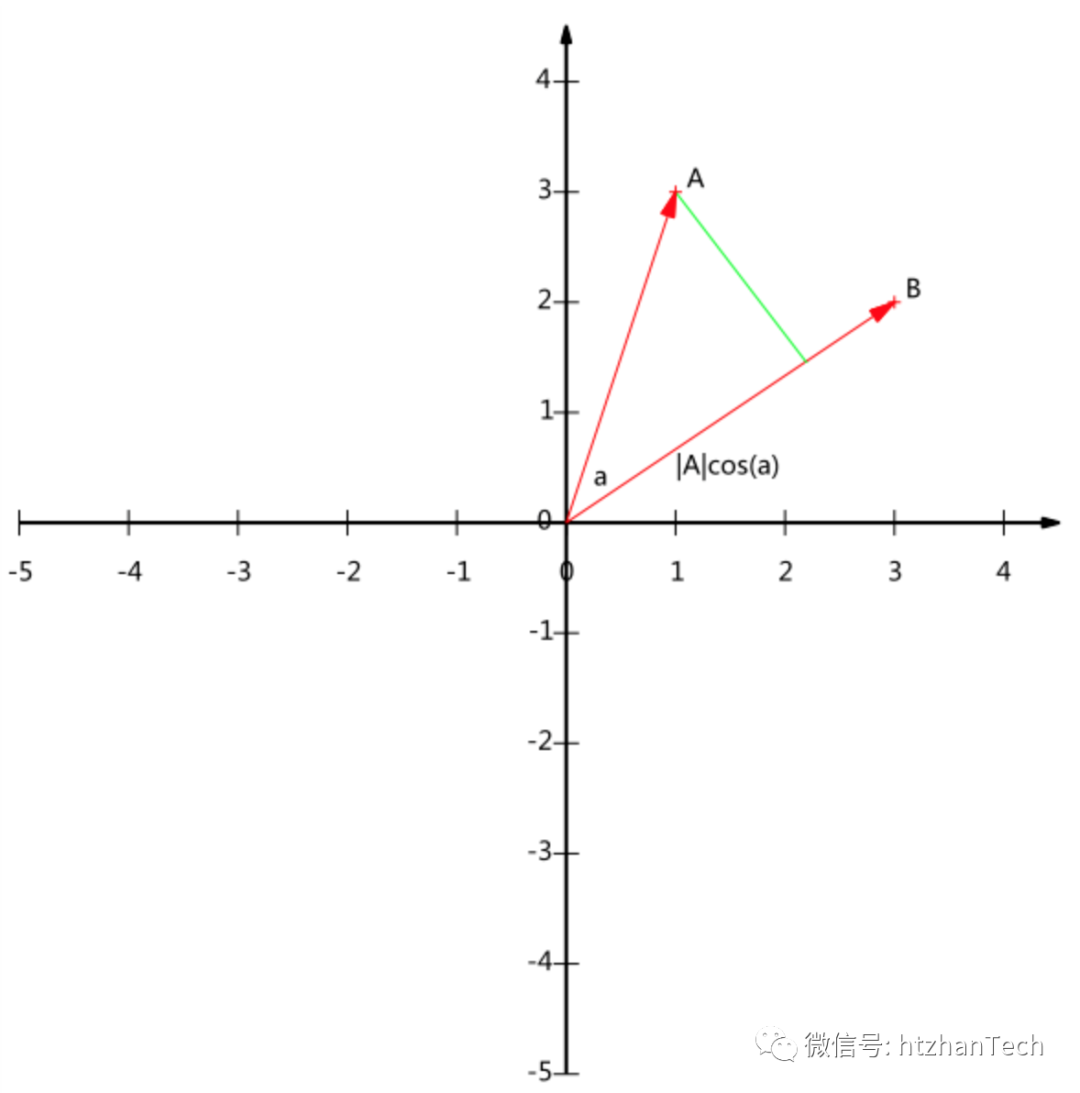
4.2 基
基即坐标系，即某个向量在一组向量上的投影。例如左图的基为 (1,0 ) (0,1)，然后向量(3,2)T可以表示为：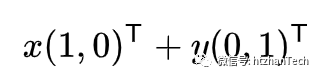
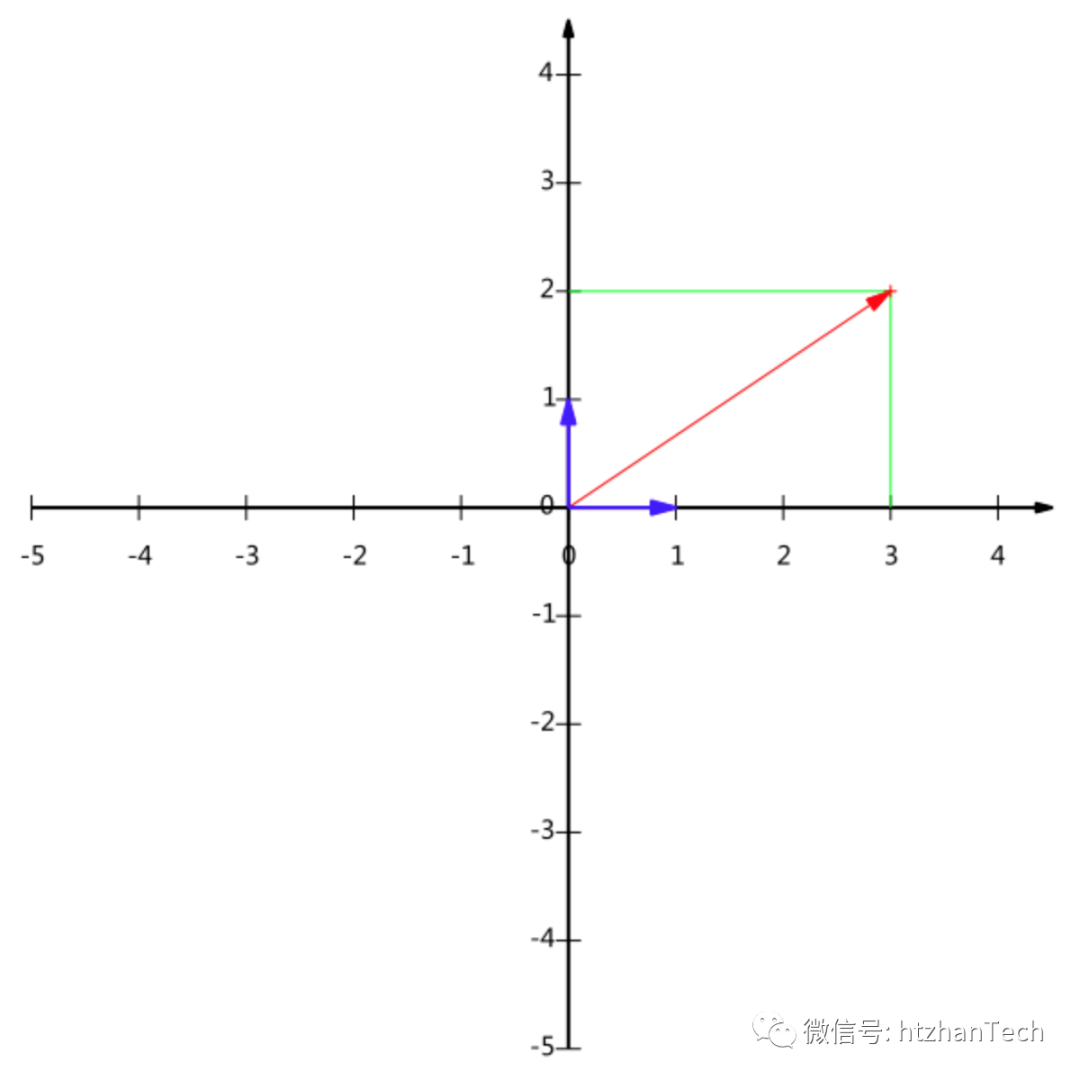
4.3 基变换
例如现在要将(3,2)T转换到 (1/sqrt(2), 1/sqrt(2)), (-1/sqrt(2), 1/sqrt(2)) 这组基上，采取的方式就是投影，也即向量的点乘：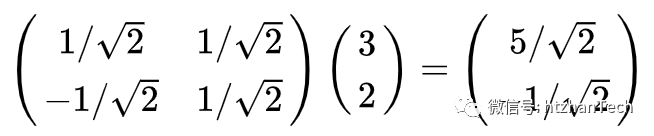
OK，现在我们发现，协方差矩阵将方差和协方差统一到了一个矩阵中，为了让方差大，协方差趋于0，即对角线的值大，非对角线上的数值趋近于0。
现在我们将高方差，低关联换个更为准确的解释：
我们将M维的数据X降维到N维，就是我们找一个基变换矩阵P，将数据转化到N维的基(坐标系)，使得原数据转化到N维基后的数据Y，数据Y尽可能保留原数据X的信息，即方差高，协方差趋于0。
假设基变化的矩阵为P，那么换基后的Y=PX，
Y的协方差矩阵为D:
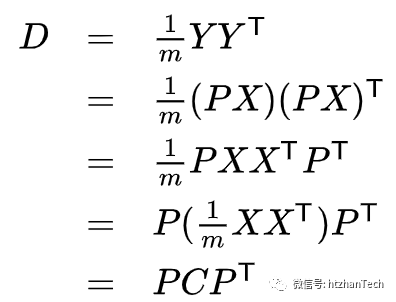
所以，我们要找的基变换矩阵P不是别的矩阵，就是能够将X的协方差对角化的矩阵。
同时发现，协方差矩阵是个对称矩阵，对称矩阵有良好的数学性质，一定可以正角化，而且对称矩阵的基是正交基。
所以，我们通过计算特征值和特征向量，按照特征值大小排序，挑选出新的基，即能得到方差尽可能大的降维后结果
所以，我们得到了PCA的算法流程如下：
数据0均值化
求出协方差矩阵
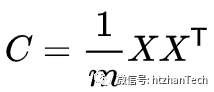
求出协方差矩阵的特征值及对应的特征向量
将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P
Y=PX即为降维到k维后的数据
2.2 Linear Discriminant Analysis (LDA：线性判别分析）
LDA和PCA最大的不同在于，LDA是监督学习，需要用到样本的类别信息，于1936年由Fisher提出。[2]
LDA希望降维后的数据，不同类别的数据尽可能的分开，希望降维后的数据依然能够较好分开，类似聚类的思想，这可能意味着两点：
不同类别数据的均值距离尽可能的大
同类别的数据之间的数据尽可能的小，即类内方差小
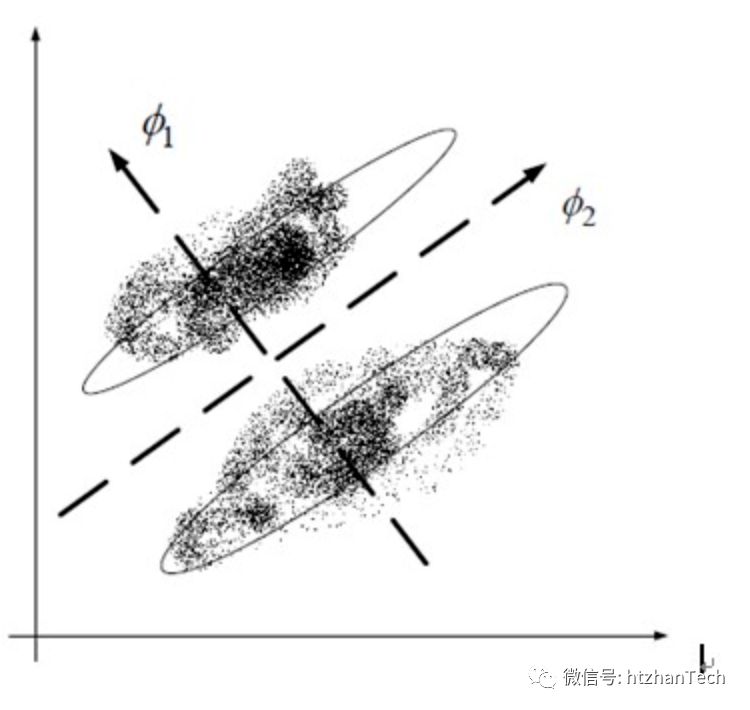
如果使用PCA降维，那么PCA会选择2方向，因为投影到这个方向的数据方差更大。而考虑类别信息的LDA则会选择方向1，这样降维后，依然能够很好的完成分类。
即可得到优化目标：
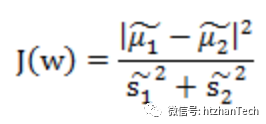
其中，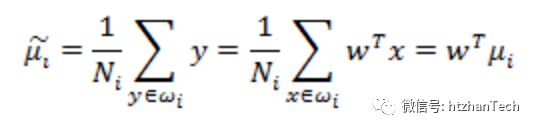
表示降维后的数据均值。
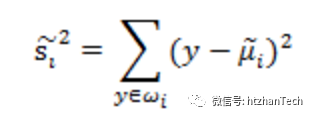是降维后数据的方差。
对上诉公式进行数学变换：
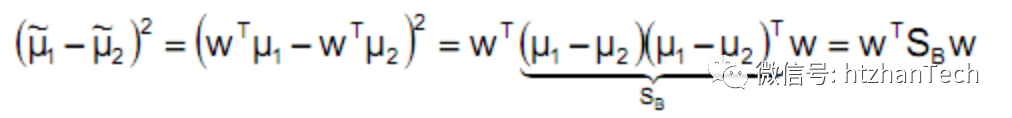
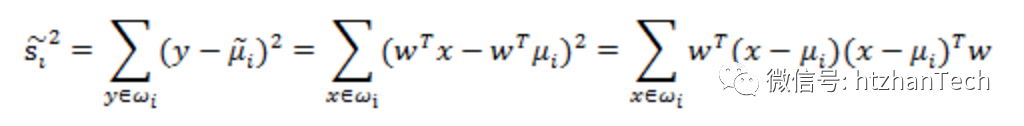
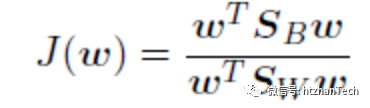
其中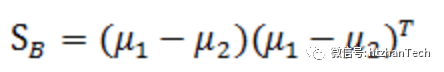
，称为类间散度矩阵，
Sw=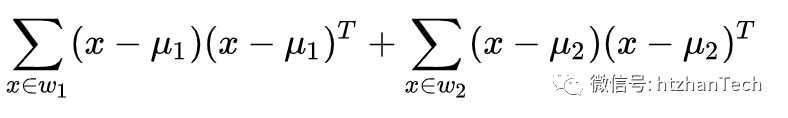
称为类内散度矩阵。
对J(w)求导然后令其等于0，可以得到
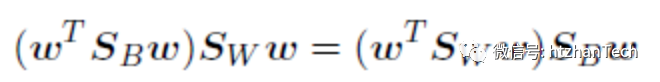
，忽略两边等式左侧的标量，等式改为
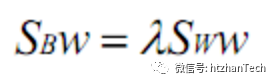
，两边乘以Sw的逆，得
，
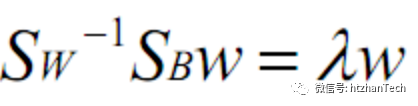即问题再次被转化为求特征值和特征向量问题，参考PCA方法的相关步骤
2.3 PCA和LDA的异同[3]
相同点
1）两者均可以对数据进行降维。
2）两者在降维时均使用了矩阵特征分解的思想。
不同点
1）LDA是有监督的降维方法，而PCA是无监督的降维方法
2）LDA降维最多降到类别数k-1的维数，而PCA没有这个限制。
3）LDA除了可以用于降维，还可以用于分类。
4）LDA选择分类性能最好的投影方向，而PCA选择样本点投影具有最大方差的方向。
参考文献：
[1] https://zhuanlan.zhihu.com/p/21580949
[2] https://zhuanlan.zhihu.com/p/21580949
[3] https://www.cnblogs.com/pinard/p/6244265.html
