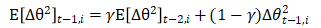点击上方“IT那活儿”公众号--专注于企业全栈运维技术分享,不管IT什么活儿,干就完了!!! 使用全部数据计算梯度,进而更新参数因为我们需要遍历整个数据集,再执行一次更新参数,所以批量梯度下降更新参数速度慢。另外批量梯度下降也不适合大数据集。批量梯度下降也不适合实时场景,不能在线更新模型。算法计算每个样本的损失,进而更新参数SGD由于每次只使用一个训练数据计算梯度更新参数,所以SGD更新参数更快。另一方面由于SGD执行频繁的更新参数,计算的梯度方差高,导致目标函数剧烈波动。SGD的波动性一方面可以使目标函数能够跳到更好的局部极小值,另一方面会使目标函数在最小值周围上下波动。计算一个批次内的样本的损失,进而更新参数计算的梯度方差小(训练稳定) ,计算速度快,使用内存小。现在一般深度学习使用小批量梯度下降算法来更新模型, n 常取2的指数倍。一般来说,很多人都会把SGD默认为是MSGD。所以有时候看到不要奇怪。现在常用SGD指代小批量梯度下降。
动量优化方法引入物理学中的动量思想,有Momentum和Nesterov两种算法。引入了一阶动量。Momentum 是各个时刻梯度的指数移动平均值。这个动量很有意思,一般动量是mv,m是质量,这里没有,就是我们的一个超参数,比如0.9;Momentum是一种有助于抑制SGD振荡并加快SGD向最小值收敛的方法。Momentum将过去时间的梯度向量添加到当前梯度向量。这个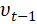 类比到动量就是速度,前面的参数就是质量,这里是我们自己定义的超参数。下面谈到的牛顿加速,是先往前走了一步,怎么走的呢? 是用了第一个公式的前半部分。
类比到动量就是速度,前面的参数就是质量,这里是我们自己定义的超参数。下面谈到的牛顿加速,是先往前走了一步,怎么走的呢? 是用了第一个公式的前半部分。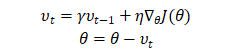
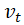 的计算方式类似于指数加权平均数,其中 γ 常取0.9。γ 决定过去一段时间的梯度向量和当前时间的梯度和权重比。普通SGD和带Momentum的SGD练过程对比如下图
的计算方式类似于指数加权平均数,其中 γ 常取0.9。γ 决定过去一段时间的梯度向量和当前时间的梯度和权重比。普通SGD和带Momentum的SGD练过程对比如下图
- 优化算法寻找目标函数最小值的过程就像使用一个小球在一个超平面滚来滚去最终滚到最低点的过程。SGD每次通过一个批次的数据决定小球接下来要滚的方向,由于每次只使用一个小批次的数据计算梯度,得到的梯度只是损失函数在这一小批次数据上的梯度。所以各个批次数据得到的梯度有一定的方差,小球每次滚的方向和距离都不一样。但是大致方向上小球还是朝着最低点前进的。
- 带Momentum的SGD在训练时仿佛有惯性一样,会沿着前面一段时间的梯度方向往前“冲”,就像本身具有“动量”一样。这也是Momentum名字的由来。每当小球要转变方向时,例如从“向右上”转到“向右下”,由于“动量”的存在,之前一段时间“向上"方向的动量和当前时刻“向下”方向的动量抵消,之前一段时间“向右”的动量和现在时刻“向右”的动量叠加,所以小球可以少走弯路,更快的滚向最低点。动量可以在方向错误时将其“拉”回来,方向正确时将其再“推”快点。
2.2 Nesterov accelerated gradient (NAG) 牛顿加速法先根据当前的动量往前走一步(注意是只根据了当前的动量这一部分),然后到达了下一个点,计算此时的梯度,然后更新。取决于下一个时刻的梯度和此时的动量。在前面的小球的例子中,如果小球能够事先知道自己在下一时刻的位置,那么小球就可以提前知道自己是应该“拉”回来还是“推”快点。那么小球就可以提前改变方向和速度。NAG从这一想法出发,从Momentum的参数更新公式我们知道不管当前时刻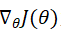 为多少,θ 总是要先更新
为多少,θ 总是要先更新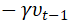 的。那么我们不妨先计算
的。那么我们不妨先计算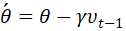 ,让参数
,让参数 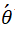 离下一时刻的值更一些让我们知道我们的参数 θ 大概会更新到哪,我们的损失函数在下一时刻大概会到哪然后用距离下一时刻更近的 θ 值来计算损失函数的值和梯度的值。
离下一时刻的值更一些让我们知道我们的参数 θ 大概会更新到哪,我们的损失函数在下一时刻大概会到哪然后用距离下一时刻更近的 θ 值来计算损失函数的值和梯度的值。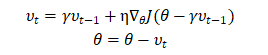
前面都是非自适应学习率优化算法,也就是所有参数,不管维度多少,不管更新的幅度大小,不管更新的频率大小,统一使用同一个学习率。接下来,就是引入二阶动量,出现了自适应学习率优化算法。
AdaGrad考虑对于不同维度的参数采用不同的学习率,具体的,对于那些更新幅度很大的参数,通常历史累计梯度的平方和会很大,相反的,对于那些更新幅度很小的参数,通常其累计历史梯度的平方和会很小。所以Adagrad在学习率下除了一个根号的历史梯度平方和,所以整体这个学习率是在变化的。要注意的是,虽然你没办法确定你除以的这个数字是一个小于1 的数字,但是除以的这个数字是一直在增大的,所以我认为学习率是一直在减小的。而且同时要注意不同的参数的学习率也不同。所以在一个固定学习率的基础上除以历史累计梯度的平方和就能使得那些更新幅度很大的参数的学习率变小,同样也能使得那些更新幅度很小的参数学习率也会减小。但是减小的幅度就相比较很慢。缺点很明显:
- 因为学习率下面有一个根号平方,所以这个值会越来越大,导致学习率会越来越小。最后导致模型的参数虽然还具有较大梯度,但是参数却无法更新。
思想很简单,Adagrad使用的是所有梯度的平方和,但是我们知道对于当前时刻离得非常远的梯度可能并不重要,所以对梯度做了一个指数加权移动平均。这就是RMSProp。首先看最简单直接版的RMSProp,RMSProp就是在AdaGrad的基础上将普通的历史累计梯度平方和换成历史累计梯度平方和的指数加权移动平均值,所以只需将AdaGrad中的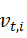 的公式改成指数加权移动平均值的形式即可,也即:
的公式改成指数加权移动平均值的形式即可,也即: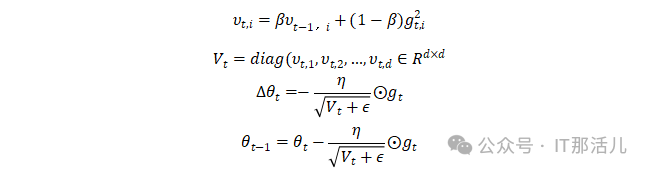
它的一点就是学习率不一定是单调递减,有可能增大,也有可能降低。解决了adagrad的缺点。而AdaDelta除了对二阶动量计算指数加权移动平均以外,还对当前时刻的下降梯度也计算一个指数加权移动平均,具体地: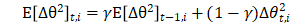
由于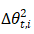 目前是未知的,所以只能用 t-1 时刻的指数加权移动平均来近似替换,也即:
目前是未知的,所以只能用 t-1 时刻的指数加权移动平均来近似替换,也即: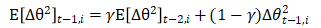
除了计算出 t-1 时刻的指数加权移动平均以外,AdaDelta还用此值替换我们预先设置的学习率,因此,AdaDelta的参数更新公式为: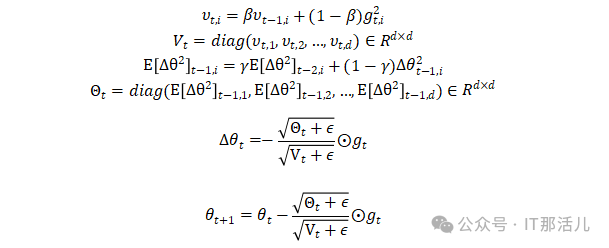
显然,对于AdaDelta算法来说,已经不需要我们自己预设学习率 η 了,只需要预设 β 和 γ 这两个指数加权移动平均值的衰减率即可。
Adam 是Momentum SGD 和RMSProp的结合体。引入一阶动量同时引入二阶动量。
附:《数学符号释义》
https://baike.baidu.com/item/%E6%95%B0%E5%AD%A6%E7%AC%A6%E5%8F%B7/685756?fr=ge_ala
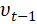 类比到动量就是速度,前面的参数就是质量,这里是我们自己定义的超参数。
类比到动量就是速度,前面的参数就是质量,这里是我们自己定义的超参数。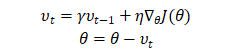
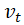 的计算方式类似于指数加权平均数,其中 γ 常取0.9。γ 决定过去一段时间的梯度向量和当前时间的梯度和权重比。普通SGD和带Momentum的SGD练过程对比如下图
的计算方式类似于指数加权平均数,其中 γ 常取0.9。γ 决定过去一段时间的梯度向量和当前时间的梯度和权重比。普通SGD和带Momentum的SGD练过程对比如下图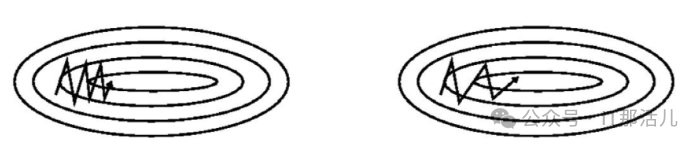
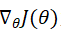 为多少,θ 总是要先更新
为多少,θ 总是要先更新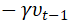 的。
的。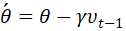 ,让参数
,让参数 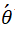 离下一时刻的值更一些让我们知道我们的参数 θ 大概会更新到哪,我们的损失函数在下一时刻大概会到哪然后用距离下一时刻更近的 θ 值来计算损失函数的值和梯度的值。
离下一时刻的值更一些让我们知道我们的参数 θ 大概会更新到哪,我们的损失函数在下一时刻大概会到哪然后用距离下一时刻更近的 θ 值来计算损失函数的值和梯度的值。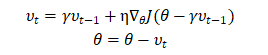
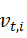 的公式改成指数加权移动平均值的形式即可,也即:
的公式改成指数加权移动平均值的形式即可,也即: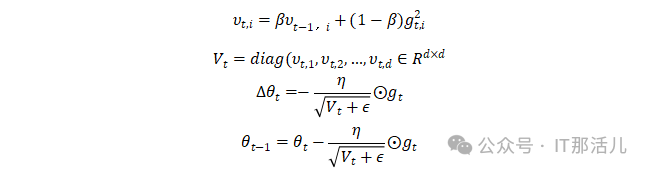
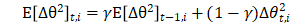
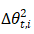 目前是未知的,所以只能用 t-1 时刻的指数加权移动平均来近似替换,也即:
目前是未知的,所以只能用 t-1 时刻的指数加权移动平均来近似替换,也即: